高等光学作业

第一次光学大作业-------双光束干涉的计算机模拟此次实验用matlab进行，软件版本为r2014a，操作界面如图：1.模拟双光束干涉条纹的强度分布曲线源程序为：lam=500e-9;d=0.001;D=1;ymax=0.002;xs=ymax;ny=101;ys=linspace(-ymax,ymax,ny);for i=1:nyL1=sqrt((ys(i)-d/2).^2+D/2);L2=sqrt((ys(i)+d/2).^2+D/2);phi=2*pi*(L1-L2)/lam;b(i,:)=4*cos(phi/2).^2;endclf;figure(gcf);nclevels=255;br=(b/4.0)*nclevels;subplot(1,2,1)image(xs,ys,br);colormap(gray(nclevels));subplot(1,2,2)plot(b(:),ys)此时设定波长λ=500nm，双缝之间的距离d=1mm,缝到屏幕之间的距离D=1m。

2．当S1，S2之间的距离发生变化时，屏上条纹变化规律。

上面的源程序红色部分代表S1，S2之间的距离，修改可研究其变化规律当d=2mm时，所的条纹为：当d=1.5mm时，所的条纹为：当d=2.5mm时，屏上条纹为：结论：由多次试验所得条纹可知，随着d的增大，屏上的条纹变细，间距变大，随着d的减小，屏上的条纹变粗，间距变小。

3.当光源S上下移动时，屏上条纹分布的变化规律源程序：当S上移0.1mm时，lam=500e-9;bc=0.0002;d=0.002;L=1;D=2;ymax=0.0005;xs=ymax;ny=101;ys=linspace(-ymax,ymax,ny);for i=1:nyL1=sqrt((ys(i)-d/2).^2+D/2);L2=sqrt((ys(i)+d/2).^2+D/2);phi=2*pi*(L1-L2+0.5*bc*d/L)/lam;b(i,:)=4*cos(phi/2).^2;endclf;figure(gcf);nclevels=255;br=(b/4.0)*nclevels;subplot(1,2,1)image(xs,ys,br);colormap(gray(nclevels));subplot(1,2,2)plot(b(:),ys)修改源程序红色部分，即改变了光源的位置，可研究相应的规律当bc=0.2mm时，当bc=0.4mm时，结论：由此可见，当光源向上或向下平移时，条纹也将发生平移，光强不变，条纹间距不变。

习题1010.1选择题（1）在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是[](A)使屏靠近双缝．(B)使两缝的间距变小．(C)把两个缝的宽度稍微调窄．(D)改用波长较小的单色光源．[答案：B]（2）两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的[](A)间隔变小，并向棱边方向平移．(B)间隔变大，并向远离棱边方向平移．(C)间隔不变，向棱边方向平移．(D)间隔变小，并向远离棱边方向平移．[答案：A]（3）一束波长为λ的单色光由空气垂直入射到折射率为n的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为[](A)λ / 4．(B)λ/(4n)．(C)λ / 2．(D)λ/(2n)．[答案：B]（6）在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹[](A)对应的衍射角变小．(B)对应的衍射角变大．(C)对应的衍射角也不变．(D)光强也不变．[答案：B]（7）波长λ=500 nm(1nm=10-9m)的单色光垂直照射到宽度a=0.25mm的单缝上，单缝后面放一凸透镜，在凸透镜的焦平面上放置一屏幕，用以观测衍射条纹。

今测得屏幕上中央明条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为d=12mm，则凸透镜的焦距是[](A)2m.(B)1m.(C)0.5m.(D)0.2m.(E)0.1m[答案：B]（8）波长为λ的单色光垂直入射于光栅常数为d、缝宽为a、总缝数为N的光栅上．取k=0，±1，±2．．．．，则决定出现主极大的衍射角θ 的公式可写成[](A)N a sinθ=kλ．(B)a sinθ=kλ．(C)N d sinθ=kλ．(D)d sinθ=kλ．[答案：D]（9）在光栅光谱中，假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上，因而实际上不出现，那么此光栅每个透光缝宽度a和相邻两缝间不透光部分宽度b的关系为[](A)a=0.5b(B)a=b(C)a=2b(D)a=3b[答案：B]（10）一束光强为I0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I为[](A)4/0I2．(B)I0/4．(C)I0/2．(D)2I0/2。

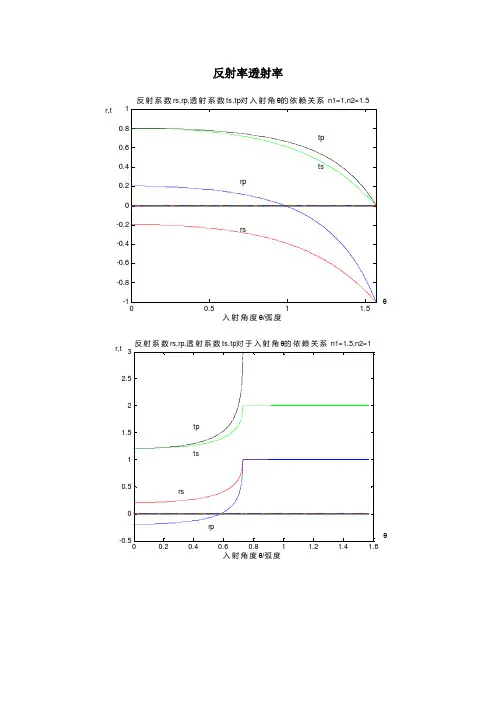
反射率透射率00.51 1.5-1-0.8-0.6-0.4-0.20.20.40.60.81tpts rp rs 反射系数rs,rp,透射系数ts,tp 对入射角θ的依赖关系 n1=1,n2=1.5入射角度θ/弧度r,t θ 00.20.40.60.81 1.2 1.4 1.6-0.500.511.522.53rstsrptp 反射系数rs,rp,透射系数ts,tp 对于入射角θ的依赖关系 n1=1.5,n2=1入射角度θ/弧度r,t θ棱镜耦合法测薄膜折射率棱镜耦合法是通过在薄膜样品表面放置一块耦合棱镜，将入射光导入被测薄膜，检测和分析不同入射角的反射光，确定波导膜耦合角，从而求得薄膜厚度和折射率的一种接触测量方法。

波导模式特征方程为εθεθπsin )sin (cos sin )1()(21222122-+=+=-p m m f N N m N n kd在上式中，"k 为波数，m 为膜数，m N 为m 阶导模的有效折射率，θ,ε,p N 分别为耦合角、棱镜角和棱镜折射率。

若测得两个以上模式的耦合角，便可求出d 和f N 。

棱镜耦合法的测量精度与转盘的转角分辨率、所用棱镜折射率、薄膜的厚度和折射率范围及基底的性质等因素有关，折射率和厚度测量精度分别可达到310-±和（nm 5%5.0+±），实际精度还会高些。

L ：光源；R1.R2反射镜；A ：衰减片；F ：滤波器；Q;1/4波片;P:偏振片；D ：探测器；G:棱镜；C ：耦合头；SC ：转盘;FL:薄膜样品近场扫描光学显微镜的扫描原理和核心技术二、近场扫描光学显微镜原理及有关的技术、理论问题1·近场扫描光学显微镜的基本思想想如图1所示,近场探测原理是近场扫描光学显微镜的核心。

当一个亚波长孔径的微小光源,在一物体的近场范围内照射物体时,照射光斑的面积只和孔径大小有关,而与波长无关。

这样,在反射光或透射光中,将携带物体亚波长尺寸结构的信息,通过扫描采集样品各“点”的信号光,即可得到分辨率小于半波长的样品的近场图象。

3.3. 空间相干性和时间相干性指的是什么？如何量度？光源的角宽度和相干孔径角是如何定义的？证明相干长度 Lc = λ2/∆λ。

答：空间相干性是指光场中不同两点在同一时刻的相干程度。

时间相干性是指同一点在不同时刻的相干程度。

空间相干性的度量是采用相干面积进行度量。

时间相干性是采用相干时间或相干长度进行度量。

光源的角宽度定义为0a d λ=，d0是使得条纹可见的光源最大宽度。

相干孔径角定义为22c pλθ=。

证明：多色光源的干涉场分布的条纹可见度有：sin()22kl K kl ∆=∆ 当2klπ∆=条纹不可见，此时有： 2122l k λλπλλλ==∆∆∆证毕。

3.12.(1)当把一单色点光源放在一会聚透镜物空间焦点上, 观察屏与透镜空间焦面重合, 则观察到夫琅和费圆孔衍射图样。

现在将光源换为圆状准单色初级光源, 圆中心在光轴上, 圆面垂直于光轴, 要想仍获得夫琅和费圆孔衍射图样, 对光源大小。

频宽以及透镜直径应有什么限制? 答：这里可以认为光源在透镜前表面的场的相干性决定了衍射图样。

首先光源的频宽应该保证准单色有νν∆，光源宽度应保证相干面积大于透镜宽度，有L fd aλ<，dL 为透镜直径，a 为光源直径，f 是透镜焦距。

(2)在衍射计实验中, 光源不是单色点光源, 但仍引用夫琅和费圆孔衍射的结果,即取I Q I Q J u uu a ()()()()(()),sin 121222===πλφ根据(1)的结果, 试说明为什么可以如此处理?答：只要光源足够小，保证了其在屏处的相干面积大，同时圆孔本身面积远小于相干面积，加上光源准单色条件，即可认为屏幕上两孔光场依然具有足够的相干性，因此可以用夫琅和费圆孔衍射的结果。

3.1.已知太阳的表观角直径为0.5。

平均有效波长为6000A, 求阳光的相干面积。

解：由L zd aλ=，根据角直径定义，有2tan(0.25)0.00873az=≈ 因此可得相干线度为：68.7um ，相干面积4723um 2. 3.9.阻尼振子的辐射场中某点复扰动为V t A t t i t t t ()exp(/)exp()=--><⎧⎨⎩10200φπν式中t 1是自发辐射寿命。

n ( D1 D2 ) 0 D1n 1n E1n D1n D2 n 0 D2 n 2 n E2 n n r D1n D2 n 1n E1n 2 n E2 n
答：
n
r r 0 0
1n E1n 2 n E2 n n E1n n E2 n
高等光学(2015-2016)考试题目
一、 判断对错 1、 对于多缝夫琅和费衍射，缺级是因为衍射因子的某级主极大值刚好与干 涉因子的某级极小值重合。 （X） 对于多缝夫琅和费衍射，缺级是因为衍射因子的某级主极小值刚好与干涉因子 的某级极大值重合。 2、 在菲涅耳衍射区，圆环衍射中为暗斑，而圆屏衍射中为亮斑。 （X） 在菲涅耳衍射区，圆环衍射中为暗斑或者亮斑，而圆屏衍射中为亮斑。 3、在电偶极子振动方向上无能量辐射。 （γ） 4、各种金属反射光的能力不用，在于它所包含的自由电子的密度不同，一般 来说，自由电子密度越大，电导率越大，反射率也越低。 （X） 各种金属反射光的能力不用，在于它所包含的自由电子的密度不同，一般来说， 自由电子密度越大，电导率越大，反射率也越高。 5、由于衍射 0 级集中最大能量无法改变，因此在闪耀光栅中通过改变干涉来 改善平面光栅 0 级集中最大能量的缺陷。 （γ） 6、在用菲涅耳波带法估算菲涅耳衍射的过程中，每个波带的面积只和照射波 长相关。 （γ） 7、两个不同频率的单色光波叠加时可以产生稳定的干涉图案。 （X） 两个不同频率的单色光波叠加时不可以产生稳定的干涉图案，可以产生拍频现 象。 8、体心立方体结构的倒格矢空间是面心立方结构。 （γ） 9、阶梯光栅的高分辨率本领来源于高光普级，因此自由光谱范围很小。 （γ） 10、点光源照明所产生的条纹一定是非定域条纹。 （X） 点光源照明产生的条纹不一定是非定域条纹，扩展光源照明的干涉条纹是定 域条纹。 11、干涉和衍射从本质上来说都是波的相干叠加，没有区别。 （γ） 12、理想的夫琅合费衍射系统是傅里叶频谱分析仪。 （γ） 13、油侵显微镜、紫外显微镜和电子显微镜具有更高的分辨本领是因所用光 波波长短或者物方折射率高的缘故。 （γ） 14、 自然光经过双折射晶体后可以得到圆偏振光、 椭圆偏振光、 线偏振光。 （X） 自然光经过双折射晶体后可以得到 o 光、e 光。 15、照相过程中为了得到更好的景深，需要把照相机的光圈开到最大。 （γ） 光圈越大景深越浅，小光圈的时候取景窗看到的景象就会比较暗，所以在取景 的时候相机是以最大光圈来取景的。 二、 简答题 1、在平静水面湖边洗脸时，我们很难看到自己对水面的反射像，但是站在平静 水面的湖边看到湖对岸的山、树以及建筑的水中倒影却十分明亮，试解释之（提 示：菲涅耳公式分析） 答：因为在湖边洗脸时，观察的是垂直入射、反射的光，在空气与水界面上， 由菲耳公式 ，这种情况下反射光能量很小，因此看不到自己 的像．而观察湖对岸的山、树以及建筑物，是观察反射、入射的光，此时光能 量几乎全部反射到人眼中来，看到的景物清晰明亮．

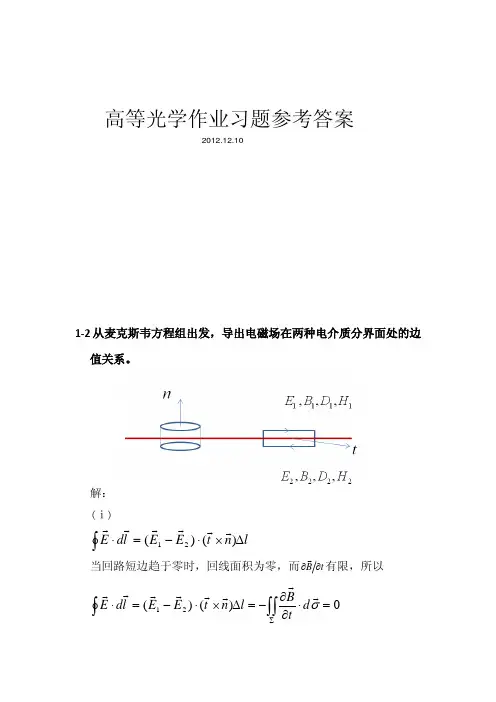
1-2 从麦克斯韦方程组出发，导出电磁场在两种电介质分界面处的边值关系。

解：(ⅰ)ln t E E l d E ∆×⋅−=⋅∫)()(21当回路短边趋于零时，回线面积为零，而t B ∂∂有限，所以0)()(21=⋅∂∂−=∆×⋅−=⋅∫∫∫Σσd t B l n t E E l d E高等光学作业习题参考答案2012.12.10即l E E n t ∆−⋅×)()(21l E E n t ∆−×⋅=))((210=得0)(21=−×E E n，即t t E E 21=(ⅱ)l t d t DJ l n t H H l d H ∆⋅=⋅∂∂+=∆×⋅−=⋅∫∫∫Σασ)()()(21t H H n t n t H H⋅=−×⋅=×⋅−α))(()()(2121当没有电流分布时0=α，得,0)(21=−×H H n即t t H H 21=(ⅲ)s n D D ds n D d D ∆⋅−=⋅=⋅∫∫)(21σ当不存在自由电荷时，0=sρ，积分0=∫∫∫Ωdv s ρ，所以0)(21=∆⋅−s n D D，即n n D D 21=(ⅳ)0)(21=∆⋅−=⋅=⋅∫∫s n B B ds n B d Bσ即n n B B 21=1-5 已知电场E 和磁场H 在直角坐标中的分量分别为：)cos(t kz A E x ω−=；);sin(wt kz B E y −=0=z E )sin(t kz B H x ωε−−=；)cos(t kz A H y ωε−=；0=z H试求电磁场的能量密度w 和玻印亭矢量S 。

解：HB E D µε==,电磁场能量密度)(21B H D E w ⋅+⋅=)(2122H E µε+= )]()([21222222z y x z y x H H H E E E +++++=µε )](sin )(cos [2)1(2222t kz B t kz A ωωµε−+−+=玻印亭矢量H E S ×=zyxz y xH H H E E E z y x =z H E H E y H E H E x H E H E x y y x z x x z y z z y)()()(−+−+−=z H E H E x y y x)(−=z t kz B t kz A))]((sin ))((cos [2222ωεωε−+−=1-6 设某一无限大介质中，,0,0==σρε、µ只是空间坐标的函数，试从麦克斯韦方程和物质方程出发证明：{}0)](ln [)()(ln 22=∇⋅∇+×∇×∇++∇εµεµωE E E E证明：)(),(r rµµεε==H B E Dµε==,E E E D⋅∇+⋅∇=⋅∇=⋅∇εεε由麦克斯韦方程 0=⋅∇D得 (ln )EE E εεε∇⋅∇⋅=−=−∇⋅取麦克斯韦方程组微分式第一式的旋度，)()(B tE ×∇∂∂−=×∇×∇其中，E E E 2)()(∇−⋅∇∇=×∇×∇2[(ln )]E E ε=−∇∇⋅−∇)()(H tB t µ×∇∂∂−=×∇∂∂− )(H H t×∇+×∇∂∂−=µµ)(µµµB t Dt×∇+∂∂∂∂= t B tE ∂∂×∇+∂∂= )(ln 22µεµ)()(ln 22E t E×∇×∇−∂∂=µεµ)()(B tE ×∇∂∂−=×∇×∇即222(ln )()[(ln )]0E E E E t εµµε∂∇−+∇×∇×+∇∇⋅=∂若ti e E E ω0 =，则22(ln )()[(ln )]0E E E E εµωµε∇++∇×∇×+∇∇⋅=1-7 从麦克斯韦方程组出发导出电磁场在有色散的非均匀介质中所满足的亥姆霍兹方程。

第9章 光学习题解9.1在双缝干涉实验中，波长nm 的单色光入射在缝间距500=λm 的双缝上，屏到双缝的距离为2m ，求(1)每条明纹的宽度；(2)中央4102-⨯=a 明纹两侧的两条第10级明纹中心的间距；(3)若用一厚度为m 的云6106.6-⨯=e 母片覆盖其中一缝后，零级明纹移到原来的第七级明纹处；则云母片的折射率为多少？解：（1）m 105102105002349---⨯=⨯⨯⨯==∆d D x λ（2）两条10级明纹间距为20＝0.1m x ∆（3）由于，所以有()λ71=-n e 53.171=+=e n λ9.2 某单色光照射在缝间距为d =m 的杨氏双缝上，屏到双缝的4102.2-⨯距离为D =m ，测出屏上20条明纹之间的距离为m ，则该单色光的81⋅210849-⨯⋅波长是多少？解： m 1084.9202-⨯=∆==∆x x d D x λnm 3.6018.1201084.9102.224=⨯⨯⨯⨯=∴--λ9.3白光垂直照射到空气中一厚度m 的肥皂膜（n = 1.33）上，在μ380=e 可见光的范围内（），哪些波长的光在反射中增强？nm 760nm 400--解：由于光垂直入射，光程上有半波损失，即时，干涉加强。

λλk ne =+22所以10101220216124-⨯-=-=k k ne λ在可见光范围内 nm 9.6732＝　时，λ=k nm 3.4043＝　时，λ=k 9.4如题图9.4所示，在双缝实验中入射光的波长为550nm ，用一厚度为的透明薄片盖住S 1缝，发现中央明纹移动3个条纹，向上移至cm 1085.24-⨯=e 。

求透明薄片的折射率。

‘O 题图9.4 解：当用透明薄片盖住S 1缝，以单色光照射时，经S 1缝的光程，在相同的几何路程下增加了，于是原光程差为零的中央明纹位置从O 点向上移动，其他条纹随之平动，但条纹宽度不变。

依题意，图中为中央明条纹的位置，加透'O 明薄片后，①光路的光程为，②光路的光程为r 2。

2016高等光学第4次作业答案4-8一对称型带状波导，宽度和厚度分别为a 和b ，导光层的折射率为n ，覆盖层和衬底的折射率为n 0.证明：波导的基模传输条件为a=b 。

解：薄膜波导在x 向有限，y 方向无限大；带状波导，在x 和y 向都有限，宽度为a 和b （类似于矩形波导，参考图（4.1.1））。

x 方向受限的波导稳定传输的条件为（4.2.8）0122a cos ++2i n k m θδδπ=Y 方向受限的波导稳定传输条件为'''0122b cos ++2i n k n θδδπ=基模传输，''112'112===,0mn δδδθθδ==，，， 故a=b 。

4-9 一阶跃型光纤的纤芯和包层的折射率分别为1 1.55n =,2 1.50n =,求光纤在空气中的数值孔径和最大入射孔径角0θ.若将该光纤放入水中(设水的折射率为1.33),问光纤的数值孔径是否会改变?如果改变,则改变量是多少?解:光纤的数值孔径大小与纤芯折射率,及纤芯－包层折射率差有关,表达式为:.所以将该光纤放入水中,其数值孔径不会改变. 最大入射孔径角0θ==023≈4-10 一阶跃型光纤的纤芯和包层的折射率分别为n1=1.52，n2=1.51，现欲使该光纤单模传输，问工作波长分别为λλ00=11.222222和λλ00=00.882222时，光纤的最大芯径应该是多少？解：单模光纤的归一化截止频率（查阅光纤相关资料）0V=k 2.4048≤a λ≤max max =1.2m a =2.64m =0.8m a =1.76mλµµλµµ，，。

高等光学第4-5章习题答案第四章标量衍射理论基础4.1证明（4-21）式所示的索末菲辐射条件成立。

证明：球面2S是中心位于1S面上的发散球面波的波面，假定2S面上的光场分布表示为rjkr)exp(=U式中r表示产生发散球面波的点光源到球面2S上任意一点的距离。

1exp()cos()cos(,)r jkrjkn r n r r r∂∂∂∂===−∂∂∂∂U U Un,r n r当∞→R时，有∞→r，所以这时有1),cos(≈rn2)exp()exp(1rjkrjkrjkrrjkjkn−≅−−=−∂∂UUU当∞→R时，上式分母中的r可用R来代替，于是2exp()1lim lim lim(cos sin)R R RjkrR jk R kr j krn R R→∞→∞→∞∂−=−=−+∂UUlim0jkrReR→∞=−=4.2 参考图4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即010110101exp()exp()()jkr jkrPr r+=+G(1)证明+G的法线方向的导数在孔径平面上为零。

(2)利用这个格林函数，求出用孔径上的任意扰动来表示()pU的表达式，要得到这个结果必须用什么样的边界条件。

(3)利用(2)的结果，求出当孔径被从2P点发散的球面波照明时()pU的表达式证明: 下面是教材中图4-8（1）)(1P +G 由两项迭加而成，它们分别表示从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球面波。

孔径平面1S 上任一点1P 的+G 值为010101011~)~exp()exp()(r r jk r jkr P +=+G （P4.2-1） 1()P +G 的法向导数为0101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n −+ −=∂∂+ （P4.2-2） 对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n −= 0101~r r = （P4.2-3）将以上关系式代入（P4.2-2）式，得到0n+∂=∂G （P4.2-4） （2）根据（4-22）式，观察点0P 的光扰动可以用整个平面1S 上的光扰动U 和它的法向导数来表示∫∫∂∂−∂∂=1d 41)(0S s n n P G U G U U π（P4.2-5） 由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式一同代入（P4.2-5）式，得到∫∫∫∫∂∂=∂∂=+11d )exp(21d 41)(01010S S s r jkr ns G n P U U U ππ（P4.2-7）为了将上式所表示的结果进一步简化，根据孔径Σ上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径Σ上，场分布的法向导数n U ∂∂与不存在衍射屏时的值完全相同。

高等光学教程--第三章参考答案第三章光学薄膜的基本知识3.1 证明在TM 波入射的情况下单层膜的特征矩阵为=22sin cos sin cos j q jq ββββ⎛⎫- ⎪⎪⎪-⎝⎭M式中=2q 220cos /θμεn，其它参数及图示参考§3.1节中图3-2。

图p3-1解答: 模仿教材§3-1中推导TE 波入射情况下求特征矩阵所用的方法。

在界面I 处： 2II 2I 1I 1I I cos cos cos cos θθθθrt r i E E E E E '-=-= (p3.1-1) II I I I I rt r i H H H H H '+=+= (p3.1-2) 由非磁性介质中E 和的关系式H E s H ⨯=n 0με (p3.1-2)式化为 )()(II I 20I I 100I rt r i E E n E E n H '+=-=μεμε (p3.1-3) 在界面II 处： 3II 2II 2II II cos cos cos θθθt r i E E E E =-= (p3.1-4)II II II II t r i H H H H =+= (p3.1-5)由(p3.1-3)式，(p3.1-5)式化为II 30II II 200II )(t r i E n E E n H μεμε=+=(p3.1-6) 两个界面上的电矢量有关系式II tI II II j i j r r E E eE E eββ-⎧=⎪⎨'=⎪⎩ (p3.1-7)(p3.1-8)由(p3.1-7)和(p3.1-8)两式，(p3.1-4)、(p3.1-6)两式化为II tI 2I 2II2tI I cos cos (p3.1-9)(p3.1-10)()j j r j j r E E e E e H E e E e ββββθθ--'⎧=-⎪⎨'=+⎪⎩由(p3.1-9)和(p3.1-10)两式解出tI 2II 2II cos E E θ⎫=⎪⎪⎭H + (p3.1-11) 和 βθμεμεθj re n E n H E --='220II 20II 2II cos 2cos (p3.1-12)将(p3.1-11)、(p3.1-12)式代入(p3.1-1)式，并令有 II 2II 1sin cos H q j E E ββ-=(p3.1-13) 22q =用同样的方法得到II II 2I cos sin H E jq H ββ+-= (p3.1-14)由(p3.1-13)和(p3.1-14)式⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡II II 22I I cos sin sin cos H E jq q jH E ββββ ⎥⎥⎦⎤⎢⎢⎣⎡--=ββββcos sin sin cos 22I jq q j M∴式中 2202cos θμεn q =3.2 如图p3-2所示，有一单层介质膜，入射光由折射率为的介质经过界面I 、单层膜及界面II 后进入折射率为 的衬底，入射光在界面I 和界面II 一次反射的振幅反射率分别为和，一次透射的振幅透射率分别为和。

高等光学第1-3章习题答案第一章光的基本电磁理论1.1 在非均匀介质中，介电系数是空间位置的函数，波动方程有下面的形式)(r εε=0)()()(222=⎦⎤⎢⎣⎡∇⋅∇+∂∂-∇r r E E r E εεμεt 解释为什么当电场的三个分量中有多于两个不为0时，电场分量之间就会出现耦合。

解答:zy x ∂∂+∂∂+∂∂=∇)()()()(r k r j r ir εεεε因而 zE E y E E x E z y x ∂∂+∂∂+∂∂=∇⋅)()()()()()()()(r r r r r r r r E εεεεεε由上式看到式的分量中含有和，分量中含有和，分⎥⎦⎤⎢⎣⎡∇⋅∇)()(r r E εεx y E z E y x E z E z 量中含有和，结合题中所给出的波动方程看到电场的三个分量中有多与两个不为0x E y E 时分量之间出现了交叉耦合。

1.2（1）在（1-57）式中若，验证平面波是波动方程z =⋅s r 12()()z vt z vt =-++U U U （1-51）的解。

（2）验证（1-62）式所示的球面波是波动方程（1-60）12()()r vt r vt r r-+=+U U U 的解。

解答：（1）波动方程为(1-51)012222=∂∂-∇tvU U 即1222222222=∂∂-∂∂+∂∂+∂∂tvzyxU U U U )()(21vt z vt z ++-=U U U 令， vt z -=ξvtz +=η则有ηξηηξξ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂+∂∂=∂∂212121U U U U U U U z z z z z(A1-1)22221222221222ηξηηξξ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂U U U U Uz z z(A1-2)2222212222ηξ∂∂+∂∂=∂∂U U U vvt将(A1-1)、(A1-2)式代入波动方程的左边，显见12222=∂∂-∇tvU U （2）波动方程为(1-60)0)(1)(22222=∂∂-∂∂t r v r r U U 即01122222=∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂t v r r r r UU 设 ， r vt r )(11-=U f rvt r )(22+=U f 令， vt r -=ξvtr +=η则有rr r r r r r r r r ∂∂++∂∂+=∂∂+∂∂=∂∂221121)()()(f f f f f f Uηξ∂∂+-∂∂+-+=221121U U U U f f r r222222212121212211)(ξξξξ∂∂+∂∂-+∂∂+∂∂-+∂∂+∂∂=∂∂U U U U U U f f U r r r r r r r r 2222222121212221211111ξξξξξξ∂∂+∂∂-+∂∂+∂∂-+∂∂+-∂∂+-=U U U U U U U U U U r r r r r r r r 222212ξξ∂∂+∂∂=U U 用同样方法可以求出 之值。

2021届新高考物理二轮复习光学精炼（2）1.下列说法正确的是( )A.各种电磁波中,最容易表现出干涉和衍射现象的是γ射线B.红外线有显著的热效应,紫外线有显著的荧光效应C.X 射线的穿透本领比γ射线更强D.在电磁波谱中,X 射线与γ射线有很大一部分重叠区域,因此两者产生机理应该是一样的 2.关于光的现象,下列说法正确的是( )A.某单色光从真空射入普通玻璃,光线传播速度将增大B.用光导纤维传输信号,应用了全反射原理C.刮胡须的刀片的影子边缘模糊不清是光的干涉现象D.在镜头前加装一个偏振片可以增强入射光的强度3.如图所示，白炽灯的右侧依次放置偏振片P 和Q A ，点位于P Q 、之间，B 点位于Q 右侧，旋转偏振片P A B ，、两点光的强度变化情况是( )A.A B 、均不变B.A B 、均有变化C.A 不变，B 有变化D.A 有变化，B 不变 4.如图所示, 12O O 是半圆柱形玻璃体的对称面和纸面的交线，A,B 是关于12O O 对称且平行的两束不同单色细光束，从玻璃体右方射出后的光路如图所示，MN 是垂直于12O O 放置的光屏，P是屏上的一个光斑，根据该光路图，下列说法正确的是( )A.在玻璃中，A 光的波长比B 光的波长短B.在真空中，A 光的频率比B 光的大C.A 光的光子动量比B 光的小D.通过同一双缝于涉装置,A 光的干涉条纹间距比B 光的小5.若甲、乙两种单色光通过同一双缝干涉装置后得到的干涉条纹间距x x ∆>∆甲乙，由此可知( )A.甲光能发生偏振现象，乙光不能发生偏振现象B.若甲、乙两种单色光从真空射入同一介质中，该介质对甲光的折射率大于对乙光的折射率C.若甲、乙两种单色光从同一介质射入真空中，甲光发生全反射的临界角大于乙光的D.在同一介质中传播，甲光的传播速度大于乙光的6.关于电磁波及其应用，下列说法正确的有( )A.无论哪一种电磁波，在真空中的传播速度都相同B.γ射线的穿透能力最强，所以最适于用来透视人体，检查骨骼和其他病变情况C.红外线是一种光波，在军事、医疗、勘测，甚至日常生活中都有广泛的应用D.第四代移动通信系统（4G ）采用1880~2690 MHz 间的四个频段，该电磁波信号的磁感应强度随时间是均匀变化的7.虹一般是由阳光射入雨滴（视为球形）时，经一次反射和两次折射而产生色散形成的。

高等光学思考题和习题一、光的电磁理论、傅里叶分析（一）思考题1.1.指出周期函数和非周期函数的频谱有何区别，实函数和偶函数的频谱有何特点，原函数的有效宽度和频带宽度之间的关系。

1.2. 光场按线性系统的本征函数展开的物理意义及其好处？分别写出坐标算子x 和梯度算子-i ∇的本征解和正交性（分连续和分立两种情形）。

1.3. 光场用复数表示的好处及其适用条件？1.4. 解释空间频率、角谱以及光场用平面波角谱展开的物理意义。

如何理解衰逝波(非均匀平面波)和全反射的古斯-汉欣位移?1.5. 平面波的波矢k 是复数时表示何物理意义? 在什么情况下k 是复数?1.6.如何理解点源含有最丰富的信息，平面波不带任何信息？(二)习题:1.1.证明平面波的平均能流密度为<>=* S E r H r 1200Re(()()]式中E 0(r)和H 0(r)分别是电矢量和磁矢量的振幅。

1.2.求准单色波列的频谱.1.3.求准单色光振动f t A t t j t ()exp[()]exp[()]=--+022002τπνϕ的频谱分布。

1.4.证明近轴近似下的球面波的空间频谱F T j k z x y j z j z f f x y .{exp[()]}exp[()]22222+=-+λπλ1.5.证明两个高斯函数的卷积仍然是高斯函数。

1.6.证明两个洛伦兹函数的卷积仍然是洛伦兹函数。

二.标量衍射理论. 成像系统的频谱分析（一）思考题:2.0.什么叫标量衍射理论? 条件, 适用范围? 并简要说明理由。

2.1.说明卷积的展宽性质和谱函数的性质及其光学意义。

2.2.说明按平面波展开的衍射积分公式的物理意义并将公式写成入射波和某个函数的卷积形式, 该函数的的物理意义是什么？在自由空间中，点扩展函数，传递函数，本征函数和本征值之间是怎样的关系？2.3.说明衍射光栅的三要素和光栅光谱仪的三个指标的意义, 光栅光谱仪与F-P光谱仪的异同。

第一章 习题11、物点A 经平面镜成像像点A ＇，A 和A ＇是一对共轭等光程点吗？ 答：A 和A ＇是一对共轭等光程点2、在什么条件下附图中的折射球面起会聚作用，在什么条件下起发散作用？(a) (b)解: r nn n f -''='(a ) ∵ r > 0 ,∴ 当 n' > n 时，0>'f ，会聚；当 n' < n 时，0<'f ,发散。

(b )∵ r < 0 ,∴ 当 n' > n 时，0<'f ，发散; 当 n' < n 时，0>'f ，会聚。

3、顶角α很小的棱镜，常称为光楔；n 是光楔的折射率。

证明光楔使垂直入射的光线产生偏向角δ = (n −1) α，δ是指入射光经两折射面折射后，出射光线与入射光线之间的夹角。

证法一： 由折射定律n sin i 1=n 0sin i 2 ， i 1、 i 2 很小，则 11sin i i ≈ ， 22sin i i ≈ 由几何关系：α=1i ，即2i n =α ∴αααδ)1(12-=-=-=n n i i证法二：由几何关系：α=1iδαδ+=+=12i i由折射定律 n sin i 1=n 0sin i 2∵ i 1、 i 2 很小，α=≈11sin i i , 22sin i i ≈， 且 10≈n1则有 δαα+=n ，∴ αααδ)1(-=-=n n4、若空气中一均匀球形透明体能将平行光束会聚于其背面顶点上，此透明体的折射率应等于多少？解：设球形透明体的半径为r ，其折射率为n ′已知r p p n 2 , , 1='-∞== 根据单球面折射成像公式rnn p n p n -'=-'' 得：r n r n 12-'=' ∴ 2='n 5、试证明：一束平行光相继经过几个平行分界面的多层介质折射时，出射光线的方向只与入射光的方向及入射空间和出射空间介质的折射率有关，与中间各层介质无关。

实验一用两次成像法测薄透镜焦距一、引言透镜是光学仪器中最基本的元件，反映透镜特性的一个主要参量是焦距，它决定了透镜成像的位置和性质(大小、虚实、倒立)。

对于薄透镜焦距测量的准确度，主要取决于透镜光心及焦点(像点)定位的准确度。

本实验在光具座上采用贝塞耳法（两次成像法）测薄凸透镜焦距，以便了解透镜成像的规律，掌握光路调节技术，为今后正确使用光学仪器打下良好的基础。

二、实验目的1.学会用贝塞耳法（两次成像法）测量透镜焦距的方法。

2.掌握简单光路的分析和光学元件同轴等高的调节方法。

3.熟悉光学实验的操作规则。

三、实验仪器He-Ne激光器，白光源，双凸透镜，反射镜，目标物，白屏，分划板四、实验原理在近轴光线的条件下，薄透镜成像的高斯公式为：''1f fs s（4-1）当将薄透镜置于空气中时，则焦距：'''s sf fs s（4-2）(4-2)式中, f ′为像方焦距； f为物方焦距；s′为像距；s为物距。

式中的各线距均从透镜中心(光心)量起，与光线进行方向一致为正，反之为负，如图4-1所示。

若在实验中分别测出物距s和像距s′，即可用式(4-2)求出该透镜的焦距f′。

但应注意:测得量须添加符号，求得量则根据求得结果中的符号判断其物理意义。

对于凸透镜焦距的测量，除用当将薄透镜上述物像公式法测量之外，还可用以下几种方法。

1.粗略估测法图4-1 薄透镜成像以太阳光或较远的灯光为光源，用凸透镜将其发出的光线聚成一光点(或像)，此时，s →∞，s ′≈f ′，即该点(或像)可认为是焦点，而光点到透镜中心(光心)的距离，即为凸透镜的焦距，此法测量的误差约在10％左右。

由于这种方法误差较大，大都用在实验前作粗略估计，如挑选透镜等。

2.自准法如图4-2所示，在待测透镜L的一侧放置被光源照明的1字形物屏AB ，在另一侧放一平面反射镜M ，移动透镜(或物屏)，当物屏AB 正好位于凸透镜之前的焦平面时，物屏AB 上任一点发出的光线经透镜折射后，将变为平行光线，然后被平面反射镜反射回来。

光学精炼（4)1.关于电磁波的应用，下列说法不正确的是（）A。

医院里常用X射线对病房和手术室进行消毒B.工业上利用γ射线检查金属部件内部有无砂眼或裂缝C。

刑侦上用紫外线拍摄指纹照片，因为紫外线波长短、分辨率高D.卫星用红外遥感技术拍摄云图照片，因为红外线衍射能力较强2。

阳光照射下的肥皂膜看起来是彩色的，下列现象与这个现象形成的物理原理不同的是（)A.透过两支并排铅笔的狭缝看日光灯，可以观察到彩色条纹B。

雨后公路积水上面漂浮的油膜，经常显现出彩色条纹C。

用激光照射挡板上的两条平行狭缝，在光屏上观察到亮暗相间的条纹D。

在眼镜片的表面镀一层特定厚度的薄膜，可以增加光的透射3。

夜晚，汽车前灯发出的强光将迎面驶来的汽车司机照得睁不开眼，严重影响行车安全.若考虑将汽车前灯玻璃改用偏振玻璃，使射出的灯光变为偏振光；同时汽车前窗玻璃也采用偏振玻璃,其透振方向正好与对面灯光的振动方向垂直，但还要能看清自己车灯发出的光所照亮的物体。

假设所有的汽车前窗玻璃和前灯玻璃均按同一要求设置，如下措施可行的是（)A。

前窗玻璃的透振方向是竖直的,车灯玻璃的透振方向是水平的B。

前窗玻璃的透振方向是竖直的，车灯玻璃的透振方向是竖直的C.前窗玻璃的透振方向是斜向右上45°，车灯玻璃的透振方向是斜向左上45°D。

前窗玻璃和车灯玻璃的透振方向都是斜向右上45°4。

两束单色光a，b沿如图所示方向射向截面为半圆形的玻璃砖的圆心O，已知a光刚好发生全反射，b光的折射光线（反射光线未画出）刚好与a光的反射光线重叠。

下列说法正确的是（)A。

若用a光照射锌板能使之发生光电效应，则用b光时也能B.若将b光沿a光的光路射向O点，b光也能发生全反射C.在玻璃中，b光的传播速度较小D.用a光检查光学平面的平整度时，呈现的明暗相间条纹比用b 光时呈现的条纹要密5。

抽制高强度纤维细丝可用激光监控其粗细，如图所示，观察光束经过细丝后在光屏上所产生的条纹即可判断细丝粗细的变化，下列说法正确的是（）A.这里应用的是光的衍射现象B。

光学作业习题及解答12-9.在干涉实验中，两缝为0.6nm,照亮狭缝S的光源是汞弧灯加上绿色滤光片。

在2.5m远处的屏幕上出现干涉条纹，测得相邻两明条纹中心距离为2.27mm 试计算入射光的波长。

如果所用仪器只能测量△ x> 5mm的距离，则对此双缝的间距d有何要求？解：根据双缝实验相邻条纹中心距离间距：—，可知，入射光波长：d也x 2.27x10’」d 0.6 10 m 二545nmD 2.5如果所用仪器只能测量△ x> 5mm的距离，则对此双缝的间距d应进一步减小，,, 入D r/口 D 九 2.5汉545汉10一’由Z = — > 5mm 可得： d = < ----------------------- -3 ----- m = 0.2725mmd A x 5 0012-11.用很薄的云母片（n= 1.58）覆盖在双缝实验中的一条缝上，这时屏幕上的零级明条纹移到原来的第七级条纹的位置上。

如果入射光波长为550nm，试问此云母片的厚度为什么？（假设光通过云母片时不考虑折射引起的光线偏折。

）解：由于插入的云母片，使到屏幕上点的两光线的光程差发生变化，这附加产生的光程差使零级明条纹移到原来第七级条纹的位置如图，覆盖云母片前，0点处是零级明纹位置，有: °=r2-打二0由于覆盖云母片很薄，忽略光线在其中的偏折，设其厚度为覆盖云母片后，零级明条纹下移，0点处成为第七级明条纹的位置，有：^7即： [亿- e) ne] - 口 =(门 - n) (n - 1)e = (n - 1)e = 7所以云母片厚度为：「七®4 10'mm12-15.白光垂直照射在空气中厚度为0.40um的玻璃片上，玻璃的折射率为1.50, 试问在可见光范围内（A400—700nm），明E些波长的光在反射中增强？哪些波长的光在透射中增强？由以上计算可知，只有取k=3时，光波长入在可见光范围内，所以:在可见光范围内只有怎=480nm 的光在反射中增强。