高等光学_赵建林_答案_课堂笔记
- 格式:pdf
- 大小:7.46 MB
- 文档页数:14

电磁波作用下介质中的电流*张涛北京师范大学低能核物理研究所,北京市辐射中心,北京,(100875)taozhang@摘要提出了在电磁波作用下介质中存在的一种电流机制,有助于深入认识电磁波与介质之间的相互作用.关键词电磁波介质电流介质与电磁波相互作用时,介质中会生成宏观意义上的附加电荷和电流,用ρ和j分别表示所有宏观附加电荷的密度和所有宏观附加电流的密度. 为了便于分析,这里的“介质”是指无限大各向同性介质. 一般认为ρ和j组成如下[1]ρ=ρ0+ρ′, (1)j=j0+j P+j M, (2)式中ρ0和ρ′分别是介质中自由电荷密度和极化电荷密度,j0、j P和j M分别是介质中传导电流密度、极化电流密度和磁化电流密度,这是根据电荷和电流的形成机制而划分的.最近提出了电子云导体模型:电子云之中存在的变化外磁场会在电子云上诱发一个感生电流. 这一模型应用于光的折射方面取得一些合理结果,并将氦气的折射率与抗磁性联系起来[2]. 麦克斯韦认为:变化的磁场在周围激发了一种电场,这种电场称为感生电场,它的存在不依赖于在变化的磁场周围是否有闭合导体. 根据法拉第电磁感应原理,电磁波变化的磁B.来轨道运动上的附加运动造成的,这是对电子运动统计平均的结果. 一个分子内所有电子的周向运动形成一个等效环电流(称之为“分子感生环电流”或“分子感生电流”),如图2. 如同介质磁化会在介质中形成宏观的磁化电流一样,介质各个分子感生环电流最终形成一个宏观电流(如图3). 为方便起见,称这个宏观电流为“合成感生电流”,并且用j F表示合成感生电流密度. 总之,每一分子内各个电子的周向运动形成分子感生环电流,介质中各个分子合成感生电流与磁化电流都是分子大小级别的环电流合成宏观电流的结果,但它们的生成机理是不同的:合成感生电流生成机理是法拉第电磁感应原理,合成感生电流随变化的外磁场而产生,在稳定的外磁场下j F=0;磁化电流是介质顺磁、抗磁等性质的结果,无论外磁场变化与否,只要外磁场不为0,j M就不为0.可以借助介质的极化电流机制来说明合成感生电流的合理性. 绝缘介质的一种电极化机制是电子极化,即分子内的电子在交变外电场作用下往复运动,类似一个振子[3, 4],这种往复运动具有统计意义. 这表明,绝缘介质分子内的电子虽然不能在分子之间自由流动,但它在自己的电子云空间内可以有一定程度的自由运动,可以视为分子内的自由电子(分子内每一电子的活动区域限于其电子云范围)[5]. 既然分子内的电子能在交变外电场作用下形成统计意义上往复定向运动,并且导致介质的极化电流,那么,分子内的电子也应该能在变化外磁场诱发的感生电动势作用下形成统计意义上的环形定向运动,并且导致合成感生电流. 实际上,电子在介质内或分子内的定向运动均是统计意义上的结果.在外场作用下原子光谱的分裂现象、介质的抗磁性、介质在电场下的击穿等现象均是外场改变分子内电子运动的例子.2下面考察j F 的表达形式. 类似于磁化电流的统计处理方法,可以假定:只要所考察的各个分子处的电磁波∂B /∂t 相同,则在电磁波∂B /∂t 作用下各个分子形成的感生环电流的强度和尺寸是相同的. 分子感生环电流i 正比于感生电动势从而正比于磁通量变化的负值,即tS U ∂∂−==Bi Fσσ. (3) 式中U = −S F (∂B /∂t )是感生电动势(法拉第电磁感应原理),S F 是感生环电流面积,B 是介质中的磁感应强度,σ是一比例系数. 每个分子感生环电流的磁矩(称之为“分子感生磁矩”)tS S ∂∂−==Bi m 2FF F σ. (4) m F 指向阻止B 变化的方向.分子感生磁矩造成的磁化强度(称之为“感生磁化强度”,区别于介质磁化造成的磁化强度)tt S N N ∂∂−=∂∂−==BB m M βσ2FF F . (5) 式中N 是介质分子的密度,β=N σ S F 2. N 、σ、S F 与介质性质有关,在一定情况下它们随外界条件变化而变化,将它们合并为一个介质的宏观性质参数β,称之“感生磁化率”,其单位:S •m(西门子•米). 类似于磁化电流密度与磁化强度之间的关系[1],最终有合成感生电流密度j F 与感生磁化强度M F 之间关系)(F F t∂∂−×∇=×∇=BM j β. (6) 与磁化电流一样,合成感生电流不会引起电荷的积累,因此式(1)保持不变. 根据上面论述,式(2)j 变为j =j 0+j P +j M +j F . (7)式(7)比式(2)多了j F 项.总之,在电磁波作用下,介质中应该至少存在4种电流机制,它们分别是传导电流、极化电流、磁化电流和合成感生电流机制. 其中传导电流是电子(或其它载流子)在导电物质分子之间的定向运动造成的,在光频下其余三种电流是电子在其分子内的定向运动造成的. 只要有电子云存在,就会有分子感生环电流的机制,因此推论电磁波与介质相互作用时导致合成感生电流的现象应该是普遍存在的.参考文献[1]蔡圣善,朱耘,徐建军.电动力学. 北京:高等教育出版社,2002年7月第二版,第1章. [2]张涛. 光在介质中的折射. ,2005年9月1日. [3]赵建林.高等光学. 北京:国防工业出版社,2002年9月,第2章.[4]Gerald Burns. Solid State Physics. Orlando, Florida: Academic Press, Inc., 1985,Chapter 13.3[5]同[1],352页.Currents in medium interacted with electromagnetic waveZhang TaoInstitute of Low Energy Nuclear Physics, Beijing Radiation Center, Beijing Normal University,Beijing 100875, ChinaAbstractA mechanism of current in medium was presented. This helps to understand the interaction between medium and electromagnetic wave.Keywords:medium, electromagnetic wave, current4。

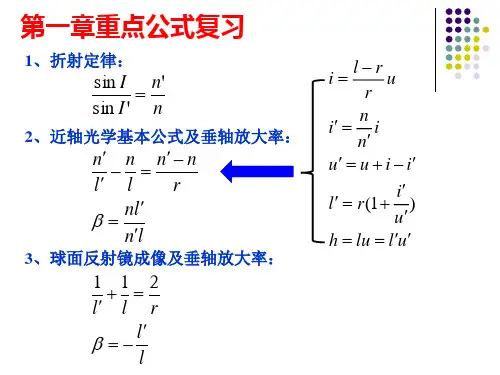
3.1 证明反射定律符合费马原理。
证明:设两个均匀介质的分界面是平面,它们的折射率为n 1和n 2。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
为了确定实际光线的路径,通过A,B 两点作平面垂直于界面,'OO 是它们的交线,则实际光线在界面上的反射点C 就可由费马原理来确定,如下图所示。
(1)反证法:如果有一点'C 位于线外,则对应于'C ,必可在'OO 线上找到它的垂足''C .由于''AC 'AC >,''BC 'BC >,故光线B AC'总是大于光程B ''AC 而非极小值,这就违背了费马原理,故入射面和反射面在同一平面内得证。
(2)在图中建立坐XOY 坐标系,则指定点A,B 的坐标分别为(x1,y1)和(x2,y2),未知点C 的坐标为(x ,0)。
C 点是在'A 、'B 之间的,光程必小于C 点在''B A 以外的相应光程,即21v x x <<,于是光程ACB 为y x x n y x x n CB n AC n ACB n 2211221221111)()(+-++-=+=根据费马原理,它应取极小值,即0)(1=n dxd0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n B C C A n y x x x x n y x x x x n ACB n dx d 所以当11'i i =,取的是极值,符合费马原理。
3.2 根据费马原理可以导出在近轴条件下,从物点发出并会聚倒像点的所有光线的光程都相等。
由此导出薄透镜的物象公式。
解:略3.3 眼睛E 和物体PQ 之间有一块折射率为1.5的玻璃平板(见题3.3图),平板的厚度d 为30cm 。

高考物理最新光学知识点之几何光学知识点总复习附答案解析一、选择题1.如图所示是一透明玻璃球体,其半径为R,O为球心,AB为水平直径。
M点是玻璃球的最高点,一条平行于AB的光线自D点射入球体内,其折射光线为DB,已知∠ABD=30°,光在真空中的传播速度为c、波长为λ,则A.此玻璃的折射率为B.光线从D传播到B的时间是C.光在玻璃球体内的波长为λD.光在B点会发成全反射2.华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”.光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所示,其内芯和外套材料不同,光在内芯中传播.下列关于光导纤维的说法中正确的是A.内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射B.内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射C.波长越短的光在光纤中传播的速度越大D.频率越大的光在光纤中传播的速度越大3.如图所示,一束光由空气射入某种介质,该介质的折射率等于A.sin50 sin55︒︒B.sin55 sin50︒︒C.sin40 sin35︒︒D.sin35 sin40︒︒4.一束光线从空气射向折射率为1.5的玻璃内,人射角为45o下面光路图中正确的是A. B.C. D.5.如图所示的四种情景中,属于光的折射的是().A.B.C.D.6.频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示,下列说法正确的是()A.单色光1的波长小于单色光2的波长B.在玻璃中单色光1的传播速度大于单色光2的传播速度C.单色光1通过玻璃板所需的时间小于单色光2通过玻璃板所需的时间D.单色光1从玻璃到空气的全反射临界角小于单色光2从玻璃到空气的全反射临界角7.一细光束由a、b两种单色光混合而成,当它由真空射入水中时,经水面折射后的光路如图所示,则以下看法正确的是A.a光在水中传播速度比b光小B.b光的光子能量较大C.当该两种单色光由水中射向空气时,a光发生全反射的临界角较大D.用a光和b光在同一装置上做双缝干涉实验,a光的条纹间距大于b光的条纹间距8.如图所示,一束平行光经玻璃三棱镜折射后分解为互相分离的a、b、c三束单色光.比较a、b、c三束光,可知A.当它们在真空中传播时,c光的波长最大B.当它们在玻璃中传播时,c光的速度最大C.若它们都从玻璃射向空气,c光发生全反射的临界角最小D.对同一双缝干涉装置,a光干涉条纹之间的距离最小9.如图所示,一束复色光由空气射向玻璃,发生折射而分为a、b两束单色光.则A.玻璃对a、b光的折射率满足n a>n bB.a、b光在玻璃中的传播速度满足v a>v bC.逐渐增大入射角,a光将先消失D.分别通过同一双缝干涉实验装置时,相邻亮条纹间距离a光大于b光10.红、黄、绿三种单色光以相同的入射角从水中射向空气,若黄光恰能发生全反射,则A.绿光也一定能发生全反射B.红光也一定能发生全反射C.红、绿光都能发生全反射D.红、绿光都不能发生全反射11.ABCDE为单反照相机取景器中五棱镜的一个截面示意图,AB⊥BC,由a、b两种单色光组成的细光束从空气垂直于AB射入棱镜,经两次反射后光线垂直于BC射出,且在CD 、AE 边只有a 光射出,光路图如图所示,则a 、b 两束光( )A .在真空中,a 光的传播速度比b 光的大B .在棱镜内,a 光的传播速度比b 光的小C .以相同的入射角从空气斜射入水中,b 光的折射角较小D .分别通过同一双缝干涉装置,a 光的相邻亮条纹间距小12.光在真空中的传播速度为c ,在水中的传播速度为v 。

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。

工程光学笔记总结一、几何光学基本定律与成像概念。
1. 直线传播定律。
- 光在均匀介质中沿直线传播。
例如小孔成像现象,就是光直线传播的体现。
- 应用:针孔相机的原理就是基于光的直线传播,光线通过小孔在成像面上形成倒立的实像。
2. 独立传播定律。
- 不同光线在空间相遇后互不干扰,各自沿原方向传播。
- 例如多束光在空间交叉时,每束光的传播路径不会因为其他光线的存在而改变。
3. 反射定律。
- 反射光线位于入射光线和法线所决定的平面内;反射光线和入射光线分别位于法线的两侧;反射角等于入射角,即i = i'。
- 在平面镜成像中,像与物关于镜面对称,这是反射定律的重要应用。
4. 折射定律。
- n_1sinθ_1=n_2sinθ_2,其中n_1、n_2分别是两种介质的折射率,θ_1是入射角,θ_2是折射角。
- 全反射现象:当光线从光密介质射向光疏介质,且入射角大于临界角θ_c=arcsin(n_2)/(n_1)时,发生全反射。
光纤通信就是利用了全反射原理,光在光纤内部通过不断全反射来传输信号。
5. 成像概念。
- 物点发出的光线经光学系统后,重新会聚于一点(实像)或光线的反向延长线会聚于一点(虚像)。
- 像的大小、正倒、虚实等性质取决于光学系统的特性和物像之间的相对位置。
二、理想光学系统。
1. 基点和基面。
- 焦点(F,F'):平行于光轴的光线经光学系统后会聚(或其反向延长线会聚)的点。
- 主点(H,H'):物方主点和像方主点,通过主点的光线方向不变。
- 节点(N,N'):通过节点的光线,其出射光线与入射光线平行。
- 焦平面:过焦点且垂直于光轴的平面。
- 主平面:过主点且垂直于光轴的平面。
2. 成像公式。
- 高斯成像公式(1)/(l')+(1)/(l)=(1)/(f),其中l为物距,l'为像距,f为焦距。
- 牛顿成像公式xx' = f f',其中x为物点到物方焦点的距离,x'为像点到像方焦点的距离。
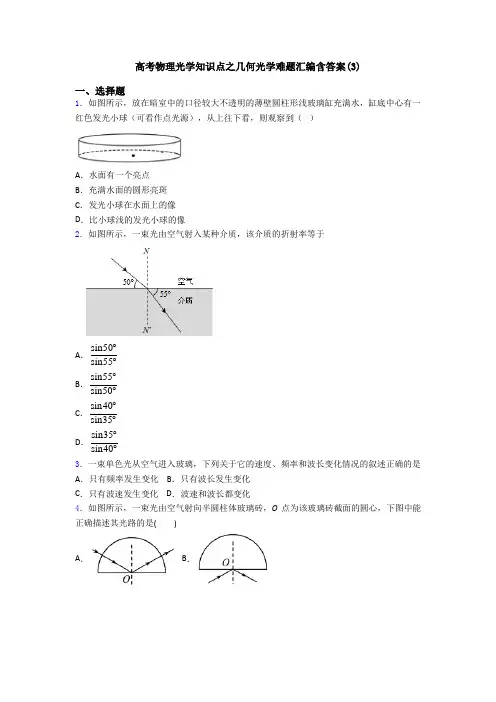
高考物理光学知识点之几何光学难题汇编含答案(3)一、选择题1.如图所示,放在暗室中的口径较大不透明的薄壁圆柱形浅玻璃缸充满水,缸底中心有一红色发光小球(可看作点光源),从上往下看,则观察到()A.水面有一个亮点B.充满水面的圆形亮斑C.发光小球在水面上的像D.比小球浅的发光小球的像2.如图所示,一束光由空气射入某种介质,该介质的折射率等于A.sin50 sin55︒︒B.sin55 sin50︒︒C.sin40 sin35︒︒D.sin35 sin40︒︒3.一束单色光从空气进入玻璃,下列关于它的速度、频率和波长变化情况的叙述正确的是A.只有频率发生变化 B.只有波长发生变化C.只有波速发生变化 D.波速和波长都变化4.如图所示,一束光由空气射向半圆柱体玻璃砖,O点为该玻璃砖截面的圆心,下图中能正确描述其光路的是()A. B.C. D.5.两束不同频率的平行单色光。
、从空气射入水中,发生了如图所示的折射现象(a>)。
下列结论中正确的是()A.光束的频率比光束低B.在水中的传播速度,光束比小C.水对光束的折射率比水对光束的折射率小D.若光束从水中射向空气,则光束的临界角比光束的临界角大6.一束单色光由玻璃斜射向空气,下列说法正确的是A.波长一定变长 B.频率一定变小C.传播速度一定变小 D.一定发生全反射现象7.a、b两种单色光以相同的入射角从半圆形玻璃砖的圆心O射向空气,其光路如图所示.下列说法正确的是()A.a光由玻璃射向空气发生全反射时的临界角较小B.该玻璃对a光的折射率较小C.b光的光子能量较小D.b光在该玻璃中传播的速度较大8.如图所示,为观察门外情况,居家防盗门一般都会在门上开一小圆孔.假定门的厚度为a=8cm,孔的直径为d=6cm,孔内安装一块折射率n=1.44的玻璃,厚度可]的厚度相同,已知sin37°=0.6,cos37°=0.8.则A.如未装玻璃,室内的人通过小孔能看到外界的角度范围为106°B.装人玻璃后,室内的人通过玻璃能看到外界的角度范围约为106°C.装人玻璃的折射率越大,室内的人通过玻鵯能看到外界的角度范围就越小D.若要将视野扩大到180°,需嵌入折射率大于或等于53的玻璃9.明代学者方以智在《阳燧倒影》中记载:“凡宝石面凸,则光成一条,有数棱则必有一面五色”,表明白光通过多棱晶体折射会发生色散现象.如图所示,一束复色光通过三棱镜后分解成两束单色光a、b,下列说法正确的是A.若增大入射角i,则b光最先消失B.在该三棱镜中a光波速小于b光C.若a、b光通过同一双缝干涉装置,则屏上a光的条纹间距比b光宽D.若a、b光分别照射同一光电管都能发生光电效应,则a光的遏止电压高10.如图所示为用a、b两种单色光分别通过同一双缝干涉装置获得的干涉图样.现让a、b两种光组成的复色光穿过平行玻璃砖或三棱镜时,光的传播路径与方向可能正确的是()A.①③B.①④C.②④D.只有③11.ABCDE为单反照相机取景器中五棱镜的一个截面示意图,AB⊥BC,由a、b两种单色光组成的细光束从空气垂直于AB射入棱镜,经两次反射后光线垂直于BC射出,且在CD、AE边只有a光射出,光路图如图所示,则a、b两束光()A.在真空中,a光的传播速度比b光的大B .在棱镜内,a 光的传播速度比b 光的小C .以相同的入射角从空气斜射入水中,b 光的折射角较小D .分别通过同一双缝干涉装置,a 光的相邻亮条纹间距小12.光在真空中的传播速度为c ,在水中的传播速度为v 。


1.1波长为500nm的绿光投射在间距d为0.022cm的双缝上,在距离r。
为180cm处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为700nm的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离。
解:相邻两个亮条纹之间的距离为扎丄r。
=y = y i i yd180 10,_9 /二 2 500 10 : 0.409 10 m0.022 疋10若改用700nm的红光照射时,相邻两个亮条纹之间的距离为人▲「0 2y = % 1 yi - ■d180 10' _9 _22 700 10 : 0.573 10 m0.022 疋10这两种光第2级亮条纹位置的距离为=2 180 10之[(700 -500) 10』]:3.27 10^m0.022 101.2在杨氏实验装置中,光源波长为640nm,两狭缝间距d为0.4mm,光屏离狭缝的距离r。
为50cm试求:⑴光屏上第1亮条纹和中央亮条纹之间的距离;(2)若P点离中央亮条纹0.1mm,问两束光在P点的相位差是多少?(3)求P点的光强度和中央点的强度之比。
解:⑴因为y = j「0(j=0,1)。
d所以第1亮条纹和中央亮条纹之间的距离为A丄r0, 50 汉10’」/y 二y1 y。
二(1-0)-03 640 10 =8.0 10 md 0.4汉10⑵因为「1 -「2 -皿,若P点离中央亮纹为0.1mm,贝U这两束光在P点的相位差为r02二yd _ 2二0.1 10“ 0.4 10“=£y = y2 ■ z700nm '<■ 500nmD九r0一640"0亠50"0“- 42(3)由双缝干涉中光强l(p) =2A1 (p)[1 cos「:(p)],得P点的光强为l(p) =2A 12(p)[1 cos : :(p)] =2A 12(p)[1 ;] =A 12(p)[2 .、2],中央亮纹的光强为 2I 0 = 4A 1 (p)。


2013年高考物理备考30分钟课堂专练系列专题11 光学(教师版)1.(2013年苏北四市期末调研)香港中文大学第三任校长高锟荣获了2009年诺贝尔物理学奖.诺贝尔奖委员会高度评价了高锟的贡献,评委会指出:高锟1966年发现如何通过光学玻璃纤维远距离传输光信号的工作,成为今日电话和高速互联网等现代通信网络运行的基石.下列关于“光纤”及原理的说法中,正确的是( )A.光纤通信具有传输容量大、衰减小、抗干扰性强等优点B.光纤通信、全息照相、数码相机及医用纤维式内窥镜都是利用了光的全反射原理C.实用光导纤维是由内芯和外套两层组成.内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射D.当今社会,在信号的传输领域中,光纤电缆(“光缆”)已经几乎完全取代了传统的铜质“电缆”,成为传播信息的主要工具,是互联网的骨架,并已联接到普通社区解析:选AD.全息照相利用了光的干涉原理,数码相机利用了光电传感器,B错;光导纤维内芯的折射率比外套的大,C错.2.(2013年衡水中学模拟)一束光从空气射向折射率n=2的某种玻璃的表面,如图所示.θ1代表入射角,则( )A.当θ1>45°时会发生全反射现象B.无论入射角θ1是多大,折射角θ2都不会超过45°C.当入射角θ1=45°时,折射角θ2=30°D.当入射角θ1=60°时,反射光线与折射光线垂直sinθ1=2sin30°3. (2013年南京质检)如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则( )A.该棱镜的折射率为3B.光在F点发生全反射C .光从空气进入棱镜,波长变小D .从F 点出射的光束与入射到E 点的光束平行 解析:选AC.在E 点作出法线可知入射角为60°,折射角为30°,折射率为3,A 对;由光路的可逆性可知,在BC 边上的入射角小于临界角,不会发生全反射,B 错;由公式λ介=λ空气n ,可知C 对;三棱镜两次折射使得光线都向底边偏折,不会与入射到E 点的光束平行,故D 错.4.(2013年辽宁铁岭调研)如图所示,ABC 为等腰棱镜,a 、b 两束不同频率的单色光垂直AB 边射入棱镜,两束光在AB 面上的入射点到OC 的距离相等,两束光折射后相交于图中的P 点,以下判断正确的是( )A .在真空中,a 光光速大于b 光光速B .在真空中,a 光波长大于b 光波长C .a 光通过棱镜的时间大于b 光通过棱镜的时间D .a 、b 两束光从同一介质射入真空过程中,a 光发生全反射的临界角大于b 光发生全反射的临界角5. (2013年海口一中模拟)如图,一透明半圆柱体折射率为n =2,半径为R 、长为L .一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出.求该部分柱面的面积S .答案:π3RL 6.(2013年哈尔滨模拟)透明光学材料制成的直角三棱镜,∠B =30°,其折射率为2,一束波长为566 nm 的单色光垂直于AC 面射向棱镜(如图所示),入射点为O ,求:(1)此单色光在棱镜中的波长;(2)该光射出棱镜的折射角.7.(2013年湖北联考)如图所示,半圆玻璃砖的半径R =10 cm ,折射率为n =3,直径AB 与屏幕垂直并接触于A 点.激光a 以入射角i =30°射向半圆玻璃砖的圆心O ,结果在水平屏幕MN 上出现两个光斑.求两个光斑之间的距离L .解析:画出如图光路图,设折射角为r ,根据折射定律n =sin r sin i,解得r =60°,由几何知识得,∠POA =30°,∠AOQ =60°,所以两个光斑PQ 之间的距离L =PA +AQ =R tan30°+R tan60°,解得L =4033≈23.1 cm.答案:23.1 cm8.(2013年上海宝山区模拟)在光的单缝衍射实验中可观察到清晰的亮暗相间的图样,下列四幅图片中属于光的单缝衍射图样的是( )A .a 、cB .b 、cC .a 、dD .b 、d解析:选D.a 图是双缝干涉图样,b 图是单缝衍射图样,c 是小孔衍射图样,d 是单缝衍射图样,故D 正确.9.(2013年银川一中模拟)用如图所示的实验装置观察光的薄膜干涉现象.图甲是点燃的酒精灯(在灯芯上洒些盐),图乙是竖立的附着一层肥皂液薄膜的金属丝圈.将金属丝圈在其所在的竖直平面内缓慢旋转,观察到的现象是( )A.当金属丝圈旋转30°时干涉条纹同方向旋转30°B.当金属丝圈旋转45°时干涉条纹同方向旋转90°C.当金属丝圈旋转60°时干涉条纹同方向旋转30°D.干涉条纹保持原来状态不变解析:选D.金属丝圈在竖直平面内缓慢旋转时,楔形薄膜各处厚度几乎不变.因此,形成的干涉条纹保持原状态不变,D正确,A、B、C错误.10.(2013年宁波质检)劈尖干涉是一种薄膜干涉,其装置如图甲所示,将一块平板玻璃放置在另一平板玻璃之上,在一端夹入两张纸片,从而在两玻璃表面之间形成一个劈形空气薄膜.当光垂直入射后,从上往下看到的干涉条纹如图乙所示,干涉条纹有如下特点:(1)任意一条明条纹或暗条纹所在位置下面的薄膜厚度相等;(2)任意相邻明条纹和暗条纹所对应的薄膜厚度差恒定.现若在图甲装置中抽去一张纸片,则当光垂直入射到新的劈形空气薄膜后,从上往下观察到的干涉条纹( )A.变疏B.变密C.不变D.消失11.(2013年温州模拟)在观察光衍射的实验中,分别观察到如图甲、乙所示的清晰的明暗相间的图样,图中黑线为暗纹.那么障碍物应是( )A.乙图对应的是很小的不透明圆板B.甲图对应的是很大的不透明圆板C.乙图对应的是很大的中间有大圆孔的不透明挡板D.甲图对应的是很大的中间有小圆孔的不透明挡板12.利用薄膜干涉的原理可以用干涉法检查平面和制造增透膜,回答以下两个问题:(1)用如图所示的装置检查平面时,是利用了哪两个表面反射光形成的薄膜干涉图样?(2)为了减少光在透镜表面由于反射带来的损失,可在透镜表面涂上一层增透膜,一般用折射率为1.38的氟化镁,为了使波长为5.52×10-7 m的绿光在垂直表面入射时使反射光干涉相消,求所涂的这种增透膜的厚度?13.(上海市闸北区2013届高三模拟)利用发波水槽可以观察“波的干涉现象”。
第十二章光的干涉(一)一、学时安排:6学时二、教学要求(重点,难点)1、了解光源发光机理,理解获得相干光的方法。
2、掌握杨氏双缝实验的光干涉条件,明、暗条纹分布规律的计算。
3、理解光程概念,掌握其计算方法。
4、掌握薄膜干涉的形成、干涉条件及其应用。
5、掌握劈尖干涉和牛顿环的形成、干涉条件及其应用6、了解Michelson interferometer 的结构和光路以及用其测量微小长度原理。
三、教学参考书1、WA VES . F.S Crawford, Berkeley PhysicsCourse, Vol3.2 、University Physics, Part 2.3 、杨仲耆《大学物理学》波动与光学4、张三慧《大学物理》波动与光学前言光学是物理学发展较早的一个分支。
我国古代关于光现象的文字记载首推“墨经,”其中有“景,光之人,煦若射;下者之人也高,高者之人也下,足蔽下光,故成景于上,首蔽上光,故成景于下 ”总结了光直进的原理。
还有其它一些记载,在世界科学史上占有崇高的地位。
除了反射、折射、成像等现象外(表征光的直线传播),关于光的本性和传播问题,也很早就引起人们的注意。
在17世纪,关于光的本性问题,有两派不同的学说,一派是牛顿的微粒说,认为光是从发光体发出的且以一定速度向空间传播的一种机械微粒。
另一派是惠更斯所倡议的光的波动说(认为光是在媒质中传播的机械波)。
由于当时科学水平的局限,他们或者把光看作由机械微粒所组成,或者把光看作一种机械波,这两种观点都没有正确地反映光的客观本质。
微粒说和波动说当时都能解释光的反射和折射现象,但在解释光线从空气进入水中的折射现象时,微粒说的结论是空水v v >,波动说的结论是水空v v >,因为当时人们还不能准确地用实验方法测定光速,所以无法判断这两种学说的优劣。
19世纪初,人们发现光有干涉、衍射和偏振等现象,这些现象是波动的特征,和微粒子说是不相容的。
高考物理新光学知识点之几何光学全集汇编及答案解析(2)一、选择题1.如图所示是一透明玻璃球体,其半径为R,O为球心,AB为水平直径。
M点是玻璃球的最高点,一条平行于AB的光线自D点射入球体内,其折射光线为DB,已知∠ABD=30°,光在真空中的传播速度为c、波长为λ,则A.此玻璃的折射率为B.光线从D传播到B的时间是C.光在玻璃球体内的波长为λD.光在B点会发成全反射2.华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”.光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所示,其内芯和外套材料不同,光在内芯中传播.下列关于光导纤维的说法中正确的是A.内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射B.内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射C.波长越短的光在光纤中传播的速度越大D.频率越大的光在光纤中传播的速度越大3.如图所示,一束光由空气射入某种介质,该介质的折射率等于A.sin50 sin55︒︒B.sin55 sin50︒︒C.sin40 sin35︒︒D .sin35sin40︒︒ 4.某单色光在真空中传播速度为c ,波长为λ0,在水中的传播速度为v ,波长为λ,水对这种单色光的折射率为n ,当这束单色光从空气斜射入水中时,入射角为i ,折射角为r ,下列正确的是( )A .v=nc ,λ=n c 0λ B .λ0=λn,v=sini csinr C .v=cn ,λ=c v0λD .λ0=λ/n,v=sinrcsini 5.如图所示,两束单色光a 、b 同时从空气中斜射入平行玻璃砖的上表面,进入玻璃砖中后形成复合光束c 则下列说法中正确的是A .a 光的能量较大B .在玻璃中a 光的传播速度小于b 光的传播速度C .在相同的条件下,a 光更容易发生衍射D .a 光从玻璃到空气的全反射临界角小于b 光从玻璃到空气的全反射临界角6.如图所示,一束光由空气射向半圆柱体玻璃砖,O 点为该玻璃砖截面的圆心,下图中能正确描述其光路的是( )A .B .C .D .7.一束单色光由玻璃斜射向空气,下列说法正确的是A .波长一定变长B .频率一定变小C .传播速度一定变小D .一定发生全反射现象8.如图所示为用a 、b 两种单色光分别通过同一双缝干涉装置获得的干涉图样.现让a 、b 两种光组成的复色光穿过平行玻璃砖或三棱镜时,光的传播路径与方向可能正确的是( )A.①③B.①④C.②④D.只有③9.如图所示,将一个折射率为n的透明长方体放在空气中,矩形ABCD是它的一个截面,一单色细光束入射到P点,入射角为θ.12AP AD=,则( )A.若要使光束进入长方体后能射至AD面上,角θ的最小值为arcsin 1 2 nB.若要使光束进入长方体后能射至AD面上,角θ的最小值为arcsin5 5nC.若要此光束在AD面上发生全反射,角θ的范围应满足arcsin 12n<θ≤arcsin21n-D.若要此光束在AD面上发生全反射,角θ的范围应满足arcsin 25n<θ≤arcsin21n-10.ABCDE为单反照相机取景器中五棱镜的一个截面示意图,AB⊥BC,由a、b两种单色光组成的细光束从空气垂直于AB射入棱镜,经两次反射后光线垂直于BC射出,且在CD、AE边只有a光射出,光路图如图所示,则a、b两束光()A.在真空中,a光的传播速度比b光的大B .在棱镜内,a 光的传播速度比b 光的小C .以相同的入射角从空气斜射入水中,b 光的折射角较小D .分别通过同一双缝干涉装置,a 光的相邻亮条纹间距小11.在杨氏干涉实验中,从两个狭缝到达像屏上的某点的光走过的路程相等,该点即为中央亮条纹的位置(即k=0对应的那条亮条纹),双缝屏上有上下两狭缝,设想在双缝屏后用一块极薄的玻璃片遮盖上方的缝,则屏上中央亮条纹的位置将( )A .向上移动B .向下移动C .不动D .可能向上移动,也可能向下移动12.光在真空中的传播速度为c ,在水中的传播速度为v 。