(推荐下载)30度角所对直角边专练

九上数学每日一练：含30度角的直角三角形练习题及答案_2020年解答题版答案解析答案解析答案解析答案解析答案解析2020年九上数学：图形的性质_三角形_含30度角的直角三角形练习题1.(2018北京.九上期末) 如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，连接BC ．若AB ＝6，∠B ＝30°，求弦CD 的长．考点： 含30度角的直角三角形;勾股定理;垂径定理;圆周角定理;2.(2018垣曲.九上期末) 如图，小明坐在堤边A 处垂钓，河堤AC与水平面的夹角为30°，AC 的长为米，钓竿AO 与水平线的夹角为60°，其长为3米，若AO 与钓鱼线OB 的夹角为60°，求浮漂B与河堤下端C 之间的距离.考点： 等边三角形的判定与性质;含30度角的直角三角形;3.(2018阜宁.九上期末) 大海中某小岛周围10 范围内有暗礁，一海轮在该岛的南偏西 方向的某处，由西向东行驶了 后到达该岛的南偏西 方向的另一处，如果该海轮继续向东行驶，会有触礁的危险吗？（≈1.732）．考点： 等腰三角形的性质;含30度角的直角三角形;勾股定理的应用;解直角三角形的应用﹣方向角问题;4.(2017德惠.九上期末) 如图，在∠ABC 中，∠B=30°，AC= ，等腰直角△ACD 斜边AD 在AB 边上，求BC 的长．考点： 等腰直角三角形;直角三角形的性质;含30度角的直角三角形;勾股定理;5.(2016西湖.九上期末) 如图，BM 是⊙O的直径，四边形ABMN 是矩形，D 是⊙O 上的点，DC ⊥AN ，与AN 交于点C ，己知AC=15，⊙O 的半径为30，求 的长．考点： 含30度角的直角三角形;矩形的性质;弧长的计算;2020年九上数学：图形的性质_三角形_含30度角的直角三角形练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：。

八上数学每日一练：含30度角的直角三角形练习题及答案_2020年综合题版答案解析答案解析2020年八上数学：图形的性质_三角形_含30度角的直角三角形练习题1.(2020慈溪.八上期中) 阅读下列材料，然后解决问题：和、差、倍、分等问题中有着广泛的应用，截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题.（1） 如图1，在△ABC 中，若AB=12，AC=8，求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法：延长AD 到点E 使DE=AD ，再连接BE ，把AB 、AC 、2AD 集中在△ABE 中.利用三角形三边的关系即可判断中线AD 的取值范围是；（2） 问题解决：如图2，在四边形ABCD 中，AB=AD ，∠ABC+∠ADC=180°，E 、F 分别是边BC ，边CD 上的两点，且∠EAF= ∠B AD ，求证：BE+DF=EF.（3） 问题拓展：如图3，在△ABC 中，∠ACB=90°，∠CAB=60°，点D 是△ABC 外角平分线上一点，DE ⊥AC 交CA 延长线于点E ，F 是AC 上一点，且DF=DB.求证：AC-AE= AF.考点： 三角形三边关系;全等三角形的判定与性质;含30度角的直角三角形;2.(2020通榆.八上期末) △ABC 是边长为6的等边三角形，P 是AC 边上一动点，由A 向C 运动(与A 、C 不重合)，Q 是CB 延长线上一动点，与点P 同时以相同的速度山B 向CB 延长线方向运动(Q 不与B 重合)，过P 作PF ∥BC ，交AB 于F ，连接PQ 交A B 于D 。

（1） 如图①，△AFP 是（判定三角形形状）（2） 当∠BQD=30°时，求AP 的长；（3） 证明：在运动过程中，点D 是线段PQ 的中点；（4） 如图②，作PE ⊥AB 于E ，运动过程中线段ED 的长是定值，则这个定值是。

八上数学每日一练：含30度角的直角三角形练习题及答案_2020年解答题版答案解析答案解析答案解析2020年八上数学：图形的性质_三角形_含30度角的直角三角形练习题1.(2020历下.八上期末)如图，在等边中，点（2，0），点 是原点，点 是 轴正半轴上的动点，以 为边向左侧作等边 ，当时，求 的长．考点： 坐标与图形性质;等边三角形的性质;含30度角的直角三角形;勾股定理;2.(2020厦门.八上期中) 如图，在平面直角坐标系中，点A 在y 轴上，点B 在x 轴上，∠OAB ＝30°．（Ⅰ）若点C 在y 轴上，且△ABC 为以AB 为腰的等腰三角形，求∠BCA 的度数；（Ⅱ）若B （1，0），沿AB 将△ABO 翻折至△ABD ． 请根据题意补全图形，并求点D的横坐标．考点： 坐标与图形性质;等腰三角形的性质;含30度角的直角三角形;翻折变换（折叠问题）;3.(2020重庆.八上期中) 如图所示,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB 的高.考点： 等腰三角形的性质;含30度角的直角三角形;4.(2020安陆.八上期末)如图， 中，，，一同学利用直尺和圆规完成如下操作：分别以点 、 为圆心，以大于的长为半径画弧，两弧交于点，两点，直线 交 于 ，交 于 .请你观察图形，猜想 与 之间的数量关系，并证明你的结论.答案解析答案解析考点： 线段垂直平分线的性质;含30度角的直角三角形;5.(2017卢龙.八上期中) 如图，在Rt △ABC 中，∠C=90°，BD 平分∠ABC 交AC 于D ，DE ⊥AB 于E ，若DE=1cm ，∠CBD =30°，求∠A 的度数和AC 的长．考点： 角平分线的性质;含30度角的直角三角形;2020年八上数学：图形的性质_三角形_含30度角的直角三角形练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：。

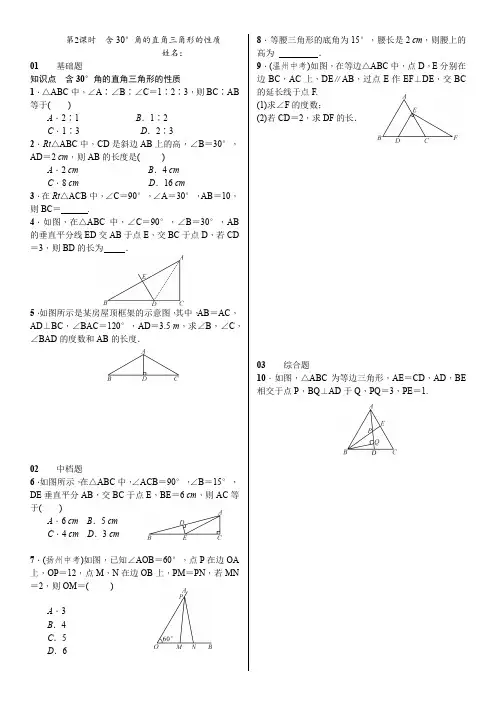
第2课时 含30°角的直角三角形的性质姓名：01 基础题知识点 含30°角的直角三角形的性质1．△ABC 中，∠A ∶∠B ∶∠C ＝1∶2∶3，则BC ∶AB 等于( )A ．2∶1B ．1∶2C ．1∶3D ．2∶32．Rt △ABC 中，CD 是斜边AB 上的高，∠B ＝30°，AD ＝2 cm ，则AB 的长度是( )A ．2 cmB ．4 cmC ．8 cmD ．16 cm 3．在Rt △ACB 中，∠C ＝90°，∠A ＝30°，AB ＝10，则BC ＝ .4．如图，在△ABC 中，∠C ＝90°，∠B ＝30°，AB 的垂直平分线ED 交AB 于点E ，交BC 于点D ，若CD ＝3，则BD 的长为 ．5．如图所示是某房屋顶框架的示意图，其中，AB ＝AC ，AD ⊥BC ，∠BAC ＝120°，AD ＝3.5 m ，求∠B ，∠C ，∠BAD 的度数和AB 的长度．02 中档题 6．如图所示，在△ABC 中，∠ACB ＝90°，∠B ＝15°，DE 垂直平分AB ，交BC 于点E ，BE ＝6 cm ，则AC 等于( )A ．6 cmB ．5 cmC ．4 cmD ．3 cm7．(扬州中考)如图，已知∠AOB ＝60°，点P 在边OA 上，OP ＝12，点M ，N 在边OB 上，PM ＝PN ，若MN ＝2，则OM ＝( )A ．3B ．4C ．5D ．68．等腰三角形的底角为15°，腰长是2 cm ，则腰上的高为 ．9．(温州中考)如图，在等边△ABC 中，点D ，E 分别在边BC ，AC 上，DE ∥AB ，过点E 作EF ⊥DE ，交BC 的延长线于点F. (1)求∠F 的度数；(2)若CD ＝2，求DF 的长．03 综合题10．如图，△ABC 为等边三角形，AE ＝CD ，AD ，BE 相交于点P ，BQ ⊥AD 于Q ，PQ ＝3，PE ＝1.。

八年级上册数学第2课时含30°角的直角三角形的性质精选练习2°角的直角三角形的性质精选练习2
1.在Rt△A BC中，∠C=90°∠A=30°，若AB=4cm,则BC=_______________.
2.等腰三角形一底角是30°，底边上的高为9cm，则其腰长为__________,顶角是
__________.
3.在△A BC中，∠ACB=90°，CD⊥AB于点D，∠A=30°，则
CD=____AC,BC=____AB,BD=____BC,BD=_____AB.
4.在△ABC中，∠B=∠C=15°，AB=2cm,CD⊥AB交BA的延长线与点D，则CD的长为
___________.
5.如右图所示，△ABC为等边三角形，AD∥BC，
CD⊥AD,若△ABC的周长为36cm,求AD的长。

6.如右图所示，在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于点D,AB=10，求DB
的长。

7.如右图所示，在△ABC中，∠ACB=90°，∠A=30°，CD⊥AB于点D,AB=4cm,求BC ﹨AD﹨BD的长和∠BCD的度数。

8.如下图所示，∠AOP=∠BOP=15°，PC∥OA,若PC=4，求PD的长。

9.如下图所示，在Rt△ABC中，∠C=90°，∠ABC=75°，从顶点B引射线BD与CA 交于点D，使∠CDB=30°.求证：AD=2BC.。

九上数学每日一练：含30度角的直角三角形练习题及答案_2020年综合题版答案解析答案解析答案解析2020年九上数学：图形的性质_三角形_含30度角的直角三角形练习题1.(2020德城.九上期末) (如图，⊙O 是△ABC 的外接圆，圆心O 在AB 上，且∠B ＝2∠A ，M 是OA 上一点，过M 作AB 的垂线交AC 于点N ，交BC 的延长线于点E ，直线CF 交EN 于点F ，EF ＝FC.（1） 求证：CF 是⊙O 的切线；（2） 若⊙O 的半径为2，且AC ＝CE ，求AM 的长．考点： 含30度角的直角三角形;勾股定理;圆周角定理;切线的判定;2.(2020宜兴.九上期中) 如图，在平面直角坐标系中，以点M （0， ）为圆心，以 长为半径作⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，连接AM 并延长交⊙M 于P 点，连接PC 交x 轴于E.（1） 求出CP 所在直线的解析式；（2） 连接AC ，请求△ACP 的面积.考点： 待定系数法求一次函数解析式;等边三角形的判定与性质;含30度角的直角三角形;垂径定理;圆周角定理;3.(2020农安.九上期中) 我们定义：如图1、图2、图3，在中，把绕点顺时针旋转得到，把绕点逆时针旋转得到，连接 ，当时，我们称是的“旋补三角形”，边上的中线 叫做 的“旋补中线”，点叫做“旋补中心”.图1、图2、图3中的 均是的“旋补三角形”.（1）①如图2，当为等边三角形时，“旋补中线” 与的数量关系为： ；②如图3，当，时，则“旋补中线” 长为.（2） 在图1中，当 为任意三角形时，猜想“旋补中线” 与 的数量关系，并给予证明.考点： 等边三角形的性质;含30度角的直角三角形;平行四边形的判定;4.(2019三门.九上期末) 如图，▱ABCD 的对角线AC 、BD 相交于点M ，点M 在以AB 为直径的⊙O 上，AD 与⊙O 相交于点E ，连接ME.答案解析答案解析（1） 求证：ME ＝MD ；（2） 当∠DAB ＝30°时，判断直线CD 与⊙O 的位置关系，并说明理由.考点： 含30度角的直角三角形;菱形的判定与性质;圆周角定理;圆内接四边形的性质;切线的判定;5.(2019婺城.九上期末) 如图1，在中，，， ，于点D ，将绕点B 顺时针旋转 得到（1） 如图2，当 时，求点C 、E 之间的距离；（2） 在旋转过程中，当点A 、E 、F 三点共线时，求AF 的长；（3） 连结AF ，记AF 的中点为P ，请直接写出线段CP 长度的最小值.考点： 含30度角的直角三角形;直角三角形斜边上的中线;三角形中位线定理;旋转的性质;2020年九上数学：图形的性质_三角形_含30度角的直角三角形练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：。

专题1.3 含30°角的直角三角形性质专项训练（30道）【北师大版】考卷信息：本套训练卷共30题，选择题10道，填空题10道，解答题10道，题型针对性较高，覆盖面广，选题有深度，综合性较强！一．选择题（共10小题）1．（2021秋•娄星区校级月考）如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，∠A＝30°，则下列结论中正确的是（ ）A．AC＝2AD B．CD＝2BD C．BC＝2CD D．BC＝2BD【解题思路】根据直角三角形的性质可得在直角三角形ACB中AB＝2BC，在直角△CDB中BC＝2BD，在直角△ACD中AC＝2CD．【解答过程】解：在△ABC中，∠ACB＝90°，∴△ACB是直角三角形，∵∠A＝30°，∴AB＝2BC，∵CD是AB边上的高，∴∠CDA＝∠CDB＝90°，∴∠ACD＝60°，∴∠DCB＝30°，∴BC＝2BD，AC＝2CD．故选：D．2．（2021春•丹东期末）如图，在△ABC中，AB＝AC，AD⊥AB交BC于点D，∠BAC＝120°，AD＝4，则BC的长为（ ）A．8B．10C．11D．12【解题思路】依据等腰三角形的内角和，即可得到∠C＝∠B＝30°，依据AD⊥AB交BC于点D，即可得到BD＝2AD＝8，∠CAD＝30°＝∠B，CD＝AD＝4，进而得出BC的长．【解答过程】解：∵△ABC中，AB＝AC，∠BAC＝120°，∴∠C＝∠B＝30°，∵AD⊥AB交BC于点D，∴BD＝2AD＝8，∠CAD＝30°＝∠B，∴CD＝AD＝4，∴BC＝BD+CD＝8+4＝12．故选：D．3．如图，∠AOB＝60°，点P在OA上，PC＝PD，若OC＝5cm，OD＝8cm，则OP的长是（ ）A．13cm B．12cm C．8cm D．5cm【解题思路】过点P作PE⊥OB于点E，根据△PCD为等腰三角形，则E为CD的中点，再由△POE为直角三角形，∠AOB＝60°，即可得出答案．【解答过程】解：如图，过点P作PE⊥OB于点E，则PE⊥CD，∵PC＝PD，∴△PCD为等腰三角形，∴点E为CD的中点，∵OC＝5cm，OD＝8cm，∴CD＝3cm，∴OE＝6.5cm，∵∠AOB＝60°，∴∠OPE＝90°﹣60°＝30°，∴OP＝2OE＝13cm，故选：A．4．（2021春•濮阳期末）如图，在△ABC中，AB＝AC，∠B＝30°，AD⊥AC，交BC于点D，AD＝4，则BC的长为（ ）A．8B．4C．12D．6【解题思路】由等腰三角形的性质得出∠B＝∠C＝30°，∠CAD＝90°，可得∠DAB＝∠B＝30°，即BD＝AD＝4．Rt△ACD中，根据30°角所对直角边等于斜边的一半，可求得CD＝2AD＝8，由此可求得BC的长．【解答过程】解：∵AB＝AC，∠B＝30°，∴∠B＝∠C＝30°，∵AD⊥AC，AD＝4，∴CD＝2AD＝2×4＝8，∵∠C+∠ADC＝90°，∴∠ADC＝90°﹣30°＝60°，∵∠ADC＝∠DAB+∠B，∴∠DAB＝30°，∴∠DAB＝∠B，∴DB＝AD＝4，∴BC＝BD+DC＝4+8＝12，故选：C．5．（2021春•新城区期中）如图，△ABC是等边三角形，AB＝10，点D是BC边上任意一点，DE⊥AB于点E，DF⊥AC于点F，则BE+CF的长是（ ）A．5B．6C．8D．10【解题思路】先设BD＝x，则CD＝10﹣x，根据△ABC是等边三角形得出∠B＝∠C＝60°，求出∠BDE ＝30°，∠CDF＝30°，根据含30°角的直角三角形的性质求出CF和CF，再相加即可．【解答过程】解：设BD＝x，则CD＝10﹣x，∵△ABC是等边三角形，∴∠B＝∠C＝60°，∴∠BDE＝30°，∠CDF＝30°，∴BE=12BD=x2同理可得，CF=10x 2，∴BE+CF=x2+10x2=5，故选：A．6．（2021春•岳麓区校级期末）如图，△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线交AC于D，交AB于E，CD＝2，则AD等于（ ）A．10B．8C．6D．4【解题思路】先由直角三角形的性质求出∠ABC的度数，由AB的垂直平分线交AC于D，交AB于E，垂足为E，可得BD＝AD，由∠A＝30°可知∠ABD＝30°，故可得出∠DBC＝30°，根据CD＝2可得出BD的长，进而得出AD的长．【解答过程】解：连接BD，∵在△ABC中，∠C＝90°，∠A＝30°，∴∠ABC＝60°．∵AB的垂直平分线交AC于D，交AB于E，∴AD＝BD，DE⊥AB，∴∠ABD＝∠A＝30°，∴∠DBC＝30°，∵CD＝2，∴BD＝2CD＝4，∴AD＝4．故选：D．7．（2020秋•朝阳县期末）如图，在△ABC中，AB＝AC＝11，∠BAC＝120°，AD是△ABC的中线，AE 是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为（ ）A．4.5B．5C．5.5D．6【解题思路】根据等腰三角形三线合一的性质可得到AD⊥BC，∠BAD＝∠CAD，从而可得到∠BAD＝60°，∠ADB＝90°，再根据角平分线的性质即可得到∠DAE＝∠EAB＝30°，从而可推出AD＝DF，根据直角三角形30度角的性质即可求得AD的长，即得到了DF的长．【解答过程】解：∵△ABC是等腰三角形，D为底边的中点，∴AD⊥BC，∠BAD＝∠CAD，∵∠BAC＝120°，∴∠BAD＝60°，∠ADB＝90°，∵AE是∠BAD的角平分线，∴∠DAE＝∠EAB＝30°．∵DF∥AB，∴∠F＝∠BAE＝30°．∴∠DAF＝∠F＝30°，∴AD＝DF．∵AB＝11，∠B＝30°，∴AD＝5.5，∴DF＝5.5故选：C．8．（2020秋•丛台区校级期末）如图，△ABC与△DCE都是等边三角形，B，C，E三点在同一条直线上，若AB＝3，∠BAD＝150°，则DE的长为（ ）A．3B．4C．5D．6【解题思路】根据等边三角形的性质得出AB＝AC＝3，DE＝DC，∠BAC＝∠DCE＝∠ACB＝60°，求出∠ACD＝60°，∠CAD＝90°，求出∠ADC＝30°，根据很30度角的直角三角形性质得出DC＝2AC，求出即可．【解答过程】解：∵△ABC与△DCE都是等边三角形，AB＝3，∠BAD＝150°，∴AB＝AC＝3，DE＝DC，∠BAC＝∠DCE＝∠ACB＝60°，∴∠ACD＝60°，∠CAD＝150°﹣60°＝90°，∴∠ADC＝30°，∴DC＝2AC＝6，∴DE＝DC＝6，故选：D．9．（2021•海淀区校级模拟）如图，在△ABC中，∠C＝60°，AD是BC边上的高，点E为AD的中点，连接BE并延长交AC于点F．若∠AFB＝90°，EF＝2，则BF长为（ ）A．4B．6C．8D．10【解题思路】根据三角形内角和定理求出∠DAC＝30°和∠EBD＝30°，根据含30°角的直角三角形的性质得出AE＝2EF，BE＝2DE，代入求出即可．【解答过程】解：∵在△ABC中，∠C＝60°，AD是BC边上的高，∴∠DAC＝90°﹣∠C＝90°﹣60°＝30°，∵∠AFB＝90°，EF＝2，∴AE＝2EF＝4，∵点E为AD的中点，∴DE＝AE＝4，∵∠C＝60°，∠BFC＝180°﹣90°＝90°，∴∠EBD＝30°，∴BE＝2DE＝8，∴BF＝BE+EF＝8+2＝10，故选：D．10．（2021春•织金县期末）如图，在△ABC中，∠BAC＝90°，∠ABC＝2∠C，BE平分∠ABC交AC于E，AD⊥BE于D，下列结论：①AC﹣BE＝AE；②点E在线段BC的垂直平分线上；③∠DAE＝∠C；④BC＝3AD，其中正确的个数有（ ）A．4个B．3个C．2个D．1个【解题思路】根据三角形内角和定理、线段垂直平分线的判定定理、直角三角形的性质判断即可．【解答过程】解：∵∠BAC＝90°，∠ABC＝2∠C，∴∠ABC＝60°，∠C＝30°，∵BE平分∠ABC，∴∠EBC＝∠ABE=12∠ABC＝30°，∴∠EBC＝∠C，∴EB＝EC，∴AC﹣BE＝AC﹣EC＝AE，①正确；∵EB＝EC，∴点E在线段BC的垂直平分线上，②正确；∵∠BAC＝90°，∠ABE＝30°，∴AEB＝60°，∵AD⊥BE，∴∠DAE＝30°，∴∠DAE＝∠C，③正确；∵∠BAC＝90°，∠C＝30°，∴BC＝2AB，同法AB＝2AD,∴BC＝4AD,④错误，故选：B．二．填空题（共10小题）11．（2020秋•抚顺县期末）右图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB＝7.4m，∠A＝30°，则DE长为　1.85m　．【解题思路】根据直角三角形的性质求出BC，根据三角形中位线定理计算即可．【解答过程】解：∵∠A＝30°，BC⊥AC，∴BC=12AB＝3.7，∵DE⊥AC，BC⊥AC，∴DE∥BC，∵点D是斜梁AB的中点，∴DE=12BC＝1.85m，故答案为：1.85m．12．（2020秋•沂水县期末）如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，AB＝6，点D，E分别是边BC，AC上的点，且BD＝2CD，DE∥AB，则DE的长是　2　．【解题思路】由∠ACB＝90°，∠ABC＝60°得∠A＝30°，根据含30°角的直角三角形的性质可得BC=12AB＝3，由BD＝2CD可得CD＝1，根据平行线的性质得∠DEC＝∠A＝30°，即可得DE＝2CD＝2．【解答过程】解：∵∠ACB＝90°，∠ABC＝60°，∴∠A＝30°，∴BC=12AB＝3，∵BD＝2CD，∴CD＝1，∵DE∥AB，∴∠DEC＝∠A＝30°，∵∠ACB＝90°，∴DE＝2CD＝2．故答案为：2．13．（2021春•普宁市期末）如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F，若BF＝2，则CF的长为　4　．【解题思路】连接AF，根据三角形的内角和定理及等腰三角形的性质可求解∠B＝∠C＝30°，利用线段垂直平分线的性质可求解∠BAF＝30°，即可求解∠FAC＝90°，再利用含30°角的直角三角形的性质可求解CF的长．【解答过程】解：连接AF，∵AB＝AC，∠BAC＝120°，∴∠B＝∠C＝30°，∵EF垂直平分AB，∴BF＝AF，∴∠BAF＝∠B＝30°，∴∠CAF＝120°﹣30°＝90°，∴CF＝2AF＝2BF，∵BF＝2，∴CF＝4．故答案为4．14．（2021春•垦利区期末）如图，△ABC是等边三角形，AD∥BC，CD⊥AD．若AD＝2cm，则△ABC的周长为　12　cm．【解题思路】利用平行线的性质和CD⊥AD，先得到∠DCB的度数，再求出∠ACD的度数，再直角三角形中，利用30°角所对的边与斜边的关系求出AC，最后求出等边三角形的周长．【解答过程】解：∵△ABC是等边三角形，∴AB＝AC＝BC，∠ACB＝60°．∵AD∥BC，CD⊥AD，∴∠D+∠DCB＝180°，∠D＝90°．∴∠DCB＝90°．∴∠ACD＝∠∠DCB﹣∠ACB＝30°．在Rt△ACD中，∵AD＝2cm，∠ACD＝30°，∴AC＝2AD＝4（cm）．L＝AB+AC+BC＝12（cm）．△ABC故答案为：12．15．（2021春•九江期末）如图，在△ABC中，∠A＝30°，F为AC上一点，FD垂直平分AB，交AB于点D，线段DF上点E满足EF＝2DE＝2，连接CE、EB，若BE＝EC，则CF的长为　4　．【解题思路】连接AE，过点E作EG⊥AC交AC于点G，根据已知条件，可得等腰三角形AEC，利用等腰三角形的三线合一解题即可．【解答过程】解：如图，连接AE，过点E作EG⊥AC交AC于点G．在△ABC 中，∠CAB ＝30°，FD 垂直平分AB ，EF ＝2DE ＝2，∴FD ＝3DE ＝3，AF ＝2FD ＝6，AE ＝BE ，∵BE ＝EC ，∴AE ＝EC ，∴GF =12EF ＝1，AG ＝GC ＝5，∴CF ＝GC ﹣GF ＝5﹣1＝4．故答案为：4．16．（2021春•沂源县期末）如图，在△ABC 中，AB ＝AC ＝8，∠ABC ＝15°，则△ABC 的面积为 16　．【解题思路】过B 点作BD ⊥AC ，交CA 的延长线于点D ，由等腰三角形的性质结合三角形外角的性质可求得∠BAD 的度数，由含30°角的直角三角形的性质可求解BD 的长，利用三角形的面积公式可求解△ABC 的面积．【解答过程】解：过B 点作BD ⊥AC ，交CA 的延长线于点D ，，∵AB ＝AC ，∠ABC ＝15°，∴∠C ＝∠ABC ＝15°，∴∠DAB ＝∠ABC +∠C ＝30°，∵AB ＝AC ＝8，∴BD =12AB ＝4，∴△ABC 的面积为：12AC ⋅BD =12×8×4=16．故答案为16．17．（2021春•济宁期末）如图，△ABC 是等边三角形，点D 为AB 的中点，DE ⊥AC 于点E ，EF ∥AB ，AD ＝6，则△EFC 的周长为　27　．【解题思路】利用含30度角的直角三角形求出AE 的长，根据平行线的性质、等边三角形的性质和判定求出△EFC 各边长，周长即可求．【解答过程】解：∵△ABC 是等边三角形，∴∠A ＝∠B ＝∠C ＝60°，AB ＝AC ．∵点D 为AB 的中点，AD ＝6，∴AB ＝2AD ＝12．∵DE ⊥AC 于点E ，AD ＝6，∴∠ADE ＝30°，∴AE =12AD ＝3，∴CE ＝AC ﹣AE ＝9．∵EF ∥AB ，∴∠FEC ＝∠A ＝60°，∵∠C ＝60°，∴△EFC 是等边三角形．∴△EFC 的周长＝9+9+9＝27．故答案为27．18．（2020秋•西城区期末）如图，△ABC 是等边三角形，AD ⊥BC 于点D ，DE ⊥AC 于点E ．若AD ＝12，则DE ＝　6　；△EDC 与△ABC 的面积关系是：S △EDC S △ABC =　18　．【解题思路】由等边三角形的性质得出∠C ＝∠BAC ＝60°，由直角三角形的性质得出DE ＝6，由直角三角形的性质得出BC ＝4EC ，根据三角形的面积公式可得出答案．【解答过程】解：∵△ABC是等边三角形，∴∠C＝∠BAC＝60°，∵AD⊥BC，∴BD＝CD，∠DAC=12∠BAC＝30°，∵AD＝12，∴DE=12AD＝6；∵DE⊥AC，∴∠EDC＝90°﹣∠C＝90°﹣60°＝30°，∴EC=12 DC，∴BC＝4EC，∵S△EDC =12ED⋅EC=12×6×EC＝3EC，S△ABC=12AD×BC=12×12×BC＝6BC＝24EC，∴S△EDCS△ABC=3EC24EC=18．故答案为：6，1 8．19．（2020秋•海珠区校级期末）如图，在Rt△ABC中，∠A＝90°，∠B＝30°，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，若AN＝1，则BC的长为　6　．【解题思路】根据三角形的内角和定理求出∠ACB，根据平行线的性质求出∠AMN＝30°，根据角平分线的定义求出∠NMC＝∠ACM＝30°，根据含30°角的直角三角形的性质求出即可≤【解答过程】解：在Rt△ABC中，∠A＝90°，∠B＝30°，∴∠ACB＝60°，∵MN∥BC，∴∠AMN＝∠B＝30°，∵∠A＝90°，AN＝1，∴MN＝2AN＝2，∵MN平分∠AMC，∠AMN＝30°，∴∠AMC＝∠AMN+∠NMC＝60°∵CM平分∠ACB，∠ACB＝60°，∴∠ACM=12∠ACB＝30°，∴∠ACM＝∠NMC，∴MN＝CN＝2，∴AC＝AN+CN＝1+2＝3，∵在Rt△ABC中，∠A＝90°，∠B＝30°，∴BC＝2AC＝2×3＝6，故答案为：6．20．（2020秋•梁园区期末）如图，∠ABC＝60°，AB＝3，动点P从点B出发，以每秒1个单位长度的速度沿射线BC运动，设点P的运动时间为t秒，当△ABP是钝角三角形时，t满足的条件是　0＜t＜32或t＞6　．【解题思路】过A作AP⊥BC和过A作P'A⊥AB两种情况，利用含30°的直角三角形的性质解答．【解答过程】解：①过A作AP⊥BC时，∵∠ABC＝60°，AB＝3，∴BP=3 2，∴当0＜t＜32时，△ABP是钝角三角形；②过A作P'A⊥AB时，∵∠ABC＝60°，AB＝3，∴BP'＝6，∴当t＞6时，△ABP'是钝角三角形，故答案为：0＜t＜32或t＞6．三．解答题（共10小题）21．（2021春•渠县校级期末）如图，已知：在△ABC中，AB＝AC，∠BAC＝120°，D为BC边的中点，DE⊥AC．求证：CE＝3AE．【解题思路】连接AD，根据等腰三角形三线合一的性质可得AD⊥BC，再根据等腰三角形两底角相等求出∠C＝30°，再求出∠ADE＝30°，然后根据直角三角形30°角所对的直角边等于斜边的一半进行求解即可．【解答过程】证明：如图，连接AD，∵AB＝AC，D是BC的中点，∴AD⊥BC，∵∠BAC＝120°，AB＝AC，∴∠C=12（180°﹣120°）＝30°，∵DE⊥AC，∴∠ADE＝∠C＝30°，在Rt△ADE中，AD＝2AE，在Rt△ACD中，AC＝2AD＝4AE，∴CE＝AC﹣AE＝4AE﹣AE＝3AE，即CE＝3AE．22．（2020秋•无棣县期末）如图，在等边△ABC中，D、E分别在边BC、AC上，且DE∥AB，过点E作EF⊥DE交BC的延长线于点F．若CD＝3cm，求DF的长．【解题思路】由等边三角形性质和平行线的性质证得∠EDC＝60°，再根据利用直角三角形30°角所对的直角边等于斜边的一半即可求解．【解答过程】解：∵△ABC是等边三角形，∴∠A＝∠B＝60°，∵DE∥AB，∴∠EDC＝∠B＝60°，∠DEC＝∠A＝60°，∴△EDC是等边三角形．∴DE＝CD＝3（cm），∵EF⊥DE，∴∠DEF＝90°，∴∠F＝90°﹣∠EDC＝30°，∴DF＝2DE＝6（cm）．23．（2020秋•丰台区期中）如图，△ABC是等边三角形，BD⊥AC于点D，AE∥CB，∠AEB＝90°．求证：AE＝CD．【解题思路】由等边三角形的性质得出CD＝AD=12AB，由平行线的性质得出∠BAE＝∠ABC＝60°，则∠ABE＝30°，由直角三角形的性质得出AE=12AB，则可得出答案．【解答过程】证明：∵△ABC是等边三角形，∴∠ABC＝60°，AB＝BC＝AC，∵BD⊥AC，∴CD＝AD=12 AB，∵AE∥BC，∴∠BAE＝∠ABC＝60°，∵∠AEB＝90°，∴∠ABE＝30°，∴AE=12 AB，∴AE＝CD．24．（2020秋•温岭市期中）一艘轮船自西向东航行，在A处测得小岛P的方位是北偏东75°，航行7海里后，在B处测得小岛P的方位是北偏东60°，若小岛周围3.8海里内有暗礁，问该船一直向东航行，有无触礁的危险？并说明原因．【解题思路】作PD⊥AB，利用直角三角形性质求出PD长，和3.8海里比较即可看出船不改变航向是否会触礁．【解答过程】解：有触礁危险．理由如下：作PD⊥AB于D，∵A处测得小岛P在北偏东75°方向，∴∠PAB＝15°，∵在B处测得小岛P在北偏东60°方向，∴∠APB＝15°，∴AB＝PB＝7海里，∵∠PBD＝30°，∴PD=12PB＝3.5＜3.8，∴该船继续向东航行，有触礁的危险．25．（2020春•揭西县期末）如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB的垂直平分线分别交AB 和AC于点D，E．（1）求证：AE＝2CE；（2）连接CD，请判断△BCD的形状，并说明理由．【解题思路】（1）连接BE，由垂直平分线的性质可求得∠EBC＝∠ABE＝∠A＝30°，在Rt△BCE中，由直角三角形的性质可证得BE＝2CE，则可证得结论；（2）由垂直平分线的性质可求得CD＝BD，且∠ABC＝60°，可证明△BCD为等边三角形．【解答过程】（1）证明：连接BE，∵DE是AB的垂直平分线，∴AE＝BE，∴∠ABE＝∠A＝30°，∴∠CBE＝∠ABC﹣∠ABE＝30°，在Rt△BCE中，BE＝2CE，∴AE＝2CE；（2）解：△BCD是等边三角形，理由如下：连接CD．∵DE垂直平分AB，∴D为AB中点，∵∠ACB＝90°，∴CD＝BD，∵∠ABC＝60°，∴△BCD是等边三角形．26．（2020秋•西华县期中）如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边上的中线，且BD ＝BE，CD的垂直平分线MF交AC于F，交BC于M，MF的长为2．（1）求∠ADE的度数；（2）△ADF是正三角形吗？为什么？（3）求AB的长．【解题思路】（1）根据等腰三角形的性质和三角形内角和定理求出∠B和∠C，求出∠BDE，即可求出答案；（2）求出DF＝CF，根据等腰三角形的性质求出∠FDC＝∠C，求出∠AFD和∠DAF，根据等边三角形的判定得出即可；（3）求出CF和DF，根据等边三角形的性质求出AF，求出AC，即可求出AB．【解答过程】解：（1）∵在△ABC中，AB＝AC，∠BAC＝120°，∴∠B＝∠C=12×（180°﹣∠BAC）＝30°，∵BD＝BE，∴∠BDE＝∠BED=12×（180°﹣∠B）＝75°，∵在△ABC中，AB＝AC，AD是BC边上的中线，∴AD⊥BC，∴∠ADB＝90°，∴∠ADE＝∠ADB﹣∠BDE＝15°；（2）△ADF是正三角形，理由是：∵CD的垂直平分线MF交AC于F，交BC于M，∴DF＝CF，∵∠C＝30°，∴∠FDC＝∠C＝30°，∴∠AFD＝∠C+∠FDC＝60°，∵AD⊥BC，∴∠ADC＝90°，∴∠DAF＝90°﹣∠C＝60°，∴∠ADF＝60°，即∠FAD＝∠ADF＝∠AFD＝60°，∴△ADF是正三角形；（3）∵CD的垂直平分线MF，∴∠FMC＝90°，∵∠C＝30°，MF＝2，∴FC＝2MF＝4，∵DF＝FC，∴DF＝4，∵△ADF是等边三角形，∴AF＝DF＝4，∴AC＝AF+CF＝4+4＝8，∵AB＝AC，∴AB＝8．27．（2021秋•官渡区期末）如图，四边形ABCD中，AD＝4，BC＝1，∠A＝30°，∠B＝90°，∠ADC＝120°，求CD的长．【解题思路】先延长AD、BC交于E，根据已知证出△EDC是等边三角形，设CD＝CE＝DE＝x，根据AD＝4，BC＝1和30度角所对的直角边等于斜边的一半，求出x的值即可．【解答过程】解：延长AD、BC交于E，∵∠A＝30°，∠B＝90°，∴∠E＝60°，∵∠ADC＝120°，∴∠EDC＝60°，∴△EDC是等边三角形，设CD＝CE＝DE＝x，∵AD＝4，BC＝1，∴2（1+x）＝x+4，解得；x＝2，∴CD＝2．28．（2021春•昌图县期末）如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝4cm，动点P、Q同时从A、B两点出发，分别在AB、BC边上匀速移动，它们的速度分别为V P＝2cm/s，V Q＝1cm/s，当点P到达点B时，P、Q两点同时停止运动，设点P的运动时间为ts．（1）当t为何值时，△PBQ为等边三角形？（2）当t为何值时，△PBQ为直角三角形？【解题思路】用含t的代数式表示出BP、BQ．（1）由于∠B＝60°，当BP＝BQ时，可得到关于t的一次方程，求解即得结论；（2）分两种情况进行讨论：当∠BOP＝90°时，当∠BPQ＝90°时．利用直角三角形中，含30°角的边间关系，得到关于t的一次方程，求解得结论．【解答过程】解：在△ABC中，∵∠C＝90°，∠A＝30°，∴∠B＝60°．∵4÷2＝2，∴0≤t≤2，BP＝4﹣2t，BQ＝t.（1）当BP＝BQ时，△PBQ为等边三角形．即4﹣2t＝t．∴t=4 3．当t=43时，△PBQ为等边三角形；（2）若△PBQ为直角三角形，①当∠BQP＝90°时，BP＝2BQ，即4﹣2t＝2t，∴t＝1．②当∠BPQ＝90°时，BQ＝2BP，即t＝2（4﹣2t），∴t=8 5．即当t=85或t＝1时，△PBQ为直角三角形．29．（2021秋•禹州市期中）如图，△ABC是等边三角形，P是△ABC的角平分线BD上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q．（1）若BQ＝2，求PE的长（2）连接PF，EF，试判断△EFP的形状，并说明理由．【解题思路】（1）先根据△ABC是等边三角形，BP是∠ABC的平分线，可知∠EBP＝30°，由PE⊥AB于点E，进而可得PE=12BP，然后由线段BP的垂直平分线交BC于点F，可得BP＝2BQ＝4，进而可求PE的长；（2）由等边三角形的性质得出∠ABC＝60°，∠ABP＝∠CBD＝30°，求出∠BPE＝60°，由线段垂直平分线的性质得出FB＝FP，由等腰三角形的性质得出∠FBQ＝∠FPQ＝30°，得出∠EPF＝∠EPB+∠BPF＝90°即可．【解答过程】解：（1）∵△ABC是等边三角形，BP是∠ABC的平分线，∴∠EBP＝∠PBC＝30°，∵PE⊥AB于点E，∴∠BEP＝90°，∴PE=12 BP，∵QF为线段BP的垂直平分线，∴BP＝2BQ＝2×2＝4，∴PE=12×4＝2；（2）△EFP是直角三角形．理由如下：连接PF、EF，如图所示：∵△ABC是等边三角形，BD平分∠ABC，∴∠ABC＝60°，∠ABP＝∠CBD＝30°，∵PE⊥AB，∴∠PEB＝90°，∴∠BPE＝60°，∵FQ垂直平分线段BP，∴FB＝FP，∴∠FBQ＝∠FPQ＝30°，∴∠EPF＝∠EPB+∠BPF＝90°，∴△EFP是直角三角形．30．（2021•沙坪坝区校级二模）如图，Rt△ACB中，∠ACB＝90°，∠A＝30°，∠ABC的角平分线BE 交AC于点E．点D为AB上一点，且AD＝AC，CD，BE交于点M．（1）求∠DMB的度数；（2）若CH⊥BE于点H，证明：AB＝4MH．【解题思路】（1）根据角平分线的性质得到∠ABE＝∠CBE＝30°，根据等腰三角形的性质得到∠ACD ＝∠ADC＝75°，根据三角形的外角性质计算，得到答案；（2）根据含30度角的直角三角形的性质，等腰直角三角形的性质计算，即可证明．【解答过程】（1）解：∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BE是∠ABC的角平分线，∴∠ABE＝∠CBE＝30°，∵∠A＝30°，AC＝AD，∴∠ACD＝∠ADC＝75°，∴∠DMB＝∠ADC﹣∠ABE＝45°；（2）证明：∵∠ACB＝90°，∠A＝30°，∴AB＝2BC，∵CH⊥BE，∠CBE＝30°，∴BC＝2CH，∴AB＝4CH，在Rt△CHM中，∠CMH＝45°，∴CH＝MH，∴AB＝4MH．。