伺服电机低惯量及高惯量的区别
- 格式:docx
- 大小:9.26 KB
- 文档页数:2
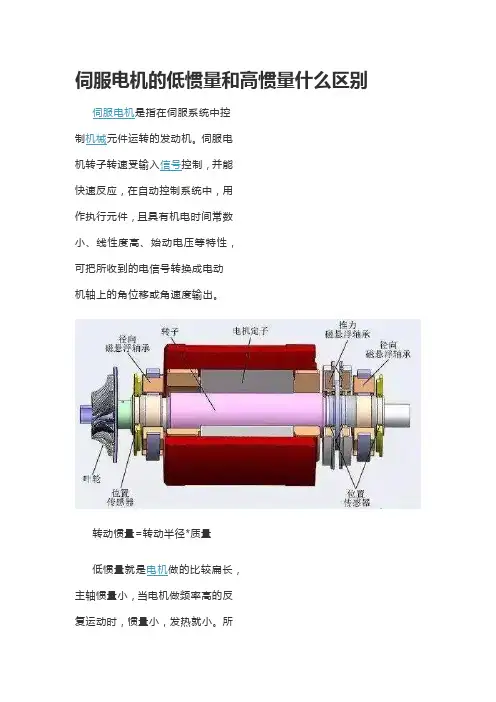
伺服电机的低惯量和高惯量什么区别伺服电机是指在伺服系统中控制机械元件运转的发动机。
伺服电机转子转速受输入信号控制,并能快速反应,在自动控制系统中,用作执行元件,且具有机电时间常数小、线性度高、始动电压等特性,可把所收到的电信号转换成电动机轴上的角位移或角速度输出。
转动惯量=转动半径*质量低惯量就是电机做的比较扁长,主轴惯量小,当电机做频率高的反复运动时,惯量小,发热就小。
所以低惯量的电机适合高频率的往复运动使用。
但是一般力矩相对要小些。
高惯量的伺服电机就比较粗大,力矩大,适合大力矩的但不很快往复运动的场合。
因为高速运动到停止,驱动器要产生很大的反向驱动电压来停止这个大惯量,发热就很大了。
惯量就是刚体绕轴转动的惯性的度量,转动惯量是表征刚体转动惯性大小的物理量。
它与刚体的质量、质量相对于转轴的分布有关。
(刚体是指理想状态下的不会有任何变化的物体),选择的时候遇到电机惯量,也是伺服电机的一项重要指标。
它指的是伺服电机转子本身的惯量,对于电机的加减速来说相当重要。
如果不能很好的匹配惯量,电机的动作会很不平稳。
一般来说,小惯量的电机制动性能好,启动,加速停止的反应很快,高速往复性好,适合于一些轻负载,高速定位的场合,如一些直线高速定位机构。
中、大惯量的电机适用大负载、平稳要求比较高的场合,如一些圆周运动机构和一些机床行业。
如果负载比较大或是加速特性比较大,而选择了小惯量的电机,可能对电机轴损伤太大,选择应该根据负载的大小,加速度的大小等等因素来选择,一般的选型手册上有相关的能量计算公式。
伺服电机驱动器对伺服电机的响应控制,最佳值为负载惯量与电机转子惯量之比为一,最大不可超过五倍。
通过机械传动装置的设计,可以使负载。
惯量与电机转子惯量之比接近一或较小。
当负载惯量确实很大,机械设计不可能使负载惯量与电机转子惯量之比小于五倍时,则可使用电机转子惯量较大的电机,即所谓的大惯量电机。
使用大惯量的电机,要达到一定的响应,驱动器的容量应要大一些。

伺服电机的转子惯量伺服电机的转子惯量是电机设计和使用中很重要的一个参数,它直接关系到电机的控制性能和响应能力。
本文将详细介绍伺服电机的转子惯量的定义、计算方法、影响因素以及优化方法。
一. 定义伺服电机的转子惯量是指电机转子固有的惯性矩,它表示电机对于转速变化所表现出的惯性特性。
一般来说,转子惯量越大,电机的响应性能越差,控制难度也越大。
二. 计算方法伺服电机转子惯量的计算可以采用多种方法,其中比较常用的方法包括动态法和静态法。
1. 动态法动态法计算转子惯量的思路是将电机加速到一定速度,然后停电,记录电机在停电后继续旋转的时间和加速度,通过运动学方程可得出电机转子的惯性矩。
公式如下:J = τ / α其中,J为转子惯量,τ为电机停电后继续旋转的转矩,α为电机停电后继续旋转的加速度。
2. 静态法静态法计算转子惯量的思路是将电机旋转到一定速度,然后施加一定大小的扭矩,记录电机的加速度和加速时间,通过牛顿第二定律可得出电机转子的惯性矩。
公式如下:J = T / (ω2 - ω1)其中,J为转子惯量,T为施加的扭矩,ω1和ω2分别为电机起始和结束的转速。
三. 影响因素伺服电机转子惯量的大小受到多种因素的影响,主要包括电机结构、材料、质量和工作状态等因素。
1. 结构电机结构的复杂度、定子和转子的形状、定位方式等因素都会影响电机转子惯量的大小。
一般来说,定子和转子的惯性矩越接近,电机转子惯量就越小。
2. 材料电机转子的材料也会对其惯性矩产生影响,一般来说,质量越大的材料转子惯量越大。
同时,材料的弹性模量、热膨胀系数等物理特性也会对电机转子惯量产生影响。
3. 质量电机转子的质量也是影响其惯性矩的一个重要因素,除了质量本身的大小外,质量的分布情况也很重要。
如果电机转子的质量分布不均匀,则转子惯量也会增加。
4. 工作状态电机的工作状态也会对其转子惯量产生影响。
不同的工作条件下,电机的转子惯量也可能会产生变化。
四. 优化方法为了优化伺服电机的转子惯量,可以采用以下方法:1. 优化材料采用质量轻、强度高的材料可以有效减小电机转子的惯性矩,提高电机的相应能力。

伺服电机惯量是什么意思伺服电机惯量是伺服电机的一项重要指标。
它指的是转子本身的惯量,对于电机的加减速来说相当重要。
惯性大小与物质质量相应惯量J= ∫r dm 其中r为转动半径,m为刚体质量惯量。
电机的转子惯量是电机本身的一个参数。
单从响应的角度来讲,电机的转子惯量应小为好。
但是,电机总是要接负载的,负载一般可分为二大类,一类为负载转矩,一类为负载惯量。
一般来说,小惯量的电机制动性能好,启动,加速停止的反应很快,适合于一些轻负载,高速定位的场合。
如果你的负载比较大或是加速特性比较大,而选择了小惯量的电机,可能对电机轴损伤太大,选择应该根据负载的大小,加速度的大小等等因素来选择,一般有理论计算公式。
伺服电机的惯量由转子自身的质量,以及外加的负载而组成。
惯量越大,物体的运动状态越不容易改变。
无论旋转运动的部件,还是直线运动的部件,都成为电机的负载惯量,它们的大小有不同的计算方法,因为计算公式较多,就不一一列举。
惯量对伺服电机运行的影响电机轴上的负载惯量大小,对电机的灵敏度和整个伺服系统的精度将产生很大的影响,通常,当负载小于电机转子惯量时,上述影响不大。
但当负载惯量达到甚至超过转子惯量的5倍时,会使伺服放大器不能在正常调节范围内工作。
所以对这类惯量应避免使用。
所以在设计负载时,应尽可能地减小体积和重量。
在伺服系统选型及调试中,常会碰到惯量问题。
其具体表现为:在伺服系统选型时,除考虑电机的扭矩和额定速度等等因素外,我们还需要先计算得知机械系统换算到电机轴的惯量,再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机;在调试时,正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。
此点在要求高速高精度的系统上表现尤为突出,这样,就有了惯量匹配的问题。
什么是“惯量匹配”?1、根据牛顿第二定律:“进给系统所需力矩T = 系统传动惯量J ×角加速度θ角”。
加速度θ影响系统的动态特性,θ越小,则由控制器发出指令到系统执行完毕的时间越长,系统反应越慢。

伺服电机惯量比小于1伺服电机惯量比小于1:探索精准控制的奇迹1. 导言在现代工业领域中,高精度和高效率的运动控制对于机械设备的性能至关重要。
而伺服电机作为一种常见的运动控制元件,其能够通过闭环控制实现高精度的位置和速度调节。
而伺服电机惯量比则是评估这种控制性能的一个重要指标。
对于伺服电机惯量比小于1的情况,其具有较低的惯量,从而能够实现更快的响应速度和更精确的位置控制。
本文将深入探讨伺服电机惯量比小于1的意义、影响因素以及应用案例,以便更全面地理解这一主题。
2. 伺服电机惯量比的定义和意义伺服电机惯量比是指电机转子惯量与负载惯量的比值。
在控制系统中,这一比值直接影响到伺服电机的动态特性。
当惯量比小于1时,即电机转子的惯量较小,相对于负载来说,电机更容易迅速响应控制信号并实现精确的位置调节。
这种控制特性是伺服电机惯量比小于1的主要意义所在。
3. 影响伺服电机惯量比的因素要实现伺服电机惯量比小于1的控制特性,有几个关键因素需要考虑和优化:3.1 电机选择与设计:选择合适的低惯量电机并进行相应的设计,以确保电机转子的惯量尽可能低。
可以通过采用轻量化的材料、优化转子形状以及减少转子和轴承的摩擦来实现。
3.2 感知与反馈:对于精确的位置调节,准确的传感器和反馈系统至关重要。
通过有效的传感器和高精度的反馈系统,可以实现对电机位置、速度和加速度等参数的实时感知和反馈,从而更好地控制电机的运动。
3.3 控制算法与参数调节:选择合适的控制算法,并通过适当的参数调节来实现对电机的精确控制。
此过程需要考虑负载特性、控制要求以及系统静态与动态响应等因素,从而优化控制算法和参数设置,以实现最佳的控制性能。
4. 伺服电机惯量比小于1的应用案例伺服电机惯量比小于1的控制特性在许多应用中都能发挥重要作用。
以下是一些常见的应用案例:4.1 机床加工:在数控机床中,伺服电机的控制性能对于实现高精度和高效率的加工至关重要。
通过采用惯量比小于1的伺服电机,可以实现更精细的位置控制,从而提高加工质量和加工效率。

在伺服系统选型及调试中,常会碰到惯量问题。
其具体表现为:在伺服系统选型时,除考虑电机的扭矩和额定速度等等因素外,我们还需要先计算得知机械系统换算到电机轴的惯量,再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机;在调试时,正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。
此点在要求高速高精度的系统上表现尤为突出,这样,就有了惯量匹配的问题。
一、什么是“惯量匹配”?1、根据牛顿第二定律:“进给系统所需力矩T = 系统传动惯量J ×角加速度θ角”。
加速度θ影响系统的动态特性,θ越小,则由控制器发出指令到系统执行完毕的时间越长,系统反应越慢。
如果θ变化,则系统反应将忽快忽慢,影响加工精度。
由于马达选定后最大输出T值不变,如果希望θ的变化小,则J应该尽量小。
2、进给轴的总惯量“J=伺服电机的旋转惯性动量JM +电机轴换算的负载惯性动量JL。
负载惯量JL由(以平面金切机床为例)工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到马达轴上的惯量组成。
JM为伺服电机转子惯量,伺服电机选定后,此值就为定值,而JL则随工件等负载改变而变化。
如果希望J变化率小些,则最好使JL所占比例小些。
这就是通俗意义上的“惯量匹配”。
二、“惯量匹配”如何确定?传动惯量对伺服系统的精度,稳定性,动态响应都有影响。
惯量大,系统的机械常数大,响应慢,会使系统的固有频率下降,容易产生谐振,因而限制了伺服带宽,影响了伺服精度和响应速度,惯量的适当增大只有在改善低速爬行时有利,因此,机械设计时在不影响系统刚度的条件下,应尽量减小惯量。
衡量机械系统的动态特性时,惯量越小,系统的动态特性反应越好;惯量越大,马达的负载也就越大,越难控制,但机械系统的惯量需和马达惯量相匹配才行。
不同的机构,对惯量匹配原则有不同的选择,且有不同的作用表现。
不同的机构动作及加工质量要求对JL与JM大小关系有不同的要求,但大多要求JL与JM的比值小于十以内。

伺服惯量
伺服惯量指的是伺服电机在转动过程中产生的惯量,它是由电机的转子、机械传动系统和负载的惯量组成。
具体来说,伺服惯量的大小取决于电机的转子惯量和机械传动系统的惯量。
对于高速高精度的系统,需要特别关注惯量匹配问题。
因为如果伺服电机的转动惯量与负载的转动惯量不匹配,可能会导致系统动态特性不佳,定位精度下降,甚至出现振荡等问题。
此外,对于不同负载情况,伺服电机的转动惯量可能会有不同的影响。
例如,在高速往复运动的场合,需要选择转动惯量较小的伺服电机,以减小负载惯量对系统的影响。
而在需要平稳运行的场合,需要选择转动惯量较大的伺服电机,以减小机械系统的振动和噪声。
因此,在实际应用中,需要根据具体的负载情况和系统要求,选择合适的伺服电机和传动系统,以获得最佳的系统性能。

伺服电机惯量伺服电机是一种将电能转化为机械能的装置,具有较高的精度和可控性。
而惯量则是伺服电机的一个重要参数,它描述了电机在转动过程中的惯性特性,对于电机的动态响应和控制性能有着重要影响。
惯量是指物体对于改变自身运动状态的抵抗能力,可以通过物体的质量和几何形状来计算。
对于伺服电机而言,惯量的计算是十分复杂的,需要考虑到电机的转子、定子和传动系统等多个组成部分的质量和几何参数。
伺服电机的转子是主要质量集中的部分,它由磁钢、线圈和轴等组成。
转子的质量决定了电机惯量的大小,质量越大,惯量也就越大。
此外,转子的几何形状也会对惯量产生影响,比如转子的半径、长度等参数。
伺服电机的定子也会对惯量产生一定影响。
定子是电机的固定部分,它由铁芯和线圈等组成。
定子的质量和几何形状也会对惯量产生影响,但相对于转子而言,定子的贡献较小。
伺服电机的传动系统也是影响惯量的重要因素。
传动系统通常由减速器和传动轴等组成,它们的质量和几何形状也会对惯量产生影响。
减速器的减速比越大,传动轴的长度越长,惯量也就越大。
伺服电机的惯量对于其动态响应和控制性能有着重要影响。
惯量越大,电机的加速和减速过程就会越慢,对于频繁改变运动状态的应用场景,惯量较小的电机更加适用。
而在对位置和速度要求较高的应用场景,惯量较大的电机更加稳定可靠。
为了降低伺服电机的惯量,可以采取以下措施:1. 选择轻量化的材料:使用轻质材料来制造电机的转子和定子,可以有效减小质量,从而减小惯量。
2. 优化结构设计:通过优化电机的结构设计,减少不必要的质量,降低惯量。
例如,可以采用空心结构或镂空设计来减小转子和定子的质量。
3. 使用高效减速器:选择高效的减速器可以实现较大的减速比,从而减小传动系统的惯量。
同时,减速器的结构设计也要考虑减小自身质量和惯量。
总的来说,伺服电机的惯量是影响其动态响应和控制性能的重要参数。
通过合理选择材料、优化结构设计以及使用高效减速器等措施,可以降低电机的惯量,提高其控制性能和运动精度。



1、机电领域中伺服电机的选择原则现代机电行业中经常会碰到一些复杂的运动,这对电机的动力荷载有很大影响。
伺服驱动装置是许此,伺服电机的选择就变得尤为重要。
首先要选出满足给定负载要求的电动机,然后再从中按价格济指标选择最适合的电机。
各种电机的T- 曲线(1)传统的选择方法这里只考虑电机的动力问题,对于直线运动用速度v(t),加速度a(t)和所需外力F(t)速度 (t),角加速度 (t)和所需扭矩T(t)表示,它们均可以表示为时间的函数,与其他因素无关率P电机,最大应大于工作负载所需的峰值功率P峰值,但仅仅如此是不够的,物理意义上的功率但在实际的传动机构中它们是受限制的。
用峰值,T峰值表示最大值或者峰值。
电机的最大速度限,n上限= 峰值,最大/ 峰值,同样,电机的最大扭矩决定了减速比的下限,n下限=T峰值/T电大于n上限,选择的电机是不合适的。
反之,则可以通过对每种电机的广泛类比来确定上下限之间用峰值功率作为选择电机的原则是不充分的,而且传动比的准确计算非常繁琐。
(2)新的选择方法一种新的选择原则是将电机特性与负载特性分离开,并用图解的形式表示,这种表示方法使得驱动同系统间的比较更方便,另外,还提供了传动比的一个可能范围。
这种方法的优点:适用于各种负的特性分离开;有关动力的各个参数均可用图解的形式表示并且适用于各种电机。
因此,不再需要机是否能够驱动某个特定的负载。
在电机和负载之间的传动比会改变电机提供的动力荷载参数。
比如,一个大的传动比会减小外部扭而且,为输出同样的运动,电机就得以较高的速度旋转,产生较大的加速度,因此电机需要较大的适的传动比就能平衡这相反的两个方面。
通常,应用有如下两种方法可以找到这个传动比n,它会地协调起来。
一是,从电机得到的最大速度小于电机自身的最大速度电机,最大;二是,电机任机额定扭矩M额定。
2、一般伺服电机选择考虑的问题(1)电机的最高转速电机选择首先依据机床快速行程速度。
快速行程的电机转速应严格控制在电机的额定式中,为电机的额定转速(rpm);n为快速行程时电机的转速(rpm);为直线运行速度(m/min 电机/n丝杠;丝杠导程(mm)。
伺服电机高低惯量的区别伺服电机是一种专门用来控制运动的电机,广泛应用于工业自动化、机器人、数控设备等领域。
在选择伺服电机时,一个重要的考虑因素就是其高低惯量。
高低惯量对于伺服电机的性能和适用场景有着重要的影响。
我们来了解一下什么是惯量。
惯量是物体抵抗改变其运动状态的性质,可以理解为物体在运动中的惯性大小。
在电机中,惯量通常指转动惯量,即转动质量的大小。
惯量越大,电机转动的惯性越大,需要更大的力矩才能改变其运动状态。
高低惯量对于伺服电机的影响主要体现在以下几个方面:1. 响应速度:惯量越大,伺服电机的响应速度越慢。
这是因为惯量大的电机需要更长的时间才能改变其运动状态,需要更大的力矩才能加速或减速。
因此,在需要快速响应的场景下,低惯量的伺服电机更加适用。
2. 控制精度:惯量越大,伺服电机的控制精度越高。
这是因为惯量大的电机具有更强的稳定性和抗干扰能力,可以更精确地控制运动状态。
在需要高精度控制的场景下,高惯量的伺服电机更加适用。
3. 能耗效率:惯量越大,伺服电机的能耗越高。
这是因为惯量大的电机需要更大的力矩才能改变其运动状态,因此消耗的能量更多。
在需要节能环保的场景下,低惯量的伺服电机更加适用。
4. 负载能力:惯量越大,伺服电机的负载能力越强。
这是因为惯量大的电机具有更大的惯性,可以更好地抵抗外部负载的影响。
在需要承载大负载的场景下,高惯量的伺服电机更加适用。
除了以上几点,高低惯量还会影响伺服电机的动态响应和稳定性。
惯量越大,电机的动态响应越慢,即速度和位置变化的速度越慢。
而惯量小的电机则可以更快地响应变化。
另外,高低惯量还会影响电机的振动和噪音水平。
惯量大的电机由于惯性大,通常会有更大的振动和噪音。
伺服电机的高低惯量对于其性能和适用场景有着重要的影响。
在选择伺服电机时,需要根据具体的应用需求来确定惯量的大小。
如果需要快速响应、高精度控制和节能环保,可以选择低惯量的伺服电机;如果需要承载大负载和稳定性较高,可以选择高惯量的伺服电机。
“旺材电机与电控”提醒您不要走开,文末有福利!在伺服系统选型及调试中,常会碰到惯量问题。
其具体表现为:在伺服系统选型时,除考虑电机的 扭矩和额定速度等等因素外,我们还需要先计算得知机械系统换算到电机轴的惯量,再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机;在调试时,正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。
此点在要求高速高精度的系统上表现尤为突出,这样,就有了惯量匹配的问题。
一、什么是“惯量匹配”?1、根据牛顿第二定律:“进给系统所需力矩T = 系统传动惯量J × 角加速度θ角”。
加速度θ影响系统的动态特性,θ越小,则由控制器发出指令到系统执行完毕的时间越长,系统反应越慢。
如果θ变化,则系统反应将忽快忽慢,影响加工精度。
由于马达选定后最大输出T值不变,如果希望θ的变化小,则J应该尽量小。
2、进给轴的总惯量“J=伺服电机的旋转惯性动量JM + 电机轴换算的负载惯性动量JL 。
负载惯量JL由(以平面金切机床为例)工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到马达轴上的惯量组成。
JM为伺服电机转子惯量,伺服电机选定后,此值就为定值,而JL则随工件等负载改变而变化。
如果希望J变化率小些,则最好使JL所占比例小些。
这就是通俗意义上的“惯量匹配”。
二、“惯量匹配”如何确定?传动惯量对伺服系统的精度,稳定性,动态响应都有影响。
惯量大,系统的机械常数大,响应慢,会使系统的固有频率下降,容易产生谐振,因而限制了伺服带宽,影响了伺服精度和响应速度,惯量的适当增大只有在改善低速爬行时有利,因此,机械设计时在不影响系统刚度的条件下,应尽量减小惯量。
衡量机械系统的动态特性时,惯量越小,系统的动态特性反应越好;惯量越大,马达的负载也就越大,越难控制,但机械系统的惯量需和马达惯量相匹配才行。
不同的机构,对惯量匹配原则有不同的选择,且有不同的作用表现。
电机招聘专家所谓的PUU (Pulse of User Unit)使用者单位,為一个经过电子齿轮比的使用者单位,这样的设计,可以让使用者不必自行转换外部实际物理Encoder回授量与电子齿轮间的关係。
例如:ASDA-A2的encoder,每转一圏,物理量将回授1280000个脉波,如果想要改变马逹走一圏时的回授脉波数,例如100000个脉波当作一圏,则可以设P1-44(N) =128;P1-45(M) =10,当马逹转完一圏时,ASDA-A2会收到100000个脉波,这个经过电子齿轮比运算的100000,其单位即為PUU,如果要在控制器内部下逹马逹走两圏的命令时,只需根据所定义的PUU下200000个PUU命令,控制器内部会自动换回其实际的物理量,这个用法狠直觉,下图為其运算原理。
一般一直认為同样的负载、同样的惯量(切刀伺服),使用同等转速的2kW马达,惯量比大的马达应该只有好处没有坏处,但事实上在实验过程中发现:切刀驱动不换,原来使用130框号, 2kW的马达,负载率约120 ~ 140%,负载惯量比1%的马达总是过热,因此当尝试将马达更换為180框号, 2kW,结果换上去后发现速度只要开到800r/min,就会发生ALE02(过电压)或ALE05(回生异常)警示。
两台马达的扭力是一样的,但是原来使用130框号, 2kW的马达,当转速达到1200r/min才会达到极限。
从这个例子来看,并不是马达惯量越大越好,那麼请问在那些应用场合下惯量比发挥的作用影响大,那些应用场合下扭力的影响大?1. 并不是高惯量就一定好,低惯量就一定差,要看其应用场合。
T= I x α(扭力= 惯量x 角加速度) P= T x ω(功率= 扭力x 角速度) P = I x αx ω所以,同样的功率之下,若惯量提升,加速度必下降,即加减速的特性变差了,当然,角速度也会相对变化,在此我们先假设其运转速度不变。
I是固定的,当一个系统设定好后(如飞刀系统,因為飞刀不变,但如果用於输送带,惯量则会变,当输送带上的物品变多时,拖的力量需加大)。
伺服电机的惯量指的的是什么?在伺服系统选型及调试中,常会碰到惯量问题。
其具体表现为:在伺服系统选型时,除考虑电机的扭矩和额定速度等等因素外,我们还需要先计算得知机械系统换算到电机轴的惯量,再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机;在调试时,正确设定惯量比参数是充分发挥机械及伺服系统效能的前提。
此点在要求高速高精度的系统上表现尤为突出,这样,就有了惯量匹配的问题。
一、“惯量匹配”是什么1、根据牛顿第二定律:“进给系统所需力矩T=系统传动惯量J×角加速度θ角”。
加速度θ影响系统的动态特性,θ越小,则由控制器发出指令到系统执行完毕的时间越长,系统反应越慢。
如果θ变化,则系统反应将忽快忽慢,影响加工精度。
由于马达选定后输出T值不变,如果希望θ的变化小,则J应该尽量小。
2、进给轴的总惯量“J=伺服电机的旋转惯性动量JM+电机轴换算的负载惯性动量JL。
负载惯量JL由(以平面金切机床为例)工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到马达轴上的惯量组成。
JM为伺服电机转子惯量,伺服电机选定后,此值就为定值,而JL则随工件等负载改变而变化。
如果希望J变化率小些,则使JL所占比例小些。
这就是通俗意义上的“惯量匹配”。
二、如何确定“惯量匹配”传动惯量对伺服系统的精度,稳定性,动态响应都有影响。
惯量大,系统的机械常数大,响应慢,会使系统的固有频率下降,容易产生谐振,因而限制了伺服带宽,影响了伺服精度和响应速度,惯量的适当增大只有在改善低速爬行时有利,因此,机械设计时在不影响系统刚度的条件下,应尽量减小惯量。
衡量机械系统的动态特性时,惯量越小,系统的动态特性反应越好;惯量越大,马达的负载也就越大,越难控制,但机械系统的惯量需和马达惯量相匹配才行。
不同的机构,对惯量匹配原则有不同的选择,且有不同的作用表现。
不同的机构动作及加工质量要求对JL与JM大小关系有不同的要求,但大多要求JL与JM的比值小于十以内。
伺服电机高低惯量的区别以伺服电机高低惯量的区别为标题,本文将从以下几个方面进行阐述:伺服电机的概念及应用、高低惯量的定义与作用、高低惯量对伺服电机性能的影响、如何选择适合的高低惯量等。
一、伺服电机的概念及应用伺服电机是一种能够根据外部信号控制自身运动的电机。
它通过传感器感知负载的位置、速度和加速度等参数,并通过控制器对电机施加适当的控制信号,使电机能够精确地跟踪和控制负载的运动状态。
伺服电机广泛应用于自动化设备、机械加工、机器人、医疗设备等领域。
二、高低惯量的定义与作用惯量是物体抵抗改变其运动状态的性质。
在伺服电机中,惯量反映了电机转动过程中抵抗改变转动状态的能力。
高低惯量分别指的是电机转子惯量和负载惯量的大小。
高惯量意味着电机的转子和负载惯量较大,低惯量则相反。
高低惯量对伺服电机的性能影响很大。
高惯量电机转动惯性大,转动时需要较大的力矩来克服惯性,因此响应速度较慢。
而低惯量电机转动惯性小,转动时需要较小的力矩,响应速度较快。
高低惯量还与电机的精度、稳定性、动态响应等性能指标密切相关。
三、高低惯量对伺服电机性能的影响1. 动态响应:高低惯量对伺服电机的动态响应速度有直接影响。
高惯量电机惯性大,转动起来比较缓慢,响应速度较慢;而低惯量电机惯性小,转动起来比较迅速,响应速度较快。
2. 精度:高低惯量对伺服电机的定位精度有一定的影响。
高惯量电机由于惯性大,容易产生回差,导致定位精度下降;而低惯量电机惯性小,定位精度相对较高。
3. 稳定性:高低惯量也会影响伺服电机的稳定性。
高惯量电机转动惯性大,抵抗外部干扰能力强,稳定性较好;而低惯量电机转动惯性小,对外部干扰较为敏感,稳定性相对较差。
四、如何选择适合的高低惯量在选择伺服电机的高低惯量时,需要根据具体应用需求来进行选择。
一般来说,如果应用场景对动态响应速度要求较高,可以选择低惯量电机;如果应用场景对定位精度要求较高,可以选择高惯量电机。
同时还需要考虑负载的惯性大小,以及电机本身的功率和转速等参数。
伺服电机低惯量及高惯量的区别
摘要: 转动惯量=转动半径*质量低惯量就是电机做的比较扁长,主轴惯量小,当电机做频率高的反复运动时,惯量小,发热就小。
所以低惯量的电机适合高频率的往复运动使用。
但是一般力矩相对要小些。
高惯量的伺服电机就比较粗...
转动惯量=转动半径*质量
低惯量就是电机做的比较扁长,主轴惯量小,当电机做频率高的反复运动时,惯量小,发热就小。
所以低惯量的电机适合高频率的往复运动使用。
但是一般力矩相对要小些。
高惯量的伺服电机就比较粗大,力矩大,适合大力矩的但不很快往复运动的场合。
因为高速运动到停止,驱动器要产生很大的反向驱动电压来停止这个大惯量,发热就很大了。
惯量就是刚体绕轴转动的惯性的度量,转动惯量是表征刚体转动惯性大小的物理量。
它与刚体的质量、质量相对于转轴的分布有关。
(刚体是指理想状态下的不会有任何变化的物体),选择的时候遇到电机惯量,也是伺服电机的一项重要指标。
它指的是伺服电机转子本身的惯量,对于电机的加减速来说相当重要。
如果不能很好的匹配惯量,电机的动作会很不平稳.
一般来说,小惯量的电机制动性能好,启动,加速停止的反应很快,高速往复性好,适合于一些轻负载,高速定位的场合,如一些直线高速定位机构。
中、大惯量的电机适用大负载、平稳要求比较高的场合,如一些圆周运动机构和一些机床行业。
如果负载比较大或是加速特性比较大,而选择了小惯量的电机,可能对电。