华东师大版八年级下册17.3.3一次函数的性质

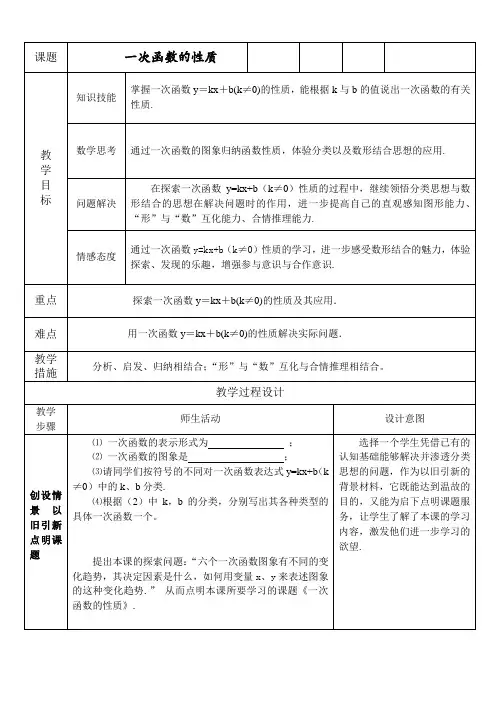
2019-2020学年八年级数学下册 17.3.3 一次函数的性质教案 华东师大版教学目标知识与技能：重点：掌握一次函数y ＝kx ＋b (k ≠0)的性质. 利用一次函数的有关性质解决有关问题。

难点:探索一次函数图象的性质。

感受一次函数中k 与b 的值对函数性质的影响。

过程与方法：实践探究、 讲练结合。

情感态度与价值观：通过师生共同交流、探讨，使学生在掌握知识的基础上，引导学生通过分析、归纳，培养学生用类比的方法探索新知识的能力。

教学过程一、知识链接：1、在同一直角坐标系中，画出正比例函数x y 5.0=，x y 5.0-=,y=x; y=-x ;的图象。

二、新课导学1.）观察图象、研究性质提出问题1：观察图像探究正比例函数)0,(≠=k k kx y 为常数中，k 对函数图象有何影响？y 随x 的变化的趋势？并填写实验报告填写实验报告如下：实验报告：k 对正比例函数)0,(≠=k k kx y 为常数的图象的影响1,0.5,0.5,1,k =--引导学生观察正比例)0,(≠=k k kx y 为常数的图象的变化并归纳出它的性质： 当0>k 时，图象在 象限，y 随x 的增大而 ； 当0<k 时，图象在 象限，y 随x 的增大而 。

2.）类比联想、探索性质1.在同一直角坐标系中，画出函数112y x=+和y＝x-2的图象.问题1;观察，分析函数y＝12x＋l和y＝x-2图象经过几个象限？有何变化规律？生:讨论、交流,并举手逐个回答,不断补充完善.在自主探索的基础上合作交流.观察图象发现在直线112y x=+和y＝x-2上，当一个点在直线上从左向右移动时，（即自变量x从小到大时），点的位置也在逐步从低到高变化（函数y的值也从小变到大）.即：函数值y随自变量x的增大而增大.上述两条直线都经过一、三象限．又由于直线与y轴的交点坐标是(0,b)所以，当b＞0时，直线与x轴的交点在y轴的正半轴，也称在x轴的上方；当b＜0时，直线与x轴的交点在y轴的负半轴，也称在x轴的下方．所以当k＞0,b≠0时，直线经过一、三、二象限或一、三、四象限.问题2、画出函数y＝－x＋2和y＝－x－1的图象。

一次函数的性质多媒体教 学目 标掌握一次函数y ＝kx ＋b(k ≠0)的性质. 利用一次函数的有关性质解决有关问题。

一次函数性质的探索、语言的准确描述、归纳总结及逐步培养学生从特殊到一般、一、提出问题： 1. 小明家离学校2千米，小明骑自行车的速度平均每小时10千米， （1）他离家的距离s （千米）与时间t （小时）的函数关系式为： （2）他离学校的距离s （千米）与时间t （小时）的函数关系式为： 2. 一次函数图象是怎样的？一般情况下我们画一次函数y ＝kx ＋b(k ≠0)的图象，取哪两个点比较简便？ 二、知识探究：在同一直角坐标系中，画出函数132+=x y 和y ＝3x -2的图象.问： 1.在你所画的一次函数图象中，直线经过几个象限. 2.观察图象直线132+=x y ，当一个点在直线上从左向右移动时，（即自变量x 从小到大时），这个点的位置发生怎样变化？ 即：函数值y 随自变量x 的增大而 . x 132+=x y xy ＝3x -2x探究：在同一坐标系中，画出函数y ＝-x ＋2和123--=x y 的图象。

根据上面分析的过程，请同学们研究这两个函数图象是否也有相应的性质？你能发现什么规律？ 即：函数值y 随自变量x 的增大而 . 一次函数y ＝kx ＋b 有下列性质： 例1. 已知一次函数y ＝(1-2m )x ＋m -1，若函数y 随x 的增大而减小，并且函数的图象经过二、三、四象限,求m 的取值范围. （变形：函数的图象经过二、三、四象限改为不经过第一象限或 图象与y 轴交点在x 轴下方呢？） 例2. 画出函数y ＝-2x ＋2的图象，结合图象回答下列问题：(1)这个函数中，随着x 的增大，y 将增大还是减小？它的图象从左到右怎样变化？(2)当x 取何值时，y ＝0? (3)当x 取何值时，y ＞0？（0<y <1？） 课堂练习：y ＝-x ＋2xy=123--x x y ＝-2x ＋2。

17.3.3一次函数的性质一、做一做：分别在同一个坐标系中作出下列函数的图象：①y= x+1 ，y=3x+2 , y= x+2 ②y=- x-1 ，y=-x+2 , y=-3x-2 ③y=x-2 ，y= x+1 , y=2x+1 ④y=- x+2 ，y=-2x-1 , y=- x+1二、观察：观察①③这三组函数的图象发现：1、直线从左到右 (“上升”还是“下降”)。

2、当一个点在直线上从左向右移动，它的位置也在逐步从低到 变化；3、自变量x 的值从小到大变化时，函数y 的值也随之从 到 变化。

也就是说，函数值y 随自变量x 的增大而 。

三、探索：再观察 ②④两组函数的图象，你能得到类似的结论吗？ 请从以下几个方面作研究：1、直线从左到右的变化趋势。

2、当一个点在直线上从左向右移动时，它的位置高低变化情况3221232321323、自变量x 的值从小到大变化时，函数值y 如何变化得出性质，函数值y 随自变量x 如何变化四、观察并思考：分别观察①③和②④两组函数图象，思考：1、函数和函数图象有哪些异同？2、你得出的性质有何异同？3、这些异同跟k 或b 的值有关系吗？五、概括：当k＞0时，y随x的增大而增大，这时函数的图象从左到右上升；当k＜0时，y随x的增大而减小，这时函数的图象从左到右下降。

六、试一试，你能行：画出函数y=-2x+2的图象，结合图象回答下列问题：⑴这个函数中，随着自变量x的增大，函数值y是增大还是减小？它的图象从左到右怎样变化？⑵当x取何值时，y=0？⑶当x取何值时，y＞0？七、练习：已知函数y=(m-3)x-2 (m是常数)，回答下列问题：⑴当m取何值时，y随x的增大而增大？⑵当m取何值时，y随x的增大而减小？八、练习：1、已知点(-1, a)和点(2 , b)都在直线y= -2x+3上，试比较a和b的大小。

2、已知点(-1, a)和点(2 , b)都在直线y=(m2+1)x+n 上，试比较a和b的大小。

17.3.3一次函数的性质知识点梳理1、正比例函数的图像及性质正比例函数是一条过原点的直线①K>0, 函数图像过一、三象限，y 随x 的增大而增大； 函数图像从左到右上升； 字母表述：k>0, 当x 1>x 2时，y 1>y 2②K<0, 函数图像过二、四象限，y 随x 的增大而减小；函数图像从左到右下降； 字母表述：k<0, 当x 1<x 2时，y 1<y 22、一次函数的图像及性质①K>0, b>0函数图像过一、二、三象限，交于y 轴正半轴，y 随x 的增大而增大； ②K>0, b<0函数图像过一、三、四象限，交于y 轴负半轴，y 随x 的增大而增大； ③K<0, b>0函数图像过一、二、四象限，交于y 轴正半轴，y 随x 的增大而减小； ④K<0, b<0函数图像过二、三、四象限，交于y 轴负半轴，y 随x 的增大而减小；典例精析1．关于 一次函数31y x =-+，下列结论不正确的是（ ） A ．图象与直线3y x =-平行 B ．图象与y 轴的交点坐标是()01， C ．图象经过第一、二、四象限D ．y 随自变量x 的增大而增大2．关于一次函数12y x =-，下列说法正确的是（ ） A ．它的图象过点(1,2)- B ．它的图象经过第一、二、三象限 C ．y 随x 的增大而增大D ．当0x >时，总有1y <3．下列函数的图象经过（0，1），且y 随x 的增大而减小的是（ ） A ．y=一xB ．y=x-1C ．y=2x+1D ．y=一x+14．下列描述一次函数y=－2x+5图象性质错误的是（ ） A ．y 随x 的增大而减小 B ．直线经过第一、二、四象限 C ．直线从左到右是下降的D ．直线与x 轴交点坐标是（0，5）5．如图，一次函数y=kx+b 图象与x 轴的交点坐标是（2，0），则下列说法：①y 随x 的增大而减小；②b＞0；③关于x 的方程kx+b=0的解为x=2．其中说法正确的是（ ）A ．①和②B ．①和③C ．②和③D ．①②③都正确6．已知正比例函数y=(k+5)x ，且y 随x 的增大而减小，则k 的取值范围是( ) A ．k>5B ．k<5C ．k>−5D ．k<−57．一次函数y =kx ﹣1的图象经过点P ，且y 的值随x 值的增大而增大，则点P 的坐标可以为（ ） A ．()5,3- B ．(2,3)-C ．(2,2)D ．(3,1)-8．一次函数的图象过点（0,2），且随的增大而增大，则m=（ ）A ．-1B ．3C ．1D ．-1或39．已知正比例函数y =（1﹣m ）x 的图象过二、四象限，则m 的取值范围是（ ） A ．m ＜1B ．m ＞1C ．m ≤1D ．m ≥110．若2y kx =+的函数值y 随着x 的增大而增大，则k 的值可能是（ ） A ．0B ．1C ．-3D ．-211．已知P 1（﹣1，y 1），P 2（2，y 2）是一次函数y ＝﹣x+1图象上的两个点，则y 1，y 2的大小关系是（ ） A ．y 1＝y 2B ．y 1＜y 2C ．y 1＞y 2D ．不能确定12．已知点M (1，a )和点N (2，b )是一次函数y =－2x ＋1图象上的两点，则a 与b 的大小关系是( ) A ．a ＞bB ．a =bC ．a ＜bD ．以上都不对13．下列函数的图象不经过第三象限，且y 随x 的增大而减小的是（ ） A ．31y x =-+B ．31y x =--C ．31yx D ．31y x =-14．下列函数的图象经过()0,1，且y 随x 的增大而减小的是（ ）A ．y x =-B ．1y x =-C ．21y x =+D ．1y x =-+15．若正比例函数y ＝(1－2m)x 的图象经过点A(x 1，y 1)和点B(x 2，y 2)，当x 1＜x 2时，y 1＞y 2，则m 的取值范围是（ ）A ．m ＜0B ．m ＞0C ．m ＜12D ．m ＞1216．已知正比例函数y=kx(k≠0)的函数值y 随x 的增大而减小，则函数y=kx ﹣k 的图象大致是( )A ．B ．C ．D ．17．若0mn >，则一次函数y mx n =+的图象一定过（ ） A ．第一、二象限B ．第二、三象限C ．第二象限D ．第四象限18．当k ＜0时，一次函数y=kx ﹣k 的图象不经过（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限19．一次函数y ＝﹣bx ﹣k 的图象如下，则y ＝﹣kx ﹣b 的图象大致位置是（ ）A ．B ．C ．D ．20．已知点(k ，b)为第二象限内的点，则一次函数y kx b =-+的图象大致是( )A ．B ．C ．D ．21．当a ＜0，b ＞0函数y ＝ax +b 与y ＝bx +a 在同一平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．22．已知函数()315y m x m =-++. （1）若函数图象经过原点，求m 的值；（2）若这个函数是一次函数，且y 随着x 的增大而减小，求m 的取值范围.23．已知一次函数()226y k x k =--+. (1)k 满足何条件时，y 随x 的增大而减小； (2)k 满足何条件时，图像经过第一、二、四象限； (3)k 满足何条件时，它的图像与y 轴的交点在x 轴的上方.24．已知函数()13y m x m =++-． （1）若函数图象经过原点，求m 的值；（2）若函数图象与y 轴交点的纵坐标为2-，求m 的值；（3）若这个函数是一次函数，且y 随x 的增大而减小，求m 的取值范围； （4）若这个函数是一次函数，且图象不经过第二象限，求m 的取值范围．25．已知一次函数()()21y m x m =++-，若y 随x 的增大而减小，且该函数图象与x 轴的交点在原点右侧，求m 的取值范围。