模糊综合评价法与例题
- 格式:ppt
- 大小:1.43 MB
- 文档页数:51

关于模糊综合评价的矩阵算法:1、按模糊矩阵运算(培训教材课堂上的例题):a、权重系数会事先给出,由此会得出集合A = [ 0.2, 0.2, 0.2, 0.4 ]b、指标集和评价集按下式列出,代入数据表示成集合R评价集V1V2V3V4V5指U10 0.1 0.2 0.3 0.4标U2 0.1 0.1 0.4 0.2 0.2 代入数据表示成集U3 0 0.1 0.2 0.6 0.1U4 0 0.2 0.5 0.3 0C、综合评价集合的计算B=A·R即用集合A中第一个数和集合R中的沿第一列方向的第一个数模糊相乘(0.2︿0),然后再模糊相加(﹀)集合A中第二个数和集合R中的沿第一列方向的第二个数模糊相乘(0.2︿0.1),依次类推得到下式(0.2︿0)﹀(0.2︿0.1) ﹀(0.2︿0) ﹀(0.4︿0)按相乘取小,相加取大得出= 0 ﹀0.1﹀0 ﹀0 = 0.1然后再用集合A中第一个数和集合R中的沿第二列方向的第一个数模糊相乘(0.2︿0.1),然后再模糊相加(﹀)集合A中第二个数和集合R中的沿第二列方向的第二个数模糊相乘(0.2︿0.1),依次类推得到下列各算式,按相乘取小,相加取大得出各数值(0.2︿0.1)﹀(0.2︿0.1)﹀(0.2︿0.1)﹀(0.4︿0.2)= 0.2(0.2︿0.2)﹀(0.2︿0.4)﹀(0.2︿0.2)﹀(0.4︿0.5)= 0.4(0.2︿0.3)﹀(0.2︿0.2)﹀(0.2︿0.6)﹀(0.4︿0.3)= 0.3(0.2︿0.4)﹀(0.2︿0.2)﹀(0.2︿0.1)﹀(0.4︿0)= 0.2即A·R = [ 0.1, 0.2, 0.4, 0.3, 0.2 ]归一化:[0.1/1.2, 0.2/1.2, 0.4/1.2, 0.3/1.2, 0.2/1.2]= [ 0.083, 0.167,0.333,0.250,0.167 ]2、按经典矩阵运算(新第二版教材上的例题):a、权重系数会事先给出,由此会得出集合A = [ 0.2, 0.2, 0.2, 0.4 ]b、指标集和评价集按下式列出,代入数据表示成集合R评价集V1V2V3V4V5指U10 0.1 0.2 0.3 0.4标U2 0.1 0.1 0.4 0.2 0.2 代入数据表示成集U3 0 0.1 0.2 0.6 0.1U4 0 0.2 0.5 0.3 0C、综合评价集合的计算B=A·R即用集合A中第一个数和集合R中的沿第一列方向的第一个数相乘0.2×0,然后再相加(+)集合A 中第二个数和集合R中的沿第一列方向的第二个数相乘0.2×0.1,依次类推得到下式(0.2×0)+(0.2×0.1)+(0.2×0 )+(0.4×0)=0.02然后再用集合A中第一个数和集合R中的沿第二列方向的第一个数相乘0.2×0.1,然后再相加(+)集合A中第二个数和集合R中的沿第二列方向的第二个数相乘0.2×0.1,依次类推得到下列各算式及值(0.2×0.1)+(0.2×0.1)+(0.2×0.1)+(0.4×0.2)= 0.14(0.2×0.2)+(0.2×0.4)+(0.2×0.2)+(0.4×0.5)= 0.36(0.2×0.3)+(0.2×0.2)+(0.2×0.6)+(0.4×0.3)= 0.34(0.2×0.4)+(0.2×0.2)+(0.2×0.1)+(0.4×0)= 0.14即A·R = [ 0.02, 0.14, 0.36,0.34, 0.14](因0.02+0.14+0.36+0.34+0.14=1,无需再归一化)3、考试时采用模糊矩阵运算,因教材上给出的全是模糊矩阵运算公式,而此节讲的又是模糊理论方法,理应采用模糊矩阵运算,但不知为啥教材上用经典矩阵计算。

模糊综合评价模型模糊综合评价模型(Fuzzy Synthetic Evaluation Model)目录[隐藏]1 什么是模糊综合评价模型?2 模糊评价的基本思想3 模糊综合评价模型类别[1]o 3.1 模糊评价基本模型o 3.2 置信度模糊评价模型4 模糊综合评价模型的运用5 模糊综合评价模型案例分析o 5.1 案例一:模糊综合评价模型在企业跨国并购风险评价中的应用[2]6 参考文献[编辑]什么是模糊综合评价模型?模糊综合评价方法是模糊数学中应用的比较广泛的一种方法。
在对某一事务进行评价时常会遇到这样一类问题,由于评价事务是由多方面的因素所决定的,因而要对每一因素进行评价;在每一因素作出一个单独评语的基础上,如何考虑所有因素而作出一个综合评语,这就是一个综合评价问题。
[编辑]模糊评价的基本思想许多事情的边界并不十分明显,评价时很难将其归于某个类别,于是我们先对单个因素进行评价,然后对所有因素进行综合模糊评价,防止遗漏任何统计信息和信息的中途损失,这有助于解决用“是”或“否”这样的确定性评价带来的对客观真实的偏离问题。
[编辑]模糊综合评价模型类别[1][编辑]模糊评价基本模型设评判对象为P: 其因素集 ,评判等级集。
对U中每一因素根据评判集中的等级指标进行模糊评判,得到评判矩阵:(1)其中,r ij表示u i关于v j的隶属程度。
(U,V,R) 则构成了一个模糊综合评判模型。
确定各因素重要性指标(也称权数)后,记为,满足,合成得(2)经归一化后,得 ,于是可确定对象P的评判等级。
[编辑]置信度模糊评价模型(1) 置信度的确定。
在(U,V,R)模型中,R中的元素r ij是由评判者“打分”确定的。
例如 k 个评判者,要求每个评判者u j对照作一次判断,统计得分和归一化后产生, 且 , 组成 R0。
其中既代表 u j关于v j的“隶属程度”,也反映了评判u j为 v j的集中程度。
数值为1 ,说明 u j为 v j是可信的,数值为零为忽略。

可编辑修改精选全文完整版第三节 模糊综合评判法的应用案例二、在物流中心选址中的应用物流中心作为商品周转、分拣、保管、在库管理和流通加工的据点,其促进商品能够按照顾客的要求完成附加价值,克服在其运动过程中所发生的时间和空间障碍。
在物流系统中,物流中心的选址是物流系统优化中一个具有战略意义的问题,非常重要。
基于物流中心位置的重要作用,目前已建立了一系列选址模型与算法。
这些模型及算法相当复杂。
其主要困难在于:(1) 即使简单的问题也需要大量的约束条件和变量。
(2) 约束条件和变量多使问题的难度呈指数增长。
模糊综合评价方法是一种适合于物流中心选址的建模方法。
它是一种定性与定量相结合的方法,有良好的理论基础。
特别是多层次模糊综合评判方法,其通过研究各因素之间的关系,可以得到合理的物流中心位置。
1.模型⑴ 单级评判模型① 将因素集U 按属性的类型划分为k 个子集,或者说影响U 的k 个指标,记为12(,,,)k U U U U =且应满足:1, ki ij i U U U U φ===② 权重A 的确定方法很多,在实际运用中常用的方法有:Delphi 法、专家调查法和层次分析法。
③ 通过专家打分或实测数据,对数据进行适当的处理,求得归一化指标关于等级的隶属度,从而得到单因素评判矩阵。
④单级综合评判B A R⑵多层次综合评判模型一般来说,在考虑的因素较多时会带来两个问题:一方面,权重分配很难确定;另一方面,即使确定了权重分配,由于要满足归一性,每一因素分得的权重必然很小。
无论采用哪种算子,经过模糊运算后都会“淹没”许多信息,有时甚至得不出任何结果。
所以,需采用分层的办法来解决问题。
2.应用运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级,三级模糊评判的数学模型见表3-7.表3-7 物流中心选址的三级模型因素集U 分为三层: 第一层为 {}12345,,,,U u u u u u =第二层为 {}{}{}111121314441424344551525354,,,;,,,;,,,u u u u u u u u u u u u u u u === 第三层为 {}{}5151151251352521522,,;,u u u u u u u ==假设某区域有8个候选地址,决断集{},,,,,,,V A B C D E F G H =代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3-8所示。




第三节 模糊综合评判法的应用案例二、在物流中心选址中的应用物流中心作为商品周转、分拣、保管、在库管理和流通加工的据点,其促进商品能够按照顾客的要求完成附加价值,克服在其运动过程中所发生的时间和空间障碍。
在物流系统中,物流中心的选址是物流系统优化中一个具有战略意义的问题,非常重要。
基于物流中心位置的重要作用,目前已建立了一系列选址模型与算法。
这些模型及算法相当复杂。
其主要困难在于:(1) 即使简单的问题也需要大量的约束条件和变量。
(2) 约束条件和变量多使问题的难度呈指数增长。
模糊综合评价方法是一种适合于物流中心选址的建模方法。
它是一种定性与定量相结合的方法,有良好的理论基础。
特别是多层次模糊综合评判方法,其通过研究各因素之间的关系,可以得到合理的物流中心位置。
1.模型⑴ 单级评判模型① 将因素集U 按属性的类型划分为k 个子集,或者说影响U 的k 个指标,记为12(,,,)k U U U U =且应满足:1, ki ij i U U U U φ===② 权重A 的确定方法很多,在实际运用中常用的方法有:Delphi 法、专家调查法和层次分析法。
③ 通过专家打分或实测数据,对数据进行适当的处理,求得归一化指标关于等级的隶属度,从而得到单因素评判矩阵。
④ 单级综合评判B A R =⑵多层次综合评判模型一般来说,在考虑的因素较多时会带来两个问题:一方面,权重分配很难确定;另一方面,即使确定了权重分配,由于要满足归一性,每一因素分得的权重必然很小。
无论采用哪种算子,经过模糊运算后都会“淹没”许多信息,有时甚至得不出任何结果。
所以,需采用分层的办法来解决问题。
2.应用运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级,三级模糊评判的数学模型见表3-7.表3-7 物流中心选址的三级模型因素集U 分为三层: 第一层为 {}12345,,,,U u u u u u =第二层为 {}{}{}111121314441424344551525354,,,;,,,;,,,u u u u u u u u u u u u u u u === 第三层为 {}{}5151151251352521522,,;,u u u u u u u ==假设某区域有8个候选地址,决断集{},,,,,,,V A B C D E F G H =代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3-8所示。

模糊综合评价方法在物流中心选址的应用物流中心作为商品周转、分拣、保管、在库管理和流通加工的据点,其促进商品能够按照顾客的要求完成附加价值,克服在其运动过程中所发生的时间和空间障碍。
在物流系统中,物流中心的选址是物流系统优化中一个具有战略意义的问题,非常重要。
基于物流中心位置的重要作用,目前已建立了一系列选址模型与算法。
这些模型与算法相当复杂。
其主要困难在于:(1)即使简单的问题也需要大量的约束条件和变量; (2)约束条件和变量多使问题的难度呈指数增长。
模糊综合评判方法是一种适合于物流中心选址的建模方法。
它是一种定性与定量相结合的方法,有良好的理论基础。
特别是多层次模糊综合评判方法,其通过研究各因素之间的关系,可以得到合理的物流中心位置。
1、模型(1)单级评判模型①将因素集U 按属性的类型划分为k 个子集,或者说影响U 的k 个指标,记为且应满足:1,ki i j i U U U U ===∅②权重A 的确定方法很多,在实际运用中常用的方法有:层次分析法、Delphi 法、专家调查法、加权平均法。
③通过专家打分或实测数据,对数据进行适当的处理,求得归一化指标关于等级的隶属度,从而得到单因素评判矩阵。
④单级综合评判B A R =. (2)多层次综合评判模型一般来说,在考虑的因素较多时会带来两个问题:一方面,权重分配很难确定;另一方面,即使确定了权重分配,由于要满足归一性,每一因素分得的权重必然很小。
无论采用哪种算子,经过模糊运算后都会“淹没”许多信息,有时甚至得不出任何结果。
所以,需采用分层的办法来解决问题。
2、应用运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级,三级模糊评判的数学模型见下表:物流中心选址的三级模型 第一级指标 第二级指标第三级指标 自然环境1u(0.1) 气象条件11u (0.25) 地质条件12u (0.25) 水文条件13u (0.25) 地形条件14u (0.25)交通运输2u(0.2) 经营环境3u(0.3)侯选址4u(0.2) 面积41u (0.1)形状42u (0.1) 面积43u (0.4) 面积44u (0.4)公共设施5u(0.2)三供51u (0.4)供水511u (1/3) 供电512u (1/3) 供气513u (1/3) 废物处理52u (0.3)排水521u(0.5)固体废物处理513u(0.5)通信53u (0.2) 道路设施54u (0.1)因素集U 分为三层:第一层为{}12345,,,,U u u u u u =第二层为}{111121314,,,u u u u u =;}{441424344,,,u u u u u =;}{551525354,,,u u u u u = 第三层为}{51511512513,,u uu u =;}{52521522,u u u = 假设某区域有8个候选地址,决断集}{,,,,,,,V A B C D E F G H =代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3-8所示。

模糊综合评价法举例企业进行年度绩效评价时,需要综合考虑多个指标,包括销售额、利润率、市场份额等。
为了进行绩效评价,需要将这些指标进行量化,按照一定的评价标准进行评分。
首先,我们需要确定多个评价指标的权重。
假设销售额的权重为0.4,利润率的权重为0.3,市场份额的权重为0.3、权重的确定可以根据不同的评价对象和评价目标进行调整。
接下来,我们需要将每个指标的实际值进行归一化处理,将其转化为[0,1]之间的数值。
假设销售额的最小值为1000万,最大值为2000万;利润率的最小值为10%,最大值为20%;市场份额的最小值为5%,最大值为15%。
通过将每个指标的实际值减去最小值,然后除以最大值减去最小值,得到归一化后的值。
例如,企业的销售额为1500万元,利润率为15%,市场份额为10%,那么归一化后的销售额值为(1500-1000)/(2000-1000)=0.5,归一化后的利润率值为(15-10)/(20-10)=0.5,归一化后的市场份额值为(10-5)/(15-5)=0.5接下来,我们需要确定模糊综合评价的判断矩阵。
判断矩阵是一个n×n的矩阵,其中n是指标的个数。
假设我们有3个指标,判断矩阵如下:归一化指标1归一化指标2归一化指标3归一化指标110.70.4归一化指标20.310.6归一化指标30.60.81判断矩阵的元素表示对应指标之间的重要程度比较,数值越大表示权重越高。
然后,我们需要确定评价等级。
评价等级一般根据实际情况确定,可以是五级评价(优秀、良好、合格、差、很差)等。
最后,我们需要计算模糊矩阵。
模糊矩阵是一个n×r的矩阵,其中n是指标的个数,r是评价等级的个数。
模糊矩阵的元素表示对应指标在不同评价等级下的隶属度。
我们可以根据实际情况给出每个指标在各个评价等级下的隶属度。
例如,企业的销售额在不同评价等级下的隶属度如下:优秀良好合格差很差0.10.40.50.30.1利润率在不同评价等级下的隶属度如下:优秀良好合格差很差0.20.60.40.30.1市场份额在不同评价等级下的隶属度如下:优秀良好合格差很差0.30.70.60.20.1根据判断矩阵和模糊矩阵,我们可以通过计算得出企业的综合评价结果。

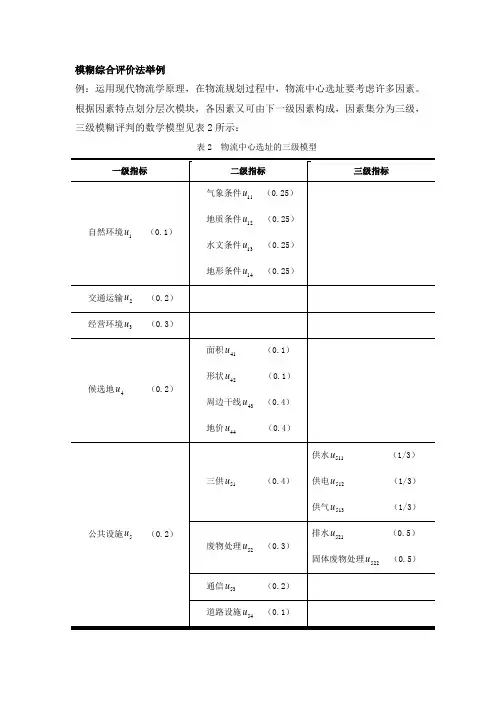
模糊综合评价法举例例:运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级,三级模糊评判的数学模型见表2所示:表2 物流中心选址的三级模型因素集U 分为三层: 第一层为 {}12345,,,,Uu u u u u =第二层为 {}{}{}111121314441424344551525354,,,;,,,;,,,u u u u u u u u u u u u u u u === 第三层为 {}{}5151151251352521522,,;,u u u u u u u ==假设某区域有8个候选地址,决断集{},,,,,,,V A B C D E F G H =代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3所示。
表3 某区域的模糊综合评判⑴ 分层作综合评判{}51511512513,,u u u u =,权重{}511/3,1/3,1/3A =,由表3对511512513,,u u u 的模糊评判构成的单因素评判矩阵:510.600.710.770.600.820.950.650.760.600.710.700.600.800.950.650.760.910.900.930.910.950.930.810.89R ⎛⎫ ⎪= ⎪ ⎪⎝⎭用模型(,)M •+(矩阵运算)计算得:515151(0.703,0.773,0.8,0.703,0.857,0.943,0.703,0.803)B A R ==类似地:525252(0.895,0.885,0.785,0.81,0.95,0.77,0.775,0.77)B A R ==5550.7030.7730.80.7030.8570.9430.7030.8030.8950.8850.7850.810.950.770.7750.77(0.40.30.20.1)0.810.940.890.600.650.950.950.890.900.600.920.600.600.840.650.81B A R ⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭=(0.802,0.823,0.826,0.704,0.818,0.882,0.769,0.811)4440.600.950.600.950.950.950.950.950.600.690.920.920.870.740.890.95(0.10.10.40.4)0.950.690.930.850.600.600.940.780.750.600.800.930.840.840.600.80B A R ⎛⎫⎪⎪== ⎪⎪⎝⎭=(0.8,0.68,0.844,0.899,0.758,0.745,0.8,0.822)1110.910.850.870.980.790.600.600.950.930.810.930.870.610.610.950.87(0.250.250.250.25)0.880.820.940.880.640.610.950.910.900.830.940.890.630.710.950.91B A R ⎛⎫⎪⎪== ⎪⎪⎝⎭=(0.905,0.828,0.92,0.905,0.668,0.633,0.863,0.91)(2)高层次的综合评判{}12345,,,,U u u u u u =,权重{}0.1,0.2,0.3,0.2,0.2A =,则综合评判12345B B B A R A B B B ⎛⎫ ⎪ ⎪⎪== ⎪ ⎪ ⎪⎝⎭0.9050.8280.920.9050.6680.6330.8630.910.950.900.90.940.600.910.950.94 =(0.10.20.30.20.2)0.900.900.870.950.870.650.740.610.80.680.8440.8990.7580.7450.80.8220.8020.8230.8260.7040.8180.8820.7690.811⎛ ⎝⎫⎪⎪⎪⎪⎪ ⎪⎭ =(0.871,0.833,0.867,0.884,0.763,0.766,0.812,0.789)由此可知,8块候选地的综合评判结果的排序为:D,A,C,B ,G,H,F,E ,选出较高估计值的地点作为物流中心。
模糊综合评价模型[编辑]什么是模糊综合评价模型?模糊综合评价方法是模糊数学中应用的比较广泛的一种方法。
在对某一事务进行评价时常会遇到这样一类问题,由于评价事务是由多方面的因素所决定的,因而要对每一因素进行评价;在每一因素作出一个单独评语的基础上,如何考虑所有因素而作出一个综合评语,这就是一个综合评价问题。
[编辑]模糊评价的基本思想许多事情的边界并不十分明显,评价时很难将其归于某个类别,于是我们先对单个因素进行评价,然后对所有因素进行综合模糊评价,防止遗漏任何统计信息和信息的中途损失,这有助于解决用“是”或“否”这样的确定性评价带来的对客观真实的偏离问题。
[编辑]模糊综合评价模型类别[1][编辑]模糊评价基本模型设评判对象为P: 其因素集 ,评判等级集。
对U中每一因素根据评判集中的等级指标进行模糊评判,得到评判矩阵:(1)其中,rij表示u i关于v j的隶属程度。
(U,V,R)则构成了一个模糊综合评判模型。
确定各因素重要性指标(也称权数)后,记为,满足,合成得(2)经归一化后,得 ,于是可确定对象P的评判等级。
[编辑]置信度模糊评价模型(1) 置信度的确定。
在(U,V,R)模型中,R中的元素rij是由评判者“打分”确定的。
例如k 个评判者,要求每个评判者uj对照作一次判断,统计得分和归一化后产生, 且 , 组成R0。
其中既代表uj关于v j的“隶属程度”,也反映了评判u j为v j的集中程度。
数值为1 ,说明u j为v j是可信的,数值为零为忽略。
因此,反映这种集中程度的量称为“置信度”。
对于权系数的确定也存在一个信度问题。
在用层次分析法确定了各个专家对指标评估所得的权重后,作关于权系数的等级划分,由此决定其结果的信度。
当取N个等级时,其量化后对应于[0,l]区间上N次平分。
例如,N取5,则依次得到[0,0.2],[0.2,0.4],[0.2,0.6],[0.6,0.8],[0.8,l]。
对某j个指标,取遍k个专家对该指标评估所得的权重,得。
模糊综合评价法案例模糊综合评价法是一种综合评价方法,它能够有效地处理评价指标之间的模糊性和不确定性,广泛应用于各种决策和评价场景中。
下面我们通过一个案例来具体了解模糊综合评价法的应用。
某公司需要对几位员工进行绩效评价,评价指标包括工作态度、工作成绩、团队合作能力和创新能力。
每个指标的评价等级分为优秀、良好、一般和差,我们将采用模糊综合评价法来进行绩效评价。
首先,我们需要建立模糊评价矩阵。
对于每个员工的每个评价指标,我们需要确定其隶属度函数,即确定其在各个评价等级下的隶属度值。
例如,对于工作态度这一指标,我们可以设定“优秀”评价等级的隶属度为0.8,良好为0.6,一般为0.4,差为0.2。
通过这样的方式,我们可以建立出完整的模糊评价矩阵。
接下来,我们需要确定各个评价指标的权重。
在这个案例中,我们可以采用层次分析法或者专家打分法来确定各个指标的权重。
假设我们确定工作态度的权重为0.3,工作成绩的权重为0.2,团队合作能力的权重为0.25,创新能力的权重为0.25。
然后,我们可以计算出每个员工在每个评价指标下的模糊评价值。
以员工A为例,我们可以通过模糊综合评价法计算出其工作态度、工作成绩、团队合作能力和创新能力的模糊评价值。
最后,我们可以利用模糊综合评价法计算出每位员工的综合评价值。
通过综合评价值的比较,我们可以得出每位员工的绩效排名,从而为公司的绩效奖金分配、晋升评定等决策提供参考依据。
通过以上案例,我们可以看到模糊综合评价法在实际应用中的优势和效果。
它能够有效地处理评价指标之间的模糊性和不确定性,为决策提供科学、客观的依据。
在实际工作中,我们可以根据具体情况对模糊综合评价法进行适当的调整和改进,以更好地满足实际需求。
总的来说,模糊综合评价法在绩效评价、风险评估、项目选择等领域具有广泛的应用前景,它为我们提供了一种全新的综合评价方法,帮助我们更好地应对复杂多变的决策和评价问题。
希望通过本案例的介绍,能够增进大家对模糊综合评价法的理解,为其在实际工作中的应用提供一些借鉴和启发。
二、在物流中心选址中的应用物流中心作为商品周转、分拣、保管、在库管理和流通加工的据点,其促进商品能够按照顾客的要求完成附加价值,克服在其运动过程中所发生的时间和空间障碍。
在物流系统中,物流中心的选址是物流系统优化中一个具有战略意义的问题,非常重要。
基于物流中心位置的重要作用,目前已建立了一系列选址模型与算法。
这些模型及算法相当复杂。
其主要困难在于:(1) 即使简单的问题也需要大量的约束条件和变量。
(2) 约束条件和变量多使问题的难度呈指数增长。
模糊综合评价方法是一种适合于物流中心选址的建模方法。
它是一种定性与定量相结合的方法,有良好的理论基础。
特别是多层次模糊综合评判方法,其通过研究各因素之间的关系,可以得到合理的物流中心位置。
1.模型⑴ 单级评判模型① 将因素集U 按属性的类型划分为k 个子集,或者说影响U 的k 个指标,记为12(,,,)k U U U U =且应满足:1, ki ij i U U U U φ===② 权重A 的确定方法很多,在实际运用中常用的方法有:Delphi 法、专家调查法和层次分析法。
③ 通过专家打分或实测数据,对数据进行适当的处理,求得归一化指标关于等级的隶属度,从而得到单因素评判矩阵。
④ 单级综合评判B A R = ⑵ 多层次综合评判模型一般来说,在考虑的因素较多时会带来两个问题:一方面,权重分配很难确定;另一方面,即使确定了权重分配,由于要满足归一性,每一因素分得的权重必然很小。
无论采用哪种算子,经过模糊运算后都会“淹没”许多信息,有时甚至得不出任何结果。
所以,需采用分层的办法来解决问题。
2.应用运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级,三级模糊评判的数学模型见表3-7.表3-7 物流中心选址的三级模型因素集U 分为三层: 第一层为 {}12345,,,,U u u u u u =第二层为 {}{}{}111121314441424344551525354,,,;,,,;,,,u u u u u u u u u u u u u u u === 第三层为 {}{}5151151251352521522,,;,u u u u u u u ==假设某区域有8个候选地址,决断集{},,,,,,,V A B C D E F G H =代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3-8所示。