初中数学解题模型专题讲解10---“将军饮马”模型详解与拓展

将军饮马模型“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现． 模型1：直线与两定点模型作法结论lB A当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使P A ＋PB 最小．lPAB连接AB 交直线l 于点P ，点P即为所求作的点．P A ＋PB 的最小值为ABl AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得P A ＋PB 最小．lPB'AB作点B 关于直线l 的对称点B '， 连接AB '交直线l 于点P ，点P 即为所求作的点．P A ＋PB 的最小值为AB 'l AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得PA PB -最大．lPAB连接AB 并延长交直线l 于点P ，点P 即为所求作的点．PA PB -的最大值为ABlAB当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使得PA PB -最大．l B'AB P作点B 关于直线I 的对称点B '，连接AB '并延长交直线l 于点P ，点P 即为所求作的点．PA PB -的最大值为AB 'l AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得PA PB -最小．l PAB连接AB ，作AB 的垂直平分线交直线l 于点P ，点P 即为所求作的点．PA PB -的最小值为0模型实例例1：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，则PD ＋PE 最小值是 ．EBC ADP解答：如图所示，∵点B 与点D 关于AC 对称，∴当点P 为BE 与AC 的交点时，PD ＋PE 最小，且线段BE 的长． ∵正方形ABCD 的面积为12，∴其边长为23∵△ABE 为等边三角形，∴BE ＝AB ＝23PD ＋PE 的最小值为3例2：如图，已知△ABC 为等腰直角三角形，AC ＝BC ＝4，∠BCD ＝15°，P 为CD 上的动点，则PA PB -的最大值是多少？DPPA'B解答：如图所示，作点A 关于CD 的对称点A ′，连接A ′C ，连接A ′B 并延长交CD 于点P ，则点P 就是PA PB -的值最大时的点，PA PB -＝A ′B ．∵△ABC 为等腰直角三角形，AC ＝BC 等于4，∴∠ACB ＝90°． ∵∠BCD ＝15°，∴∠ACD ＝75°．∵点A 、A ′关于CD 对称，∴AA ′⊥CD ，AC ＝CA ′， ∵∠ACD ＝∠DCA ′＝75°，∴∠BCA ′＝60°．∵CA ′＝AC ＝BC ＝4，∴△A ′BC 是等边三角形，∴A ′B ＝BC ＝4．∴PA PB -的最大值为4． 练习1．如图，在△ABC 中，AC ＝BC ＝2，∠ACB ＝90°，D 是BC 边的中点，E 是AB 边上一动点，则EC ＋ED 的最小值是 ．DACB E解：解：过点C 作CO ⊥AB 于O ，延长CO 到C '，使O C '=OC ，连接D C '，交AB 于E ，连接C 'B ，此时DE+CE=DE+E C '=D C '的值最小．连接B C '，由对称性可知∠C 'BE=∠CBE=45°，∴∠CB C '=90°，∴B C '⊥BC ， ∠BC C '=∠B C 'C=45°，∴BC=B C '=2，∵D 是BC 边的中点，∴BD=1， 根据勾股定理可得：D C '=5，故EC+ED 的最小值是5． 2．如图，点C 的坐标为（3，y ），当△ABC 的周长最短时，求y 的值．xyB (2,0)A (0,3)O解：解：（1）作A 关于x=3的对称点A′，连接A′B 交直线x=3与点C ． ∵点A 与点A′关于x=3对称，∴AC=A′C ．∴AC+BC=A′C+BC ．当点B 、C 、A′在同一条直线上时，A′C+BC 有最小值，即△ABC 的周长有最小值． ∵点A 与点A′关于x=3对称，∴点A′的坐标为（6，3）．设直线BA′的解析式y=kx+b，将点B和点A′的坐标代入得：k＝34，b＝−32．∴y=34x-32．将x=3代入函数的解析式，∴y的值为3 43．如图，正方形ABCD中，AB＝7，M是DC上的一点，且DM＝3，N是AC上的一动点，求|DN－MN|的最小值与最大值．C解：解：当ND=NM时，即N点DM的垂直平分线与AC的交点，|DN-MN|=0，因为|DN-MN|≤DM，当点N运动到C点时取等号，此时|DN-MN|=DM=3，所以|DN-MN|的最小值为0，最大值为3于D ，点C 、点D 即为所求．PB OAQ点P 、Q 在∠AOB 内部，在OB 边上找点D ，OA 边上找点C ，使得四边形PQDC 周长最小．分别作点P 、Q 关于OA 、OB 的对称点P ′、Q ′，连接P ′Q ′，分别交OA 、OB 于点C 、D ，点C 、D 即为所求．PC ＋CD ＋DQ 的最小值为P ′Q ′，所以四边形PQDC 周长的最小值为PQ ＋P ′Q ′模型实例如图，∠AOB=30°，∠AOB 内有一定点P ，且10OP =.在OA 上有一点Q ，OB 上 一点R ．若立△PQR 周长最小，则最小周长是多少？解答如图，作点P 分别关于OA 、OB 的对称点E 、F ，连接EF ，分别交OA 、OB 于点Q 、R ，连接OE 、OF 、PE 、PF .EQ OP =，FR RP =．△PQR 的周长的最小值为EF 的长.由对称性可得∠EOQ=∠POQ ，∠FOR=∠POR ， ∠EOF=2∠AOB=60°． △EOF 是正三角形．10EF OE OP ===．即△PQR 周长最小值为10.模型2/角与定点1．已知，40MON °?，P 为MON Ð内一定点，A 为OM 上的点，B 为ON 上的点，当△PAB 的周长取最小值时：OBAP(1)找到A 、B 点，保留作图痕迹；(2)求此时APB Ð等于多少度.如果∠MON =θ，∠APB 又等于多少度？ON1.解答（1）做点P 分别关于OM ON 、的对称点E F 、，连接EF 分别交OM ON 、于点A B 、．点A B 、即为所求，此时△PAB 的周长最小．（２）∵点E 与点P 关于直线OM 对称，点F 与点P 关于ON 对称， ∴∠E ＝∠APE ，∠F =∠BPF ，∠CPD =180°-∠MON =140°． ∴在△EFP 中，∠E +∠F =180°-140°=40°， ∴∠CPA +∠BPD =40°．∴∠APB =100°．如果∠MON =θ， ∴∠CPD =180°-θ，∠E +∠F =θ． 又∵∠PAB =2∠E ，∠PBA =2∠F ∴∠PAB +∠PBA =2（∠E +∠F ）=2θ ∴∠APB =180°-2θ．ONE2．如图，四边形中ABCD ，110BAD °?,90B D °??，在BC 、CD 上分别找 一点M 、N ，使△AMN 周长最小，并求此时+AMN ANM ∠∠的度数．A DBMN2．解答如图，作点A关于BC的对称点A'，关于CD的对称点A''，连接A A'''与BC、CD的交点即为所求的点M、N．此时△AMN周长最小．∵∠BAD=110°，∴∠A'+∠A''=180°-110°=70°．由轴对称的性质得：∠A'=∠A AM'，∠A''=∠A AN''，∴∠AMN+∠ANM=2(∠A'+∠A'')=2×70°=140°．3．如图，在x轴上找一点C，在y轴上找一点D，使AD CD BC++最小，并求直线CD的解析式及点C、D的坐标．yxOB(3,1)A(1,3)3．解答作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A B''分别交x轴、y轴于点C、D，此时AD CD BC++最小．由对称性可知A'（-1,3），B'（3，-1）．易求得直线A B''的解析式为2y x=-+，即直线CD的解析式2y x=-+．当0y=时，2x=，∴点C坐标为（2,0）．当0x=时，2y=，∴点D坐标为（0,2）．xy (1，3)(3，1)OB 'BA 'AD C4．如图，20MON°?，A 、B 占分别为射线OM 、ON 上两定点，且2OA =，4OB =，点P 、Q 分别为射线OM 、ON 上两动点，当P 、Q 运动时，线段AQ PQ PB ++ 的最小值是多少？ONMAB4．解答作A 点关于ON 的对称点A '，点B 关于OM 的对称点B '，连接A B ''，分别交OM ON 、于点P Q 、，连接OA '、OB '．则AQ PQ PB A Q PQ PB A B ''''++=++=，此时AQ PQ PB ++最小． 由对称可知，PB PB '=，AQ A Q '=，2OA OA '==，4OB OB '==，20MOB NOA MON ''∠=∠=∠=︒． 60A OB ''∠=︒．作A D '⊥OB '于点D ， 在Rt △ODA '中，∴1OD =，3A D '= ∴413B D '=-=，23A B ''= ∴AQ PQ PB ++的最小值是23．模型作法结论如图，在直线l上找M、N两点(M在左)，使得AM＋MN＋NB最小，且MN＝d.将A向右平移d个单位到A′，作A′关于l的对称点A"，连接A"B与直线l交于点N，将点N向左平移d个单位即为M，点M，N即为所求.AM＋MN＋NB的最小值为A"B＋d如图，l1∥l2，l1、l2间距离为d，在l1、l2分别找M、N两点，使得MN⊥l1，且AM＋MN＋NB最小．将A向下平移d个单位到A，连接A′B交直线l2于点N，过点N作MN⊥l1，连接AM.点M、N即为所求．AM＋MN＋NB的最小值为A'B＋d.例题：在平面直角坐标系中，矩形OABC如图所示，点A在x轴正半轴上，点C在y轴正半轴上，且OA＝6，OC＝4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF＝2.当四边形BDEF的周长最小时，求点E的坐标．解答：如图，将点D向右平移2个单位得到D'(2，2)，作D'关于x轴的对称点D"(2，－2)，连接BD"交x轴于点F，将点F向左平移2个单位到点E，此时点E和点F为所求作的点，且四边形BDEF周长最小.理由：∵四边形BDEF的周长为BD＋DE＋EF＋BF，BD与EF是定值.∴BF＋DE最小时，四边形BDEF周长最小，∵BF＋ED＝BF＋FD'＝BF＋FD"＝BD"ABl2l1A′NMABl2l1BAlM NA′A"BAld设直线BD "的解析式为y ＝kx ＋b ，把B (6，4)，D "(2，－2)代入，得6k ＋b ＝4，2k ＋b ＝－2，解得k ＝32，b ＝－5，∴直线BD "的解析式为y ＝32x －5．令y ＝0，得x ＝103，∴点F 坐标为(103，0)．∴点E 坐标为(43，0)．练习1．在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，A (3，0)，B (0，4)，D 为边OB 的中点． (1)若E 为边OA 上的一个动点，求△CDE 的周长最小值；(2)若E 、F 为边OA 上的两个动点，且EF ＝1，当四边形CDEF 的周长最小时，求点E 、F 的坐标．解答：(1)如图，作点D 关于x 轴的对称点D '，连接CD '与x 轴交于点E ，连接DE ，由模型可知△CDE 的周长最小．∵在矩形OACB 中，OA ＝3，OB ＝4，D 为OB 的中点， ∴D (0，2)，C (3，4)，D '(0，－2).设直线CD '为y ＝kx ＋b ，把C (3，4)，D '(0，－2)代入， 得3k ＋b ＝4，b ＝－2，解得k ＝2，b ＝－2， ∴直线CD '为y ＝2x －2. 令y ＝0，得x ＝1， ∴点E 的坐标为(1，0). ∴OE ＝1，AE ＝2.利用勾股定理得CD ＝13，DE ＝5，CE ＝25， ∴△CDE 周长的最小值为13＋35．(2)如图，将点D 向右平移1个单位得到D '(1，2)，作D '关于x 轴的对称点D ″(1，－2)，连接CD ″交x 轴于点F ，将点F 向左平移1个单位到点E ，此时点E 和点F 为所求作的点，且四边形CDEF 周长最小．理由：∵四边形CDEF 的周长为CD ＋DE ＋EF ＋CF ，CD 与EF 是定值，∴DE ＋CF 最小时，四边形BDEF 周长最小，∴DE ＋CF ＝D 'F ＋CF ＝FD ″＋CF ＝CD ″， 设直线CD ″的解析式为y ＝kx ＋b ，把C (3，4)，D (1，－2)代入，得3k ＋b ＝4，k ＋b ＝－2，解得k ＝3，b ＝－5．∴直线CD ″的解析式为y ＝3x －5， 令y ＝0，得x ＝53，∴点F 坐标为(53，0)，∴点E 坐标为(23，0)．112．村庄A 和村庄B 位于一条小河的两侧，若河岸彼此平行，要架设一座与河岸垂直的桥，桥址应如何选择，才使A 与B 之间的距离最短？解答：设l 1和l 2为河岸，作BD ⊥l 2，取BB '等于河宽，连接AB '交l 1于C 1，作C 1C 2⊥l 2于C 2， 则A →C 1→C 2→B 为最短路线，即A 与B 之间的距离最短.AB l 2l 1。

最值问题之将军饮马问题最值问题是老师们最爱考的热门题型之一，综合性较强，需要一定的基本功，一般考察时一般放在压轴位置。

模型讲解【基本模型】问题：在直线l上找一点P，使得P A＋PB的值最小解析：连接AB，与直线l交点即为点P(两点之间线段最短)【拓展模型1】问题：在直线/上找一点P，使得P A＋PB的值最小解析：点A作关于l的对称点A'，连接BA'，与直线l的交点即为点P，此时P A＋PB的最小值即为线段BA′的长度．【练习】1、尺规作图：在直线MN上找一点P，使得∠APN＝∠BPN．(保留作图痕迹)【模型拓展2】1、如图，已知点P为定点，定长线段AB在直线MN上运动，在什么位置时，P A＝PB最小？思维转化：将线段AB移动，点P不动，理解为线段AB不动，点P在直线CD上移动，将模型转化为最基本模型【模型拓展3】问题：∠MON内一定点A，点P、Q分别为OM、ON上的动点，求△APQ周长的最小值．解析：点A作关于ON和OM的对称点A1、A2，，连接A1A2，与ON、OM交点即为Q、P，线段A1A2的长度即为△APQ周长的最小值．基本结论：①△A1OA2必为等腰三角形，且腰长等于线段OA的长．②∠A1OA2＝2∠MON．四边形ABPQ周长最小的模型，最小值即为线段AB＋A'B'的长度和．【模型拓展4】问题：求AB＋BC＋CD的最小值问题解析：作点A关于ON的对称点A'，点D关于OM的对称点D′，连接A'D′，最小值即为线段A'D'的长度．(作点A和点D的对称点的过程中，也可以直接将OM、ON整个对称过去，使得图形更加完整)【模型拓展5】MN垂直两平行线，求AM＋MN＋NB的最小值模型．其中MN 为定值，故只需求AM ＋NB 的最小值，将点A 向下平移MN 的长度得到A ′，连接A ′B ，线段A ′B 的长度即为AM ＋NB 的最小值直线l 上有一长度不变线段MN 移动，求AM ＋MN ＋NB 最小值的模型．将A 点向右平移MN 的长度，以此转化为基本模型，最小值即为MN ＋A 2B【例题讲解】例题1、如图，在平面直角坐标系中，Rt △OAB 的顶点A 在x 轴的正半轴上，顶点B 的坐标为(3，点C 的坐标为(12，0)，点P 为斜边OB 上的一动点，则P A ＋PC 的最小值为 ．解：作A 关于OB 的对称点D ，连接CD 交OB 于P ，连接AP ，过D 作DN ⊥OA 于N ，则此时P A ＋PC 的值最小，∵DP ＝P A ，∴P A ＋PC ＝PD ＋PC ＝CD ，∵B (3，∴AB OA ＝3，∵tan ∠AOB ＝AB OA AOB ＝30°，∴OB ＝2AB ＝ 由三角形面积公式得：12×OA ×AB ＝12×OB ×AM ，∴AM ＝32，∴AD ＝2×32＝3，∵∠AMB ＝90°，∠B ＝60°，∴∠BAM ＝30°，∵∠BAO ＝90°，∴∠OAM ＝60°，∵DN ⊥OA ，∴∠NDA ＝30°，∴AN ＝12AD ＝32，由勾股定理得：DN ，∵C (12，0)，∴CN ＝3﹣12﹣32＝1，在Rt △DNC 中，由勾股定理得：DC ，即P A＋PC．【思考】若把题中条件点“C的坐标为(12，0)”改为“点C为OA边上一动点”，其它条件不变，那么此时P A＋PC最小值又是多少呢？解答：∵P A＋PC＝PC＋PD＝CD≥DN，∴P A＋PC．例题2、某长方体的长、宽、高分别为4、3、5，(1)如图1，点A、B分别为该长方体的两个顶点，已知蚂蚁从点A沿长方体侧面爬到点B，则最短路线长是多少？(2)如图2，点A、C分别为该长方体的两个顶点，如果用一根细线从点A开始经过4个侧面缠绕一圈到达点C，那么所用细线最短长度是．(3)如图2，点A、C分别为该长方体的两个顶点，如果用一根细线从点A开始经过4个侧面缠绕三圈到达点C，那么所用细线最短长度是．(4)如图3，已知圆柱高4米，底面周长1米．如果用花圈从上往下均匀缠绕圆柱3圈(如图)，那么螺旋形花圈的长至少米．答案：例题3、如图，在五边形ABCDE中，∠BAE＝120°，∠B＝∠E＝90°，AB＝BC＝1，AE＝DE＝2，在BC、DE上分别找一点M、N．(1)当△AMN的周长最小时，∠AMN＋∠ANM＝；(2)求△AMN的周长最小值．解：作A 关于BC 和ED 的对称点A ′，A ″，连接A ′A ″，交BC 于M ，交ED 于N ，则A ′A ″即为△AMN 的周长最小值．⑴作EA 延长线的垂线，垂足为H ，∠BAE ＝120°，∴∠AA ′A ″＋∠AA ″A ′＝60°，∠AA ′A ″＝∠A ′AM ，∠AA ″A ′＝∠EAN ，∴∠CAN ＝120°－∠AA ′A ″－∠AA ″A ′＝60°，也就是说∠AMN ＋∠ANM ＝180°－60°＝120°.⑵过点A ′作EA 延长线的垂线，垂足为H ，∵AB ＝BC ＝1，AE ＝DE ＝2，∴AA ′＝2BA ＝2，AA ″＝2AE ＝4，则Rt △A ′HA 中，∵∠EAB ＝120°，∴∠HAA ′＝60°，∵A ′H ⊥HA ，∴∠AA ″H ＝30°，∴AH ＝12AA ′＝1，∴A ′H ，A ″H ＝1＋4＝5，∴A ′A ″＝例题4、如图，正方形ABCD 的边长为4，点E 在边BC 上且CE ＝1MN 在AC 上运动．(1)求四边形BMNE 周长最小值；(2)当四边形BMNE 的周长最小时，则tan ∠MBC 的值为 ．解：作EF ∥AC 且EF DF 交AC 于M ，在AC 上截取MN DF 交BC 于P ，作FQ ⊥BC 于Q ，作出点E 关于AC 的对称点E ′，则CE ′＝CE ＝1，将MN 平移至E ′F ′处，则四边形MNE ′F ′为平行四边形，当BM ＋EN ＝BM ＋FM ＝BF ′时，四边形BMNE 的周长最小，由∠FEQ ＝∠ACB ＝45°，可求得FQ ＝EQ ＝1，∵∠DPC ＝∠FPQ ，∠DCP ＝∠FQP ，∴△PFQ ∽△PDC ， ∴PQ PQ QE EC ++＝PQ CD ，∴2PQ PQ +＝14，解得：PQ ＝23，∴PC ＝83，由对称性可求得tan∠MBC＝tan∠PDC＝23．例题5、在平面直角坐标系中，已知点A(一2，0)，点B(0，4)，点E在OB上，且∠OAE＝∠OB A．如图，将△AEO沿x轴向右平移得到△AE′O′，连接A'B、BE'．当AB＋BE'取得最小值时，求点E'的坐标．【提示】将△AEO向右平移转化为△AEO不动，点B向左平移，则点B移动的轨迹为一平行于x轴的直线，所以作点E关于该直线的对称点E1，连接AE1，与该直线交点F即为最小时点B的位置，求出BF长度即可求出点E向右平移的距离．例题6、如图，已知正比例函数y＝kx(k＞0)的图像与x轴相交所成的锐角为70°，定点A的坐标为(0，4)，P为y轴上的一个动点，M、N为函数y＝kx(k＞0)的图像上的两个动点，则AM＋MP＋PN的最小值为．解：如图所示，直线OC 、y 轴关于直线y ＝kx 对称，直线OD 、直线y ＝kx 关于y 轴对称，点A ′是点A 关于直线y ＝kx 的对称点．作A ′E ⊥OD 垂足为E ，交y 轴于点P ，交直线y ＝kx 于M ，作PN ⊥直线y ＝kx 垂足为N ，∵PN ＝PE ，AM ＝A ′M ，∴AM ＋PM ＋PN ＝A ′M ＋PM ＋PE ＝A ′E 最小(垂线段最短)，在RT △A ′EO 中，∵∠A ′EO ＝90°，OA ′＝4，∠A ′OE ＝3∠AOM ＝60°，∴OE ＝12OA ′＝2，A ′E ．∴AM ＋MP ＋PN 的最小值为【巩固练习】1、如图所示，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD ＋PE 的和最小，则这个最小值为 ．2、在菱形ABCD 中，对角线AC ＝6，BD ＝8，点E 、F 、P 分别是边AB 、BC 、AC 上的动点，PE ＋PF 的最小值是 ．3、如图，在边长为2的等边△ABC 中，D 为BC 的中点，E 是AC 边上一点，则BE ＋DE 的最小值为 ．4、如图，钝角三角形ABC 的面积为9，最长边AB ＝6，BD 平分∠ABC ，点M 、N 分别是BD 、BC 上的动点，则CM ＋MN 的最小值为 ．5、如图，在△ABC 中，AM 平分∠BAC ，点D 、E 分别为AM 、AB 上的动点，(1)若AC ＝4，S △ABC ＝6，则BD ＋DE 的最小值为(2)若∠BAC ＝30°，AB ＝8，则BD ＋DE 的最小值为 ．(3)若AB ＝17，BC ＝10，CA ＝21，则BD ＋DE 的最小值为 ．AB C DEM6、如图，在△ABC 中，AB ＝BC ＝4，S △ABC ＝，点P 、Q 、K 分别为线段AB 、BC 、AC 上任意一点，则PK ＋QK 的最小值为 ．7、如图，AB 是⊙O 的直径，AB ＝8，点M 在⊙O 上，∠MAB ＝20°，N 是弧MB 的中点，P 是直径AB 上的一动点，则PM ＋PN 的最小值为 ．B8、如图，在锐角△ABC 中，AB ＝4，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM ＋MN 的最小值是．9、如图，圆柱形玻璃杯高为12cm 、底面周长为18cm ，在杯内离杯底4cm 的点C 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm 与蜂蜜相对的点A 处，则蚂蚁到达蜂蜜的最短距离为cm ．10、如图，菱形OABC中，点A在x轴上，顶点C的坐标为(1，动点D、E分别在射线OC、OB上，则CE＋DE＋DB的最小值是．11、如图，点A(a，1)、B(－1，b)都在双曲线y＝－3x(x＜0)上，点P、Q分别是x轴、y轴上的动点，当四边形P ABQ的周长取最小值时，PQ所在直线的解析式是．12、如图，点P是∠AOB内任意一点，OP＝5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是．13、如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM＝1，ON＝3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是．14、如图，在Rt△ABC中，∠ACB＝90°，点D是AB边的中点，过D作DE⊥BC于点E．(1)点P是边BC上的一个动点，在线段BC上找一点P，使得AP＋PD最小，在下图中画出点P；(2)在(1)的条件下，连接CD交AP于点Q，求AQ与PQ的数量关系；AC E D15、在矩形ABCD 中，AB ＝6，BC ＝8，G 为边AD 的中点．(1)如图1，若E 为AB 上的一个动点，当△CGE 的周长最小时，求AE 的长．(2)如图2，若E 、F 为边AB 上的两个动点，且EF ＝4，当四边形CGEF 的周长最小时，求AF 的长．16、图1，图2为同一长方体房间的示意图，图2为该长方体的表面展开图．(1)蜘蛛在顶点A ′处，①苍蝇在顶点B 处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线；②苍蝇在顶点C 处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD 爬行的最近路线A 'GC 和往墙面BB 'C 'C 爬行的最近路线A 'HC ，试通过计算判断哪条路线更近？(2)在图3中，半径为10dm 的OM 与D 'C '相切，圆心M 到边CC ′的距离为15dm ，蜘蛛P 在线段AB 上，苍蝇Q 在OM 的圆周上，线段PQ 为蜘蛛爬行路线．若PQ 与OM 相切，试求PQ 的长度的范围．17.如图，抛物线21242y x x =-++交y 轴于点B ，点A 为x 轴上的一点，OA =2，过点A 作直线MN ⊥AB 交抛物线与M 、N 两点.（1）求直线AB 的解析式；（2）将线段AB 沿y 轴负方向平移t 个单位长度，得到线段11A B ，求11MA MB +取最小值时实数t 的值.参考答案1.解：连接BD，∵点B与D关于AC对称，∴PD＝PB，∴PD＋PE＝PB＋PE＝BE最小．∵正方形ABCD的面积为12，∴AB＝又∵△ABE是等边三角形，∴BE＝AB＝．2.解：∵四边形ABCD是菱形，对角线AC＝6，BD＝8，∴AB＝5，作E关于AC的对称点E′，作E′F⊥BC于F交AC于P，连接PE，则E′F即为PE＋PF的最小值，∵12⋅AC⋅BD＝AD⋅E′F，∴E′F＝245，∴PE＋PF的最小值为245.3.解：作B关于AC的对称点B′，连接BB′、B′D，交AC于E，此时BE＋ED＝B′E＋ED＝B′D，根据两点之间线段最短可知B′D就是BE＋ED的最小值，∵B、B′关于AC的对称，∴AC、BB′互相垂直平分，∴四边形ABCB′是平行四边形，∵三角形ABC是边长为2，D为BC的中点，∴AD⊥BC，AD BD＝CD＝1，BB′＝2AD＝，作B′G⊥BC的延长线于G，∴B′G＝AD，在Rt△B′BG中，BG＝3，∴DG＝BG﹣BD＝3﹣1＝2，在Rt△B′DG中，B′D故BE ＋ED4.解：过点C 作CE ⊥AB 于点E ，交BD 于点M ，过点M 作MN ⊥BC 于N ，∵BD 平分∠ABC ，ME ⊥AB 于点E ，MN ⊥BC 于N ，∴MN ＝ME ，∴CE ＝CM ＋ME ＝CM ＋MN 是最小值．∵三角形ABC 的面积为9，AB ＝6，∴12×6 CE ＝9，∴CE ＝3．即CM ＋MN 的最小值为3．5.H E'A C DEM提示：作点E 关于AM 的对称点E ′，BH ⊥AC 于H ，易知BD ＋DE 的最小值即为BH 的长.答案：(1)3；(2)4；(3)8．6.解：如图，过A 作AH ⊥BC 交CB 的延长线于H ，∵AB ＝CB ＝4，S △ABC ＝AH ＝∴cos ∠HAB ＝AH ABHAB ＝30°，∴∠ABH ＝60°，∴∠ABC ＝120°， ∵∠BAC ＝∠C ＝30°，作点P 关于直线AC 的对称点P ′，过P ′作P ′Q ⊥BC 于Q 交AC 于K ，则P′Q的长度＝PK＋QK的最小值，∴∠P′AK＝∠BAC＝30°，∴∠HAP′＝90°，∴∠H＝∠HAP′＝∠P′QH＝90°，∴四边形AP′QH是矩形，∴P′Q＝AH＝即PK＋QK的最小值为7.解：作点N关于AB的对称点N′，连接OM、ON、ON′、MN′，则MN′与AB的交点即为PM＋PN的最小时的点，PM＋PN的最小值＝MN′，∵∠MAB＝20°，∴∠MOB＝2∠MAB＝2×20°＝40°，∵N是弧MB的中点，∴∠BON＝12∠MOB＝12×40°＝20°，由对称性，∠N′OB＝∠BON＝20°，∴∠MON′＝∠MOB＋∠N′OB＝40°＋20°＝60°，∴△MON′是等边三角形，∴MN′＝OM＝OB＝12AB＝182⨯＝4，∴PM＋PN的最小值为4，8.解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′＋M′N′为所求的最小值．∵AD是∠BAC的平分线，∴M′H＝M′N′，∴BH是点B到直线AC的最短距离，∵AB＝4，∠BAC＝45°，∴BH＝AB⋅sin45°＝4＝∵BM＋MN的最小值是BM′＋M′N′＝BM′＋M′H＝BH＝9.解：沿过A 的圆柱的高剪开，得出矩形EFGH ，过C 作CQ ⊥EF 于Q ，作A 关于EH 的对称点A ′，连接A ′C 交EH 于P ，连接AP ，则AP ＋PC 就是蚂蚁到达蜂蜜的最短距离，∵AE ＝A ′E ，A ′P ＝AP ，∴AP ＋PC ＝A ′P ＋PC ＝A ′C ，∵CQ ＝12×18cm ＝9cm ，A ′Q ＝12cm ﹣4cm ＋4cm ＝12cm ，在Rt △A ′QC 中，由勾股定理得：A ′C ＝15cm ，故答案为：15．10.解：连接AC ，作B 关于直线OC 的对称点E ′，连接AE ′，交OC 于D ，交OB 于E ，此时CE ＋DE ＋BD 的值最小，∵四边形OCBA 是菱形，∴AC ⊥OB ，AO ＝OC ，即A 和C 关于OB 对称，∴CE ＝AE ，∴DE ＋CE ＝DE ＋AE ＝AD ，∵B 和E ′关于OC 对称，∴DE ′＝DB ，∴CE ＋DE ＋DB ＝AD ＋DE ′＝AE ′，过C 作CN ⊥OA 于N ，∵C (1)，∴ON ＝1，CN由勾股定理得：OC ＝2，即AB ＝BC ＝OA ＝OC ＝2，∴∠CON ＝60°，∴∠CBA ＝∠COA ＝60°， ∵四边形COAB 是菱形，∴BC ∥OA ，∴∠DCB ＝∠COA ＝60°，∵B 和E ′关于OC 对称，∴∠BFC ＝90°，∴∠E ′BC ＝90°﹣60°＝30°，∴∠E ′BA ＝60°＋30°＝90°，CF ＝12BC ＝1，由勾股定理得：BF E ′F ，在Rt △EBA 中，由勾股定理得：AE ′＝4，即CE ＋DE ＋DB 的最小值是4．11.解：把点A(a，1)、B(﹣1，b)代入y＝﹣3x(x＜0)得a＝﹣3，b＝3，则A(﹣3，1)、B (﹣1，3)，作A点关于x轴的对称点C，B点关于y轴的对称点D，所以C点为(﹣3，﹣1)，D点为(1，3)，连结CD分别交x轴、y轴于P点、Q点，此时四边形P ABQ的周长最小，设直线CD的解析式为y＝kx＋b，则313k bk b-+=-⎧⎨+=⎩，解得12kb=⎧⎨=⎩，所以直线CD的解析式为y＝x＋2．12.解：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：∵点P关于OA的对称点为D，关于OB的对称点为C，∴PM＝DM，OP＝OD，∠DOA＝∠POA；∵点P关于OB的对称点为C，∴PN＝CN，OP＝OC，∠COB＝∠POB，∴OC＝OP＝OD，∠AOB＝12∠COD，∵△PMN周长的最小值是5cm，∴PM＋PN＋MN＝5，∴DM＋CN＋MN＝5，即CD＝5＝OP，∴OC＝OD＝CD，即△OCD是等边三角形，∴∠COD＝60°，∴∠AOB＝30°；13.解：作M关于OB的对称点M′，作N关于OA的对称点N′，连接M ′N ′，即为MP ＋PQ ＋QN 的最小值．根据轴对称的定义可知：∠N ′OQ ＝∠M ′OB ＝30°，∠ONN ′＝60°，∴△ONN ′为等边三角形，△OMM ′为等边三角形，∴∠N ′OM ′＝90°，∴在Rt △M ′ON ′中，M ′N ′14.A'AB PC EDQA'A B P C E D解：(1)作点A 关于BC 的对称点A ′，连DA ′交BC 于点P.(2)由(1)可证得PA 垂直平分CD ，∴AQCQ ＝3PQ15.解：(1)∵E 为AB 上的一个动点，∴作G 关于AB 的对称点M ，连接CM 交AB 于E ，那么E 满足使△CGE 的周长最小； ∵在矩形ABCD 中，AB ＝6，BC ＝8，G 为边AD 的中点，∴AG ＝AM ＝4，MD ＝12， 而AE ∥CD ，∴△AEM ∽△DCM ，∴AE ：CD ＝MA ：MD ，∴AE ＝CD MA MD＝2； (2)∵E 为AB 上的一个动点，∴如图，作G 关于AB 的对称点M ，在CD 上截取CH ＝4，然后连接HM 交AB 于E ，接着在EB 上截取EF ＝4，那么E 、F 两点即可满足使四边形CGEF 的周长最小．∵在矩形ABCD 中，AB ＝6，BC ＝8，G 为边AD 的中点，∴AG ＝AM ＝4，MD ＝12，而CH ＝4，∴DH ＝2，而AE∥CD，∴△AEM∽△DHM，∴AE：HD＝MA：MD，∴AE＝HD MAMD⨯＝23，∴AF＝4＋23＝143．16.解：(1)①根据“两点之间，线段最短”可知：线段A′B为最近路线，如图1所示．②Ⅰ．将长方体展开，使得长方形ABB′A′和长方形ABCD在同一平面内，如图2①．在Rt△A′B′C中，∠B′＝90°，A′B′＝40，B′C＝60，∴ACⅡ．将长方体展开，使得长方形ABB′A′和长方形BCC′B′在同一平面内，如图2②．在Rt△A′C′C中，∠C′＝90°，A′C′＝70，C′C＝30，∴A′C＝ABCD爬行的最近路线A′GC更近；(2)过点M作MH⊥AB于H，连接MQ、MP、MA、MB，如图3．∵半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，BC′＝60dm，∴MH＝60﹣10＝50，HB＝15，AH＝40﹣15＝25，根据勾股定理可得AM，MB∴50≤MP∵⊙M 与PQ 相切于点Q ，∴MQ ⊥PQ ，∠MQP ＝90°，∴PQ当MP ＝50时，PQ当MP时，PQ55．∴PQ 长度的范围是≤PQ ≤55dm ．17.解：（1）依题意，易得B （0，4），A （2，0），则AB 解析式：42+-=x y（2）∵AB ⊥MN∴直线MN ：121-=x y 与抛物线联立可得：⎪⎪⎩⎪⎪⎨⎧-=++-=12142212x y x x y 解得：M （-2，-2）将AB 向负方向平移t 个单位后，A 1（2，-t ），B 1（0，4-t ） 则A 1关于直线x =-2的对称点A 2为（-6，-t ）当A 2、M 、B 1三点共线时，11MA MB +取最小值 ∴314=t。

将军饮马五大模型七类题型(模型梳理与题型分类讲解)第一部分【知识点归纳】【理论依据】路径最短、线段和最小、线段差最大、周长最小等一系列最值问题。

【方法原理】1.两点之间，线段最短；2.三角形两边之和大于第三边，两边之差小于第三边；3.中垂线上的点到线段两端点的距离相等；4.垂线段最短.【基本模型】【模型一：两定交点型】如图1，直线l和l的异侧两点A.B，在直线l上求作一点P，使P A+PB最小；图1【模型二：两定一动型】如图2，直线l和l的同侧两点A.B，在直线l上求作一点P，使P A+PB最小(同侧转化为异侧)；图2【模型三：一定两动型】如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△P AB 的周长最小。

图3【模型四：两定两动型】如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形P AQB的周长最小。

图4【模型五：一定两动(垂线段最短)型】如图5，点A是∠MON外的一点，在射线ON上作点P，使P A 与点P到射线OM的距离之和最小。

图5【模型六：一定两动，找(作)对称点转化型】如图6，点A是∠MON内的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小。

图6【题型目录】【题型1】两定一动型.......................................................3;【题型2】一定两动(两点之间线段最短)型...................................6;【题型3】一定两动(垂线段最短)型.........................................9；【题型4】两定两动型.......................................................12;【题型5】一定两动(等线段)转化型.........................................14;【题型6】直通中考.........................................................18;【题型7】拓展延伸.........................................................21;第二部分【题型展示与方法点拨】【题型1】两定一动型；1.(23-24八年级上·河北廊坊·期中)如图，在△ABC中，∠BAC=90°，AB=12，AC=16，BC=20，将△ABC沿射线BM折叠，使点A与BC边上的点D重合．(1)线段CD的长是；(2)若点E是射线BM上一动点，则△CDE周长的最小值是．【答案】824【分析】本题主要考查了的折叠的性质、两点之间线段最短，熟练掌握折叠的性质是解此题的关键．(1)由折叠的性质可得BD=AB=12，再由CD=BC-BD进行计算即可得到答案；(2)设BM与AC的交点为点F，连接AE，由折叠的性质可得：DF=AF，DE=AE，∠BDF=∠BAF，再根据两点之间线段最短可得当点E与点F重合时，AE+CE取最小值，最小值为AC，由此即可得到答案．解：(1)由折叠的性质可得：BD=AB=12，∴CD=BC-BD=20-12=8，故答案为：8；(2)如图，设BM与AC的交点为点F，连接AE，由折叠的性质可得：DF=AF，DE=AE，∠BDF=∠BAF，由(1)得：CD=8，∴△CDE的周长=CD+DE+CE=8+AE+CE，要是△CDE的周长最小，只需AE+CE最小，由两点之间线段最短可知，当点E与点F重合时，AE+CE取最小值，最小值为AC，∴△CDE的周长=8+AC=8+16=24，故答案为：24．2.(22-23八年级上·广西南宁·期末)如图，点E在等边△ABC的边BC上，BE=4，射线CD⊥BC，垂足为点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+FP的值最小时，BF=5，则AB 的长为．【答案】7【分析】本题考查最短路径问题、等边三角形的性质、含30度角的直角三角形的性质，熟练掌握利用轴对称性质求最短距离的方法是解答的关键．作点E 关于射线CD 的对称点E ，过E 作E F ⊥AB 于F ，交射线CD 于P ，连接PE ，此时EP +FP 的值最小，利用等边三角形的性质和三角形的内角和定理求得∠E =90°-∠B =30°，然后利用含30度角的直角三角形的性质求得BE =2BF =10，进而求得CE =3即可求解．解：作点E 关于射线CD 的对称点E ，过E 作E F ⊥AB 于F ，交射线CD 于P ，连接PE ，如图，则E P =EP ，∴EP +FP =E P +FP =E F ，此时EP +FP 的值最小，则BF =5，∵△ABC 是等边三角形，∴∠B =60°，AB =BC ，在Rt △BFE 中，∠E =90°-∠B =30°，∴BE =2BF =10，∵BE =4，CE =CE ，∴2CE +4=10，∴CE =3，∴AB =BC =3+4=7，故答案为：7．3.(23-24八年级下·河南郑州·阶段练习)如图，在△ABC 中，AB =AC ．在AB 、AC 上分别截取AP 、AQ ，使AP =AQ ．再分别以点P ，Q 为圆心，以大于12PQ 的长为半径作弧，两弧在∠BAC 内交于点R ，作射线AR ，交BC 于点D ．已知BC =5，AD =6．若点M 、N 分别是线段AD 和线段AB 上的动点，则BM +MN 的最小值为．【答案】6013【分析】本题考查作图-复杂作图，角平分线的定义，等腰三角形的性质等知识，解题关键是读懂图形信息，灵活运用所学知识解决问题，属于中考常考题型．过点B 作BH ⊥AC 于点H ，交AD 于点M ，根据等腰三角形的性质和勾股定理求出AC ，然后根据S ΔABC =12⋅BC ⋅AD =12⋅AC ⋅BH ，可得BH =6013．作点H 关于解：如图，过点B 作BH ⊥AC 于点H ，交AD 于点M ，由作图可知，AD 平分∠BAC ，∵AB =AC ，∴AD ⊥BC ，∴BD =CD =12BC =52，∵AD =6．∴AC =AD 2+DC 2=62+52 2=132，∵S ΔABC =12⋅BC ⋅AD =12⋅AC ⋅BH ，∴5×6=132BH ，∴BH =6013．∵AB =AC ，AD ⊥BC ，作点H 关于AD 的对称点交AB 于点N ，连接M N ，当M 与M 重合时，此时BM +MN 最小，∴M H =M N ，∴BH =BM +M H =BM +M N ，则BM +MN 的最小值为6013．故答案为：6013【题型2】一定两动(两点之间线段最短)型；4.(23-24七年级下·陕西西安·期末)如图，在锐角△ABC 中，∠ABC =30°，AC =4，△ABC 的面积为5，P 为△ABC 内部一点，分别作点P 关于AB ，BC ，AC 的对称点P 1，P 2，P 3，连接P 1P 2，PP 3，则2P 1P 2+PP 3的最小值为．【答案】5【分析】首先由△ABC 的面积为5，12AC ⋅BM =5，求出BM =52，然后由∠ABC =30°和对称构造正三角形，将P 1P 2转化成BP ，将2P 1P 2+PP 3提取系数2，最终转化成垂线段最短．解：设PP3与AC 交于点Q ，则PQ =12PP 3，连接BP 、BQ 、BP 1、BP 2，作BM ⊥AC ，垂足为M ，AC =4，△ABC 的面积为5，∴12AC ⋅BM =5，即12×4BM =5∴BM =5，根据对称性得BP=BP1=BP2，∠ABP=∠ABP1，∠CBP=∠CBP2，∴∠P1BP2=2∠ABC=60°，∴△P1BP2是正三角形，∴P1P2=BP1=BP，∴2P1P2+PP3=2P1P2+12PP3=2(BP+PQ)≥2BQ≥2BM=5，故答案为：5．【点拨】本题考查了轴对称、正三角形、三角形面积、垂线段最短等知识，解题的关键是将P1P2转化成BP，将2P1P2+PP3提取系数2，最终转化成垂线段最短．形式上易与胡不归混淆．5.(23-24八年级上·北京海淀·期中)如图，已知∠MON=30°，在∠MON的内部有一点P，A为OM上一动点，B为ON上一动点，OP=a，当△P AB的周长最小时，∠APB=度，△P AB的周长的最小值是．【答案】120a【分析】分别作出点P关于OM，ON两条射线的对称点，连接两个对称点的线段与OM，ON的交点即为所确定的点；连接OP，OP ，OP ，由轴对称的性质得：OP=OP =OP =a，∠P OA=∠POA，∠P OB=∠POB，证得△P OP 是等边三角形，即可得到结论．解：①分别作点P关于OM，ON的对称点P ，P ；连接P ，P ，分别交OM，ON于点A、点B，则此时△P AB的周长最小．连接OP，OP ，OP ，由轴对称的性质得：OP=OP =OP =a，∠P OA=∠POA，∠P OB=∠POB，∵∠MON=30°，∴∠P OP =2∠MON=60°，∴△P OP 是等边三角形，∴P P =OP=a，∠AP O=∠APO，∠BP O=∠BPO，∴∠APB=∠AP O+∠BP O=120°，∴△P AB的周长=P P =a，故答案为：120，a．【点拨】此题主要考查了轴对称-最短路径问题，解决本题的关键是理解要求周长最小问题可归结为求线段最短问题，通常是作已知点关于所求点所在直线的对称点．6.(22-23八年级上·新疆乌鲁木齐·期末)如图，已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP=5，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于5，则α=()A.30°B.45°C.60°D.90°【答案】A【分析】设点P关于OA的对称点为C，关于OB的对称点为D，当点E、F在CD上时，△PEF的周长为PE+ EF+FP=CD，此时周长最小，根据CD=5可求出α的度数．解：如图，作点P关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F．此时，△PEF 的周长最小．连接OC，OD，PE，PF．∵点P与点C关于OA对称，∴OA垂直平分PC，∴∠COA=∠AOP，PE=CE，OC=OP，同理，可得∠DOB=∠BOP，PF=DF，OD=OP．∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α，OC=OD=OP=5，∴∠COD=2α．又∵△PEF的周长为：PE+EF+FP=CE+EF+FD=CD=5，∴OC=OD=CD=5，∴△COD是等边三角形，∴2α=60°，∴α=30°．故选：A．【点拨】此题主要考查了最短路径问题，本题找到点E和F的位置是解题的关键．要使△PEF的周长最小，通常是把三边的和转化为一条线段，运用三角形三边关系解决．【题型3】一定两动型(垂线段最短)；7.(2024八年级上·全国·专题练习)如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD是∠BAC的平分线，若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是()A.2.4B.3C.4D.5【答案】A【分析】本题考查了轴对称最短路径问题，角平分线定义，勾股定理，作点Q关于AD的对称点Q ，连接PQ ，股定理求出AB 的长，再利用三角形面积求出CH 的长即可得到结果．解：如图，作点Q 关于AD 的对称点Q ，连接PQ ，CQ ，过点C 作CH ⊥AB 于点H ，∵AD 是△ABC 的角平分线，Q 与Q 关于AD 对称，∴点Q 在AB 上，PC +PQ =PC +PQ ≥CH ，∵AC =3，BC =4，∴AB =AC 2+BC 2=5，12⋅AC ⋅BC =12⋅AB ⋅CH 即12×3×4=12×5×CH ，∴CH =2.4，∴CP +PQ ≥2.4，∴PC +PQ 的最小值为2.4，故选：A ．8.(23-24七年级下·广东深圳·期末)如图，在等腰三角形ABC 中，AB =AC ，AD ⊥BC ，点D 为垂足，E 、F 分别是AD 、AB 上的动点．若AB =6，△ABC 的面积为12，则BE +EF 的最小值是()A.2B.4C.6D.8【答案】B 【分析】本题考查等腰三角形的性质，轴对称-最短路线问题，垂线段最短．解此题的关键是正确作出辅助线．作点F 关于AD 的对称点M ，连接BM 、EM ，过点B 作BN ⊥AC 于点N ，从而可确定BE +EF ≥BM ，即BM 最小时，BE +EF 最小．再根据垂线段最短可知BN 的长即为BM 最小时，最后根据三角形面积公式求出BN 的长即可．解：如图，作点F 关于AD 的对称点M ，连接BM 、EM ，过点B 作BN ⊥AC 于点N ，∴EF =EM ，∴BE +EF =BE +EM ≥BM ，∴BM 最小时，BE +EF 最小．当BM ⊥AC 时BM 最小，即为BN 的长，∵S △ABC =12AC ⋅BN =12，AB =AC =6，∴BN =2×12÷6=4，∴BE +EF 的最小值是4．故选B ．9.(23-24八年级·江苏·假期作业)如图，在△ABC 中，AB =AC =10,BC =12,AD =8，AD 是∠BAC 的平分线．若P ，Q 分别是AD 和AC 上的动点，则PC +PQ 的最小值是．【答案】9.6【分析】本题考查了轴对称--最短路线问题、等腰三角形的性质以及三角形的面积，线段垂直平分线的性质．连接PB ，PQ ，根据线段垂直平分线的性质可得BP =CP ，从而得到当点B ，P ，Q 三点共线时，PC +PQ 取得最小值，最小值为BQ 的长，且当BQ ⊥AC 时，BQ 最小，再由S △ABC =12BC ⋅AD =12AC ⋅BQ ，求出BQ 的长，即可．解：如图，连接PB ，PQ ，∵AB =AC ，AD 是∠BAC 的平分线，∴AD 垂直平分BC ，∴BP =CP ，∴PC +PQ =PB +PQ ≥PQ ，∴当点B ，P ，Q 三点共线时，PC +PQ 取得最小值，最小值为BQ 的长，且当BQ ⊥AC 时，BQ 最小，∵S △ABC =12BC ⋅AD =12AC ⋅BQ ，∴12×12×8=12×10BQ ，∴BQ =9.6．故答案为：9.6【题型4】两定两动型；10.(22-23八年级上·湖北武汉·期末)如图，∠AOB =20°，M ，N 分别是边OA ，OB 上的定点，P ，Q 分别是边OB ，OA 上的动点，记∠OPM =α，∠OQN =β，当MP +PQ +QN 最小时，则关于α，β的数量关系正确的是()A.β-α=30°B.β+α=210°C.β-2α=30°D.β+α=200°【答案】D 【分析】如图，作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N 交OA 于Q ，交OB 于P ，则MP +PQ +QN 最小，易知∠OPM =∠OPM ′=∠NPQ ，∠OQP =∠AQN ′=∠AQN ，∠OQN =180°-20°-∠ONQ ，∠OPM =∠NPQ =20°+∠OQP ，∠OQP =∠AQN =20°+∠ONQ ，由此即可解决问题．PQ +QN 最小，解:由轴对称的性质得∠OPM =∠OPM ′=∠NPQ ，∠OQP =∠AQN ′=∠AQN ，∠OQN =180°-20°-∠ONQ ，∠OPM =∠NPQ =20°+∠OQP ，∠OQP =∠AQN =20°+∠ONQ ，∴α+β=180°-20°-∠ONQ +20°+20°+∠ONQ =200°．故选：D ．【点拨】本题考查轴对称-最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．【变式】(20-21八年级上·天津·期末)如图，∠AOB =25°，点M ，N 分别是边OA ，OB 上的定点，点P ，Q 分别是边OB ，OA 上的动点，记∠MPQ =α，∠PQN =β，当MP +PQ +QN 的值最小时，β-α的大小=_______(度)．【答案】50【分析】本题主要考查最短路径问题、轴对称的性质，三角形外角的性质，作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N ，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，可知此时MP +PQ +QN 最小，此时∠OPM =∠OPM =QPN ，∠OQP =∠AQN =∠AQN ，再根据三角形外角的性质和平角的定义即可得出结论．解：作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N ，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，如图所示．根据两点之间，线段最短，可知此时MP +PQ +QN 最小，即MP +PQ +QN =M N ，∴∠OPM =∠OPM =QPN ，∠OQP =∠AQN =∠AQN ，∵∠MPQ =α，∠PQN =β，∴∠QPN =12180°-α ，∠OQP =12180°-β ，∵∠QPN =∠AOB +∠OQP ，∠AOB =25°,∴12180°-α =25°+12180°-β ，∴β-α=50°，故答案为：50．【题型5】一定两动(等线段)转化型；11.(23-24九年级下·广西南宁·开学考试)如图，△ABC 是等边三角形，AB =4．过点A 作AD ⊥BC 于点D ，点P 是直线AD 上一点，以CP 为边，在CP 的下方作等边△CPQ ，连接DQ ，则DQ 的最小值为．【答案】1【分析】连接BQ ，先证△ACP ≌△BCQ (SAS )，则可得∠CBQ =∠CAP =30°，由此可知Q 点在过B 点且与BC 成30°角的直线上运动．根据垂线段最短可知，当DQ ⊥BQ 时，DQ 最小，求出DQ 的值即可．本题主要考查了等边三角形的性质，全等三角形的判定和性质，以及垂线段最短．熟练掌握以上知识，找出Q 点的运动轨迹是解题的关键．解：连接BQ ，∵△ABC 和△CPQ 都是等边三角形，∴AC =BC ，PC =QC ，∠ACB =∠PCQ =60°，∴∠ACB -∠PCB =∠PCQ -∠PCB ，即∠ACP =∠BCQ ，∴△ACP ≌△BCQ (SAS )，∴∠CBQ =∠CAP ，∵△ABC 是等边三角形，AB =4，∴BC =AB =4，∠BAC =60°，∵AD ⊥BC ，∴BD =DC =12BC =2，∠CAP =12∠BAC =30°，∴∠CBQ =30°，∴Q 点在过B 点且与BC 成30°角的直线上运动．当DQ ⊥BQ 时，DQ 最小，此时DQ =12BD =1，∴DQ 的最小值为1．故答案为：1．12.(23-24八年级下·湖北武汉·阶段练习)如图，在Rt △ABC 中，∠BAC =90°，AC =6，BC =10，D 、E 分别是AB 、BC 上的动点，且CE =BD ，连接AE 、CD ，则AE +CD 的最小值为．【答案】234【分析】本题主要考查了全等三角形的判定及性质，勾股定理，两点之间，线段最短，过点C 作CN ∥AB 且使CN =BC ，连接EN ，AN ，证明△CEN ≌△BDC SAS ，得EN =DC 进而可得AE +CD =AE +EN ，再由两点之间线段最短可得：AE +EN ≥AN ，所以当点E 在AN 上时，AE +EN 有最小值,即AE +CD 有最小值为AN ，利用勾股定理计算即可，熟练掌握相关知识点是解题的关键．解：过点C 作CN ∥AB 且使CN =BC ，连接EN ，AN ，∵CN ∥AB ，∴∠ECN =∠ABC ，∠ACN =180°-∠BAC =90°，在△CEN 和△BDC 中，EC =BD∠ECN =∠DBC CN =BC，∴△CEN ≌△BDC SAS ，∴EN =DC ，∴AE +CD =AE +EN ，由两点之间线段最短可得：AE +EN ≥AN ，所以当点E 在AN 上时，AE +EN 有最小值,即AE +CD 有最小值为AN ，∵AC =6，BC =CN =10，∴Rt △ACN 中，AN =AC 2+CN 2=62+102=234，∴AE +CD 最小值为：234，故答案为：234．13.(2024·安徽合肥·二模)如图，△ABC 和△ADE 都是等腰三角形，且∠BAC =∠DAE =120°，AB =8，O 是AC 的中点，若点D 在直线BC 上运动，连接OE ，则在点D 运动过程中，OE 的最小值为()A.42B.433C.32D.2【答案】D 【分析】设AB 的中点为Q ，连接DQ ，过点Q 作QH ⊥BC 于H ，证△AQD 和△AOE 全等得QD =OE ，因此当QD 为最小时，OE 为最小，根据“垂线段最短”得QD ≥QH ，故点D 与点H 重合时，QD 为最小，最小值为QH 的长，然后在Rt △BQH 中求出QH 的长即可．解：设AB 的中点为Q ，连接DQ ，过点Q 作QH⊥BC 于H ，如下图所示：∵△ABC 和△ADE 都是等腰三角形，且∠BAC =∠DAE =120°，∴AB =AC ，AD =AE ，∠QAD +∠DAC =∠DAC +∠OAE =120°，∴∠QAD =∠OAE ，∵点Q 是AB 的中点，点O 是AC 的中点，AB =AC ，∴AQ =AO ，在△AQD 和△AOE 中，AQ =AO∠QAD =∠OAE AD =AE，∴△AQD ≌△AOE (SAS )，∴QD =OE ，∴当QD 为最小时，OE 为最小，∵点Q 为AB 的中点，AB =8，点D 在直线BC 上运动，∴根据“垂线段最短”得：QD ≥QH ，∴当点D 与点H 重合时，QD 为最小，最小值为QH 的长，在△ABC 中，AB =AC =8，∠BAC =120°，∴∠B =∠C =12(180°-∠BAC )=30°，在Rt △BQH 中，∠B =30°，BQ =12AB =4，∴QH =12BQ =2，∴QD 的最小值为2，即OE 的最小值为2.故选：D ．【点拨】此题主要考查了等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，垂线段的性质，熟练掌握等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，理解垂线段最短是解决问题的关键，难点是正确地作出辅助线构造全等三角形和直角三角形．第三部分【中考链接与拓展延伸】【题型6】直通中考14.(2023·辽宁锦州·中考真题)如图，在Rt △ABC 中，∠ACB =90°，∠ABC =30°，AC =4，按下列步骤作图：①在AC 和AB 上分别截取AD 、AE ，使AD =AE ．②分别以点D 和点E 为圆心，以大于12DE 的长为半径作弧，两弧在∠BAC 内交于点M ．③作射线AM 交BC 于点F ．若点P 是线段AF 上的一个动点，连接CP ，则CP +12AP 的最小值是．【答案】23【分析】过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，先利用角平分线和三角形的内角和定理求出∠BAF =30°，然后利用含30°的直角三角的性质得出PQ =12AP ，则CP +12AP =CP +PQ ≥CH ，当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，利用含30°的直角三角的性质和勾股定理求出AB ，BC ，最后利用等面积法求解即可．解：过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，由题意知：AF 平分∠BAC ，∵∠ACB =90°，∠ABC =30°，∴∠BAC =60°，∴∠BAF =12∠BAC =30°，∴PQ =12AP ，∴CP +12AP =CP +PQ ≥CH ，∴当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，∵∠ACB =90°，∠ABC =30°，AC =4，∴AB =2AC =8，∴BC =AB 2-AC 2=43，∵S △ABC =12AC ⋅BC =12AB ⋅CH ，∴CH =AC ⋅BC AB =4×438=23，1故答案为：23．【点拨】本题考查了尺规作图-作角平分线，含30°的直角三角形的性质，勾股定理等知识，注意掌握利用等积法求三角形的高或点的线的距离的方法．15.(2020·新疆·中考真题)如图，在△ABC 中，∠A =90°,∠B =60°,AB =4，若D 是BC 边上的动点，则2AD+DC 的最小值为．【答案】12【分析】过点C 作射线CE ，使∠BCE =30°，再过动点D 作DF ⊥CE ，垂足为点F ，连接AD ，在Rt △DFC 中，∠DCF =30°，DF =12DC ，2AD +DC =2AD +12DC =2(AD +DF )当A ，D ，F 在同一直线上，即AF ⊥CE 时，AD +DF 的值最小，最小值等于垂线段AF 的长．解：过点C 作射线CE ，使∠BCE =30°，再过动点D 作DF ⊥CE ，垂足为点F ，连接AD ，如图所示：在Rt △DFC 中，∠DCF =30°，∴DF =12DC ，∵2AD +DC =2AD +12DC =2(AD +DF )，∴当A ，D ，F 在同一直线上，即AF ⊥CE 时，AD +DF 的值最小，最小值等于垂线段AF 的长，此时，∠B =∠ADB =60°，∴△ABD 是等边三角形，∴AD =BD =AB =4，在Rt △ABC 中，∠A =90°，∠B =60°，AB =4，∴BC =8，∴DC =4，∴DF =12DC =2，∴AF =AD +DF =4+2=6，∴2(AD +DF )=2AF =12，∴2AD +DC 的最小值为12，故答案为：12．【点拨】本题考查垂线段最短、等边三角形的判定和性质，含30度的直角三角形等知识，解题的关键是学会添加辅助线，构造数学模型，学会用转化的思想思考问题，属于中考填空题中的压轴题．【题型7】拓展延伸16.(2024·辽宁葫芦岛·二模)在△ABC 中，∠ABC =60°，BC =4，AC =5，点D ，E 在AB ，AC 边上，且AD=CE ，则CD +BE 的最小值是．【答案】61【分析】本题考查两点之间线段最短、勾股定理，全等三角形的性质和判定等知识，学会构造全等三角形解决问题是解题的关键．如图作CK∥AB，使得CK=CA．作BG⊥KC交KC的延长线于G．首先证明EK=CD，可得CD+BE =EK+EB≥BK，推出CD+BE的最小值为BK的长．解：如图作CK∥AB，使得CK=CA．作BG⊥KC交KC的延长线于G．∵CK∥AB，∴∠KCE=∠A，∵CK=CA，CE=AD，∴△CKE≌△CAD SAS，∴CD=KE，∵CD+BE=EK+EB≥BK，∴CD+BE的最小值为BK的长，∵KG∥AB，∴∠GCB=∠ABC=60°，∴∠CBG=90°-∠GCB=30°，在Rt△BCG中，∵∠G=90°，BC=4，∴CG=12BC=2，BG=BC2-CG2=23，∴GK=KC+CG=AC+CG=5+2=7，在Rt△KBG中，BK=GK2+BG2=72+(23)2=61．故答案为：61．17.(23-24八年级上·湖北武汉·阶段练习)如图，等腰△ABC中，∠BAC=100°，BD平分∠ABC，点N为BD上一点，点M为BC上一点，且BN=MC，若当AM+AN的最小值为4时，AB的长度是．【答案】4【分析】由等腰△ABC中，∠BAC=100°，可得∠ABC=∠ACB=180°-∠BAC2=40°，由BD平分∠ABC，可得∠ABD=12∠ABC=20°，如图，作∠BCE=∠ABD=20°，使CE=AB，连接EM，则∠ACE=∠ACB+E三点共线时，AM+AN最小，即AE=4，证明△ACE是等边三角形，则AC=AE=4，进而可求AB．解：∵等腰△ABC中，∠BAC=100°，=40°，∴∠ABC=∠ACB=180°-∠BAC2∵BD平分∠ABC，∠ABC=20°，∴∠ABD=12如图，作∠BCE=∠ABD=20°，使CE=AB，连接EM，∴∠ACE=∠ACB+∠BCE=60°，∵CE=AB，∠BCE=∠ABD，MC=BN，∴△CEM≌△BAN SAS，∴ME=AN，CE=AB，∴AM+AN=AM+ME，∴当A、M、E三点共线时，AM+AN最小，即AE=4，∵CE=AC，∠ACE=60°，∴△ACE是等边三角形，∴AC=AE=4，∴AB=4，故答案为：4．【点拨】本题考查了等腰三角形的性质，角平分线，全等三角形的判定与性质，等边三角形的判定与性质等知识．熟练掌握等腰三角形的性质，角平分线，全等三角形的判定与性质，等边三角形的判定与性质是解题的关键．。

将军饮马模型将军饮马问题是一类最值问题，常常与直线、角、三角形、四边形、圆、抛物线等图形结合出现在中考和竞赛中。

该问题主要利用构造对称图形的方法来解决求两条线段和差、三角形周长、四边形周长等问题。

通常作为压轴题出现。

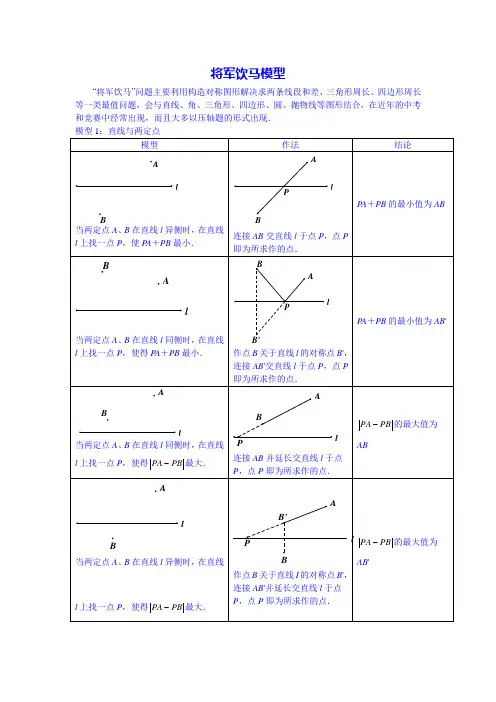
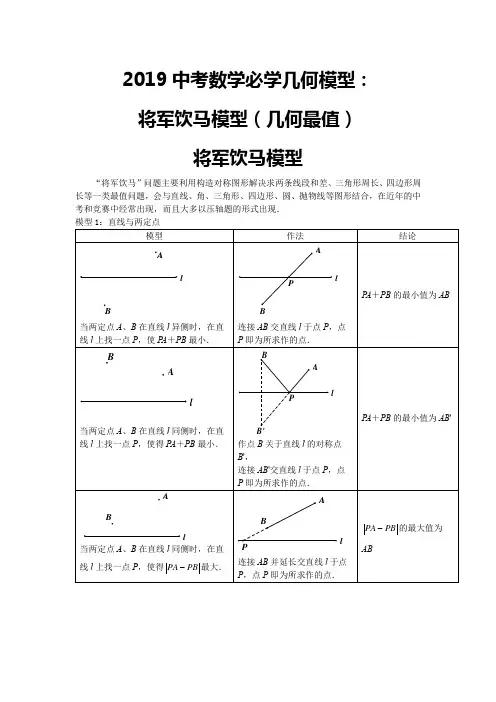
模型1：直线与两定点模型作法结论A当两定点A、B在直线l异侧时，在直线l上找一点P，使PA＋PB最小。

连接AB交直线l于点P，点P即为所求作的点。

当两定点A、B在直线l同侧时，先作点B关于直线l的对称点B'，再在直线l上找一点P，使PA＋PB最小。

连接AB'交直线l于点P，点P即为所求作的点。

当两定点A、B在直线l同侧时，先作点B关于直线l的对称点B'，再在直线l上找一点P，使PA PB最大。

连接AB'并延长交直线l于点P，点P即为所求作的点。

当两定点A、B在直线l异侧时，在直线l上找一点P，使PA PB最大。

作点B关于直线l的对称点B'，连接AB'并延长交直线l于点P，点P即为所求作的点。

当两定点A、B在直线l同侧时，在直线l上找一点P，使PA PB最小。

连接AB，作AB的垂直平分线交直线l于点P，点P即为所求作的点。

例1：如图，正方形ABCD的面积是12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，则PD＋PE最小值是23.解答：如图所示，点B与点D关于对角线AC对称。

因此，当点P为BE与AC的交点时，PD＋PE最小，且线段BE 的长。

由于正方形ABCD的面积为12，其边长为23.因为△ABE为等边三角形，所以BE＝AB＝23.因此，PD＋PE的最小值为23.例2：如图，已知△ABC为等腰直角三角形，AC＝BC＝4，∠BCD＝15°，P为CD上的动点，则PA PB的最大值是A′B。

解答：如图所示，作点A关于CD的对称点A′，连接A′C，连接A′B并延长交CD于点P，则点P就是PA PB的值最大时的点，PA PB＝A′B。

第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l异侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是，在OA 上找一点M ，在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、（M 在左），使NB MN AM ++最小,且d MN =.如图，21//l l ，21l l 、之间的距离为d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，且NB MN AM ++最小.如图，21//l l ，43//l l ,21l l 、之间的距离为1d ，43//l l 之间的距离为2d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，在43l l 、上分别找Q P 、两点，使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图，在⊙O 上找一点N ，在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1：如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值．P OBAMN例2：如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值．例3：如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)第3题图 第4题图 第5题图例4：如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．7例5：如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________． PDCBAA BCDMNNMDCBA例6：如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值．例7：如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3 B ．4 C ． D ．第7题图 第8题图 第9题图例8：如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) A B ．2 C ．D ．4例9：如图，在菱形ABCD 中，AC =BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( ) A ．6B ．C ．D ．4.5NMDBA E AFCDBNM DCBAEPDCBAM例10：如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)3第10题图 第11题图 第12题图例11：如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A ．B ．C ．D 例12：如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( )A ．B ．C ．D ．例13：如图，∠AOB =60°，点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )A B C ．6D ．3第13题图 第14题图 CBH FGEDCB AA BMOPN例14：如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为 ．例15：如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为___________．第15题图例16：如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．例17：如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．AB CD EFMx例18：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，求PD+PE 的最小值。

将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB 最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.关键：找对称点作法：作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PAC中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM 交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d（动点M位于动点N左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l于点N，将点N向左平移长度d，得到点M。

专题02 最值模型之将军饮马（遛马、过桥）模型将军遛马模型和将军过桥（造桥）模型是将军饮马的姊妹篇，它是在将军饮马的基础上加入了平移的思想，主要还是考查转化与化归等的数学思想。

在各类考试中都以中高档题为主，本专题就将军遛马模型和将军过桥（造桥）模型进行梳理及对应试题分析，方便掌握。

在解决将军遛马和将军过桥（造桥），不管是横向还是纵向的线段长度（定长），只要将线段按照长度方向平移即可，即可以跨越长度转化为标准的将军饮马模型，再依据同侧做对称点变异侧，异侧直接连线即可。

利用数学的转化思想，将复杂模型变成基本模型就简单容易多了，从此将军遛马和将军过桥（造桥）再也不是问题！模型1.将军遛马模型【核心思路】去除定量，组合变量（通过几何变换将若干段原本彼此分类的线段组合到一起）。

【模型解读】已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA +PQ +QB 的值最小。

（原理用平移知识解）（1）点A 、B 在直线m 两侧：（2）点A 、B 在直线m 同侧：如图1 如图2（1）如图1，过A 点作AC ∥m ,且AC 长等于PQ 长，连接BC ,交直线m 于Q ,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。

（2）如图2，过A 点作AE ∥m ,且AE 长等于PQ 长，作B 关于m 的对称点B ’,连接B ’E ,交直线m 于Q ,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。

【最值原理】两点之间线段最短。

例1．（2023·黑龙江·九年级校考期中）问题背景（1）如图（1），在公路l 的一侧有A ，B 两个工厂，A ，B 到公路的垂直距离分别为1km 和3km ，A ，B 之间的水平距离为3km ．现需把A 厂的产品先运送到公路上然后再转送到B 厂，则最短路线的长是_____km ．问题探究（2）如图（2），ACB △和DEF V 是腰长为2的两个全等的等腰直角三角形，90ACB DEF Ð=Ð=°，点A ，D 重合，点B ，F 重合，将ACB △沿直线AB 平移，得到A C B ¢¢¢△，连接QQ P【答案】（1）5km （2）存在，最小值为25（3）最短路线长为15km【分析】（1）根据最短路径的作法，找出最短路径A B ¢，再利用矩形的性质，求出BE 和A E ¢利用勾股定理即可求出最短路径；（2）根据平移的性质可知四边形CQEC ¢和AQEA ¢均为平行四边形，再利用最短路径作法得出则 AQ A Q ¢=，AQ BQ A Q ¢=\+\ 当点Q 与点P 重合时， AQ 连接AA ¢， 交l 于点C ， 过点由平移知CC AB ¢∥，CC QE ¢\∥．又 CQ EC ¢∥，\四边形 CQEC ¢是平行四边形，CC QE \¢=，CQ EC =¢由平移知CC AA ¢¢=，AA QE\¢=又n AB ∥，\四边形 AQEA ¢是平行四边形，AQ A E \=¢1A E C E AQ CQ QA CQ \+=+=+³¢¢\当点Q 与点P 重合时， A E C E ¢+¢过点C 作 1CG A A ^交 1A A 的延长线于点2AC AE ==Q ，2CG \=，13A G =例3．（2022·四川自贡·中考真题）如图，矩形ABCD 中，42AB BC ==，，G 是AD 的中点，线段EF 在边AB 上左右滑动；若1EF =，则GE CF +的最小值为____________．【答案】【分析】如图，作G关于AB的对称点G'，在CD上截取CH=1，然后连接HG'交AB于E，在EB上截取EF=1，此时GE+CF的值最小，可得四边形EFCH是平行四边形，从而得到G'H=EG'+EH=EG+CF，再由勾股定理求出HG'的长，即可求解．【详解】解：如图，作G关于AB的对称点G'，在CD上截取CH=1，然后连接HG'交AB于E，在EB上截取EF=1，此时GE+CF的值最小，∴G'E=GE，AG=AG'，∵四边形ABCD是矩形，∴AB∥CD，AD=BC=2∴CH∥EF，∵CH=EF=1，∴四边形EFCH是平行四边形，∴EH=CF，∴G'H=EG'+EH=EG+CF，∵AB=4，BC=AD=2，G为边AD的中点，∴AG=AG'=1 ∴DG′=AD+AG'=2+1=3，DH=4-1=3，+的最小值为∴HG¢===GE CF【点睛】此题主要考查了利用轴对称求最短路径问题，矩形的性质，勾股定理等知识，确定GE+CF最小时E，F位置是解题关键．【答案】35【分析】连接BD与AC交于点O，延长Q四边形ABCD是菱形，AC\\=+=，由平移性质知，246OM\+=FM FD\=，DF DE AF当点A、F、M三点共线时，\+的最小值为：AMDF DE模型2.将军过桥（造桥）模型【核心思路】去除定量，组合变量（通过几何变换将若干段原本彼此分类的线段组合到一起）。

将军饮马模型讲解【模型1】如图，定点A，B分布在定直线l的两侧，在直线l上找一点P，使得PA+PB的值最小.【作法】如图，连接AB，与直线l的交点即为所求点P.【模型2】如图，定点A，B分布在定直线的同侧，在直线l上找一点P，使得PA+PB的值最小.【作法】如图，作点B关于直线l的对称点B'，连接AB'，与直线l的交点即为所求点P.【模型3】如图，点P为角内一点，在射线l1，l2上分别找点M，N，使得△PMN的周长最小.【作法】如图，分别作点P关于两直线l1，l2的对称点P'和P"，连接P' P"，与两射线的交点即为所求点M，N.【模型4】如图，P，Q为角内的两个定点，在射线l1，l2上分别找点M，N，使得四边形PQMN的周长最小.【作法】如图，分别作点Q，P关于直线l1，l2的对称点Q'和P'，连接Q'P'，与两射线的交点即为所求点M，N.【模型5】如图，直线m∥n，A，B分别为m上方和n下方的定点(直线AB不与m垂直)，在m，n上分别求点M，N，使得MN⊥m，且AM+MN+BN的值最小.【作法】如图，将点A向下平移，使AA'=MN，连接A'B，交n于点N，过点N作MN⊥m于点M，则点M和点N即为所求.【模型6】如图，定点A，B分布在直线l的同侧，长度为a(a为定值）的线段MN在l上移动(点M在点N的左边)，在直线l上求两点M，N(点M在左)，使得MN=a，并使得AM+MN+NB的值最小.【作法】如图，将点A向右平移a个单位长度得到点A'，作点A'关于l的对称点A"，连接A"B，交直线l于点N，将点N向左平移a个单位长度得到点M，则点M和点N即为所求.典型例题典例1如图，∠AOB=30"，OC为∠AOB内部的一条射线，P为射线OC上一点，OP=4，点M，N分别为OA，OB边上的动点，则△PMN周).长的最小值为( ).A.2B.4C.8D.4√3典例2如图，BD平分∠ABC，E，F分别为线段BC，BD上的动点，AB=8，△ABC的面积为20，求EF+CF的最小值.典例3四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使△AMN的周长最小，则∠AMN+∠ANM的度数为( ).A.80°B.90°C.100°D.130°初露锋芒1.如图，直线L是一条河，P，Q是两个村庄.欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是( ).2.如图，在等腰△ABC 中，AB=AC ，D,E 分别是BC ，AC 的中点，点P 是线段AD 上的一个动点.当△PCE 的周长最小时，点P 的位置是( ).A.AD 与BE 的交点处B.AD 的中点处C.A 点处D.D 点处3.如图，∠AOB=60°，点P 是∠AOB 内的定点，且OP= √3，点M ，N 分别是射线OA ，OB 上异于点O 的动点，则△PMN 周长的最小值是( ).A.3√62B. 3√32C.6D.34. 如图所示，在边长为2的正三角形ABC 中，E 、F 、G 分别为AB 、AC 、BC 的中点，点P 线段EF 上一个动点，连接BP 、GP ，则△BPG 周长的最小值是________.感受中考1.(2016江苏苏州中考真题)矩形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标为(3，4)，D 是OA 的中点，点E 在AB 上，当△CDE 的周长最小时，点E 的坐标为( ).A.(3，1)B.(3，43) c.(3,53) D.(3,2)2.(2020贵州毕节中考模拟)如图，正方形ABCD 的边长为4，点E 是AB 的中点，点P 是边BC 上的动点，点Q 是对角线AC 上的动点(包括端点A ，C ），则EP+PQ 的最小值是__________.参考答案典例1【答案】B【解析】如图，作点P关于OA的对称点P1，作点P关于OB的对称点P2，连接P1 P2，与OA的交点为点M，与OB的交点为点N,则PM=P1M,PN=P2N.此时，△PMN的周长最小，为PM+MN+PN=P1M +MN+P2N=P1P2.连接OP1，OP2，则OP1=OP2=OP=4.又∵∠P1OP2=2∠AOB=60°，∴△OP1P2是等边三角形，∴P1P2=OP1=4.∴△PMN周长的最小值是4.故选B.典例2【答案】5【解析】如图，作E关于BD对称交于点E'，则EF= E'F∴EF+CF= E'F+ CF∴当C E'⊥AB时，EF+CF最小.∵S△ABC= 12×AB×C E'=12×8×C E' =20C E'=5∴EF+CF的最小值为5.典例3【答案】C【解析】如图，延长线段AB到点A'使得BA'=AB，延长线段AD到点A"使得DA"=AD，连接A'A"，与BC.CD分别交于点M，N，此时△AMN的周长最小.∴点A，A'关于直线BC对称，点A，A"关于直线CD对称.∵BA=BA',MB⊥AB. ∴MA=MA'.同理，NA=NA"，∴∠A'=∠MAB，∠A"=∠NAD.∵∠AMN=∠A'+∠MAB=2∠A', ∠ANM=∠A"+∠NAD=2∠A",∴∠AMN+∠ANM=2(∠A'+∠A").又∵∠BAD=130°, ∴∠A'+∠A"=180°-∠BAD=50°，∴∠AMN+∠ANM=100°.故选C.初露锋芒1. 【答案】D .【解析】根据两点之间，线段最短，作点P 关于直线L 的对称点P '，连接QP '交直线L 于点M 即可.故选D.2. 【答案】A【解析】∵EC 的长度固定，∴△PCE 的周长大小与PE+PC 的值有关， ∴当PE+PC 的值最小时，△PCE 的周长最小. 连接BE ，交AD 于点P '，如图，此时BP '+P 'E 的值最小，即BP+PE 的值最小. ∵点C 关于直线AD 的对称点为点B. ∴此时PE+PC 的值最小，∴当点P 在BE 与AD 的交点处时，△PCE 的周长最小. 故选A.3. 【答案】D.【解析】如图，分别作点P 关于射线OA. OB 的对称点C ，D ，连接CD 分别交OA ，OB 于点M ，N ，连接OC ，OD ， 则MP=MC ，NP=ND ，OC=OD=OP=√3, ∠BOP=∠BOD.∠AOP=∠AOC,∴PN+PM+MN=ND+MC+MN=DC.∠COD=∠BOP +∠BOD+∠AOP+∠AOC=2∠AOB=120°,∴∠OCD=∠ODC=30°.作OH ⊥CD 于点H ，则CH=DH.∵∠OCH=30°. ∴OH= 12 0C= √32, ∴CH=√3OH= 32，∴CD=2CH=3, 即△PAMN 周长的最小值是3.故选D.4. 【答案】3.【解析】要使△PBG 的周长最小，而BG=1一定，只要使BP+PG 最短即可，如图：连接AG 交EF 于M ，因为等边△ABC ，E 、F 、G 分别为AB 、AC 、BC 的中点，所以AG ⊥BC,EF ∥BC,则AG ⊥EF ，AM=MG,A 、G 关于EF 对称，即当P 和E 重合时，此时BP+PG 最小，即△PBG 的周长最小，AP =PG ，BP=BE ，最小值是：PB+ PG+ BG= AE+BE+ BG=AB+BG=2+1=3感受中考1.【答案】B【解析】如图，作点D 关于直线AB 的对称点H ，连接CH 交AB 于点E ，此时△CDE 的周长最小.∵B(3，4)，四边形OABC 是矩形，∴A(3,0)，C(0,4).∵D 是OA 的中点，∴D( 32，0)，H( 92，0). 设直线CH 的解析式为y=kx + b ，把C(0，4).H( 92，0)代人y= kx + b , 得{4=b 0= 92k + b 解得{k =−89b =4 ∴直线CH 的解析式为y=−89x+4， 当x=3时；y= 43， ∴点E 的坐标为(3，43). 故选B.2. 【答案】3√2【解析】如图，作点B关于BC的对称点E'，作E'Q'⊥AC于点Q'，交BC于点P.∴PE=PE'.∴PQ+PE=PE'+PQ.分析知，当Q与Q'重合时，PE+PQ的值最小(垂线段最短)，∵四边形ABCD是正方形，∴∠E'AQ'=45°.∵AE'=6，∴E'Q'=3√2∴PE+PQ的最小值为3√。

“将军饮马”模型详解与拓展平面几何中涉及最值问题的相关定理或公理有:① 线段公理：两点之间，线段最短. 并由此得到三角形三边关系；② 垂线段的性质：从直线外一点到这条直线上各点所连的线段中,垂线段最短. 在一些“线段和最值”的问题中,通过翻折运动，把一些线段进行转化即可应用①、② 的基本图形,并求得最值，这类问题一般被称之为“将军饮马"问题.问题提出:唐朝诗人李欣的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题．如图所示，诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营．请问怎样走才能使总的路程最短？模型提炼：模型【1】一定直线、异侧两定点直线l和l的异侧两点A、B，在直线l上求作一点P，使PA+PB最小解答：根据“两点之间,线段距离最短”，所以联结AB交直线l于点P，点P即为所求点模型【2】一定直线、同侧两定点直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最小解答：第一步：画点A关于直线l的对称点A’(根据“翻折运动”的相关性质,点A、A’到对称轴上任意点距离相等,如图所示，AP=A'P,即把一定直线同侧两定点问题转化为一定直线异侧两定点问题)第二步：联结A'B交直线l于点Q，根据“两点之间，线段距离最短”，此时“A’Q+QB”最短即“AQ+QB”最短模型【3】一定直线、一定点一动点已知直线l和定点A，在直线k上找一点B（点A、B在直线l同侧)，在直线l上找点P,使得AP+PB最小解答：第一步:画点A关于直线l的对称点A’第二步：过点A'做A'B⊥k于点B且交直线l于点P，根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短",可知A’P+PB最小即AP+PB最小模型【4】一定点、两定直线点P是∠MON内的一点，分别在OM，ON上作点A，B，使△PAB的周长最小解答:策略：两次翻折第一步：分别画点P关于直线OM、ON的对称点P1、P2第二步:联结P1P2，交OM、ON于点A、点B（根据“翻折运动”的相关性质,AP=AP1，BP=BP2；根据“两点之间，线段距离最短”可知此时AP1+BP2+AB最短即△ABP周长最短）拓展如果两定点、两定直线呢？“如图,点P，Q为∠MON内的两点,分别在OM，ON上作点A,B。

中考数学最值问题：将军饮马模型
“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

模型1：“两点一线”模型
模型2：“定点两线”模型
模型3：“两定点一定长”模型
2
1
2
1
几何中的将军饮马题型1：正方形中的将军饮马问题
【关于对角线对称】
【假装不存在的正方形】
【隐身的正方形】
题型2：三角形中的将军饮马【等边系列】
【隐身的等边三角形】
【角平分线系列之点点】
【角分线系列之点线】
题型3：矩形、菱形中的将军饮马【菱形高】
【折点在边上】
【折点与面积】
【全等与对称】
题型4：特殊角的对称【60°角的对称】
【30°角的对称】
【20°角的对称】
题型5：直角梯形中的将军饮马
题型6：圆形中的将军饮马
题型7：一次函数中的将军饮马
题型8：二次函数中的将军饮马。

华东师大版八年级数学下册“将军饮马模型”专题讲义及解析一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB 最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PAC中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM 交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d（动点M位于动点N左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l于点N，将点N向左平移长度d，得到点M。

将军饮马”模型详解与拓展 (1)A，B，C，D，使得四边形ABCD的周长最小。

该问题可以通过两次翻折来解决。

第一步：分别画点P、Q关于直线OM、ON的对称点P1、Q1、P2、Q2.第二步：联结P1Q2、P2Q1，交OM、ON于点A、B、C、D。

根据“翻折运动”的相关性质，AP=AP1，BP=BP2，CQ=CQ1，DQ=DQ2；根据“两点之间，线段距离最短”可知此时AP1+P1Q2+QC1+CD+DQ2+BP2最短即四边形ABCD周长最短。

将军饮马”问题源于唐朝诗人XXX的诗《古从军行》。

在这首诗中，将军从山脚下的A点出发，走到河边饮马后再到B点宿营。

问题是，怎样走才能使总的路程最短？该问题可以通过“线段和最值”问题中的“一定直线、异侧两定点”模型来解决。

根据“两点之间，线段距离最短”的原理，联结AB交直线l于点P，点P即为所求点。

除了“一定直线、异侧两定点”模型外，还有“一定直线、同侧两定点”、“一定直线、一定点一动点”和“一定点、两定直线”等模型。

这些模型都可以通过“翻折运动”来转化为“一定直线、异侧两定点”问题，然后应用“两点之间，线段距离最短”的原理来求解。

对于“一定点、两定直线”问题，需要通过两次翻折来解决。

分别画点P、Q关于直线OM、ON的对称点P1、Q1、P2、Q2，然后联结P1Q2、P2Q1，交OM、ON于点A、B、C、D。

根据“翻折运动”的相关性质和“两点之间，线段距离最短”的原理，可以得到四边形ABCD周长最短。

总之，“将军饮马”问题是一个典型的“线段和最值”问题，可以通过不同的模型和翻折运动来解决。

掌握这些模型和原理，可以帮助我们更好地解决类似的几何问题。

如何使四边形PAQB的周长最小？在数学问题中，我们经常需要优化某些值。

这个问题的目标是最小化四边形PAQB的周长。

为了解决这个问题，我们需要先找到四边形的特征。

四边形PAQB是由四个点P、A、Q和B组成的。

我们可以使用坐标系来表示这些点。

专题11 动点最值之将军饮马模型模型一、两定一动模型例题1. 如图，在矩形ABCD中，AB＝10，AD＝6，动点P满足S△P AB＝S矩形ABCD，则点P到A，B两点距离之和P A+PB的最小值为．【解答】解：设△ABP中AB边上的高是h．∵S△P AB＝S矩形ABCD，∴AB•h＝AB•AD，∴h＝AD＝4，∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．在Rt△ABE中，∵AB＝10，AE＝4+4＝8，∴BE＝＝＝2，即P A+PB的最小值为2．故答案为：2．【变式训练1】如图，正方形ABEF的面积为4，△BCE是等边三角形，点C在正方形ABEF外，在对角线BF 上有一点P，使PC＋PE最小，则这个最小值的平方为（）A. B. C. 12 D.【答案】B【解析】连接AC、AE，过点C作CG⊥AB，如图所示：∵正方形ABEF，∴AE⊥BF,OA＝OE，即可得：E关于BF的对称点是A，连接AC交BF于P，则此时EP＋CP的值最小，EP＋CP＝AC，∵正方形ABEF的面积为4，△BCE是等边三角形，∴AB＝BE＝2，BE＝BC＝2，在Rt△BCG中，∠CBG＝90º－60º＝30º，BC＝2，∴CG＝1，，，.【变式训练2】如图Rt△ABC和等腰△ACD以AC为公共边，其中∠ACB＝90°，AD＝CD，且满足AD⊥AB，过点D作DE⊥AC于点F，DE交AB于点E，已知AB＝5，BC＝3，P是射线DE上的动点，当△PBC 的周长取得最小值时，DP的值为（）A．B．C．D．【解答】解：连接PB、PC、P A，要使得△PBC的周长最小，只要PB+PC最小即可，∵PB+PC＝P A+PB≥AB，∴当P与E重合时，P A+PB最小，∵AD＝CD，DE⊥AC，∴AF＝CF，∵∠ACB＝90°，∴EF∥BC，∴AE＝BE＝AB＝2.5，∴EF＝BC＝1.5，∵AD⊥AB，∴△AEF∽△DEA，∴＝，∴DE＝＝，故选：B．【变式训练3】如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE＝2，当EF＋CF取得最小值时，则∠ECF的度数为多少？【答案】∠ECF＝30º【解析】过E作EM∥BC，交AD于N，如图所示：∵AC＝4，AE＝2，∴EC＝2＝AE，∴AM＝BM＝2，∴AM＝AE，∵AD是BC边上的中线，△ABC是等边三角形，∴AD⊥BC，∵EM∥BC，∴AD⊥EM，∵AM＝AE，∴E和M关于AD对称，连接CM交AD于F，连接EF，则此时EF＋CF的值最小，∵△ABC是等边三角形，∴∠ACB＝60º，AC＝BC，∵AM＝BM，∴∠ECF＝∠ACB＝30º.模型二、一定两动例.如图，∠AOB＝30°，点M、N分别是射线OB、OA上的动点，点P为∠AOB内一点，且OP＝4，则△PMN的周长的最小值为（）A．2B．4C．6D．8【解析】分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M′、N′，连接OC、OD、PM′、PN′．∵点P关于OA的对称点为C，∴PM′＝CM′，OP＝OC，∠COB＝∠POB；∵点P关于OB的对称点为D，∴PN′＝DN′，OP＝OD，∠DOA＝∠POA，∴OC＝OD＝OP＝4，∠COD＝∠COB+∠POB+∠POA+∠DOA＝2∠POA+2∠POB＝2∠AOB＝60°，∴△COD是等边三角形，∴CD＝OC＝OD＝4．∴当M、N与M′、N′重合时，△PMN周长最小＝PM′+M′N′+PN′＝DN′+M′N′+CM′＝CD＝4，选B．【变式训练1】如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB 上的动点，当△PMN周长取最小值时，则∠MPN的度数为（）A．140°B．100°C．50°D．40°【解答】解：分别作点P关于OA、OB的对称点P1、P2，连接P1P2，交OA于M，交OB于N，则OP1＝OP＝OP2，∠OP1M＝∠MPO，∠NPO＝∠NP2O，根据轴对称的性质，可得MP＝P1M，PN＝P2N，则△PMN的周长的最小值＝P1P2，∴∠P1OP2＝2∠AOB＝80°，∴等腰△OP1P2中，∠OP1P2+∠OP2P1＝100°，∴∠MPN＝∠OPM+∠OPN＝∠OP1M+∠OP2N＝100°，故选：B．【变式训练2】如图，在菱形ABCD中，AB，∠A＝120º，点P,Q,K分别为线段BC,CD，BD上的任意一点，则PK＋QK的最小值为.【解析】过点C作CE⊥AB，如图所示：∵菱形ABCD中，AB＝2，∠A＝120º，∴∠ABC＝60º，BC＝2，BD平分∠ABD，∴BE＝，CE＝BE＝，∵BD平分∠ABD，∴在AB上作点P关于BD的对称点P'，∴PK＋QK＝P'K＋KQ，当P',K,Q三点共线且P'Q⊥AB时，PK＋QK有最小值，即最小值为平行线AB,CD的距离，则最小值为.【变式训练3】如图所示，在四边形ABCD中，∠A＝90º，∠C＝90º，∠D＝60º，AD＝3，AB＝，若点M、N分别为边CD，AD上的动点，则△BMN的周长最小值为（）A. B. C. 6 D. 3【答案】C【解析】作点B关于CD、AD的对称点分别为点B'和点B''，连接B'B''交DC和AD于点M和点N，连接MB、NB；再DC和AD上分别取一动点M’和N’（不同于点M和N），连接M'B，M'B'，N’B和N'B''，如图1所示：∵B'B''＜M'B'＋M'N'＋N'B"，B'M'＝BM'，B"N'＝BN'，∴BM'＋M'N'＋BN'＞B'B"，又∵B'B"＝B'M＋MN＋NB"，MB＝MB'，NB＝NB''，∴NB＋NM ＋BM＜BM'＋M’N'＋BN'NB＋NM＋BM时周长最小；连接DB，过点B'作B'H⊥DB''于B’’D的延长线于点H，如图示2所示：在Rt△ABD中，AD＝3，AB＝，，∴∠2＝30º，∴∠5＝30º，DB＝DB''，又∵∠ADC＝∠1＋∠2＝60º，∴∠1＝30º，∴∠7＝30º，DB'＝DB，∴∠B'DB''＝∠1＋∠2＋∠5＋∠7＝120º，DB'＝DB''＝DB，又∵∠B'DB"＋∠6＝180º，∴∠6＝60º，∴HD＝，HB'＝3，在Rt△B'HB''中，由勾股定理得：B'B"＝，NB＋NM＋BM＝6，故选C.【变式训练4】如图，在△ABC中，∠C＝90°，CB＝CA＝4，∠A的平分线交BC于点D，若点P、Q分别是AC和AD上的动点，则CQ+PQ的最小值是2．【解答】解：如图，作点P关于直线AD的对称点P′，连接CP′交AD于点Q，则CQ+PQ＝CQ+P′Q＝CP′．∵根据对称的性质知△APQ≌△AP′Q，∴∠P AQ＝∠P′AQ．又∵AD是∠A的平分线，点P在AC边上，点Q在直线AD上，∴∠P AQ＝∠BAQ，∴∠P′AQ＝∠BAQ，∴点P′在边AB上．∵当CP′⊥AB时，线段CP′最短．∵在△ABC中，∠C＝90°，CB＝CA＝4，∴AB＝4，且当点P′是斜边AB的中点时，CP′⊥AB，此时CP′＝AB＝2，即CQ+PQ的最小值是2．故填：2．模型三、两段之差模型例.如图，在△ABC中，AB＝AC,AC的垂直平分线交AC于点N，交AB于点M，AB＝12，△BMC的周长是20，若点P在直线MN上，则PA－PB的最大值为（）A. 12B. 8C. 6D. 2【解答】B【解析】∵MN垂直平分AC，∴MA＝MC，BM＋MC＋BC＝20，BM＋MA＝AB＝12，∴BC＝20－12＝8，在MN上取点P，∵MN垂直平分AC，如图所示，连接PA、PB、PC，∴PA＝PC，∴PA－PB＝PC－PB，在△PBC中PC－PB＜BC当P、B、C共线时（PC－PB）有最大值，此时PC－PB＝BC＝8，故选B.【变式训练1】如图，在菱形ABCD中，AB＝6，∠ABC＝60º，AC与BD交于点O，点N在AC上且AN＝2，点M在BC上且BM＝BC,P为对角线BD上一点，则PM－PN的最大值为.【解答】2【解析】如图所示，作以BD为对称轴作N的对称点N'，连接PN',MN'，根据轴对称性质可知，PN＝PN'，∴PM－PN＝PM－PN'≤MN'，当P,M,N'三点共线时，取“＝”,∵在菱形ABCD中，AB＝6，∠ABC＝60º，∴AC＝6，∵O为AC中点，∴AO＝OC＝3，∵AN＝2，∴ON＝1，∴ON'＝1，CN'＝2，∴AN'＝4，，∴CM＝AB－BM＝6－4＝2，，∴PM∥AB∥CD，∠CMN'＝60º，∵∠N'CM＝60º，∴△N'CM为等边三角形，∴CM＝MN'＝2，即PM－PN的最大值为2.【变式训练2】如图，两点A、B在直线MN外的同侧，A到MN的距离AC＝16，B到MN的距离BD＝10，CD＝8，点P在直线MN上运动，则|P A﹣PB|的最大值等于10．【答案】10【解答】解：延长AB交MN于点P′，∵P′A﹣P′B＝AB，AB＞|P A﹣PB|，∴当点P运动到P′点时，|P A﹣PB|最大，∵BD＝10，CD＝8，AC＝16，过点B作BE⊥AC，则BE＝CD＝8，AE＝AC﹣BD＝16﹣10＝6，∴AB＝＝＝10，∴|P A﹣PB|的最大值等于10，故答案为：10．模型四、特殊型例1.如图，矩形ABCD中，AB＝4，BC＝8，E为CD的中点，点P、Q为BC上两个动点，且PQ＝3，当CQ＝时，四边形APQE的周长最小．【解答】解：点A向右平移3个单位到M，点E关于BC的对称点F，连接MF，交BC于Q，此时MQ+EQ最小，∵PQ＝3，DE＝CE＝2，AE＝＝2，∴要使四边形APQE的周长最小，只要AP+EQ最小就行，即AP+EQ＝MQ+EQ，过M作MN⊥BC于N，设CQ＝x，则NQ＝8﹣3﹣x＝5﹣x，∵△MNQ∽△FCQ，∴＝，∵MN＝AB＝4，CF＝CE＝2，CQ＝x，QN＝5﹣x，解得：x＝，则CQ＝故答案为：．【变式训练】如图，已知A（3，1）与B（1，0），PQ是直线y＝x上的一条动线段且PQ＝（Q在P的下方），当AP+PQ+QB最小时，Q点坐标为（）A．（，）B．（，）C．（0，0）D．（1，1）【解答】解：作点B关于直线y＝x的对称点B'（0，1），过点A作直线MN，使得MN平行于直线y＝x，并沿MN向下平移单位后得A'（2，0），连接A'B'交直线y＝x于点Q，如图理由如下：∵AA'＝PQ＝，AA'∥PQ，∴四边形APQA'是平行四边形，∴AP＝A'Q∵AP+PQ+QB＝B'Q+A'Q+PQ且PQ＝，∴当A'Q+B'Q值最小时，AP+PQ+QB值最小根据两点之间线段最短，即A'，Q，B'三点共线时A'Q+B'Q值最小∵B'（0，1），A'（2，0），∴直线A'B'的解析式y＝﹣x+1∴x＝﹣x+1，即x＝∴Q点坐标（，），故选：A．，课后训练1.如图，在锐角△ABC中，∠ACB＝50°；边AB上有一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最小时，∠MPN的度数是（）A．50°B．60°C．70°D．80°【答案】D【解析】∵PD⊥AC，PG⊥BC，∴∠PEC＝∠PFC＝90°，∴∠C+∠EPF＝180°，∵∠C＝50°，∠D+∠G+∠EPF＝180°，∴∠D+∠G＝50°，由对称可知：∠G＝∠GPN，∠D＝∠DPM，∴∠GPN+∠DPM＝50°，∴∠MPN＝130°﹣50°＝80°，选D．2.如图，在四边形ABCD中，DA⊥AB，DA＝6，∠B＋∠C＝150º，CD与BA的延长线交于E点，A刚好是EB 中点，P、Q分别是线段CE、BE上的动点，则BP＋PQ最小值是( )A. 12B. 15C. 16D. 18【答案】D【解析】如图，作点B关于CE的对称点F，连接BF，EF，则EB＝EF，∵∠B＋∠C＝150º，∴∠BEC＝30º，∴∠BEF＝60º，∴△BEF是等边三角形，连接BP，PF，PQ，则BP＝FP，∴BP＋QP＝FP＋PQ，当F，P，Q在同一直线上且FQ⊥EB时，BP＋PQ的最小值为FQ的长，此时，Q为EB的中点，故与A重合，∵DA⊥AB.DA＝6，∴AE ，∴Rt△QEF中，FQ＝AE＝18，∴BP＋PQ最小值值为18，故选D.3.如图，已知等边△ABC的面积为4，P、Q、R分别为边AB、BC、AC上的动点，则PR+QR的最小值是（）A．3B．2C．D．4【解答】解：如图，作△ABC关于AC对称的△ACD，点E与点Q关于AC对称，连接ER，则QR＝ER，当点E，R，P在同一直线上，且PE⊥AB时，PR+QR的最小值是PE的长，设等边△ABC的边长为x，则高为x，∵等边△ABC的面积为4，∴x×x＝4，解得x＝4，∴等边△ABC的高为x＝2，即PE＝2，故选：B．4.如图，平面直角坐标系中，分别以点A（2，3）、点B（3，4）为圆心，1、3为半径作⊙A、⊙B，M，N 分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值为（）A．5﹣4B．﹣1C．6﹣2D．【解答】解：作⊙A关于x轴的对称⊙A′，连接BA′分别交⊙A′和⊙B于M、N，交x轴于P，如图，则此时PM+PN最小，∵点A坐标（2，3），∴点A′坐标（2，﹣3），∵点B（3，4），∴A′B＝＝5，∴MN＝A′B﹣BN﹣A′M＝5﹣3﹣1＝5﹣4，∴PM+PN的最小值为5﹣4．故选：A．5.如图，矩形ABCD中，AB＝4，BC＝6，点P是矩形ABCD PC＋PD的最小值为.【解析】如图，作PM⊥AD于M，作点D关于直线PM的对称点E，连接PE，EC.设AM＝，∵四边形ABC都是矩形，AB//CD，AB＝CD＝4，BC＝AD＝6，，∴，∴＝2，∴AM＝2，DM＝EM＝4，在Rt△ECD，∵PM垂直平分线段DE，∴PD＝PE，∴PC＋PD＝PC＋PE≥EC，∴PD＋PC，∴PD＋PC.6.如图，矩形ABCO的边OC在x轴上，边OA在y轴上，且点C的坐标为（8，0），点A的坐标为（0，6），点E、F分别足OC、BC的中点，点M，N分别是线段OA、AB上的动点（不与端点重合），则当四边形EFNM 的周长最小时，点N的坐标为（4，6）．【解答】解：如图所示：作点F关于AB的对称点F′，作点E关于y轴的对称点E′，连接E′F′交AB与点N．∵C的坐标为（8，0），点A的坐标为（0，6），点E、F分别足OC、BC的中点，∴OE＝OE′＝4，FB＝CF＝3，∴E′C＝12，CF′＝9．∵AB∥CE′，∴△F′NB∽△F′E′C．∴＝＝，即＝，解得BN＝4，∴AN＝4．∴N（4，6）．故答案为：（4，6）．7.如图，在△ABC中，∠ACB＝90º，以AC为边在△ABC外作等边三角形ACD，过点D作AC的垂线，垂足为F，与AB相交于点E，连接CE（1）说明：AE＝CE＝BE；（2）若DA⊥AB,BC＝6，P是直线DE上的一点，则当P在何处时，PB＋PC最小，并求出此时PB＋PC的值.【答案】（1）见解析；（2）12【解析】（1）∵△ADC是等边三角形，DF⊥AC，∴DF垂直平分线段AC，∴AE＝EC，∴∠ACE＝∠CAE，∵∠ACB＝90º，∴∠ACE＋∠BCE＝90º＝∠CAE＋∠B＝90º，∴∠BCE＝∠B，∴CE＝EB，∴AE＝CE＝BE；（2）连接PA,PB,PC，如图所示：∵DA⊥AB，∴∠DAB＝90º，∵∠DAC＝60º，∴∠CAB＝30º，∴∠B＝60º，∴BC＝AE＝EB＝CE＝6.∴AB＝12，∵DE垂直平分AC，∴PC＝AP，∴PC＝PB＋PA，∴当PB＋PC最小时，也就是PB＋PA最小，即P,B,A共线时最小，∴当点P与点E共点时，PB＋PC的值最小，最小值为12.8.已知：矩形ABCD中，AD＝2AB，AB＝6，E为AD中点，M为CD上一点，PE⊥EM交CB于点P，EN平分∠PEM交BC于点N.（1）求证：PE＝EM；（2）用等式表示BP2、PN2、NC2三者的数量关系，并加以证明；（3）过点P作PG⊥EN于点G，K为EM中点，连接DK、KG，求DK＋KG＋PG的最小值.【答案】（1）见解析；（2）BP2＋NC2＝PN2；（3）【解析】（1）证明：过P作PQ⊥AD于Q，则PQ＝AB，如图所示：∵AD＝2AB，E为AD中点，∴AD＝2DE，∴PQ＝DE，∵PE⊥EM，∴∠PQE＝∠D＝∠PEM＝90º，∴∠QPE＋∠PEQ＝∠PEQ＋∠DEM＝90º，∴∠QPE＝∠DEM，∴△PQE≌△EDM（ASA），∴PE＝EM；（2）三者的数量关系是：BP2＋NC2＝PN2①点N与点C重合时，P为BC的中点，显然BP2＋NC2＝PN2成立；②点P与点B重合时，N为BC的中点，显然BP2＋NC2＝PN2成立；③证明：连接BE、CE，如图所示：∵四边形ABCD为矩形，AD＝2AB，E为AD中点，∴∠A＝∠ABC＝90º，AB＝CD＝AE＝DE，∴∠AEB＝45º，∠DEC＝45º，在△ABE和△DCE中，，∴△ABE≌△DCE（SAS），∠BEC＝90º，∴BE＝CE，∴∠EBC＝∠ECB＝45º，∴∠EBC＝∠ECD，又∵∠BEC＝∠PEM＝90º，∴∠BEP＝∠MEC，∠EBP＝∠ECM在△BEP和△CEM中，，∴△BEP≌△CEM（ASA），∴BP＝MC，PE＝ME，∵EN平分∠PEM，∴∠PEN＝∠MEN＝45º，在△EPN和△EMN中，，∴△EPN≌△EMN（SAS），∴PN＝MN，在Rt△MNC中有：MC2＋NC2＝MN2，∴BP2＋NC2＝PN2；（3）连接PM，如图所示：由（2），可得PN ＝MN，PE＝ME，∴EN垂直平分PM，PG⊥EN，∴P、G、M三点共线，且G为PM的中点，∵K为EM中点，D＝90º，，由（2），可得△PEM为等腰直角三角形，根据勾股定理，可得，，∴当ME取得最小值时，DK＋GK＋PG取得最小值，即当ME＝DE＝6时，DK＋GK＋PG有最小值，最小值为.。

初中数学几何模型（十）将军饮马模型1、两定一动：在直线l上作一点P，使AP+BP最短。

如图：作法：作点A关于直线l的对称点A1，连接A1B，与l的交点就是所求作的P点。

即：AP+BP=A1B（两点之间，线段最短。

）2、一定两动：在∠AOB的两边上分别求点M、N，使△PMN周长最小。

作法：分别作点P关于OA、OB的对称点P1、P2，连接P1P2，与OA交于点M，与OB交于点N，点M、N为所求作的点。

即：PM+MN+PN=P1P2（两点之间，线段最短。

），此时，△PMN周长最小。

3、两定两动：（1）如图，点P、Q使是∠AOB内的两个定点，在∠AOB的两边上分别求作点M、N，使四边形PMNQ周长最小。

作法：作点P关于OA的对称点P1，作点Q关于OB的对称点Q1；连接P1Q1，与OA交于点M，与OB交于点N，点M、N即为所求作的点。

即：PM+MN+NQ=P1Q1，（两点之间，线段最短。

）此时，四边形PMNQ周长最小。

（2）如图，点A、B在直线l外，在直线l上求两点M、N（M在左），使得MN=a，并使AM+MN+NB最短。

作法：如图，将点A向右平移a个单位到A1，作点A1关于直线l 的对称点A2，连接A2B，与直线l交于点N，将点N向左平移a个单位即为点M。

即：AM+MN+NB=a+A2B（两点之间，线段最短。

），此时，AM+MN+NB最短。

4、点-线：点与直线的连线中，垂线段最短。

如图，点P在∠AOB内，在OA、OB上分别取M、N，使得PM+PN 最小。

作法：过点P作关于OA的对称点P1，过点P1作OB的垂线，交OA于点M，交OB于点N。

点M、N即为所求作的点。

即：PM+MN=P1M+MN=P1N（点直线的距离垂线段最短），此时，PM+PN最小。

5、PA—PB型：三角形两边之差小于第三边。

如图，点A、B在直线l两侧，在直线l上取点P，使得|PA-PB|最大。

作法：过点B作关于直线l的对称点B1，连接A B1并延长交直线l于一点，即为所求的点P。