货币时间价值系数表
- 格式：docx
- 大小：107.31 KB
- 文档页数：7
下载文档原格式
合集下载
货币的时间价值
+50000=281855 元
14
普通年金终值计算：
更一般的， 假设每年收付的金额为A， 利率为i, 期数为n, 则计算复利终值的年金终值FVAn的公 式如下：
从这个公式可以看出来， 这是一个等比数列求 和公式， 简化后可以得到：
记：
15
普通年金终值计算：
例6：某父母为孩子在10年后上大学准备5万元 钱， 假设银行的存款年利率为6%， 复利计息， 那么在这10年中， 每年年末要存入多少元？
Lecture 2：货币的时间价值 (Time Value of Money)
潘贵芳 宁波诺丁汉大学
金融与投资
1
教学内容：
货币的时间价值 单利/复利的现值与终值 年金（普通年金、预付年金、递延年金、永
续年金） 货币时间价值应用中的几个问题 （利率或
折现率、期限、名义利率和实Fra bibliotek利率）2
货币的时间价值概述：
10
复利计息现值与终值：
例4 （改例3， p6）：王先生计划于5年后买车， 需购车款13万元， 王先生打算现在存笔钱到银 行， 5年后正好用于购车， 银行目前的存款利 率为6%, 且复利计息，一年一计， 则王先生需 要存入的金额为：
PV=13*（P/F，6%，5）=13*0.7473=9.71 （万元） 按单利计息时，王先生需要存入10万元，而当
这一问题， 第二年计算利息的本金是上一年的年末终值， 也就是1080， 又再按8%的利息计算， 也就是说 FV2=FV1*（1+i）=PV*（1+i）*（1+i）=PV*（1+i）2 =1000*（1+8%）2 =1166.4元 第三年末， 该账户金额为： FV3=FV2*（1+i）=PV*（1+i）2（1+i）=PV（1+i）3=1000*（1+8%） 3=1259.7元 所以， 更一般的， 在第n年末， 该账户的终值FVn应该为： FVn=PV (1+i)n=PV (F/P, i, n) (p.25)
14
普通年金终值计算：
更一般的， 假设每年收付的金额为A， 利率为i, 期数为n, 则计算复利终值的年金终值FVAn的公 式如下：
从这个公式可以看出来， 这是一个等比数列求 和公式， 简化后可以得到：
记：
15
普通年金终值计算：
例6：某父母为孩子在10年后上大学准备5万元 钱， 假设银行的存款年利率为6%， 复利计息， 那么在这10年中， 每年年末要存入多少元？
Lecture 2：货币的时间价值 (Time Value of Money)
潘贵芳 宁波诺丁汉大学
金融与投资
1
教学内容：
货币的时间价值 单利/复利的现值与终值 年金（普通年金、预付年金、递延年金、永
续年金） 货币时间价值应用中的几个问题 （利率或
折现率、期限、名义利率和实Fra bibliotek利率）2
货币的时间价值概述：
10
复利计息现值与终值：
例4 （改例3， p6）：王先生计划于5年后买车， 需购车款13万元， 王先生打算现在存笔钱到银 行， 5年后正好用于购车， 银行目前的存款利 率为6%, 且复利计息，一年一计， 则王先生需 要存入的金额为：
PV=13*（P/F，6%，5）=13*0.7473=9.71 （万元） 按单利计息时，王先生需要存入10万元，而当
这一问题， 第二年计算利息的本金是上一年的年末终值， 也就是1080， 又再按8%的利息计算， 也就是说 FV2=FV1*（1+i）=PV*（1+i）*（1+i）=PV*（1+i）2 =1000*（1+8%）2 =1166.4元 第三年末， 该账户金额为： FV3=FV2*（1+i）=PV*（1+i）2（1+i）=PV（1+i）3=1000*（1+8%） 3=1259.7元 所以， 更一般的， 在第n年末， 该账户的终值FVn应该为： FVn=PV (1+i)n=PV (F/P, i, n) (p.25)
投资管理考核试题及答案
投资管理考核试题及答案一、单项选择题6.1 下列投资活动中，属于间接投资的是（ ）。
A.建设新的生产线B.开办新的子公司C.吸收合并其他企业 D.购买公司债券6.2 A公司某项设备近期正在进行更新改造，该设备的原值为50 000元，已计提折旧30 000元，目前市面上同类新设备的价格为80 000元。
如果A公司将该旧设备出售，预计的售价为10 000元。
假设所得税税率为25%，则该项目建设期现金净流量为（ ）元。
A.-80 000 B.-70 000 C.-72 500 D.-67 5006.3 某投资项目需要在第一年年初投资840万元，寿命期为10年，每年可带来营业现金流量180万元，已知按照必要收益率计算的10年期年金现值系数为7.0，则该投资项目的年金净流量为（ ）万元。
A.60 B.120 C.96D.1266.4 下列各项中，由于计提折旧而减少的所得税额可用（）进行计算。
A.折旧额×所得税税率 B.折旧额×（1-所得税税率）C.（付现成本+折旧）×所得税税率 D.（付现成本+折旧）×（1-所得税税率）6.5 某公司投资18.6万元购入一台设备，预计使用5年，预计净残值0.6万元，按照直线法计提折旧。
设备投产后预计每年净利润为2.4万元，则该项目的投资回收期为（ ）年。
A.2.8 B.3.1 C.3.9 D.4.26.6 某公司计划投资建设一条新生产线，投资总额为60万元，预计新生产线投产后每年可为公司新增税后营业利润4万元，生产线的年折旧额为6万元，则该投资的静态回收期为（ ）年。
A.5 B.6 C.10 D.156.7 某公司拟投资900万于一个游乐园建设项目，预计该项投资的周期为4年，每年现金净流量依次为240万、300万、400万、360万，则该项目的投资回收期为（ ）年。
A.2.7 B.3 C.2.9D.2.86.8 采用静态回收期法进行项目评价时，下列表述错误的是（）。
终值现值系数表
终值现值系数表
终值现值系数表是一种用于计算未来一段时间内资金的终值与现值的比例的工具。
它可以帮助人们在投资和财务决策中考虑时间价值的因素。
终值现值系数是根据给定的利率和时间期限计算得出的。
它可以用于计算资金在未来某个时点的价值，或者用于计算未来一段时间内的利息或回报。
下面是一个简单的终值现值系数表的示例：
时间期限利率(%) 终值现值系数
1年 5% 1.05
2年 5% 1.1025
3年 5% 1.1576
4年 5% 1.2167
5年 5% 1.2815
终值现值系数是根据复利计算得出的。
在上面的示例中，假设每年的利率为5%。
例如，如果你有100元的现金，并且把它存入一个年利率为5%的银行账户，那么在一年后你的账户上将有105元。
根据上面的表格，我们可以知道，这100元现金在两年后的价值为110.25元。
使用终值现值系数表可以方便地计算资金在未来某个时点的价值，或者计算未来一段时间内的利息或回报。
财务管理计算分析题母题
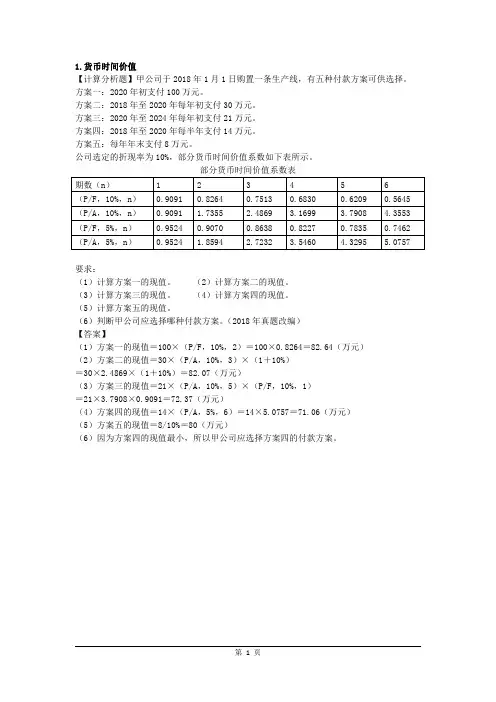
1.货币时间价值【计算分析题】甲公司于2018年1月1日购置一条生产线，有五种付款方案可供选择。
方案一：2020年初支付100万元。
方案二：2018年至2020年每年初支付30万元。
方案三：2020年至2024年每年初支付21万元。
方案四：2018年至2020年每半年支付14万元。
方案五：每年年末支付8万元。
公司选定的折现率为10%，部分货币时间价值系数如下表所示。
部分货币时间价值系数表期数（n）123456（P/F，10%，n）0.90910.82640.75130.68300.62090.5645（P/A，10%，n）0.9091 1.7355 2.4869 3.1699 3.7908 4.3553（P/F，5%，n）0.95240.90700.86380.82270.78350.7462（P/A，5%，n）0.9524 1.8594 2.7232 3.5460 4.3295 5.0757要求：（1）计算方案一的现值。
（2）计算方案二的现值。
（3）计算方案三的现值。
（4）计算方案四的现值。
（5）计算方案五的现值。
（6）判断甲公司应选择哪种付款方案。
（2018年真题改编）【答案】（1）方案一的现值＝100×（P/F，10%，2）＝100×0.8264＝82.64（万元）（2）方案二的现值＝30×（P/A，10%，3）×（1＋10%）＝30×2.4869×（1＋10%）＝82.07（万元）（3）方案三的现值＝21×（P/A，10%，5）×（P/F，10%，1）＝21×3.7908×0.9091＝72.37（万元）（4）方案四的现值＝14×（P/A，5%，6）＝14×5.0757＝71.06（万元）（5）方案五的现值＝8/10%＝80（万元）（6）因为方案四的现值最小，所以甲公司应选择方案四的付款方案。
2-货币时间价值
② 扣除法，其基本思路是假定递延期中也进行收付，先将递 延年金视为正常的普通年金，计算普通年金现值，然后再扣 除递延期内未发生的普通年金，其结果即为递延年金的现值。 其计算公式为：
PV AP / A, r, n P / A, r, m
7.永续年金现值（已知永续年金A，求永续年金现值PV） 永续年金的现值可以通过普通年金现值的计算公式推导得出。
1 (1 r ) ( n 1) PV A 1 r
也可以写成：
PV A( P / A, r , n 1) 1
PV A( P / A, r , n)(1 r )
5.递延年金终值（已知递延年金A，求递延年金终值FV）
递延年金的第一次现金流量并不是发生在第一期的，但
FV（Future value的简写）表示。
（四）单一支付款项和系列支付款项
单一支付款项是指在某一特定时间内只发生一次的简单现
金流量，如投资于到期一次偿还本息的公司债券就是单一支 付款项的问题。
系列支付款项是指在n期内多次发生现金流入或现金流出。
年金是系列支付款项的特殊形式，是在一定时期内每隔相同
时点： 0 1 2 3
现金流：
-100
-150
+50
+200
发生时间：
现在
第1年末 或 第2年初
第2年末 或 第3年初
第3年末 或 第4年初
图2-1 货币时间价值时间轴
需要注意两点：
（1）除0点以外，每个时点数字代表的都是两个含义，即当期的期末和 下一期的期初，如时点t=1就表示第1期的期末和第2期的期初。 （2）现金流数字前面的正负号表示的是现金流入还是现金流出，其中正 号表示的数值是从公司外部流入到公司内部的现金，如收回的销售收入、 固定资产的残值收入等，而负号表示的数值则是指从公司内部流入到外
3 含时间因素的货币等值
–所谓单利既是指每期均按原始本金计算利息 –计算公式： I=Pni
F=P(1+ni)
I--利息 P--借入本金 n--计息期数 i--利率 F—n年末的本利和
例：假如以年利率6%借入资金1000元,共借4年,其偿还的情况如下表
年 1 2 3 4
年初欠款 1000 1060 1120 1180
年末应付利息 1000 × 0.06=60 1000 × 0.06=60 1000 × 0.06=60 1000 × 0.06=60
式中[(1+i)n-1]/[i(1+i)n]称为等额支付系列 现值系数，记为（P/A i,n)
• 某工程项目每年获净收益100万元，利率为 10%，项目可用每年获净收益在6年内回收 初始投资，问初始投资为多少？
解：P=100（P/A 10，6）万元
=100*4.3553万元 =435.53万元
均匀梯度系列公式
n－1 n
A2= G [
1 n － （A/F,i,n）] i i
梯度系数（A/G,i,n） （可查表）
支付系列为均匀增加，则有 支付系列为均匀减少，则有
A=A1+A2 A=A1－A2
• 若某人第1年支付一笔10000元的保险金， 之后9年内每年少支付1000元，若10年内采 用等额支付的形式，则等额支付款为多少 时等价于原保险计划?
=100（P/F 12，5） =100*0.5674 =56.74万元
等额支付系列复利公式
(1 i) 1 FA i
n
式中（1+i)n-1/i称为等额支付系列复利系数， 记为（F/A i,n)
F 0 1 2 3 n-1 n
A
A
F=P(1+ni)
I--利息 P--借入本金 n--计息期数 i--利率 F—n年末的本利和
例：假如以年利率6%借入资金1000元,共借4年,其偿还的情况如下表
年 1 2 3 4
年初欠款 1000 1060 1120 1180
年末应付利息 1000 × 0.06=60 1000 × 0.06=60 1000 × 0.06=60 1000 × 0.06=60
式中[(1+i)n-1]/[i(1+i)n]称为等额支付系列 现值系数，记为（P/A i,n)
• 某工程项目每年获净收益100万元，利率为 10%，项目可用每年获净收益在6年内回收 初始投资，问初始投资为多少？
解：P=100（P/A 10，6）万元
=100*4.3553万元 =435.53万元
均匀梯度系列公式
n－1 n
A2= G [
1 n － （A/F,i,n）] i i
梯度系数（A/G,i,n） （可查表）
支付系列为均匀增加，则有 支付系列为均匀减少，则有
A=A1+A2 A=A1－A2
• 若某人第1年支付一笔10000元的保险金， 之后9年内每年少支付1000元，若10年内采 用等额支付的形式，则等额支付款为多少 时等价于原保险计划?
=100（P/F 12，5） =100*0.5674 =56.74万元
等额支付系列复利公式
(1 i) 1 FA i
n
式中（1+i)n-1/i称为等额支付系列复利系数， 记为（F/A i,n)
F 0 1 2 3 n-1 n
A
A
《财务管理学》第二章 货币的时间价值
普通年金终值计算公式的推导如下：
0 1 2 n-2 n-1 n
理 财
A
A
A
A
A
A(1+i)0 A(1+i)1 A(1+i)2
FVAn = A(1+i)0+A(1+i)1+A(1+i)2+…+A(1+i)n-2+A(1+i)n-1
其中(1+i)0+(1+i)1+(1+i)2+…+(1+i)n-2+(1+i)n-1为一公比为 1+i的等比数列求和式，其值由i和n确定，称其为利率为i期 数为n的年金终值系数，简写为FVIFAi,n。
第二节 风险报酬
思考：你认为什么是风险？
理 财
一、风险的概念
•
在做某件事乊前我们就知道这件事必然会 出现什么样的结果，那么做这事有风险吗？ 答：没有风险。 • 如果我们判断：这事八九成是一个什么什 么结果，我们会得出什么结论？
答：做这事很有把握，风险不大。
如果我们说这事结果很难说，你会得 出什么结论？ 答：做这事风险很大。
理 财
课堂作业
1.某人准备为他刚读初中一年级的小 孩存一笔 款以支付其读大学的学费。预计６年以后的 学费是４万元，现银行存款利率为５％，那 么此人现在应存入多少钱？
当2中每年存款额相等时则有简便算 法，这就是年金的计算。
理 财
四、年金终值与年金现值的计算
年金是一定时期内发生的一系列金额相等的 收支款项，如折旧、租金、养老金、银行按 揭贷款的等额还款额、零存整取或整存零取 储蓄等等。年金按款项收付发生的时点不同 分为普通年金（后付年金）、先付年金、延 期年金、永续年金等。
货币的时间价值
货币的时间价值货币时间价值第一节资金时间价值一、资金时间价值的概念我国经济学家认为：资金时间价值是指货币在周转过程中随着时间推移发生的增值二、货币时间价值的计算(一)单利终值和现值的计算1、单利终值基本公式：Vn=V0×(1+n×i)终值本金期数利率例如，将*****元存入银行，年利息率为10%,5年后单利终值应为：Vn=V0×(1+n×i)=*****×(1+5×10%)=*****(元)2、单利现值Vn 基本公式：V0 = ――――― 1+n×i 例如，某人打算5年后得到*****元，若年利率10%,按单利计算，现在应存多少钱？Vn ***** V0 = ――――― = ――――――― 1+n×i 1+ 5 × 10% =6666.67(元)(二)复利终值和现值的计算1、复利终值基本公式：Vn=V0×(1+i)n =V ×(F/P,i,n) 0 例如，将*****元存入银行，年利息率10%,按复利计算，5年后应得多少钱？Vn=V0×(1+i)n =*****×(1+10%)5=*****.1元复利现值系数Vn 2、复利现值Vn (P/ Fn,i,n)复利终值系数(F / P,i,n)基本公式：V0 =―――― (1+i)n= Vn (P/ Fn,i,n)例如，某人打算5年后得到*****元，年利息率10%,按复利计算，现在应存多少钱？Vn V0 =―――― (1+i)n***** = ―――― =*****×0.6209=6209元(1+10%)5(三)年金及其计算1、年金是指相同的间隔期收付同等数额的款项。
如：计提折旧、收付租金等年金终值或年金现值的计算实际上是复利终值或复利现值计算的简化形式。
年金的种类普通年金：每期期末发生的年金预付年金：每期期初发生的年金永续年金：无限期连续收付的年金递延年金：第一期末以后某一时点开始收入或支出的年金。
知识点3：货币时间价值
2.单利现值
•
【例题】某人为了5年后能从银行取出
500元，在年利率2%的情况下，目前应存入
银行的金额是多少？假设银行按单利计息。
•
•
• 『解答』P＝F/（1＋n×i）＝500/（1＋ 5×2%）＝454.55（元）
• 单利终值
单利现值
• F＝P（1＋n×i）
P＝F/（1＋n×i）
• 单利的终值和单利的现值互为逆运算； 单利终值系数（1＋n×i）和单利现值系数 1/（1＋n×i）互为倒数。
93.312 1259.712×8%
1080
0
1166.4
0
1259.712 0
1360.489 1360.489
＝100.777
一次支付的终值和现值
• 一、单利模式下的终值和现值
•
【例题】某人将100元存入银行，年利
率2%，假设单利计息，求5年后的终值。
•
•
• 『解答』F＝P×（1＋n×i）＝100×（1＋ 5×2%）＝110（元）
0 0 0 1320
80
• 【例题】假如以复利方式借入1000元，年
利率8%，四年末偿还，则各年利息和本利
和，如表所示。（单位：元）
使用期 年初款额 年末利息
年末本利 和
年末偿还
1000×8%＝80
1 2 3 4
1000 1080 1166.4 1259.712
1080×8%＝
86.4 1166.4×8%＝
二、复利模式下的终值和现值
• 利生利、利滚利
•
【例题】某人将100元存入银行，复利
年利率2%，求5年后的终值。
•
•
• 『解』F＝P×（1＋i）n＝100×（1＋2%）5 ＝100×（F/P，2%，5）＝100×1.1041＝ 110.41（元）
第08讲_投资管理(2)
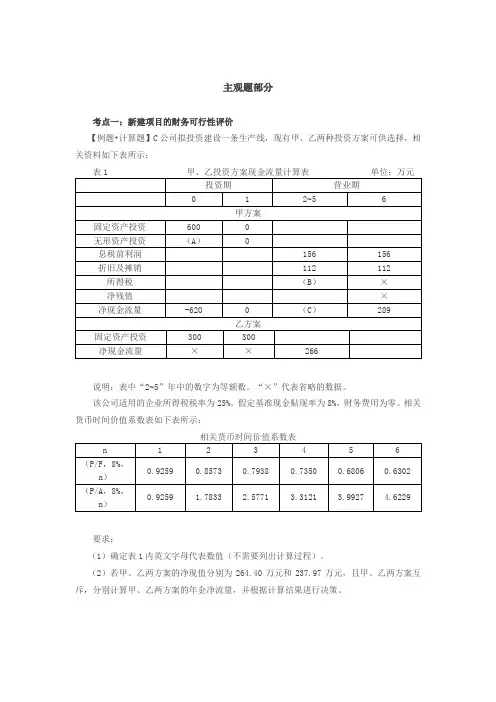
要求：（1）确定表1内英文字母代表数值（不需要列出计算过程）。
（2）若甲、乙两方案的净现值分别为264.40万元和237.97万元，且甲、乙两方案互斥，分别计算甲、乙两方案的年金净流量，并根据计算结果进行决策。
要求：（1）根据资料1和资料2，计算新生产线项目的下列指标：①原始投资额；②NCF1-7；③NCF8；④NPV。
（2）判断是否应该购置该生产线，并说明理由。
【答案】（1）原始投资额=50000+5500=55500（万元）每年折旧额=（50000-2000）/8=6000（万元）时预计生产线最终残值为500万元。
资料三：乙公司目前资本结构（按市场价值计算）为：总资本40000万元，其中债务资本16000万元（市场价值等于其账面价值，平均年利率为8%），普通股股本24000万元（市价6元/股，4000万股），公司今年的每股股利（D0）为0.3元，预计股利年增长率为10%；且未来股利政策保持不变。
资料四：乙公司投资所需资金7200万元需要从外部筹措，有两种方案可供选择：方案一为全部增发普通股，增发价格为6元/股。
方案二为全部发行债券，债券年利率为10%，按年支付利息，到期一次性归还本金。
假设不考虑筹资过程中发生的筹资费用。
乙公司预期的年息税前利润为4500万元。
要求：（1）根据资料一和资料二，计算A方案的下列指标：①投资期现金净流量；②年折旧额；③生产线投入使用后第1~5年每年的营业现金净流量；④生产线投入使用后第6年的现金净流量；⑤净现值。
（2）分别计算A、B方案的年金净流量，据以判断乙公司应选择哪个方案，并说明理由。
（3）根据资料二，资料三和资料四：①计算方案一和方案二的每股收益无差别点（以息税前利润表示）；②计算每股收益无差别点的每股收益；③运用每股收益分析法判断乙公司应选择哪一种筹资方案，并说明理由。
（4）假定乙公司按方案二进行筹资，根据资料二、资料三和资料四计算：①乙公司普通股的资本成本；②筹资后乙公司的加权平均资本成本。
货币时间价值的计算
货币时间价值的计算文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]货币时间价值的计算（二）单利的终值与现值在时间价值计算中，经常使用以下符号：P 本金，又称现值；i 利率，通常指每年利息与本金之比；I 利息；F 本金与利息之和，又称本利和或终值；n 期数1、单利终值单利终值的计算可依照如下计算公式：F = P + P·i·n= P (1 + i·n)【例1】某人现在存入银行1000元，利率为5%，3年后取出，问：在单利方式下，3年后取出多少钱F = 1000 × ( 1 + 3 × 5% ) = 1150 (元)在计算利息时，除非特别指明，给出的利率是指年利率。
对于不足1年的利息，以1年等于360天来折算。
2、单利现值单利现值的计算同单利终值的计算是互逆的，由终值计算现值称为折现。
将单利终值计算公式变形，即得单利现值的计算公式为：P = F / (1 + i·n)【例2】某人希望在3年后取得本利和1150元，用以支付一笔款项，已知银行存款利率为5%，则在单利方式下，此人现在需存入银行多少钱P = 1150 / ( 1 + 3 × 5% ) = 1000 (元)（三）复利的终值与现值1、复利终值复利终值是指一定量的本金按复利计算的若干期后的本利和。
若某人将P 元存放于银行，年利率为i ，则：第一年的本利和为： F = P + P ·i = P · ( 1 + i )第二年的本利和为： F = P · ( 1 + i )· ( 1 + i ) = P ·2)1(i + 第三年的本利和为： F = P ·2)1(i +· (1 + i ) = P · 3)1(i +第 n 年的本利和为： F = P ·n i )1(+式中n i )1(+通常称为复利终值系数，用符号（F/P,i,n ）表示。