学而思讲义四年级第三讲(游戏与对策)

《对策问题》（教案）四年级下册数学北师大版教案：《对策问题》四年级下册数学北师大版一、教学内容本节课的教学内容来自于北师大版四年级下册数学的第76页至第78页，主要包括对策问题的理解和解决方法。

通过本节课的学习，学生将掌握对策问题的基本概念，学会使用简单的策略来解决问题。

二、教学目标1. 让学生了解对策问题的基本概念，理解对策问题的解决方法。

2. 培养学生的逻辑思维能力，提高学生解决实际问题的能力。

3. 培养学生合作学习的能力，增强学生的团队意识。

三、教学难点与重点1. 教学难点：对策问题的解决方法，如何运用策略来解决问题。

2. 教学重点：让学生通过实际操作，理解对策问题的解决方法，并能够运用到实际问题中。

四、教具与学具准备1. 教具：黑板、粉笔、教学卡片。

2. 学具：学生用书、练习本、铅笔、尺子。

五、教学过程1. 导入：通过一个实际问题情景引入，例如：“两个朋友一起去找工作，他们有四个选择：A、B、C和D。

A工作报酬是100元，B工作报酬是200元，C工作报酬是300元，D工作报酬是400元。

他们不能同时做两个工作，每个工作只能一个人做。

请问他们应该如何选择才能使自己的利益最大化？”让学生思考并讨论，引出对策问题的概念。

2. 讲解：讲解对策问题的基本概念，解释对策问题的解决方法。

通过教学卡片，展示不同的对策问题情景，让学生理解并掌握对策问题的解决方法。

3. 练习：让学生通过练习题来巩固所学的内容。

例如：“甲、乙两人比赛跳远，甲每次跳3米，乙每次跳4米。

请问甲、乙应该如何比赛才能使自己获胜？”让学生独立思考并解答，然后进行讲解和反馈。

4. 应用：让学生通过实际问题来应用所学的内容。

例如：“一个班级有男生和女生，男生有20人，女生有15人。

如果每次只能选出一个男生和一个女生进行比赛，请问男生和女生应该如何选择才能使自己的胜率最大化？”让学生分组讨论并给出解决方案，然后进行讲解和反馈。

六、板书设计板书设计如下：对策问题的解决方法：1. 分析问题的条件和限制。

第三讲数学游戏中的必胜策略知识要点：做数学游，如果你掌握了一些策略，就一定能取。

“数”游就是两个人按照一定的流数，并将所的数逐步累加，先到定数的一方；“ 数”游与“ 数”游似，只是先到定数的一方失。

然，里藏着数学奥秘。

例题精选：例1．甲乙二人流数。

从 1 起，每人每次可一个数或两个数。

能得 20 就。

先和同学玩一玩个游。

如果由你先数，你能保？点：可以从 20 往前想，如果想，自己不要19 和 18。

因 19，方 20 一个数就了； 18，方两个数19、 20 就了。

，要想（到20）必到 17。

同理，要想到17，就要争取到14；要想到 14，就要争取到11；要想到 11，就要争取到8；要想到 8，就要争取到5；要想到 5，就要争取到2；因此，先到 2。

方 3，自己 4、5；方 3、4，自己 5。

就又到了 5。

依次方法下去，就一定会了。

例2．甲乙二人流数。

从 1 起，每人每次最多可以 3 个数。

能得 30 就。

点：是游“ 30”。

仍可以采用从后往前想的方法。

要想到 30，就要争取到 26；要想到 26，就要争取到 22；⋯⋯因此，先到 2。

再看方数情况依次 6、 10、14、18、22、26、 30 就可。

例3．按照例 1 的数方法，如果先“ 20”的一方失，怎保？点：就是“ 数游”。

20 就要 19，并且依次 16、13、 10、7、4、1。

因此，要先“ 1”，再根据方数情况依次 4、 7、 10、13、16、19，就把 20 了方。

根据上面三个例，你什么律？例4．按照例 1 的数方法，如果先“ 30”的一方，怎保？点：因每次最多两个数，所以要到“ 30”就要一次 27、24、 21、18、15、 12、9、6、3。

而先数的一方最多只能到“ 2”，因此，可以方先数，再看方数情况依次到3、 6、 9⋯⋯例5．甲乙二人流在方格中移棋子。

如下：（1）只能向右移；（2）每次只能移一格或两格；（3）占最后一格的。

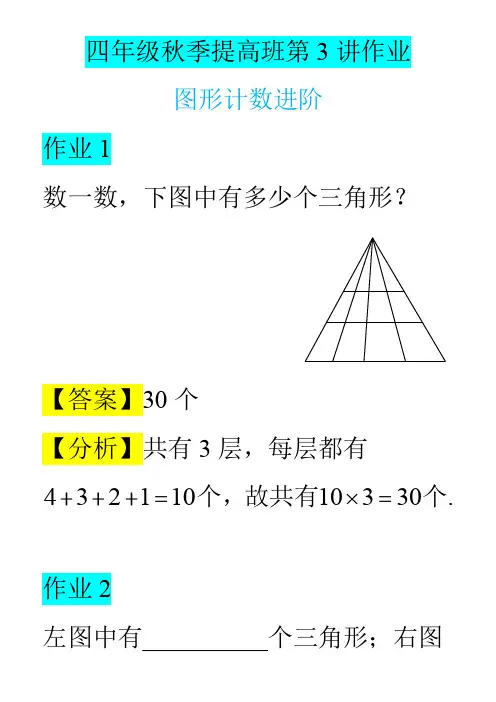
四年级秋季提高班第3讲作业图形计数进阶作业1数一数，下图中有多少个三角形？【答案】30个【分析】共有3层，每层都有432110个，故共有10330个.作业2左图中有__________个三角形；右图中有__________个三角形．【答案】35；43【分析】左：1515535；右：355343作业3下面的图形中有多少个长方形？【答案】60个【分析】长有3216种，宽是432110种，故共有61060个长方形.作业4下图中包含有“好未来”三个汉字的长方形有多少个？好未来【答案】18个【分析】3618个.作业5图中有__________个（可旋转可翻转）．【答案】34个【分析】对应到中，每个小长方形内有2个，所以有21734个．复习巩固作业6观察5*255560，7*477777777778638，推知9*5的值是__________．【答案】111105【分析】原式999999999999999111105作业7某班有3个小组，赵、钱、孙三人分属不同的小组．这次语文考试成绩公布，情况如下：赵和第3小组的那位成绩不一样，孙比第1小组的那位成绩低，三人中第3小组的那位比钱分数高：若赵、钱、孙三人按语文成绩由高到低排列，正确的顺序是__________．【答案】赵、孙、钱【分析】赵不属于第3小组，钱也不属于第3小组，所以孙属于第3小组，孙比第1小组的成绩低，且比钱的分数高，所以赵是第1小组的，分数最高，钱分数最低．作业85个足球队进行比赛，每个球队都与其他球队各比一场，胜方得3分，负方得0分，平局各得1分．最后四个队分别得1分、2分、5分和7分，那么第五个队得__________分．【答案】12【分析】前4队3胜7负，所以第5个队只能4场全胜，12分．四年级秋季提高班第3讲练习册答案图形计数进阶同步练习1．35个。

左边15个，右边15个，左右结合有5个.2．22个按大小分类（边长为1、2的三角形），共有16622个三角形；方法二：“向右”的三角形有8311个，故“向左”的三角形也有11个，共有22个.3．100个，有(4321)(4321)100个平行四边形.4．30个左下可选3个点，右上可选10个点，则共有31030个.5．（1）43213434（）个；（2）新增的三角形以新产生的线段为边，上半部分有639个，下半部分有4个，总共新增9413个；有341347个；（3）又新增一条一样的线段，所以边长在这条线段上三角形也有13个，边长同时在这两条新增线段上的三角形总共有4个；所以图中总共有三角形341313464个.6．36个中心正方形内有84416个，其外有8412个，“跨界”的有8个，故共有1612836个.深化练习7．38个添线法，原有10个，添上右倾的斜线增加了10414个，再添上左倾的斜线，增加了634114个，所以共10141438个．最后添左倾斜线时，为保证不重不漏，可将这条斜线以外的每个交点与斜线形成的新三角形个数标在点上，最后相加得到总数，如下图，共增加了63514个三角形． 1111060138．添线法，1520253590．9．85由2个例2（1）的图构成，新增加含4块的三角形有10个，含8块的三角形有5个，所以共35210585个.实战练习10．20个按大小分类枚举（正放：面积为1、4的正方形；斜放：面积为2、5的正方形），共有826420个正方形.阶段测试1．1*2=121=32．原式=101102103104105 (12345)1015101503．依题意，A A A A A*2224,A A A A A4*3=8+3=11,A A A A A11*4=22+4=26,得26260,10.A A4．图中共有19+11+5+1=36个正方形.5．观察图形可知，在题述图形中由实线和虚线构成的长方形各有9个，共计9+9=18个.6．个数=6×8=48（个）.7．“甲已经赛了4盘”，说明甲与乙、丙、丁、小强各赛了1盘(小强与甲赛了1盘)“丁赛了1盘”，肯定丁只与甲比赛. “乙赛了3盘”，说明乙与甲、丙、小强各赛了1盘(小强与乙赛了1盘).现在已经知道，丙赛的2盘是与甲、乙各赛了1盘，所以，小强赛了2盘.8．四个人循环比赛总共比赛5×4÷2=10（场），每场无论分出胜负还是打平，两人的得分和一定是2分，因此最终四个人的得分加起来一定是10×2=20（分）．9．每场平局两队共得2分，如果分出胜负则两队共得3分．6支球队共要比65215场比赛，其中有4场平局，所以有15411场分出了胜负，那么6支球队总得分为2431141分，由于有5支球队共得了31分，所以第6支球队得了413110分．10．法一：四人共赛6局，总分为6212（分），因为没有人全胜，所以得分最高的选手最多是两胜一平得5分，因此在另外的3局比赛中：如果全部是平局，则4个人的分数只能分别为5，3，2，2，就会出现分数相同的情况，如下左图（图中箭头表示有胜负，箭头指向输者，虚线表示平局）如果有2局是平局，则可以出现满足条件的情况：4人分数分别为5，4，2，1，如下右图②③②⑤D C B A ④①②⑤D C B A所以至少有3局是平局．法二：四人共赛6局，如果6局都是平局，那么四人总分相同，不合题意．如果有5局平局，那么除有胜负的两人外，另两人总分相同，不合题意．如果有4局平局，那么可分为三种情况：一个人胜两局，输的两个人总分相同；一个人输两局，胜的两个人总分相同；四个人中两人胜两人负，两个胜的人总分相同，两个负的人总分相同，都不合题意．3局平局是可能的，如下图所示，连线表示平局，箭头指向的一方为负方，图中数字为各人总分．②④①⑤四年级秋季提高班第3讲图形计数进阶例1图（1）中有__________个三角形；图（2）中有__________个三角形；图（3）中有__________个三角形；图（4）中有__________个三角形．(1)(2)(3)(4)【答案】30；20；37；50【分析】（1）151530；（2）增加一条线，线上面增加3个三角形，线下面增加2个三角形，153220个；（3）在（1）、（2）的基础上增加2个三角形，305237个；（4）在（3）的基础上增加633113个，所以共371350个．【随堂练】（1）图中有多少个三角形（2）图中有多少个三角形（3）图中有多少个三角形【答案】（1）20个（2）30个（3）27个拓展5图（1）有__________个三角形；图（2）有__________个三角形；图（3）有__________个三角形．(1)(2)(3)【答案】34；47；64【分析】（1）43213434（）个；（2）新增的三角形以新产生的线段为边，上半部分有639个，下半部分有4个，总共新增9413个；有341347个；（3）又新增一条一样的线段，所以边长在这条线段上三角形也有13个，边长同时在这两条新增线段上的三角形总共有4个；所以图中总共有三角形341313464个.例2图（1）有__________个三角形；图（2）有__________个三角形．(1)(2)【答案】35；29【分析】（1）分类枚举，含1块、2块、3块、5块的分别有10、10、10、5个，共有101010535个；（2）以去掉的线为边的三角形有6个，所以剩下35629个；练一练下图中有多少个三角形？(3)【答案】47【分析】以新增的线为边的三角形左右两边各6个，所以共有356247个．拓展9数出下图中三角形的个数.【答案】85【分析】由2个例2（1）的图构成，新增加含4块的三角形有10个，含8块的三角形有5个，所以共35210585个．例3（1）图中有__________个长方形．（2）下图中含“★”的长方形有多少个？★（3）下图中含两个“★”的长方形有多少个？★★【答案】150；54；54【分析】（1）长方形邻边对应：一条水平线段和一条竖直线段可确定一个长方形．根据乘法原理可知，长方形有（）（）1234512341510150个.（2）长方形两点对应：只要确定对角的两个顶点就可以确定一个水平的长方形，就像在电脑桌面上拖动鼠标选中文件一样．这种对应法专门用来解决包含某个区域的长方形个数．如下图所示，★的左上角有6个点，右下角有9个点，根据乘法原理，共有6954个长方形.★（3）同（2），包含两个★的长方形有9654个．★★【随堂练】1．图中有多少个长方形【答案】10660个2．图中有多少个包含“心”的长方形【答案】4624例4在下图45的方格中：（1）有__________个；（2）有__________个（可旋转可翻转）；（3）有__________个（可旋转可翻转）；（4）有__________个（可旋转可翻转）．【答案】（1）12；（2）48；（3）17；（4）34【分析】特殊图形的对应：可将特殊图形对应到能包含自身的最小长方形中．（1）4312个；（2）对应到中，每个田字格内有4个，所以有41248个；（3）横向的有339个，纵向的有248个，共9817个；（4）对应到中，每个小长方形内有2个，所以有21734个．【随堂练】图中有多少个【答案】66224（）练一练下图中，共有__________个（可旋转可翻转）．【答案】30【分析】图中有7个田字格，4728个，注意左上角与右下角还各有1个，共28230个．例5用9个钉子钉成相互间隔为1厘米的正方阵(如下图)．如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于2平方厘米的三角形有多少个？面积等于1平方厘米的三角形有多少个？【答案】8；32【分析】（1）面积等于2平方厘米的分类统计如下：3×2=6（个）1×2=2（个）所以，面积等于2平方厘米的三角形的个数有：6+2=8（个）．（2）面积等于1平方厘米的分类统计如下：3×2×4=24（个）2×4=8（个）面积等于2平方厘米的三角形有8个；面积等于1平方厘米的三角形有32个．练一练13枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等．请回答：可以构成多少个正方形？【答案】11【分析】按大小分类枚举（正放：面积为1、4的正方形；斜放：面积为2、8的正方形），共有415111个正方形.拓展1016枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等.请回答：可以构成多少个正方形？【答案】20【分析】按大小分类枚举（正放：面积为1、4的正方形；斜放：面积为2、5的正方形），共有826420个正方形.拓展练习拓1☆数一数下图中，有多少个三角形？【答案】35个【分析】左边15个，右边15个，左右结合有5个.拓2☆☆图中共有多少个三角形？【答案】22个【分析】按大小分类（边长为1、2的三角形），共有16622个三角形；方法二：“向右”的三角形有8311个，故“向左”的三角形也有11个，共有22个.拓3☆☆下面的图中共有多少个平行四边形？【答案】100个【分析】有(4321)(4321)100个平行四边形.拓4☆☆下图中有多少个同时包含2个五角星的长方形？★★【答案】30个【分析】左下可选3个点，右上可选10个点，则共有31030个.拓5☆☆☆图（1）有_________个三角形；图（2）有_________个三角形；图（3）有_________个三角形．(1)(2)(3)【答案】34；47；64【分析】（1）43213434（）个；（2）新增的三角形以新产生的线段为边，上半部分有639个，下半部分有4个，总共新增9413个；有341347个；（3）又新增一条一样的线段，所以边长在这条线段上三角形也有13个，边长同时在这两条新增线段上的三角形总共有4个；所以图中总共有三角形341313464个.拓6☆☆☆下图中有多少个三角形？【答案】36个【分析】中心正方形内有84416个，其外有8412个，“跨界”的有8个，故共有1612836个.拓7☆☆☆下图中有多少个三角形？【答案】38个【分析】添线法，原有10个，添上右倾的斜线增加了10414个，再添上左倾的斜线，增加了634114个，所以共10141438个．最后添左倾斜线时，为保证不重不漏，可将这条斜线以外的每个交点与斜线形成的新三角形个数标在点上，最后相加得到总数，如下图，共增加了63514个三角形． 111106013拓8☆☆☆图中有多少个三角形？【答案】90【分析】添线法，1520253590．拓9☆☆☆数出下图中三角形的个数.【答案】85【分析】由2个例2（1）的图构成，新增加含4块的三角形有10个，含8块的三角形有5个，所以共35210585个．拓10☆☆☆16枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等.请回答：可以构成多少个正方形？【答案】20【分析】按大小分类枚举（正放：面积为1、4的正方形；斜放：面积为2、5的正方形），共有826420个正方形.。

游戏与对策一、基本前提：游戏双方足够聪明，目的都是获胜二、方法：倒推、画图列表三、游戏类型：①田忌赛马【例1】学校举行乒乓球团体比赛，每班派出3名运动员参赛，规定有两名运动员胜出的班获胜（三局两胜制）。

四（1）班：第一名：张明；第二名：李超；第三名：郭胜四（2）班：第一名：王勇；第二名：宋佳；第三名：高祥如果你是四（1）班的班长，要想赢下这次比赛，应该怎样排兵布阵？请把你的想法填入表中。

（假设两个班相同排名的运动员的水平相当）四（2）班四（1）班获胜班级第一场第一名：王勇第二场第二名：宋佳第三场第三名：高祥【举一反三1-1】四（1）班和四（2）班举行跳绳团体比赛。

两队队员复赛成绩如下，比赛中四（1）班队员先出场，如果你是四（2）班文体委员，你怎样安排队员出场才能取胜？（用线连一连）四（1）班四（2）班张丽160次/分钟杨文爱150次/分钟吴敏147次/分钟刘苹142次/分钟王雯128次/分钟李琳琳115次/分钟【举一反三1-2】小强和小刚玩扑克牌“比大小”的游戏。

玩法是：每人每次出一张牌，出三次，赢两次者为胜。

小强三张牌分别为“2”“5”“8”，小刚三张牌分别为“1”“4”“7”。

小强先出牌，小刚怎么出牌才能取胜？请把出牌的情况填入下表。

第一次第二次第三次小强8 2 5小刚本次赢者游戏类型②：拿火柴棒或抢数解题方法：（1）找周期：周期等于可拿最大限度+1有余数：抢先拿（2）总数÷周期整除（余数为0）：抢后【例2】桌子上放着40根火柴，甲、乙二人轮流每次取走1-2根．规定谁取走最后一根火柴谁输．如果双方都采用最佳方法，甲先取，那么谁将获胜？【举一反三2-1】甲、乙二人轮流报数，报出的数只能是1至7的自然数．同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜．问谁有必胜策略？【举一反三2-2】桌上放着60根火柴，青青和亮亮二人轮流每次取走1-3根，规定谁取走最后一根火柴谁就获胜。

四年级高斯数学导引第三讲超越篇（原创实用版）目录1.导引简介2.高斯数学导引的内容3.四年级高斯数学导引第三讲的主要内容4.超越篇的含义和作用5.超越篇的主要知识点6.总结正文一、导引简介《四年级高斯数学导引》是一本针对小学四年级学生的数学辅导教材，以德国数学家高斯的教学理念为基础，结合我国的教育实际，为学生提供系统、全面的数学知识。

本书的内容涵盖了四年级数学课程的全部知识点，旨在帮助学生更好地理解和掌握数学知识，提高学生的数学素养和解题能力。

二、高斯数学导引的内容《四年级高斯数学导引》共分为十讲，内容包括：算术、代数、几何、测量、组合、概率、逻辑、方法、策略、竞赛等。

每讲都按照知识点的难易程度和学生的接受能力进行编排，既有基本概念的讲解，也有综合运用的训练，让学生在掌握知识的同时，也能学会解题的方法和技巧。

三、四年级高斯数学导引第三讲的主要内容第三讲为超越篇，主要介绍了一些基本的超越数及其性质。

超越数是指不能表示为两个整数的比值的实数，例如圆周率π和自然对数的底数 e等。

本讲的主要内容包括：超越数的概念、性质、分类和一些著名的超越数等。

四、超越篇的含义和作用超越篇的含义是指那些不能用有理数表示的实数，它们在数学中有着广泛的应用。

学习超越数，有助于学生更好地理解实数的概念，丰富学生的数学知识，提高学生的数学素养。

同时，超越数的学习也为以后学习更高级的数学知识打下基础。

五、超越篇的主要知识点1.超越数的概念：不能表示为两个整数的比值的实数。

2.超越数的性质：无理数、无限不循环小数、不能表示为整系数方程的根等。

3.超越数的分类：代数无理数、无理代数数、超越代数数等。

4.著名的超越数：圆周率π、自然对数的底数 e、黄金分割比例φ等。

六、总结《四年级高斯数学导引》第三讲超越篇为学生介绍了一些基本的超越数及其性质，让学生了解到超越数的概念、性质、分类和一些著名的超越数等知识。

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题，处理多个对象时可采用列表的形式，在年龄问题中，通常采用和差倍问题的分析方法，有时需注意任意两人的年龄差保持不变。

典型问题兴趣篇1. 某数加上6，再乘以6，再减去6，再除以6，其结果等于6，则这个数是多少？答案：这个数是详解：+6 x6 -6 +662. 有一个人非常喜欢喝酒，他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦，看到一个酒店就把酒葫芦中的酒加一倍，然后喝下8两酒，这天他一共遇到3家酒店，在最后一家酒店喝完酒后，葫芦里的酒刚好喝完. 问：原来酒葫芦里有多少两酒？答案：7两酒。

详解：每经过一个酒店，葫芦里酒的数量就先乘2，再减8，利用倒推法，我们反过来应该先加8，再除以2.那么到酒店C之前葫芦里应该有（0+8）÷2=4两酒，他在到酒店B的时候应该有（4+8）÷2=6两酒，所以他原来的酒葫芦应该有（6+8）÷2=7两酒。

0+8=8，8÷2=4，4+8=12，12÷2=6，6+8=14，14÷2=73. 某人发现了一条魔道，下面有一个存钱的小箱子，当他从魔道走过去的时候，箱子里的一些钱会飞到人的身上使人身上的钱增加一倍，这人很高兴；当他从魔道走回来时，身上的钱会飞到箱子里，使箱子里的钱增加一倍；这人一连走了3个来回后，箱子里的钱和人身上的钱都是64枚一元的硬币，那么原来这人身上有多少元？箱子里有多少元？答案：原来这个人身上有43元，箱子里有85元。

详解：4. 三棵树上共有48只鸟. 后来，第一棵树上有一半的鸟飞到了第二棵树上；之后，第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上；最后，第三棵树上又有10只鸟飞到了第一棵树上，此时三棵树上的鸟一样多. 问：一开始三棵树上各有几只鸟？答案：第一棵树上有12，第二棵23，第三棵13详解：5. 1997年张伯伯45岁，小方9岁，在哪一年张伯伯的年龄是小方年龄的4倍？答案：小方12岁那年。

学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形，已知AB＝22厘米，BC＝20厘米，那么每一个正方形的面积是多少平方厘米？【难度级别】★★★★★2、【学案2】在四边形ABCD中，线段BC长为6厘米，∠ABC＝90°，∠BCD＝135°，且点A到边CD 的垂线段AE＝12厘米，线段ED＝5，求四边形ABCD 的面积。

D C3、【学案3】等腰梯形ABCD 中，交于O 点的两条对角线互相垂直，三角形ECB 是直角三角形，OC 比AO长20厘米。

已知三角形ADE 的面积是250平方厘米，则梯形ABCD 的面积是多少平方厘米？4、【学案4】一块边长为180厘米的正方形铁片，四角各被截去一个边长为40厘米的小正方形铁片，现在要从剩下的铁片中剪出一块完整的正方形铁片来，剪出的正方形面积最大为多少平方厘米？5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形，保留必要的作图痕迹。

O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中，有多少个与5678相加时，至少发生一次进位？7、【例8】有______个四位数满足下列条件：它的各位数字都是奇数，它的各位数字互不相同，它的每个数字都能整除它本身。

8、【学案1】计算机上编程序打印出前10000个正整数：1,2,3,……,10000时，不幸打印机有毛病，每次打印数字3时，它都打印出x，问其中被错误打印的共有多少个数？9、【学案4】有9张同样大小的圆形纸片，其中标有数码“1”的有1张，标有数码“2”的有2张，标有数码“3”的有3张，标有数码“4”的有3张，把这9张圆形纸片如图所示放置在一起，但标有相同数码的纸片不许挨在一起。

(1)如果M处放标有数码“3”的纸片，一共有多少种不同的放置方法？(2)如果M处放标有数码“2”的纸片，一共有多少种不同的放置方法？10、【越玩越聪明】在例6的后面。

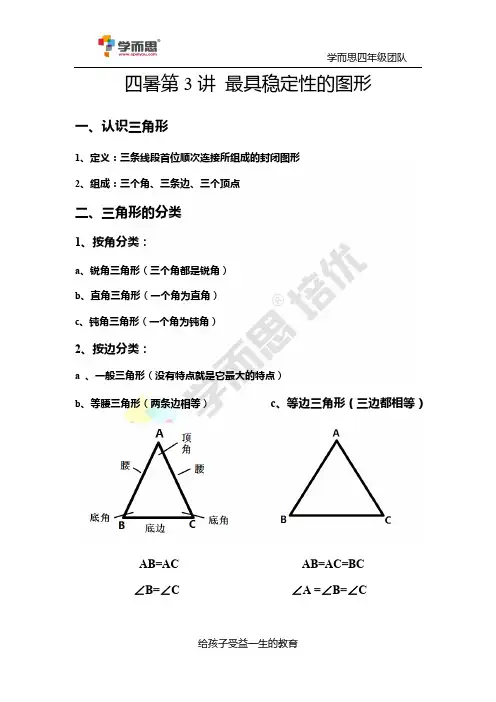
四暑第3讲最具稳定性的图形一、认识三角形1、定义：三条线段首位顺次连接所组成的封闭图形2、组成：三个角、三条边、三个顶点二、三角形的分类1、按角分类：a、锐角三角形（三个角都是锐角）b、直角三角形（一个角为直角）c、钝角三角形（一个角为钝角）2、按边分类：a 、一般三角形（没有特点就是它最大的特点）b、等腰三角形（两条边相等）c、等边三角形（三边都相等）AB=AC AB=AC=BC∠B=∠C ∠A =∠B=∠C3）特殊三角形AB=AC，∠B=∠C,∠A=90°三、三角形边的关系任意两边之和大于第三边四、内角和三角形的内角和：180°多边形的内角和：（n-2）×180°例题1、以下三角形属于哪一类三角形？例题2、1)下列各组线段能组成一个三角形的是（）(A) 3cm,3cm,6cm (B) 2cm,3cm,6cm(C) 5cm,8cm,12cm (D) 4cm,98cm,101cm2)若等腰三角形的两个边长分别为3和7，则它的周长为________若等腰三角形的两个边长分别为3和4，则它的周长为________例题3、1)左图等腰直角三角形中，∠B=______，∠C=______右图等边三角形中，∠A=______，∠B=______，∠C=______2)在等腰三角形中，已知其中一角为30°，那么三角形的另外两个角分别是多少？例题4、如图，∠1=∠2，∠3=∠4，∠5=130°，那么∠A=______度例题5、1）以下图形内角和分别为多少？2）n边形的内角和：_____________。

第三讲 游戏与对策一、基本前提游戏双方足够聪明，目的都是获胜。

二、方法：倒推三、游戏类型（一）拿火柴棍/抢数如：桌子上放着10根火柴，二人轮流每次取走1—2根，规定谁取走最后一根火柴谁获胜。

你知道必胜的方法吗？分析：如果从开始分析，“局面”太大，有太多种取法要讨论。

所以我们尝试从结果倒推。

如上图，要必胜，也就是要让自己拿到10号火柴，那就应给对方留下8，9,10三根火柴供他取，这样对方不管取一根还是两根，自己都能拿到最后的10号火柴。

照这样分析，自己应该拿到7号火柴（这样就是给对方留下了8,9,10号三根）就必胜。

同理分析，要想取7号，就应该取4号，要想取4号，就应该取1号。

那么，本题的制胜点就是1,4,7,10号火柴，对于足够聪明的人来说，拿到第一个制胜点1号火柴，一定能拿到其余的制胜点。

所以本题要必胜，就要抢先取1根，然后对方取a 根，自己就取3-a 根，这样保证自己能取到每一个制胜点，最终取到10号火柴。

总结一下，同学们应该能看出，这里面有周期现象（只是周期是从后往前排布的），周期是几呢？是可取的最大限度2再加1等于3，制胜点是哪些呢？是每个周期的最后一根。

掌握此规律，就不难总结出这类题的解题方法了：解题方法：（1）找周期：周期等于可拿最大限度+1（2）总数÷周期1 桌子上放着60根火柴，聪明昊、神奇涛二人轮流每次取走1—3根，规定谁取走最后一根火柴谁获胜。

你知道必胜的方法吗？解析： 周期为 3+1=4（根）60÷4=15（组） （整除，应该抢后）制胜点：4,8,12 (60)做法：1、让对方先取2、对方取a 根，自己就取4-a 根2 有一种抢数游戏，是两个人从自然数1开始轮流报数，规定每次至少报几个数与至多报几个数（都是自然数），最后谁报到规定的“某个数字”为胜。

如“抢50”，规定每次必须报1或2个1 2 3 4 5 6 7 8 9 10有余数：抢先拿余数整除（余数为0）：抢后自然数，从1开始，谁抢报到50为胜。