1.2库仑定律

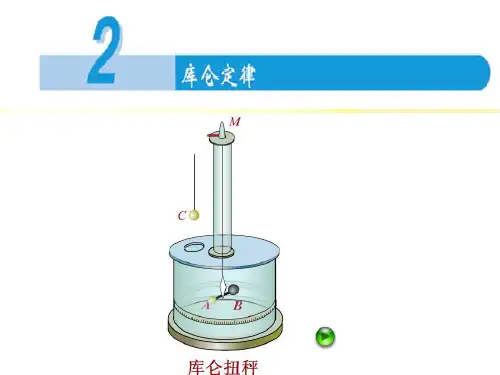
1.2 库仑定律简介库仑定律是电磁学中的基本定律之一，描述了带电物体之间相互作用力的大小与它们之间距离、电荷量的关系。

该定律是由法国物理学家库仑于18世纪末提出的，被认为是电磁学的基石之一，对于理解电荷之间的相互作用以及电磁现象的发生和演化具有重要意义。

定义库仑定律可以表述如下：两个电荷之间的静电力的大小与它们之间直线距离的平方成反比，在恒定吸引或排斥力的情况下，与这两个电荷的数量成正比。

公式表示为：F = k * (q1 * q2) / r^2其中，F表示两个电荷之间的静电力，k是库仑常数，q1和q2分别表示两个电荷的电荷量，r表示它们之间的距离。

库仑常数库仑常数是一个物理常数，用于计算两个电荷之间的静电力。

它的数值约为9.0 x 10^9 Nm2/C2，其中Nm2/C2是国际单位制中的单位。

电荷的性质根据库仑定律，电荷有两种性质：正电荷和负电荷。

正电荷尽可能地排斥彼此，而负电荷也尽可能地排斥彼此。

正电荷和负电荷之间会产生吸引力，这是导致电荷之间相互作用的原因。

实例分析下面我们通过一个实例来分析和应用库仑定律。

假设有两个电荷，电荷q1的电荷量为2C，电荷q2的电荷量为-4C，它们之间的距离r为1m。

我们可以使用库仑定律来计算它们之间的静电力。

根据库仑定律的公式，我们有：F = k * (q1 * q2) / r^2代入具体数值得到：F = (9.0 x 10^9 Nm2/C2) * (2C * -4C) / (1m)^2简化计算得到：F = -7.2 x 10^9 N由此可见，这两个电荷之间的静电力是-7.2 x 10^9 N（牛顿）。

负号表示这两个电荷之间的力是吸引力，而不是排斥力。

应用库仑定律在众多领域中都有广泛的应用。

以下是一些常见的应用场景：1.静电学：库仑定律对于描述静电现象和静电力的大小提供了基本的理论基础。

2.电荷的分布与运动：在电荷的分布和运动方面，库仑定律有很多应用，比如计算静电场的大小、电荷在电场力作用下的运动等。

第二讲 库仑定律[知识要点]1．点电荷：无大小、无形状、且有电荷量的一个点叫 ．它是一个理想化的模型．2．库仑定律的内容：真空中两个静止点电荷之间的相互作用力跟它们电荷量的 成正比，跟它们的距离的 成反比，作用力的方向在它们的 ．3．库仑定律的表达式：F = 221r q q k ； 其中q 1、q 2表示两个点电荷的电荷量，r 表示它们的距离，k 为比例系数，也叫静电力常量， k = 9.0×109N m 2/C 2.[典型例题]例1 半径为r 的两个相同金属球，两球心相距为L (L ＝3r)，它们所带电荷量的绝对值均为q ，则它们之间相互作用的静电力FA ．带同种电荷时,F ＜22L q kB ．带异种电荷时,F ＞22Lq k C ．不论带何种电荷,F ＝22Lq k D ．以上各项均不正确 例2 如图1—2—2所示，三个完全相同的金属球a 、b 、c 位于等边三角形的三个顶点上．a 和c 带正电，b 带负电，a 所带电荷量的大小比b 的小．已知c 受到a 和b 的静电力的合力可用图中有向线段中的一条来表示，它应是A ．F 1B ．F 2C ．F 3D ．F 4图1—2—2例3 两个大小相同的小球带有同种电荷（可看作点电荷），质量分别为m 1和m 2，带电荷量分别是q 1和q 2，用绝缘线悬挂后，因静电力而使两悬线张开，分别与铅垂线方向成夹角θ1和θ2,且两球同处一水平线上，如图1—2—3所示，若θ1＝θ2,则下述结论正确的是A.q 1一定等于q 2B.一定满足q 1/ m 1＝q 2/ m 2C.m 1一定等于m 2D.必须同时满足q 1＝q 2, m 1＝ m 2图1—2—3例4 a 、b 两个点电荷，相距40cm ，电荷量分别为q 1和q 2，且q 1＝9 q 2，都是正电荷；现引入点电荷c ，这时a 、b 、c 三个电荷都恰好处于平衡状态．试问：点电荷c 的性质是什么?电荷量多大?它放在什么地方?例5 有三个完全相同的金属球A 、B 、C ，A 带电荷量7Q ，B 带电荷量﹣Q ，C 不带电．将A 、B 固定，然后让C 反复与A 、B 接触，最后移走C 球．问A 、B 间的相互作用力变为原来的多少倍?例6 如图1—2—5所示．在光滑绝缘的水平面上的A 、B 两点分别放置质量为m 和2m 的两个点电荷Q A 和Q B .将两个点电荷同时释放，已知刚释放时Q A 的加速度为a ，经过一段时间后(两电荷未相遇)，Q B 的加速度也为a ，且此时Q B 的速度大小为v ，问：(1) 此时Q A 的速度和加速度各多大?(2) 这段时间 内Q A 和Q B 构成的系统增加了多少动能？[经典练习]1．下列哪些带电体可视为点电荷A ．电子和质子在任何情况下都可视为点电荷B ．在计算库仑力时均匀带电的绝缘球体可视为点电荷C ．带电的细杆在一定条件下可以视为点电荷D ．带电的金属球一定不能视为点电荷2．对于库仑定律，下面说法正确的是图1—2—5A ．凡计算真空中两个静止点电荷间的相互作用力，就可以使用公式F = 221rq q k ； B ．两个带电小球即使相距非常近，也能用库仑定律C ．相互作用的两个点电荷，不论它们的电荷量是否相同，它们之间的库仑力大小一定相等D ．当两个半径为r 的带电金属球心相距为4r 时，对于它们之间相互作用的静电力大小，只取决于它们各自所带的电荷量3．两个点电荷相距为d ，相互作用力大小为F ，保持两点电荷的电荷量不变，改变它们之间的距离，使之相互作用力大小为4F ，则两点之间的距离应是A ．4dB ．2dC ．d/2D ．d/44．两个直径为d 的带正电的小球，当它们相距100 d 时作用力为F ，则当它们相距为d 时的作用力为( )A ．F ／100B ．10000FC ．100FD ．以上结论都不对5．两个带正电的小球，放在光滑绝缘的水平板上，相隔一定的距离，若同时释放两球，它们的加速度之比将A ．保持不变B ．先增大后减小C ．增大D ．减小6．两个放在绝缘架上的相同金属球相距d ，球的半径比d 小得多，分别带q 和3q 的电荷量，相互作用的斥力为3F ．现将这两个金属球接触，然后分开，仍放回原处，则它们的相互斥力将变为A ．OB ．FC ．3FD ．4F７．如图1—2—6所示，大小可以不计的带有同种电荷的小球A 和B 互相排斥，静止时两球位于同一水平面上，绝缘细线与竖直方向的夹角分别为α和β卢，且α < β， 由此可知A ．B 球带电荷量较多B ．B 球质量较大C ．A 球带电荷量较多D ．两球接触后，再静止下来，两绝缘线与竖直方向的夹角变为α′、β′，则仍有α ′< β′ ８．两个质量相等的小球，带电荷量分别为q 1和q 2，用长均为L 的两根细线，悬挂在同一点上，静止时两悬线与竖直方向的夹角均为30°，则小球的质量为 . ９．两个形状完全相同的金属球A 和B ，分别带有电荷量q A ＝﹣7×108-C 和q B ＝3×108-C ，它们之间的吸引力为2×106-N ．在绝缘条件下让它们相接触，然后把它们又放回原处，则此时它们之间的静电力是 (填“排斥力”或“吸引力”)，大小是 ．(小球的大小可忽略不计)10．如图1—2—7所示，A 、B 是带等量同种电荷的小球，A 固定在竖直放置的10 cm 长的绝缘支杆上，B 平衡于倾角为30°的绝缘光滑斜面上时，恰与A 等高，若B 的质量为303g ，则B 带电荷量是多少?(g 取l0 m ／s 2)[课后作业] 图1—2—6 图1—2—71．两个带有等量电荷的铜球，相距较近且位置保持不变，设它们带同种电荷时的静电力为F 1，它们带异种电荷时(电荷量绝对值相同)的静电力为F 2，则F 1和F 2的大小关系为：A ．F 1＝F 2 D ．F 1> F 2 C ．F 1< F 2 D ．无法比较2．如图1—2—8所示，在A 点固定一个正点电荷，在B 点固定一负点电荷，当在C 点处放上第三个电荷q 时，电荷q 受的合力为F ，若将电荷q 向B 移近一些，则它所受合力将A ．增大 D ．减少 C ．不变 D ．增大、减小均有可能．3．真空中两个点电荷，电荷量分别为q 1＝8×109-C 和q 2＝﹣18×109-C ，两者固定于相距20cm 的a 、b 两点上,如图1—2—9所示．有一个点电荷放在a 、b 连线(或延长线)上某点，恰好能静止，则这点的位置是A ．a 点左侧40cm 处B ．a 点右侧8cm 处C ．b 点右侧20cm 处D ．以上都不对．4．如图所示，+Q 1和-Q 2是两个可自由移动的电荷，Q 2=4Q 1．现再取一个可自由移动的点电荷Q 3放在Q 1与Q 2连接的直线上，欲使整个系统平衡，那么 （ ）A.Q 3应为负电荷，放在Q 1的左边 B 、Q 3应为负电荷，放在Q 2的右边C.Q 3应为正电荷，放在Q 1的左边 D 、Q 3应为正电荷，放在Q 2的右边．5．如图1—2—10所示，两个可看作点电荷的小球带同种电，电荷量分别为q 1和q 2，质量分别为m 1和m 2，当两球处于同一水平面时，α >β，则造成α >β的可能原因是：A ．m 1>m 2B ．m 1<m 2C q 1>q 2D ．q 1>q 26．如图1—2—11所示，A 、B 两带正电小球在光滑绝缘的水平面上相向运动．已知m A ＝2m B ，A v ＝20v ，B v ＝0v ．当两电荷相距最近时，有A ．A 球的速度为0v ，方向与A v 相同B ．A 球的速度为0v ，方向与A v 相反C ．A 球的速度为20v ，方向与A v 相同D ．A 球的速度为20v ，方向与A v 相反．7．真空中两个固定的点电荷A 、B 相距10cm ，已知q A ＝+2.0×108-C ，q B ＝+8.0×108-C ，现引入电荷C ，电荷量Qc ＝+4.0×108-C ，则电荷C 置于离A cm ，离Bcm 处时，C 电荷即可平衡；若改变电荷C 的电荷量，仍置于上述位置，则电荷C 的平衡状态 (填不变或改变)，若改变C 的电性，仍置于上述位置，则C 的平衡 ，若引入C 后，电荷A 、B 、C 均在库仑力作用下平衡，则C 电荷电性图1—2—9 图1—2—8 图1—2—10 图1—2—11 图1—2—12应为，电荷量应为C．8．如图1—2—12所示，两相同金属球放在光滑绝缘的水平面上，其中A球带9Q的正电荷，B球带Q的负电荷，由静止开始释放，经图示位置时，加速度大小均为a，然后发生碰撞，返回到图示位置时的加速度均为．9．如图1—2—13所示，两个可视为质点的金属小球A、B质量都是m、带正电电荷量都是q，连接小球的绝缘细线长度都是l，静电力常量为k，重力加速度为g．则连结A、B的细线中的张力为多大? 连结O、A的细线中的张力为多大?图1—2—13 10．如图1—2—14所示，一个挂在丝线下端的带正电的小球B静止在图示位置．固定的带正电荷的A球电荷量为Q，B球质量为m、电荷量为q，θ＝30°，A和B在同一水平线上，整个装置处在真空中，求A、B两球间的距离．图1—2—14。