应用回归分析第2章课后习题参考答案
- 格式:doc
- 大小:442.51 KB
- 文档页数:18

第二章 一元線性回歸分析思考與練習參考答案2.1 一元線性回歸有哪些基本假定?答: 假設1、解釋變數X 是確定性變數,Y 是隨機變數;假設2、隨機誤差項ε具有零均值、同方差和不序列相關性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假設3、隨機誤差項ε與解釋變數X 之間不相關: Cov(X i , εi )=0 i=1,2, …,n假設4、ε服從零均值、同方差、零協方差の正態分佈 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考慮過原點の線性回歸模型 Y i =β1X i +εi i=1,2, …,n誤差εi (i=1,2, …,n )仍滿足基本假定。
求β1の最小二乘估計 解: 得:2.3 證明(2.27式),∑e i =0 ,∑e i X i =0 。
證明:∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中:即: ∑e i =0 ,∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回歸方程E (Y )=β0+β1X の參數β0,β1の最小二乘估計與最大似然估計在什麼條件下等價?給出證明。
答:由於εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函數:使得Ln (L )最大の0ˆβ,1ˆβ就是β0,β1の最大似然估計值。
同時發現使得Ln (L )最大就是使得下式最小,∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估計の目標函數相同。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=(5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。

2.1 一元线性回归模型有哪些基本假定?答:1. 解释变量 1x , ,2x ,p x 是非随机变量,观测值,1i x ,,2 i x ip x 是常数。
2. 等方差及不相关的假定条件为⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≠=====j i n j i j i n i E j i i ,0),,2,1,(,),cov(,,2,1,0)(2 σεεε 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件,简称G-M 条件。
在此条件下,便可以得到关于回归系数的最小二乘估计及误差项方差2σ估计的一些重要性质,如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。
3. 正态分布的假定条件为⎩⎨⎧=相互独立n i n i N εεεσε,,,,,2,1),,0(~212 在此条件下便可得到关于回归系数的最小二乘估计及2σ估计的进一步结果,如它们分别是回归系数的最及2σ的最小方差无偏估计等,并且可以作回归的显著性检验及区间估计。
4. 通常为了便于数学上的处理,还要求,p n >及样本容量的个数要多于解释变量的个数。
在整个回归分析中,线性回归的统计模型最为重要。
一方面是因为线性回归的应用最广泛;另一方面是只有在回归模型为线性的假设下,才能的到比较深入和一般的结果;再就是有许多非线性的回归模型可以通过适当的转化变为线性回归问题进行处理。
因此,线性回归模型的理论和应用是本书研究的重点。
1. 如何根据样本),,2,1)(;,,,(21n i y x x x i ip i i =求出p ββββ,,,,210 及方差2σ的估计;2. 对回归方程及回归系数的种种假设进行检验;3. 如何根据回归方程进行预测和控制,以及如何进行实际问题的结构分析。
2.2 考虑过原点的线性回归模型 n i x y i i i ,,2,1,1 =+=εβ误差n εεε,,,21 仍满足基本假定。
求1β的最小二乘估计。
答:∑∑==-=-=ni ni i i i x y y E y Q 1121121)())(()(ββ∑∑∑===+-=--=∂∂n i n i ni i i i i i i x y x x x y Q111211122)(2βββ 令,01=∂∂βQ即∑∑===-n i ni i i i x y x 11210β 解得,ˆ1211∑∑===ni ini i i xyx β即1ˆβ的最小二乘估计为.ˆ1211∑∑===ni ini ii xyx β2.3 证明: Q (β,β1)= ∑(y i-β0-β1x i)2因为Q (∧β0,∧β1)=min Q (β0,β1 )而Q (β0,β1) 非负且在R 2上可导,当Q 取得最小值时,有即-2∑(y i -∧β0-∧β1x i )=0 -2∑(y i-∧β0-∧β1x i ) x i=0又∵e i =yi -( ∧β0+∧β1x i )= yi -∧β0-∧β1x i ∴∑e i =0,∑e i x i =0(即残差的期望为0,残差以变量x 的加权平均值为零)2.4 解:参数β0,β1的最小二乘估计与最大似然估计在εi~N(0, 2 ) i=1,2,……n 的条件下等价。

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答:假设1解释变量X是确定性变量,丫是随机变量;假设2、随机误差项&具有零均值、同方差和不序列相关性:E( i)=0 i=1,2,…,n2Var (i)=, i=1,2, …,nCov( E £)=0 i 工j i,j= 1,2, …,nCov(X i, i )=0 i=1,2, …,n假设4、&服从零均值、同方差、零协方差的正态分布2i~N(0, ~)i=1,2,…,n2.2考虑过原点的线性回归模型Y i= 0X i+ i i=1,2,…,nn nQ e 八(Y i -Y?)2八(Y i -?i X i)2i』i=1得: f?=M羊Xi)X^0n' (X i Y i)i dn' (X i2)i =1i d2.3 证明(2.27 式),工e i =0 ,工eXi=0。
n nQ=S:(丫-Y?)2=迟(Y i —(f?°+f?X i))2 证明: 1 1其中:丫?=児+叹e=Y-丫?即: I ^(A+AA;-l;) = 0|V^o+/?rVj-T;)A;= 0^e =0 ,乞eX i=0假设3、随机误差项&与解释变量X之间不相关:误差 $ (i=1,2,解:…)n仍满足基本假定。
求仪的最小二乘估计2.4回归方程E (Y ) = 00+ 3X 的参数①,妆的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于 £ 厂N(0, ~2)i=1,2,…,n所以 Y i =场 + 0X + £~N ( [3D + [3iX i , o 2) 最大似然函数:1 nL( 0, i ,;「2)=二爲 f i (Y i ) =(2=2)』/2exp{——2、 [Y i -( o i o ,X i )]2}2 ynLn{L( o , i ,二2)}= -:帕(2二2)-2、 M -( o i o ,X i )]222<r y使得Ln (L )最大的况,瞬就是肉,0的最大似然估计值。
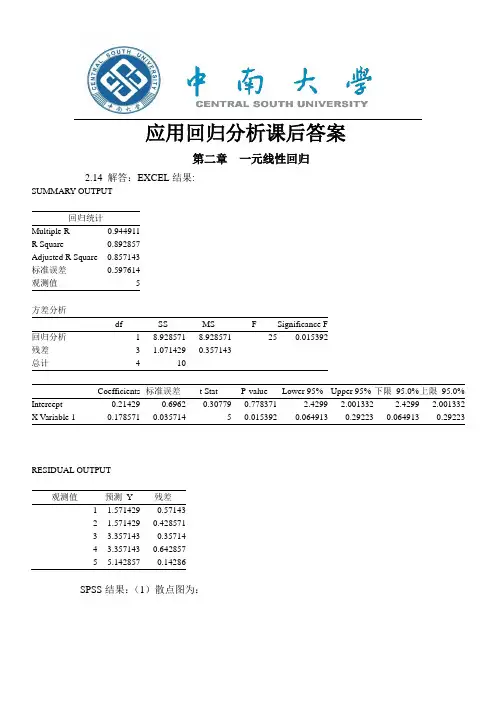
应用回归分析课后答案第二章一元线性回归2.14 解答:EXCEL结果:SUMMARY OUTPUT回归统计Multiple R0.944911R Square0.892857Adjusted R Square0.857143标准误差0.597614观测值5方差分析df SS MS F Significance F回归分析18.9285718.928571250.015392残差3 1.0714290.357143总计410Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0% Intercept-0.214290.6962-0.307790.778371-2.4299 2.001332-2.4299 2.001332 X Variable 10.1785710.03571450.0153920.0649130.292230.0649130.29223RESIDUAL OUTPUT观测值预测Y残差1 1.571429-0.571432 1.5714290.4285713 3.357143-0.357144 3.3571430.6428575 5.142857-0.14286SPSS结果:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

应用回归分析_第2章课后习题参考答案1. 简答题1.1 什么是回归分析?回归分析是一种统计建模方法,用于研究自变量与因变量之间的关系。
它通过建立数学模型,根据已知的自变量和因变量数据,预测因变量与自变量之间的关系,并进行相关的推断和预测。
1.2 什么是简单线性回归和多元线性回归?简单线性回归是指只包含一个自变量和一个因变量的回归模型,通过拟合一条直线来描述两者之间的关系。
多元线性回归是指包含多个自变量和一个因变量的回归模型,通过拟合一个超平面来描述多个自变量和因变量之间的关系。
1.3 什么是残差?残差是指回归模型中,观测值与模型预测值之间的差异。
在回归分析中,我们希望最小化残差,使得模型与观测数据的拟合效果更好。
1.4 什么是拟合优度?拟合优度是用来评估回归模型对观测数据的拟合程度的指标。
一般使用R方(Coefficient of Determination)来表示拟合优度,其值范围为0到1,值越接近1表示模型拟合效果越好。
2. 计算题2.1 简单线性回归假设我们有一组数据,其中X为自变量,Y为因变量,如下所示:X Y13253749511我们想要建立一个简单线性回归模型,计算X与Y之间的线性关系。
首先,我们需要计算拟合直线的斜率和截距。
根据简单线性回归模型的公式Y = β0 + β1*X,我们可以通过最小二乘法计算出斜率和截距的估计值。
首先,计算X和Y的均值:mean_x = (1 + 2 + 3 + 4 + 5) / 5 = 3mean_y = (3 + 5 + 7 + 9 + 11) / 5 = 7然后,计算X和Y的方差:var_x = ((1-3)^2 + (2-3)^2 + (3-3)^2 + (4-3)^2 + (5-3)^2) / 5 = 2var_y = ((3-7)^2 + (5-7)^2 + (7-7)^2 + (9-7)^2 + (11-7)^2) / 5 = 8接下来,计算X和Y的协方差:cov_xy = ((1-3) * (3-7) + (2-3) * (5-7) + (3-3) * (7-7) + (4-3) * (9-7) + (5-3) * (11-7)) / 5 = 4根据最小二乘法的公式:β1 = cov_xy / var_x = 4 / 2 = 2β0 = mean_y - β1 * mean_x = 7 - (2 * 3) = 1因此,拟合直线的方程为:Y = 1 + 2X。

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n )仍满足基本假定。
求β1的最小二乘估计 解: 得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中: 即: ∑e i =0 ,∑e i X i =02.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi ~N (0, σ2 )21112)ˆ()ˆ(i ni i ni ii e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂的假设下求得,最小二乘估计则不要求分布假设。

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n 假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n)仍满足基本假定。
求β1的最小二乘估计 解: 得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:其中:即: ∑e i =0 ,∑e i X i =0∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ21112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi ~N (0, σ2 )的假设下求得,最小二乘估计则不要求分布假设。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)22001()(,())xxx N n L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 3.66==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
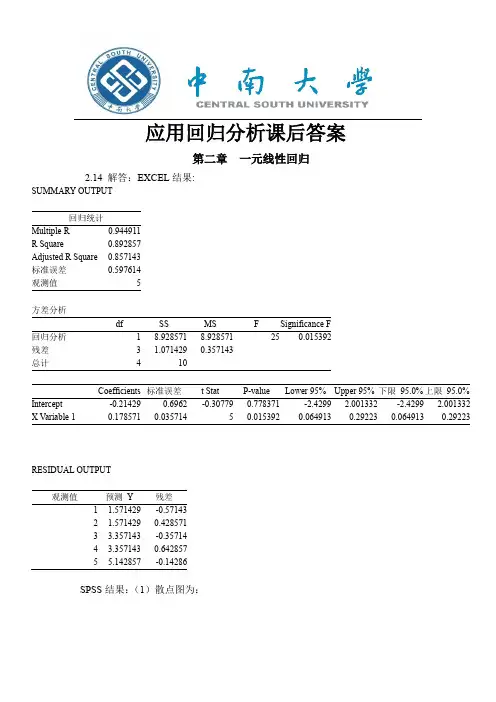
应用回归分析课后答案第二章一元线性回归2.14 解答:EXCEL结果:SUMMARY OUTPUT回归统计Multiple R0.944911R Square0.892857Adjusted R Square0.857143标准误差0.597614观测值5方差分析df SS MS F Significance F回归分析18.9285718.928571250.015392残差3 1.0714290.357143总计410Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0% Intercept-0.214290.6962-0.307790.778371-2.4299 2.001332-2.4299 2.001332 X Variable 10.1785710.03571450.0153920.0649130.292230.0649130.29223RESIDUAL OUTPUT观测值预测Y残差1 1.571429-0.571432 1.5714290.4285713 3.357143-0.357144 3.3571430.6428575 5.142857-0.14286SPSS结果:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN Lσββ∧t σ∧==服从自由度为n-2的t 分布。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n )仍满足基本假定。
求β1的最小二乘估计 解: 得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:其中:即: ∑e i =0 ,∑e i X i =0∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ21112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑ =2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈(5)由于2 11(,)xxNLσββ∧tσ∧==服从自由度为n-2的t分布。
因而/2||(2)1P t nαασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t tααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353即为:(2.49,11.5)22001()(,())xxxNn Lββσ-∧+t∧∧==服从自由度为n-2的t分布。
因而/2||(2)1P t nαα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1pβσββσα∧∧∧∧-<<+=-可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x与y的决定系数22121()490/6000.817()niiniiy yry y∧-=-=-==≈-∑∑(7)ANOVAx平方和 df均方 F显著性组间(组合) 9.000 2 4.500 9.000 .100线性项加权的 8.167 1 8.167 16.333 .056偏差.833 1 .833 1.667.326组内 1.0002 .500总数10.0004由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75))[]1169049363110/3=++++=6.1σ∧= (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)22001()(,())xxx N n L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
2.1 一元线性回归模型有哪些基本假定?答:1. 解释变量 1x ,Λ,2x ,p x 是非随机变量,观测值,1i x ,,2Λi x ip x 是常数。
2. 等方差及不相关的假定条件为⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≠=====j i n j i j i n i E j i i ,0),,2,1,(,),cov(,,2,1,0)(2ΛΛσεεε 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件,简称G-M 条件。
在此条件下,便可以得到关于回归系数的最小二乘估计及误差项方差2σ估计的一些重要性质,如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。
3. 正态分布的假定条件为⎩⎨⎧=相互独立n i n i N εεεσε,,,,,2,1),,0(~212ΛΛ 在此条件下便可得到关于回归系数的最小二乘估计及2σ估计的进一步结果,如它们分别是回归系数的最及2σ的最小方差无偏估计等,并且可以作回归的显著性检验及区间估计。
4. 通常为了便于数学上的处理,还要求,p n >及样本容量的个数要多于解释变量的个数。
在整个回归分析中,线性回归的统计模型最为重要。
一方面是因为线性回归的应用最广泛;另一方面是只有在回归模型为线性的假设下,才能的到比较深入和一般的结果;再就是有许多非线性的回归模型可以通过适当的转化变为线性回归问题进行处理。
因此,线性回归模型的理论和应用是本书研究的重点。
1. 如何根据样本),,2,1)(;,,,(21n i y x x x i ip i i ΛΛ=求出p ββββ,,,,210Λ及方差2σ的估计;2. 对回归方程及回归系数的种种假设进行检验;3. 如何根据回归方程进行预测和控制,以及如何进行实际问题的结构分析。
2.2 考虑过原点的线性回归模型 n i x y i i i ,,2,1,1Λ=+=εβ误差n εεε,,,21Λ仍满足基本假定。
求1β的最小二乘估计。
答:∑∑==-=-=ni ni i i i x y y E y Q 1121121)())(()(ββ∑∑∑===+-=--=∂∂n i n i ni i i i i i i x y x x x y Q111211122)(2βββ 令,01=∂∂βQ即∑∑===-n i ni i i i x y x 11210β 解得,ˆ1211∑∑===ni ini i i xyx β即1ˆβ的最小二乘估计为.ˆ1211∑∑===ni ini ii xyx β2.3 证明: Q (β,β1)= ∑(y i-β0-β1x i)2因为Q (∧β0,∧β1)=min Q (β0,β1 )而Q (β0,β1) 非负且在R 2上可导,当Q 取得最小值时,有即-2∑(y i -∧β0-∧β1x i )=0 -2∑(y i-∧β0-∧β1x i ) x i=0又∵e i =yi -( ∧β0+∧β1x i )= yi -∧β0-∧β1x i ∴∑e i =0,∑e i x i =0(即残差的期望为0,残差以变量x 的加权平均值为零)2.4 解:参数β0,β1的最小二乘估计与最大似然估计在εi~N(0, 2 ) i=1,2,……n 的条件下等价。
证明:因为ni N i ,.....2,1),,0(~2=σε所以),(~2110110σββεββX X Y N i i +++=其最大似然函数为已知使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
即使得下式最小 :∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ ①因为①恰好就是最小二乘估计的目标函数相同。
所以,在ni N i ,.....2,1),,0(~2=σε 的条件下, 参数β0,β1的最小二100ˆˆQQββ∂∂==∂∂乘估计与最大似然估计等价。
2.5.证明0β)是0β的无偏估计。
证明:若要证明0β)是0β的无偏估计,则只需证明E(0β))=0β。
因为0β),1β)的最小二乘估计为⎪⎩⎪⎨⎧-==x y L L xxxy 101/βββ))) 其中∑∑∑∑∑∑∑∑∑-=-=-=-=-=--=22222)(1)(1))((i i i i xx i i i i i i i i xy x nx x n x x x L y x ny x y x n y x y y x x LE(0ˆβ)=E(x y 1ˆβ-)=E(∑∑==--n i i xx i n i i y L x x x y n 111)=E[∑=--ni i xx i y L x x x n 1)1(]=E[∑=++--ni i i xxi x L x x x n 110))(1(εββ]=E(∑=--ni xx i L x x x n 10)1(β)+E(∑=--n i i xx i x L x x x n 11)1(β)+E(∑=--ni i xx i L x x x n 1)1(ε)其中∑=--ni xx i L x x x n 10)1(β=∑=--ni xx i L x x x n 10)1(β=))(1(10∑=--ni ixx x xL x n n β由于∑=-ni i x x 1)(=0,所以∑=--ni xx i L x x x n 10)1(β=0β∑=--ni i xx i x L x x x n 11)1(β=∑=--ni ixx i i x L x x x n x 11)(β=))((11∑=--ni i ixx x x xL x x β=)-)(((11∑=--ni i ixxx x x xL xx β)=)(1x x -β=0又因为一元线性回归模型为⎩⎨⎧++=),0(210σεεββN x y i i i i 独立同分布,其分布为各所以E(iε)=0所以E(∑=--ni xx i L x x x n 10)1(β)+E(∑=--n i i xx i x L x x x n 11)1(β)+E(∑=--ni i xx i L x x x n 1)1(ε=++)0()(0E E β ∑=--ni i xx i E L x x x n 1)()1(ε=0β所以0β)是0β的无偏估计。
2.6 解:因为∑==ni i yn y 11 ①,xy ∧∧-=ββ10 ②,yLx in i xxix∑=∧-=11β③联立 ①②③式,得到y L x ini xx ix x n ∑=∧--=10)1(β。
])1([)(10y L x i ni xx i x x n Var Var ∑=∧--=β)(1])1[(2y L x x x ni Var ni xx i ∑--==σ2122]2(1[)∑-=--+=ni xxi nLx L x x x nx x xxi因为∑-==ni xxx x Li 12)(,)(1=-∑=n i ix x ,所以σβ21212212])(21[)()()(nLx L x x x nxxni in i ni x x xxi Var ∑∑-∑===∧-++=σ22)(1⎪⎪⎪⎭⎫ ⎝⎛+=L x xxn σ2122)()(1⎪⎪⎪⎪⎭⎫ ⎝⎛+=∑-=ni x x x i n2.7 证明平方和分解公式:SST=SSE+SSR证明:2.8 验证三种检验的关系,即验证:()()∑∑==-+-=-=ni i i n i i y i y yy y y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni i i n i i i i n i i y y y y y y y y12112)ˆˆ)(ˆ2ˆ()()SSE SSR y y y y ni i i n i i +=-+-=∑∑==1212)ˆˆ(1)21)2(r r n t --=;(2)2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ证明:(1)因为2-n 22SSESSR L xx =∧∧=σβ和,所以SSTSSE SST SSRn SSESSR n n SSE t LLxxxx)()(22222-=-=-∧=∧=∧βσβ又因为SST SSR r=2,所以SST SSE SST SSR SST r =-=-21故21)2(r r n t --=得证。
(2)22222011111111ˆˆˆˆˆˆ()()(())(())nnnni i ii xx i i i i SSR y y x y y x x y x x L βββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xx L SSR F t SSE n βσ∴===-g2.9 验证(2.63)式:()σ2xx2i Lx -x e i-n 1-1var ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)(证明:),()()()()(∧∧∧+==y y y y y y eiiiiiii cov 2-var var -var var ))x -y cov 2var var x y x y i1ii1i(,()()(∧∧∧+-++=βββ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=--L x x L xx i n )()(22xx 22212i n 1x x σσσ()σ2xx2x -x in 11⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=L。