计算流体力学典型算例
- 格式:docx
- 大小:37.06 KB
- 文档页数:2

第二章例1:用复式水银压差计测量密封容器内水面的相对压强,如下列图。
:水面高程z 0=3m,压差计各水银面的高程分别为z 1=, z 2=, z 3=m, z 4=m, 水银密度 3/13600m kg ρ=',水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解:ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2:用如下列图的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
测压计两侧斜液柱读数的差值为L=30mm ,倾角θ=30∘,试求压强差p 1 – p 2 。
解: 224131)()(p z z γz z γp =-+-- θL γz z γp p sin )(4321=-=-∴例3:用复式压差计测量两条气体管道的压差〔如下列图〕。
两个U 形管的工作液体为水银,密度为ρ2 ,其连接收充以酒精,密度为ρ1 。
如果水银面的高度读数为z 1 、 z 2 、 z 3、z 4 ,试求压强差p A – p B 。
解: 点1 的压强 :p A )(21222z z γp p A --=的压强:点)()(33211223z z γz z γp p A -+--=的压强:点 B A p z z γz z γz z γp p =---+--=)()()(3423211224 )()(32134122z z γz z z z γp p B A ---+-=-∴例4:用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解: C gz r p +⎪⎭⎫ ⎝⎛-=2221ωρ a p gz r p +⎪⎭⎫ ⎝⎛-=∴2221ωρ在界面A-A 上:Z = - ha p gh r p +⎪⎭⎫⎝⎛+=∴2221ωρ⎪⎭⎫⎝⎛+=-=∴⎰2420218122)(ghR R rdr p p F a Rωπρπ例5:在一直径d= 300mm ,而高度H=500mm 的园柱形容器中注水至高度h 1 = 300mm ,使容器绕垂直轴作等角速度旋转。

流体力学公式流体力学是研究流体运动及其力学性质的学科。
它涉及了流体的运动、压强、温度、密度等物理性质,以及液压、气动、船舶、飞行器等领域的应用。
在流体力学中,有许多重要的公式,用于描述和计算流体的性质和行为。
本文将介绍几个流体力学公式,并探讨其应用。
1. 流体静力学公式流体静力学研究的是稳定的静止流体的力学性质。
以下是常见的流体静力学公式:压强公式在静止的流体中,压强(P)定义为单位面积上施加的力(F)与该面积(A)的比值。
压强公式如下:P = F / A其中,P为压强,单位为帕斯卡(Pa),1Pa = 1N / m²;F 为力,单位为牛顿(N);A为压力作用面积,单位为平方米(m²)。
压力的液柱公式当液体静止时,在柱状液体中,液体的压力与液柱的高度和液体密度有关。
液柱公式如下:P = ρgh其中,P为液体的压力,单位为帕斯卡(Pa);ρ为液体的密度,单位为千克/立方米(kg/m³);g为重力加速度,单位为米/秒²(m/s²);h为液柱的高度,单位为米(m)。
2. 流体动力学公式流体动力学研究的是流体在运动过程中的力学性质。
以下是常见的流体动力学公式:连续方程流体在不可压缩条件下的连续方程描述了质量守恒的原理,其表达式为:∇·v = 0其中,∇·v表示速度场的散度,v表示速度矢量。
动量方程流体运动的动量方程描述了流体在外力作用下的运动规律。
对于不可压缩流体,动量方程可表示为:∂v/∂t + (v·∇)v = -1/ρ ∇P + ν∇²v其中,∂v/∂t表示速度场对时间的偏导数;(v·∇)v表示速度场的对流项;-1/ρ∇P表示压力梯度的力学作用;ν∇²v表示速度场的粘性耗散。
能量方程流体运动的能量方程描述了流体在热力学条件下的能量转换规律。
对于不可压缩流体,能量方程可表示为:∂e/∂t + (v·∇)e = -P(∇·v) + κ∇²T其中,∂e/∂t表示能量场对时间的偏导数;(v·∇)e表示能量场的输送项;-P(∇·v)表示压强梯度的功率项;κ∇²T表示温度场的传导项。

pai 定理 工程流体力学例题例 1 开口容器内盛有液体,容器下部壁面有孔通大气。
显然在孔的不同高度上流出的速度也不同。
试计算通过此孔的流量Q 。
设自由面高度不变,不计摩擦,几何尺寸如图(4.13)所示。
解 出口面上的任一微面 dh b ⨯上的速度可以利用连续方程及动量方程求得gh 2e=V式中h 为此微元面距自由面的高度。
出口体积流量为})()2{(2322b 2/32/32/2/2/12/2/d H dH g b dh h g b Vdh Q d H d H d H d H --+===⎰⎰+-+-2a e g p p H ρ+= 例2大容器有背压的小孔流出。
开口容器内盛有液体,容器下部有小孔,小孔与另一盛有液体的容器通,如图(4.14)所示。
两容器中自由液面高度分别为1H ,2H ,压力位a p ,设不计摩擦,1H ,2H 为常数,试求小孔流出速度。
解 小孔出口压力(a )在S A 面与e A 面之间应用伯努利方程(b )利用(a )、(b ),并注意到eV V S <<,可得到出口速度公式)g 221e H H V -=(例3 文丘里管流量计为了测量管道中的流量,可以将收缩—扩张管接到管道中去。
如图(4.15)所示。
通过测量颈部及来流段的压力差以确定流体的平均速度。
为了测量这个压力差,可以利用U 型管测压器。
试建立颈部g2g p 0g 2g p 2ee 2a 1VV H S ++=+=ρρ)1)(()()g-g1212121122z p z p ρρρρρρ,,()(--=---=++l l l l l l 2/1,12212222)]1)(()/-1g2[(ρρ---==l l A A A V A Q 2/1,122122)]1)(()/(-1g 2[A ρρ---=l l A V 流速与U 型管中液面高度差的关系。
解 对1—1,2—2截面利用连续方程与伯努利方程1221A A V V = (a)z pV z p V ggg g 2222112122++=++ρρ(b)由此两式可得 )()(2)/(1221121222z p z p A A V gg g +-+=-ρρ(c ) 由此可见,只要能测出p p 12-就可完全确定V2。

课程:计算流体力学题目:FLUENT软件具体实例运用实例:在边长为1m的正方形容器,右侧壁面温度为2000K,左侧壁面温度为1000K,上下壁面均为绝热。
重力方向向下,重力加速度设为;容器部的介质密度为1000的流体介质,其定压比热,粘性系数,热传导率。
流体的介质普朗特数,基于特征长度,方腔长度L的瑞利数,普朗克数(特征温度取冷热壁面温度的平均值)。
由于传热引起的密度梯度产生了浮力驱动流动。
壁面为黑色,介质具有吸收和发射性质,增强了介质与壁面之间的辐射热交换。
利用GAMBIT建立计算区域和指定边界条件类型1、创建控制区域(1)创建点(2)创建边(3)创建面2、网络划分(1)边的网络划分(2)面的网络划分网络划分图3、边界条件类型的指定添加边界的名称、类型及对应的几何单位:edge1.2.3.4的边界名称分别为left,right,top,bottom,边界条件的类型为WALL。
4、mesh文件的输出生成"radiation.mesh"的网络文件。
一、利用Rosseland辐射模型求解Rosseland模型中的速度矢量图流函数等值线图不考虑辐射时的流函数等值线图温度分布图不考虑辐射的温度分布容器水平线上Y方向速度的显示1、首先创建y=0.5的水平直线2、直线y=0.5上Y方向速度的显示。
Rosseland模型中水平中心线Y方向速度曲线左右壁面的传热率的计算点击report,fluxes,打开Flux Reports对话框,选中Options项下的Total HeatTransfer Rate选项,选中Boundaries下的Left 和right,然后单击Compute图标,设置如下图所示左右壁面总的传热率均接近743000W二、利用P-1辐射模型进行求解P-1迭代过程P-1模型中的速度矢量图水平中心线上的Y方向速度显示。
P-1模型水平中心线Y方向速度曲线左右壁面总传热面积的计算左右壁面总传热率设置及计算结果对话框右侧壁面总的传热率约为84600W三、利用DTRM辐射模型进行求解DTRM迭代过程DTRM模型中的速度矢量图DTRM模型中水平中心线Y方向速度曲线左右壁面传热面积左右壁面总传热率设置及计算结果对话框四、利用DO辐射模型进行求解DO迭代过程DO模型中的速度矢量图DO模型中水平中心线Y方向速度曲线左右壁面总传热率计算结果比较上述四个模型计算的水平中心线上的Y方向的速度由以上图可知P-1、DTRM和DO模型计算结果几乎相同,尽管他们计算的壁面传热率不同;因为对于小的光学厚度,速度场独立于辐射场,而P-1、DTRM 和DO模型采用与不考虑辐射相近的求解流场的计算方法,可以看出Rosseland 模型不适合小的光学厚度下求解。

练习题1. 如右图所示,在一密闭容器中,上部装有密度ρ1=0.8×103kg/m 3的油,下部为密度ρ2=103 kg/m 3的水,已知h 1=0.4m ,h 2=0.2m 。
测压管中水银柱的读数h =0.5m ,水银的密度为ρ1=13.6×103 kg/m 3。
求密闭容器中油液面上的压强p 0。
2. 图示为一水暖系统,为了防止水温升高时体积膨胀将水管胀裂,在系统顶部设一膨胀水箱,使水有膨胀的余地。
若系统内水的总体积为8m3,加温前后温差为50℃,在其温度范围内水的膨胀系数为βT =9×10-4 1/℃,求膨胀水箱的最小容积。
3. 当温度不变,压强从0.20 MPa 增加到10 MPa 时,某种液体的体积减小0.49%,求该液体的体积模量。
4. 两个充满空气的封闭容器互相隔开,左边压力表M 的读数为100kPa ,右边真空计V 的读数为 3.5mH2O ,试求连接两容器的水银压差计中h 的读值。
5. 已知流体运动的速度场为:3231yv xy v y x ==,,试求t=2时过点()()x y z ,,,,=312处的流线方程。
hp ap 0h 1h 2ρ1ρ2ρ36. 如图所示,水在压强作用下从密封的下水箱沿竖直管道流入上水箱中,已知h =50cm ,H =3m ,管道直径D =25mm ,λ=0.02,各局部阻力系数分别为ζ1=0.5,ζ2=5.0,ζ3=1.0,求:为维持稳定的管中流速V =1m/s ,下水箱的液面压强应保持在多少Pa?7. 右图为毕托管示意图。
液体自左向右流动,直管和直角弯管直接插入管道内的液体中,弯管开口迎着流动方向。
测得A 点的液柱高度为hA =170 mm ,B 点的液柱高度为hB = 230 mm ,已知液体的密度为 =990 kg/m3,忽略阻力损失,试计算管内液体的流速uA 。
8. 如右图所示为一壁厚可以忽略的大容器,在其下部开一直径为d =12mm 的小孔口,水自孔口流出后进入另一液面比大容器液面低H =1.2m 的容器中,两容器内的水位始终保持不变。


《例题力学》典型例题例题1:如图所示,质量为m =5 kg 、底面积为S =40 cm ×60 cm 的矩形平板,以U =1 m/s 的速度沿着与水平面成倾角θ=30的斜面作等速下滑运动。
已知平板与斜面之间的油层厚度δ=1 mm ,假设由平板所带动的油层的运动速度呈线性分布。
求油的动力粘性系数。
解:由牛顿内摩擦定律,平板所受的剪切应力du Udy τμμδ== 又因等速运动,惯性力为零。
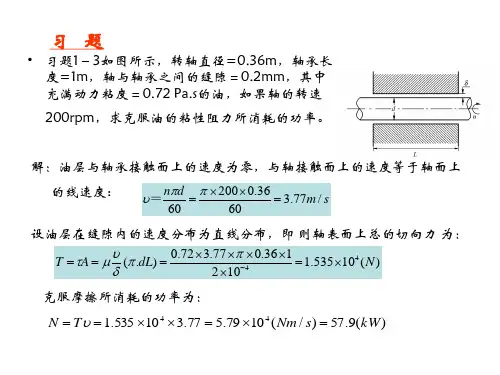
根据牛顿第二定律:0m ==∑F a ,即:gsin 0m S θτ-⋅=()324gsin 59.8sin 301100.1021N s m 1406010m U S θδμ--⋅⨯⨯⨯⨯==≈⋅⋅⨯⨯⨯ 例题2:如图所示,转轴的直径d =0.36 m 、轴承的长度l =1 m ,轴与轴承的缝隙宽度δ=0.23 mm ,缝隙中充满动力粘性系数0.73Pa s μ=⋅的油,若轴的转速200rpm n =。
求克服油的粘性阻力所消耗的功率。
解:由牛顿内摩擦定律,轴与轴承之间的剪切应力()60d d n d uy πτμμδ==粘性阻力(摩擦力):F S dl ττπ=⋅= 克服油的粘性阻力所消耗的功率:()()3223223230230603.140.360.732001600.231050938.83(W)d d n d n n lP M F dl πππμωτπδ-==⋅⋅=⨯⨯=⨯⨯⨯=⨯⨯=例题3:如图所示,直径为d 的两个圆盘相互平行,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以恒定角速度ω旋转,此时所需力矩为T ,求间隙厚度δ的表达式。
解:根据牛顿黏性定律 d d 2d r r F A r r ωωμμπδδ== 2d d 2d r T F r r r ωμπδ=⋅=42420d d 232dd d T T r r πμωπμωδδ===⎰432d Tπμωδ=例题4:如图所示的双U 型管,用来测定比水小的液体的密度,试用液柱高差来确定未知液体的密度ρ(取管中水的密度ρ水=1000 kg/m 3)。

光滑粒子流体力学计算案例光滑粒子流体力学(Smoothed Particle Hydrodynamics,SPH)是一种基于粒子方法的流体力学计算方法。
它通过离散化流体介质为一系列粒子,并利用这些粒子之间的相互作用来模拟流体的运动和变化。
下面将介绍十个光滑粒子流体力学计算案例,以展示其在不同领域的应用。
1. 大规模涡街模拟:涡街是指在流体中形成的旋转流动,具有很多实际应用,如风力发电和混合过程。
通过使用SPH方法,可以模拟大规模涡街的形成和演化,以研究其对流体流动的影响。
2. 水下爆炸冲击波模拟:水下爆炸会产生强烈的冲击波,对周围环境造成破坏。
利用SPH方法,可以准确地模拟水下爆炸的冲击波传播过程,以评估其对结构物和生物的影响。
3. 水波传播模拟:SPH方法可以用于模拟水波的传播和变形过程。
这对于海洋工程、船舶设计和海岸防护等领域非常重要,可以帮助工程师预测和防止水波对结构物的破坏。
4. 河流水动力学模拟:通过将河流离散为一系列粒子,可以使用SPH方法模拟河流的水动力学行为,包括水流速度、水位变化和悬浮颗粒的输运等。
这对于河道治理和水资源管理非常关键。
5. 波浪-结构相互作用模拟:在海洋工程和海岸防护中,波浪与结构物之间的相互作用是一个重要问题。
使用SPH方法,可以模拟波浪与结构物的相互作用,以评估结构物的稳定性和安全性。
6. 粘弹性流体模拟:SPH方法不仅适用于模拟牛顿流体,还可以模拟粘弹性流体,如聚合物溶液和纳米流体。
这对于研究材料的流变性质和设计新型流体材料非常有价值。
7. 燃烧过程模拟:SPH方法可以模拟燃烧过程中的流体动力学和热传导行为。
这对于燃烧工程和火灾安全评估非常重要,可以帮助改进燃烧设备和制定有效的火灾防护措施。
8. 多相流模拟:多相流是指同时存在多种不同相态的流体,如气液两相流和固液两相流。
SPH方法可以模拟多相流的复杂流动行为,如气泡运动、颗粒悬浮和液滴破裂等。
9. 气体动力学模拟:SPH方法可以用于模拟气体动力学过程,如爆炸、喷射和气体流动。

第一章:绪论例1-1 200 ºC体积为的2.5m3水,当温度升至800ºC时,其体积增加多少?解: 200 ºC时:ρ1=998.23kg/m3 800CºC时:ρ2=971.83kg/m3即:则:例1-2使水的体积减小0.1%及1%时,应增大压强各为多少?(K=2000MPa)d V/V =-0.1%=-2000×106×(-0.1%)=2×106Pa=2.0MPad V /V = -1%= -2000×106×(-1%)=20 MPa例1-3输水管l=200m,直径d=400mm,作水压试验。
使管中压强达到55at后停止加压,经历1小时,管中压强降到50at。
如不计管道变形,问在上述情况下,经管道漏缝流出的水量平均每秒是多少?水的体积压缩率κ =4.83×10-10m2 /N 。
解水经管道漏缝泄出后,管中压强下降,于是水体膨胀,其膨胀的水体积水体膨胀量5.95 l 即为经管道漏缝流出的水量,这是在1小时内流出的。
设经管道漏缝平均每秒流出的水体积以Q 表示,则例1-4:试绘制平板间液体的流速分布图与切应力分布图。
设平板间的液体流动为层流,且流速按直线分布,如图1-3所示。
解:设液层分界面上的流速为u,则:切应力分布:图1-3上层下层:在液层分界面上:--流速分布:上层:下层:例1-5:一底面积为40 ×45cm2,高为1cm的木块,质量为5kg,沿着涂有润滑油的斜面向下作等速运动,如图1-4所示,已知木块运动速度u =1m/s,油层厚度d =1mm,由木块所带动的油层的运动速度呈直线分布,求油的粘度。
解:∵等速∴αs =0由牛顿定律:∑F s=mαs=0m gsinθ-τ·A=0(呈直线分布)图1-4∵ θ=tan-1(5/12)=22.62°例1-6: 直径10cm的圆盘,由轴带动在一平台上旋转,圆盘与平台间充有厚度δ=1.5mm的油膜相隔,当圆盘以n =50r/min旋转时,测得扭矩M =2.94×10-4 N·m。
工程流体力学习题及答案工程流体力学习题及答案工程流体力学是研究流体在工程领域中的运动规律和力学性质的学科。
它在各个工程领域中都有广泛的应用,例如水力工程、航空航天工程、石油工程等。
在学习工程流体力学的过程中,解决习题是提高理论应用能力的重要途径。
下面,我们将介绍一些常见的工程流体力学习题及其详细解答。
1. 一个长方形截面的水槽,长为2m,宽为1m,高为1.5m。
槽中注满了水,求水的质量。
解答:水的质量可以通过体积和密度的乘积来计算。
首先计算水的体积,即长方体的体积,公式为V = 长× 宽× 高= 2m × 1m × 1.5m = 3m³。
然后,根据水的密度为1000kg/m³,将体积乘以密度,即可得到水的质量。
所以,水的质量为3m³ × 1000kg/m³ = 3000kg。
2. 一个圆柱形容器,半径为0.5m,高度为2m,容器中注满了油,油的密度为900kg/m³。
求油的质量。
解答:油的质量可以通过体积和密度的乘积来计算。
首先计算油的体积,即圆柱体的体积,公式为V = π × 半径² × 高度= 3.14 × (0.5m)² × 2m = 1.57m³。
然后,根据油的密度为900kg/m³,将体积乘以密度,即可得到油的质量。
所以,油的质量为1.57m³ × 900kg/m³ = 1413kg。
3. 一根半径为0.1m的水管,水流速度为2m/s,求水管中的水流量。
解答:水流量可以通过流速和管道截面积的乘积来计算。
首先计算管道的截面积,即圆的面积,公式为A = π × 半径² = 3.14 × (0.1m)² = 0.0314m²。
然后,将流速乘以截面积,即可得到水流量。
水水银题1图题型一:曲面上静水总压力的计算问题(注:千万注意方向,绘出压力体)1、AB 曲面为一圆柱形的四分之一,半径R=0.2m ,宽度(垂直纸面)B=0.8m ,水深H=1.2m ,液体密度3/850m kg =ρ,AB 曲面左侧受到液体压力。
求作用在AB 曲面上的水平分力和铅直分力。
(10分) 解:(1)水平分力:RB RH g A h P z c x ⋅-==)2(ργ…….(3分) N 1.14668.02.0)22.02.1(8.9850=⨯⨯-⨯⨯=,方向向右(2分)。
(2)铅直分力:绘如图所示的压力体,则B R R R H g V P z ⎥⎥⎦⎤⎢⎢⎣⎡+-==4)(2πργ……….(3分)1.15428.042.014.32.0)2.02.1(8.98502=⨯⎥⎥⎦⎤⎢⎢⎣⎡⨯+⨯-⨯⨯=,方向向下(2分)。
2.有一圆滚门,长度l=10m ,直径D=4.2m ,上游水深H1=4.2m ,下游水深H2=2.1m ,求作用于圆滚门上的水平和铅直分压力。
ldQhG BA空 气 石 油甘 油7.623.661.529.14m11解题思路:(1)水平分力:l H H p p p x )(21222121-=-=γ 方向水平向右。
(2)作压力体,如图,则l D Al V p z 4432πγγγ⨯=== 方向垂直向上。
3.如图示,一半球形闸门,已知球门的半径m R 1= ,上下游水位差m H 1= ,试求闸门受到的水平分力和竖直分力的大小和方向。
解: (1)水平分力:()2R R H A h P c πγγ⋅+===左,2R R A h P c πγγ⋅='=右右左P P P x -=kN R H 79.30114.31807.92=⨯⨯⨯=⋅=πγ,方向水平向右。
(2)垂直分力:V P z γ=,由于左、右两侧液体对曲面所形成的压力体均为半球面,且两侧方向相反,因而垂直方向总的压力为0。
典 型 例 题 1 基本概念及方程【1-1】底面积A =0.2m ×0.2m 的水容器,水面上有一块无重密封盖板,板上面放置一个重量为G 1=3000N 的铁块,测得水深h =0.5m ,如图所示。
如果将铁块加重为G 2=8000N ,试求盖板下降的高度Δh 。
【解】:利用体积弹性系数计算体积压缩率:E p v v //∆=∆ )/(00B p p np E +=p 为绝对压强。
当地大气压未知,用标准大气压Pa p 501001325.1⨯=代替。
Pa A G p p 51011076325.1/⨯=+=Pa A G p p 52021001325.3/⨯=+=因 01/p p 和 02/p p 不是很大,可选用其中任何一个,例如,选用02/p p 来计算体积弹性系数:Pa B p p np E 9020101299.2)/(⨯=+=在工程实际中,当压强不太高时,可取 Pa E 9101.2⨯=512104827.6/)(///-⨯=-=∆=∆=∆E p p E p v v h hm h h 55102413.310604827--⨯=⨯=∆【2-2】用如图所示的气压式液面计测量封闭油箱中液面高程h 。
打开阀门1,调整压缩空气的压强,使气泡开始在油箱中逸出,记下U 形水银压差计的读数Δh 1=150mm ,然后关闭阀门1,打开阀门2,同样操作,测得Δh 2=210mm 。
已知a =1m ,求深度h 及油的密度ρ。
【解】水银密度记为ρ1。
打开阀门1时,设压缩空气压强为p 1,考虑水银压差计两边液面的压差,以及油箱液面和排气口的压差,有同样,打开阀门2时,两式相减并化简得代入已知数据,得所以有2 基本概念及参数【1-3】测压管用玻璃管制成。
水的表面张力系数σ=0.0728N/m ,接触角θ=8º,如果要求毛细水柱高度不超过5mm ,玻璃管的内径应为多少? 【解】由于因此【1-4】高速水流的压强很低,水容易汽化成气泡,对水工建筑物产生气蚀。
计算流体力学典型算例
流体力学是研究液体和气体在运动中的力学性质和行为的学科。
计算
流体力学(CFD)是一种利用数学模型和数值方法来模拟和解决流体力学
问题的技术。
在实际应用中,CFD被广泛应用于工程、航空航天、天气预
报等领域。
下面将介绍一个典型的计算流体力学算例。
典型算例:空气动力学性能分析
假设我们要研究一架新型飞机的空气动力学性能,我们可以利用CFD
来模拟和计算该飞机在不同速度和攻角条件下的气动特性。
首先,我们需要建立飞机的几何模型。
这可以通过计算机辅助设计(CAD)软件来完成,将飞机的几何形状和细节信息输入到CFD软件中。
接下来,我们需要为计算设置边界条件。
边界条件包括飞机表面的边
界条件和远场环境的边界条件。
在飞机表面,我们可以设置壁面条件和粘
性条件。
远场环境的边界条件可以设置为自由流条件,即远离飞机的区域
中的流体速度和压力。
然后,我们可以选择适当的数值方法来求解流体力学方程。
CFD软件
通常提供了多种数值方法,如有限体积法、有限元法和谱方法等。
根据实
际情况,我们可以选择合适的数值方法来模拟飞机周围的流场。
接下来,我们需要设置求解参数。
这些参数包括时间步长、网格大小、迭代收敛准则等。
根据计算资源和精度要求,我们可以选择合适的参数值。
完成设置后,我们可以开始进行计算。
CFD软件将根据初始条件和边
界条件,以迭代方式求解流体力学方程。
每一步迭代都会更新飞机周围的
流场,直到达到收敛标准。
计算完成后,我们可以通过CFD软件提供的可视化工具来分析计算结果。
我们可以查看飞机周围的流线、压力分布、速度分布等信息,并进一步分析飞机的气动特性,如升力系数、阻力系数等。
通过这个典型算例,我们可以看到CFD在空气动力学性能分析中的应用。
CFD技术可以快速、准确地模拟复杂流体力学问题,并提供详细的结果分析。
这使得CFD成为现代工程设计和优化中不可或缺的工具。