第3讲_光线传输矩阵
- 格式:ppt
- 大小:1.36 MB
- 文档页数:32

传输矩阵计算电场分布
要计算电场分布,可以使用传输矩阵方法。
传输矩阵是一种用于描述光束在光学系统中传输过程的数学工具,它可以应用于电磁波的传输。
传输矩阵描述了光束经过一个光学元件(如透镜、衍射光栅等)后的变换关系。
对于电场分布来说,传输矩阵可以将初始的电场分布与光学元件之间的相互作用联系起来。
传输矩阵通常用一个2x2矩阵表示,记作M。
对于一个光学元件,其传输矩阵可以通过其折射率、厚度、曲率等参数进行计算。
如果有多个光学元件组成一个系统,可以将各个元件的传输矩阵相乘得到整个系统的传输矩阵。
对于一个初始的电场分布矢量E_in,通过与传输矩阵相乘,可以得到出射电场分布矢量E_out = M * E_in。
这样就可以计算出电场在光学系统中的传输和变换过程。
需要注意的是,传输矩阵方法是基于一些假设和近似条件的,例如,它适用于高频或平面波近似下的电磁波传输。
此外,在应用传输矩阵计算电场分布时,还需要考虑光学元件的非线性效应、衍射等其他影响因素。
综上所述,通过使用传输矩阵方法,可以计算电场在光学系统中的传输和变换过程,以获得电场分布信息。
1。


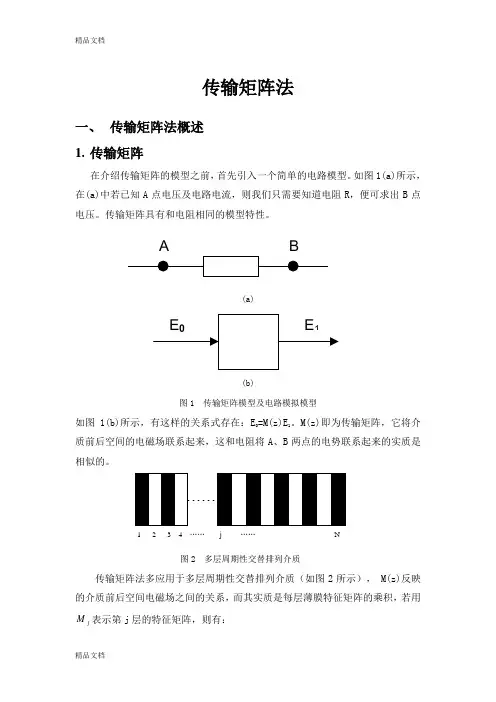
传输矩阵法一、 传输矩阵法概述 1. 传输矩阵在介绍传输矩阵的模型之前,首先引入一个简单的电路模型。
如图1(a)所示, 在(a)中若已知A 点电压及电路电流,则我们只需要知道电阻R ,便可求出B 点电压。
传输矩阵具有和电阻相同的模型特性。
(a)(b)图1 传输矩阵模型及电路模拟模型如图1(b)所示,有这样的关系式存在:E 0=M(z)E 1。
M(z)即为传输矩阵,它将介质前后空间的电磁场联系起来,这和电阻将A 、B 两点的电势联系起来的实质是相似的。
图2 多层周期性交替排列介质传输矩阵法多应用于多层周期性交替排列介质(如图2所示), M(z)反映的介质前后空间电磁场之间的关系,而其实质是每层薄膜特征矩阵的乘积,若用j M 表示第j 层的特征矩阵,则有:1 2 3 4 …… j …… N(1)其中, (2)j δ为相位厚度,有 (3)如公式(2)所示,j M 的表示为一个2×2的矩阵形式,其中每个矩阵元都没有任何实际物理意义,它只是一个计算结果,其推导过程将在第二部分给出。
2. 传输矩阵法在了解了传输矩阵的基础上,下面将介绍传输矩阵法的定义:传输矩阵法是将磁场在实空间的格点位置展开,将麦克斯韦方程组化成传输矩阵形式,变成本征值求解问题。
从其定义可以看出,传输矩阵法的实质就是将麦克斯韦方程转化为传输矩阵,也就是传输矩阵法的建模过程,具体如下:利用麦克斯韦方程组求解两个紧邻层面上的电场和磁场,从而可以得到传输矩阵,然后将单层结论推广到整个介质空间,由此即可计算出整个多层介质的透射系数和反射系数。
传输矩阵法的特点:矩阵元少(4个),运算量小,速度快;关键:求解矩阵元;适用介质:多层周期性交替排列介质。
二、 传输矩阵的基础理论——薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量:D 、E 、B 、H ,两个源量:J 、ρ以及反映它们之间关系的方程组成。
而且由媒质方程中的参数ε、μ、σ反映介质对电磁场的影响。







测量光学传输矩阵的方法说实话测量光学传输矩阵这事,我一开始也是瞎摸索。
我试过好多种方法,走了不少弯路才渐渐有点明白。
我最开始的时候,完全不知道从哪里入手。
就像在黑暗里找东西,到处乱撞。
我查了好多资料,按照一些书上说的老方法来做。
那方法看着很简单,就是调节一些光学仪器,然后记录数据,再计算。
可是我发现我做得一塌糊涂。
后来我才明白,是我对仪器的细节设置理解错了。
比如说那个调节光强的旋钮,我以为转一点点没什么差别,结果这一点点就导致数据完全不对。
这就好比你做菜的时候,盐放得稍微不对,整个菜的味道就不对了。
这算是我第一个失败的教训。
后来我又换了一种比较新的设置方法。
这个方法里要用好多个镜子和透镜来调整光路。
说实话,刚开始的时候那些镜子和透镜的位置可把我折腾死了。
光线一会儿强一会儿弱,而且方向也不对。
我就跟个无头苍蝇一样,不断调整镜子的角度。
我记得有一次因为一个镜子稍微歪了一点,整个光路就乱套了。
我当时就特沮丧,但是我也知道,做这个就得多尝试。
再之后,我开始注重每次调整后的数据记录。
光靠估计是不行的,一定要精确。
比如说光强的数值,以前我就大概写个数字,现在就得用精度高的仪器准确测量。
我发现只要这些基础数据准确了,后面计算光学传输矩阵就顺利很多。
不过我还得说,我现在对一些复杂的光路计算还是有点不确定。
但我目前的经验是,如果遇到光路交叉或者多次反射折射的情况,就把它拆分开来,一段光路一段光路地去分析。
这样虽然速度慢一点,但是不容易出错。
还有就是在参考别人的实验方法的时候,不能完全照搬。
因为每个实验室的仪器啊环境啊都有差别。
比在我之前参考一个国外的实验流程,他们那仪器的精度和我这的不一样,所以按照他们的方法做出来的数据不对。
后来我根据自己这儿仪器的具体情况,调整了一下参数,才慢慢有了正确的结果。
在这个不断尝试的过程中,我渐渐发现,测量光学传输矩阵没有一个一劳永逸的完美方法,很多时候就是要不断从错误中学习,从失败里去找可能成功的路。
1. 光学变换矩阵光学变换矩阵是指傍袖光线通过光学元件后,描述其传播特 性的参数发生变化的矩阵表达方法。
任何一条傍轴光线在某一给定横截面内都可以用两个坐标参数来表征,一个是光线离轴线的距离r,另一个是光线与轴线之间的夹角θ我们规定如下的符号规则:光线位置在轴线上方时r 取正,否则取负;光线的出射方向向上时θ取正,否则取负。
将两个坐标值组成的列向量称为光线在某一截面处的坐标向量。
通过光学元件后,坐标向量的变化可用下边的矩阵形式表示为式中, 为光学元件的出射截面处的光线坐标向量; 为光学元件的入射截面处的光线坐标向量;T 为该光学元件的光学变换矩阵,T = 是个2×2阶矩阵。
下边我们来讨论几种光学元件系统的光学变化矩阵。
1) 自由空间传播L 距离设光线出发时坐标为()11,θr ,传播L 距离后变为()22,θr 。
由图5.1.1容易得到:(3.1.1) 2θ对傍轴光线来说,1θ很小,有≈θtan 1θ。
故有:(3.1.2) 写成矩阵表达形式为:2121r r T θθ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦⎥⎦⎤⎢⎣⎡22θr 11r θ⎡⎤⎢⎥⎣⎦⎥⎦⎤⎢⎣⎡D C B A ⎩⎨⎧=+=12112tan θθθL r r ⎩⎨⎧=+=12112θθθL rr 图3.1.1 传播L 距离的光学变换矩阵(3.1.3) 因此,自由空间传播L 距离的光学变换矩阵为:(3.1.4) 2) 球面反射镜以凹面反射镜为例,设入射光线在镜面上的坐标为()11,θr ,出射光线在镜面上的坐标为()22,θr 。
如图3-1-2所示,O 为反射镜面曲率中心,A 为光线入射点,0A 为曲率半径,用R 表示,B 为镜面中心,OB 为镜面轴线,α为入射或反射线与A 点处镜面法线间夹角,β为 AB 所对圆心角。
由图可写出:(3.1.5) 式中, 和 为A 点到轴线的距离;1θ和2θ只代表大小,未考虑符号。
傍轴近似条件下,β为(3.1.6)将式(5.1.8)与式(5.1.7)中,考虑到图示情况下1θ取正、2θ取负,将2θ变号后可以得到:(3.1.7) 把式(5-1-6)与式(5-1-10)合在一起,得到球面反射镜的光学变换矩阵为: (3.1.8) 可以证明,此变换矩阵不仅适用于图5.1.2所示的入射光线 的情况,也适用于任何一种情况的入射光线。