第3讲 光线传输矩阵

光矩阵传输特点一、采用光纤传输光纤传输，即以光导纤维为介质进行的数据、信号传输。

光矩阵能够兼容基本上全部的视音频信号、同时其无损的信号传输功能也是其他模拟矩阵难以企及的。

二、传输距离远通常75-5或75-3视频线缆理论传输距离约200米，普通VGA、DVI、HDMI等线缆传输距离大于15米则依信号分辨率、刷新率会发生不同程度的拖尾、重影、像素失真、信号噪点、信号丢失等情况。

而目前利用光纤传输多模可达500米，单模可达数十公里。

三、数模信号兼容矩阵类型主要指VIDEO、VGA、DVI、HDMI、SDI等，目前大型场所信号源众多，系统所需的信号切换矩阵和各种信号格式转换器很容易造成系统设计繁琐和信号损失。

而光传输矩阵不仅能够兼容基本上全部的视音频信号、同时其无损的信号传输功能也是其他模拟矩阵所不具备的。

如下：1.支持包含数字高清信号的端到端的全数字解决方案。

通道带宽3.2G，超过DVI规范中1.65G 的数据量的要求，满足数字高清信号对带宽的传输要求。

2.全面向下兼容模拟设备。

3.对不同的信号，数字光矩阵提供光传输通道，在信号源输入前端和输出后端完成各类接口到光纤之间的转换，如DVI/HDMI/SDI/HD-SDI等。

4.系统抗干扰能力强，稳定性好。

5.信号传输过程中无衰减。

6.单膜、多膜光模块灵活配置，满足用户对传输距离的不同要求。

7.设备采用插拔式结构，配置灵活，输入/输出接口可任意配置，既可以为光纤接口或是电接口（DVI）接口（DVI接口支持DDC通道的切换）。

8.设备容量从8×8到32×32，最大可到144×144灵活配置选择。

9.光接口全部采用SFP封装的模块，接口模块（板）支持热插拔，方便设备的升级和维护。

10.设备采用双电源冗余供电，有强制散热措施，确保系统24小时连续工作。

四、抗干扰，更安全能够抵抗电磁干扰，包括核子造成的电磁脉冲；对电信号的阻抗极高，所以能在高电压或是地面电位不同的状况下安全工作；重量较轻，接头线缆不会产生火花；没有电磁辐射、不易被窃听，对于需要高度安全的系统而言十分重要；光纤另外一项重要的优点是即使跨越长距离的数条光纤并行，光纤与光纤之间也不会产生串讯的干扰，这和传输电信号的传输线正好相反。

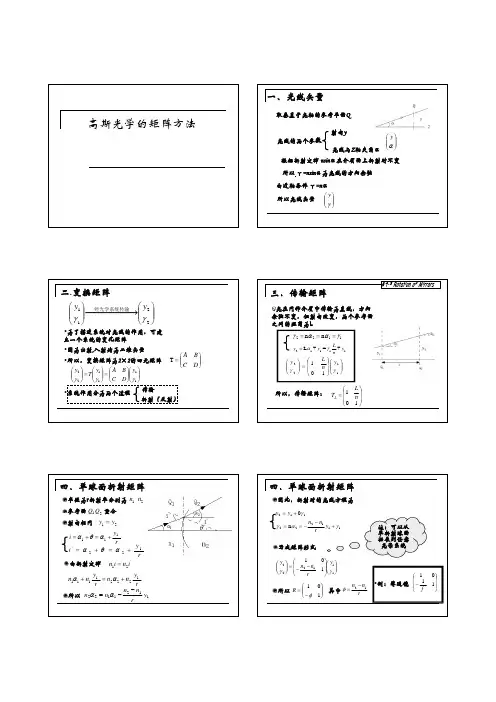
传输矩阵法概述1.传输矩阵在介绍传输矩阵的模型之前，首先引入一个简单的电路模型。

如图1(a)所示, 在(a)中若已知A 点电压及电路电流，贝賊们只需要知道电阻 R,便可求出B 点 电压。

传输矩阵具有和电阻相同的模型特性。

(b)图1传输矩阵模型及电路模拟模型如图1(b)所示，有这样的关系式存在：B=M(z)E i 。

M(z)即为传输矩阵，它将介 质前后空间的电磁场联系起来，这和电阻将 A 、B 两点的电势联系起来的实质是 相似的。

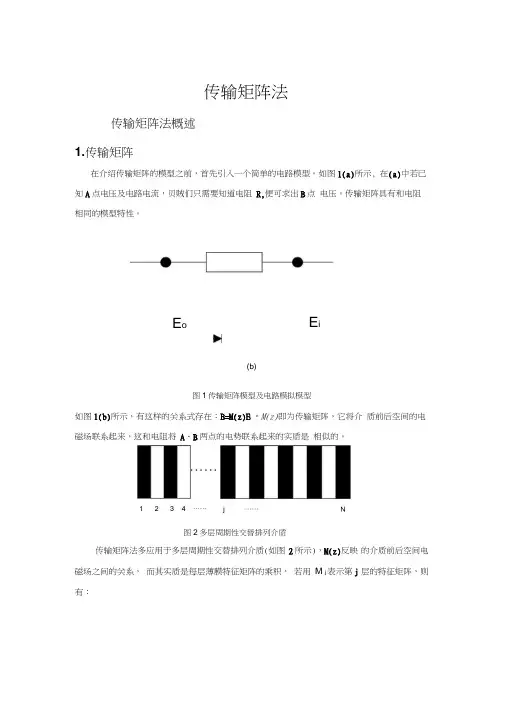
传输矩阵法多应用于多层周期性交替排列介质(如图 2所示)，M(z)反映 的介质前后空间电磁场之间的关系， 而其实质是每层薄膜特征矩阵的乘积， 若用 M j 表示第j 层的特征矩阵，则有：传输矩阵法E oE i图2多层周期性交替排列介质(1)NM ⑵二…M j =如公式（2）所示，M j 的表示为一个2X 2的矩阵形式，其中每个矩阵元都 没有任何实际物理意义，它只是一个计算结果，其推导过程将在第二部分给出。

2•传输矩阵法在了解了传输矩阵的基础上，下面将介绍传输矩阵法的定义：传输矩阵法是将磁场在实空间的格点位置展开，将麦克斯韦方程组化成传输 矩阵形式，变成本征值求解问题。

从其定义可以看出，传输矩阵法的实质就是将麦克斯韦方程转化为传输矩 阵，也就是传输矩阵法的建模过程，具体如下：利用麦克斯韦方程组求解两个紧 邻层面上的电场和磁场，从而可以得到传输矩阵，然后将单层结论推广到整个介 质空间，由此即可计算出整个多层介质的透射系数和反射系数。

传输矩阵法的特点：矩阵元少（4个），运算量小，速度快；关键：求解矩 阵元；适用介质：多层周期性交替排列介质。

传输矩阵的基础理论 一一薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量： D E 、B 、H,两个源量：J 、，以及反映它们之间关系的方程组成。

而且由媒质方程中的参数 "■、匚反映介质对电磁场的 影响。

方程组的实质是描述电磁场的传播， 即: 一个变化的磁场引起邻近区域的 电场变化，而此电场的变化又引起邻近磁场的变化， 如此进行下去，便可抽象出 电磁场的传播。

abcd光学矩阵计算光学矩阵是光学系统中的一种重要工具，能够用来描述光线通过光学系统时的传播和变换规律。

其中，abcd矩阵是一种常用的光学矩阵，用来描述光线通过光学元件时的光学行为。

abcd矩阵是一个2×2的矩阵，表示光线的传输和变换过程。

矩阵的元素a、b、c、d分别代表了光线的传输系数和变换系数。

通过计算abcd矩阵，可以得到光线通过光学元件后的位置和方向的变化关系。

在光学系统中，光线的传输可以通过矩阵乘法来描述。

假设有一个光学元件，其光学矩阵为M，光线的入射位置和方向分别为(x, θ)，则光线的出射位置和方向可以通过以下公式来计算：(x', θ') = M * (x, θ)其中，(x', θ')为光线的出射位置和方向，M为光学矩阵，(x, θ)为光线的入射位置和方向。

在实际应用中，光学系统通常由多个光学元件组成。

假设光学系统由n个光学元件组成，其光学矩阵分别为M1、M2、...、Mn，光线的入射位置和方向为(x, θ)，则光线的出射位置和方向可以通过以下公式来计算：(x', θ') = Mn * ... * M2 * M1 * (x, θ)通过以上公式，我们可以计算出光线在整个光学系统中的传输和变换过程。

这对于光学系统的设计和分析非常重要。

需要注意的是，abcd矩阵描述的是近轴光线的传输和变换过程。

对于大角度入射的光线，abcd矩阵的应用会有一定的限制。

此外，abcd矩阵的计算也需要考虑光学元件的非理想性，如光学元件的形状误差、材料非均匀性等因素。

在实际应用中，光学矩阵的计算可以通过多种方法实现。

一种常用的方法是使用矩阵乘法和矩阵求逆的操作。

通过将光学元件的传输和变换关系表示为矩阵形式，并进行矩阵运算，可以得到光学矩阵的结果。

除了abcd矩阵，还有其他表示光线传输和变换的方法，如传输矩阵法和物方传输函数法等。

这些方法在不同的光学系统分析和设计中有着各自的应用。

《激光原理与技术》习题一《激光原理与技术》习题一班级序号姓名等级一、选择题1、波数也常用作能量的单位，波数与能量之间的换算关系为1cm-1 = eV。

×10-7 (B) ×10-6 (C) ×10-5 (D) ×10-42、若掺Er光纤激光器的中心波长为波长为μm，则产生该波长的两能级之间的能量间隔约为cm-1。

6000 (B) 6500 (C) 7000 (D) 100003、波长为λ=的He-Ne激光器，谱线线宽为Δν=×109Hz。

谐振腔长度为50cm。

假设该腔被半径为2a=3mm的圆柱面所封闭。

则激光线宽内的模式数为个。

6 (B) 100(C) 10000 (D) ×1094、属于同一状态的光子或同一模式的光波是 . (A) 相干的(B) 部分相干的(C) 不相干的(D) 非简并的二、填空题1、光子学是一门关于、、光子的科学。

2、光子具有自旋，并且其自旋量子数为整数，大量光子的集合，服从统计分布。

3、设掺Er磷酸盐玻璃中，Er离子在激光上能级上的寿命为10ms，则其谱线宽度为。

三、计算与证明题1．中心频率为5×108MHz的某光源，相干长度为1m，求此光源的单色性参数及线宽。

2．某光源面积为10cm2，波长为500nm，求距光源处的相干面积。

3．证明每个模式上的平均光子数为11。

exp(hv/kT)?1《激光原理与技术》习题二班级姓名等级一、选择题1、在某个实验中，光功率计测得光信号的功率为-30dBm，等于W。

1×10-6 (B) 1×10-3 (C) 30 (D) -302、激光器一般工作在状态.(A) 阈值附近(B) 小信号 (C) 大信号(D) 任何状态二、填空题1、如果激光器在?=10μm输出1W连续功率，则每秒从激光上能级向下能级跃迁的粒子数是。

2、一束光通过长度为1m的均匀激励的工作物质。

tmm传输矩阵原理TMM传输矩阵原理传输矩阵法（Transfer Matrix Method，简称TMM）是一种用于计算光学系统传输特性的数学方法。

它广泛应用于光学系统设计、分析和优化中，尤其在光纤通信和光学薄膜领域具有重要作用。

TMM是基于波动光学理论的一种近似方法，它通过将光学系统分割成一系列的薄片，并将每个薄片的传输特性表示为一个传输矩阵，从而描述整个系统的传输特性。

传输矩阵是一个二阶方阵，它能够完全描述光的传输过程。

在TMM中，每个薄片都被描述为一个传输矩阵，该矩阵将入射光的振幅和相位转换为出射光的振幅和相位。

在光学系统的分析中，TMM的基本思想是将整个系统分解为多个子系统，并通过将每个子系统的传输矩阵相乘，得到整个系统的传输矩阵。

通过对传输矩阵的乘法运算，可以方便地计算出系统的传输特性，如透过率、反射率、相位延迟等。

TMM的应用广泛而灵活。

在光纤通信领域，TMM可以用于分析和优化光纤连接中的损耗、色散和非线性效应。

在光学薄膜领域，TMM可以用于设计和优化光学薄膜的传输特性，如反射率、透过率和相位调制等。

TMM的优点之一是计算简便快速。

通过将光学系统分解为多个子系统并计算传输矩阵的乘积，可以避免复杂的微分方程求解或数值模拟，从而大大加快了计算速度。

然而，TMM也存在一些限制和假设。

首先，TMM是基于波动光学理论的近似方法，适用于波长远大于物体特征尺寸的情况。

其次，TMM假设光在每个薄片中的传输是均匀的，忽略了传输中的非均匀性和散射效应。

此外，TMM也没有考虑到光的偏振效应和非线性效应。

为了提高TMM的准确性和适用性，研究人员也提出了一些改进和扩展的方法。

例如，矢量TMM考虑了光的偏振效应，非线性TMM考虑了光的非线性效应，色散TMM考虑了光的色散特性等。

TMM是一种基于传输矩阵的光学系统分析方法，广泛应用于光纤通信和光学薄膜领域。

通过将光学系统分解为多个子系统，并通过传输矩阵的乘积运算，TMM可以方便地计算出系统的传输特性。