当前位置：文档之家 › 生物统计学3-抽样分布4-ok

生物统计学3-抽样分布4-ok

  • 格式：pdf
  • 大小：1.43 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

抽样分布知识点总结

抽样分布知识点总结

抽样分布知识点总结抽样分布是统计学中一个重要的概念，它描述了在进行抽样时得到的样本统计量的分布情况。

抽样分布是统计推断的基础，它可以帮助我们理解抽样误差以及估计参数的可信度。

在本文中，我们将对抽样分布的基本概念、性质和相关理论进行总结和讨论。

一、基本概念1.1 抽样与总体在统计学中，总体是指我们想要研究的所有个体的集合，而抽样则是从总体中选取一部分个体作为样本，以获得对总体特征的估计。

抽样可以是随机抽样、分层抽样、系统抽样等方法，目的是代表性地反映总体的特征。

1.2 样本统计量在抽样中，对样本数据进行统计分析得到的统计量称为样本统计量，常见的样本统计量有均值、方差、标准差、比例等。

样本统计量能够提供有关总体参数的估计和推断。

1.3 抽样分布抽样分布是描述样本统计量的分布情况的统计学概念。

当我们从总体中抽取多个样本，并计算每个样本的统计量时，得到的这些统计量的分布就是抽样分布。

抽样分布可以反映出样本统计量的可变性、偏移和分布形态等特征。

二、性质2.1 中心极限定理中心极限定理是抽样分布理论中的重要定理，它描述了在一定条件下，样本均值的抽样分布近似服从正态分布。

中心极限定理对于理解抽样分布的性质和应用具有重要意义，也为许多统计推断方法提供了理论基础。

2.2 大数定律大数定律是另一个重要的抽样分布性质，它描述了当样本容量足够大时，样本均值会收敛于总体均值，即样本均值的抽样分布会集中在总体均值附近。

大数定律为我们理解样本统计量的稳定性和准确性提供了重要参考。

2.3 置信区间置信区间是根据抽样分布推断总体参数的一种方法，通过对抽样分布的分布情况进行分析，我们可以建立对总体参数的置信区间，从而对总体特征进行推断。

置信区间对于统计推断的可信度和精度有着重要的作用。

三、理论基础3.1 样本容量样本容量是影响抽样分布的一个重要因素，在实际抽样中，样本容量的大小对于样本统计量的分布情况有着重要的影响。

通常情况下，样本容量越大，抽样分布的稳定性和准确性越高。

统计学第3章抽样与抽样分布PPT资料(正式版)

统计学第3章抽样与抽样分布PPT资料(正式版)

统计学第3章抽样与抽样分布
3.1 常用的抽样方法
概率抽样
(probability sampling)
1. 也称随机抽样
按一定的概率以随机原则抽取样本
简单随机抽样
(simple random sampling)
1. 从总体N个单位中随机地抽取n个单位作为样本， 每个单位入抽样本的概率是相等的
2. 有重复抽样和不重复抽样
3 2.0 2.5 3.0 3.5
4
.3
2.5
.2
3.0
3.5 .1
4.0 0
P (X ) 1.0 1.5 2.0 2.5 3.0 3.5 4.0 X
样本均值的抽样分布
样本均值的分布与总体分布的比较 P101
总体分布
.3
.2
.1 0
1
234
= 2.5
σ2
.3 P ( X ) 抽样分布
.2
.1
0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 X
当样本容量足够大时(n 30) ，样本均值的抽样分布逐渐趋于正态分布
有重复抽样和不重复抽样
既可以 对总体 参数进 行估计 ，也可 以对 从总体N个单位中随机地抽取n个单位作为样本，每个单位入抽样本的概率是相等的
各层的目标量进行估计
3.1.3 系统抽样
(systematic sampling)
1. 将总体中的所有单位按一定顺序排列，按 某规则确定一个随机起点, 然后每隔一定 的间隔抽取一个单位,直到抽取n个样本单 位.
2. 优点：操作简便，可提高估计的精度
3.1.4 整群抽样
1. 将总体中若干个单位合并为组(群),抽样 时直接抽取群，然后对中选群中的所有单 位全部实施调查
生物统计学3

生物统计学3

正态分布
1 f (x) = e σ 2π
( x− µ )2 − 2σ 2
, −∞ < x<∞
记作 X ~ N ( µ , σ 2 )
设X~ N ( µ , σ ) ,
2
X的分布函数是 的分布函数是
( t − µ )2 − 2σ 2
1 F (x) = σ 2π
∫
x
−∞
e
dt , − ∞ < x < ∞
x−µ t= s/ n
服从自由度为n-1的t分布
F t ( d f ) = P ( t < t1 ) =
∫− ∞
t1
f (t ) d t
F t (df)
1-F t (df)
例如:当df=15时，查t分布表得两尾概率等于 0.05的临界t值为 =2.131，其意义是： P(-∞<t<-2.131)= P(2.131<t<+∞)=
σ x2 − x = σ x21 + σ x22
1 2
(2) 样本平均数差数的方差等于两样本平均数
（总体方差除以各样本容量之和）
σ 12 σ 22 = + n1 n 2
(3) 从两个正态总体中抽出的样本平均数差数的
分布是正态分布， 记作
N ( µ1 − µ 2 ,σ
2 x1 − x 2
)
三、t分布 分布
µx =
σ
2 x
∑
Nn
f x / N n = 48 . 0 / 16 = 3 = µ
∑ =
f ( x − µ x )2
∑ =
fx 2 −ቤተ መጻሕፍቲ ባይዱ( ∑ fx ) 2 / N n Nn
生物统计学课件-3正态分布和抽样分布

生物统计学课件-3正态分布和抽样分布


近似性
当样本量足够大时，样本 统计量近似服从正态分布。
抽样分布在生物学中的应用
01
实验设计
在生物学实验中，常常需要从总体中随机抽取一定数量的样本进行实验，
以评估实验结果的可重复性和可靠性。抽样分布理论为实验设计提供了
理论基础。
02
数据处理和分析
在生物学数据分析和统计推断中，常常需要利用样本统计量来估计总体
生物统计学课件-3正态分布 和抽样分布
目录
• 正态分布 • 抽样分布 • 正态分布与抽样分布的关系 • 实例分析
01
正态分布
正态分布的定义
正态分布是一种连续概率分布，其概率密度函数呈钟形，对称轴为均值所在直线。
在正态分布中，数据点在均值附近最为集中，向两侧逐渐减少，形成钟形曲线。
正态分布是自然界和人类社会中最为常见的分布形态之一，许多随机变量都服从或 近似服从正态分布。
02
抽样分布
抽样分布的定义
01
02
03
抽样分布
描述样本统计量（如样本 均值、样本方差等）的概 率分布。
样本统计量
从总体中随机抽取的样本 所计算出的各种统计指标， 如样本均值、样本方差等。
总体
研究对象全体个体的集合。
抽样分布的性质
独立性
样本统计量之间相互独立。
随机性
样本统计量的取值具有随 机性。
中心极限定理
在大量独立随机抽样的前提下，不论总体分布如何，样本均值的分布趋近于正态分布。
样本均值的方差与总体方差的关系
样本均值的方差随着样本量的增加而趋近于总体方差的1/n，其中n为样本量。
正态分布与抽样分布的区别
定义不同
正态分布是对总体特征的描述，而抽样分布是对样本统计 量的描述。
生物统计学之抽样原理与方法

生物统计学之抽样原理与方法


sp
pq n
样本频率的标准误和置信区间
则总体频率在（1-α）置信水平上的置信区间 为：
( p uasp , p uasp )
2平均数资料样本容量的确定
确定样本容量前，必须先明确能够接受误差的 范围，并了解两类错误的概率和变量标准差的 大小，并根据试验和经验作出估计。
L t0.05sx
sx
n
2u2 pq L2
8 pq L2
其中：p 为合并百分率；q (1 p)。
例题7
对两个食品厂进行抽查后，发现甲厂产品 合格率为95％，乙厂为91％，若要推断 两厂间食品的合格率是否确实相差4％， 取α=0.05时至少要检验多少批食品？ p 0.95 0.91 0.93 2
q 1 0.93 0.07
n
4s2 L2
4 102 22
100
（棵）
例题2
条件同例题1，若要求估计误差不超过5 kg，问应抽取多少果树做样本？
n
4s2 L2
4 102 52
16
（棵）
n
t2
0.05
s2
L2
2.1312 102 52
18 （棵）
n
t2
0.05
s2
2.112 102
18
（棵）
L2
52
频率资料样本容量的确定
随机抽样
随机抽样要求在进行抽样的过程中，应该 使总体内所有个体均有同等机会被抽取。
由于抽样的随机性，可正确地估计试验误 差，从而得出科学合理的结论。
随机抽样可分为：简单随机抽样、分层随 机抽样、整体抽样、双重抽样。
随机抽样
简单随机抽样 是最简单、最常用的抽样方法，要求被 抽总体内每一个体被抽的机会均等。即 采用随机的方法直接从总体中抽出若干 抽样单位构成样本。
生物统计课件：随机抽样和抽样分布

生物统计课件：随机抽样和抽样分布

例. 求7, 9, 4, 4, 6, 6, 6, 8, 8, 11的众数. 例. 众数是否唯一？
6. 极差 数据中最大值与最小值之差
例. 甲大学学生年龄的极差是6岁。 乙大学学生年龄的极差是10岁。
平均数、中位数 和众数关系
抽样分布
样本均数的分布 三大分布
抽样分布
精确抽样分布 渐近分布
• 统计量是随机变量； • 统计量的“抽样分布”
(Xi
−
X
)2
∑ ∑ =
1
n
[
n − 1 i=1
X
2 i
−
1( n n i=1
X i)2]
3. 标准误 SX 即样本均数的标准差
DX = 1 σ 2 = 1 DX
n
n
DX = 1 DX = DX
n
n
SX =
S n
S 2 = DX
4. 中位数
成绩 2 10 78 80 90 人数 1 1 1 22 5
nπ Γ( n)
(1
+
t2 n
)
−
n+1 2
2
E(t) = 0, D(t) = n ( when n > 2 ) n−2
n → ∞, t(n) ~ N (0,1)
iid
Theorem : if X1,L, X n ~ N (µ,σ 2 ), then X − µ ~ t(n −1) S/ n
X −µ X −µ = σ / n = S/ n S/ n
8 8
2.5 ≤ x < 2.7 2.7 ≤ x < 3
7 / 8 3 ≤ x < 3.5
1
x ≥ 3.5
正态概率纸原理
生物统计学课件2、抽样分布及应用一

生物统计学课件2、抽样分布及应用一

体均值的置信区间。
样本量确定
在确定样本量时，我们需要考虑 抽样误差和总体变异程度。通过 抽样分布，我们可以确定一个具
有足够精确度的样本量。
在假设检验中的应用
假设检验
在假设检验中，我们通常会根据已知的抽样分布来构建拒 绝域或临界值，以判断样本数据是否符合预期的假设。
检验效能
在假设检验中，我们还需要考虑检验效能，即当原假设为 假时，我们能够正确拒绝原假设的概率。通过抽样分布， 我们可以计算检验效能。
抽样分布的期望值和方差
总结词
抽样分布的期望值等于总体均值，而方差则与样本大小和总体方差有关。
详细描述
在统计学中，抽样分布的期望值（或平均值）等于总体均值，这是大数定律的一个结果。此外，抽样 分布的方差与样本大小和总体方差有关。随着样本量的增加，样本方差趋于总体方差，这是样本方差 估计总体方差的基础。
02
抽样的方法
随机抽样
简单随机抽样
每个样本被选中的概率相等，不受其 他因素的影响。
分层随机抽样
将总体分成不同的层，然后在每一层 内进行随机抽样。
系统抽样
等距抽样
将总体分成若干个部分，然后每隔一定距离抽取一个样本。
时间序列抽样
按照时间顺序抽取样本，例如每天、每周或每月抽取一个样 本。
分层抽样
分类抽样
单一样本方差的区间估计
使用卡方分布或F分布的临界值，结合样本方差和样本大小，计算 总体方差的置信区间。
两独立样本均值的比较
1 2
两独立样本均值的比较方法
使用t检验或Z检验等方法比较两组独立样本的均 值。
t检验的前提条件
两组样本应来自正态分布的总体，且方差应相等 。
3
Z检验的前提条件
生物统计学1-统计数据的收集与整理4-ok

生物统计学1-统计数据的收集与整理4-ok


2. 质量性状资料（qualitative character） ——能观察到而不能直接测量的性状（颜色、性别）。
处理方法：质量性状数量化。 1）统计次数法：以次数或者分数作为质量性状的数据。
<例1.1> 表1.1 一批鲤鱼健康情况（100条）
2）评分法或分级法（等级、半定量资料）：对某一性状根据其类别 或重要性不同，分级给予评分或划分等级。
2.两个性质(仅对直接法得到的算术平均值有效) 1）离均差之和等于零，即
(x x) (x1 x) (xn x)
x1
xn
nx
x
n
n
x
x
x
0
2）离均差平方和最小，即
(x x) 2 (x a)2 (x2 2xx x2 ) (x2 2xa a2 ) x2 2x x x2 x2 2a x a2
M
。
o
常用来表示生物某些较为稳定的性状，即大多数个体相同，变异仅发生 在较少个体上。如鱼类的脊椎骨数、鳍条数或对虾额角齿数等。
第四节 变异数——数据的离散性
观测值离散程度的表示，用来表示平均值代表性的 强弱。
变异数大，离散程度大，平均值的代表性差，反之 亦然。
主要有极差、方差、标准差、标准误差、变异系数。
资料的构成比。
5)线图：用来表示事物或现象随时间而变化发展的情况。
第三节 平均数——数据的集中性
平均数(mean)——最常用的统计量，是反映资料中各 观测值集中较多的中心位置。
主要有算术平均数、几何平均数、中位数和众数。
一、算术平均数(arithmetic mean)
——各观测值总和除以观测值个数所得的商，简称平均数
见P6表1.1）
解： x 12.5 8.9 10.1 11.24 (cm) 100
统计学中的抽样分布和抽样误差

统计学中的抽样分布和抽样误差

统计学中的抽样分布和抽样误差统计学是一门研究数据收集、处理和分析的学科，而在进行统计分析时，抽样是一项重要的技术。

抽样分布和抽样误差是统计学中关键的概念，本文将具体介绍它们的定义、特点和应用。

一、抽样分布在统计学中，抽样分布指的是从总体中抽取样本的过程中得到的样本统计量的概率分布。

样本统计量可以是样本均值、样本方差等。

抽样分布是由大量不同的样本所形成的，它们具有一定的数学特性。

抽样分布的特点有：1. 抽样分布的中心趋向于总体参数。

当样本容量足够大时，抽样分布的中心会接近总体参数的真值。

2. 抽样分布的形状可能与总体分布相同，也可能近似于正态分布。

中心极限定理是解释抽样分布接近正态分布的重要定理。

3. 样本容量越大，抽样分布的方差越小。

样本容量增大，抽样误差减小。

抽样分布在实际应用中具有重要价值。

通过了解抽样分布的性质，我们可以进行假设检验、构建置信区间以及进行参数估计等统计推断。

二、抽样误差抽样误差是指由于从总体中抽取样本而导致的估计值与总体参数值之间的差异。

它是统计推断中常见的误差来源，也是统计分析中需要控制的重要因素。

抽样误差的大小受到多个因素的影响，包括样本容量、总体变异性以及抽样方法等。

通常情况下，样本容量越大，抽样误差越小，因为更大的样本容量能够更好地代表总体。

为了降低抽样误差，我们可以采取以下策略：1. 增加样本容量。

增大样本容量可以减小抽样误差，提高估计值的准确性。

2. 采用随机抽样方法。

随机抽样可以降低抽样误差，确保样本的代表性。

3. 控制变异性。

尽量减少总体的变异性，可以减小抽样误差。

抽样误差的存在对于统计推断的可靠性有着重要的影响。

在进行数据分析和解释时，我们需要正确理解抽样误差的概念，并将其考虑在内。

总结：统计学中的抽样分布和抽样误差是进行统计推断不可或缺的概念。

抽样分布是样本统计量的概率分布，具有一定的数学特性，可以用于进行假设检验和置信区间估计。

抽样误差是由于从总体中抽取样本而导致的估计值与总体参数值之间的差异，它的大小受到多个因素的影响。

统计学抽样与抽样分布

统计学抽样与抽样分布

3
总体和参数（续）
通常所要估计的总体指标有
X
NX
一、 几个概念
（二）样本总体与样本指标
样本总体。简称样本（Sample），它是按照随机原则， 从总体中抽取的部分总体单位的集合体 。
样本容量：样本中所包含的个体的数量，一般用n表示。 在实际工作中，人们通常把n≥30的样本称为大样本， 而把n<30的样本称为小样本。
可以看成是一组随机变量。
设X1, X2,… , Xn是来自总体X 的一个样本，g(X1, X2,… , Xn) 是 X1, X2,… , Xn的一个函数。若 g 是连续函数，且 g 中不含任何未 知参数，则称 g(X1, X2,… , Xn) 是一个统计量。统计量也是一个随
机变量。
设x1, x2,… , xn 是相应于样本X1, X2,… , Xn的一个样本值， 则 称 g(x1, x2,… , xn ) 是统计量 g(X1, X2,… , Xn) 的一个观测值。
1 n 1
n i 1
(Xi
X )2
,
（4）样本比例：P =k/n，其中k为样本中某属性出现次数 s
概率抽样
(probability sampling)
u概率抽样也叫随机抽样，是指按随机原则抽取样本。
u随机原则，就是排除主观意识的干扰，使总体每一个单位都有
一定的概率被抽选为样本单位，每个单位能否入选是随机的。
u 特点
能有效地避免主观选样带来的倾向性误差（系统偏差）， 使样本资料能够用于估计和推断总体的数量特征，而且 这种估计和推断得以建立在概率论和数理统计的科学理 论之上
可以计算和控制抽样误差，说明估计的可靠程度。
u作用：
在不可能或不必要进行全面调查时，利用概率抽样来推 断总体；
统计学之抽样与抽样分布培训课件

统计学之抽样与抽样分布培训课件

并求样本220平0 均 1 工 52 资 的60分 7布.75。元
2021/3/5
第四章 抽样和抽样分布
36
3.3 不重置抽样下的抽样分布
例 解：已知 X， N 100 000人 ； 总体
n4＝-4300 ， n1 360
样本
为 样本了签解约某率地p区 31600万 9名0％农民工签 重置订抽样劳下动： 合同的签4约00率，随机抽取
F x2 F x1
X
F x1 XXP X x1 FPx 2x1PXX x 2x2
x1
x2
2021/3/5
第四章 抽样和抽样分布
4
2.1 离散型随机变量概率分布
在统计中，通常要求 X 落入[ x1 , x2 )的概率。 对于离散型随机变量：
Px1 X x2 F x2 F x1 F X x1 F X x2
x
n
（ x11 … x1n ）
x1
X
X1
（ x21 … x2n ）
x2
X3 X2
…
……
……
XN
（xm1 …xmn ）
xm
E x X ； x X n
2021/3/5
第四章 抽样和抽样分布
25
3.2 重置抽样下的抽样分布
x
x X
X
n
X
2021/3/5
第四章 抽样和抽样分布
26
3.2 重置抽样下的抽样分布 样本平均数的分布： 1. 样本平均数的期望（平均数）
x2
3. Pf xx1 — XX 的x密2 度 函 数f xdx
x1
2021/3/5
第四章 抽样和抽样分布
9
2.2 连续型随机变量概率分布

生物统计学课件 3、抽样分布及应用二

=
ˆ np np npq
第一节
二项总体抽样
习题 给定一个二项总体 ｛0,1,0,0,1,1,0,1,1,0｝，现从中以 n = 4进行复置抽样, 则分析如下:
例3.1 假定调查某地全部棉株受盲椿危 害的情况，发现704株受害，且 N = 2000， 得μ= 0.352,σ= 0.4776；现从中以n = 200 ˆ = 74，受害 抽取一个样本，知受害株数np ˆ = 0.37，试计算获此抽样误差的概率。 率p
ˆ y或 np
Ӯ或 p ˆ
0 0
1 0.25
2 0.5
3 0.75
4 1.0
ˆ –p|≥0.018) 解 依题意应求P( | p n = 0.4776÷√200 = 0.034 ∵ p ˆ ∴原式 = P(|u| ≥ 0.53)= 2 P(u ≤ - 0.53) = 2 Φ(- 0.53) = 2×0.2981= 0.5962
0 N(1- p)
μ=Σfy /N = Np/N = p σ2 = Σf ( y –μ)2/N = Np(1- p) /N = pq 可见二项总体的两个参数 μ,σ2 都由平均数p (即个体出现某种性状的概率) 唯一确定。
ˆ～N(μΣy ，σ2Σy )且： Σy或 np μΣy = nμ= np, 2 2 = npq， σ2Σy = n = nσ ˆ p 于是: u = (Ӯ – μӮ ) /σӮ ˆ p p pq n = u = (Σy – μΣy ) /σΣy
ˆq ˆ n 1 是σ2= pq的无偏估计值 ⑵∵S 2 np
∴ Sp ˆq ˆ n 1 =√(0.4×0.6÷19)=0.1124 p ˆ
tc= ( | p = 0.667 ˆ – p | – 0.5/n ) / S p ˆ = ( 0.1－0.025 ) / 0.1124

生物统计学(第三版)

概论名词：生物统计：将概率论和数理统计的原理应用到生物学中以分析和解释其数量资料的科学试验设计：试验工作未进行之前应用生物统计原理，来制定合理的试验方案，包括选择动物，分组和对比以及相应的资料搜集整理和统计分析的方法。

总体与样本⏹数据具有不齐性。

⏹根据研究目的确定的研究对象的全体称为总体(population)；⏹含有有限个个体的总体称为有限总体；⏹包含有无限多个个体的总体叫无限总体；⏹总体中的一个研究单位称为个体(individual)；⏹从总体中随机抽出一部分具有代表性的个体称为样本(sample)；⏹样本中所包含的个体数目叫样本容量或大小，常记为n。

⏹通常把n≤30的样本叫小样本，n >30的样本叫大样本。

随机抽取(random sampling) 的样本是指总体中的每一个个体都有同等的机会被抽取组成样本。

变数与变异数列、变量：⏹变数：研究中对样本个体的观察值。

⏹变量：相同性质的事物间表现差异性的某种特征。

如：身高、体重。

⏹变异数列：将变数按从小到大的顺序排列的一组数列。

参数与统计量⏹由总体计算的特征数叫参数（parameter）；⏹由样本计算的特征数叫统计量（staistic）。

准确性与精确性⏹准确性（accuracy）也叫准确度，指观测值与其真值接近的程度。

若x与μ相差的绝对值|x－μ|小，则观测值x的准确性高；反之则低。

⏹精确性（precision）也叫精确度，指重复观测值彼此接近的程度。

若观测值彼此接近，即任意二个观测值xi、xj相差的绝对值|xi －xj |小，则观测值精确性高；反之则低。

⏹调查或试验的准确性、精确性合称为正确性。

由于真值μ常常不知道，所以准确性不易度量，但利用统计方法可度量精确性。

随机误差与系统误差随机误差也叫抽样误差(sampling error) ，是由于许多无法控制的内在和外在的偶然因素所造成。

带有偶然性质，在试验中，即使十分小心也难以消除。

随机误差影响试验的精确性。

第三章 抽样分布


F分布特征及查表方法：
F分布的上侧和下侧分位点见下图。 根据df1值和df2值及α值可在附表7中查出。如F4，20，0.01=4.431 附表7给出的是上侧分位数，要求下侧分位数需将df1和df2位置 对调再求倒数。 如F4，20，0.99=1/F20，4，0.01=1/14.0=0.0714 有些自由度下的 F 值附表 7 没有给出，可用线性内插方法求出。 F12,17,0.05=F12,15,0.05+(F12,20,0.05－F12,15,0.05)/(20-15)×(17-15)=2.396
(x x )
1 2
12
n1
n2
标准化(
u
( x 1 x 2 ) ( 1 2 )
12
n1

2 2
)后的变量服从
n2
标准的正态分布，这样可以推断在标准差已
知时，两个样本平均数的差异是否显著。
二、总体标准差未知但相等时,两个样本平均数和与差 的分布---t分布
例1：查df＝9，α＝0.05的χ 2值 例2：设随机变量k服从分布χ 2(5),求λ的值使其满足 P{k≤λ}=0.05
4.2 从两个正态分布总体中抽取的样本统计量的分布
假定有两个正态总体，分别具有(μ1，σ1)和(μ2，σ2)。 从第一个总体中随机抽取含量为 n1 的样本，并独立地从第二 个总体中抽取含量为 n2的样本。求出x1,s1和x2,s2。下面我们 研究x1±x2的分布。
X 0.1 1 2 F 0.1 即， P 0.5 0.997 0.5 0.5 n n n
解：P {∣ X －μ∣<0.1｝= 0.997

生物统计学课件--3正态分布和抽样分布备课讲稿

生物统计学课件--3正态分布和 抽样分布
正态分布密度函数在直角坐标上的图象称正态曲线
x
决定正态曲线最高点横坐标的值，决定正态曲线最 高点纵坐标的值和曲线的开张程度， 越小，曲线越 陡峭，数据越整齐。
N（ ，2 ） N（156，4.82），N（15，4）
正态曲线有一组而不是一条
2、正态分布的累积函数
f (x)
1
x2
e2
2
三、标准正态分布
称=0，=1时的正态分布为标准正态分布，记为N（0，1）。
1、标准正态分布的密度函数和累积函数
密度函数：
(u)
1
u 2
e2
2
其中：-∞ u∞
累积函数：
(u)P(Uu) 1
u u2
e 2du
2
标准正态分布的分布曲线
u 标准正态分布的累积分布曲线
u
服从正态分布，且有：
x ,
2 x
2
n
即： X N(,2 )
n
将平均数标准化，则：u
x
， u服从N（0，1）
n
例：假如某总体由三个数字2、4、6组成，现在从该总体中做放回式抽样，
样本容量
样本
样本数
n=1
2
4
6
31
平均数
2
4
6
n=2
2 2 ，2 4 ，4 2，2 6，6 2， 4 4， 4 6，6 4，6 6
310=59049
n=20
5904959049
2、标准差未知时的样本平均数的分布----t 分布 若总体的方差是未知的，即标准差 未知，可以用样 本的标准差 s代替总体的标准差 ，
则变量

生物统计学

生物统计学1．总体：我们研究的全部对象2．样本：从总体中抽出的一个部分3．方差：4．对立事件：如果事件A1和A2必发生其一，但不能同时发生，我们称事件A1和A2为对立事件。

5．小概率事件：若随机事件的概率很小，例如小于0.05、0.01、0.001，称之小概率事件。

6．小概率事件：原理小概率事件在一次试验中几乎是不会发生的。

若根据一定的假设条件计算出来该事件发生的概率很小，而在一次试验中竟然发生了，则可以认为假设的条件不正确，从而否定假设。

7．抽样分布：从一个已知的总体中，独立随机地抽取含量为 n 的样本，研究所得样本的各种统计量的概率分布。

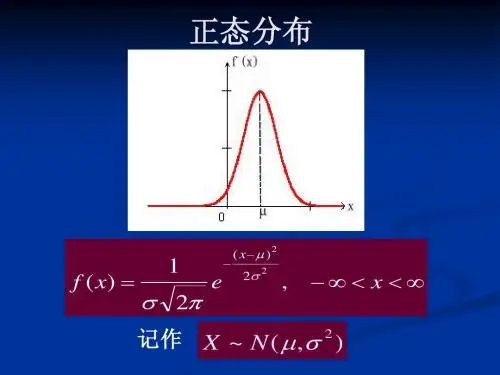
8．标准正态分布：期望值μ=0，即曲线图象对称轴为Y 轴，标准差σ=1条件下的正态分布，记为N(0，1)。

9．统计推断：根据抽样分布律和概率理论，由样本结果（统计数）来推论总体特征（参数）。

10．单尾测验：否定区位于分布的一尾的测验。

11．备择假设：与零假设相对立的假设称为备择假设。

12．接受区：接受无效假设的区间。

13．数学期望：随机变量Y 或者Y 的函数的理论平均数。

14．点估计：用样本数据所计算出来的单个数值，对总体参数所做的估计称为点估计1．算术平均数的重要特征之一是离均差之和（ C ）A 最小B 最大C 等于零D 接近零2．统计推断过程中，若我们拒绝H0，则（ C ）A 犯α错误B 犯β错误C 犯α错误或不犯错误D 犯β错误或不犯错误3．两个平均数的假设测验用测验。

（ C ）A uB tC u 或tD F4．总体参数在区间[L1,L2]内的概率为1-α,其中L1和L2在统计上称为（ D ）A 置信区间B 区间估计C 置信距D 置信限5．下列不是方差分析基本假定的是假定。

（ C ）A 可加性B 正态性C 无偏性D 同质性6．人口调查中，以人口性别所组成的总体是( C )总体A 正态分布B 对数正态C 二项分布D 指数分布7．下列有关标准正态分布概率公式的计算中错误的是（ D ）A P （0<u</uB P （U>u ）=f (-u)C P （| U| > u ）= 2 f (-u)D P (u1<u<="" -="" =="" bdsfid="119" f="" p=""></u8．在抽样分布的研究中，当总体标准差σ未知时样本平均数分布服从（ B ）分布。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

标准化的方法如下：
2
(n 1)s2
2
~
2 (n 1)
2服从自由度为n-1的卡方（chi-square）分布
2分布具有如下性质和特点：
1. 2分布的变量值始终为正； 2. 2分布的形状取决于其自由度 的大小，通常为不对称的右偏分 布，但随着自由度的增大逐渐趋 于对称； 3. 对于 2 分布来说，抽出样本的 总体必须是正态分布。
F
s12 s22
12
2 2
~ F (n1 1, n2 1)
F分布的临界值
临界值（上侧、下侧及双侧临 界值表示同卡方分布）（见附 表6）
附表6没有下侧临界值，可利用 公式求出
F1 (df1, df2 )
1 F (df2, df1)
简便算法：求F值时，用较小 方差作分母，较大方差作分子 ，采用上侧临界值。
2 2
பைடு நூலகம்
~
2 (n2
1)
两个独立的卡方分布除以自由度后相比即得到F分布，即
(n1 1)s12 / 12(n1 1)
(n2 1)s22 22(n2 1)
s12
/
2 1
s
2 2
/
2 2
~ F(n1 1,n2
1)
从均值和方差分别为
N (1,12 )
和
N
(2
,
2 2
)
的两个
正态总体中，抽取含量分别为n1和n2的样本，并分 别求出它们的样本方差s12和s22，标准化的样本方 差之比称为F。
t 分布的临界值
P(t t ) P(t t ) 此时，t 为上侧临界值，- t为下侧临界值；
P( t t ) 此时，t 为双侧临界值。
t 分布的图示跟正态分布十分相似。
注意：本教材中附表4给出的临界值均为双侧临界值，当使
用单侧临界值时需要注意。
<例2.28> 查表求 t0.05(9) ? ，t0.025(9) ?
(n1 1)s12 (n2 1)s22 ( 1
1
)
~ t(n1 n2 2)
n1 n2 2
n1 n2
其中
se2
(n1
1)s12 (n2 1)s22 n1 n2 2
为两样本的合并方差
s x1x2
se2
(
1 n1
1 n2
)
为样本平均数差数的标准误。
3.
方差比
s2 1
s22
的分布——F 分布
样本标准差s代替，这时标准化的样本均值
x 的抽样分布
x s
- 不
n
再服从标准正态分布，而服从具自由度为n-1的t分布，即：
t x - ~ t(n 1) sn
其中 s 称为样本标准误差，df n 1 称为自由度。
n
t 分布的密度曲线特点：
a）受df 制约，每个df 都有一条 t 分 布密度曲线； b）以 y 轴为对称轴左右对称，且在t =0时取极大值； c）与标准正态分布比， t 分布曲线 顶部略低，两尾部稍高而平， df 越 大越趋近于标准正态分布。 d）一般当df >35时，t 值可由Φ值近 似代替。
抽 样 分 布
两个正态总体
均值
σ已知 σ未知
方差
均值差 方差比
σ i已知
σ i未知但相等 σ i未知且不等
u分布 t分布 χ2分布 u分布 t分布
近似t分布
F分布
作业5
•习题2（P43）6、7
2分布的临界值
P( 2 2 )
2 ——上侧临界值
2 1
——下侧临界值
2
、 2 1-
——双侧临界值
2
2
例子：求 2 (9) ? 0.05 2 (9) 16.92 0.05
含义：自由度为9，概率α=0.05的 2值等于 16.92，就是说 2大于16.92的概率为0.05， 或写成 P( 2 16.92) 0.05
与从单个总体抽样的情况类似。 当总体标准差已知时，两个平均数差的分布对总体正态性的
要求并不十分严格，只要样本含量足够大就可以。 当总体标准差未知时，两个总体应尽量为正态总体，如果不
能达到正态总体，也必须是近似正态总体。 对于方差比的分布，要求抽出样本的两个总体必须是正态总
体。
本章小结
单个正态总体
即在大量重复抽样试验的基础上得到统计量取值的集合以及 其相应的概率。
统计学的一个主要任务是研究总体和样本之间的关系，可从两个 方面进行： ① 从总体到样本，即研究抽样分布的问题； ② 从样本到总体，即统计推断。
抽样分布是统计推断的基础。
设一个总体只有4个个体，即N=4，取值分别为x1=1，x2=2，x3=3， x4=4。具体可以视为一个黑布袋中有4个球，分别标明1,2,3,4号球，xi取 每一个值的概率都相同，P(x)=0.25，总体的分布情况如图：
X的总体均值μ=21/6=3.5；各样本平均值与 总体均值μ所表现的差异称为随机抽样误 差。
由于随机误差（个体变异、抽样）的原因，抽取的各个样本所计算的 统计量之间以及样本统计量与总体参数之间会存在一定的的差异，称 为抽样误差。
我们从一个已知的总体中，独立随机地抽取含量为n的样本， 研究所得样本的各统计量的概率分布，即所谓的抽样分布 （sample distribution）；
第三章 抽样分布
样本统计量本身 是随机变量
例子：掷一枚均匀的骰子，并且令X为掷 出的点数。假设骰子被掷3次，产生的样 本 观 察 值 是 2,2,6 ， 则 此 样 本 的 均 值 是 3.33；现在再掷3次骰子并得到样本观察 值3,4,6，这次样本的均值为4.33。
不同的样本会导致各样本的统计量取不同 的值；
总体的分布 总体的均值和方差为：
若从该总体中采取重复抽样的方法抽取容量为n=2的随机样本，即先摸 出一个球，记下号码后放回袋中再摸第二个球，来看看样本均值 的抽 样分布。
从该总体中采取重复抽样的方法抽取容量为n=2的随机样本，共有42=16 个可能的样本，计算每一个样本的均值 。
16个可能的样本及其均值与方差列表
2 1
2 2
n1 n2
当
12
2 2
2，n1
n2
n
时，
2 x1
x2
2 2
n
，而
2 x
2
n
表明：两样本平均数差数的抽样分布比平均数的分布分散 得多。
2. i 未知但相等时，x1 - x2的分布
可以用
s12与
s22
代替
12和
2 2
，仿照单个总体的
t
分布：
t n1n2 2
( x1 x2 ) (1 2 )
， x1-x2
x1 x2
。
x1x2 是样本平均数差数的标准误。
可以证明：
1. i 已知时， x1 - x2 的分布
X1
~
N (1,12 )
，X 2
~
N
(
2
,
2 2
)
， x1 -
x2
~
N (1
2
,
2 1
n1
2 2
)
n2
则标准化后
u (x1 - x2 ) (1 2 ) ~ N (0,1)
解： t0.05(9) 2.262
t0.025(9) 2.685
2. 样本方差的抽样分布—— 2 分布
从正态总体中重复选取容量为n的样本时，由样本方差的所有
可能取值形成的抽样分布，称为样本方差的抽样分布。
在讨论样本方差的分布时，通常并不直接谈s2的分布，而是将
它标准化，并讨论标准化后的变量 2 的分布。
例：查表求
F0.01(4,20) ? F0.01(20,4) ? F0.99 (4,20) ?
解：
F0.01(4,20) 4.43
F0.01(20,4) 14.02
F0.99 (4,20)
1 F0.01 (20,4)
1 14.02
0.0714
注： 从两个总体中抽取的样本统计量的分布，对总体分布的要求
样本均值经整理后的分布 把 的抽样分布绘成频数分布图： 抽样分布的形成过程可以概括成下图：
一、从一个正态总体中抽取的样本统计量的分布
1. 样本平均数的抽样分布
1.1 u分布( z分布)
若随机变量X服从总体均值为μ，方差为σ2的正态分布，从该总体 中独立随机地抽取含量为n的样本，样本均值的数学期望（即样
本均值的均值记为 x），样本均值的方差记为 x 2 ，则：
x
x
n
x 称为平均数 x 的标准误差（standard error of mean），简称标准误。
当 X ~ N(, 2) 时，x ~ N (, 2 ) ，则标准化后
n
u x ~ N (0,1) n
称为u分布（有的教材称为z分布）。
设 X1 ~ 2(n1) , X2 ~ 2(n2 ) , X1、X2 相互独立，则称
F
X1 X2
n1 n2
~ F (n1, n2 )
服从df =(n1，n2)的F分布，其中n1为第一自由度，n2为第二自由度。
样本方差的抽样分布服从卡方分布：
(n1 1)s12
2 1
~
2 (n1 1)
(n2 1)s22
二、从两个正态总体中抽取的样本统计量的分布
假定有两个正态总体 N (1,12)
，
N
(2
,
2 2
)
，从第一个总体随
机抽取含量为n1的样本，并独立地从第二个总体抽取含量为n2的
样本，然后计算样本平均数差数 x1 - x2，其所有可能取值形成的
分布称为样本平均数差数的抽样分布。