当前位置：文档之家 › 吉林大学《线性代数》线性代数1-7.ppt

吉林大学《线性代数》线性代数1-7.ppt

  • 格式：ppt
  • 大小：327.01 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

《线性代数讲义》课件

《线性代数讲义》课件

在工程学中，性变换也得到了广泛的应用。例如，在图像处理中，可
以通过线性变换对图像进行缩放、旋转等操作；在线性控制系统分析中
，可以通过线性变换对系统进行建模和分析。
THANKS
感谢观看
特征向量的性质
特征向量与特征值一一对应，不同的 特征值对应的特征向量线性无关。
特征值与特征向量的计算方法
01
定义法
根据特征值的定义，通过解方程 组Av=λv来计算特征值和特征向 量。
02
03
公式法
幂法
对于某些特殊的矩阵，可以利用 公式直接计算特征值和特征向量 。
通过迭代的方式，不断计算矩阵 的幂，最终得到特征值和特征向 量。
矩阵表示线性变换的方法
矩阵的定义与性质
矩阵是线性代数中一个基本概念，它可以表示线性变 换。矩阵具有一些重要的性质，如矩阵的加法、标量 乘法、乘法等都是封闭的。
矩阵表示线性变换的方法
通过将线性变换表示为矩阵，可以更方便地研究线性 变换的性质和计算。具体来说，如果一个矩阵A表示 一个线性变换L，那么对于任意向量x，有L(x)=Ax。
特征值与特征向量的应用
数值分析
在求解微分方程、积分方程等数值问题时， 可以利用特征值和特征向量的性质进行求解 。
信号处理
在信号处理中，可以利用特征值和特征向量的性质 进行信号的滤波、降噪等处理。
图像处理
在图像处理中，可以利用特征值和特征向量 的性质进行图像的压缩、识别等处理。
05
二次型与矩阵的相似性
矩阵的定义与性质
数学工具
矩阵是一个由数字组成的矩形阵列，表示为二维数组。矩阵具有行数和列数。矩阵可以进行加法、数 乘、乘法等运算，并具有相应的性质和定理。矩阵是线性代数中重要的数学工具，用于表示线性变换 、线性方程组等。

线性代数ppt课件

线性代数ppt课件


x1

b1a22 a11a22
a12b2 a12a21

x2

a11b2 a11a22
b1a21 a12a21

x1

b1a22 a11a22
a12b2 a12a21

x2

a11b2 a11a22
b1a21 a12a21

5
第一章 行列式
我们用符号
aa1211表aa示1222代数和a11a22a12a21
解： 1 3 … （2n-1） 2 4 … 2k… （2n)
D3x24x189x2x212x25x6
即x25x60
x2或x3
值得注意的是：四阶及四阶以上行列式没有像二、三阶 行列式那样的对角线法则
13
第一章 行列式 §1-2 全排列及其逆序数
[引例]用1、2、3三个数字 可以组成多少个没有重复数字的 三位数？
[解依] 次选定百位数、十位数、个位数。 百位数有3种选法 十位数有2种选法 个位数有1种选法 所以可以组成6个没有重复数字的三位数 这6个三位数是 123 132 213 231 312 321
十八世纪开始，行列式开始作为独立的数学概念被研究。 十九世纪以后，行列式理论进一步得到发展和完善。
3
第一章 行列式
莱布尼茨：历史上少见的通才，被誉为 十七世纪的亚里士多德。在数学上，他 和牛顿先后独立发明了微积分。在哲学 上，莱布尼茨的“乐观主义”最为著名 。 他对物理学的发展也做出了重大贡献 。
并称它为三阶行列式。
10
第一章 行列式
2、行列式中的相关术语
行列式的元素、行、列、主对角线、副对角线 3、三阶行列式的计算 （对角线法则或沙路法则 ）

线性代数全套课件

线性代数全套课件
a 21 D ai 1 a i1 a n1 a 22 a2n ai 2 a a in a i2 in an 2 a nn
则行列式D等于下列两个行列式之和：
a11 a 21 D ai 1 a n1 a12 a 22 ai 2 an 2 a1n a11 a 2 n a 21 a in a i1 a nn a n1 a12 a1n a 22 a 2 n a a i2 in a n 2 a nn
i j r[ j i ( k )] a j 2 a jn (a j 1 ka i 1 ) (a j 2 ka i 2 ) (a jn ka in ) an 2 a nn a n1 an 2 a nn
例 计算四阶行列式
1 1
M 11 a11 A11
an 3 ann
对一般情形，只要适当交换D的行与列的位置， 即可得到结论。
定理3 行列式等于它的任一行（列）的各元素与其 对应的代数余子式乘积之和，即
D ai 1 Ai 1 ai 2 Ai 2 ain Ain ( i 1,2, , n) 或 D a1 j A1 j a2 j A2 j anj Anj
a11 a12 a13 a 23 0 0 a 21 a 22 D a 31 a 32 a41 0
n n 1 2
a1na2,n1 an1, 2an1
a14 0 a14a 23a 32a41 0 0
§3 对 换
定义5 排列中，将某两个数对调，其余的数不动， 这种对排列的变换叫对换，将相邻两数对换，叫做 相邻对换（邻换）。 定理1 一个排列中的任意两数对换， 排列改变奇偶性。

线性代数课件ppt

线性代数课件ppt
aij bij i 1,2,,m; j 1,2,,n,
则称矩阵A与B相等,记作A B.
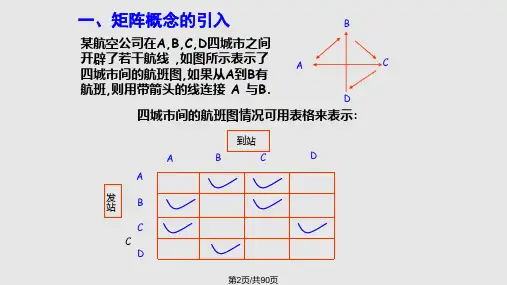
第12页/共90页
例3: 设 A 1 2 3, 3 1 2
B 1 x 3, y 1 z
已知 A B,求 x, y, z. 解: A B,
x 2, y 3, z 2.
第13页/共90页
0 0 1 a31 a32 a33 a31 a32 a33
a11 x1 a12 x2 a1n xn a21 x1 a22 x2 a2n xn
b1
b2
,
am1 x1 am2 x2 amn xn bm
所以方程组可以用矩阵的乘法来表示．方程组中 系数组成的矩阵A称为系数矩阵，
第28页/共90页
方程组中系数与常数组成的矩阵
3 3 6 2 8 1 6 8 9
第16页/共90页
2、 矩阵加法的运算规律
1 A B B A;
2 A B C A B C .
a11
3
A
a21
a12
a22
am1 am1
称为矩阵A的负矩阵.
a1n a2n amn
aij ,
4 A A 0, A B A B.
主对角线 a11 a12
A
a21
a22
副对角线 am1 am2
a1n
a2n
amn
矩阵A的
m, n元
简记为
A Amn
aij
mn
aij
.
这m n个数称为A的元素,简称为元.
元素是实数的矩阵称为实矩阵,
元素是复数的矩阵称为复矩阵.
第5页/共90页
例1:线性方程组
a11 x1 a12 x2

线性代数第一章ppt

线性代数第一章ppt
线性代数第一章
目录
CONTENTS
• 绪论 • 线性方程组 • 向量与向量空间 • 矩阵 • 特征值与特征向量
01
绪论
线性代数的定义与重要性
线性代数是数学的一个重要分支，主要研究线性方程组、向量空间、矩阵 等线性结构。它在科学、工程、技术等领域有着广泛的应用。
线性代数的重要性在于其提供了一种有效的数学工具，用于解决各种实际 问题中的线性关系问题，如物理、化学、生物、经济等。
向量空间中的零向量是唯一确定的，且对于任意 向量a，存在唯一的负向量-a。
向量空间的运算与性质
向量空间中的加法满足交换律和结合 律，即对于任意向量a和b，存在唯一 的和向量a+b；且对于任意三个向量a、 b和c，(a+b)+c=a+(b+c)。
向量空间中的数乘满足结合律和分配 律，即对于任意标量k和l，任意向量a 和b，存在唯一的结果k*(l*a)=(kl)*a 和(k+l)*a=k*a+l*a。
圆等。
经济学问题
线性方程组可以用来描述经济现象和 规律，例如供需关系、生产成本、利
润最大化等。
物理问题
线性方程组可以用来描述物理现象和 规律，例如力学、电磁学、热力学等。
计算机科学
线性方程组在计算机科学中有广泛的 应用，例如机器学习、图像处理、数 据挖掘等。
03
向量与向量空间
向量的定义与性质
01 向量是具有大小和方向的量，通常用有向线 段表示。 02 向量具有模长，即从起点到终点的距离。
特征值与特征向量的计算方法
定义法
幂法
谱分解法
根据特征值和特征向量的定义， 通过解方程组Ax=λx来计算特征 值和特征向量。这种方法适用于 较小的矩阵，但对于大规模矩阵 来说效率较低。

线性代数知识点全面总结PPT课件

线性代数知识点全面总结PPT课件

量 组 的
维 向 量 线性相关
判定 概念 判定
充要条件
线
概念
充分条件
性 相
线性无关
判定
充要条件 充分条件
关 性
概念
向
极大无关组 求法
量
概念
空
向量空间的基
间
线 Ax = b
解
有解判定R(A)≠R(B)无解 的
性 方 程 组
初行变换等阶梯形
R(A)=R(B)有解 结
构
R(A)=n仅有零解 基
Ax = 0
2、矩阵的乘法
(1)(AB)C = A ( BC ) ;
(2) A ( B + C ) =
(3) (kA)(lB) = (kl)AB;
(4) AO =OA = O.
3、矩阵的转置
(1)(AT)T = A; (3)(kA)T =kAT;
(2) (A+B)T = AT+BT; (4) (AB)T = BTAT.
A
A12
A22
An1
An2
A1n A2n
Ann
概 如果AB=BA=E,则A可逆， 念 B是A的逆矩阵.
用定义
逆 矩求
用伴随矩阵 A1 1 A
A
阵
法
分块对 A
角矩阵
0
0 1 A1
B
0
0 0
B1
B
A1 0
0
A1
B1
0
|A| ≠ 0 , A
证 法
可|A逆| =.0 , A不可 逆AB .= E , A与B互逆.
总 有 解R(A)<n有非零解
A+B = ( aij + biAj与) B同型

线性代数完整版ppt课件

线性代数完整版ppt课件
a11x1 a12x2 b1 a21x1 a22x2 b2
求解公式为
x1
x
2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12a 21 b1a 21 a12a 21
请观察，此公式有何特点？ Ø分母相同，由方程组的四个系数确定. Ø分子、分母都是四个数分成两对相乘再
a11 a12 a13 D a21 a22 a23
a31 a32 a33
实线上的三个元素的乘积冠正号， 虚线上的三个元素的乘积冠负号.
a11a22a33 a12a23a31 a13a21a32 a13a22a31a12a21a33 a11a23a32
注意：对角线法则只适用于二阶与三阶行列式.
.
13
(方程组的系数行列式)
D1
b1 b2
a12 a22
D2
a11 a 21
b1 b2
则上述二元线性方程组的解可表示为
x1
b1a22 a11a22
a12b2 a12a21
D1 D
x2
a11b2b1a21 a11a22a12a21.
D2 D
10
例1
求解二元线性方程组
32x1x1 2xx22
12 1
3 2
显然 P n n ( n 1 ) ( n 2 )3 2 1 n !
即n 个不同的元素一共有n! 种不同的排法.
.
18
3个不同的元素一共有3! =6种不同的排法 123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前.
线性代数（第五版）

线性代数第一章、矩阵PPT课件

线性代数第一章、矩阵PPT课件
矩阵的秩的计算方法
可以通过初等行变换或初等列变换将矩阵转化为行阶梯形或列阶梯形，然后数非零行的个数即为矩阵的秩。
矩阵的秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
矩阵的秩
通过初等行变换将增广矩阵化为行阶梯形，然后回代求解。
高斯消元法
克拉默法则
迭代法
适用于线性方程组系数行列式不为0的情况，通过解方程组求出方程的解。
n阶方阵A的行列式记为det(A)，是一个n阶的方阵，其值是一个实数。
行列式与转置矩阵的行列式相等，即det(A^T) = det(A)；行列式的乘法性质，即det(kA) = k^n * det(A)；行列式的初等变换性质，即行列式在初等变换下保持不变。
行列式的定义与性质
行列式的性质
行列式的定义
线性代数第一章、矩阵ppt课件
目录
CONTENTS
矩阵的定义与性质 矩阵的逆与行列式 矩阵的秩与线性方程组 矩阵的特征值与特征向量 矩阵的分解与正交矩阵 矩阵在实际问题中的应用
01
矩阵的定义与性质
CHAPTER
矩阵的定义与性质
about the subject matter here refers to the subject matter here.
相似法
如果存在可逆矩阵P，使得P^(-1)AP=B，则矩阵A的特征值和特征向量可以通过矩阵B的特征值和特征向量来求解。
特征值与特征向量的计算方法
如果矩阵A的所有特征值都是实数且没有重复，则矩阵A可以对角化。
判断矩阵是否可对角化
求解线性方程组
判断矩阵是否相似
优化问题
通过将线性方程组Ax=b转化为特征值问题，可以求解线性方程组。

线性代数ppt课件

线性代数ppt课件

c12 1
c1r c2r 1
dr1 0且rn时，唯一解；
dr1 0且rn时，无穷多解。
c1n d1 c2n d2
crn 0
ddrr1
x1x23x4x5 2 例、求解方程组4x1x1x22x22x36x3x43x144x5 7
2x14x22x34x47x5 1
x1 c12x2

x2

c1nxn d1 c2nxn d2

xr crnxn dr 0dr1
(r n)
（其中r为阶梯形方程组中方程式的个数。）
5
线性代数
第二章 线性方程组
第1节 Gauss消元法
由阶梯形方程组知原方程组（*）的解有以下三种情况：
（ 1 ） d r 1 0 ， 则 方 程 组 无 解 ；
（2）dr1 0且rn，则方程组（*）可化为如下
x1 c12x2 ...c1nxn d1
阶梯形方程组...... x2 ...c2nxn d2

xn dn
1 c12 由于系数行列式D 1
c1n c2n 10，
1
由Cramer法则，方程组（*）解唯一。
6
线性代数

6 x2 9 x2
3x3 5 10 x3 2
x1 3x2 2 x3 6
（3） 2x1x1 3x62x2 5x33x351 x1 3x2 5x3 4
第1节 Gauss消元法
4
线性代数
第二章 线性方程组
第1节 Gauss消元法
用Gauss消元法可以解一般的线性方程组（*），消元的结 果得到一个与原方程组同解的“标准”的阶梯形方程组或 出现矛盾式，可得如下一般形式：

线性代数全套课件

线性代数全套课件
2
它们的和
j1 jn
J 1 a1 j a2 j
1
2
anjn
称为n阶行列式。
a11 a12 a1n
记为
a21 a22 a2 n an1 an 2 ann a11 a12 a1n a21 a22 a2 n an1 an 2 ann
aij 称为行列式的元素
行列式中，除对角线上的元素以外，其他元素全为 零（即i≠j时元素aij＝0）的行列式称为对角行列式， 它等于对角线上元素的乘积。
例 证明
a a n 1 ,1 a n1 a a n 1, 2 an 1
n ( n 1 ) 2
a1n a2,n1 an1, 2 an1
i1 i p i q i n 与 i1 iq i p in 只经过一次对换
a11 a12 a13 a 23 0 0 a 21 a 22 D a 31 a 32 a41 0
n n 1 2
a1na2,n1 an1, 2an1
a14 0 a14a 23a 32a41 0 0
§3 对 换
定义5 排列中，将某两个数对调，其余的数不动， 这种对排列的变换叫对换，将相邻两数对换，叫做 相邻对换（邻换）。 定理1 一个排列中的任意两数对换， 排列改变奇偶性。
此式称为n阶行列式的 展开式或行列式的值
D

j1 jn
1
J
a1 j1 a2 j2 anjn
例
计算4阶行列式
a11 D
0
0 0 a 33 a43
0 0 0 a44
a 21 a 22 a 31 a 32 a41 a42
解： 根据定义，D是4！＝24项的代数和，但每一 项的乘积 a1 j1 a2 j 2 a3 j3 a4 j中只要有一个元素为 0，乘积 n 就等于0，所以只需展开式中不明显为0 的项。

线性代数行列式的概念和性质

线性代数行列式的概念和性质
det A a11 a12
a11 a21
a21 a22
—
a12 a22
+
a11 1 11 det S11 a12 1 12 det S12
a11a22 a12a21
当前您浏览的位置是第六页，共三十二页。
1 3
例
设
A
2
4
3 7
a11 解 det A
an1
7 3 , 计算 det A 的值. 2
注 行列式的每个元素都分别对应一个余子式和一个代数余子
式.
根据该定义，可重新表达行列式的值
a11
det A
a1n def
n
1 k
a1k 1 det S1k
an1 ann
k 1
n
a1k A1k
k 1
其中 A1k 是元 a1k 对A 或 det A 的代数余子式.
相当于把行列式按第一行展开
cnk bn1
bnn
a1k
b11
, D2 det(bij )
akk
bn1
b1n ,
bnn
当前您浏览的位置是第二十三页，共三十二页。
内容总结
线性代数课件行列式的概念和性质。对 n = 2, 3,。项,每一项都是位于不同行,不同列的 三个元素的乘积, 其中三项为正, 三项为负.。个不同项的代数和，其中的每一项都是处于行 列式不同行又不同列的n 个元之乘积.。说明 行列式中行与列具有同等的地位,因此行列式的 性质凡是对行成立的对列也同样成立.。性质5 把行列式的某一列(行)元素的k倍加到另一列 (行)对应的元素上去，行列式的值不变．
AC
det U
det A det B
OB

线性代数总复习讲义PPT课件

线性代数总复习讲义PPT课件
在金融学中，线性代数用于描述资产价格和风险等经济量，以及计算收益 率和波动率等金融指标。
在计算机科学中的应用
01
Байду номын сангаас
02
03
04
线性代数在计算机科学中也有 着广泛的应用，如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用，如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用，如图像处理、 机器学习和数据挖掘等领域。
100%
相似变换法
通过相似变换将矩阵对角化，从 而得到其特征值和特征向量。
80%
数值计算法
对于一些大型稀疏矩阵，可以使 用数值计算方法来计算其特征值 和特征向量。
特征值与特征向量的应用
01
在物理、工程等领域中，特征值和特征向量被广泛 应用于求解振动、波动等问题。
02
在图像处理中，特征值和特征向量被用于图像压缩 和图像识别。
二次型的应用与优化问题
总结词
了解二次型在解决优化问题中的应用
详细描述
二次型的一个重要应用是在解决优化问题中， 特别是在求解二次规划问题时。通过将问题 转化为二次型的形式，可以方便地应用各种 优化算法进行求解，如梯度下降法、牛顿法 等。此外，二次型在统计分析、机器学习等 领域也有着广泛的应用。
06
矩阵的逆与行列式的值
要点一
总结词
矩阵的逆和行列式的值是线性代数中的重要概念，它们在 解决线性方程组、向量空间和特征值等问题中有着广泛的 应用。
要点二
详细描述
矩阵的逆是矩阵运算的一个重要概念，它表示一个矩阵的 逆矩阵与其原矩阵相乘为单位矩阵。逆矩阵的存在条件是 矩阵的行列式值不为零。行列式的值是一个由n阶方阵构 成的代数式，表示n个未知数的n阶线性方程组的解的系数 。行列式的值可以用来判断线性方程组是否有解以及解的 个数。同时，行列式的值也与特征值和特征向量等问题密 切相关。

(完整版)《大学线性代数》PPT课件

(完整版)《大学线性代数》PPT课件

下特页点
结束
a11 a12 … a1n
a21
…
a22 … a2n … ……
=
(-1) N ( j1 j2 jn ) a1 j1 a2 j2 anjn 。
an1 an2 … ann
n阶行列式共有n!项，且冠以正号的项和冠以负号的 项各占一半。
在行列式中，a1 j1 a2 j2 anjn 是取自不同行不同列
结束
例2．计算 n 阶下三角形行列式D的值： a11 0 0 … 0 a21 a22 0 … 0
D = a31 a32 a33 … 0 … … … …… an1 an2 an3 … ann
其中aii0(i=1, 2, , n)。
解：为使取自不同行不同列的元素的乘积不为零，
第一行只能取a11，第二行只能取a22，第三行只能取a33， ， 第 n 行只能取ann。 这样不为零的乘积项只有
结束
对换：
在一个排列i1isitin中，将两个数码 is与it对调， 就得到另一个排列 i1 it is in ，这样的变换称为一个 对换，记为对换(is , it)。
例如，排列 21354 经对换(1, 4)，得到排列24351。 提问：
排列 21354 经对换 (1, 4)，得到的排列是 24351， 排列的奇偶性有无变化？ 提示：
的 n 个元素的乘积。
a1 j1 a2 j2 anjn 之前的符号是 (-1) N(j1 j2 jn) 。
行列式有时简记为| a ij |。一阶行列式|a|就是a。
首页
上页
四阶行列式
a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44

线性代数课件

线性代数课件
a11 a21 a31 a12 a22 a32 a13 a23 a33
偶排列
奇排列
1
N ( j1 j2 j3 )
a1 j1 a2 j2 a3 j3
线性代数 第一章 行列式
11
定义 设有 n 2 个数，排成 n 行 n 列的数表
a11 a12 n 称为n 阶行列式. 简记为 a ij
it 这种变换称为对换，记作（ i s ，）
定理1.1 任一 排列经过一次对换后奇偶性发生改变。
定理1.2
n! n级排列共有 n! 个，其中奇、偶排列相等，各为 2
线性代数 第一章 行列式
10
2
a11 a21 a31
n 阶行列式的定义
a12 a22 a32 a13 a23 a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32 a33
主讲
田立芳
统计与数学学院
目录 线性代数 第一章 行列式 退出
1
目
录
行列式 矩阵 线性空间 线性方程组 矩阵的特征值 二次型
线性代数 第一章 主页 行列式 线性代数
退出
2
第一章 行列式
§1 n 阶行列式的定义
§2 行列式的性质 §3 行列式的计算 §4 克莱姆法则
线性代数 第一章 行列式
3
§1.1
线性代数 第一章 行列式
18
性质1 对任何行列式D，有D=DT（行列式与其转置行列式相等） 证
D
T
将DT记为
于是有 bij a ji ( i , j 1,2, , n) 按行列式的定义

j1 j2 jn

线性代数第一章第一节PPT课件

线性代数第一章第一节PPT课件

01递Biblioteka 公式法02递推公式法是根据行列式的性质和结构特点，利用递推公式来
计算行列式的方法。
递推公式法可以大大简化高阶行列式的计算过程，提高计算效
03
率。
行列式的计算方法
分块法
1
2
分块法是将高阶行列式分成若干个小块，然后利 用小块来计算整个行列式的方法。
3
分块法可以简化高阶行列式的计算过程，特别是 当行列式具有特定的结构特点时，分块法可以大 大提高计算效率。
01
向量空间
02
向量空间是线性代数中的一个重要概念，而行列式在向量 空间的定义和性质中也有着重要的应用。例如，通过行列 式可以判断一个向量集合是否构成向量空间，以及向量空 间的一些基本性质。
03
行列式在向量空间中的应用可以帮助我们更好地理解线性 代数的本质和结构特点。
05
特征值与特征向量
特征值与特征向量的定义
转置等特殊运算。
向量与矩阵的关系
关联性
04
向量可以用矩阵来表示，矩 阵中的每一行可以看作是一 个向量。
01 03
•·
02
向量和矩阵在数学中是密切 相关的概念，矩阵可以看作 是向量的扩展。
04
行列式
行列式的定义与性质
基本概念
行列式是由数字组成的方阵，按照一定的规则计 算出的一个数。
行列式具有一些基本的性质，如交换律、结合律、 分配律等。
向量可以用有向线段、坐 标系中的点或有序数对来 表示。
向量有大小和方向两个基 本属性，大小表示向量的 长度，方向表示向量的指 向。
矩阵的定义与运算
•·
02
基础运算
01
03
矩阵是一个由数字组成的矩 形阵列，表示二维数组。

线性代数相关知识培训教程PPT课件( 93页)

线性代数相关知识培训教程PPT课件( 93页)
那末 A称为对称阵.
例如A162
6 8
1 0
为对称. 阵
1 0 6
说明 对称阵的元素以主对角线为对称轴对应相
等.
同型矩阵与矩阵相等
1）两个矩阵的行数相等,列数相等时,称为同型矩阵.
例如
1 5
2 6
与

14 8
3 4
为同型矩阵.
3 7 3 9
Aij (1)i j Mij, Aij叫做元素 aij的代数余子.式
A a i1 A i1 a i2 A i2 a iA n in ( i 1 ,2 , ,n ) A a i1 A j1 a i2 A j2 a iA n jn ( i j)
例1 3 1 1 2 5 1 3 4
p1p2pn
列取 . 和
N阶行列式是一个数,该数是n!项的代数和, 每项为取自表中不同行不同列n个元素的乘 积,符号由这n个元素列标排列的逆序数决定 (行标按自然顺序排列),奇排列带负号,偶排 列带正号.
2. 行列式的性质
1)行列式与它的转置行式列相等,即D DT. 2)互换行列式的两行 (列),行列式变号. 3)如果行列式有两行 (列)完全相同,则此行列式 等于零. 4)行列式的某一行(列)中所有的元素都乘以同 一数k,等于用数k 乘此行列式.
6）逆矩阵
伴随矩阵定义
行列式 A 的各个元素的代数余子式A ij 所
构成的如下矩阵
A11
A


A12
A1n
A21 An1 A22 An2 A2n Ann
称为矩阵 A 的伴随矩阵.
伴随矩阵性质
AA A AA E .
逆矩阵定义
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

424 8
D1 3
3
9
36 27
3 4 16 64
13 1 1
14 4 8
D2 1 3
18 9 27
1 3 16 64
11 3 1
12 4 8
D3 1 3
3
24 27
1 4 3 64
11 1 3
12 4 4
D4 1 3 9
6 3
1 4 16 3
D 12
y 3 3 x 2x2 1 x3
6x 4y 24
❖ 无解3x 2y 12
6x 4y 25
3 2
D
0
21
3 2
D
0
6 4
3 2
D
0
6 4
x2
y
3
x
4
2 3
t
,
(t
R)
y t
3x 2y 12
0 1
齐次方程组
a11x1 a12 x2 a21x1 a22 x2 an1x1 an2 x2
a1n xn 0 a2n xn 0
0 4 7 6
21 8 1
1 3 9 6
D3 0
2
5
27 2
14 0 6
2 8 5 1
1 9 0 6
D2 0 5 1
108 2
1 0 7 6
2 1 5 8
1 3 0 9
D4 0
2
27 1 5
1 4 7 0
D 27, x1 3, x2 4, x3 1, x4 1
求曲线方程系数
y a0 a1x a2 x2 a3 x3
0 7 5 13
1 3 D
0
6 r1 2r2 1 3
0
6
0 2 1 2 r4 r2 0 2 1 2
1 4 7 6
0 7 7 12
7 5 13
3 5 3
2 1
2 c1 2c2 0
1
3 0
3 27
7 7 12 c3 2c2 7 7 2 7 2
8 1 5 1
9 3 0 6
D1 5
2
1
61 2
ann xn 0
❖ 必然有零解 x1 x2 ❖ 关心是否有非零解。
xn 0
齐次线性方程组的解
❖ 只有零解
3x 2y 0
2x
y
0
3 2
D
0
21
❖ 无穷多组解
3x 2y 0 6x 4y 0
3 2
D
0
6 4
2 3
t
, (t
R)
y t
有非零解？
(5 )x 2 y 2z 0
D2 D
,
, xn
Dn D
,
a11
a1, j1 b1 a1, j1
a11
❖ 其中 Dj
an1
an. j1 bn an, j1
an1
解线性方程组
2x1 x2 5x3 x4 8
x1 3x2
6x4 9
2x2 x3 2x4 5
x1 4x2 7x3 6x4 0
2 1 5 1
(1,3) (2, 4) (3,3) (4, 3)
a0 a1 a2 a3 3 a0 2a1 4a2 8a3 4 a0 3a1 9a2 27a3 3 a0 4a1 16a2 64a3 3
11 1 1
12 4 8
D
12
1 3 9 27
1 4 16 64
范德蒙德行列式
311 1
2x
(6
)
y
0
2x
(4 )z 0
5 2 2 D 2 6 0
2 0 4 (5 )(2 )(8 )
2,5,8 D 0 唯一零解
❖ 其它情况下，验证之后都有非零解。
2
2
解的唯一性与存在性
❖ 定理4:如果线性方程组的系数行列式非零， 则方程组一定有解，且解是唯一的。
D 0 唯一解
❖ 定理4’：如果方程组无解或者有两个不同的 解，则它的系数行列式必为零。
无解或不唯一解 D 0
方程解的三种情形
❖
唯一解
3x 2y 12
2x y 1
❖ 无穷多3解x 2y 12
第一章
7、克拉默法则
n个线性方程的n元方程组
a11x1 a12 x2 a21x1 a22 x2 an1x1 an2 x2
a1n xn b1 a2n xn b2
ann xn bn
克拉默法则
❖ 如果
a11 D
an1
a1n 0
ann
❖ 则方程组有唯一解：
x1
D1 D
, x2