动力学习题20150513
- 格式:docx
- 大小:30.84 KB
- 文档页数:3

动力学测试题及答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分考试用时120分钟第Ⅰ卷(选择题共40分)一、本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.全部选对的得4分,选不全的得2分,有选错或不答的得0分.1.在静止的小车内,用细绳a 和b 系住一个小球。
绳a 与竖直方向成θ角,拉力为T a ,绳b 成水平状态,拉力为T b 。
现让小车从静止开始向右做匀加速直线运动,如图1所示。
此时小球在车内的位置仍保持不变(角θ不变)。
则两根细绳的拉力变化情况是 ( )A .T a 变大,T b 不变B .T a 变大,T b 变小C .T a 变大,T b 变 大D .T a 不变,T b 变小2.在光滑的水平面上,有一个物体同时受到两个水平力F 1和F 2的作用,在第1s 内保持静止。
若两个力F 1、F 2随时间变化如图2所示,则下列说法正确的是( )A .在第2s 内,物体做匀加速运动,加速度的大小恒定, 速度均匀增大B .在第3s 内,物体做变加速运动,加速度均匀减小,速度逐渐减小C .在第5s 内,物体做变加速运动,加速度均匀减小,速度逐渐增大D .在第6s 末,物体的加速度与速度均为零3.如图3所示,在一无限长的小车上,有质量分别为m 1和m 2的两个滑块(m 1>m 2)随车一起向右匀速运动。
设两滑块与小车间的动摩擦因数均为μ,其它阻力不计,当车突然停止,以下说法中正确的是( )A .若μ=0,两滑块一定相碰B .若μ=0,两滑块一定不相碰C .若μ≠0,两滑块一定相碰图1 图3图2D .若μ≠0,两滑块一定不相碰 4.如图4所示,滑轮A 可沿倾角为θ的足够长光滑轨道下滑,滑轮下用轻绳挂着一个重力为G 的物体B ,下滑时,物体B 相对于A 静止,则下滑过程中 ( ) A .B 的加速度为g sin θ B .绳的拉力为G sin θC .绳的拉力为GD .绳的方向保持竖直。

动力学综合练习一1、在轻绳两端各系一小球,一人用手拿着上端的小球站在三层楼的阳台上,放手后让小球自由下落,两球相继落地的时间差为Δt 1,如果人站在四楼的阳台上,同样放手让小球自由地下落,两球相继落地的时间差为Δt 2,则Δt 1和Δt 2相比较有:( )A 、Δt 1<Δt 2B 、Δt 1=Δt 2C 、Δt 1>Δt 2D 、无法判断2、如图,为三个物体运动的v-t 图象,其中A 、B 两物体是从不同地点出发,A 、C 是从同一地点出发,则以下说法正确的是:( )A 、A 、C 两物体的运动方向相反B 、t=4s 时,A 、B 两物体相遇C 、t=4s 时,A 、C 两物体相遇D 、t=2s 时,A 、B 两物体相距最近3、两光滑平板MO 、NO 构成一具有固定的夹角0θ=750的V 型槽,一球置于槽内,用θ表示NO 板与水平面之间的夹角,如图所示。
若球对NO 板的压力大小正好等于球所受重力的大小,则下列θ值中哪个是正确的:( )A 、150B 、300C 、450D 、6004、如图所示,小圆环A 吊着一个质量为m 2的物块并套在另一个竖直放置的大圆环上,有一细线一端栓在小圆环A 上,另一端跨过固定在大圆环最高点B 的一个小滑轮后吊着一个质量为m 1的物块,若各处摩擦力均不计,绳不可伸长,若平衡时,弦AB 所对应的圆心角为α,则两物体的质量之比m 1:m 2应为:( )A 、cos α/2B 、sin α/2C 、2sin α/2D 、2cos α/25、如图所示,木板B 放在粗糙水平面上,木块A 放在B 的上面,A的右端通过一不可伸长的轻绳固定在竖直墙上,用水平恒力F 向左拉动B ,使其以速度V 做匀速运动,此时绳水平且拉力大小为T ,下列说法正确的是:( )A 、绳上拉力T 与水平恒力F 大小相等T αC 、木板B 受到A 和地面施加的两个滑动摩擦力的合力大小等于FD 、若木板B 以2V 匀速运动,则拉力仍为F6、一滑块在水平地面上沿直线滑行,t =0时其速度为1 m/s 。

动力学强化训练1.如图所示,从H=45m 高处水平抛出的小球,除受重力外,还受到水平风力作用,假设风力大小恒为小球重力的0.2倍,g=10m/s 2.问:(1)有水平风力与无风时相比较,小球在空中的飞行时间是否相同?如不相同,说明理由;如相同,求出这段时间?(2) 为使小球能垂直于地面着地, 水平抛出的初速度v 0=?2.为了安全,在公路上行驶的汽车之间应保持必要的距离。
我国公安部门规定:高速公路上行驶汽车的安全距离为200m ,汽车行驶的最高速度为120km/h ,g=9.8m/s 2,请你根据下面提供的资料。
说明计算安全距离为200m资料一:驾驶员的反应时间:0.3s —0.6s 之间风3.为了体现人文关怀,保障市民出行安全和严格执法,成都市交管部门强行推出了“电子眼”,据了解,在城区内全方位装上“电子眼”后立马见效,机动车擅自闯红灯的大幅度减少,因闯红灯引发的交通事故也从过去的5%下降到1%。
现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为10m/s.当两车快要到一十字路口时,甲车司机看到绿灯已转换成了黄灯,于是紧急刹车(反应时间忽略不计),乙车司机为了避免与甲车相撞也紧急刹车,但乙车司机反应较慢(反应时间为0.5s)。
已知甲车紧急刹车时制动力为车重的0.4倍,乙车紧急刹车制动力为车重的0.5倍,求:(g=10m/s2)(1)若甲司机看到黄灯时车头距警戒线15m,他采取上述措施能否避免闯红灯?(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中至少应保持多大距离?4.如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD 为水平面,B点在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达B点。
求:Array⑴释放点距A点的竖直高度.⑵落点C与A点的水平距离.5.如图所示,A和B是两个相同的带电小球,视为质点,质量均为m,电荷量均为q.A固定在绝缘地面上,B放在以恒定的加速度a(a<g)竖直下落的绝缘板上,当下落高度h时,B与绝缘板脱离.若静电力常量为k.求:(1)B脱离绝缘板时的动能;(2)B在脱离绝缘板前的运动过程中,电场力和绝缘板的支持力对B做功的代数和W;(3)B脱离绝缘板时离A的高度x.6.如图所示,薄木板A长l=5.0m,质量M=5.0kg,放在水平桌面上,板右端与桌面相齐,在A上距右端s=3.0m处放一小物块B,质量m=2.0kg,已知A、B间动摩擦因数μ1=0.1,A与桌面间和B与桌面间的动摩擦因数μ2=0.2,原来系统静止,现对平板A施加一个水平向右、大小恒定的拉力F,作用一段时间,将平板A从小物块B的下面抽出,且小物块B最后恰好停在桌面的右端边缘。

动力学练习题及解答动力学练习题及解答动力学练习题一:小球滑动题目:一个小球位于斜面上,斜面的角度为30度。
小球的质量为0.5kg,通过绳子与一个固定的点相连,绳子的长度为1m,小球从静止开始沿着斜面滑下。
设斜面上摩擦系数为0.2,重力加速度为10m/s²。
(1)求小球滑动的加速度。
(2)求小球滑动的摩擦力。
(3)求小球滑动时的速度。
解答:(1)小球在斜面上受到的合力为斜面上的重力分力与摩擦力之和,根据牛顿第二定律可得\(\Sigma F_x=ma_x \Rightarrow m \cdot a = m \cdot g \cdot sin(\Theta) - F_f = m \cdot g \cdot sin(\Theta) - \mu \cdot m \cdot g \cdot cos(\Theta). \)其中,\(\Theta\)为斜面角度,m为小球质量,g为重力加速度,\(\mu\)为摩擦系数。
代入数值可求得: \(a = g \cdot (sin(\Theta) - \mu \cdot cos(\Theta))\)代入数值可得:\(a = 10 \cdot (sin(30°) - 0.2 \cdot cos(30°)) ≈5.317m/s²\)(2) 小球的摩擦力为:\(F_f = \mu \cdot m \cdot g \cdot cos(\Theta)\)代入数值可得:\(F_f = 0.2 \cdot 0.5 \cdot 10 \cdot cos(30°) ≈ 0.86N\)(3) 小球在滑动过程中会不断加速,因此速度随时间的增加而增加。
根据运动学中的公式可以计算速度\(v\):\( v = v_0 + a \cdot t\)由题可知小球从静止开始滑动,即\(v_0 = 0\),代入数值可得:\(v = 0 + 5.317 \cdot t\)。



动力学课后习题习题 1某溶液中反应 A + B Y 开始时 A 与 B 的物质的量相等,没有 Y ,1h 后 A 的转化率为75%,问2h 后 A 尚有多少未反应?假设:(1)对 A 为一级,对 B 为零级;(2)对 A ,B 皆为一级;(3)对 A ,B 皆为零级。
习题 2某反应 A → Y + Z ,在一定温度下进行,当-3-1的初始速率υA,0 =0.01mOl·dm·s。
试计算反应物-3及 x A =0.75 时,所需时间,若对反应物 At= 0,c A,0 =1mOl ·dm-3时,测定反应A 的物质的量浓度 c A= 0.50mOl ·dm (i) 0 级; (ii) 1 级; (iii) 2 级;习题 3已知气相反应 2A + B2Y 的速率方程为dp Akp A p B。
将气体 A 和 B 按物质的量dt比 2:1 引入一抽空的反应器中,反应温度保持400 K 。
反应经 10min 后测得系统压力为84 kPa,经很长时间反应完了后系统压力为63 kPa。
试求:(1)气体 A 的初始压力 p A,0及反应经 10 min 后 A 的分压力 p A;(2)反应速率系数 k A;(3)气体 A 的半衰期。
习题 4反应 2A(g)+B(g)Y(g)的动力学方程为-dcB= k B c1A.5 c B0. 5。
今将 A 与 B 的摩尔比为dt2∶ 1 的混合气体通入400 K 定容容器中,起始总压力为 3.04 kPa,50s 后,总压力变为 2.03 kPa,试求反应的反应速率系数k B及 k A。
习题 5已知反应 2HI → I2 + H 2,在 508℃下,HI 的初始压力为 10132.5 Pa 时,半衰期为 135 min ;而当 HI 的初始压力为 101 325 Pa 时,半衰期为 13.5 min 。
试证明该反应为二级,并求出反应速率系数 (以 dm3·mol -1· s-1及以P a-1· s-1表示 )。

第一部分:1.对元反应A+2B→C,若将其反应速率方程写为下列形式, 则k A 、k B 、k C 间的关系应为:( )A k A = kB = kC B k A =2 k B = k C C k A =1/2 k B = k C [解]C ,反应速率之比r A :r B :r C =1:2:1,k A :k B :k C=1:2:12.某反应,无论反应物初始浓度为多少, 在相同时间和温度时, 反应物消耗的浓度为定值,此反应是A 负级数反应B 一级反应C 零级反应D 二级反应 [解]C ,一级反应积分速率方程C A ,0-C A =kt ,反应物浓度的消耗C A ,0-C A 就是与k 和t 有关,k 和温度有关,当温度和时间相同时,反应物浓度的消耗是定值。
3.关于反应级数的各种说法中正确的是 A 只有基元反应的级数是正整数 B 反应级数不会小于零C 反应总级数一定大于对任一反应物级数D 反应级数都可通过实验来确定 [解]D ,4.某反应,A→Y,其速率系数k A =6.93min -1,则该反应物A 的浓度从1.0mol ×dm -3变到0.5 mol ×dm -3所需时间是( )A 0.2minB 0.1minC 1min[解]B ,从速率系数的单位判断是一级反应,代入积分速率方程,0lnA AC kt C =,1ln6.930.5t =,t=0.1min 。
5.某反应,A→Y,如果反应物A 的浓度减少一半,它的半衰期也缩短一半,则该反应的级数为( )A 零级B 一级C 二级[解]A ,半衰期与浓度成正比,所以是零级反应。
6.某化学反应的速率常数为2.0mol ·l -1·s -1,该化学反应的级数为 A.1 B.2 C.0 D.-1 [解]C ,从速率常数的单位判断是零级反应。
7.放射性Pb 201的半衰期为8小时,1克放射性Pb 201经24小时衰变后还剩 A.1/3g B.1/4g C.1/8g D.0gBA B B d d c c k t c =-B A C C d d c c k t c =B A A A d d c c k t c =-[解]C ,放射性元素的衰变是一级反应,通过半衰期公式12ln 2t k =,ln 28k =,再代入一级反应积分速率方程,,0lnA AC ktC =,起始浓度为1g ,1ln 2n*248A C =,18A C g =。

动力学1A一、选择题1. 连串反应A k1B k2 C 其中k1= 0.1 min-1,k2= 0.2 min-1,假定反应开始时只有A,且浓度为1 mol·dm-3,则B 浓度达最大的时间为:( )(A) 0.3 min (B) 5.0 min(C) 6.93 min (D) ∞2. 平行反应A k1 B (1);A k2 D (2),其反应(1)和(2)的指前因子相同而活化能不同,E1为120 kJ·mol-1,E2为80 kJ·mol-1,则当在1000K 进行时,两个反应速率常数的比是:( )(A) k1/k2= 8.138×10-3(B) k1/k2= 1.228×102(C) k1/k2= 1.55×10-5(D) k1/k2= 6.47×1043. 如果臭氧(O3) 分解反应2O3→3O2的反应机理是:O3→O + O2(1)O + O3→2O2(2)请你指出这个反应对O3而言可能是:( )(A) 0 级反应(B) 1 级反应(C) 2 级反应(D) 1.5 级反应4. 化学反应速率常数的Arrhenius 关系式能成立的范围是:( )(A) 对任何反应在任何温度范围内(B) 对某些反应在任何温度范围内(C) 对任何反应在一定温度范围内(D) 对某些反应在一定温度范围内5. 如果反应2A + B =2D 的速率可表示为:r = -12d c A /d t = - d c B /d t = 12d c D /d t 则其反应分子数为: ( )(A) 单分子 (B) 双分子(C) 三分子 (D) 不能确定6. 实验测得反应 3H 2+ N 2→ 2NH 3 的数据如下:由此可推知该反应的速率方程 d p (NH 3)/2d t 等于: ( )(A) kp H 23 p N 2(B) kp H 22p N 2 (C) kp H 2 p N 2 (D) kp H 2 p N 227. 在反应 A k 1B k 2C ,A k 3 D 中,活化能 E 1> E 2> E 3,C 是所需要的产物,从动力学角度考虑,为了提高 C 的产量,选择反应温度时,应选择: ( )(A) 较高反应温度(B) 较低反应温度 (C) 适中反应温度(D) 任意反应温度 8. [X]0 [Y]0 [Z] 增加 0.0050 mol ·dm -3 所需的时间/ s0.10 mol ·dm -3 0.10 mol ·dm -3 720.20 mol ·dm -3 0.10 mol ·dm -3 180.20 mol·dm-30.05 mol·dm-336对于反应X + 2Y →3Z,[Z] 增加的初始速率为:( )(A) 对X 和Y 均为一级(B) 对X 一级,对Y 零级(C) 对X 二级,对Y 为一级(D) 对X 四级,对Y 为二级9. 一级反应,反应物反应掉1/n所需要的时间是:( )(A) -0.6932/k(B) (2.303/k) lg[n/(n-1)](C) (2.303/k) lg n(D) (2.303/k) lg(1/n)10. 关于反应速率理论中概率因子P的有关描述,不正确的是:( )(A) P与≠S m有关(B) P体现空间位置对反应速率的影响(C) P与反应物分子间相对碰撞能有关(D) P值大多数<1,但也有>1的二、填空题12. 60Co广泛用于癌症治疗, 其半衰期为5.26 a (年), 则其蜕变速率常数为:_________________, 某医院购得该同位素20 mg, 10 a后剩余______________ mg。

化学动力学基础练习题一 选择1 基元反应的分子数取值为( )A 可以为 0、1、2、3B 只能是 1、2、3;C 可以是小于1的数值;D 可正、可负、可为0。
2 基元反应中反应级数与反应分子数的关系( )A 反应级数与反应分子数一致B 反应级数大于反应分子数C 反应级数小于反应分子数D 反应级数小于或等于反应分子数 3 对于一个化学反应,测得的浓度与时间成直线关系,则该反应为( )A 一级反应B 零级反应C 二级反应D 不确定 4 光化反应与黑暗反应的相同之处在于( )A 反应都需要活化能B 温度系数小C 反应都向ΔG (恒温恒压,W ˊ=0时)减少的方向进行D 平衡常数可用通常的热力学函数计算 5 按照光化当量定律( )A 在整个光化过程中,一个光子只能活化一个原子或分子B 在光化反应的初级阶段,一个光子活化1moL 原子或分子C 在光化反应的初级阶段,一个光子活化一个原子或分子D 在光化反应的初级阶段,一个爱因斯坦的能量活化一个原子或分子 6 对于复杂反应,一下说法中不正确的是( )A 复杂反应无反应级数而言B 复杂反应至少包括两个基元步骤C 复杂反应的级数不会是正整数D 反应级数为分数的反应一定是复杂反应 7 放射性元素P b 201的半衰期为8小时,1克放射性P b 20124小时后还剩下( )A 1/2 gB 1/3 gC 1/4 gD 1/8 g 8 两个H ·与M 粒子同时相碰撞,发生下列反应H ·+H ·+M →H 2 (g) + M 此反应的活化能E a 是( ) A 大于零 B 等于零 C 小于零 D 不能确定9 对于1100m U kJ m ol -∆=⋅的某吸热反应,其逆反应的活化能符合下列哪种情况( )A 一定小于100kJ/moL C 可能小于100kJ/moL ,也可能大于100kJ/moLB 一定大于100kJ/moL D 一定大于正反应的活化能10 某反应的速率常数K =4.62×10-2min -1,初始浓度为0.1moL/dm 3,则该反应的半衰期t 1/2为( ) A221m in 6.93100.1-⨯⨯ B 15 min C 30 min D21m in 4.62100.1⨯⨯11 某反应A →Y ,其速率系数k A =6.93min -1,则该反应物A 的浓度从1.0 moL/dm 3变到0.5moL/dm 3所需的时间是( )A 0.2minB 0.1minC 1min12 基元反应:H + Cl 2 → HCl + Cl 的反应分子数是( ) A 单分子反应 B 双分子反应 D 四分子反应13 某反应速率常数与各基元反应速率常数的关系为121242k k k k ⎛⎫= ⎪⎝⎭,则该反应的表观活化能与各基元反应活化能的关系是( ) A 21412a E E E E =+- B ()21412a E E E E =+- C ()122142a E E E E =+-14 一反应,如果起始浓度减少一半,半衰期缩短一半,则反应级数为(C )A 1B 2C 0D 1.515 平行反应:A (g)已知反应①的活化能E a1=80KJ mol -1 ,反应②活化能E a2=40KJ mol -1,为有利于产物B (g)的生成,应当采用( B )的方法。
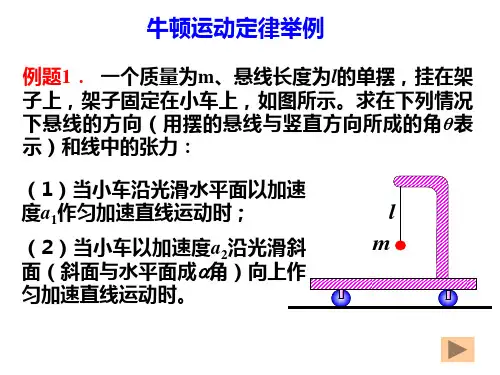
动力学练习题1、题图所示系统中,各杆均为均质杆。
已知:杆OA ,CD 的质量各为m ,杆AB 的质量为2m ,l CD CB AC OA ====,杆OA 以角速度ω转动,求图示瞬时各杆动量的大小,并在图中标明各杆动量的方向。
2、如图所示,均质细圆环质量为M ,半径为R ,圆心为C ,其上固接一质量为m 的均质细杆AB ,系统在铅垂面内以角速度ω绕轴O 转动,已知060=∠CAB 。
求图示位置系统对轴O 的动量和动量矩。
3、质量为M ,半径为R 的均质圆盘,以角速度ω转动,其边缘上焊接一质量为m ,长为b 的均质细杆AB ,如题图所示。
求图示位置系统动量的大小以及对轴O 的动量矩的大小。
4、如题图所示,两个重物M 1和M 2的质量各为m 1与m 2,分别系在两条不计质量的绳上,此两绳又分别绕在半径为r 1和r 2的塔轮上。
塔轮质量为m 3,对质心轴O 的回转半径为ρ。
重物受重力作用而运动,求塔轮的角加速度α。
5、如题图所示的卷扬机,轮B,C的半径分别为R,r,对通过点O1,O2的水平轴的转动惯量分别为J1,J2,物体A重P,在轮C上作用一常转矩M。
试求物体A上升的加速度。
6、在图示机构中,鼓轮A和圆盘B为均质,重量各为P,半径均为R,物体C重为Q,轮A上作用一矩为M的常值力偶,试求此瞬时系统中物块C的加速度及轮A上绳子的拉力。
7、均质圆柱体的质量为m1、半径为R,沿固定水平面作纯滚动;重物B的质量为m2;定滑轮D质量不计;弹簧的弹性系数为k,初始时弹簧长度为其原长L0的一半,系统从静止无初速释放。
试求重物下降h=2L0时的速度和加速度以及水平段绳索拉力。
8、图示机构中,沿斜面纯滚动的圆柱体O'和鼓轮O为均质物体,质量均为m,半径均为R。
绳子不能伸缩,其质量略去不计。
粗糙斜面的倾角为θ,不计滚动摩擦。
如在鼓轮上作用一常力偶M。
求:(1)鼓轮的角加速度;(2)绳索的拉力;(3)轴承O的水平反力。
1.速率方程:速率方程不浮上固体及水的浓度;气体反应物可用分压代替浓度;k-速率常数质量作用定律:对于基元反应:mA+nB→C2. 影响化学反应速率的因素内因:反应物的本性;外因:(1)浓度/分压升高,单位体积分子数增多,单位体积活化分子数增多;(2)催化剂,可降低活化能(3)温度升高,一方面使分子能量普遍升高;另一方面还可以使碰撞次数增多,有效碰撞增多.3. 封闭体系、恒温恒压、只做体积功时,自发反应总是朝着Gibbs自由能减小方向举行,至△rGm=0达平衡,体系自由能降至最小值△rGm<0 正向自发反应;△rGm>0逆向自发反应△G=△H-T△S例一:有基元反应,A+B=C ,下列讲述准确的是( )A. 此反应为一级反应B. 两种反应物中,无论哪一种的浓度增强一倍,都将使反应速度增强一倍C. 两种反应物的浓度同时减半,则反应速度也将减半D. 两种反应物的浓度同时增大一倍,则反应速度增大两倍例二:对于反应速度常数k ,下列说法准确的是( )A. 速度常数值随反应物浓度增大而增大;B. 每个反应惟独一个速度常数;C. 速度常数的大小与浓度有关;D. 速度常数随温度而变化;例三:某化学反应在任何温度下都可以自发举行,此反应需满意的条件是:(A )∆H<0, ∆S>0; (B )∆H>0, ∆S<0;(C )∆H>0, ∆S>0; (D )∆H<0, ∆S<0例四:对于一个化学反应,下列各组中关系准确的是:ΘΘΘΘm m ΘΘΘΘm m (A) ΔrG >0, K <1; (B) ΔrG >0, K <1;(C) ΔrG <0, K =1; (D) ΔrG <0, K <1;例一:答案B 利用基元反应化学反应速率方程式求解例二:答案D 速率常数与温度、活化能、指前因子A有关例三:答案A ∆G=∆H-T∆S<0 能自发举行例四:答案A。
动力学问题1.一质量为M 的探空气球在匀速下降,若气球所受浮力F 始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g .现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为A.)(2g F M - B.gFM 2-C.g FM -2 D.02.两个分别带有电荷量Q 和+3Q 的相同金属小球(均可视为点电荷),固定在相距为r 的两处,它们间库仑力的大小为F 。
两小球相互接触后将其固定距离变为2r ,则两球间库仑力的大小为A .112FB .34FC .43FD .12F3.用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为10N,为使绳不断裂,画框上两个挂钉的间距最大为(g取210m/s)A.3m2B.2m2C.1m2D.3m44.在无风的情况下,跳伞运动员从水平飞行的飞机上跳伞,下落过程中受到空气阻力,下列描绘下落速度的水平分量大小x v、竖直分量大小y v与时间t的图像,可能正确的是5.如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度(A)大小和方向均不变(B)大小不变,方向改变(C)大小改变,方向不变(D)大小和方向均改变6.如图所示,置于水平地面的三脚架上固定着一质量为m的照相机.三脚架的三根轻质支架等长,与竖直方向均成30 角,则每根支架中承受的压力大小为(A)13mg(B)23mg(C)36mg(D)239mg7.如图所示,石拱桥的正中央有一质量为m 的对称楔形石块,侧面与竖直方向的夹角为α,重力加速度为g ,若接触面间的摩擦力忽略不计,旵石块侧面所受弹力的大小为A .2sin mg αB .2s mgco αC .1tan 2mg αD .1t 2mgco α8.将一只皮球竖直向上抛出,皮球运动时受到空气阻力的大小与速度的大小成正比。
下列描绘皮球在上升过程中加速度大小a与时间t关系的图象,可能正确的是9.如图所示,一夹子夹住木块,在力F 作用下向上提升。
《动力学 I 》第一章运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将 030=θ代入得34cos cos 22lk lk l y v ====θθθ98cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动 , 所以 n t a a a +=, 设质点的速度为 v , 由图可知 : a a vv y n cos ==θ,所以 : yv va a n = 将c v y =, ρ2n va =代入上式可得ρc v a 3=证毕 1-7证明:因为 n2a v=ρ, va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时 , 绳索 AB 的长度为 L , 时刻 t 时的长度为 s , 则有关系式: t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= , x x s s 22= 由此解得:xsv x-= (a (a式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b 将 (a式代入 (b式可得:3220220xlv x x v x a x -=-==(负号说明滑块 A 的加速度向上1-11解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上 A 、 B 两点的速度在 A、 B 两点连线上的投影相等,即: θcos A B v v = (a 因为xR x 22cos -=θ (b 将上式代入(a 式得到 A 点速度的大小为: 22Rx x Rv A -=ω (c由于 x v A -=, (c 式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222 (x R R x x ω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222 (2ω=-- 将上式消去 x 2后,可求得:22242(R x xR x--=ω由上式可知滑块 A 的加速度方向向左,其大小为 2 2242(R x xR a A -=ω1-13解:动点:套筒 A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。
动力学练习1与答案-05级(化学、高分子)一、选择题1.反应A k1B (I);Ak2D (II),已知反应I 的活化能E1大于反应II 的活化能E2,以下措施中哪一种不能改变获得B 和D 的比例?( )(A) 提高反应温度(B) 延长反应时间(C) 加入适当催化剂(D) 降低反应温度2 如果某反应的△r H m= 100kJ·mol-1,那么活化能E a将:( )(A) E a≠100kJ·mol-1(B) E a≥100kJ·mol-1(C) E a≤100kJ·mol-1(D) 都可以3. 2A k1产物上述反应对A 为二级,下列何者对时间作图可得一直线,且直线斜率等于速率常数k?( )(A) 2[A](B) [A]2(C) 1/[A](D) 1/[A]24. 某反应进行时,反应物浓度与时间成线性关系,则此反应的半衰期与反应物初始浓度:( )(A) 成正比(B) 成反比(C) 平方成反比(D) 无关5.此反应的速率方程为:( )(A) r = k c B(B) r = k c A c B(C) r = k c A(c B)2(D) r = k c A6. 400 K 时,某气相反应的速率常数k p= 10-3(kPa)-1·s-1,如速率常数用k C表示,则 k C 应为: ( )(A) 3.326 (mol ·dm -3)-1·s -1(B) 3.0×10-4 (mol ·dm -3)-1·s -1(C) 3326 (mol ·dm -3)-1·s -1(D) 3.0×10-7 (mol ·dm -3)-1·s -17. 均相反应 A + B k 1 C + D , A + B k 2 E + F 在反应过程中具有 ∆[C]/∆[E] = k 1/k 2的关系, ∆[C],∆[E] 为反应前后的浓差,k 1,k 2是反应 (1),(2)的速率常数。
1、判断下列说法是否正确:
(1)反应级数等于反应分子数;(2)反应级数不一定是简单的正整数;(3)具有简单级数的反应是基元反应;(4)不同反应若具有相同级数形式,一定具有相同反应机理;(5)反应分子数只能是正整数,一般不会大于三;(6)某化学反应式为A+B=C ,则该反应为双分子反应 (7) 零级反应是基元反应
2. 反应物转化掉1/2, 3/4和7/8所需的时间之比对于一级、二级(起始反应物浓度相等)、三级(起始反应物浓度相等)反应各有何规律?
3、阿累尼乌斯经验式的适用条件是什么?如果表观速率常数的表示式为2/14
12)2(
k k k k =,写出其表观指前因子和表观活化能的表示式.
4.碰撞理论中阈能的物理意义是什么? 它与Arrhenius 的实验活化能Ea 有何关系?过渡态理论中的活化焓与m r H ≠∆Arrhenius 的实验活化能Ea 又有何关系?
5. 试定性比较如下三个反应的概率因子P 的大小:
(1) Br ·+ Br · Br 2
(2) CH 4 + Br 2 CH 3Br + HBr
(3)C 2H 5OH + CH 3COOH CH 3COOC 2H 5 + H 2O
6. 进行反应A + 2D →3G 在298K 及2dm 3容器中进行,若某时刻反应进度随时间变化率为0.3
mol·s -1,则此时G 的生成速率为(单位:mol·dm -3·s -1) ( )
(A) 0.15 ; (B) 0.9 ; (C) 0.45 ; (D) 0.2
7. 某一基元反应,2A(g) + B(g) →E(g),将2mol 的A 与1mol 的B 放入1升容器中混合并反应,那么反应物消耗一半时的反应速率与反应起始速率间的比值是( )
(A) 1∶2 ; (B) 1∶4 ; (C) 1∶6 ; (D) 1∶8
8. 反应3O 2→2O 3,其速率方程 -d[O 2]/d t = k [O 3]2[O 2] 或 d[O 3]/d t = k '[O 3]2[O 2],那么k
与k '的关系是( )
(A) 2k = 3k ' ; (B) k = k ' ; (C) 3k = 2k ' ; (D) ½k = k ' 。
9. 净重为8 g 的某物质的分解反应为一级反应,其半衰期为10 d,则40 d 后其净重为( )
(A) 4 g ; (B) 2 g ; (C) 1 g ; (D) 0.5 g
10.某反应进行时,反应物浓度与时间成线性关系,则此反应之半衰期与反应物最初浓度有何关系? ( )
(A) 无关 ; (B) 成正比 ; (C) 成反比 ; (D) 平方成反比
11. 某反应只有一种反应物,其转化率达到75%的时间是转化率达到50%的时间的两倍,反应转化率达到64%的时间是转化率达到x %的时间的两倍,则x 为( )
(A) 32 ; (B) 36 ; (C) 40 ; (D) 60
12.某一反应在有限时间内可反应完全,所需时间为c 0/k ,该反应级数为( )
(A) 零级 ; (B) 一级 ; (C) 二级 ; (D) 三级
13. 某一级反应,反应物转化99.9%所需的时间是半衰期的 倍
14. 某反应物转化掉5/9所需的时间是转化掉1/3所需时间的2倍,则该反应的级数是
15.起始浓度都相同的三级反应的直线图应是 (c 为反应物浓度,n 为级数)( )
16.下列各式中,活化能E a 、临界能E 0和标准活化焓的关系正确的是( ) (A) E a > E c > ;(B) > E a > E c ;(C) E c > > E a ;(D)E c > E a > 。
17.若两个同类的气相反应的活化焓值相等,在400K 时,两个反应的活化熵
(1) - (2) = 10 J·mol -1,则这两个反应的速率之比( )
(A) k 1/k 2 = 0.300 ; (B) k 1/k 2 = 0.997 ;(C) k 1/k 2 = 1.00 ; (D) k 1/k 2 = 3.33 。
18.双分子气相反应A + B = D ,其阈能为50.0 kJ·mol -1,反应在400K 时进行,该反应的活
化焓为( )
(A) 46.674 kJ·mol -1 (B) 48.337 kJ·mol -1 (C) 45.012 kJ·mol -1 (D) 43.349 k J·mol -1 。
19. 双分子气相反应A + B = D ,其阈能为40 kJ·mol -1,有效碰撞分数是6×10-4
,该反应进行的温度是( )
(A) 649K ; (B) 921K ; (C) 268K ; (D) 1202K 。
20. 在碰撞理论中,概率因子P 小于1的主要原因是( )
(a) 反应系统是非理想的; (b) 空间的位阻效应; (c) 分子碰撞不够激烈; (d) 分子间有作
用力
21. 有一平行反应(1)A
k1 B, (2) A k2 D,已知反应(1)的活化能大于反应(2)的活化能,如下措施哪种不能改变产物B 和D 的比例?
(A) 提高反应温度 (B) 加入合适催化剂 (C )延长反应时间 (D )降低反应温度
22. 两个都是一级的平行反应 (1)A k1 B, (2) A k2 D, 设反应开始时产物的浓度为零,下列结论不正确的是 ( )
(A )k 表观=k 1+k 2 (B )k1/k2=[B]/[D] (C) E 表观=Ea,1+ Ea,2 (D) t1/2=ln2/( k 1+k 2)
23. 一个复杂化学反应可用平衡态近似法处理的条件是 ( )
(A) 反应速率快, 迅速达到化学平衡态
(B) 包含可逆反应且很快达到平衡, 其后的基元步骤速率慢
(C) 中间产物浓度小, 第二步反应慢
(D) 第一步反应快, 第二步反应慢
24. 温度对光化反应速度的影响
(A) 与热反应大致相同
(B) 与热反应大不相同,温度增高,光化反应速度下降
(C) 与热反应大不相同,温度增高,光化反应速度不变
(D) 与热反应大不相同,温度的变化对光化反应速度的影响较小
25.计算: 某药物分解30%即为失效.若放置在3 o C 的冰箱中保质期为两年,某人购回此新药物,因故在室温(25 o C)下搁置了两周,试通过计算说明此药物是否已经失效?已知该药物分解
m r
H ≠∆m r H ≠∆m r H ≠∆m r H ≠∆m r
H ≠∆≠∆m r H ≠∆m r S ≠∆m r S ≠
∆m r H
百分数与初始浓度无关,且分解活化能为130.0kJ.mol-1.
26.计算: 已知反应 NO2(g) =NO(g) + (1/2)O2(g) 以NO2的消耗速率表示的反应速率常数与温度的关系为
ln(k/dm3·mol-1·s-1)=-12884K/T +20.2664
(1)试求反应的级数,活化能E a及指前因子A。
(2) 若在400 ℃ 时将压力为26664Pa的NO2(g)通入反应器中,使之发生分解反应,试计算反应器的压力达到31997Pa时所需时间。
27. 某溶液中反应A+B C,设开始时A与B物质的量相等,没有C,1 h后A的转化率为75%, 求 2 h后A还剩多少未反应? 假设: (1) 对A为1 级,对B为0 级; (2) 对A、B均为1级;
(3)对A、B均为0级。