结构动力学基础课后习题答案--张亚辉-大连理工大学出版社(新)

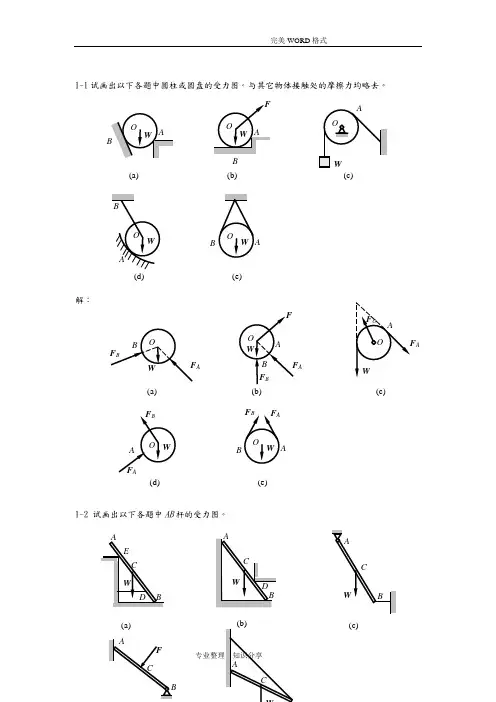
完美WORD 格式1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

ABAOW (a) B AO W F(b)OW (c)AAOW(d)BAOW (e)BF BF ABO W(a) B AO W F(b) F AF B AO W(c)F AF O A O W(d)F B F AAOW (e)BF B F A AWC B(c)D (a) A WC E B(b)AW CD B解：1-3 试画出以下各题中AB 梁的受力图。

解：ABW (e)CF B F AAB F(d)CF BF A(a) F D F BF ED A WCE B(b)AWC D B F D F BF A(c)AWC BF BF AAW CB(a)WABC D(c)ABF q D(b)CC A BFWDA ’ D ’B ’(d)ABFq(e)F BF AF qABC F B1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：CA BFWD(d)F BF AF DAB Fq(e)F BxF ByF AAB F (a) DCWAF (b) DB(c) FABD D ’ABF(d)CDW ABC D(e)WABC (f)AB F (a)D CWF AxF AyF DA F (b)BF BF A(c)FABDF BF D A FCA F AF AB1-5 试画出以下各题中指定物体的受力图。

(a) 结点A，结点B；(b) 圆柱A和B及整体；(c) 半拱AB，半拱BC及整体；(d) 杠杆AB，切刀CEF及整体；(e) 秤杆AB，秤盘架BCD及整体。

解：(a)(b)ABW(a)(c)BC W1 W2FAFDABCE F(d)AF ABF ATF ABF BAF BTWABPP(b)WA BCC’DOG (e)(c)(d)(e)F CAPCF BB PCF ’ CF AABPPF BF NBC W 1W 2 F AF Cx F CyF AxF AyB W 1F A F Ax F AyF Bx F By B C W 2 F Cx F CyF ’Bx F ’By F A BC F C F BDC E F F E F ’C F F FDAB C E F F EF FF BB C D G F B F C WAB CC ’ DO GF Oy F OxF C ’A B O W F BF OyF Ox2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：以 m1 − k 体系静平衡位置作为原点 则 m1 , m2 共同作用的静平衡位置 u st = 碰撞之前 m2 的速度 v2 = m2 2 gh 碰撞之后：动量守恒
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程： ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时，发生共振有： Rd 1 =
当 w wn = 1 10 时， Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解：
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理： δ Ws
+ δ WI + δ W D +δ W p = 0 得：
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解：
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭

1，集中质量法 2，广义坐标法 3，有限单元法
2019/9/16
38
2019/9/16
39
2019/9/16
40
2019/9/16
41
2019/9/16
42
2019/9/16
43
三. 自由度的确定
广义坐标法：广义坐标个数即为自由度个数； 有限元法：独立结点位移数即为自由度数； 集中质量法：独立质量位移数即为自由度数；
11

l3 3EI
柔度系数
my(t) 3 EI l3y( Nhomakorabea)
P(t)
2019/9/16
柔度法步骤： 1.在质量上沿位移正向加惯性力； 2.求外力和惯性力引起的位移； 3.令该位移等于体系位移。
49
二、刚度法
P(t)
m
1
my(t)
y(t)
l EI
y
k11
k11 y(t )
k11y(t) P(t) my(t)
变分法（Hamilton原理）以及lagrange等。
我们这节课主要介绍达朗泊尔原理建立的动力学微分方程，用能量法建立 微分方程的方法在以后的章节中介绍。
达朗泊尔原理
质点系运动的任意瞬时，除了实际作用于每个质点的主动力和约束反力外， 在加上假象的惯性力，则在该瞬时质点系处于假象的平衡状态。
m P(t) my(t)
结构动力学
2019/9/16
1/
思考问题
1，结构动力学和静力学的区别和联系在哪里？
运动方程为：
m y(t) c y(t) k y(t) p(t)
静力学方程为：
k y p
201所9/9/以16 两者的区别在于：动力学问题多了惯性力项以及由运动产生的阻尼力。 2

《结构动力学》习题答案1~151． 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1）建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2）进行振型和频率分析对无阻尼自由振动，这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3）求广义质量和荷载依次取每一个振型向量n φ，计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4）求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5）求对荷载的振型反应根据荷载类型，用适当的方法解这些单自由度方程，每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6）振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7）求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然，它反映了各个振型贡献的叠加。

因此命名为振型叠加法。

8）弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时，可以采用另一种弹性力的表达式。

1.5 结构的动力特性
结构受动荷载作用，它的反应不仅和动荷载有关， 结构受动荷载作用，它的反应不仅和动荷载有关， 而且还和结构本身固有的特性（包括结构阻尼、 而且还和结构本身固有的特性（包括结构阻尼、频率 谱和振型等）有关。 谱和振型等）有关。 设有单自由度的刚架和桁架， 设有单自由度的刚架和桁架，如果它们具有相同 的阻尼、频率，在相同动荷载下将具有相同的反应。 的阻尼、频率，在相同动荷载下将具有相同的反应。 可见结构的固有特性能确定动荷下的反应程度， 可见结构的固有特性能确定动荷下的反应程度，因此 称作结构的动力特性。 将他们称作结构的动力特性 将他们称作结构的动力特性。 1.5.1 自振频率和频率谱 外界干扰消除後， 外界干扰消除後，系统在平衡位置附近所产生的 自由振动（ ）。自由振 振动，称作自由振动 无外荷作用的振动）。 振动，称作自由振动（无外荷作用的振动）。自由振 动的频率称自振频率 简称自频 自振频率， 自频。 动的频率称自振频率，简称自频。
1.3结构动力学的研究内容和任务 结构动力学的研究内容和任务
结构动力学是研究动荷作用下结构动力反应规律的 学科。 学科。 1.3.1 结构动力学的研究内容 当前结构动力学的研究内容可用下图表示 输入 动力荷载） （动力荷载） 结构 系统） （系统） 输出 动力反应） （动力反应）
第二类问题：参数（或称系统）识别 第二类问题：参数（或称系统） 控制系统 （装置、能量） 装置、能量）
1.4 结构动力分析中的自由度
3) 有限单元法 和静力问题一样， 和静力问题一样，可通过将实际结构离散化为有限 个单元的集合，将无限自由度问题化为有限自由度来 个单元的集合， 解决。由于将专门介绍，这里不再赘述。 解决。由于将专门介绍，这里不再赘述。 虽将简单介绍有限单元法，但本部分主要讨论集 虽将简单介绍有限单元法， 中质量法。对集中质量而言，自由度并不难理解， 中质量法。对集中质量而言，自由度并不难理解，但 如果错误判断了自由度个数， 如果错误判断了自由度个数，象超静定问题基本未知 量个数一样，由于它的错误，后面再算是无意义的。 量个数一样，由于它的错误，后面再算是无意义的。 因此，必须熟练地掌握自由度的确定。 因此，必须熟练地掌握自由度的确定。

λ/nm
v /1014s－1
312.5 9.59
365.0 8.21
404.7 7.41
546.1 5.49
Ek/10－19J
3.41
2.56
1.95
0.75
由表中数据作图，示于图 1.2 中
4
Ek /10-19J
3
2
1
0 4 5 6 7 8 9 10 ν/1014g-1
图 1.2 金属的 Ek −ν 图
由式
hv = hv0 + Ek
推知
h = Ek = ∆Ek v − v0 ∆v
即 Planck 常数等于 Ek − v 图的斜率。选取两合适点，将 Ek 和 v 值带入上式，即可求出 h 。
例如：
h
=
(2.70 −1.05) ×10−19 J (8.50 − 600)×1014 s−1
=
6.60×1034 J is
( ) ( ) n 和 n' 皆为正整数，因而 n − n' 和 n + n' 皆为正整数，所以积分：
l
∫ψ n ( x)ψ n' ( x) dτ = 0
0
ψ
根据定义，
n
(
x
)
ψ
和
n'
(
x)
互相正交。
【1.15】已知在一维势箱中粒子的归一化波函数为
ϕn ( x) =
2 sin nπ x ll
n = 1, 2,3⋅⋅⋅
压加速电子）。
解：解法一：根据不确定度关系，电子位置的不确定度为：
△x
=
h △ px
h =
h/λ
= 1.226 ×10−9 i

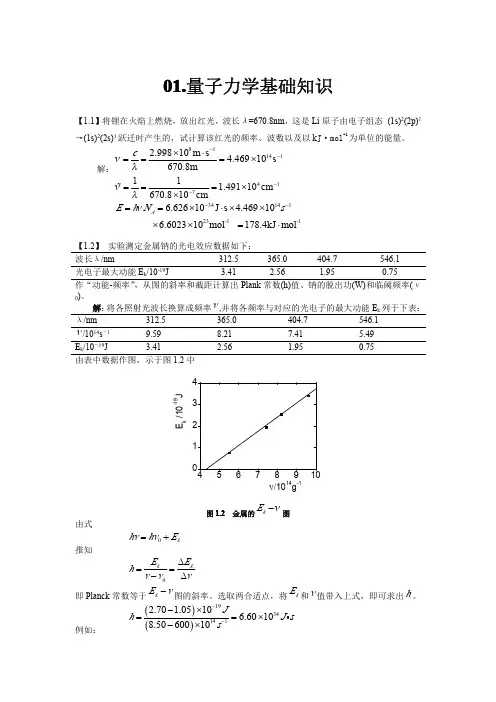
机械工程材料 课后习题答案大连理工版1-1、可否通过增加零件尺寸来提高其弹性模量。

解：不能，弹性模量的大小主要取决于材料的本性，除随温度升高而逐渐降低外，其他强化材料的手段如热处理、冷热加工、合金化等对弹性模量的影响很小。

所以不能通过增大尺寸来提高弹性模量。

1-2、工程上的伸长率与选取的样品长度有关，为什么？解：伸长率等于，当试样(d)不变时，增加，则伸长率δ下降，只有当/为常数时，不同材料的伸长率才有可比性。

所以伸长率与样品长度有关。

1-3、和两者有什么关系？在什么情况下两者相等？解：为应力强度因子，为平面应变断裂韧度，为的一个临界值，当增加到一定值时，裂纹便失稳扩展，材料发生断裂，此时，两者相等。

1-4、如何用材料的应力-应变曲线判断材料的韧性？解：所谓材料的韧性是指材料从变形到断裂整个过程所吸收的能量，即拉伸曲线（应力-应变曲线）与横坐标所包围的面积。

2-1、从原子结构上说明晶体与非晶体的区别。

解：原子在三维空间呈现规则排列的固体称为晶体，而原子在空间呈无序排列的固体称为非晶体。

晶体长程有序，非晶体短程有序。

2-2、立方晶系中指数相同的晶面和晶向有什么关系？解：相互垂直。

2-4、合金一定是单相的吗？固溶体一定是单相的吗？解：合金不一定是单相的，也可以由多相组成，固溶体一定是单相的。

3-1、说明在液体结晶的过程中晶胚和晶核的关系。

解：在业态经书中存在许多有序排列飞小原子团，这些小原子团或大或小，时聚时散，称为晶胚。

在以上，由于液相自由能低，晶胚不会长大，而当液态金属冷却到以下后，经过孕育期，达到一定尺寸的晶胚将开始长大，这些能够连续长大的晶胚称为晶核。

3-2、固态非晶合金的晶化过程是否属于同素异构转变？为什么？解：不属于。

同素异构是物质在固态下的晶格类型随温度变化而发生变化，而不是晶化过程。

3-3、根据匀晶转变相图分析产生枝晶偏析的原因。

解：①枝晶偏析：在一个枝晶范围内或一个晶粒范围内，成分不均匀的现象叫做枝晶偏析。

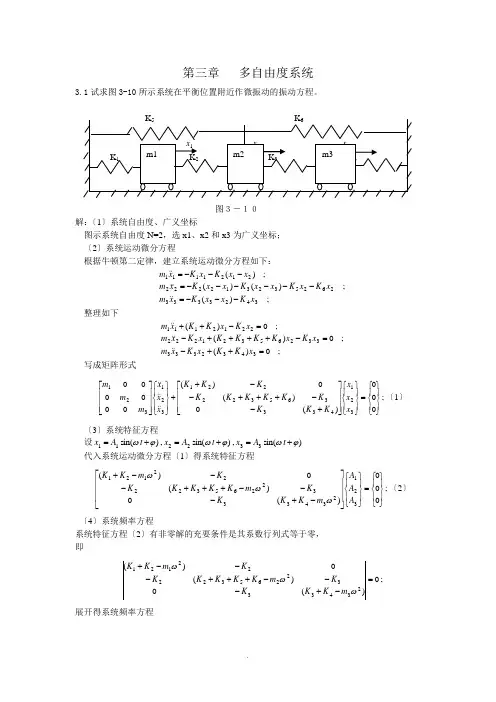
第三章 多自由度系统3.1试求图3-10所示系统在平衡位置附近作微振动的振动方程。

图３－１０解：〔1〕系统自由度、广义坐标图示系统自由度N=2，选x1、x2和x3为广义坐标； 〔2〕系统运动微分方程根据牛顿第二定律，建立系统运动微分方程如下：;)(;)()(;)(34233332625323122222121111x K x x K x m x K x K x x K x x K xm x x K x K xm ---=------=---= 整理如下;0)(;0)(;0)(3432333332653212222212111=++-=-++++-=-++x K K x K xm x K x K K K K x K xm x K x K K xm 写成矩阵形式;000)(0)(0)(00000321433365322221321321⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+++--++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x K K K K K K K K K K K K x x x m m m 〔1〕 〔3〕系统特征方程设)sin(,)sin(,)sin(332211ϕωϕωϕω+=+=+=t A x t A x t A x 代入系统运动微分方程〔1〕得系统特征方程;000)(0)(0)(321234333226532222121⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+---+++---+A A A m K K K K m K K K K K K m K K ωωω〔2〕 〔4〕系统频率方程系统特征方程〔2〕有非零解的充要条件是其系数行列式等于零， 即;0)(0)(0)(234333226532222121=-+---+++---+ωωωm K K K K m K K K K K K m K K展开得系统频率方程;0))(())(()))(())(()((21212323432223432265322121=-+--+--+-+++-+ωωωωωm K K K m K K K m K K m K K K K m K K进一步计算得;0;0)()())()(()))(())((())()()(()()()()())(()())(())(())()(())(())(()))(()()())((())(())(()))(())(()((02244662123432265324321236532214321231233224316532214332216321231232123232243226321421434322124321243165322165324323653221653243212121232343222343421221265322165322121212323432223432265322121==++++-+-+++++++++++-++-+++++++++++-=++-++--++++++-++++++++-++++-+++++=-+--+--+++-+++-++++=-+--+--+-+++-+a a a a K K K K K K K K K K K K K K m K K K K K K K K K K m m m K m K m m K K K K m m K K m m K K m m m m m K K K K m K K K K m m m m m K K m m K K K K K K m m m K K K K m K K K K K K m K K K K K K K K K K K K K K m K K K m K K K m K K m m K K m K K K K m K K K K K K m K K K m K K K m K K m K K K K m K K ωωωωωωωωωωωωωωωωωωωωωωωωωω (3)其中;3216m m m a -= ;)()()(316532214332214m m K K K K m m K K m m K K a +++++++=;))(())((36532214321231233222m K K K K K K K K K K m m m K m K a ++++-++-+=);()())()((21234322653243210K K K K K K K K K K K K K K a +-+-+++++=求解方程〔3〕得系统固有频率;)3,2,1(),,,,,,,,,(654321321==i K K K K K K m m m f i i ω 〔4〕 〔5〕系统固有振型 将系统固有频率代入系统特征方程〔2〕得系统固有振型， 即各阶振型之比：)3(3)3(1)3(3)3(2)3(1)3(2)2(3)2(1)2(3)2(2)2(1)2(2)1(3)1(1)1(3)1(2)1(1)1(21,1;1,1,1,1A A A A A A A A A A A A ======γγγγγγ 〔5〕 〔6〕系统振动方程)sin()sin()sin()sin()sin()sin(33)3(1)3(3)3(1)3(2)3(122)2(1)2(3)2(1)2(2)2(111)1(1)1(3)1(1)1(2)1(133)3(3)3(2)3(122)2(3)2(2)2(111)1(3)1(2)1(1321ϕωγγϕωγγϕωγγϕωϕωϕω+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧t A A A tA A A tA A A t A A A t A A A t A A A x x x 〔6〕在方程〔6〕中含有6个待定常数：)1(1A 、)2(1A 、)3(1A 、1ϕ、2ϕ和3ϕ。

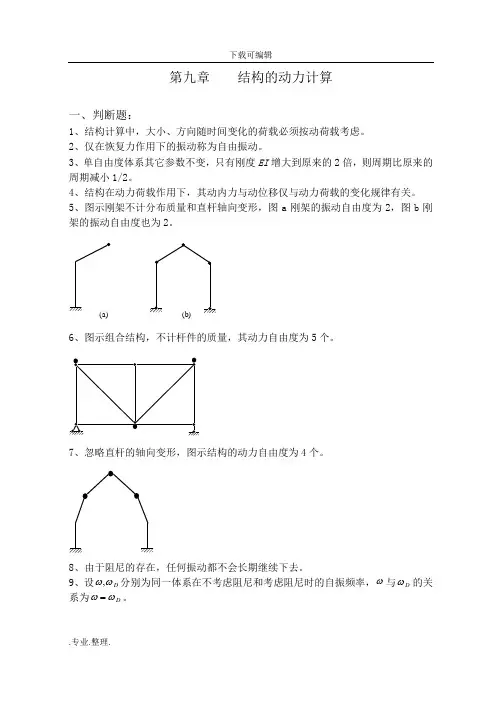
第九章 结构的动力计算一、判断题：1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。

2、仅在恢复力作用下的振动称为自由振动。

3、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。

4、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。

5、图示刚架不计分布质量和直杆轴向变形，图a 刚架的振动自由度为2，图b 刚架的振动自由度也为2。

6、图示组合结构，不计杆件的质量，其动力自由度为5个。

7、忽略直杆的轴向变形，图示结构的动力自由度为4个。

8、由于阻尼的存在，任何振动都不会长期继续下去。

9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率，ω与ωD 的关系为ωω=D 。

二、计算题：10、图示梁自重不计，求自振频率ω。

l l /411、图示梁自重不计，杆件无弯曲变形，弹性支座刚度为k ，求自振频率ω。

l /2l /212、求图示体系的自振频率ω。

l l 0.5l 0.513、求图示体系的自振频率ω。

EI = 常数。

l l 0.514、求图示结构的自振频率ω。

l l15、求图示体系的自振频率ω。

EI =常数，杆长均为l 。

16、求图示体系的自振频率ω。

杆长均为l 。

17、求图示结构的自振频率和振型。

l /2l /2l /18、图示梁自重不计，W EI ==⨯⋅2002104kN kN m 2,，求自振圆频率ω。

B 2m 2m19、图示排架重量W 集中于横梁上，横梁EA =∞，求自振周期ω。

EI EI W20、图示刚架横梁∞=EI 且重量W 集中于横梁上。

求自振周期T 。

EI EI WEI 221、求图示体系的自振频率ω。

各杆EI = 常数。

a a a22、图示两种支承情况的梁，不计梁的自重。

求图a 与图b的自振频率之比。

l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ，各杆EA 相同，杆重不计。

求水平自振周期T 。

.. .
m u + c u + ku = Pu (t ) 2.13 一根均匀杆，图 P2.13 其单位体积质量密度 ρ ，并具有顶部质量 M，应 用假定法ψ ( x) = x L 来推导该系统轴向自由振动的运动方程。假定 AE = 常数。 解：
.. 1 EA ( ρAL + M ) u + u = P(t ) 3 L
结构动力学习题 参考答案
1
2.3 一根刚梁 AB，用力在弹簧 BC 上去激励它，其 C 点的运动规定为 Z（t）,如 图 P2.3. 按 B 点的垂直运动 u 来确定系统的运动方程，假定运动是微小的。 解： 4M u + 3c u + (3k1 + 12k 2 )u = 12k 2 Z (t )
.. .
4
4.17 在振动的结构上一个点，已知其运动为 Ζ = Ζ1 cos(Ω1t ) + Ζ 2 cos(Ω 2 t ) =
0.05 cos ( 60π t ) + 0.02 cos(120π t ) 。
（a）用一加速度计其阻尼因数 ξ = 0.70 和 20 KHz 共振频率来确定振动记录 w p (t ) 。 (b) 加速度计是否会引起有效幅值或相位畸变？ 解： （a） w p (t ) = w p1 (t ) + w p 2 (t ) = 6.339 × 10 −11 A1 cos 60π (t − 1.1145 × 10 −5 ) + 6.339 × 10 −11 A2 • cos 120π (t − 1.1146 × 10 −5 ) （b） w p (t ) = C[ A1 cos Ω1 (t − τ ) + A2 cos Ω 2 (t − τ )] A1 , A2 分别表示 Z1 , Z 2 的加速度幅值，所以输出 w p (t ) 与加速度输 入成正比，所以不会发生幅值畸变或相位畸变。 5.2 运送一件仪器设备重 40 1b，是用泡沫包装在一容器内。该容器的有效刚度 k=100 1b/in，有效阻尼因数 ξ = 0.05 ，若整个容器和它的包装以垂直速度 V=150 in/s 碰撞在地面上，求泡沫包装在仪器设备的最大总应力。 （如图 P5.2 所示） 解： f max = 451.739 (1b) 6.5 例 题 4.3 中的 车辆 ， 已知 k = 400 × 10 3 , m = 1200kg , ξ = 0.4。 当满 载时以

i (0) i (l ) 0
--基函数（或形状函数） 课件 i ( x)PPT
9
ai ---广义坐标
3) 有限元法 和静力问题一样，可通过将实 际结构离散化为有限个单元的集合， 将无限自由度问题化为有限自由度 来解决。
m
三. 自由度的确定
集中质量法：独立质量位移数即为自由度数； 广义坐标法：广义坐标个数即为自由度个数； 有限元法：独立结点位移数即为自由度数；
第三类问题：荷载识别。
PPT课件
5
第四类问题：控制问题
输入 （动力荷载） 结构 （系统） 控制系统 （装置、能量） 输出 （动力反应）
本课程主要介绍结构的反应分析 任务 讨论结构在动力荷载作用下反应的分析的方法。寻找 结构固有动力特性、动力荷载和结构反应三者间的相互关 系，即结构在动力荷载作用下的反应规律，为结构的动力 可靠性（安全、舒适）设计提供依据。
PPT课件
10
例. 自由度的确定
1) 平面上的一个质点 3) 计轴向变形时 W=2 不计轴向变形时 W=1 W=2 为减少动力自由度，梁与 刚架一般可不计轴向变形。
y2
y1
W=2
2)Βιβλιοθήκη 弹性支座不减少动力自由度PPT课件
11
4)
y1
W=1
5) W=2
6)
EI
W=1
PPT课件
12
§1.4
体系的运动方程
形式上的平衡方程，实质上的运动方程
PPT课件
13
一、柔度法
P(t )
l
EI
m m (t ) y y(t )
=1
11
(t )] 11[ P(t ) m y

结构动力学*本章讨论结构在动力荷载作用下的反应。

**学习本章注重动力学的特征------惯性力。

*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律，从而找出其最大值作为设计的依据。

*动力学研究的问题：动态作用下结构或构件的强度、刚度及稳定性分析。

一、本章重点1．振动方程的建立2．振动频率和振型的计算3．振型分解法求解多自由度体系4．最大动位移及最大动应力二、基础知识1．高等数学2．线性代数3．结构力学三、动力荷载的特征1．大小和方向是时间t的函数例如：地震作用，波浪对船体的作用，风荷载，机械振动等2．具有加速度，因而产生惯性力四、动力荷载的分类1．周期性动力荷载例如：①机械运转产生的动力荷载，②打桩时的锤击荷载。

P（t） Pt t（机械运转荷载）（打桩荷载）2．冲击荷载例如：①爆炸力产生的动力荷载，②车轮对轨道连接处的冲击。

P（t）P（t）P（t）t t t（爆炸力动力荷载）（吊车起吊钢索的受力）（随机动力荷载）3．突加常量荷载例如：吊车起吊重物时钢索的受力。

4．随机动力荷载前3类荷在是时间t的确定函数，称为确定性动力荷载；而地震作用，波浪对船体的作用，风荷载等其作用大小只能用统计的方法获得。

五、动力荷载的计算方法1．原理：达朗贝尔原理，动静法建立方程2．计算工具：微分方程，线性代数，结构力学六、体系振动的自由度---------动力自由度结构具有质量，有质量在运动时就有惯性力。

在进行动力计算时，一般把结构的质量简化为若干质点的质量，整个结构的惯性力就成为各质点的惯性力问题。

1．质点简化的一般要求①简单，②能反映主要的振动特性例如：楼房；质量集中在各层楼板平面内水塔：质量集中在水箱部分梁：无限自由度集中质量（楼房质量集中）（水塔质量集中）（梁的质量集中）2．位移y（t）即指质点的位移y（t），其加速度为y&&)(t3．动力自由度的确定即质点位移数量的确定。

刚性圆柱体涡激振动响应模态特性研究冯绍军;熊友明;高云【摘要】基于改进的尾流振子模型对刚生圆柱体涡激振动响应模态特性进行了研究.建立了刚生圆柱体与尾流振子的耦合模型,对耦合模型进行了线性简化,同时对简化后的模型进行解耦得到圆柱体的模态特性参数.对不同质量比情况下的刚性圆柱体频率、相位角以及主导模态等参数进行了分析.分析结果表明:圆柱体涡激振动响应模态可分为结构模态及流场模态,以流场模态为主导模态;结构模态频率分布在圆柱体固有频率附近,而流场模态频率则分布在斯脱哈尔漩涡泄放频率附近.【期刊名称】《石油工程建设》【年(卷),期】2018(044)002【总页数】5页(P17-21)【关键词】尾流振子模型;频率实部;频率虚部;流场模态;结构模态【作者】冯绍军;熊友明;高云【作者单位】西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500【正文语种】中文圆柱体在一定的来流下，会在其尾部两侧形成交替脱落的漩涡，漩涡脱落会引起圆柱体产生周期性的振动，称为涡激振动（Vortex induced vibration，VIV）[1]。

圆柱体涡激振动现象广泛存在于工程应用中，如处于空气中的桅杆、烟囱、桥梁悬索以及处于水中的立管、海底管道、锚链等结构，均有可能出现涡激振动响应。

当尾部漩涡泄放频率靠近结构固有频率时，便会出现锁定现象，此时圆柱体会发生大幅的、危险的涡激振动响应，这种响应会给结构带来很大的疲劳损伤。

圆柱体涡激振动问题是一种典型的非线性流固耦合问题，该问题的研究方法主要分为实验方法[2-5]、计算流体动力学（Computational fluid dynamics，以下简称CFD）方法[6-9]以及经验模型方法[10-13]。

实验方法分析数据可靠、分析现象直观，但研究成本较高；CFD方法与经验模型方法之间最主要的一个区别在于流体力的获取，CFD方法可通过对模型的计算实时地获取流体力，而经验模型方法则是基于经验系数去近似地模拟流体力；显然CFD方法在计算精度上占有一定的优势，但经验模型方法在计算资源上更占优势，经验模型方法由于计算时间快，更适用于实际海洋工程中的多工况问题。

my cy ky FP (t)
§2-5 广义单自由度体系：刚体集合
➢刚体的集合（弹性变形局限于局部弹性 元件中）
➢分布弹性（弹性变形在整个结构或某些 元件上连续形成）
➢只要可假定只有单一形式的位移，使得 结构按照单自由度体系运动，就可以按 照单自由度体系进行分析。
E2-1
x
p( x,t
)
=p
x a
作用时间： 恒载 活载 作用位置： 固定荷载 移动荷载 对结构产生的动力效应： 静荷载 动荷载
静荷载： 动荷载：
大小、方向和作用点不随时间变 化或变化很缓慢的荷载。
大小、方向或作用点随时间变化 很快的荷载。
快慢标准： 是否会使结构产生显著的加速度
显著标准： 质量运动加速度所引起的惯性力 与荷载相比是否可以忽略
FP (t ) FI FD FS1 FS2 0
其中各力的大小：
惯性力： FI my 弹性力Fs=Fs1+Fs2： 位移法：柱子一端产生单位平移时的杆端剪力
1
12i
l2
柱端发生平移 y 时产生的梁-柱间剪力：
EI
12 EI FS1 l13 y
12EI
FS 2
l
3 2
y
l
等效粘滞阻尼力： FD cy
大型桥梁结构 的有限元模型
第二章 运动方程的建立
定义
在结构动力分析中，描述体系质量运动规律的数学 方程，称为体系的运动微分方程，简称运动方程。
▪ 运动方程的解揭示了体系在各自由度方向的位移 随时间变化的规律。
▪ 建立运动方程是求解结构振动问题的重要基础。 ▪ 常用方法：直接平衡法、虚功法、变分法。
8
比较：
c k

输出 （动力反应）
.
第四类问题：控制问题
输入 （动力荷载）
结构 （系统）
输出 （动力反应）
控制系统 （装置、能量）
本课程主要介绍结构的反应分析
任务 讨论结构在动力荷载作用下反应的分析的方法。寻找
结构固有动力特性、动力荷载和结构反应三者间的相互关 系，即结构在动力荷载作用下的反应规律，为结构的动力 可靠性（安全、舒适）设计提供依据。
集中质量法 广义坐标法 有限单元法
.
1) 集中质量法 将实际结构的质量看成（按一定规则）集中在某些
几何点上，除这些点之外物体是无质量的。这样就将无 限自由度系统变成一有限自由度系统。
m
2) 广义坐标法
y(x) aii(x) i1 n
y(x) aii(x) i1
a i ---广义坐标
m y(x)
EI
m
l/2
l/2
W
m y(t)
1
11
st y(t)
Y(t)y(t)st
加速度为
Y(t) y(t)
y (t) s t 1[P 1 (t) W m y (t)]
st W11
结构动力学是研究结构、动荷载、结构反应三者关 系的学科。
.
当前结构动力学的研究内容为:
第一类问题：反应分析（结构动力计算）
输入 （动力荷载）
结构 （系统）
输出 （动力反应）
第二类问题：参数（或称系统）识别
输入 （动力荷载）
结构 （系统）
第三类问题：荷载识别。
输出 （动力反应）
输入 （动力荷载）
结构 （系统）
其他确定规律的动荷载 风荷载
不确定
地震荷载 其他. 无法确定变化规律的荷载

第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。

单自由度系统固有频率求法有：牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。

1、 牛顿第二定律法适用范围：所有的单自由度系统的振动。

解题步骤：（1） 对系统进行受力分析,得到系统所受的合力；（2） 利用牛顿第二定律∑=F x m,得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

2、 动量距定理法适用范围：绕定轴转动的单自由度系统的振动。

解题步骤：（1） 对系统进行受力分析和动量距分析；（2） 利用动量距定理J ∑=M θ,得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

3、 拉格朗日方程法：适用范围：所有的单自由度系统的振动。

解题步骤：（1）设系统的广义坐标为θ，写出系统对于坐标θ的动能T 和势能U 的表达式；进一步写求出拉格朗日函数的表达式：L=T-U ； （2）由格朗日方程θθ∂∂-∂∂∂LL dt )( =0，得到系统的运动微分方程； （3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

4、 能量守恒定理法适用范围：所有无阻尼的单自由度保守系统的振动。

解题步骤：（1）对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式；进一步写出机械能守恒定理的表达式 T+U=Const （2）将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ，进一步得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。

用衰减法求单自由度系统阻尼比的方法有两个：衰减曲线法和共振法。

方法一：衰减曲线法。

求解步骤：（1）利用试验测得单自由度系统的衰减振动曲线，并测得周期和相邻波峰和波谷的幅值i A 、1+i A 。