当前位置：文档之家 › 5分子平均动能按自由度均分的统计规律

5分子平均动能按自由度均分的统计规律

  • 格式：ppt
  • 大小：408.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

§3.4 能量按自由度均分定理

§3.4 能量按自由度均分定理


1 ε s = (n + )hv, n = 0,1,2,... 2
n，振动量子数，h= 6.63x10-34JS(焦耳秒），v振动频 振动量子数， 焦耳秒），v ）， 率。hv=103k，气体温度几十K时，动能也只有几十K，在 气体温度几十K 动能也只有几十K 碰撞时就不可能是振动能发生变化。 碰撞时就不可能是振动能发生变化。
能均分定理.exe
（3）能量均分定理不仅适用于理想气体，一般也可用于 能量均分定理不仅适用于理想气体，
三、理想气体的内能
理想气体的内能 ：分子动能和分子内原子间的势能之 和. 1 m U = N A ⋅ ( t + r + 2 s ) kT 2 M 理想气体的内能 m 1 = ( t + r + 2 s ) RT M 2
kT /2 。
• 能量均分定理是指每个分子的每一个自由度均分 kT 平均动能。 /2 平均动能。
0℃时几种气体 表2.2 在0℃时几种气体 CV,m /R 的实验值
单原子气体 He Ne CV,m /R 1.49 1.55 O2 双原子气体 H2 CV,m /R 2.53 2.55 Ar Kr 1.50 1.47 N2 CO 2.49 2.49 Xe 1.51 NO 2.57 单原子N 单原子 1.49 Cl2 3.02 NH3 3.42
§3.4
能量均分定理
处于平衡态的理想气体每个分子的平均平动动 能为
ε t = 3 kT / 2
• 本节将在此基础上，通过与实验测量值的比较，得到 本节将在此基础上， 通过与实验测量值的比较， 能量均分定理, 能量均分定理, • 并指出这一定理的局限性。 并指出这一定理的局限性。
从理想气体热运动无择优取向知
能量按自由度均分定理

能量按自由度均分定理

深化人们对能量转换和利用的认识
该定理帮助人们认识到能量的分布和转换规律，为能量的高效转换和利用提供了理论支持 。
启发新的科学研究方法
能量按自由度均分定理所采用的研究方法为其他科学研究提供了启示，有助于推动其他领 域的发展。
对工程实践的影响
提高能源利用效率
根据能量按自由度均分定理，工程师可以优化能源利用方案，提高 能源利用效率，降低能耗。
定理的证明
01
证明能量按自由度均分定理需要用到热力学的基本原理和统计方法。
02
首先，我们需要引入微观状态和宏观状态的概念，然后通过计算系统的微观状 态数和熵，推导出系统的宏观热力学性质。
03
通过分析系统的能量分布和自由度的关系，我们可以证明每个自由度平均分配 系统总能量的一半。这个证明过程涉及到一些数学推导和物理概念的应用，需 要一定的专业知识和理解能力。
能量按自由度均分定理用于研究 化学反应过程中能量的变化和分 配。
02
03
化学键能计算
热化学研究
通过该定理，可以计算化学键的 键能，从而预测化学反应的活化 能和反应速率。
能量按自由度均分定理用于研究 化学反应的热力学性质，如反应 焓和熵变。
在工程领域中的应用
热工控制
在热工控制中，该定理用于设计和优化热工系统的能量转换和传 递过程。
此外，我们也可以将该定理与其 他物理原理和理论相结合，以解 决更复杂的问题。例如，将能量 按自由度均分定理与量子力学、 相对论等理论结合起来，可以更 深入地理解物质的本质和性质。
在实际应用方面，我们可以利用 该定理来研究和设计新型材料、 能源技术、环保技术等领域的材 料和系统，以提高其性能和效率。 因此，能量按自由度均分定理在 未来仍将是一个重要的研究和应 用领域。
大学物理4-2 能均分定理

大学物理4-2 能均分定理


pV
p
可知是N2或CO气体
1.25 103 8.31 273 0.028 kg / mol 101 .3
§5. 动能按自由度均分的统计规律/六、瘵例
(3)气体分子的平均平动动能和平均转动动能？
t
3 2
kT
3 1.381023 2
273
5.651021 J
r kT 1.381023 273 3.77 1021 J
k
1 mv2 2
1 2
m
(vx2
v
2 y
v
2 z
)
3 kT 2
v
2 x
v
2 y
v
2 z
1 2
mvx2
1 2
m
v
2 y
1 2
m
v
2 z
1 2
kT
每个平动自由度上分配了一份 1 kT的能量。
2
§5. 动能按自由度均分的统计规律/三、统计规律
由于分子的激烈碰撞（几亿次/秒）, 使 平动动能与转动动能不断转换，
能均分定理 理想气体内能
一、自由度 确定物体的空间位置所需的独立坐标数。 质点的自由度: t 3 气体分子的自由度: 1) 单原子分子气体 t 3 例如：氦气（He）、氖气（Ne）、氩气 （Ar）等为单原子分子气体。
ቤተ መጻሕፍቲ ባይዱ§5.分子动能按自由度均分的统计规律/一、自由度
2.双原子分子气体 例如：氢气（H2）、氧气（O2）、氮气 （N2）等为双原子分子气体。
(4)单位体积内气体分子的总平动动能?
Et
nt
p kT
101.3 1.38 1023
273
5.65 1021
03能量按自由度均分原理理想气体内能

03能量按自由度均分原理理想气体内能


1.自由度 ——描述物体运动自由程度的物理量。
在力学中，自由度是指决定一个物体的空间位置所 需要的独立坐标数.
所谓独立坐标数是指描写物体位置所需的最少的坐 标数。
2
例如：物体沿一维直线运动，最少
x
只需一个坐标，则自由度数为1。
轮船在海平面上行驶，要描 写轮船的位置至少需要两维坐 标，则自由度为 2。
11
v2vx2vy2vz2且 vx2 vy2 vz2
t
1 mv2 2
12m(vx2 vy2 vz2)
3 2
mvx
2
6
2. 1 mol气体分子的能量为:
E
i 2
NAk
T
i 2
RT
3.M 千克气体的内能为：E M i RTiRT
Mmol2
2
对于一定量的理想气体，它的内能只是温度 的函数而且与热力学温度成正比。
但对于火车在轨道上行驶时 自由度是多少呢？
自由度是 1，由于受到轨道限 制有一维坐标不独立。
飞机在天空中飞翔，要描写飞 机的空间位置至少需要三维坐 标，则自由度为 3。
3
1. 一个质点 描写它的空间位置，需要 3
个平动自由度， t 3
2.两个刚性质点
z o
P(x,y,z)
y
描写其质心位置需3个平动
自由度， t 3
x
z
描写其绕x、y轴转动需2个转动自
由度，绕z轴的转动能量可不计，
r2
o
y
总自由度数：i t r 3 2 5
3.三个或三个以上的刚性质点
x
平动自由度 转动自由度
t 3
r3
总自由度
i t r 3 3 6
能量均分定理

能量均分定理


z
C( x, y, z)
y
x
单原子分子 平动自由度t=3 平动自由度
H e
i = t +r= 3
（25）能量均分定律 25）
理想气体内能
气体动理论
（2）对双原子分子 ）
O2
对直线 确定线上一个点，需 （x、y、z） t =3 个平动自由度， 个平动自由度， 确定线上一个点， ） 确定线的方位， 确定线的方位，似乎还需 （α、β、γ）3 个转动自由度 但因 cos2 α + cos2 β + cos2 γ = 1 r = 2 个转动自由度 故只需 所以，直线需要的自由度数为： 所以，直线需要的自由度数为： i = t + r = 5 平动自由度t=3 转动自由度 转动自由度r=2 平动自由度
εk =52 kT
（25）能量均分定律 25）
气体动理论 理想气体内能 分子平均动能按自由度均分的原则是统计规律
平动动能 （1）分子平均平动动能 εt 按自由度均分 ）分子平均平动 （2）分子平均动能 εk 按自由度均分 ） 六、理想气体的内能 气 体 内 能 分子平均动能的总和（平动、振动、转动） 分子平均动能的总和（平动、振动、转动）
i εk = kT 2
注意： 注意： （1）该公式是对大量分子的统计规律。 ）该公式是对大量分子的统计规律。 （2）平衡态 ） （3）理想气体 ）
如：刚性双原子分子，分子平均动能为： 刚性双原子分子，分子平均动能为： 刚性三原子分子，分子平均动能为： 刚性三原子分子，分子平均动能为：
εk = 6 kT 2
3 RT ⑥ 2
1摩尔自由度为 的分子（单原子分子）组成的 摩尔自由度为3 的分子（单原子分子） 摩尔自由度为 系统的内能。 系统的内能。 或是所有分子平均平动动能的总和。 或是所有分子平均平动动能的总和。
能量按自由度均分定理(李椿热学3-4节ppt)

能量按自由度均分定理(李椿热学3-4节ppt)


CH
等，有三个平动、
4
三个转动共六个自由度，
6 2
kT，U
m
3RT，CV ,m
3R
。
非刚性分子：常温下振动自由度部分解冻的分子。如 Cl2， CO2，NH3，C3H6 等。一般是一些价键较弱的大分子。
虽小分子，但价键较弱！
上页 下页 作业 退出 17
刚性分子理想气体内能：既无分子间相互作用势能，又
3. 被限制在一条直线或曲线上运动的质点：x、y、z 三个坐 标中只有一个是独立的，即这里只有一个自由度。如火车。
N个自由质点的自由度数：3N 。
上页 下页 作业 退出 2
空间自由运动的刚体的自由度数：6
如抛出去的砖头：质心的平动 + 砖头绕质心的转动 （定点转动）。要想知道砖头在空间的位置，就必须知道
y 原子间距离 ξ（表示振动）.
因此，双原子分子有三个平动、
两个转动和一个振动共 6 个自由度！
上页 下页 作业 退出 4
根据理论力学，分子转动动能为
m1
kr
1 2
I 2
1 2
I2
1 2
I 2
C
m2
由于原子质量 99.9% 集中在原子核
（质点），因此分子绕 轴的转动惯量
I 0
因此分子转动动能实际为
r
2v)
注意：这些都是温度足够高即能量均分定理能够完全成 立时的理想结论。实际分子的平均总能量通常会明显地小于 这些结果！
上页 下页 作业 退出 11
三、理想气体的内能(ideal gas internal energy)
气体内能：所有分子的热运动动能、分子内原子间振动 势能，以及分子间相互作用势能的总和。
能均分定理

能均分定理


例:一容器内理想气体的温度为T=273K, 压强为p=1.013 10 Pa, 密度为 1.25g / m ，
5 3
求:(1)气体分子运动的方均根速率,
(2)气体的摩尔质量，是何种气体？
(3)气体分子的平均平动动能和转动动能,
(4)单位体积内气体分子的总平动动能,
(5)设该气体有0.3mol , 求气体的内能。 （设气体分子为钢性）
已知T=273K,
5Pa, 1.25g / m3 P=1.013*10
解:(1)气体分子运动的方均根速率？ pV
v
2
M

RT
3RT


3p
3 1.013 105 493(m / s) 3 1.25 10
(2)气体的摩尔质量，是何种气体？ M RT RT pV p 可知是N2或CO气体
刚性： 3，r 2， s 0， t
i5
3.多原子分子气体 例如：二氧化碳气体（CO2）、水蒸气 （H2O）、甲烷气体（CH4）等.
i 一般： 3n , 刚性： i 6
§5. 动能按自由度均分的统计规律/二、分子自由度
二、能均分定理 由温度公式, 分子平均平动动能 3 1 1 2 2 2 2 k mv m(vx vy vz ) kT 2 2 2
U mol
1 1. 分子的平均内能为: t r 2 s kT 2
1 N A t r 2s RT 2
M U mol M t r 2s RT 2
3. M千克气体的内能为：
U

§5. 动能按自由度均分的统计规律/四、气体能量
对单原子分子理想气体 3 U mol RT 2 对刚性双原子分子理想气体 5 U mol RT 2 对非刚性双原子分子理想气体 7 U mol RT 2 理想气体内能仅与温度T有关, 与P、V无关。
能量均分定理

能量均分定理


3
2
5
多原子分子
3
3
6
第七章 气体动理论
7 – 5 能量均分定理 理想气体内能 二 能量均分定理（玻尔兹曼假设）
物理学教程 （第二版）
气体处于平衡态时，分子任何一个自由度的平
均能量都相等，均为 1 k T，这就是能量按自由度
2
均分定理 . 分子的平均能量
i kT
2
刚性分子能量自由度
t r i 自由度
分子平均碰撞次数：单位时间内一个分子和其 它分子碰撞的平均次数 .
简化模型
1 . 分子为刚性小球 ,
d 2 . 分子有效直径为 （分子碰撞靠近时距离的平均值）， 3 . 其它分子皆静止, 某一分子以平均速率u 相
对其他分子运动 .
第七章 气体动理论
7 – 7 分子平均碰撞次数和平均自由程
物理学教程 （第二版）
M
M2
2Leabharlann （物质的量 m M ）
理想气体内能变化
第七章 气体动理论
dE i RdT
2
7 – 5 能量均分定理 理想气体内能
物理学教程 （第二版）
理想气体的内能 理想气体内能变化
E m' i RT i RT
M2
2
dE i RdT
2
几种刚性分子理想气体的内能
1mol 单原子分子气体
v vf (v)dv
8kT
0
πm
o
v
v 1.60 kT 1.60 RT
m
M
第七章 气体动理论
7 – 6 麦克斯韦气体分子速率分布律
物理学教程 （第二版）
3）方均根速率 v2
06-4能量均分定理

06-4能量均分定理


z
确定分子绕质心的转动需要三个 转动自由度 O 分子的总自由度 x
y
i = t + r = 3+3 = 6
z
如果是非刚体分子， 如果是非刚体分子，原子之间的距 离可以发生变化， 离可以发生变化，原子之间可以看 成是由一根不计质量的弹簧相连 非刚体分子的原子之间还存在一个 振动自由度
o
x
y
常温下这种原子之间的振动可以被忽略（自由度被 常温下这种原子之间的振动可以被忽略（ 冻结）， ），所以常温下一般的分子都可以视为刚性分 冻结），所以常温下一般的分子都可以视为刚性分 子，一般只有在高温时才需要考虑振动自由度
z
o
x
y
确定双原子分子绕质心的转动需要两个转动自由度 确定双原子分子绕质心的转动需要两个转动自由度 不考虑原子体积， 不考虑原子体积，所以两原子连线方向的转动忽略不计 分子的总自由度
i = t + r = 3+ 2 = 5
5 刚性多原子分子（如H2O、CO2、CH4等） 刚性多原子分子（ 、 确定分子质心的运动需要三个平 确定分子质心的运动需要三个平 动自由度
3 ε k = kT 2
5 εk = kT 2
εk = 3kT
能量均分定理不仅适用于理想气体， 能量均分定理不仅适用于理想气体，也可以用于液体 和固体。对于气体， 和固体。对于气体，能量按自由度均分是依靠分子间 的无规则碰撞；对于液体和固体， 的无规则碰撞；对于液体和固体，能量均分是通过分 子之间很强的作用力来实现的 能量均分定理仅限于均分平均动能。 能量均分定理仅限于均分平均动能。 对于振动能量，除动能外， 对于振动能量，除动能外，还有原 子之间的势能， 子之间的势能，所以一个振动自由 度要均分kT的能量 的能量（ 度要均分 的能量（我们仅限于讨 o 论刚体分子， 论刚体分子，振动自由度不在我们 x 讨论的范围内） 讨论的范围内）
气体动理论公式总结

气体动理论公式总结


1.自由度i=t+r
单原子分子 i=t=3
刚性双原子 i=t+r=3+2 刚性三原子i=t+r=3+3
2.分子平均平动动能
t
t 2
kT
3 2
kT
3.分子平均转动动能
r
r 2
kT
4.分子平均动能
k
i kT 2
5.气体内能
E
i RT
2
i pV 2
2
四、麦克斯韦速率分布律
1.速率分布函数： f (v) dN Ndv
3、均匀带电无限长直导线
E 2 0 r
4.半径为R的均匀带电球面
E外
q
4 0r 2
E内 0
q
q
U外 4 0r U内 40R
5.无限大均匀带电平面
E
2 0
15
七、静态平衡时的导体 1. 导体内部场强为0。导体表面附近场强方向与导
体表面垂直。 2.导体为等势体（电势处处相等）。
3. 导体内无电荷，所有电荷分布于表面。
(1)
D dS q0 电场的高斯定律
(2)
E dl
L
S
B
d
S
电 场 的
环路定理
t
(变化的磁场激发电场)
(3) B d S 0
磁场的高斯定律
(4)
S
H dl
L
Ic
d D
dt
Ic
D dS t
磁 场 的 环 路 定 理 （变化的电场激发磁场）
27
第13 章量子物理
一、黑体辐射
v2 b v2 f (v)dv / b f (v)dv
a
10.3 能量按自由度均分原理

10.3 能量按自由度均分原理


一个氮气(或一氧化碳)分子的转动动能为
J
2 kT 1.381023 273 3.7 1021 J 2
（4）单位体积内分子的总平均平动动能为
3 kTn 3 kT p 3 p 1.5103 J
2
2 kT 2
大学物理 第三次修订本
第10章 气体动理论及热力学
（5）0.3摩尔氮气(或一氧化碳)分子的内能为
u 2v
则
Z 2vn 2πd 2vn
二、平均自由程
每两次连续碰撞之间，分子自由运动的平 均路程。
平均自由程 v 1
Z 2πd 2n
19
大学物理 第三次修订本
第10章 气体动理论及热力学
利用 P nkT 得 kT
2πd 2P
T 一定时,
1
p
标况下多数气体 ~10-8m，氢气约为10-7m。 一般分子直径 d~10-10m， 故 d。
E
M
NA
i 2
kT
i RT
2
5 0.38.31 273 1.7 103 J 2
大学物理 第三次修订本
第10章 气体动理论及热力学
10.9 气体分子的平均自由程
前面讨论了气体处于平衡态的性质和一些 统计规律，在其中起关键作用的是分子间的碰 撞。不仅如此，系统由非平衡态向平衡态的转 变过程中，如热传递过程、扩散过程，气体分 子间的碰撞也起关键作用。
可求得: Z ~109/秒。每秒钟一个分子竟发 生几十亿次碰撞！
20
大学物理 第三次修订本
第10章 气体动理论及热力学
例 估计两种情况下空气分子的平均自由程。 (1) 273 K ,1.013×105pa 时;
(2)273 K ,1.333 ×10-3pa 时。

能量均分原理


分子热运动的平均动能都等于 1 k T
2
—— 能量均分定理 5
能量均分定理不仅适用于气体，也适用于液体和固体 甚至适用于任何具有统计规律的系统。
刚性理想气体分子的自由度和平均动能：
分子类型
单原子分子 双原子分子 多原子分子
平动 自由度
3
3
3
转动 自由度
0
2
3
自由度i
3 5 6
分子热运动
平均动能
3 kT 2
8
5 2
kT
6 kT 2
6
三. 理想气体热力学能（内能）
热力学能：系统内部各种动能和势能的总和。 （不包括系统整体质心运动的能量）
对理想气体：分子间没有相互作用力，势能为零
自由度为 i 的 分子平均动能
w ikT
2
N
NA
i2(N
Ak
)T i2RT
热力学能（内能）：U
N
i 2
kT
i
2RT
：气体系统的摩尔（mol）数 7
例：贮存有氮气的容器以速度100米/秒运动。若 该容器突然停止，问容器中温度将升多少？
已知： v 1 0 0 m / s i 5
M 28 103 kg / mol
求： T ?
解：氮气的宏观动能将转化为热力学能。
1 mv2 2
i 2
R(T2
T1 )
m
M
T2 T1
Mv2 iR
28103 1002 6.74(K ) 5 8.31
3
总自由度 i = 3 +3 = 6
x
4
二 . 能量均分定理
由
1 2
m
0
v

能量按自由度均分原理


2M
利用理想气体物态方程 pV m RT
M
得
E i pV
2
氧气旳内能 E i pV 5 21.013105 200103
2
2
1.013105 J
17
大学物理 第三次修订本
E NA
NA
i kT 2
i RT 2
质量为m 旳理想气体
E i m RT 2M
理想气体旳内能只是温度旳函数，与热力
学温度成正比。
11
大学物理 第三次修订本
第10章 气体动理论
四、气体旳摩尔热容
由 E i m RT 2M
内能变化 dE m i RdT M2
而
m dE M CvmdT
比较，得
Cvm
i 2
R
12
大学物理 第三次修订本
第10章 气体动理论
Cpm Cvm R
i RR i2R
2
i
得
Cpm
i
i
2
R
摩尔热容比
Cpm i 2 i 2
Cvm
i
i
13
大学物理 第三次修订本
第10章 气体动理论
例1 1mol刚性多原子分子气体（可视为理想气 体），压强为1.0atm，温度为27℃。若经过一 绝热过程，使其压强增长到16atm。试求 (1)该 过程中气体内能旳增量和对外所作旳功；(2)末
第10章 气体动理论
10.7 能量按自由度均分原理
一、自由度旳概念 自由度 拟定一种物体在空间旳位置所必需旳 独立坐标数目。
做直线运动旳质点： 一种自由度 做平面运动旳质点： 二个自由度 做空间运动旳质点： 三个自由度
1
大学物理 第三次修订本

能量按自由度均分原理

气体分子的方均根速率μ
RT
m kT v 332=
=
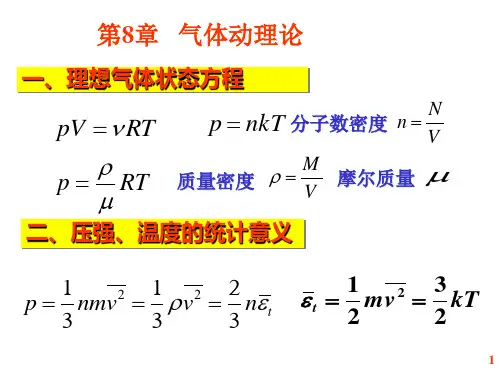
T (273K) 2H 2O 2N 空气 2v （m/s ） 1830 461 493 485 （5）压强的另一个公式
P =K n ε32=kT n 2
3
32⋅=nkT
P =nkT 理想气体状态方程的另一种表达式 比 PV=νRT 适用范围更广泛
例：推导道尔顿分压定律：混合气体压强等于各种气体分压强之和 解：设容器中有几种理想气体组成混合气体
T 相同，K K K εεε=== 21
总分子数密度 ++=21n n n P=K n ε32=K n n ε⋅++)(3221 =K n ε132+K n ε232
+ P = ++21P P
第4节 能量按自由度均分原理 理想气体内能
P =K n ε32，K ε=kT 2
3
考虑到分子结构，分子运动：平动，转动，振动
（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

可复制、编制，期待你的好评与关注）。

能量按自由度均分定理

能量按自由度均分定理能量按自由度均分定理能量按自由度均分定理是热力学的基本定理之一，它描述了一个系统中分子所具有的能量如何分布。

该定理表明，系统中每个自由度上的平均能量相等。

1. 能量和自由度在热力学中，一个系统的能量可以被划分为不同类型的能量，例如动能、势能、内能等。

而自由度则指一个分子或者原子可以在空间中运动的方向数。

例如，在三维空间中，一个粒子有三个自由度：x、y和z方向上的运动。

2. 能量按自由度均分定理的表述根据这个定理，一个系统中每个自由度上的平均能量相等。

具体而言，假设一个系统有N个粒子，每个粒子有f个自由度，则该系统总共有Nf个自由度。

如果该系统处于温度为T的热平衡状态下，则每个自由度上平均能量为：E = (1/2)kT其中k是玻尔兹曼常数。

3. 推导过程这个结论可以通过统计力学推导得出。

假设我们考虑一个单原子气体，它处于温度为T的热平衡状态下。

在这种情况下，我们可以将每个原子看作一个简谐振子，它在三个方向上都有能量。

根据统计力学，我们可以得到每个简谐振子的平均能量为：<E> = (1/2)kT因此，对于一个单原子气体而言，它的总能量就是每个原子的平均能量之和。

由于每个原子都有三个自由度（x、y、z方向），因此总共有3N个自由度。

根据能量按自由度均分定理，每个自由度上的平均能量相等，因此该系统中每个自由度上的平均能量为：E = (1/2)kT4. 应用能量按自由度均分定理在热力学中具有广泛的应用。

例如，在化学反应中，该定理可以用来预测反应物和产物之间转移的能量。

在材料科学中，该定理可以用来计算材料内部各种不同类型粒子（如电子、离子等）所占据的位置和状态。

5. 局限性虽然能量按自由度均分定理是热力学中非常重要的一个基本定理，但它也存在一些局限性。

例如，在低温下或者非常小尺寸的系统中，该定理可能不再适用。

此外，在分子之间存在相互作用的情况下，该定理也可能不再适用。

6. 结论能量按自由度均分定理是热力学中非常重要的一个基本定理，它描述了一个系统中分子所具有的能量如何分布。

能量均分定理


在重力场中气体分子的密度n随高度 的增加按指数而减小。 在重力场中气体分子的密度 随高度Z的增加按指数而减小。 随高度 的增加按指数而减小 分子的质量m越大 越大， 的减小就越迅速， 分子的质量 越大，重力的作用就越显著 ，n的减小就越迅速， 的减小就越迅速 气体的温度越高，分子的无规则运动越剧烈， 的减小就越缓 气体的温度越高，分子的无规则运动越剧烈， n的减小就越缓 慢。
鞍山科技大学 姜丽娜 8
§2.6 玻尔兹曼分布律 重力场中粒子按高度的分布 1. 玻尔兹曼分布律 玻尔兹曼把麦克斯韦速率分布律推广到气体分子在任意力 场中运动的情形 。 当气体处于平衡状态时,在一定温度下 在速度分布间隔 当气体处于平衡状态时 在一定温度下,在速度分布间隔 在一定温度下
和坐标分布间隔
鞍山科技大学 姜丽娜 5
三、理想气体的内能 问题： 问题： 1. 气体的内能包括哪些？ 气体的内能包括哪些？ 气体的内能=气体分子的总能量 气体的内能 气体分子的总能量 + 分子间相互作用势能 2. 理想气体的内能包括哪些？ 理想气体的内能包括哪些？ 理想气体的内能=所有气体分子各种运动能量的总和 理想气体的内能 所有气体分子各种运动能量的总和 3. 内能与机械能有什么区别？ 内能与机械能有什么区别？ 机械能可以为零，而内能永不为零。 机械能可以为零，而内能永不为零。 一摩尔理想气体的内能
7
);
摩尔气体分子的总转动动能( ⑷1摩尔气体分子的总转动动能 摩尔气体分子的总转动动能 摩尔气体的内能( ⑸1摩尔气体的内能 摩尔气体的内能 )。 。
鞍山科技大学 姜丽娜
3.有一个处于恒温条件下的容器 其内贮有 有一个处于恒温条件下的容器,其内贮有 某种理想气体, 有一个处于恒温条件下的容器 其内贮有1mol某种理想气体 某种理想气体 若容器发生缓慢漏气,试问容器内气体分子的平均平动动能是 若容器发生缓慢漏气 试问容器内气体分子的平均平动动能是 否改变?气体的内能是否改变 气体的内能是否改变? 否改变 气体的内能是否改变 （答案: 不变 变) 答案 不变,变 4.两个容器中分别贮有理想气体氦和氧，已知氦气的压强是氧 两个容器中分别贮有理想气体氦和氧， 两个容器中分别贮有理想气体氦和氧 气的1/2,氦气的容积是氧气的 倍。试问氦气的内能是氧气内能 氦气的容积是氧气的2倍 气的 氦气的容积是氧气的 的多少倍? 的多少倍 （答案:3 /5倍) 答案 倍 5.质量相等的的理想气体氧和氦 分别装 在两个容积相等的容 质量相等的的理想气体氧和氦,分别装 质量相等的的理想气体氧和氦 器内,在温度相同的情况下 在温度相同的情况下,氧和氦的压强之比为 ;氧 器内 在温度相同的情况下 氧和氦的压强之比为 氧 ;氧和氦内能之 氧和氦内能之 分子和氦分子的平均平动动能之比为 比为_________. 比为 (答案 1:8; 1:1; 5:24) 答案: 答案

高职高专《物理学》课程标准

《物理学》课程标准适用专业：高职电气自动化、生产过程自动化、机电一体化、应用电子技术、焊接自动化技术、检测技术、石化、分析、药分、安全、精细、应用化工技术适用学制：三制《物理学》课程标准课程名称：物理学总学时数： 88/60适用专业：高职电气自动化、生产过程自动化、机电一体化、应用电子技术、焊接自动化技术、检测技术、石化、分析、药分、安全、精细、应用化工技术一、课程定位1、课程性质公共基础课2、课程作用物理学是研究物质的基本结构、基本运动形式、相互作用的自然科学。

它的基本理论渗透在自然科学的各个领域，应用于生产技术的许多部门，是其他自然科学和工程技术的基础。

大学物理课程是高等学校理工科学生的一门重要基础课,它所阐述的物理学基本概念、基本思想、基本规律和基本方法不仅是学生学习后续专业课程的基础，而且也是培养和提高学生综合素质和科技创新能力的重要内容。

作为一名工程应用型技术人员，其物理基础的厚薄、掌握的好坏将影响到他们工作中的适应性、创造性。

二、课程设计（以能力目标指导下，基于职业教育[校企合作、工学结合、基于生产过程等]的课程整体开发设计说明）；三、课程目标1、能力目标通过众多的理想模型的建立和应用，培养学生能根据问题的性质和需要，抓住主要因素，略去次要因素，对所研究的复杂问题进行合理简化处理的能力。

注意培养学生抽象思维的能力和理论联系实际的能力．培养学生运用物理的理论、观点和方法以及所掌握的高等数学工具分析、研究、计算或估算一般难度的物理问题的能力，并能把典型数据结果在量级上加以比较，对结果的合理性做出判断。

创造条件使学生多接触各种物理现象，在教学中加强观察和实验有利于激发起学生学习物理的兴趣，而对物理学习的兴趣又能对观察能力的培养起积极作用。

培养学生的自学能力。

在整个教学过程中，应注意有计划地、循序渐进地培养学生独立阅读教材和参考书的能力，并要求学生达到理解其主要内容和写出条理较清楚的笔记、小结和心得体会。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

山东科技大学济南校区
§5.分子 动能按自由度均分的统计规律
§5. 动能按自由度均分的统计规律/二、分子自由度
三、分子动能按自由度均分的统计规律 由温度公式有分子平均平动动能 3 1 1 2 2 2 2 k mv m(vx vy vz ) kT 2 2 2
v v v
2 x 2 y
2 z
3 3 2 mvx kT 2 2 1 1 2 mvx kT 2 2
§5. 动能按自由度均分的统计规律/四、分子能量
五、气体的内能 1.一个分子的能量为:
i kT 2
2. 1 mol气体分子的能量为: i i N 0 kT RT 2 2 3. m千克气体的能量为： 气体内能
m i E RT M 2
§5. 动能按自由度均分的统计规律/四、气体能量
设计制作
干耀国
第五节 分子平均动能 按自由度均分 的统计规律
在研究气体的能量时，需要确定其物 理模型，这个物理模型就是自由度。用自 由度模型描写气体能量是有局限性的，对 少原子分子气体，在常温下理论值与实验 值符合得较好，但对多原子分子或在高温 情况下，理论值与实验值相差较大。这得 用量子物理方法进行研究。本节我们使用 自由度模型和能量均分的统计原理来研究 理想气体在常温下的气体能量。
y
3.三个或三个以上的刚性质点 需3个平动自由度和3个转动自由度。 t3 平动自由度 r3 转动自由度 总自由度 i tr 33 6
二、气体分子自由度
对于理想气体在常温下，分子内各 原子间的距离认为不变，只有平动自由 度、转动自由度。
§5. 动能按自由度均分的统计规律/二、分子自由度
§5. 动能按自由度均分的统计规律/二、分子自由度
t3 平动自由度 r2 转动自由度 i tr 32 5 总自由度 3.多原子分子气体 例如：二氧化碳气体（CO2）、水蒸气 （H2O）、甲烷气体（CH4）等为多原子 分子气体。其模型可用多个刚性质点来代 替。 t3 平动自由度 r3 转动自由度 总自由度 i tr 33 6
§5.分子动能按自由度均分的统计规律
一、什么是自由度
自由度是描写物体在空间位置所需数。 例如：物体沿一维直线运动，最少只需一 个坐标，则自由度数为1。
x
§5.分子动能按自由度均分的统计规律/一、自由度
轮船在海平面 上行驶，要描写轮 船的位置至少需要 两维坐标，则自由 度为 2。
z
P ( x , y, z )
y
§5.分子动能按自由度均分的统计规律/一、自由度
2.两个刚性质点
描写其质心位置需3个 平动自由度， t3
z
o 描写其绕x、y轴 转动需2个转动自 由度，绕z轴的转 x 动能量可不计， r2 i tr 32 5 总自由度数
§5.分子动能按自由度均分的统计规律/一、自由度
每个平动自由度上分配了一份kT/2的能量，
§5. 动能按自由度均分的统计规律/三、统计规律
由于分子的激烈碰撞（几亿次/秒）， 使平动动能与转动动能不断转换， 平动动能 转动动能
使平动动能与转动动能达到相同，即每个 转动自由度上也平均分配了kT/2能量。 由此可知，分子有 i 个自由度，其平均动 能就有i 份 kT/2 的能量。 分子平均动能
飞机在天空中 飞翔，要描写飞机 的空间位置至少需 要三维坐标，则自 由度为 3。
§5.分子动能按自由度均分的统计规律/一、自由度
但对于火车在 轨道上行驶时自由 度是多少呢？
自由度是 1，由于 受到轨道限制有一 维坐标不独立。 1. 一个质点，描写它 的空间位置，需要 3 个平动自由度， t3
o x
i kT 2
§5. 动能按自由度均分的统计规律/三、统计规律
四、气体分子的能量
=分子平均动能 + 分子与分子间的势能
+分子中原子与原子间的势能 •对于理想气体而言，分子间的作用力忽 略不计，分子与分子间的势能为 0。 •由于只考虑常温状态，分子内的原子间 的距离可认为不变，则分子内原子与原子 间的势能也可不计。 一个分子的能量为 i kT =分子平均动能 2
§5. 动能按自由度均分的统计规律/三、统计规律
1 1 2 mvx kT 2 2 即在 x 方向的自由度上平均分配了 kT / 2 的能量。 由于分子运动在哪个方向都不占优势，因 此，在 y、z 方向的自由度上也都平均分配 了 kT / 2 的能量。 1 1 1 2 2 mvy mvz kT 2 2 2
1.单原子分子气体 例如：氦气（He）、氖气（Ne）、氩气 （Ar）等为单原子分子气体。其模型可 用一个质点来代替。 t3 平动自由度 r0 转动自由度 i tr 30 3 总自由度 2.双原子分子气体 例如：氢气（H2）、氧气（O2）、氮气 （N2）等为双原子分子气体。其模型可 用两个刚性质点模型来代替。