高中数学知识点(表格格式)

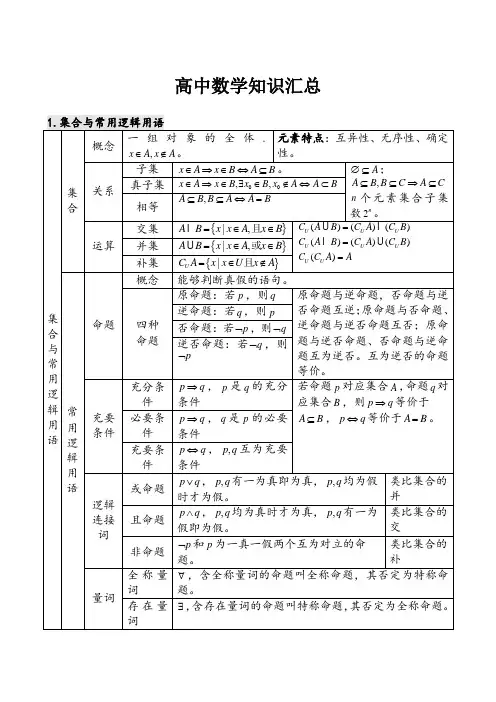
高中数学知识汇总9. 导数及其应用,n k【注：标准d 根据上下文理解为圆心到直线的距离与两圆的圆心距】注：1.表中两种形式的双曲线方程对应的渐近线方程分别为y x a =±， y x b=±。

2.表中四种形式的抛物线方程对应的准线方程分别是,,,2222p p p px x y y =-==-=。

型随机变量及其分布及其分布列分布列离散型随机变量的所有取值及取值的概率列成的表格。

性质（1）0(12)ip i n=≥L，，，；（2）121np p p+++=L。

事件的独立性条件概率概念：事件A发生的条件下，事件B发生的概率，()()()P ABP B AP A=|。

性质：0()1P B A|≤≤．,B C互斥，()()()P B C A P B A P C A=+U|||．独立事件事件A与事件B满足()()()P AB P A P B=，事件A与事件B相互独立。

n次独立重复试验每次试验中事件A发生的概率为p，在n次独立重复试验中，事件A恰好发生k次的概率为()(1)(012)k k n knP X k C p p k n-==-=L，，，，，。

典型分布超几何分布()012k n kM N MnNC CP X k kC--===L，，，，，m，其中{}minm M n=，，且n N≤，且,,,n N M N n M N*∈≤≤N，．＂二项分布分布列为：()(1)(012)k k n knP X k C p p k n-==-=L，，，，，，~()X B n p，。

数学期望EX np=、方差(1)DX np p=-【1n=时为两点分布】正态分布22()21()2πxax eμϕσ--=图象称为正态密度曲线，随机变量X满足()()baP a X b x dxϕ<=⎰≤，则称X的分布为正态分布．正态密度曲线的特点。

数字特征数学期望1122i i n nEX x p x p x p x p=+++++L L()E aX b aEX b+=+方差和标准差方差：21()ni iiDX x EX p==-∑，标准差：X DXσ=2()D aX b a DX+=23. 函数与方程思想,数学结合思想排序不等式设1212,n n a a a b b b ≤≤≤≤≤≤L L 为两组实数，12,,,n c c c L 是12,,,n b b b L 的任意排列， 则121111221122n n n n n n n a b a b a b a c a c a c a b a b a b -+++≤+++≤+++L L L 14444244443144424443144424443反序和乱序和顺序和， 当且仅当12n a a a ===L 或12n b b b ===L 时反序和等于顺序和。

高考数学回归知识必备
n 个元素集合子集数2)()()U U B C A C B =
)U A A =
{|x B ={|U x x A =能够判断真假的语句。

原命题：若p 原命题与逆命题，否命题与逆否命题互逆；原命题与否命题、逆命题与逆否命逆命题：若q ,,)b c d ∈R
←−−−
→一一对应
复平面内的点向量OZ 向量OZ 的模叫做复数的模，
投影
cos b θ叫做在a 方向上的投影。

一般表示,a b （b ≠112212(,)(,)x y x y x y x λ=⇔=a b +的平行四边形法则、三角形法则。

()(a b c a ++=+a b -的三角形法则。

MN (N M MN x x =-a λ⋅为向量，0λ>与a 方向相同， 与a 方向相反，a a λ=。

(,a x λλ=a )λμ，a a λμλ=+)(b a λλ++(
cos ,a b a b a b =⋅<>
2
a a =，a
b a b ≤⋅。

2a x y =+2121y y x ≤+
b a =，()a b
c a c +=+()()()a b a b a b λλλ==。

与上面的数量积、数乘等具有同样
n m 种不同的方法个元素的组合数，用符号1)
(!
n m m -+11
n n a C a b -+1+；n n n C C C C ++++ 241123
n -
)()g x ⎦⎣复合函数求导法则[](())''(())'()y f g x f g x g x ==大值中的最大者，最小值和区间端点和区间内的极小值中的最小者。

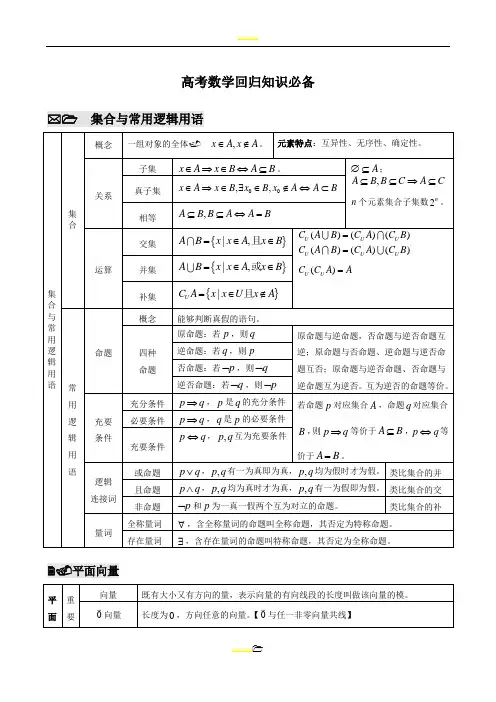
高考数学回归知识必备✉ 集合与常用逻辑用语)()()U U B C A C B =)U A A ={|x B x ={|U x x A =能够判断真假的语句。

原命题：若p 平面向量cos b 12e e μ+。

若为,x y 轴上的单位正交向量，(,)λμ就是向量a 的坐标。

坐标表示（向量坐标上下文理解）存在唯一实数λ，a b a ⊥⇔的平行四边形法则、三角形法则。

a +，()a b c a ++=+a b -1(a b x -=-MN ON OM =-。

为向量，0λ>与与a 方向相反，a a λλ=。

a )()λμ=，a a λ+=)b a b a λλλ+=+)(与数乘运算有同样的坐标表示。

cos a b =⋅122a a =，ab a b ≤⋅。

2a x =+2121y y x ≤+b a =，()a bc a c b c +=+，✉不等式、线性规划✉函数﹑基本初等函数✋的图像与性质✉ 函数与方程﹑函数模型及其应用✉✉ 三角函数的图像与性质✉ 三角恒等变换与解三角形sin sin αβtan tan 1tan tan αβα±sin c C=。

2sin R B =✉ 等差数列﹑等比数列✉ 数列求和及其数列的简单应用=12n-++(136==(12)2n n =+++=⎢⎥⎣⎦。

knn n kC C ++++。

基本特征是指数增长，常见的是增产率问题、存款复利问题。

注：表中,n k 均为正整数✉空间几何体（其中r 为半径、h 为高、l 为母线等）S h')S S h +h 底高S h✉空间点、直线、平面位置关系（大写字母表点、小写字母表直线、希腊字母表平面）：c ⇒a 共面和异面。

共面为相交和平行。

不同在任何一个平面内的两条直线称为异面直线。

,B αα∉。

α β，αβ=判定定理,,//a b a αα⊄⊂线线平行⇒线面平行b αβ=⇒⇒线线平行a b P =⎫⇒⎬⎭⇒面面平行,//a b a αγβ==⇒面面平行⇒线线平行m n P =⎫⇒⎬⎭⇒线面垂直a a b αα⊥⎫⇒⎬⊥⎭b 线线垂直⇒ααβ⇒⊥⇒,l a αβ=⊂面面垂直⇒✉ 空间向量与立体几何不共线）共面⇔存在实数对,,a b c 不共面，空间任意向量存在唯一的(,,)x y z ，使所在直线与已知直线l 平行或者重合的非零向量叫做直线l 的方向向量。

高中数学知识汇总n 个元素集合子集数2)()()U U B C A C B =)U A A ={|x B x ={|U x x A =能够判断真假的语句。

原命题：若p 原命题与逆命题，否命题与逆否命题互逆；原命题与否命题、逆命题与逆否命逆命题：若q 否命题：若⌝←−−−→一一对应复平面内的点向量OZ 向量OZ 的模叫做复数的模，di，则首先要进行分母实数化（分母乘以自己的共轭复数），在进行四则运算时，可以把字母，按照实数的四则运算律直接进行运算，并随时把投影cos b 在a 方向上的投影。

2为,x y 轴上一般表示,a b （0b ≠12(,)(,)x y x y x y x λ=⇔=a b +的平行四边形法则、三角形法则。

()(a b c a ++=+a b -的三角形法则。

MN (N M MN x x =-a λ⋅为向量，0λ>与a 方向相同， 与a 方向相反，a a λ=。

(,a x λλ=a )λμ，a a λμλ=+)(b a λλ++(cos ,a b a b a b =⋅<>2a a =，ab a b ≤⋅。

2a x y =+2121y y x ≤+b a =，()ac a c +=+()()()a b a b a b λλλ==。

与上面的数量积、数乘等具有同样4.算法、推理与证明圆的方程 圆心x 2+ y 2= r 2（0，6.计数原理与二项式定理n m 种不同的方法个元素的组合，所有不同组合的个数，叫做从!m 11n n a C a b -+11++；n n n C C C C 210++++ 8. 函数与方程﹑函数模型及其应用9. 导数及其应用)()g x ⎦⎣复合函数求导法则[](())''(())'()y f g x f g x g x ==()10. 三角函数的图像与性质11. 三角恒等变换与解三角形sin sin αβtan tan 1tan tan αβα±sin c C=。

高考数学知识必备n 个元素集合子集数2{|x B x =)()()U U A B C A C B = )()()U U B C A C B =)U A A ={|x B x ={|U x x A =能够判断真假的语句。

原命题：若p 原命题与逆命题，否命题与逆否命题互逆；原命题与否命题、逆命题与逆否命题互否；原命题与逆否命题、否命题与逆命题互为逆否。

互为逆否的命题等价。

逆命题：若q 否命题：若⌝逆否命题：若q ⇒，p 是,,)b c d ∈R←−−−→一一对应复平面内的点向量OZ 向量OZ 的模叫做复数的模，向量既有大小又有方向的量，表示向量的有向线段的长度叫做该向量的模。

0向量0与任一非零向量共线】平行向量 方向相同或者相反的两个非零向量叫做平行向量，也叫共线向量。

向量夹角 起点放在一点的两向量所成的角，范围是[,a b 的夹角记为,a b >。

投影,a b θ<>=，cos b θ叫做b 在a 方向上的投影。

【注意：投影是数量】基本定理12,e e 不共线，存在唯一的实数对(,)λμ，使12a e e λμ=+。

若12,e e 为,x y 轴上的单位正交向量，(,)λμ就是向量a 的坐标。

一般表示坐标表示（向量坐标上下文理解）,a b （0b ≠共线⇔存在唯一实数λ，a b λ=112212(,)(,)x y x y x y x λ=⇔=0a b a b ⊥⇔=。

11220x y x y +=。

a b +的平行四边形法则、三角形法则。

1(,)a b x x y y +=++。

a b b a +=+，()()a b c a b c ++=++与加法运算有同样的坐标表示。

a b -的三角形法则。

1(a b x x -=-MN ON OM =-。

(N M MN x x =-a λ⋅为向量，0λ>与a 方向相同， 0λ<与a 方向相反，a a λλ=。

(,a x y λλλ=a a )()(λμμ=，a a a μλμλ+=+)(，b a b a λλλ+=+)(与数乘运算有同样的坐标表示。

高考数学知识点归纳总结表一、代数部分1. 一次函数- 定义与性质- 直线图象与斜率- 解一次方程与不等式- 应用问题2. 二次函数- 定义与性质- 平移与伸缩- 求解二次方程与不等式- 抛物线图象与最值- 应用问题3. 绝对值与不等式- 定义与性质- 解绝对值方程与不等式- 绝对值函数与图象- 应用问题4. 等比数列- 定义与性质- 通项与求和公式- 应用问题5. 三角函数- 弧度与角度的转换- 正弦、余弦、正切函数- 特殊角的值与图象- 解三角函数方程与不等式 - 应用问题6. 指数与对数- 定义与性质- 指数函数与对数函数的图象 - 指数方程与对数方程- 应用问题二、几何部分1. 平面几何- 点、线、面的基本概念- 形状与性质：三角形、四边形、多边形、圆等 - 平行、垂直、相似、全等等关系- 面积与周长计算2. 空间几何- 直线、平面与空间的关系- 空间中的直线相交关系- 空间几何体的形状与性质：球、柱、锥等- 体积与表面积计算3. 三角关系- 同角三角比- 正弦定理、余弦定理与正弦定理的应用- 直角三角形的特殊关系与性质4. 解析几何- 平面直角坐标系- 点、直线、圆的方程- 直线与圆的位置关系三、概率与统计部分1. 概率基础- 随机事件与样本空间- 概率的定义与性质- 古典概型与几何概型2. 排列与组合- Permutation与Combination- 应用问题3. 统计与数据分析- 数据收集与整理- 数据的表示与分析：频率分布表、频率直方图等 - 平均数、中位数、众数的计算与应用四、三角函数部分1. 基本概念与关系- 弧度与角度的关系- 正弦、余弦、正切的定义与关系- 同角三角比2. 特殊角的计算- 30°、45°、60°及其倍角的值计算- 特殊角的简化3. 解三角函数方程与不等式- 基本解与普通解- 解三角函数方程与不等式的步骤与技巧以上是高考数学知识点的归纳总结表，包括代数部分、几何部分、概率与统计部分以及三角函数部分。

高中数学知识汇总6.计数原理与二项式定理16. 空间向量与立体几何注：1.表中两种形式的双曲线方程对应的渐近线方程分别为y x a =±， y x b=±。

2.表中四种形式的抛物线方程对应的准线方程分别是,,,2222p p p p x x y y =-==-=。

21.离散型随机变量及其分布等式柯西不等式二维形式()()()()22222,,,ab c d ac bd a b c d ++≥+∈R ，等号当且仅当ad bc =时成立。

向量形式α,β是两个向量，则⋅≤αβαβ，当且仅当β是零向量或存在实数k ，使k =αβ时，等号成立。

一般形式()22211n n b a b a b a +++Λ()()222221222221n n b b b a a a ++++++≤ΛΛ()n i R b a i i Λ2,1,=∈等号当且仅当021====n a a a Λ或i i ka b =时成立（k 为常数，n i Λ2,1=）。

排序不等式 设1212,n n a a a b b b ≤≤≤≤≤≤L L 为两组实数，12,,,n c c c L 是12,,,n b b b L 的任意排列，则121111221122n n n n n n n a b a b a b a c a c a c a b a b a b -+++≤+++≤+++L L L 14444244443144424443144424443反序和乱序和顺序和，当且仅当12n a a a ===L 或12n b b b ===L 时反序和等于顺序和。

证明方法比较法 作差和作商比较综合法 根据已知条件、不等式的性质、基本不等式，通过逻辑推理导出结论 分析法 执果索因的证明方法 反证法 反设结论，导出矛盾放缩法通过把不等式中的部分值放大或缩小的证明方法数学归纳法 证明与正整数有关的不等式。

27.二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：判别式24b ac ∆=-0∆> 0∆= 0∆<二次函数2y ax bx c =++()0a >的图象一元二次方程20ax bx c ++=()0a >的根有两个相异实数根1,22b x a-±∆=()12x x <有两个相等实数根122b x x a==-没有实数根。

高考数学基础知识点归纳总结表1. 代数
- 代数表达式
- 方程与不等式
- 函数与图像
- 数列与数列的通项公式
2. 几何
- 基本几何概念
- 直线与曲线
- 三角形与三角函数
- 圆与圆相关的性质
3. 概率与统计
- 随机事件
- 概率的计算
- 统计与数据分析
- 概率与统计的应用
4. 解析几何
- 平面直角坐标系
- 直线与曲线的方程
- 二次曲线
- 空间坐标系与空间几何图形5. 三角函数
- 三角函数的定义和基本性质 - 三角函数的图像与性质
- 三角函数的运算与应用
- 三角恒等变换与解三角形6. 数列与数学归纳法
- 数列与数列的通项公式
- 等差数列与等比数列
- 数学归纳法的原理与应用 - 递推关系与递归方程
7. 数与数量关系
- 实数与复数
- 数的性质与运算
- 数量关系的表示与求解
- 数与数量关系在实际问题中的应用8. 导数与微分
- 导数的概念与定义
- 基本导数公式与常见函数导数
- 高阶导数与导数的应用
- 微分与微分近似
9. 不等式与极值
- 不等式的性质与解法
- 一元不等式组的解法
- 函数的极值与最优问题
- 不等式与极值问题的应用
10. 指数与对数
- 指数函数与对数函数
- 指数与对数的性质与运算
- 指数方程与对数方程的解法
- 指数与对数在实际问题中的应用
以上是高考数学基础知识点的归纳总结表。

希望对你的学习有所帮助。

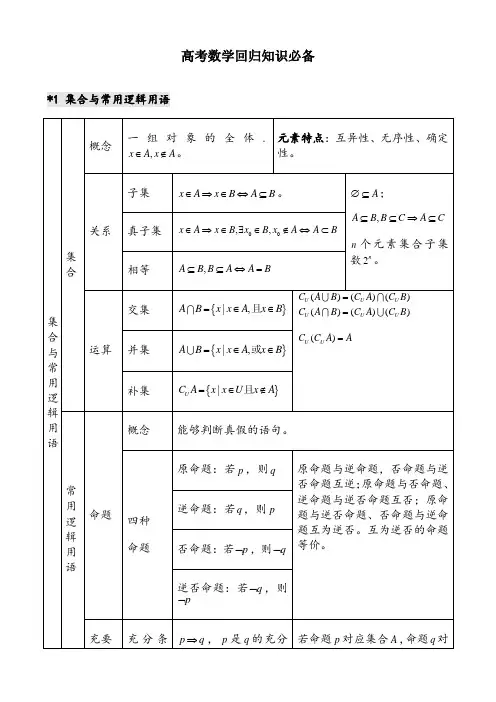
高考数学回归知识必备*1 集合与常用逻辑用语)()()U U B C A C B = )U A A ={|x B x ={|U x x A =2.平面向量平行向量方向相同或者相反的两个非零向量叫做平行向量，也叫共线b θ>=，cos b 【注意：投影是数一般表示坐标表示（向量坐标上下文0a b a b ⊥⇔=。

a b +的平行四边形法则、三角形法则。

与加法运算有同样的坐标a b -的三角形法则。

a -MN ON OM =-(N MN x x =-a λ⋅为向量，0λ>(,a x λλ=a aλ=。

cosa b=⋅2a=b a b≤⋅。

2a x y=+ *3.不等式、线性规划*4.函数﹑基本初等函数I的图像与性质*5. 函数与方程﹑函数模型及其应用**6. 三角函数的图像与性质*7. 三角恒等变换与解三角形sin sin αβtan tan 1tan tan αβα±sin c C=。

*8. 等差数列﹑等比数列)n型*9. 数列求和及其数列的简单应用=(136==2⎢⎣。

knn n kC C ++++。

注：表中,n k均为正整数*10.空间几何体（其中r为半径、h为高、l为母线等）S hS h''S S ++*11.空间点、直线、平面位置关系（大写字母表点、小写字母表直线、希腊字母表平面）：个公共点。

α∥β，αβ公共点。

bαβ=⇒线线平行a b P=⎫⇒⎬⎭面面平行,//a b a αγβ==⇒⇒线线平行m n P=⎫⇒⎬⎭线面垂直,l aαβ=⊂面面垂直⇒线面垂直*12. 空间向量与立体几何存在唯一实数λ，aλ=p与,a b、（,a b存在实数对xa b c不共面，空间任意向量,,=++。

p xa yb zc所在直线与已知直线平行或者重合的非零向量线l的方向向量。

叫做平面α的b 。

a ，平面的法向量为n ，sin n θ。

两平面的法向量分别为1n 和12cos n θ=。

最新高中数学知识点汇总(表格格式)高中数学知识汇总)()()UUB C A C B = )UA A = {|xB x ={|Ux x A =能够判断真假的语句。

原命题：若←−−−→一一对应复平面内的点向量OZ 向量OZ 的模叫做复数的模，di，则首先要进行分母实数化（分母乘以自己的共轭复数），在进行四则运算时，可以把字母，按照实数的四则运算律直接进行运算，并随时把的夹角记为cos b 叫做意：投影是数量】2,e 不共线，存在唯一的实数对(,)λμ就是向量一般表示 a b a b ⊥⇔的平行四边形法则、三角形法则。

b b a +=+，的坐标表示。

a b -的三角形法则。

MN =(,N M MN x x =-相同，a λ=a aλ=。

b a b λλ+=+) cos a b =⋅2a =b a b ≤⋅。

2a x y =+圆的方程 圆心x 2+ y 2= r 2（!m()()g x⎦复合函数求导法则[],n ），()lim nbb f x dx =∑⎰()f x 是sin sin αβtan tan 1tan tan αβα±sin c C=。

13. 数列求和及其数列的简单应用===(136⎢⎣2基本特征是均匀增加或者减少。

注：表中,n k 均为正整数S h')S S h+'0S =↓ S hh ')S S h+15.空间点、直线、平面位置关系（大写字母表点、小写字母表直线、希腊字母表平面）：∥c⇒a∥公共点、无数个公共点。

α∥β，α平面有无数个公共点。

判定定理bβ=⇒线面平行⇒线线平行a b P=⎫⇒⎬⎭线面平行⇒面面平行,//a b aαγβ==⇒面面平行⇒线线平行m n P=⎫⇒⎬⎭⇒线面垂直aabαα⊥⎫⇒⎬⊥⎭∥bαβ=⊂,l a 面面垂直⇒特殊情况λ，a b λ=。

p与,a b 、（,a b ，使,,a b c 不共面，空间任意向量，使p xa yb zc =++。

高中数学知识汇总1.集合与常用逻辑用语集合与常用逻辑用语 集合概念 一组对象的全体. ,x A x A ∈∉。

元素特点：互异性、无序性、确定性。

关系子集 x A x B A B ∈⇒∈⇔⊆。

A ∅⊆； ,AB BC A C ⊆⊆⇒⊆n 个元素集合子集数2n 。

真子集 00,,x A x B x B x A A B ∈⇒∈∃∈∉⇔⊂ 相等 ,A B B A A B ⊆⊆⇔=运算交集 {}|,x x B x B A A ∈∈=且 ()()()U U U C A B C A C B = ()()()U U U C A B C A C B =()U U C C A A =并集 {}|,x x B x B A A ∈∈=或 补集 {}|U x x U C A x A ∈=∉且常用逻辑用语命题概念能够判断真假的语句。

四种 命题 原命题：若p ，则q 原命题与逆命题，否命题与逆否命题互逆；原命题与否命题、逆命题与逆否命题互否；原命题与逆否命题、否命题与逆命题互为逆否。

互为逆否的命题等价。

逆命题：若q ，则p 否命题：若p ⌝，则q ⌝ 逆否命题：若q ⌝，则p ⌝充要条件充分条件p q ⇒，p 是q 的充分条件 若命题p 对应集合A ，命题q 对应集合B ，则p q ⇒等价于A B ⊆，p q ⇔等价于A B =。

必要条件 p q ⇒，q 是p 的必要条件 充要条件 p q ⇔，,p q 互为充要条件 逻辑连接词或命题p q ∨，,p q 有一为真即为真，,p q 均为假时才为假。

类比集合的并 且命题p q ∧，,p q 均为真时才为真，,p q 有一为假即为假。

类比集合的交 非命题p ⌝和p 为一真一假两个互为对立的命题。

类比集合的补 量词全称量词 ∀，含全称量词的命题叫全称命题，其否定为特称命题。

存在量词 ∃，含存在量词的命题叫特称命题，其否定为全称命题。

2.复数复数概念 虚数单位规定：21i =-；实数可以与它进行四则运算，并且运算时原有的加、乘运算律仍成立。