410a热力性质表

常见制冷剂的热力性质目录R-134a 四氟乙烷制冷剂 (2)R-404A(Suva HP62) 制冷剂 (4)R-407C 制冷剂 (5)R-410A 制冷剂 (7)R-417A（ISCEON MO59）环保制冷剂 (9)F-11 一氟三氯甲烷制冷剂/发泡剂 (13)R-12 二氟二氯甲烷制冷剂 (14)R-13 三氟一氯甲烷制冷剂 (15)R-13 三氟一氯甲烷制冷剂 (16)R-23 三氟甲烷制冷剂 (17)R-22 二氟一氯甲烷制冷剂 (19)R-123 三氟二氯乙烷制冷剂 (20)R-124一氯四氟乙烷制冷剂 (22)HCFC-142b 二氟一氯乙烷制冷剂 (23)R-502 制冷剂 (24)R-503 制冷剂 (25)R-507 制冷剂 (26)R-508A 制冷剂 (27)杜邦DuPontTM 制冷剂—ISCEON? MO89 制冷剂 (29)R-134a 四氟乙烷制冷剂HFC-134a 化学名：1,1,1,2-- 四氟乙烷，分子组成：CH2FCF3，CAS 注册号：811-97-2，分子量：102.0，HFC 型制冷剂，ODP 值为零。

HFC-134a 可用在目前使用CFC-12( 二氯二氟甲烷) 的许多领域，包括：制冷，聚合物发泡和气雾剂产品。

但是，为使HFC-134a 在这些领域达到最佳性能，有时需要设备设计改变。

由于HFC-134a 的低毒和不易燃性，它被研制用于药物吸入剂的载体。

HFC-134a 也可用于那些对毒性和可燃性要求严格的气雾剂中。

HFC-134a 的热力和物理性质，以及其低毒性，使之成为一种非常有效和安全的替代品，用以替代制冷工业中使用的CFC-12 。

HFC-134a 主要用在汽车空调、家用电器、小型固定制冷设备、超级市场的中温制冷、工商业的制冷机。

压缩机生产商通常建议使用POE （Polyol Ester）多元醇酯和PAG （Polyalkylene Glycol）聚二醇（汽车空调）冷冻机油。

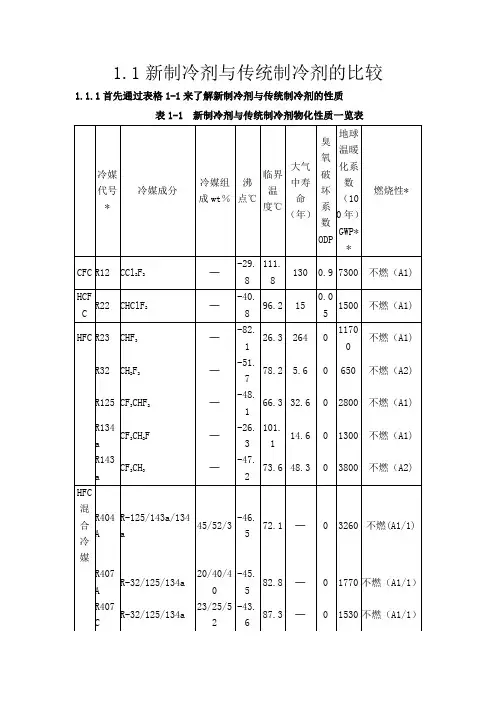
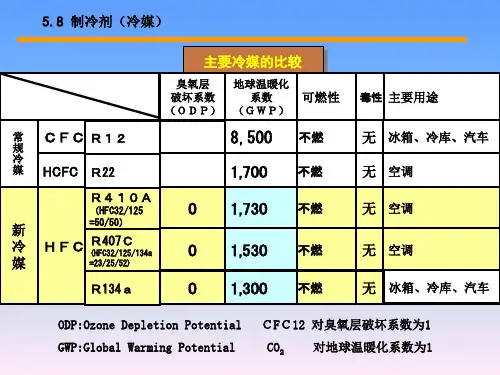
1.1新制冷剂与传统制冷剂的比较1.1.1首先通过表格1-1来了解新制冷剂与传统制冷剂的性质表1-1 新制冷剂与传统制冷剂物化性质一览表*:ASHRAE standard 34，**:IPCC-1995(累计时间100年)从上面的表格我们可以分析得出，从分子组成来分，制冷剂可以分为几种：1)CFC，以R12为典型代表，它的分子组成有C、F、Cl，其中Cl离子会与大气平流层中能吸收太阳紫外线辐射的臭氧层中的O3相结合，使O3分解成O2，失去抵挡辐射的功能，因此这种制冷剂虽然制冷能力高，但是考虑到环保，目前已经被禁止使用。

2)HCFC，以R22为典型代表，它的分子组成有H、C、F、Cl，尽管它比R-12对臭氧层的破坏小17倍，地球暖化系数小3.7倍左右，但是制冷能力小了很多，而且毕竟对环境还有一定的影响，因此也被逐步禁用。

3)HFC，主要的代表有R23、R32、R125、R134a、R143a，它们的分子组成有H、C、F，由于没有Cl离子，因此可以达到环保的要求。

4)HFC混合制冷剂，主要代表有R404、R407A、R407C、R410A、R507C等，它们是由两种或两种以上的HCF制冷剂混合而成，特点是制冷能力比HFC 单质制冷剂的制冷能力好得多，而且还能达到环保要求，因此是一种目前正在努力开发的制冷剂。

5)HC，主要代表有丙烷、异丁烷，它们最大的缺点是可燃，对于有高压而且有电气系统的空调器来说，从安全角度考虑是不会最起码是很少采用这种制冷剂的。

通过对制冷剂的分类，我们可以找准HFC及其混合物类制冷剂作为环保冷媒机型的突破口，但是在这个范围内选择哪一个制冷剂作为最佳选择有待我们下一步对他们的性质进行比较，以下就是我们将HFC制冷剂与R22进行比较。

表1-2 R22与HFC制冷剂的比较注：EER比（压缩机排气容积相同）、COP比冷凝压力比为NIST的理论循环计算值蒸发温度0℃过热度5℃冷凝温度50℃过冷度5℃分析表1-2我们可以得出：在制冷与制热综合性能上，只有R32、R407C和R410A能与R22基本持平。

R410A和R407C热力性质简化计算论文作者：沈宇纲黄冬平张春路丁国良摘要：采用隐式三次多项式拟合了R22主要替代工质R410A和R407C的热力性质,给出了形式统一的制冷剂热力性质简化模型,分析了隐式拟合过程中出现的分岔问题并提出了解决方法,从而进一步完善了模型的一致性和稳定性。

与参考模型比较,该模型在饱和区的相对误差绝对值的最大值为0.19，平均误差为0.07，过热区的相对误差绝对值的最大值为0.61，平均误差为0.18，算速度平均提高一个数量级,适用于基于计算机辅助设计的产品设计和优化计算。

关键词：制冷剂R410A R407C 热力性质制冷空调行业的各种探索和研究表明,混合工质在制冷工质替代中具有很大的潜力,其中R4 10A和R407C作为R22的替代物更是倍受瞩目.为了更好地研究它们对现有制冷系统的影响,计算机仿真是个很好的手段.而热物性程序作为仿真程序的基础部分,对仿真计算的效率和结果有相当的影响.但国内在这方面的研究很少,一般直接采用复杂的状态方程进行迭代计算,这样在相当程度上降低了仿真的速度和稳定性.为了弥补这一不足,本文采用隐式拟合显式计算的方法,参照DuPont公司的数据,对R410A和R407C的热力性质重新拟合,结果可以避免迭代,在显著提高计算速度的同时又能保证所需的精度.1 拟合模型本文对根据文献[1,2]编制的热力性质程序进行简化,并以该热力性质程序作为拟合的参考数据源和检验简化热力性质的相对精度.饱和热力性质的简化模型采用了文献[3]提出的拟合函数形式:对于过热区的热力性质,文献[4]没能给出形式完全统一的拟合函数.作者统一了过热区简化模型的形式,以便拟合和降低模型的复杂性,具体形式:简化模型是在常用的制冷空调运行工况内进行简化,在饱和区-40～60°C和过热区-4 0～120°C内保证精度,在温度外推20°C范围内保证变化趋势,以确保仿真计算的正确进行.2 隐式拟合的分岔问题和解决方法隐式拟合的最大问题就是分岔问题.在隐式拟合方程向显式的计算方程转化时,涉及到根的判别问题.三次方程涉及到3个根,分别代表了不同的根轨迹.但最后需要的可能是其中一条或多条根轨迹组合而成.然而根轨迹的衔接处会出现很小的断裂,这便是分岔现象.断裂处称为分岔点,它造成曲线不连续(分岔点处误差大)和曲线不光滑(分岔点处一阶导数不连续).虽然分岔点的范围很小,在大部分情况下对制冷系统的仿真模型不会产生大的影响,但却是个巨大的隐患(可能导致仿真模型计算值的异常).通过一系列的尝试,在不改变模型的前提下提出一种解决方法:通过改变拟合数据来调整拟合过程,把分岔点移出拟合范围,同时保证拟合精度.这一方法的数学原理是通过改变拟合数据点可以改变拟合函数的曲率.因此,只要令拟合函数在拟合范围内曲率变化减小,就可使分岔点(即曲率变化最大的点)外移.通过这种方法建立的模型在拟合范围内没有分岔问题,少数模型在外推范围内有分岔,但这对常见制冷空调工况范围内的系统仿真没有影响.具体方法:1改变拟合范围,通常是扩大拟合范围以保证拟合范围内的精度;2改变拟合的点数,大部分情况是减少点数;3用非均匀的数据点拟合(增加某区域内数据个数).相比之下,1对分岔点的位置影响最大,3则最小.从目前情况看,拟合数据范围、点数和分布的选择对不同的热力参数是不同的,在很大程度上取决于经验.3 拟合结果与计算速度比较拟合结果如表1～3所示.在表1和表3中,e1和e*1分别为在拟合范围和外推范围内,已知温度T,利用函数f(x,T)求物性x时最大相对误差的绝对值;e2和e*2分别为在拟合范围和外推范围内,已知物性x,利用函数f(x,T)求温度T时最大相对误差的绝对值;表中的T0和x0为实际拟合范围的左边界;对于x为防止拟合系数过大或过小而导致的计算困难,本文没有直接采用基本国际单位,而是采取一定的缩放比例,缩放比例在单位一栏中示出,例如表1中ρL的单位为(×103kg/m3),这说明表中系数是ρL在乘以10-3后拟合的后果.下标v 表示饱和蒸汽,L表示饱和液体.在表2中,e1和e*1分别为在拟合范围和外推范围内,已知压力p和温度T,求过热气体比容v、焓值h或熵值s时最大相对误差的绝对值;e2和e*2分别为在拟合范围和外推范围内,已知压力p和过热气体比容v、焓值h或熵值s,求过热气体温度T时最大相对误差的绝对值.表4为简化模型和参考模型的计算速度结果比较.为了突出简化模型的优越性,故对于精确模型中没有迭代计算的函数不予比较,而只选出一些比较典型的函数来比较.为了准确地测量计算速度,每个函数都调用了上万次,最后得出每调用一次所需的平均时间,由表可见,简化模型在速度方面的优势非常明显.4 结论建立的R410A和R407C的简化热物性模型与参考物性比较,在饱和区的相对误差绝对值的最大值是0.19%、平均误差为0.07%;在过热区的相对误差绝对值的最大值是0.61%、平均误差为0.18%.由于采用了隐式拟合的方法,同时在拟合范围内避免了分岔点,故简化模型在各方面都能表现良好,特别是因避免了迭代计算而大大提高了计算速度,同时也确保了计算的稳定性.参考文献[1] Thermodynam ic properties of Suva 9100 refrigerant(R410A) [R]. DuPont Technical Inform ation,1996.[2] Thermodynamic properties of Suva 9000refrigerant(R407C) [R].DuPont Technicalnform ation,1995.[3] 张春路,丁国良,李灏.制冷剂饱和热力性质的隐式拟合方法[J].工程热物理学报,1999,20(6):673～676.[4] 张春路,丁国良,李灏.制冷剂过热气体热力性质的隐式拟合方法[A].中国工程热物理学会工程热力学与能源利用学术年会论文集[C].镇江,1999. 91～95.。