1.3算法案例1

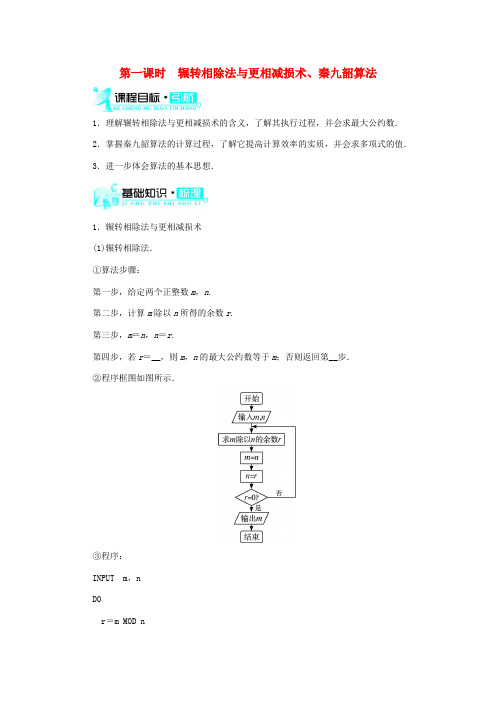
第一课时辗转相除法与更相减损术、秦九韶算法1．理解辗转相除法与更相减损术的含义，了解其执行过程，并会求最大公约数．2．掌握秦九韶算法的计算过程，了解它提高计算效率的实质，并会求多项式的值．3．进一步体会算法的基本思想．1．辗转相除法与更相减损术(1)辗转相除法．①算法步骤：第一步，给定两个正整数m，n.第二步，计算m除以n所得的余数r.第三步，m＝n，n＝r.第四步，若r＝__，则m，n的最大公约数等于m；否则返回第__步．②程序框图如图所示．③程序：INPUT m，nDOr＝m MOD nm＝nn＝rLOOP UNTIL ____PRINT __END(2)更相减损术．算法分析：第一步，任意给定两个正整数，判断它们是否都是____．若是，用__约简；若不是，执行第二步．第二步，以较大的数__去较小的数，接着把所得的差与较小的数比较，并以__数减__数．继续这个操作，直到所得的差与减数相等为止，则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数．【做一做1】用更相减损术求294和84的最大公约数时，第一步是__________．2．秦九韶算法(1)概念：求多项式f(x)＝a n x n＋a n－1x n－1＋…＋a1x＋a0的值时，常用秦九韶算法，这种算法的运算次数较少，是多项式求值比较先进的算法，其实质是转化为求n个____多项式的值，共进行__次乘法运算和__次加法运算．其过程是：改写多项式为：f(x)＝a n x n＋a n－1x n－1＋…＋a1x＋a0＝(a n x n－1＋a n－1x n－2＋…＋a1)x＋a0＝((a n x n－2＋a n－1x n－3＋…＋a2)x＋a1)x＋a0＝…＝(…((a n x＋a n－1)x＋a n－2)x＋…＋a1)x＋a0.设v1＝__________，v2＝v1x＋a n－2，v3＝v2x＋a n－3，…，v n＝____________.(2)算法步骤：第一步，输入多项式的次数n、最高次项的系数a n和x的值．第二步，将v的值初始化为a n，将i的值初始化为n－1.第三步，输入i次项的系数a i.第四步，v＝vx＋a i，i＝____.第五步，判断i是否大于或等于__．若是，则返回第三步；否则，输出多项式的值__．(3)程序框图如图所示．(4)程序：INPUT “n＝”；nINPUT “an＝”；aINPUT “x＝”；xv＝ai＝n－1WHILE ______PRINT “i＝”；iINPUT “ai＝”；av＝________i＝i－1WENDPRINT __ END【做一做2】 设计程序框图，用秦九韶算法求多项式的值，所选用的结构是( ) A ．顺序结构B ．条件结构C ．循环结构D ．以上都有答案：1．(1)①0 二 ③r ＝0 m (2)偶数 2 减 大 小 【做一做1】 用2约简 由于294和84都是偶数，先用2约简．2．(1)一次 n n a n x ＋a n －1 v n －1x ＋a 0 (2)i －1 0 v (4)i ＞＝0 v x ＋a v 【做一做2】D1．更相减损术与辗转相除法的区别与联系 剖析：如表所示．辗转相除法更相减损术区别①以除法为主．②两个整数差值较大时运算次数较少．③相除余数为零时得结果. ①以减法为主．②两个整数的差值较大时，运算次数较多． ③相减，差与减数相等得结果． ④相减前要做是否都是偶数的判断.联系 ①都是求最大公约数的方法．②二者的实质都是递归的过程．③二者都要用循环结构来实现. 2．秦九韶算法是比较先进的算法剖析：计算机的最重要特点就是运算速度快.2003年2月26日，以色列科学家宣布研制出一台依靠DNA 运行、速度达每秒运算330万亿次的生物计算机．这种计算机的运算速度比现在普通计算机的运算速度要快10万倍，但是即便如此，计算机也不是万能的．同一个问题有多种算法，如果某个算法比其他算法的步骤少，运算的次数少，那么这个算法就是比较先进的算法．算法好坏的一个重要标志就是运算的次数越少越好．求多项式f (x )＝a n x n＋a n －1xn －1＋…＋a 1x ＋a 0的值时，通常是先计算a n x n，进行n 次乘法运算；再计算a n －1xn －1，进行n －1次乘法运算；这样继续下去共进行n ＋n －1＋…＋2＋1＝n n ＋12(其计算方法以后学习)次乘法运算，还需要进行n 次加法运算，总共进行n n ＋12＋n 次运算．但是用秦九韶算法时，改写多项式为f (x )＝a n x n ＋a n －1x n －1＋…＋a 1x ＋a 0＝(a n xn －1＋a n －1xn －2＋…＋a 1)x ＋a 0 ＝((a n x n －2＋a n －1xn －3＋…＋a 2)x ＋a 1)x ＋a 0…＝(…((a n x ＋a n －1)x ＋…＋a 2)x ＋a 1)x ＋a 0.先计算v 1＝a n x ＋a n －1，需1次乘法运算，1次加法运算；v 2＝v 1x ＋a n －2，需1次乘法运算，1次加法运算；…v n ＝v n －1x ＋a 0，需1次乘法运算，1次加法运算．所以需进行n 次乘法运算，n 次加法运算，共进行2n 次运算． 由于⎣⎢⎡⎦⎥⎤n n ＋12＋n －2n ＝n n －12≥0，则n n ＋12＋n ≥2n .因此说秦九韶算法与其他算法相比运算次数少，秦九韶算法是比较先进的算法．题型一 求最大公约数【例题1】 (1)用辗转相除法求840与1 785的最大公约数； (2)用更相减损术求612与468的最大公约数．分析：本题是关于辗转相除法和更相减损术的直接应用．辗转相除法的操作是较大的数除以较小的数；更相减损术的操作是以大数减小数．反思：(1)利用辗转相除法求最大公约数时经常会取错最后一个余数．因为辗转相除法有有限个除法式子，而最后一个余数在倒数第二个式子的最后．(2)利用更相减损术求解最大公约数时，最大公约数是直到差等于减数时的那个差，或是该差与约简的数的乘积．题型二求多项式的值【例题2】用秦九韶算法求多项式f(x)＝7x7＋6x6＋5x5＋4x4＋3x3＋2x2＋x当x＝3时的值．分析：解决本题首先需要将原多项式化成f(x)＝((((((7x＋6)x＋5)x＋4)x＋3)x＋2)x ＋1)x的形式，其次再弄清v0，v1，v2，…，v7分别是多少，再针对这些式子进行计算．反思：本题中比较容易出现的问题主要集中在计算上，多步计算必须保证每一步的正确性，否则最后不但将题目算错，而且浪费了宝贵的时间．题型三易错辨析【例题3】已知f(x)＝3x4＋2x2＋4x＋2，利用秦九韶算法求f(－2)的值．错解：f(x)＝((3x2＋2)x＋4)x＋2，v1＝3×(－2)2＋2＝14；v2＝14×(－2)＋4＝－24；v3＝－24×(－2)＋2＝50.故f(－2)＝50.错因分析：所求f(－2)的值是正确的，但是错解中没有抓住秦九韶算法原理的关键，正确改写多项式，并使每一次计算只含有x的一次项．答案：【例题1】解：(1)用辗转相除法求840和1 785的最大公约数．1 785＝840×2＋105，840＝105×8.所以840和1 785的最大公约数是105.(2)首先612和468都是偶数，所以用2约简，得到306和234，但它们还都是偶数，需要再用2约简，得到153和117，最后用更相减损术计算得153－117＝36，117－36＝81，81－36＝45，45－36＝9，36－9＝27，27－9＝18，18－9＝9.所以612和468的最大公约数是9×2×2＝36.【例题2】解：f(x)＝((((((7x＋6)x＋5)x＋4)x＋3)x＋2)x＋1)x，所以有v0＝7；v1＝7×3＋6＝27；v2＝27×3＋5＝86；v3＝86×3＋4＝262；v4＝262×3＋3＝789；v5＝789×3＋2＝2 369；v6＝2 369×3＋1＝7 108；v7＝7 108×3＝21 324.故当x＝3时，多项式f(x)＝7x7＋6x6＋5x5＋4x4＋3x3＋2x2＋x的值为21 324.【例题3】正解：f(x)＝3x4＋0·x3＋2x2＋4x＋2＝(((3x＋0)x＋2)x＋4)x＋2，v1＝3×(－2)＋0＝－6；v2＝－6×(－2)＋2＝14；v3＝14×(－2)＋4＝－24；v4＝－24×(－2)＋2＝50.故f(－2)＝50.1．用更相减损术可求得78与36的最大公约数是( )A．24 B．18 C．12 D．62．用秦九韶算法计算f(x)＝3x6＋4x5＋5x4＋6x3＋7x2＋8x＋1当x＝0.4时的值，需要进行乘法运算和加法运算的次数分别为( )A．6,6 B．5,6 C．6,5D．6,123．利用辗转相除法求3 869与6 497的最大公约数时，第二步是________．4．用秦九韶算法求多项式f(x)＝x5＋5x4＋10x3＋10x2＋5x＋1在x＝－2时的值为________．5．用辗转相除法求242与154的最大公约数．答案：1．D 先用2约简得39,18；然后辗转相减得39－18＝21，21－18＝3，18－3＝15,15－3＝12,12－3＝9,9－3＝6，6－3＝3.所以所求的最大公约数为3×2＝6.2．A 改写多项式f(x)＝(((((3x＋4)x＋5)x＋6)x＋7)x＋8)x＋1，则需进行6次乘法和6次加法运算．3．3 869＝2 628×1＋1 241 第一步：6 497＝3 869×1＋2 628，第二步：3 869＝2 628×1＋1 241.4．－1 改写多项式为f(x)＝((((x＋5)x＋10)x＋10)x＋5)x＋1，当x＝－2时，v0＝1；v1＝1×(－2)＋5＝3；v2＝3×(－2)＋10＝4；v3＝4×(－2)＋10＝2；v4＝2×(－2)＋5＝1；v5＝1×(－2)＋1＝－1；故f(－2)＝－1.5．解：242＝154×1＋88，154＝88×1＋66，88＝66×1＋22，66＝22×3.所以242与154的最大公约数是22.。

1.3 算法案例1.3 算法案例——案例1 辗转相除法与更相减损术8**学习目标**1．理解辗转相除法与更相减损术求最大公约数的方法。

2．把辗转相除法与更相减损术的方法转换成程序框图与程序语言．**要点精讲**1．辗转相除法例如，求两个正数8251和6105的最大公约数。

分析与解：8251与6105两数都比较大，而且没有明显的公约数，可以考虑用两数中较大的数除以较小的数，求得商和余数：8251＝6105×1＋2146显然8251与6105的公约数也必是2146的约数，同样6105与2146的公约数也必是8251的约数， 所以8251与6105的最大公约数也是6105与2146的最大公约数。

6105＝2146×2＋1813，2146＝1813×1＋333，1813＝333×5＋148333＝148×2＋37，148＝37×4＋0则37为37与148的最大公约数，也是148与333的最大公约数，也是333与1813的最大公约数，也是1813与2146的最大公约数，也是2146与6105的最大公约数。

所以，2146与6105的最大公约数是37。

以上我们求最大公约数的方法就是辗转相除法。

也叫欧几里德算法，它是由欧几里德在公元前300年左右首先提出的。

2．更相减损术我国早期也有解决求最大公约数问题的算法，就是更相减损术。

在《九章算术》中记载了更相减损术求最大公约数的步骤：可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之。

翻译为：（1）任意给出两个正数；判断它们是否都是偶数。

若是，用2约简；若不是，执行第二步。

（2）以较大的数减去较小的数，接着把较小的数与所得的差比较，并以大数减小数。

继续这个操作，直到所得的数相等为止，则这个数（等数）就是所求的最大公约数。

**范例分析**例1．试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。