超高过渡段长度计算
- 格式:docx
- 大小:36.32 KB
- 文档页数:1

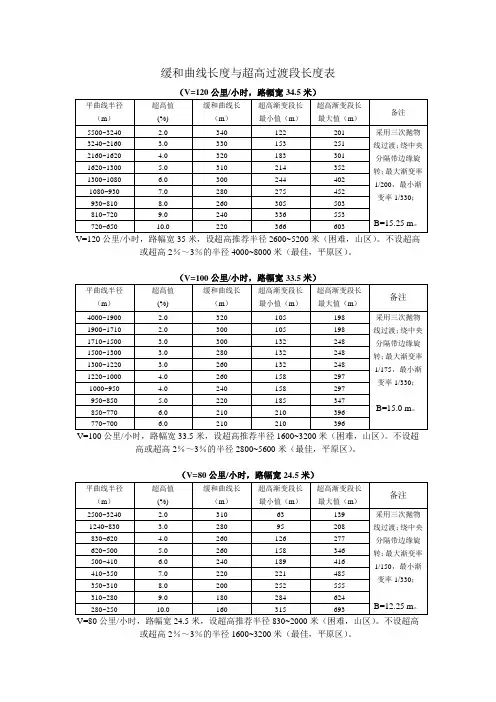



超高过渡介绍公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路,设计速度为40km/h,其中一平曲线半径R=150m,缓和曲线Ls=70m,路面宽度为B=7.0m,路肩宽度为0.75m,路拱坡度为iG=2%,路肩坡度iJ=3%,该曲线的主点桩号分别为:ZH=K1+028.665 、HY=K1+098.665 、QZ=K1+131.659 、YH=K1+164.653 、HZ=K1+234.653。
试计算各主点桩以及下列桩号:K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值(设计高为路基边缘)。
(1)确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy=5%,新建公路一般采用绕边线旋转,超高渐变率p=1/100,所以超高缓和段长度:Lc=B'△i/p=7×5%/(1/100)=35.0(m)而缓和曲线Ls=70m,先取Lc=Ls=70m,然后检查横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率:p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc=Ls=70m。
(2)计算临界断面x0X0=iG/ih×Lc=2%/5%×70=28.0m(3)计算各桩号处的超高值超高起点为ZH(HZ)点,分别计算出x值,然后分别代入超高值计算公式(见《道路勘测设计》书)中计算,加宽过渡采用比例过渡,加宽值b=1.0m。
土路肩在超高起点前1m变成与路面相同的横坡,且在整个超高过过渡段保持与相邻行车道相同的横坡。
计算结果见下表。
超高值计算结果表桩号 x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665(ZH) 0.000<x0=28 0.000 0.008 0.093 0.008+040 11.335< x0=28 0.162 0.073 0.093 0.004+070 41.335 >x0=28 0.591 0.245 0.126 -0.017+098.665(HY) 1.000 0.410 0.198 -0.065+131.659(QZ) 1.000 0.410 0.198 -0.0651+164.653(YH) 1.000 0.410 0.198 -0.065+180 54.653> x0=28 0.781 0.322 0.159 -0.037+210 24.653< x0=28 0.352 0.149 0.093 0.000+234.653(HZ) 0.000< x0=28 0.000 0.008 0.093 0.008(已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1)二.超高缓和段长度计算超高缓和段的长度按下式计算:Lc=B'×△i/P式中: Lc——超高缓和段长度(m);B' ——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);△i——旋转轴外侧的超高与路拱坡度的代数差;P ——超高渐变率,其值根据计算行车速度和超高过渡方式从下表中查取。

路基过渡段长度计算
路基过渡段长度的计算是道路建设中非常重要的一个步骤。
在实际施工过程中,为了确保道路的平稳过渡以及行车的安全,需要对路基过渡段的长度进行科学合理的计算。
路基过渡段是指道路两个不同路面等级之间的过渡区域,通常是由坡度逐渐过渡、依次改变的。
它的主要作用是消除路面高差、减小车辆的颠簸感、保证行车的舒适性。
路基过渡段的长度计算一般基于以下几个因素进行。
首先,需要考虑道路两个不同路面等级的高差。
根据国家相关标准和规范,确定不同路面等级之间的高差限制范围,然后根据实际情况确定具体的高差数值。
其次,需要考虑车辆在过渡段的行驶速度。
根据车辆的行驶速度和加速度要求,计算出车辆在过渡段内所需的最小路程。
此外,还需要考虑道路的地形和土质等因素。
根据地形情况,确定合适的路基过渡段的长度。
同时,还需要考虑土质的稳定性和承载能力,确保过渡段可以承受车辆的荷载。
最后,需要综合考虑各种因素,经过计算和实际测量,确定最终的路基过渡段长度。
需要注意的是,路基过渡段长度的计算必须符合国家相关标准和规范,确保道路建设的安全性和质量。
在实际施工中,还应进行严密的监测和检验,及时调整和修正过渡段的长度,以确保道路的平稳过渡和行车的安全。

公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路,设计速度为40km/h,其中一平曲线半径R=150m,缓和曲线Ls=70m,路面宽度为B=7.0m,路肩宽度为0.75m,路拱坡度为iG=2%,路肩坡度iJ=3%,该曲线的主点桩号分别为:ZH=K1+028.665 、HY=K1+098.665 、QZ=K1+131.659 、YH=K1+164.653 、HZ=K1+234.653。
试计算各主点桩以及下列桩号:K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值(设计高为路基边缘)。
(1)确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy=5%,新建公路一般采用绕边线旋转,超高渐变率p=1/100,所以超高缓和段长度:Lc=B'△i/p=7×5%/(1/100)=35.0(m)而缓和曲线Ls=70m,先取Lc=Ls=70m,然后检查横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率:p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc=Ls=70m。
(2)计算临界断面x0X0=iG/ih×Lc=2%/5%×70=28.0m(3)计算各桩号处的超高值超高起点为ZH(HZ)点,分别计算出x值,然后分别代入超高值计算公式(见《道路勘测设计》书)中计算,加宽过渡采用比例过渡,加宽值b=1.0m。
土路肩在超高起点前1m变成与路面相同的横坡,且在整个超高过过渡段保持与相邻行车道相同的横坡。
计算结果见下表。
超高值计算结果表桩号x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665(ZH)0.000<x0=28 0.000 0.008 0.093 0.008+040 11.335< x0=28 0.162 0.073 0.093 0.004+070 41.335 >x0=28 0.591 0.245 0.126 -0.017+098.665(HY) 1.000 0.410 0.198 -0.065+131.659(QZ) 1.000 0.410 0.198 -0.0651+164.653(YH) 1.000 0.410 0.198 -0.065+180 54.653> x0=28 0.781 0.322 0.159 -0.037+210 24.653< x0=28 0.352 0.149 0.093 0.000+234.653(HZ)0.000< x0=28 0.000 0.008 0.093 0.008(已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1)二.超高缓和段长度计算超高缓和段的长度按下式计算:Lc=B'×△i/P式中:Lc——超高缓和段长度(m);B' ——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);△i——旋转轴外侧的超高与路拱坡度的代数差;P ——超高渐变率,其值根据计算行车速度和超高过渡方式从下表中查取。

公路超高过渡段超高值的简便计算方法摘要:本文提出了根据超高过渡的特点、类型来确定超高过程中的特征断面,并对超高过渡过程进行分段处理的思路;然后给出了任意超高过渡段内任意断面的超高横坡和超高值的简单计算公式。
关键词:超高;特征断面;超高过渡段;横坡Model of calculating Superelevation forHighway Superelevation TransitionAbstract:The thought of defining characteristic section and dividing the superelevation transition segment into several smaller segments according to the characteristics and types of superelevation transition segment is put forward . On this base, the simple method for calculating cross section gradient and superelevation value of any cross section within any superelevation transition segment is presented.Key words:superelevation;characteristic section;superelevation transition segment;cross section gradient0 引言当平曲线半径小于不设超高的平曲线半径时,圆曲线上就需要设置全超高,由直线路段的双向横坡过渡到圆曲线上的单向全超高横坡时,需要设置超高过渡段。
因为圆曲线段的超高横坡度为定值,所以圆曲线上的超高值的计算相对较简单。
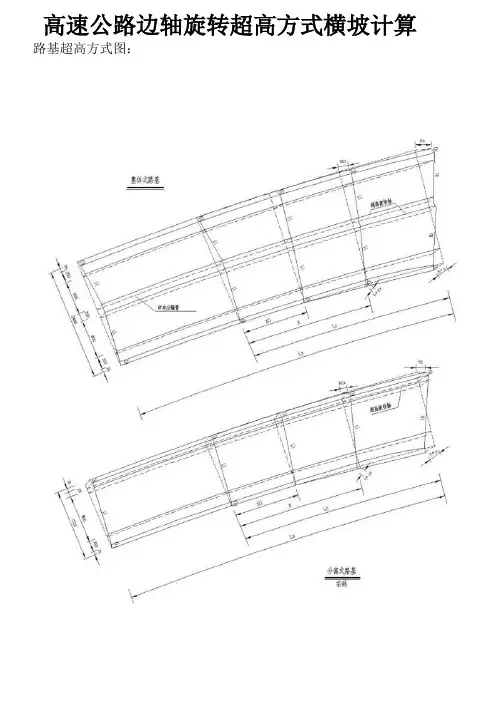
高速公路边轴旋转超高方式横坡计算路基超高方式图:说明∶1.路基超高采用边轴旋转,整体式路基旋转轴为中央分隔带边缘线;分离式路基为行车道前进方向左侧路基边缘内侧1.0米处。
2.行车道和硬路肩超高,土路肩不超高。
3.图中所示符号∶Ls--缓和曲线长,Lc--超高过渡段长;X0--与路拱同坡的单向超高点至超高过渡段起点的距离,I1--路拱横坡度;X--过渡段上任意点至超高过渡段起点的距离,I0--路肩横坡度;Ib--弯道超高横坡度,hc--路基外缘最大抬高值,h″c--路基内缘最大降低值;h″cx--x点路基内缘降低值,hcx--x点路基外缘抬高值.4.超高方式:圆曲线为全超高路段,超高过渡段长度(LC)从缓圆点(HY)往直缓点(ZH)或从圆缓点(YH)往缓直点(HZ)点计算。
先按超高渐变率p=1/330算出超高过渡段长度Lc,若Lc<Ls,则超高渐变率p=1/330。
若算出的Lc>Ls,则取Lc=Ls,超高过渡段长度等于缓和曲线长度。
5.图中尺寸均以厘米为单位,适用于设计时速V=80Km/h。
备注:正常路拱横坡(即直线段)为-2%;横坡计算按硬路肩比路缘带低为负。
一、整体式路基:图上为一左转直线到圆曲线的超高方式图。
半径为800m,缓和曲线长250m。
读图可得:R=800m,所以Ib弯道超高横坡度=4%;左转曲线,则黑线表示右幅,红线表示左幅;红点为直缓点;黑点为右幅超高起点;黄点为左幅超高起点;蓝点为缓圆点。
R=800,那么Lc=205<Ls=250.则:红点与黑点距离为:Ls-Lc=45m;黄点到蓝点距离为TX:(lb-|i左|)/(lb+|i右|)*Lc=(4-2)/(4+2)*205=68.333m; 黑点到黄点距离(与路拱同坡的单向超高点至超高过渡段起点):X0=Lc-68.333=136.667m 。
由此可得:1.直线段左右幅横坡都为-2%;2.圆曲线上分2种情况:曲线左转则:左幅横坡为-lb;右幅横坡为lb;曲线右转则:左幅横坡为lb;右幅横坡为-lb;3缓和曲线分为4种情况设桩号K:曲线左转:第一缓和曲线上则:左幅横坡= -2% -(K - (HY - TX)) / TX * (lb - 2%)右幅横坡= -2% +(K - (HY - Lc)) / lc * (lb + 2%)第二缓和曲线上则:左幅横坡= -lb + (K - YH) / TX * (lb - 2%)右幅横坡= lb - (K - YH) / lc * (lb + 2%)曲线右转:第一缓和曲线上则:左幅横坡= -2% +(K - (HY - Lc)) / Lc * (lb +2%)右幅横坡= -2% -(K - (HY - TX)) / TX * (lb -2%)第二缓和曲线上则:左幅横坡= lb - (K - YH) / Lc * (lb + 2%)右幅横坡=-lb + (K - YH) / TX * (lb - 2%)将缓和曲线公式汇总:设转向ZX,左转为-1,右转为1;设路幅A,左幅为-1,右幅为1;设与路拱同坡的过渡长TX,左转左幅或右转右幅Lc=TX,,即当ZX*A=1时,Lc=TX;公式为:第一缓和曲线:HP = -2% - ZX * A * (K - (HY - lc)) / lc * (lb - A * ZX * lz)第二缓和曲线:HP = -ZX * A * lb + ZX * A * (K - YH) / lc * (lb - ZX * A * lz)附:整体式路基excel VBA公式宏。

路线平曲线小于600m 时,在曲线上设置超高。
超高方式为,整体式路基采用绕路基中线旋转。
超高设计和计算3.6.1确定路拱及路肩横坡度:为了利于路面横向排水,应在路面横向设置路拱。
按工程技术标准,采用折线形路拱,路拱横坡度为2%。
由于土路肩的排水性远低于路面,其横坡度一般应比路面大1%~2%,故土路肩横坡度取3%。
3.6.2超高横坡度的确定:为抵消车辆在曲线路段上行驶时所产生的离心力,当平曲线半径小于不设高的最小半径值时,应在路面上设置超高,而当平曲线半径大于不设超高时的最小半径时,即可不设超高。
拟建公路为山岭重丘区三级公路,设计行车速度为40km/小时。
按各平曲线所采用的半径不同,对应的超高值如表: 表3-1 圆曲线半径与超高 圆曲线半径(m) 超高值(%) 圆曲线半径(m) 超高值(%) 600~390 1 150~120 5 390~270 2 120~90 6 270~200 3 90~60 7 200~150 4 当按平曲线半径查表5-11所得超高值小于路拱横坡度值(2%)时,取2%。
(3)、缓和段长度计算:超高缓和段长度按下式计算:PB L c i'∆=式中:c L ——超高缓和段长度(m);'B ——旋转轴至行车道外侧边缘的(m); i ∆——旋转轴外侧的超高与路拱横坡度的代数差;P ——超高渐变率,根据设计行车速度40km/小时,若超高旋转轴为路线中时,取1/150,若为边线则取1/100。
根据上式计算所得的超高缓和段长度应取成5m 的整数倍,并不小于10m 的长度。
拟建公路为无中间带的三级公路,则上式中各参数的取值如下:绕行车道中心旋转:z y i i BB +=∆=i ' , 2绕边线旋转:y i B B =∆=i ' ,式中:B ——行车道宽度(m); y i ——超高横坡度; z i ——路拱横坡度。
(4)、超高缓和段的确定:超高缓和段长主要从两个方面来考虑:一是从行车舒适性来考虑,缓和段长度越长越好;二是从排水来考虑,缓和段越短越好,特别是路线纵坡度较小时,更应注意排水的要求。
高速公路边轴旋转超高方式横坡计算高速公路边轴旋转超高方式横坡计算路基超高方式图:说明∶1.路基超高采用边轴旋转,整体式路基旋转轴为中央分隔带边缘线;分离式路基为行车道前进方向左侧路基边缘内侧1.0米处。
2.行车道和硬路肩超高,土路肩不超高。
3.图中所示符号∶Ls--缓和曲线长,Lc--超高过渡段长;X0--与路拱同坡的单向超高点至超高过渡段起点的距离,I1--路拱横坡度;X--过渡段上任意点至超高过渡段起点的距离,I0--路肩横坡度;Ib--弯道超高横坡度,hc--路基外缘最大抬高值,h″c--路基内缘最大降低值;h″cx--x点路基内缘降低值,hcx--x点路基外缘抬高值.4.超高方式:圆曲线为全超高路段,超高过渡段长度(LC)从缓圆点(HY)往直缓点(ZH)或从圆缓点(YH)往缓直点(HZ)点计算。
先按超高渐变率p=1/330算出超高过渡段长度Lc,若LcLs,则取Lc=Ls,超高过渡段长度等于缓和曲线长度。
5.图中尺寸均以厘米为单位,适用于设计时速V=80Km/h。
备注:正常路拱横坡(即直线段)为-2%;横坡计算按硬路肩比路缘带低为负。
一、整体式路基:图上为一左转直线到圆曲线的超高方式图。
半径为800m,缓和曲线长250m。
读图可得:R=800m,所以Ib弯道超高横坡度=4%;左转曲线,则黑线表示右幅,红线表示左幅;红点为直缓点;黑点为右幅超高起点;黄点为左幅超高起点;蓝点为缓圆点。
R=800,那么Lc=205< p="">红点与黑点距离为:Ls-Lc=45m;黄点到蓝点距离为TX:(lb-|i左|)/(lb+|i右|)*Lc=(4-2)/(4+2)*205=68.333m;黑点到黄点距离(与路拱同坡的单向超高点至超高过渡段起点):X0=Lc-68.333=136.667m 。
由此可得:1.直线段左右幅横坡都为-2%;2.圆曲线上分2种情况:曲线左转则:左幅横坡为-lb;右幅横坡为lb;曲线右转则:左幅横坡为lb;右幅横坡为-lb;3缓和曲线分为4种情况设桩号K:曲线左转:第一缓和曲线上则:左幅横坡= -2% -(K - (HY - TX)) / TX * (lb - 2%)右幅横坡= -2% +(K - (HY - Lc)) / lc * (lb + 2%)第二缓和曲线上则:左幅横坡= -lb + (K - YH) / TX * (lb - 2%)右幅横坡= lb - (K - YH) / lc * (lb + 2%)曲线右转:第一缓和曲线上则:左幅横坡= -2% +(K - (HY - Lc)) / Lc * (lb +2%)右幅横坡= -2% -(K - (HY - TX)) / TX * (lb -2%)第二缓和曲线上则:左幅横坡= lb - (K - YH) / Lc * (lb + 2%)右幅横坡=-lb + (K - YH) / TX * (lb - 2%)将缓和曲线公式汇总:设转向ZX,左转为-1,右转为1;设路幅A,左幅为-1,右幅为1;设与路拱同坡的过渡长TX,左转左幅或右转右幅Lc=TX,,即当ZX*A=1时,Lc=TX;公式为:第一缓和曲线:HP = -2% - ZX * A * (K - (HY - lc)) / lc * (lb - A * ZX * lz)第二缓和曲线:HP = -ZX * A * lb + ZX * A * (K - YH) / lc * (lb - ZX * A * lz)附:整体式路基excel VBA公式宏。
超高过渡段长度计算
超高过渡段长度是指在高速公路上,为了使车辆从平稳路段过渡到下坡路段或上坡路段时,设置的特殊路段长度。
其长度可通过以下公式计算得出:
超高过渡段长度 = (车辆行驶速度/重力加速度)×(车辆高度差/道路曲率半径)
其中,车辆行驶速度是指车辆在进入超高段前的平稳路段上的速度;重力加速度为9.81m/s²;车辆高度差是指车辆在通过超高段时,车辆底部与路面之间的高度差;道路曲率半径为超高段所在路段的曲率半径。
需要注意的是,在实际计算中,应该将超高段的长度向上取整,确保车辆能够平稳通过超高段,保证行车安全。