超高值计算

轨道超高计算公式在铁路运输中，轨道超高可是一个相当重要的概念，而计算轨道超高就需要用到特定的公式啦。

轨道超高，简单来说，就是为了让列车在弯道上平稳行驶，轨道会一侧高一侧低，形成一个倾斜度。

那这个倾斜度到底怎么算呢？这就得提到轨道超高计算公式。

咱们先来说说为啥要有轨道超高。

想象一下，一列长长的火车快速地拐过一个弯道，如果轨道没有超高，那外侧的车轮可能就会受到很大的压力，甚至有可能脱轨，这多危险呐！所以，合理的轨道超高能保证列车安全又顺畅地转弯。

轨道超高计算公式一般是这样的：h = 11.8*V²/R 。

这里的 h 就是要计算的轨道超高值，单位是毫米；V 代表列车通过曲线时的速度，单位是千米每小时；R 则是曲线的半径，单位是米。

比如说，有一个弯道，列车要以 100 千米每小时的速度通过，弯道半径是 500 米。

那咱们来算算轨道超高值：先把速度换算一下，100 千米每小时约等于 27.8 米每秒。

然后把数值代入公式，h = 11.8 * 27.8² / 500 ，经过计算，得出的轨道超高值就是 184.8 毫米。

我记得有一次坐火车回老家，经过一个弯道的时候，明显感觉到车身有一点点倾斜。

当时我就在想，这轨道超高设置得还挺巧妙的，要是没有这恰到好处的倾斜，估计这火车拐弯的时候就得晃悠得厉害了。

而且我还发现，当列车速度比较慢通过弯道时，那种倾斜感就没那么明显，这也说明轨道超高的设置是和列车速度紧密相关的。

在实际的铁路建设和维护中，准确计算轨道超高至关重要。

如果计算不准确，轨道超高设置得过高或者过低，都会影响列车的运行安全和舒适度。

过高的话，列车可能会向内倾斜过度，乘客会感觉不舒服；过低的话，外侧车轮压力太大，容易磨损甚至出现危险。

所以啊，那些铁路工程师们在计算轨道超高的时候，可真是得小心翼翼，不能有一点马虎。

他们要考虑到各种各样的因素，比如列车的类型、载重、行驶速度，还有弯道的具体情况等等。

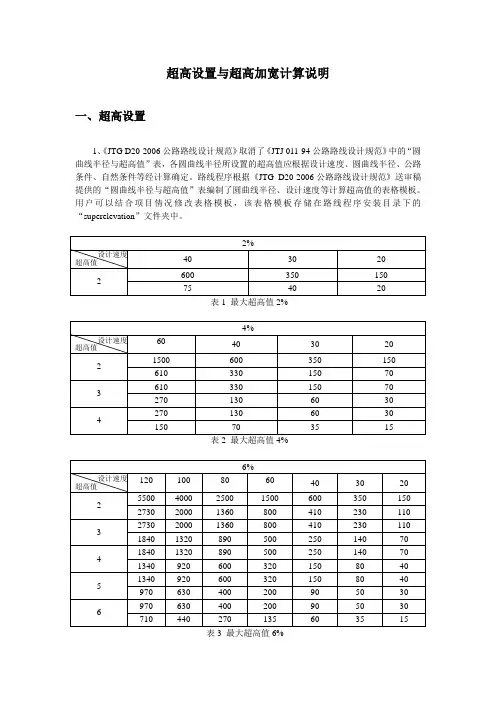
超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表，各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。

路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。

用户可以结合项目情况修改表格模板，该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。

表5 最大超高值10%2、在超高自动计算前，用户可以先进行超高设置，程序中的命令：[数据处理]→[超高分段] →[超高值设置]，设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表，若用户需要修改表格模板可点击“浏览”按钮弹出表格模板，然后修改表格模板。

点击“确定”按钮后，程序就会把用户设置的超高值存入数据库，超高自计算就会以用户设置的超高值进行计算。

若用户不进行超高设置，程序会按程序内默认的超高值进行计算。

4、表格模板格式不能修改，只能修改模板中的数据。

二、超高计算命令：[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”，程序不考虑渐变率计算的超高缓和长度，默认超高在缓和曲线上完成；反之考虑渐变率计算的超高缓和长度。

1、2 当选中窗体中的“S型曲线YH(HY)全超高”，程序认为S型曲线YH（HY）刚好达到全超高，然后向GQ点推；反之由GQ点向YH（HY）推。

1．3 当选中窗体中的“S型曲线公切点横坡0%”，则公切点超高为0%，若未选中，则公切点为正常路拱。

2、超高自动计算时，线元划分成如下单元进行计算：2、1直线——圆曲线和圆曲线——直线（1）中间没有缓和曲线，超高缓和长度直线和圆曲线上各一半。

铁路轨道超高计算公式铁路轨道超高计算公式，这可真是个有趣又重要的话题！咱们先来说说啥是铁路轨道超高。

简单来讲，就是为了让列车在弯道上能更平稳地行驶，轨道会故意做成一边高一边低的样子，这个高度差就叫超高。

那为啥要有这超高呢？想象一下，列车快速拐弯，如果轨道是平的，那离心力可就容易让列车“飘”出去，这得多危险呀！有了合适的超高，就能平衡离心力，让列车稳稳地转弯。

接下来就讲讲这计算公式。

常见的铁路轨道超高计算公式是：h = 11.8×V²÷R 。

这里的“h”就是超高值，单位是毫米；“V”是列车通过曲线的速度，单位是千米每小时；“R”是曲线半径，单位是米。

比如说，一列火车要以 120 千米每小时的速度通过一个半径为 800 米的弯道，那超高值就是：h = 11.8×120²÷800 = 212.4 毫米。

这公式看着简单，可实际运用起来得考虑好多因素呢。

就像我之前去一个铁路施工现场，工程师们正在为一段新的弯道计算超高。

他们拿着各种测量仪器，一丝不苟地测量着弯道的半径，还得考虑列车的实际运行速度，以及轨道的材质和条件等等。

我在旁边看着，心里都跟着紧张起来。

而且呀，这超高计算可不是一锤子买卖。

随着铁路线路的使用，轨道会有磨损，列车的速度也可能会调整，这都需要定期重新计算和调整超高值，以确保列车的安全和稳定运行。

还有啊，不同类型的列车，比如高速列车和普通列车，对超高的要求也不一样。

高速列车速度快，需要更大的超高来平衡离心力；而普通列车速度相对较慢，超高值就会小一些。

另外，地理环境也会影响超高的计算。

比如说在山区，弯道可能更急，半径更小，这就需要更精确的计算来保证列车安全通过。

总之，铁路轨道超高计算公式虽然看起来只是一个简单的数学式子，但背后涉及到的是铁路运输的安全和效率。

每一次准确的计算和调整，都是为了让我们的列车能更平稳、更安全地奔驰在铁轨上。

希望我这大白话能让您对铁路轨道超高计算公式有个大概的了解，这可真是铁路工程里一个不容小觑的环节呢！。

铁路曲线超高计算例题铁路曲线通常由圆曲线和缓和曲线两部分组成，其中圆曲线主要用于转弯处，而缓和曲线则用于连接直线段与圆曲线。

超高是指列车在曲线中行驶时车身与轨道之间的垂直距离差，计算超高是铁路设计中的一项重要工作。

下面举一个例题进行计算：一条铁路线路，限速120公里/小时，列车长度200米，弯曲半径800米。

计算该曲线的超高值。

解题思路：根据铁路设计规定，车辆在曲线上行驶时需要满足一定的超高限制，以确保列车安全稳定。

为了计算出该曲线的超高值，首先需要确定列车在曲线的最大超高值。

1. 确定最大超高限制首先，根据铁路行车规定，列车在曲线上的最大超高值应为铁路限速值除以25，再加上1.5米。

因此，在本题中最大超高值为：MaxH = 120 / 25 + 1.5 = 6.5米2. 确定最大列车超高其次，需要根据列车长度和弯曲半径计算出列车在曲线上可能出现的最大超高值，以便确定超高是否符合安全要求。

根据铁路设计公式，列车在圆曲线上行驶时的最大超高可以用以下公式计算：Maxh = (L^2 / 24R) + (R/2)其中，L是列车长度，R是弯曲半径。

带入数据可得：Maxh = (200^2 / (24×800)) + (800/2) = 3.47米因此，该曲线上可能出现的最大超高值是3.47米。

3. 确定实际超高值最后，根据弯曲半径和曲线长度的关系，可以利用铁路设计公式计算出该曲线的实际超高值：H = (L/2) × (L/(24×R))带入数据可得：H = (200/2) × (200/(24×800)) = 0.65米因此，该曲线的超高值为0.65米，低于最大允许超高值6.5米，符合安全要求。

结论：通过计算，我们得出该曲线的超高值为0.65米，符合安全要求。

因此，该曲线可以使用，列车可以在曲线上正常通行。

绕中轴旋转超高值计算
绕中轴旋转超高值计算是指在高空飞行中，飞机绕其中轴线进行旋转的最大高度。

计算方法如下：
首先，需要确定飞行器的绕轴转速。

假设该飞行器的绕轴转速为100度/秒。

其次，需要测量出飞行器的最大抗过载系数。

假设该飞行器的最大抗过载系数为8。

然后，需要确定飞行器的轨迹半径。

假设该飞行器的轨迹半径为500米。

最后，通过以下公式计算绕中轴旋转超高值：
绕中轴旋转超高值 = (0.95 * 最大抗过载系数 * 轨迹半径) / 标准重力加速度 * sin(绕轴转速 * 时间)
假设时间为30秒，则绕中轴旋转超高值为：
绕中轴旋转超高值 = (0.95 * 8 * 500) / 9.8 * sin(100 * 30) = 约3059米
因此，该飞行器的绕中轴旋转超高值为约3059米。

曲线外轨超高计算公式
曲线外轨超高计算公式，是指在铁路铺设过程中，为确保列车行驶的安全与稳定，需根据曲线半径、列车速度和弯道超高等参数，计算出适当的超高值，以保证列车在曲线通行过程中实现平稳转弯。

具体而言，曲线外轨超高计算公式如下：
超高值 =v^2/ (127 × R)
其中，v代表列车速度（单位：km/h），R代表曲线半径（单位：m）。

这个计算公式的原理是基于牛顿运动定律和切线加速度的理论基础。

随着列车速度的增加和曲线半径的减小，列车需要更大的超高值来保持平稳的行驶姿态，以克服离心力带来的侧向力。

通过使用曲线外轨超高计算公式，铁路工程师能够准确计算出每个曲线段的维护或建设所需的超高值。

这将有助于设计出符合安全标准、能够确保列车行驶稳定的曲线轨道。

总而言之，曲线外轨超高计算公式在铁路工程中起到至关重要的作用，它为工程师们提供了一种有效的方式来确保曲线铁路的安全性和运行稳定性。

这个计算公式的使用将有助于优化铁路设计和维护，提高列车运行的安全性和舒适性。

超高加宽计算公式
超高加宽是一种建筑设计中常用的增加层高和建筑宽度的技术手段。

通常情况下，建筑物的楼层高度和建设限制规定会对建筑物的高度和宽度有一定的限制。

而超高加宽技术则可以在不超出规定限制的情况下，通过增加楼层高度和建筑宽度，来满足建筑物的功能需求和美观要求。

1.超高计算公式
超高计算的公式可以通过考虑楼层高度的增加和结构强度的要求来确定。

一般情况下，超高的计算可以遵循以下公式：
H=h_i+ρ×n×Ts
其中，H为超高值，h_i为原始层高，ρ为楼层施工增加的层高，n 为楼层数，Ts为楼层面积。

超宽计算的公式需要考虑建筑结构的承载能力和建筑外墙保温隔热要求等因素。

W=W_i+ρ×n×Ts×Dv
其中，W为超宽值，W_i为原始建筑物的宽度，ρ为建筑物施工增加的宽度，n为楼层数，Ts为楼层面积，Dv为楼层地下深度。

总之，超高加宽计算公式可以通过考虑楼层高度和建筑宽度的增加需求，并结合建筑结构和外观设计的要求来确定。

具体的计算公式需要根据建筑设计师和结构工程师的专业知识和实践经验进行确定，以确保建筑物的结构安全和功能要求的满足。

路线平曲线小于600m时，在曲线上设置超高。

超高方式为，整体式路基采用绕路基中线旋转。

超高设计和计算361确定路拱及路肩横坡度：为了利于路面横向排水，应在路面横向设置路拱。

按工程技术标准，采用折线形路拱，路拱横坡度为2%由于土路肩的排水性远低于路面，其横坡度一般应比路面大1%-2%故土路肩横坡度取3%362超高横坡度的确定：为抵消车辆在曲线路段上行驶时所产生的离心力，当平曲线半径小于不设高的最小半径值时，应在路面上设置超高，而当平曲线半径大于不设超高时的最小半径时，即可不设超高。

拟建公路为山岭重丘区三级公路，设计行车速度为40km/小时。

按各平曲线所采用的半径不同，对应的超高值如表：表3-1圆曲线半径与超高表3-1当按平曲线半径查表5-11所得超高值小于路拱横坡度值(2%时，取2%(3)、缓和段长度计算：超高缓和段长度按下式计算：,B，\L cP式中：L c——超高缓和段长度(m);B ------ 旋转轴至行车道外侧边缘的(m);i――旋转轴外侧的超高与路拱横坡度的代数差；P——超高渐变率，根据设计行车速度40km/小时，若超高旋转轴为路线中时，取1/150，若为边线则取1/100根据上式计算所得的超高缓和段长度应取成5m的整数倍，并不小于10m的长度。

拟建公路为无中间带的三级公路，则上式中各参数的取值如下：绕行车道中心旋转：B‘ = B ,冷=i y i z2绕边线旋转：B^B , . ^-i y式中：B ――行车道宽度(m)；i y ――超高横坡度；i z ――路拱横坡度。

(4)、超高缓和段的确定：超高缓和段长主要从两个方面来考虑：一是从行车舒适性来考虑，缓和段长度越长越好；二是从排水来考虑，缓和段越短越好，特别是路线纵坡度较小时，更应注意排水的要求。

3.6.3确定缓和段长度时应考虑以下几点：⑴、一般情况下，取缓和段长度和缓和曲线长相等，即L c = L s，使超高过渡在缓和曲线全长范围内进行。

超高计算公式随着计算机技术的快速发展，超高计算（high performance computing，HPC）已经成为最前沿的技术领域之一。

超级计算机已经成为厂商和国家之间争夺科技领先地位的必备武器之一。

超高计算公式则是衡量超级计算机性能的关键指标之一。

超高计算公式是计算机性能指标之一，用来衡量计算机在单位时间内所处理的数据量。

其计算公式为R = N × P ，其中 R 表示计算机性能的峰值速度，单位为 Flops/s；N 表示计算机中的处理器个数；P 表示单个处理器的性能，单位为 Flops。

超高计算公式的设计背景在现代科技领域，特别是在工程、天气预报、医学、金融和科学领域，都需要对大量的数据进行处理，因此需要超级计算机来实现高效计算。

从上世纪90年代起，HPC技术成为科技竞争中的一个焦点，各国开始积极研发自己的超级计算机。

为衡量计算机性能指标，人们创造了超高计算公式。

超高计算公式的意义超高计算公式是衡量超级计算机性能的关键指标，它在很大程度上体现了计算机处理速度的快慢和数据处理能力的高低。

超高计算公式的设计使得计算机生产商和客户在选择计算机和进行测算时更为直观，也为大规模、复杂高性能计算提供了帮助。

认识超高计算公式超高计算公式R = N × P 在实现高性能计算中，有两个核心因素：处理器数目和单个处理器性能。

处理器数越多，性能随之提高。

但是，只增加处理器数量并不能直接提高计算机性能，需要依靠处理器性能的提高。

另外，高速IO（Input/Output）系统和优秀的软件算法也是需要考虑的因素。

总之，超高计算公式是计算机运算速度的重要依据，也是评估计算机配置和性能的重要参考。

正是计算机科学家和工程师的不断努力，使得超级计算机与HPC的运用领域越来越广泛，这也促进了全球科学技术和经济发展。