第十八讲 静电场中的导体与电介质一、金属导体的电结构导体：当物体的某部分带电后，能够将获得的电荷迅速向其它部分传布开，这种物体称为导电体（导体）。
绝缘体（电介质）：物体的某部分带电后，其电荷只能停留在该部分，不能显著地向其它部分传布，这种物体称为绝缘体。
半导体：导电能力介于导体和电介质之间的物质。
★ 注意：导体、半导体和电介质之间无严格的界限，只是导电的程度不同。
金属导体的电结构：在各种金属导体中，由于原子最外层的价电子与原子核之间的吸引力很弱，很容易摆脱原子的束缚，脱离原来所属的原子在金属中自由移动，成为自由电子；组成金属的原子，由于失去部分价电子成为带正电的离子（晶体点阵）。
（如图）金属导体的电结构：带负电的自由电子和带正电的晶体点阵。
当导体不带电也不受外电场作用时，两种电荷在导体内均匀分布，没有宏观移动，只有微观的热运动。
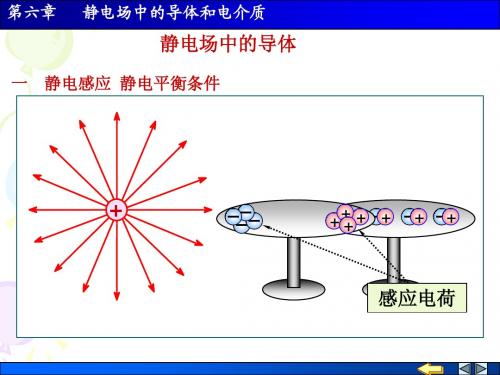
二、静电感应与静电平衡如果我们把导体放入静电场0E中，电场将驱动自由电荷定向运动，形成电流，使导体上的电荷重新分布，见下图（a ）。
在电场的作用下导体上的电荷重新分布的过程叫静电感应，感应所产生的电荷分布称为感应电荷，按电荷守恒定律，感应电荷的总电量是零。
感应电荷会产生一个附加电场E '，见下图（b ），在导体内部这个电场的方向与原场0E相反，其作用是削弱原电场。
随着静电感应的进行，感应电荷不断增加，附加电场增强，当导体中总电场的场强00E E E '=+=时，自由电荷的再分布过程停止，静电感应结束，导体达到静电平衡，见下图（c ）.三、导体的静电平衡条件导体的静电平衡条件：导体处于静电平衡时，导体内部各点的场强为零。
根据静电平衡的条件，可得出如下结论：（1）静电平衡下的导体是等势体，导体的表面是等势面。
（解释）（2）在导体表面外，靠近表面处一点的场强的大小与导体表面对应点处的电荷面密度成正比，方向与该处导体表面垂直。
对结论（2）给予证明：方向：由于电场线处处与等势面垂直，所以导体表面附近若存在电场，则场强方向必与表面垂直。
大小（高斯定理）：如图所示：在导体外紧靠表面处任取一点P ，过P 作导体表面的外法线矢量0n，则 0n E E n =并过P 作如图所示的圆柱型高斯面。
整个柱体的表面（上底、下底和侧面）构成封闭曲面，根据高斯定理，可得e n SE S σε∆Φ=∆=所以 0n E σε=矢量式：00E n σε= 0000E n E n σσ⎧>⎪⎨⎪<⎩当时，沿方向当时，与反向四、导体表面上的电荷分布当导体处于静电平衡时，导体内部处处无净电荷存在，电荷只能分布在导体的表面上（用高斯定理给予证明）。
若导体内部有空腔存在（如图），而且在空腔内部没有其他带电体，可证明不仅导体内部没有净电荷，而且在空腔的内表面上处处也没有净电荷存在，电荷只能分布在外表面。
实验表明：导体所带电荷在表面上的分布一般是不均匀的。
对于孤立导体，其表面上电荷的分布与表面曲率有关：曲率越大处，电荷面密度越大；反之越小。
尖端放电现象：具有尖端的带电导体，其尖端处电荷面密度很大，场强很大，以至于使周围的空气电离而引起放电的现象。
（举例说明） 五、静电屏蔽1．空腔内无带电体处于静电场中的空腔导体在达到静电平衡时，电荷只能分布在导体的外表面，空腔导体内表面上处处无感应电荷。
（可用高斯定理给予证明）表明：电场线将终止于导体的外表面而不能穿过导体的内表面进入内腔，因此，可用空腔导体屏蔽外电场，使空腔内的物体不受外电场的影响。
2．空腔内有带电体若一导体球壳的空腔内有一正电荷，则球壳的内表面上 将产生感应负电荷，外表面上将产生感应正电荷，如图（a ）。
球壳外面的物体将受到影响，此时把球壳接地，则外表面上的正电荷和从地上来的负电荷中和，球壳外面的电场消失。
用空腔导体屏蔽外电场结论：接地空腔导体将使外部空间不受空腔内的电场的影响。
如图（b ） ★ 空腔导体的静电屏蔽作用：空腔导体（无论接地与否）将使腔内空间不受外电场的影响，而接地的空腔导体将使外部空间不受空腔内的电场的影响。
应用：高压带电作业 电容，电容器一、孤立导体的电容定义：qC U=； 孤立导体所带电量与其电势的比值。
单位：法拉（F ） VCF 111=；PF F F 12610101==μ物理意义：反映了导体的容电本领。
二、电容器及电容当导体周围有其他导体时，其本身的电荷分布会受到其他导体上的感应电荷的影响，不能再用qC U=来描述q 与U 之间的关系。
采用静电屏蔽方法消除其他导体的影响：把导体A 放入空腔导体B 中，则A 所带电荷与A 、B 间电势差的关系为A B ABq qC U U U ==- （1） 该系统称为电容器，C 成为电容器的电容。
三种电容器电容的计算：1．球形电容器：有一个金属球和一个与它同心的金属球壳构成。
如图所示。
求它的电容方法：设内球所带电荷为q +，外球壳所带电荷为q -，(a) 计算球与球壳之间的电场分布和电势差 （b ）根据ABqC U =求电容。
由于是球形导体且实现了静电屏蔽，内球上的电荷和球壳内表面上的感应电荷均为球对称分布，因此球与球壳间的电场分布具有球对称性，由高斯定理可求得两者间任一点r 处的场强为 02014q E r r πε=球与球壳间的电势差为：21212012012()11()444R AB R q R R qqU dr rr R R R R πεπεπε-==-=⎰所以 ()012214R R C R R πε=-当2R →∞时，014C R πε=（孤立球形导体的电容） 2．平行板电容器如图所示：两板之间的场强可认为是匀强电场（除板的边缘部分有少量电场泄漏外），两板之间的场强为00E n σε=两板之间的电势差为00BABA B A d qdU U U E dl Ed Sσεε=-=⋅===⎰ 平行板电容器的电容为0AB S qC U dε== 3．圆柱形电容器如图所示：利用高斯定理，可求得两导体间任一点r 处的电场强度为000022q E r r r lrλπεπε==内外导体之间的电势差为212001ln22R AB R R q q U dr lrlR πεπε==⎰圆柱形电容器的电容为0212ln AB l qC R U R πε==★计算电容器的电容的一般步骤：（1）令电容器的两极板带电荷q ±，即对电容器充电； （2）求出两极板之间的场强分布 ； （3）由场强积分求出两极板之间的电势差；（4）由电容器的电容的定义式/AB C q U =计算其电容。
结论：电容器的电容取决于电容器的几何形状，尺寸大小和极板间的相对位置等因素，与两极板所带电荷和电势差无关。
另外，填入绝缘材料可增大电容器的电容。
三、电容器的连接方式电容器的连接方式：串联和并联电容器组的等值电容：电容器组所带的电荷与两端电势差之比。
并联（如图）：电容器组所带的总电荷q 为各个电容器上所带电荷之和，电容器组两端的电势差U 与各电容器上的电势差相等，即12q q q =+，12U U U ==并联电容器的等值电容为1212q q q C C C U U U==+=+ ★注意：电容器并联时，总电容增大，但电容器组的耐压值与电容器组中耐压最小的电容器的耐压值相等。
串联（如图）：各电容器所带电荷均为q ，若两端电势差为U ，则12U U U =+等值电容的倒数为1212111U U U C q q q C C ==+=+★ 注意：电容器串联时，总电容减小，耐压值增大，但电容器组的耐压值并不是将各电容器的耐压值简单相加。
电介质中的静电场 电位移一、电介质的电结构电介质的主要特征：它的分子中电子被原子核束缚得很紧，在宏观上几乎没有自由电荷，其导电性很差，故也称绝缘体。
电偶极子模型：在离开分子的距离比分子本身的线度大得多的地方观察，分子中全部正电荷所起的作用可用一个等效的正电荷来代替，全部负电荷所起的作用可用一个等效的负电荷来代替，若两者不重合，构成电偶极子。
电介质的分类（按分子中正、负电荷中心的分布）：无极分子：分子中的正、负电荷的等效中心在没有外场时互相重合。
如：氢、氮、甲烷等。
有极分子：分子中的正、负电荷的等效中心在没有外场时互相不重合，构成一个电偶极子（分子电矩m p）。
整块的有机分子电介质，可看成无数多个分子电矩的集合。
如甲醇、水、硫化氢等。
当无外电场时，有极分子的电矩m p的取向由于分子的热运动而表现出空间的各向等几率性，就介质中任意一个小区域来看，分子电矩都互相抵消，宏观电矩等于零，即0m p =∑ ，处于电中性状态。
对于无极分子来说，也是处于宏观电中性状态。
二、电介质的极化电介质的极化：当电介质置于电场中时，原子中的正、负电荷都将受到电场力的作用，从而发生一定程度的微小移动，这将导致原子内部的电荷分布发生微小变化，从而出现微小的反向附加电场，这种现象称为电介质的极化。
无极分子电介质—位移极化：无外电场时，分子的正、负电荷中心重合，电介质不带电。
加外电场时，如图所示：产生沿电场方向的电偶极矩，极化的效果：端面出现束缚电荷，如下图所示：有极分子电介质—取向极化：无外电场：有极分子的电偶极矩由于热运动，在空间的取向是杂乱无章的，但表现出空间的各向等几率性，介质不带电。
加外电场：有极分子的电矩m p将取向外电场排列，在介质任一小区域出现宏观电矩0mp≠∑。
极化的效果：端面出现束缚电荷，如下图所示。
00E = 00E ≠电介质在电场中极化，会出现极化电荷（束缚电荷）——不能在介质中自由移动，受到分子的束缚。
极化电荷在介质中产生附加电场E '（退极化场），则介质中的总场强0E E E '=+E ' 与0E 的方向相反，介质中的总场强E 比0E 小。
（以平行板电容器为例介绍） 三、电极化强度为了定量地描述电介质内各处极化的强弱程度，引入了电极化强度P 。
电极化强度P：电介质中某点附近单位体积内分子电偶极矩的矢量和。
m p P V=∆∑ （1）V ∆：宏观小、微观大的体积元。
极化状态：各分子电偶极矩的矢量和不会完全相互抵消。
均匀极化：电介质中各点的P的大小和方向都相同。
在各向同性的电介质中，反映介质中某一点极化强弱的P 矢量与该点的总场强E的关系为0e P E εχ=（2）式中e χ称为电介质的电极化率，取决于电介质的性质。
若e χ是一个大于零的常数，则这样的电介质称为均匀电介质。
四、电介质中的高斯定理 电位移矢量当静电场中有电介质时，在高斯面内不仅有自由电荷，还有极化电荷，这时，高斯定理应有什么样的变化呢？以两带电平行板中充满均匀各向同性的的电介质为例进行讨论。
在电介质中，高斯定理应改为Sq q E dS ε'+⋅=⎰⎰（3） 其中，0q 为高斯面内包围自由电荷的代数和，q '为高斯面内包围束缚电荷的代数和。
