《3.2.1常数与幂函数的导数》教学案2

3.2.1 常数与幂函数的导数3.2.2 导数公式表学习目标：1．能利用导数的定义推导函数y ＝c ，y ＝x ，y ＝x 2，y ＝x 3，y ＝1x，y ＝x 的导数，能根据基本初等函数的求导公式，求简单函数的导数．2．通过利用导数定义推导及归纳导数公式的过程，掌握利用导数公式求函数导数的方法． 学习重点：常数函数、幂函数的导数．学习难点：由常见幂函数的求导公式发现规律，得到幂函数的求导公式． 学习过程：知能自主梳理：一、基本初等函数的求导公式*11.(),()0;2.()(),();3.()sin ,()cos ;4.()cos ,()sin ;5.(),()ln ;6.(),();17.()log ,();ln 18.()ln ,().n n x x x x a f x c f x f x x n Q f x x f x x f x x f x x f x x f x a f x a x f x e f x e f x x f x x af x x f x x-'=='=∈='=='==-'=='=='=='==若则若则若则若则若则若则若则若则 二、例题讲解例1：求下列函数的导数(1)y ＝x 3；(2)y ＝x x ；(3)y ＝2sin x 2cos x 2； (4)y ＝1x 2.例2：求双曲线y ＝1x 在点(2，12)处的切线方程．例3：求过曲线y ＝sin x 上的点P ⎝⎛⎭⎫π4，22且与在这点处的切线垂直的直线方程． 变式应用：求曲线y ＝cos x 在点A (π6，32)处的切线方程．课堂巩固训练：1．函数f (x )＝0的导数是 ( )A ．0B ．1C ．不存在D ．不确定2．若函数f (x )＝3x ，则f ′(1)等于 () A ．0 B ．－13C ．3 D.133．已知直线y ＝kx 是y ＝ln x 的切线，则k 的值为( )A.12 B ．－12 C.1eD ．－1e 4．曲线y ＝cos x 在点P (π3，12)处的切线的斜率为____________．5．曲线y ＝xn 在x ＝2处的导数为12，则n 等于____________．6．求曲线y ＝ln x 在x ＝e 2处的切线方程．参考答案学习过程：二、例题讲解例1：解：(1)y ′＝3x 2.(2)y ＝32x ，y ′＝3212x ＝32x . (3)∵y ＝sin x ，∴y ′＝cos x .(4)∵y ＝x －2，∴y ′＝－2x －3＝－2x3 例2：解：∵y ′＝(1x )′＝－1x 2，点(2，12)在双曲线y ＝1x上， ∴双曲线y ＝1x 在点(2，12)处的切线斜率为y ′|x ＝2＝－122＝－14， 由直线方程的点斜式，得切线方程为y －12＝－14(x －2)，即y ＝－14x ＋1. 例3：解：∵y ＝sin x ，∴y ′＝(sin x )′＝cos x .∴y ′|x ＝π4＝cos π4＝22. ∴经过这点的切线的斜率为22，从而可知适合题意的直线的斜率为－ 2. ∴由点斜式得适合题意的直线方程为y －22＝－2(x －π4)，即2x ＋y －22－24π＝0. 变式应用：解：∵y ＝cos x ，∴y ′＝－sin x .y ′|x ＝π6＝－sin π6＝－12，∴k ＝－12. ∴在点A 处的切线方程为y －32＝－12(x －π6)． 即6x ＋12y －63－π＝0.课堂巩固训练：1．【答案】A【解析】常数函数的导数为0.2．【解析】∵f (x )＝3x ＝13x ，∴f ′(x )＝1323x ， ∴f ′(1)＝13.3．【解析】y ′＝1x ＝k ，∴x ＝1k，切点坐标为⎝⎛⎭⎫1k ，1， 又切点在曲线y ＝ln x 上，∴ln 1k＝1， ∴1k ＝e ，k ＝1e. 4．【解析】∵y ′＝(cos x )′＝－sin x ，∴y ′|x ＝π3＝－sin π3＝－32. 5．【答案】36．解：∵y ＝ln x ，y ′＝1x， ∴y ′|x ＝e 2＝1e 2，∴在(e 2,2)处的切线方程为y －2＝1e 2(x －e 2)，即x －e 2y ＋e 2＝0.。

3.2.1 常数与幂函数的导数3.2.2 导数公式表学习目标1.能够由定义根据求导数的三个步骤，推导常数函数与幂函数的导数；2.在教学过程中，注意培养学生归纳、探求规律的能力.学习重点利用前面已学的求导数的三个步骤对常数函数与幂函数进行探究；学习难点用从特殊到一般的规律来探究公式.学习过程例题讲解例1：求函数f (x )＝1x在x ＝1处的导数.例2：已知函数f (x )在R 上满足f (x )＝2f (2－x )－x 2＋8x －8，求曲线y ＝f (x )在点(2，f (2))处的切线方程．课堂练习1．下列命题中正确的是( )①若f ′(x )＝cos x ，则f (x )＝sin x②若f ′(x )＝0，则f (x )＝1③若f (x )＝sin x ，则f ′(x )＝cos xA ．①B ．②C ．③D ．①②③2．正弦函数y ＝sin x 上切线斜率等于12的点为( ) A ．(π3，32) B ．(－π3，－32)或(π3，32)C ．(2k π＋π3，32)(k ∈Z ) D ．(2k π－π3，－32)或(2k π＋π3，32)(k ∈Z ) 3．给出下列函数(1)y ＝(sin x )′＋(cos x )′ (2)y ＝(sin x )′＋cos x(3)y ＝sin x ＋(cos x )′ (4)y ＝(sin x )′·(cos x )′其中值域不是[－2，2]的函数有多少个( )A ．1B ．2C ．3D ．44．下列结论正确的是( )A ．若y ＝cos x ，则y ′＝sin xB ．若y ＝sin x ，则y ′＝－cos xC ．若y ＝1x ，则y ′＝－1x2 D ．若y ＝x ，则y ′＝x 25．已知f (x )＝x 3，则f (x )的斜率为1的切线有( )A ．1条B ．2条C ．3条D ．不能确定6．求曲线y ＝sin x 在点A (π6，12)的切线方程． 7．已知函数f (x )＝x ，g (x )＝a ln x ，a ∈R .若曲线y ＝f (x )与曲线y ＝g (x )相交，且在交点处有相同的切线，求a 的值和该切线方程．回顾总结布置作业参考答案：例题讲解例1：解：f ′(x )＝(1x )′＝(12x -)′＝－12112x -- ＝－1232x -＝－12x 3, ∴f ′(1)＝－12×1＝－12, ∴函数f (x )在x ＝1处的导数为－12.例2：解：由f (x )＝2f (2－x )－x 2＋8x －8，令x ＝2－x ，得f (2－x )＝2f (x )－(2－x )2＋8(2－x )－8，即2f (x )－f (2－x )＝x 2＋4x －4，联立f (x )＝2f (2－x )－x 2＋8x －8，得f (x )＝x 2，∴f ′(x )＝2x ，f ′(2)＝4，即所求切线斜率为4，∴切线方程为y －4＝4(x －2)，即4x －y －4＝0.课堂练习1．【答案】C【解析】当f (x )＝sin x ＋1时，f ′(x )＝cos x ，当f (x )＝2时，f ′(x )＝0.2．【答案】D【解析】由(sin x )′＝cos x ＝12得x ＝2k π－π3或x ＝2k π＋π3(k ∈Z )． 所以切点坐标为(2k π－π3，－32)或(2k π＋π3，32)(k ∈Z )． 3．【答案】C【解析】(1)y ＝(sin x )′＋(cos x )′＝cos x －sin x ∈[－2，2]．(2)y ＝(sin x )′＋cos x ＝2cos x ∈[－2,2]．(3)y ＝sin x ＋(cos x )′＝sin x －sin x ＝0.(4)y ＝(sin x )′·(cos x )′＝cos x ·(－sin x )＝－12sin2x ∈⎣⎡⎦⎤－12，12. 4．【答案】C【解析】∵(cos x )′＝－sin x ，(sin x )′＝cos x ，(x )′＝(x 12)′＝12·x 12－1＝12x ，∴A 、B 、D 均不正确．而⎝⎛⎭⎫1x ′＝(x －1)′＝－1×x －1－1＝－1x 2，故C 正确． 5．【答案】B【解析】设切点为(x 0，x 30)，由(x 3)′＝3x 2得在(x 0，x 30)处的切线斜率为3x 20，由3x 20＝1得x 0＝±33，故切点为⎝⎛⎭⎫33，39或⎝⎛⎭⎫－33，－39，所以有2条． 6．解：∵y ＝sin x ，∴y ′＝cos x ，∴y ′|x ＝π6＝cos π6＝32，∴k ＝32. ∴切线方程为y －12＝32(x －π6)， 化简得63x －12y ＋6－3π＝0.7．解：f ′(x )＝12x ，g ′(x )＝a x (x >0)， 由已知得⎩⎪⎨⎪⎧ x ＝a ln x ，12x ＝a x，解得a ＝e 2，x ＝e 2， ∴两条曲线交点的坐标为(e 2，e )，切线的斜率为k ＝f ′(e 2)＝12e， ∴切线的方程为y －e ＝12e(x －e 2)．。

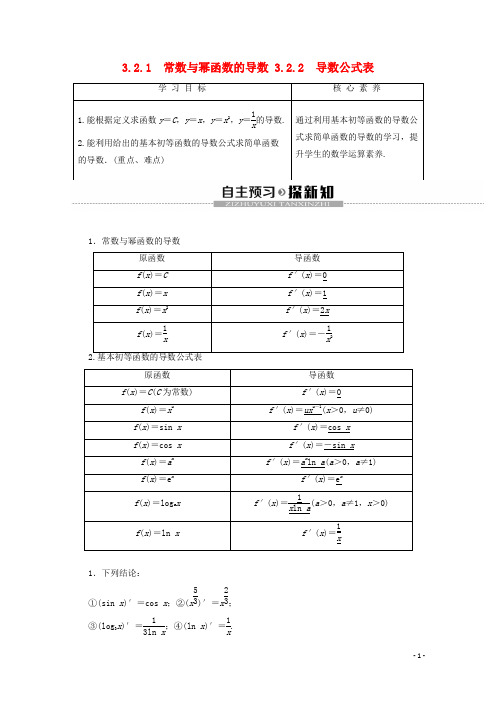
3.2.1 常数与幂函数的导数 3.2.2 导数公式表1．常数与幂函数的导数1．下列结论：①(sin x )′＝cos x ；②(x 53)′＝x 23； ③(log 3x )′＝13ln x ；④(ln x )′＝1x.其中正确的有( )A ．0个B ．1个C ．2个D ．3个C [∵②(x 53)′＝53x 23；③(log 3x )＝1x ln 3；∴②③错误，故选C.]2．若函数f (x )＝x ，则f′(1)等于( ) A ．0 B ．－12C ．12D ．1C [∵f′(x )＝(x )′＝(x 12)′＝12x 12－1＝12x ，∴f′(1)＝12，故选C.]3．曲线y ＝sin x 在⎝⎛⎭⎪⎫π4，22处的切线方程为________． 42x －8y ＋2(4－π)＝0 [∵k ＝(sin x )′|x ＝π4＝cos π4＝22，∴切线方程为y －22＝22⎝⎛⎭⎪⎫x －π4，即42x －8y ＋2(4－π)＝0.](1)y ＝x 12；(2)y ＝1x4；(3)y ＝5x 3；(4)y ＝2sin x 2cos x 2；(5)y ＝log 12x .[思路探究] 先将解析式化为基本初等函数的形式，再利用公式求导． [解] (1)y ′＝(x 12)′＝12x 12－1＝12x 11.(2)y ′＝(x －4)′＝－4x－4－1＝－4x －5＝－4x5.(3)y ′＝(5x 3)′＝(x 35)′＝35x 35－1＝35x －25＝355x2. (4)∵y ＝2sin x 2cos x2＝sin x ，∴y ′＝cos x .(5)y ′＝(log 12x )′＝1x ln12＝－1x ln 2.用导数公式求导，可以简化运算过程、降低运算难度.解题时根据所给函数的特征，将题中函数的结构进行调整，再选择合适的求导公式.提醒：若题目中所给出的函数解析式不符合导数公式，需通过恒等变换对解析式进行化简或变形后求导，如根式化成指数幂的形式求导.1．若y ＝c ，y ＝x 和y ＝x 2都表示路程关于时间的函数，则其导数的物理意义是什么？ 提示：若y ＝c 表示路程关于时间的函数，则y ′＝0可以解释为某物体的速度始终为0，即物体一直处于静止状态；若y ＝x 表示路程关于时间的函数，则y ′＝1可以解释为某物体做速度为1的匀速运动； 若y ＝x 2表示路程关于时间的函数，则y ′＝2x 可以解释为某物体做变速运动，它在x 时刻的瞬时速度为2x .2．指数函数与对数函数的导数公式各具有什么特点？[提示] (1)指数函数的导数等于指数函数本身乘以底数的自然对数，y ＝e x的导数是y ＝a x (a >0，a ≠1)导数的特例．(2)对数函数的导数等于x 与底数的自然对数乘积的倒数，y ＝ln x 的导数是y ＝log a x (a ＞0，a ≠1，x ＞0)导数的特例．【例2】 已知点P (－1,1)，点Q (2,4)是曲线y ＝x 2上两点，是否存在与直线PQ 垂直的切线，若有，求出切线方程；若没有，说明理由．[思路探究] 先求导数，再根据导数的几何意义求解． [解] 因为y ′＝(x 2)′＝2x ，假设存在与直线PQ 垂直的切线． 设切点坐标为(x 0，y 0)，由PQ 的斜率为k ＝4－12＋1＝1，又切线与PQ 垂直，所以2x 0＝－1，即x 0＝－12，所以切点坐标为⎝ ⎛⎭⎪⎫－12，14. 所以所求切线方程为 y －14＝(－1)⎝⎛⎭⎪⎫x ＋12，即4x ＋4y ＋1＝0.解决切线问题，关键是确定切点，要充分利用：(1)切点处的导数是切线的斜率.(2)切点在切线上.(3)切点又在曲线上这三个条件联立方程解决.1．思考辨析(1)若函数f (x )＝log 2π，则f′(x )＝1πln 2.( ) (2)若函数f (x )＝3x，则f′(x )＝x ·3x －1.( )(3)若函数f (x )＝4x ，则f′(x )＝4x2.( )[提示] (1)× π为常数． (2)× f′(x )＝3xln 3. (3)× f′(x )＝－4x2.2．函数f (x )＝x ，则f′(3)等于( ) A ．36B ．0C ．12xD ．32A [∵f′(x )＝12x ，∴f′(3)＝123＝36.] 3．设函数f (x )＝log a x ，f′(1)＝－1，则a ＝________. 1e [∵f′(x )＝1x ln a ，∴f′(1)＝1ln a ＝－1，∴a ＝1e .] 4．过曲线y ＝sin x 上的点P ⎝⎛⎭⎪⎫π6，12的切线方程为________．63x －12y －3π＋6＝0 [曲线y ＝sin x 在点P ⎝ ⎛⎭⎪⎫π6，12处的切线斜率为k ＝y ′|x ＝π6＝cos π6＝32.所以切线方程为y －12＝32⎝ ⎛⎭⎪⎫x －π6，即63x －12y －3π＋6＝0.]5．求下列函数的导数：(1)y ＝cos π6；(2)y ＝1x 5；(3)y ＝x2x；(4)y ＝lg x ；(5)y ＝5x；(6)y ＝cos ⎝ ⎛⎭⎪⎫π2－x .[解] (1)y ′＝0. (2)∵y ＝1x5＝x －5，∴y ′＝(x －5)′＝－5x －6＝－5x6.(3)∵y ＝x 2x＝x 32.∵y ′＝(x 32)′＝32x 12＝32x .(4)y ′＝1x ln 10. (5)y ′＝5xln 5.(6)∵y ＝cos ⎝ ⎛⎭⎪⎫π2－x ＝sin x ， ∴y ′＝(sin x )′＝cos x ．。

《常数函数与幂函数的导数》教学设计一、教学目标1、知识与技能能由定义求导数的三个步骤推导常数函数与幂函数的导数公式，并会利用它们解决简单的问题。

2、过程与方法在教学过程中，注意培养学生归纳、探求规律的能力，培养学生逻辑推理和数学运算等核心素养。

3、情感、态度与价值观教学的核心问题是让学生通过定义求导数的三个步骤，推导常数函数与幂函数的导数，通过学生的主动参与，师生、生生的合作交流，提高学生的学习兴趣，激发学生的求知欲，培养探索精神。

二、教学重点和难点教学重点：利用前面已学的求导数的三个步骤对常数函数与幂函数进行探究。

教学难点：用从特殊到一般的规律来探究公式。

三、教材分析教材的地位与作用本节内容是《普通高中课程标准实验教科书》人教版B版选修1-1第三章《导数及其应用》第二节《导数的运算》第一课时，其主要内容是常数函数与幂函数的导数公式的推导、应用。

在前面，学生们已经学会利用导数的定义能够求出函数在某一点处的导数，那么能不能利用导数的定义求出比较简单的函数及基本初等函数的导数呢？这就是本节要研究的问题。

由导数定义本身，给出了求导数的最基本的方法，但由于导数是用极限来定义的，所以求导数总是归结到求极限这在运算上很麻烦，有时甚至很困难，为了能够较快地求出某些函数的导数，这一单元我们将研究比较简单的求导数的方法，本节我们求几个常用的函数的导数。

教学重点和难点教学重点：利用前面已学的求导数的三个步骤对常数函数与幂函数进行探究。

教学难点：用从特殊到一般的规律来探究公式。

四、学情分析本节课授课对象是我校高二年级普通班的学生，数学基础比较薄弱，但是平常一直注重对他们的思想引领，所以对数学还是充满着强烈的求知欲，能够积极参与。

学生还是具备一定的观察、分析能力，具备一些从特殊到一般的归纳能力，而且学生已有导数的定义和导数的几何意义等知识储备。

本节重要是介绍求导数的方法。

根据导数定义求导数是最基本的方法。

但是，由于最终会归结为求极限，而本章并没有介绍极限知识，因此，教材只是采用这种方法计算y c =、y x =、2y x =、3y x =、1y x =、y =单函数的导数即可。

《3.2.1常数与幂函数的导数》教学案【教学目标】1.应用由定义求导数推导四种常见函数y c =、y x =、2y x =、1y x=的导数公式； 2．掌握并能运用几个基本初等函数的求导公式正确求函数的导数． 【教学难点】四种常见函数y c =、y x =、2y x =、1y x=的导数公式及应用 【教学过程】一．问题提出导数的几何意义是曲线在某一点处的切线斜率，物理意义是运动物体在某一时刻的瞬时速度．那么，对于函数()y f x =，如何求它的导数呢？由导数定义本身，给出了求导数的最基本的方法，但由于导数是用极限来定义的，所以求导数总是归结到求极限这在运算上很麻烦，有时甚至很困难，为了能够较快地求出某些函数的导数，我们将研究比较简捷的求导数的方法，下面我们求几个常用的函数的导数．二．新课讲解1．函数()y f x c ==的导数根据导数定义，因为()()0y f x x f x c c x x x ∆+∆--===∆∆∆ 所以00lim lim 00x x y y x ∆→∆→∆'===∆0y '=表示函数图像上每一点处的切线的斜率都为0．若y c =表示路程关于时间的函数，则0y '=可以解释为某物体的瞬时速度始终为0，即物体一直处于静止状态． 2．函数()y f x x ==的导数因为()()1y f x x f x x x x x x x∆+∆-+∆-===∆∆∆ 所以00limlim 11x x y y x ∆→∆→∆'===∆1y '=表示函数y x =图像上每一点处的切线的斜率都为1．若y x =表示路程关于时间的函数，则1y '=可以解释为某物体做瞬时速度为1的匀速运动．3．函数2()y f x x ==的导数 因为22()()()y f x x f x x x x x x x∆+∆-+∆-==∆∆∆ 2222()2x x x x x x x x+∆+∆-==+∆∆ 所以00lim lim(2)2x x y y x x x x ∆→∆→∆'==+∆=∆2y x '=表示函数y x =图像上点处的切线的斜率都为2x ，说明随着x 的变化，切线的斜率也在变化．另一方面，从导数作为函数在一点的瞬时变化率来看，表明：当0x <时，随着x 的增加，函数2y x =减少得越来越慢；当0x >时，随着x 的增加，函数2y x =增加得越来越快．若2y x =表示路程关于时间的函数，则2y x '=可以解释为某物体做变速运动，它在时刻x 的瞬时速度为2x ．4．函数1()y f x x==的导数 因为11()()y f x x f x x x x x x x -∆+∆-+∆==∆∆∆ 2()1()x x x x x x x x x x-+∆==-+∆∆+⋅∆ 所以220011lim lim()x x y y x x x x x∆→∆→∆'==-=-∆+⋅∆三、小试牛刀 1． 求 (1)(x 3)′ (2)(21x)′2．已知曲线y ＝x 3在点P 处的切线斜率为k ，则当k ＝3时的P 点坐标为 ( ) A ． (－2，－8) B ．(－1，－1)或(1，1)C ．(2，8)D .⎝ ⎛⎭⎪⎫－12，－18题后反思：导数的几何意义是：3．质点运动方程是51t s =， 求质点在2=t 时的速度．四、课堂练习1.求函数y =31x的导数： 2.质点的运动方程是s =t 3，(s 单位m ，t 单位s )，求质点在t =3时的速度. 3．已知直线y ＝kx 是曲线y ＝e x 的切线，则实数k 的值为( )A .1eB ．－1eC ．－eD ．e【课堂小结与反思】。

1.2.1常数函数与幂函数的导数一、学习目标1、能由定义求导数的三个步骤推导常数函数与幂函数的导数2、在教学过程中，注意培养学生探求规律的能力二、学习过程（1） 课内探究问题1：常数函数的导数是什么？问题2：运用导数的定义求下列几个幂函数的导数y=x y=x 2 y=x 3 1yx y x问题3：通过以上五个幂函数的求导过程，你有没有发现求幂函数的导数的规律？问题4：幂函数a yx 的导数是什么？（2） 典型例题例1 求 (1)(x 3)′ (2)(21x )′ (3)(x )′例2质点运动方程是51ts =, 求质点在2=t 时的速度．（3） 当堂检测1.已知语句:p 函数()y f x =的导函数是常数函数；语句:q 函数()y f x =是一次函数，则语句p 是语句q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件2.若函数()f x 的导函数为()sin f x x '=-，则函数图象在点(4(4))f ，处的切线的倾斜角为（ ）A ．90°B ．0°C ．锐角D ．钝角3.求下列函数的导数321(1) y 2 1 (2)y (3)y x x =+==213632')1(x x y =⨯=-解：33122222)(2)'()'1(': )2(x x x x x y -=-=-===----解xx x x x y 2)(21)'()'(')3(2121====-解：5252535353)(53)'()'(')4(x x x x y ====-解：（4） 课堂小结本节课学习了常数函数与幂函数的导数. 课后作业：1．()f x 与()g x 是定义在R 上的两个可导函数，若()()f x g x ，满足()()f x g x ''=，则()f x 与()g x 满足（ ）A ．()()f x g x =B ．()()f x g x -为常数C ．()()0f x g x ==D ．()()f x g x +为常数 2．设32()391f x x x x =--+，则不等式()0f x '<的解集是 ．3．曲线1y x=和2y x =在它们交点处的两条切线与x 轴所围成的三角形的面积是 ．4．求过曲线cos y x =上点π132P ⎛⎫ ⎪⎝⎭，且与过这点的切线垂直的直线方程．参考答案：典型例题例1解：(1) (x 3)′=3x 3－1=3x 2；(2) (21x)′=(x －2)′=－2x －2－1=－2x －3 (3) xx x x x 212121)()(2112121==='='-- 例2解：∵ 51t s =， ∴ 6555)()1(---='='='t t ts , ∴ 6452562-=⨯-='-=t s ． 答：质点在2=t 时的速度是645-． 当堂检测1.答案：B2.答案：C3. 3321(1) y 2 1 (2)y (3)y x (4)y x x x=+===213632')1(x x y =⨯=-解：33122222)(2)'()'1(': )2(x x x x x y -=-=-===----解xx x x x y 2)(21)'()'(')3(2121====-解：5252535353)(53)'()'(')4(x x x x y ====-解：课后作业： 1.答案：B 2.答案：(13)-，3.答案：344.解： sin y x '=-，曲线在点π132P ⎛⎫ ⎪⎝⎭，处的切线的斜率是πsin 32-=-． ∴过点P∴所求的直线方程为1π23y x ⎫-=-⎪⎭，即2π203x -=．。

人教版高中选修(B版)1-13.2.1常数与幂函数的导数教学设计一、教学目标•了解常数函数与幂函数的导函数的定义及求法。

•了解常数函数和幂函数的导数的性质和规律。

•能够计算常数函数与幂函数的导数，掌握求导法则。

二、教学重难点1.区分常数函数和幂函数的导数的不同方法；2.深入理解极限的概念；3.掌握一阶导数的求法。

三、教学过程3.1 导入新课让学生通过观察表格，找出数列之间的规律，并继而引出求导函数。

表格表格3.2 基础知识梳理•常数函数的导数–根据导数的定义，导常数函数的导数为0。

$$ y = C \\quad \\text{则} \\quad y' = 0 $$•幂函数的导数–根据导数的定义，导幂函数的导数为：$$ y = x^n \\quad \\text{则} \\quad y' = nx^{n-1} $$–特别的，当n=1时，y=x，即直线函数，其导数为1。

3.3 案例演示例1：求函数y=2x2−3x+1的导函数。

解：$$ \\begin{aligned} y' &=\\frac{d}{dx}(2x^2)-\\frac{d}{dx}(3x)+ \\frac{d}{dx}(1)\\\\ &= 4x - 3 + 0\\\\ &= 4x - 3 \\end{aligned} $$例2：求函数 $y=\\sqrt{x}$ 的导函数。

解：$$ \\begin{aligned} y'&=\\frac{d}{dx}(x^{\\frac{1}{2}})\\\\ &= \\frac{1}{2} x^{-\\frac{1}{2}}\\\\ &= \\frac{1}{2\\sqrt{x}} \\end{aligned} $$3.4 讲解要点和注意事项•常数函数的导数恒为0，可以理解为函数没有变化；•幂函数的导数可以通过直接求导来得到；•每一个导数都是一个新的函数，在常微分方程、微积分应用等领域中具有重要意义。

3.2.1 常数与幂函数的导数【教材分析】（一）三维目标（1）知识与技能能够由定义根据求导数的三个步骤，推导常数函数与幂函数的导数；（2）过程与方法在教学过程中，注意培养学生归纳、探求规律的能力；（3）情感、态度与价值观教学的核心问题是让学生能够根据定义和求导数的三个步骤，推导常数函数与幂函数的导数，通过学生的主动参与，师生、生生的合作交流，提高学生的学习兴趣，激发其求知欲，培养探索精神。

（二）教学重点利用前面已学的求导数的三个步骤对常数函数与幂函数进行探究；（三）教学难点用从特殊到一般的规律来探究公式。

（四）教学建议本节课要以教师为主导，以学生为主体，以能力的发展为目标，从学生的认知规律出发，进行启发、诱导、探索，充分调动学生的积极性，发挥学生的主体作用。

【教学过程】一．创设情景我们知道，导数的几何意义是曲线在某一点处的切线斜率，物理意义是运动物体在某一时刻的瞬时速度．那么，对于函数()y f x =，如何求它的导数呢？由导数定义本身，给出了求导数的最基本的方法，但由于导数是用极限来定义的，所以求导数总是归结到求极限这在运算上很麻烦，有时甚至很困难，为了能够较快地求出某些函数的导数，这一单元我们将研究比较简捷的求导数的方法，下面我们求几个常用的函数的导数．二．新课讲授1．函数()y f x c ==的导数根据导数定义，因为()()0y f x x f x c c x x x∆+∆--===∆∆∆ 所以00lim lim 00x x y y ∆→∆→∆'===0y '=表示函数y c =图像（图3.2-1）上每一点处的切线的斜率都为0．若y c =表示路程关于时间的函数，则0y '=可以解释为某物体的瞬时速度始终为0，即物体一直处于静止状态．2．函数()y f x x ==的导数因为()()1y f x x f x x x x x x x∆+∆-+∆-===∆∆∆ 所以00lim lim 11x x y y ∆→∆→∆'===1y '=表示函数y x =图像（图3.2-2）上每一点处的切线的斜率都为1．若y x =表示路程关于时间的函数，则1y '=可以解释为某物体做瞬时速度为1的匀速运动．3．函数2()y f x x ==的导数 因为22()()()y f x x f x x x x x x x∆+∆-+∆-==∆∆∆ 2222()2x x x x x x x x+∆+∆-==+∆∆ 所以00lim lim(2)2x x y y x x x x ∆→∆→∆'==+∆=∆2y x '=表示函数2y x =图像（图3.2-3）上点(,)x y 处的切线的斜率都为2x ，说明随着x 的变化，切线的斜率也在变化．另一方面，从导数作为函数在一点的瞬时变化率来看，表明：当0x <时，随着x 的增加，函数2y x =减少得越来越慢；当0x >时，随着x 的增加，函数2y x =增加得越来越快．若2y x =表示路程关于时间的函数，则2y x '=可以解释为某物体做变速运动，它在时刻x 的瞬时速度为2x ．4．函数1()y f x x==的导数 因为11()()y f x x f x x x x x x x-∆+∆-+∆==∆∆∆ 2()1()x x x x x x x x x x-+∆==-+∆∆+⋅∆ 所以220011lim lim()x x y y x∆→∆→∆'==-=-∆（2）推广：若*()()n y f x x n Q ==∈，则1()n f x nx -'=三．课堂练习1．课本P 87 练习A 1、2、3题2．课本P 87 练习B 1、2题3．求函数y =四．回顾总结五．布置作业。

数学选修1-1 常数与幂函数的导数 预习案【预习目标】1、了解常函数、幂函数导数的推导过程；2、尝试归纳幂函数的求导公式。

【知识回顾】1、导数的定义及符号表示：-_______________________________________ 。

2、导数的几何意义：_________________________________________。

3、函数0)(x x f 在处的切线方程：-___________________________________。

【自主探究】思考以下问题，并写下你的答案或者疑问。

问题一：常数函数的导数是什么？问题二：运用导数的定义，求下列几个幂函数的导数1、x y =2、2x y =3、3x y =4、xy 1=5、x y =思考：通过以上五个幂函数的求导过程，你有没有发现，求幂函数的导函数的规律？数学选修1-1 常数与幂函数的导数 学案【学习目标】1、掌握常函数、幂函数导数的推导过程；2、由常见幂函数的求导公式总结规律，得到幂函数的求导公式；3、常函数、幂函数导数公式的应用。

【重点】常函数、幂函数的导数及其应用。

【难点】由常见幂函数的求导公式总结规律，得到幂函数的求导公式。

【合作探究】对预案中自己不能解决的问题，请同学们组内讨论解决，并达成共识。

请同学们小组展示：附：导数公示表【典例解析】例1、求下列函数的导数（1）35=y （2）x x y = （3）31y x=；（4）x y sin = （5）x y 2= （6）x y 3log =精讲点拨：例2、求下列函数在给定点的导数（1）2,1)(==x x x f （2）4,)(==x x x f（3）0xxf==,()lnxf（4）esin,)(=x=xx精讲点拨：例3、(1)求曲线3=在点（1，1）处的切线方程;y x(2)求曲线xπ）处的切线方程.y cos=在点)1(-,例4、求与直线xy=的切线方程.y=平行的曲线x e思考讨论：点P是曲线x ey=上的任一点，求点P到直线xy=的最小距离.【自我小结】【当堂检测】1、已知()af x x=且(1)4f'=-，则实数a的值为2、若直线y x b=-+是函数1yx=图象的切线，求b及切点坐标。

高中数学第三章导数及其应用3.2.1 常数与幂函数的导数3.2.2 导数公式表学案新人教B版选修1-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章导数及其应用3.2.1 常数与幂函数的导数3.2.2 导数公式表学案新人教B版选修1-1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章导数及其应用3.2.1 常数与幂函数的导数3.2.2 导数公式表学案新人教B版选修1-1的全部内容。

3．2.1 常数与幂函数的导数3．2。

2 导数公式表1．会用导数的定义求函数的导数．(难点)2．会利用导数公式表解决一些简单的问题．（重点)［基础·初探]教材整理基本初等函数的导数公式阅读教材P86～P88例以上部分，完成下列问题．基本初等函数的导数公式原函数导函数f(x)＝c f′（x)＝0f（x)＝xα(α∈Qf′(x）＝α·xα－1＊）f(x)＝sin x f′(x）＝cos_xf（x）＝cos x f′（x)＝－sin_xf（x）＝a x f′（x)＝a x ln_a(a〉0且a≠1)f(x）＝e x f′（x）＝e xf(x）＝log a x f′(x)＝错误!(a>0且a≠1)f（x）＝ln x f′（x)＝错误!判断(正确的打“√”，错误的打“×”）(1）（log3π）′＝错误!。

( ）（2)若f(x)＝错误!，则f′(x)＝ln x．（)(3)因为（sin x）′＝cos x，所以(sin π)′＝cos π＝－1。

( )【答案】（1）×(2)×（3)×[质疑·手记］预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：_____________________________________________________解惑：______________________________________________________疑问2:_____________________________________________________解惑:______________________________________________________疑问3：_____________________________________________________解惑：_______________________________________________________[小组合作型]利用导数公式求函数的导数（0000（2）求下列函数的导数．①y＝x20；②y＝错误!；③y＝log6x.【自主解答】(1）由题意可知，f′(x0)＝1，又f′(x）＝2x，所以2x0＝1，所以x0＝错误!，y0＝错误!,x0＋y0＝错误!.【答案】错误!（2)①y′＝(x20)′＝20x20－1＝20x19.②y′＝(x－4）′＝－4x－4－1＝－4x－5。