2016届武汉高三四月湖北调考数学理科试卷及答案
- 格式:docx
- 大小:1.06 MB
- 文档页数:12
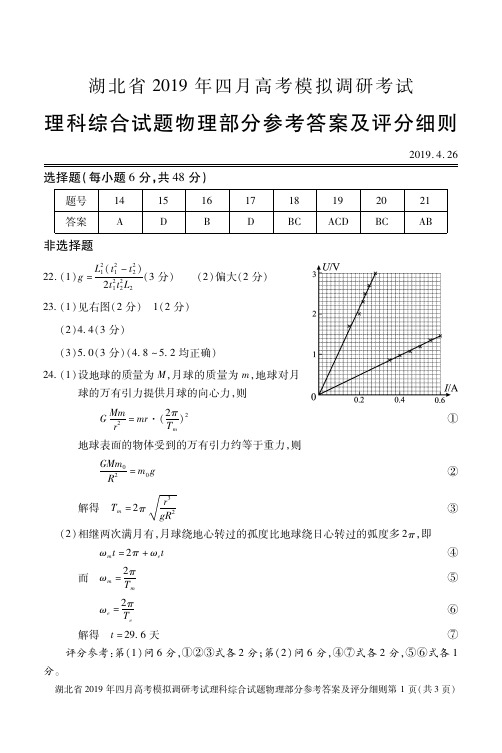
湖北省2019年四月高考模拟调研考试理科综合试题物理部分参考答案及评分细则2019.4.26选择题(每小题6分,共48分)题号1415161718192021答案ADBDBCACDBCAB非选择题22.(1)g=L21(t21-t22)2t21t22L2(3分) (2)偏大(2分)23.(1)见右图(2分) 1(2分)(2)4.4(3分)(3)5.0(3分)(4.8~5.2均正确)24.(1)设地球的质量为M,月球的质量为m,地球对月球的万有引力提供月球的向心力,则GMmr2=mr·(2πTm)2①地球表面的物体受到的万有引力约等于重力,则GMm0R2=m0g②解得 Tm=2πr3gR槡2③(2)相继两次满月有,月球绕地心转过的孤度比地球绕日心转过的弧度多2π,即ωmt=2π+ωet④而 ωm=2πTm⑤ωe=2πTe⑥解得 t=29.6天⑦评分参考:第(1)问6分,①②③式各2分;第(2)问6分,④⑦式各2分,⑤⑥式各1分。
25.(1)设小球进入复合场时,速度方向与水平方向成θ,分析小球的受力,有qvBcosθ=mg①v=v0cosθ②解得 v0=mgqB③(2)小球从A点抛出,进入复合场,由动能定理mgh=12mv2-12mv20④又由(1)知 (mg)2+(qvB)2=(qvB)2⑤解得 h=E22gB2⑥(3)设某时刻小球经过某处时速度为v,将其正交分解为vx、vy,则小球受力如图,在水平方向上,由动量定理∑(qE-qvyB)·△t=0-mv0⑦即 BqH-Eqt=mv0⑧解得 t=BHE-m2gBEq2⑨评分参考:第(1)问8分,①②式各3分,③式2分;第(2)问8分,④⑤式各3分,⑥式2分;第(3)问4分,⑦⑧式各1分,⑨式2分。
33.(1)ABD(5分)(2)(ⅰ)假设A活塞向下移动0.6L时,B活塞没有下移,对气体Ⅰ由玻意耳定律得p0LS=p1(L-0.6L)S①解得 p1=2.5p0②而 p1>2p0,故假设不成立,即活塞B向下移动。

2015~2016学年度武汉市部分学校新高三起点调研测试数学(理科)试卷 武汉市教育考试院 2015.9.9 说明:本试卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2. 选择题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
非选择题用黑色墨水的签字笔或钢笔直接答在答题卡上,答在试卷上无效。
3.考试结束后,监考人员将本试卷和答题卡一并收回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数lg y x =的定义域为集合A ,集合{}01B x x =≤≤,则A B =( )A. ()0,+∞B. []0,1C. [)0,1D. (]0,12.若i 是虚数单位,则复数21i z i-=+的实部与虚部之积为( ) A.34 B. 34- C. 34i D. 34i - 3.设随机变量服从正态分布()2,9N ,若()(2)P c P c ξξ>=<-,则c 的值是( )A.1B.2C.3D. 44.“1a = ”是“()10,,14x ax x∀∈+∞+≥”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件5.等比数列{}n a 的前n 项和为n S ,若0n a >,公比1q >,352620,64,a a a a +==则5S =( )A.31B.36C. 42D. 486. 若变量,x y 满足约束条件202x y y x y x -≥⎧⎪≥⎨⎪≥-+⎩,则2z x y =+的最小值为( )A.0B.3C. 52D. 837.已知一个棱锥的三视图如图所示,根据图中标出的尺寸(单位:cm ),8.阅读程序框图,若输入m=4,n=6,则输出a ,i 分别是( )A. 12,3a i== B. 12,4a i== C. 8,3ai == D. 8,4a i ==9.已知函数()sin()(0,)2f x wx w πϕϕ=+><的最小正周期是π,若图象向右平移3π个单位后得到的函数为奇函数,则函数()y f x =的图象( ) A. 关于点,012π⎛⎫⎪⎝⎭对称 B.关于点5,012π⎛⎫ ⎪⎝⎭对称 C.关于直线12x π=对称 D. 关于直线512x π=对称 10.已知抛物线28y x =的准线与双曲线222116x y a -=相交于,A B 两点,点F 为抛物线的焦点,ABF ∆为直角三角形,则双曲线的离心率为( )11.设数列{}n a 的通项公式为*(1)(21)cos 1()2n n n a n n N π=--⋅+∈,其前n 项和为n S ,则120S =( ) A.60- B. 120- C.180 D.24012.已知函数()(1)()f x x a x a R =+∈,设关于x 的不等式()()f x a f x +<的解集为A ,若11,22A ⎡⎤-⊆⎢⎥⎣⎦,则实数a 的取值范围是( )A. ()1,0-B. 11,2⎛-- ⎝⎭ C. 12⎛⎫ ⎪ ⎪⎝⎭ D. 10,2⎛+ ⎝⎭二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.13.对任意实数x ,有3230123(2)(2)(2)x a a x a x a x =+-+-+-,则2a 14.过点(0,2)与圆22(1)1x y -+=相切的直线方程为_________.15.已知向量,a b 是平面向量,若⊥-⊥-a (a 2b),b (b 2a),则a b 与的夹角是 _________.16.若实数a ,b ,c 满足2a +2b =2a +b ,2a +2b +2c =2a +b+c ,则c 的最大值是________.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知数列{}n a 的前n 项和为n S ,111,0,41(*)n n n n a a a a S n N +=≠=-∈( Ⅰ)证明:24n n a a +-=;( Ⅱ)求数列{}n a 的通项公式。


武汉市2016届高中毕业生四月调研测试理科综合试卷2016. 4 15选择题共21题,共126分可能用到的相对原子质量:Hl C12 Nl4 O16 Na23 Fe 56 Cu 64一、选择题:本题共l3小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关蛋白质的叙述,不正确的是A.蛋白质在常温下可与双缩脲试剂发生作用产生紫色反应B.蛋白质分子的空间结构发生改变一般不会导致其功能改变C.线粒体中能催化[H]与氧结合形成水的蛋白质分布在内膜上D.浆细胞合成和分泌抗体需要核糖体、内质网和高尔基体参与2.在置于黑暗条件下叶绿体悬浮液中加入适量NaH14CO3溶液,再给予瞬时光照。
下列说法正确的是A.黑暗条件下,叶绿体基质中不存在C3和C5B.黑暗条件下,叶绿体悬浮液不能台成A TP和[H]C.瞬时光照后,(CH2O)出现放射性比C3化合物早D.光照瞬间,C3含量迅速增加而C5含量迅速减少3.下列有关信息传递的叙述,错误的是A.遗传信息可从DNA流向RNA再流向蛋白质B.高等植物细胞之间可通过胞间连丝传递信息C.垂体与甲状腺之间可通过激素分子传递调节信息D.生态系统中信息是沿食物链从低向高营养级传递4.下图为某群落中棉蚜及其天敌瓢虫的种群数量变化,有关叙述不正确的是A.7月5日后瓢虫数量下降表明该群落中动物的丰富度降低B.棉蚜活动能力较弱,可以采用样方法调查棉蚜的种群密度C.棉蚜与瓢虫的种群数量变化反映群落内部存在负反馈调节D.瓢虫数量上升具有滞后性,棉蚜发生初期应及时人工防治5.在人体骨髓中,造血干细胞可以形成成熟的红细胞、白细胞等血细胞。
卜列说法正确的是A.造血干细胞形成不同类型血细胞的过程一般是可逆的B.造血干细胞能通过有丝分裂进行增殖而实现自我更新C.理论上人体成熟的红细胞和白细胞都具有细胞的全能性D.红细胞因细胞衰老导致细胞核逐渐退化并从细胞中排出6.红绿色盲为伴x染色体隐性遗传病,一个家庭中父母色觉正常,生了一个性染色体为XXY的孩子。

第1页 / 共12页2015-2016学年度武汉市九年级四月调考数学试卷一、选择题(共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号涂黑. 1.实数3的值在A .0与1之间.B .1与2之间.C .2与3之间.D .3与4之间. 2.分式21-x 有意义,则x 的取值范围是 A .x >2. B .x =2. C .x ≠2. D .x <2. 3.运用乘法公式计算(a —3)2的结果是A .a 2 -6a +9.B .a 2—3a +9.C .a 2—9.D . a 2 -6a -9.4.小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是A .掷一次骰子,在骰子向上的一面上的点数大于0.B .掷一次骰子,在骰子向上的一面上的点数为7.C .掷三次骰子,在骰子向上的一面上的点数之和刚好为18.D .掷两次骰子,在骰子向上的一面上的点数之积刚好是11. 5.下列计算正确的是A .3x 2—2x 2=1.B .x +x =x 2.C .4x 8÷2x 2= 2x 4.D .x ·x =x .26.如图,平行四边形ABCD 的顶点坐标分别为A (1,4),B (1,1),C (5,2),则点D 的坐标为 A . (5,5). B .(5,6). C .(6,6). D .(5,4).7.由圆柱体和长方体组成的几何体如图所示,其俯视图是8.统计学校排球队员的年龄,发现有12、13、14、15等四种年龄,统计结果如下表:年龄(岁) 12 13 14 15 人数(个)2468根据表中信息可以判断该排球队员的平均年龄为A .13.B . 14.C . 13.5.D . 5.9.如图,2×5的正方形网格,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有 A .3种. B .5种. C .8种. D .13种.yxODCBA第2页 / 共12页10.如图,在Rt △ABC 中,∠ACB = 90°,点O 在BC 上,以点O 为圆心,OC 为半径的⊙O 刚好与AB 相切,交OB 于点D .若BD =1,tan ∠AOC =2,则⊙O 的面积是A .π.B .π2.C .π49.D .π916二、填空题(共6小题,每小题3分,共18分)11.计算10+(-6)的结果为___________12.2016年全国两会在3月3日开幕,引起了传媒的极大关注.某网络平台在3月1日至8日,共监测到两会对于民生问题相关信息约290 000条,数290 000用科学记数法表示为_______________13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机取出一个小球,标号为偶数的概率为_________________14.E 为平行四边形ABCD 边AD 上一点,将△ABE 沿BE 翻折得到△FBE ,点F 在BD 上,且EF =DF .若∠C =52°,那么∠ABE =____________°.15.在平面直角坐标系中,已知A (2,4),P (1,0).B 为y 轴上的动点,以AB 为边构造△ABC ,使点C 在x 轴上,∠BAC =90°,M 为BC 的中点,则PM 的最小值为__________16.我们把函数A 的图象与直线y =x 的公共点叫做函数A 的不动点,如二次函数y =x x 4212-有两个不动点(0,0)和(10,10).直线y =m 是平行于x 轴的直线,将抛物线y =x x 4212-在直线y =m 下侧的部分沿直线y =m 翻折,翻折后的部分与没有翻折的部分组成新的函数B 的图象,若函数B 刚好有3个不动点,则满足条件的m 的值为_____________.三、解答题(共8小题,共72分)17.(本小题满分8分)解方程5x+2=2(x+4).18.(本小题满分8分)如图,线段AB,CD相交于点E,AE=BE.CE=DE.求证:AD∥C B.19.(本小题满分8分)国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.根据以上信息,回答下列问题:(1)A组的人数是__________________人,并补全条形统计图;(2)本次调查数据的中位数落在____组;(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有_________________人.第3页 / 共12页第4页 / 共12页20.(本小题满分8分)如图,双曲线y =)0(>k x k 与直线y =421+-x 相交于A ,B 两点. (1)当k =6时,求点A ,B 的坐标; (2)在双曲线y =)0(>k xk的同一支上有三点M (x 1,y 1),N (x 2,y 2),P (221x x +,0y ),请你借助图象,直接写出0y 与221y y +的大小关系.21.(本小题满分8分)已知⊙O 为△ABC 的外接圆,点E 是△ABC 的内心,AE 的延长线交BC 于点F ,交⊙O 于点D .(1)如图1,求证:BD = ED ;(2)如图2,AO 为⊙O 的直径,若BC = 6,sin ∠BAC =53,求OE 的长.第5页 / 共12页第6页 / 共12页22.(本小题满分10分)在一块矩形ABCD 的空地上划一块四边形MNPQ 进行绿化,如图,四边形的顶点在矩形的边上,且AN =AM =CP =CQ =xm .已知矩形的边BC = 200m ,边AB = am ,a 为大于200的常数,设四边形MNPQ 的面积为Sm 2.(1)求S 关于x 的函数关系式,并直接写出自变量x 的取值范围; (2)若a =400,求S 的最大值,并求出此时x 的值;(3)若a =800,请直接写出S 的最大值.23.(本小题满分10分)如图,在△ABC 中,AC >AB ,AD 是角平分线,AE 是中线.BF ⊥AD 于点G ,交AE 于点F ,交AC 于点M ,EG 的延长线交AB 于点H(1)求证:AH = BH ; (2)若∠BAC = 60°,求DGFG的第7页 / 共12页24.(本小题满分12分)如图1,在平面直角坐标系xoy 中,抛物线M :5212+-=x y 经过点C (2,3),直线y =kx +b 与抛物线相交于A ,B 两点,∠ACB = 90°.(1)探究与猜想:①探究:取点B (6,-13)时,点A 的坐标为(-25,815),直接写出直线AB 的解析式 为________________,取点B (4,-3),直接写出AB 的解析式为________________②猜想:我们猜想直线AB 必经过一个定点Q ,其坐标为___________.请取点B 的横坐标为n ,验证你的猜想;友情提醒:此问如果没有解出,不影响第(2)问的解答.(2)如图2,点D 在抛物线M 上,若AB 经过原点O ,△ABD 的面积等于△ABC 的面积,试求出一个符合条件的点D 的坐标,并直接写出其余的符合条件的D 点的坐标第8页 / 共12页第9页 / 共12页第10页 / 共12页第11页 / 共12页第12页 / 共12页。

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.已知复数1z i =+(i 是虚数单位),则22z z-的共轭..复数是( ) A . 13i -+B .13i +C .13i -D .13i --2.已知定义域为R 的函数错误!未找到引用源。
不是奇函数,则下列命题一定为真命题的是( ) A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
3.若n 是2和8的等比中项,则圆锥曲线221y x n+=的离心率是( )A .B C D 4.已知向量()()()3,1,1,3,,2a b c k ===-,若()//a c b -,则向量a 与向量c 的夹角的余弦值是( )A B .15C .D .15-5.已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据,那么该棱锥外接球的体积是( )A .B .C .D .6.如右图所示,执行程序框图输出的结果是( )A .111123411+++⋅⋅⋅+ B . 111124622+++⋅⋅⋅+C .111123410+++⋅⋅⋅+ D . 111124620+++⋅⋅⋅+7.已知g (x )是R 上的奇函数,当x <0时,g (x )=-ln(1-x ),函数()()⎩⎨⎧=x g x x f 3 00>≤x x若f (2-x 2)>f (x ),则实数x 的取值范围是 ( ) A .(-∞,1)∪(2,+∞) B .(-∞,-2)∪(1,+∞) C .(1,2) D .(-2,1)8.如下图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l ,n ∈N *)个点,相应的图案中总的点数记为n a ,则233445201520169999a a a a a a a a ++++= ( )A .20122013B .20132012C .20142015D .201420139.要得到函数()sin 33f x x π⎛⎫=+ ⎪⎝⎭的导函数()'f x 的图象,只需将()f x 的图象( ) A .向右平移3π个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) B .向右平移6π个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变)C .向左平移3π个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变)D .向左平移6π个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变)10.在双曲线22221x y a b -= (a >0,b >0)中,222c a b =+,直线2a x c=-与双曲线的两条渐近线交于A ,B两点,且左焦点在以AB 为直径的圆内,则该双曲线的离心率的取值范围为( ) A .(0,2) B . (1,2) C.⎪⎪⎭⎫⎝⎛122, D .(2,+∞) 11.从重量分别为1,2,3,4,…,10,11克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为9克的方法总数为m , 下列各式的展开式中9x 的系数为m 的选项是( ) A .2311(1)(1)(1)(1)x x x x ++++B .(1)(12)(13)(111)x x x x ++++C .2311(1)(12)(13)(111)x x x x ++++D .223211(1)(1)(1)(1)x x x x x x x x x ++++++++++12.已知函数()g x 满足121()(1)(0)2x g x g e g x x -'=-+,且存在实数0x 使得不等式021()m g x -≥成立,则m 的取值范围为( )A.(],2-∞B. (],3-∞C. [)1,+∞D.[)0,+∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.某单位为了了解用电量y 度与气温x C 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表由表中数据得回归直线方程ˆˆˆybx a =+中ˆ2b =-,预测当气温为4-C 时,用电量的度数是 . 14.设非负实数y x ,满足:⎩⎨⎧≤+-≥521y x x y ,(2,1)是目标函数y ax z 3+=()0>a 取最大值的最优解,则a的取值范围是 .15.函数()112cos 2x f x x π-⎛⎫=+ ⎪⎝⎭(46x -≤≤)的所有零点之和为 .16.已知数列3n n a =,记数列{n a }的前n 项和为n T ,若对任意的 n ∈N* ,3()362n T k n +≥-恒成立,则实数 k 的取值范围 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12 分)已知在ABC ∆中,角,,A B C 的对边分别为,,a b c , 且sin cos 0a B b A +=. (1)求角A 的大小;(2)若2a b ==,求ABC ∆的面积. 18.(本小题满分12 分)当前,网购已成为现代大学生的时尚。
试卷类型:A 武汉市2013届高中毕业生四月调研测试理科数学2013.04.23 本试卷共5页,共22题。
满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2. 选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3. 填空题和解答题的作答:用0.5毫米黑色签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4. 考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.A.-7B.-1C.1D.72. 命题“若x2+y2 =0,则X = y =0”的否命题是A. 若x2+y2 =0,则x,y中至少有一个不为0B. 若x2+y2≠0,则x,y中至少有一个不为0C. 若x2+y2≠0,则x,y都不为0D. 若x2+y2 =0, 则x,y都不为03. 对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是A. 46,45,56B. 46,45,53C. 47,45,56D. 45,47,53-0.8,c =21og 52,则 a ,b ,c 的大小关系为A. c< b < aB. c < a < b C, b < a < C D. b < C < a5. 一个几何体的三视图如图所示,则该几何体的体积是 A. 64 B. 72 C. 80 D. 112=A.1177. 已知数列{a n }的前n 项和为S n ,a 1=-(n 2) ,S A. 20122011-B. 20132012-C. 20142013-D. 20152014- 8. 如右下图,正三角形PAD 所在平面与正方形ABCD 所在平面互相垂直O 为正方形AB- CD 的中心,M 为正方形ABCD 内一点,且满足MP =MB ,则点M 的轨迹为A.42-π B.22-π41-π 10.已知抛物线M:y 2=4X ,圆N(x-1)2+y 2=r 2(其中r 为常数,r>0).过点(1,0)的直 线l 交圆N 于C,D 两点,交抛物线财于A 、B 两点,若满足丨AC 丨=|BD 丨的直线l 有三 条,则1,0(∈r 23,1(∈r 2,23(∈r ),0(+∞∈r二、填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.(一)必考题(11—14题)12 某程序框图如图所示,则该程序运行后输出的值是______(I)a 的值为______;(II)函数f(x)在(0,π)内的零点个数为________14.在Rt ΔABC 中,C ∠=90。
2016年湖北省高考数学试卷(理科)(全国新课标Ⅰ)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={x|x2﹣4x+3<0},B={x|2x﹣3>0},则A∩B=()A.(﹣3,﹣)B.(﹣3,)C.(1,)D.(,3)2.(5分)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=()A.1 B.C.D.23.(5分)已知等差数列{a n}前9项的和为27,a10=8,则a100=()A.100 B.99 C.98 D.974.(5分)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是()A.B.C.D.5.(5分)已知方程﹣=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是()A.(﹣1,3)B.(﹣1,) C.(0,3) D.(0,)6.(5分)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π7.(5分)函数y=2x2﹣e|x|在[﹣2,2]的图象大致为()A.B.C.D.8.(5分)若a>b>1,0<c<1,则()A.a c<b c B.ab c<ba cC.alog b c<blog a c D.log a c<log b c9.(5分)执行如图的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()A.y=2x B.y=3x C.y=4x D.y=5x10.(5分)以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=4,|DE|=2,则C的焦点到准线的距离为()A.2 B.4 C.6 D.811.(5分)平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.12.(5分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.5二、填空题:本大题共4小题,每小题5分,共25分.13.(5分)设向量=(m,1),=(1,2),且|+|2=||2+||2,则m=.14.(5分)(2x+)5的展开式中,x3的系数是.(用数字填写答案)15.(5分)设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为.16.(5分)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.三、解答题:本大题共5小题,满分60分,解答须写出文字说明、证明过程或演算步骤.17.(12分)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.18.(12分)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°.(Ⅰ)证明平面ABEF⊥平面EFDC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.19.(12分)某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.(Ⅰ)求X的分布列;(Ⅱ)若要求P(X≤n)≥0.5,确定n的最小值;(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?20.(12分)设圆x2+y2+2x﹣15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(Ⅰ)证明|EA|+|EB|为定值,并写出点E的轨迹方程;(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.21.(12分)已知函数f(x)=(x﹣2)e x+a(x﹣1)2有两个零点.(Ⅰ)求a的取值范围;(Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2<2.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]22.(10分)如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(Ⅰ)证明:直线AB与⊙O相切;(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.[选修4-5:不等式选讲]24.已知函数f(x)=|x+1|﹣|2x﹣3|.(Ⅰ)在图中画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.2016年湖北省高考数学试卷(理科)(全国新课标Ⅰ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={x|x2﹣4x+3<0},B={x|2x﹣3>0},则A∩B=()A.(﹣3,﹣)B.(﹣3,)C.(1,)D.(,3)【解答】解:∵集合A={x|x2﹣4x+3<0}=(1,3),B={x|2x﹣3>0}=(,+∞),∴A∩B=(,3),故选:D2.(5分)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=()A.1 B.C.D.2【解答】解:∵(1+i)x=1+yi,∴x+xi=1+yi,即,解得,即|x+yi|=|1+i|=,故选:B.3.(5分)已知等差数列{a n}前9项的和为27,a10=8,则a100=()A.100 B.99 C.98 D.97【解答】解:∵等差数列{a n}前9项的和为27,S9===9a5.∴9a5=27,a5=3,又∵a10=8,∴d=1,∴a100=a5+95d=98,故选:C4.(5分)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是()A.B.C.D.【解答】解:设小明到达时间为y,当y在7:50至8:00,或8:20至8:30时,小明等车时间不超过10分钟,故P==,故选:B5.(5分)已知方程﹣=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是()A.(﹣1,3)B.(﹣1,) C.(0,3) D.(0,)【解答】解:∵双曲线两焦点间的距离为4,∴c=2,当焦点在x轴上时,可得:4=(m2+n)+(3m2﹣n),解得:m2=1,∵方程﹣=1表示双曲线,∴(m2+n)(3m2﹣n)>0,可得:(n+1)(3﹣n)>0,解得:﹣1<n<3,即n的取值范围是:(﹣1,3).当焦点在y轴上时,可得:﹣4=(m2+n)+(3m2﹣n),解得:m2=﹣1,无解.故选:A.6.(5分)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π【解答】解:由题意可知三视图复原的几何体是一个球去掉后的几何体,如图:可得:=,R=2.它的表面积是:×4π•22+=17π.故选:A.7.(5分)函数y=2x2﹣e|x|在[﹣2,2]的图象大致为()A.B.C.D.【解答】解:∵f(x)=y=2x2﹣e|x|,∴f(﹣x)=2(﹣x)2﹣e|﹣x|=2x2﹣e|x|,故函数为偶函数,当x=±2时,y=8﹣e2∈(0,1),故排除A,B;当x∈[0,2]时,f(x)=y=2x2﹣e x,∴f′(x)=4x﹣e x=0有解,故函数y=2x2﹣e|x|在[0,2]不是单调的,故排除C,故选:D8.(5分)若a>b>1,0<c<1,则()A.a c<b c B.ab c<ba cC.alog b c<blog a c D.log a c<log b c【解答】解:∵a>b>1,0<c<1,∴函数f(x)=x c在(0,+∞)上为增函数,故a c>b c,故A错误;函数f(x)=x c﹣1在(0,+∞)上为减函数,故a c﹣1<b c﹣1,故ba c<ab c,即ab c >ba c;故B错误;log a c<0,且log b c<0,log a b<1,即=<1,即log a c>log b c.故D错误;0<﹣log a c<﹣log b c,故﹣blog a c<﹣alog b c,即blog a c>alog b c,即alog b c<blog a c,故C正确;故选:C9.(5分)执行如图的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()A.y=2x B.y=3x C.y=4x D.y=5x【解答】解:输入x=0,y=1,n=1,则x=0,y=1,不满足x2+y2≥36,故n=2,则x=,y=2,不满足x2+y2≥36,故n=3,则x=,y=6,满足x2+y2≥36,故y=4x,故选:C10.(5分)以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=4,|DE|=2,则C的焦点到准线的距离为()A.2 B.4 C.6 D.8【解答】解:设抛物线为y2=2px,如图:|AB|=4,|AM|=2,|DE|=2,|DN|=,|ON|=,x A==,|OD|=|OA|,=+5,解得:p=4.C的焦点到准线的距离为:4.故选:B.11.(5分)平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.【解答】解:如图:α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABA1B1=n,可知:n∥CD1,m∥B1D1,∵△CB1D1是正三角形.m、n所成角就是∠CD1B1=60°.则m、n所成角的正弦值为:.故选:A.12.(5分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.5【解答】解:∵x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,∴,即,(n∈N)即ω=2n+1,(n∈N)即ω为正奇数,∵f(x)在(,)上单调,则﹣=≤,即T=≥,解得:ω≤12,当ω=11时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=﹣,此时f(x)在(,)不单调,不满足题意;当ω=9时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=,此时f(x)在(,)单调,满足题意;故ω的最大值为9,故选:B二、填空题:本大题共4小题,每小题5分,共25分.13.(5分)设向量=(m,1),=(1,2),且|+|2=||2+||2,则m=﹣2.【解答】解:|+|2=||2+||2,可得•=0.向量=(m,1),=(1,2),可得m+2=0,解得m=﹣2.故答案为:﹣2.14.(5分)(2x+)5的展开式中,x3的系数是10.(用数字填写答案)==25﹣【解答】解:(2x+)5的展开式中,通项公式为:T r+1r,令5﹣=3,解得r=4∴x3的系数2=10.故答案为:10.15.(5分)设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为64.【解答】解:等比数列{a n}满足a1+a3=10,a2+a4=5,可得q(a1+a3)=5,解得q=.a1+q2a1=10,解得a1=8.则a1a2…a n=a1n•q1+2+3+…+(n﹣1)=8n•==,当n=3或4时,表达式取得最大值:=26=64.故答案为:64.16.(5分)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为216000元.【解答】解:(1)设A、B两种产品分别是x件和y件,获利为z元.由题意,得,z=2100x+900y.不等式组表示的可行域如图:由题意可得,解得:,A(60,100),目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元.故答案为:216000.三、解答题:本大题共5小题,满分60分,解答须写出文字说明、证明过程或演算步骤.17.(12分)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.【解答】解:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,整理得:2cosCsin(A+B)=sinC,即2cosCsin(π﹣(A+B))=sinC2cosCsinC=sinC∴cosC=,∴C=;(Ⅱ)由余弦定理得7=a2+b2﹣2ab•,∴(a+b)2﹣3ab=7,∵S=absinC=ab=,∴ab=6,∴(a+b)2﹣18=7,∴a+b=5,∴△ABC的周长为5+.18.(12分)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°.(Ⅰ)证明平面ABEF⊥平面EFDC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.【解答】(Ⅰ)证明:∵ABEF为正方形,∴AF⊥EF.∵∠AFD=90°,∴AF⊥DF,∵DF∩EF=F,∴AF⊥平面EFDC,∵AF⊂平面ABEF,∴平面ABEF⊥平面EFDC;(Ⅱ)解:由AF⊥DF,AF⊥EF,可得∠DFE为二面角D﹣AF﹣E的平面角;由ABEF为正方形,AF⊥平面EFDC,∵BE⊥EF,∴BE⊥平面EFDC即有CE⊥BE,可得∠CEF为二面角C﹣BE﹣F的平面角.可得∠DFE=∠CEF=60°.∵AB∥EF,AB⊄平面EFDC,EF⊂平面EFDC,∴AB∥平面EFDC,∵平面EFDC∩平面ABCD=CD,AB⊂平面ABCD,∴AB∥CD,∴CD∥EF,∴四边形EFDC为等腰梯形.以E为原点,建立如图所示的坐标系,设FD=a,则E(0,0,0),B(0,2a,0),C(,0,a),A(2a,2a,0),∴=(0,2a,0),=(,﹣2a,a),=(﹣2a,0,0)设平面BEC的法向量为=(x1,y1,z1),则,则,取=(,0,﹣1).设平面ABC的法向量为=(x2,y2,z2),则,则,取=(0,,4).设二面角E﹣BC﹣A的大小为θ,则cosθ===﹣,则二面角E﹣BC﹣A的余弦值为﹣.19.(12分)某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.(Ⅰ)求X的分布列;(Ⅱ)若要求P(X≤n)≥0.5,确定n的最小值;(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?【解答】解:(Ⅰ)由已知得X的可能取值为16,17,18,19,20,21,22,P(X=16)=()2=,P(X=17)=,P(X=18)=()2+2()2=,P(X=19)==,P(X=20)===,P(X=21)==,P(X=22)=,∴X的分布列为:X16171819202122 P(Ⅱ)由(Ⅰ)知:P(X≤18)=P(X=16)+P(X=17)+P(X=18)==.P(X≤19)=P(X=16)+P(X=17)+P(X=18)+P(X=19)=+=.∴P(X≤n)≥0.5中,n的最小值为19.(Ⅲ)解法一:由(Ⅰ)得P(X≤19)=P(X=16)+P(X=17)+P(X=18)+P(X=19)=+=.买19个所需费用期望:EX1=200×+(200×19+500)×+(200×19+500×2)×+(200×19+500×3)×=4040,买20个所需费用期望:EX2=+(200×20+500)×+(200×20+2×500)×=4080,∵EX1<EX2,∴买19个更合适.解法二:购买零件所用费用含两部分,一部分为购买零件的费用,另一部分为备件不足时额外购买的费用,当n=19时,费用的期望为:19×200+500×0.2+1000×0.08+1500×0.04=4040,当n=20时,费用的期望为:20×200+500×0.08+1000×0.4=4080,∴买19个更合适.20.(12分)设圆x2+y2+2x﹣15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(Ⅰ)证明|EA|+|EB|为定值,并写出点E的轨迹方程;(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.【解答】解:(Ⅰ)证明:圆x2+y2+2x﹣15=0即为(x+1)2+y2=16,可得圆心A(﹣1,0),半径r=4,由BE∥AC,可得∠C=∠EBD,由AC=AD,可得∠D=∠C,即为∠D=∠EBD,即有EB=ED,则|EA|+|EB|=|EA|+|ED|=|AD|=4,故E的轨迹为以A,B为焦点的椭圆,且有2a=4,即a=2,c=1,b==,则点E的轨迹方程为+=1(y≠0);(Ⅱ)椭圆C1:+=1,设直线l:x=my+1,由PQ⊥l,设PQ:y=﹣m(x﹣1),由可得(3m2+4)y2+6my﹣9=0,设M(x1,y1),N(x2,y2),可得y1+y2=﹣,y1y2=﹣,则|MN|=•|y1﹣y2|=•=•=12•,A到PQ的距离为d==,|PQ|=2=2=,则四边形MPNQ面积为S=|PQ|•|MN|=••12•=24•=24,当m=0时,S取得最小值12,又>0,可得S<24•=8,即有四边形MPNQ面积的取值范围是[12,8).21.(12分)已知函数f(x)=(x﹣2)e x+a(x﹣1)2有两个零点.(Ⅰ)求a的取值范围;(Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2<2.【解答】解:(Ⅰ)∵函数f(x)=(x﹣2)e x+a(x﹣1)2,∴f′(x)=(x﹣1)e x+2a(x﹣1)=(x﹣1)(e x+2a),①若a=0,那么f(x)=0⇔(x﹣2)e x=0⇔x=2,函数f(x)只有唯一的零点2,不合题意;②若a>0,那么e x+2a>0恒成立,当x<1时,f′(x)<0,此时函数为减函数;当x>1时,f′(x)>0,此时函数为增函数;此时当x=1时,函数f(x)取极小值﹣e,由f(2)=a>0,可得:函数f(x)在x>1存在一个零点;当x<1时,e x<e,x﹣2<﹣1<0,∴f(x)=(x﹣2)e x+a(x﹣1)2>(x﹣2)e+a(x﹣1)2=a(x﹣1)2+e(x﹣1)﹣e,令a(x﹣1)2+e(x﹣1)﹣e=0的两根为t1,t2,且t1<t2,则当x<t1,或x>t2时,f(x)>a(x﹣1)2+e(x﹣1)﹣e>0,故函数f(x)在x<1存在一个零点;即函数f(x)在R是存在两个零点,满足题意;③若﹣<a<0,则ln(﹣2a)<lne=1,当x<ln(﹣2a)时,x﹣1<ln(﹣2a)﹣1<lne﹣1=0,e x+2a<e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,当ln(﹣2a)<x<1时,x﹣1<0,e x+2a>e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)<0恒成立,故f(x)单调递减,当x>1时,x﹣1>0,e x+2a>e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,故当x=ln(﹣2a)时,函数取极大值,由f(ln(﹣2a))=[ln(﹣2a)﹣2](﹣2a)+a[ln(﹣2a)﹣1]2=a{[ln(﹣2a)﹣2]2+1}<0得:函数f(x)在R上至多存在一个零点,不合题意;④若a=﹣,则ln(﹣2a)=1,当x<1=ln(﹣2a)时,x﹣1<0,e x+2a<e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,当x>1时,x﹣1>0,e x+2a>e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,故函数f(x)在R上单调递增,函数f(x)在R上至多存在一个零点,不合题意;⑤若a<﹣,则ln(﹣2a)>lne=1,当x<1时,x﹣1<0,e x+2a<e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,当1<x<ln(﹣2a)时,x﹣1>0,e x+2a<e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)<0恒成立,故f(x)单调递减,当x>ln(﹣2a)时,x﹣1>0,e x+2a>e ln(﹣2a)+2a=0,即f′(x)=(x﹣1)(e x+2a)>0恒成立,故f(x)单调递增,故当x=1时,函数取极大值,由f(1)=﹣e<0得:函数f(x)在R上至多存在一个零点,不合题意;综上所述,a的取值范围为(0,+∞)证明:(Ⅱ)∵x1,x2是f(x)的两个零点,∴f(x1)=f(x2)=0,且x1≠1,且x2≠1,∴﹣a==,令g(x)=,则g(x1)=g(x2)=﹣a,∵g′(x)=,∴当x<1时,g′(x)<0,g(x)单调递减;当x>1时,g′(x)>0,g(x)单调递增;设m>0,则g(1+m)﹣g(1﹣m)=﹣=,设h(m)=,m>0,则h′(m)=>0恒成立,即h(m)在(0,+∞)上为增函数,h(m)>h(0)=0恒成立,即g(1+m)>g(1﹣m)恒成立,令m=1﹣x1>0,则g(1+1﹣x1)>g(1﹣1+x1)⇔g(2﹣x1)>g(x1)=g(x2)⇔2﹣x1>x2,即x1+x2<2.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]22.(10分)如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(Ⅰ)证明:直线AB与⊙O相切;(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.【解答】证明:(Ⅰ)设K为AB中点,连结OK,∵OA=OB,∠AOB=120°,∴OK⊥AB,∠A=30°,OK=OAsin30°=OA,∴直线AB与⊙O相切;(Ⅱ)因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.设T是A,B,C,D四点所在圆的圆心.∵OA=OB,TA=TB,∴OT为AB的中垂线,同理,OC=OD,TC=TD,∴OT为CD的中垂线,∴AB∥CD.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.【解答】解:(Ⅰ)由,得,两式平方相加得,x2+(y﹣1)2=a2.∴C 1为以(0,1)为圆心,以a为半径的圆.化为一般式:x2+y2﹣2y+1﹣a2=0.①由x2+y2=ρ2,y=ρsinθ,得ρ2﹣2ρsinθ+1﹣a2=0;(Ⅱ)C2:ρ=4cosθ,两边同时乘ρ得ρ2=4ρcosθ,∴x2+y2=4x,②即(x﹣2)2+y2=4.由C3:θ=α0,其中α0满足tanα0=2,得y=2x,∵曲线C1与C2的公共点都在C3上,∴y=2x为圆C1与C2的公共弦所在直线方程,①﹣②得:4x﹣2y+1﹣a2=0,即为C3 ,∴1﹣a2=0,∴a=1(a>0).[选修4-5:不等式选讲]24.已知函数f(x)=|x+1|﹣|2x﹣3|.(Ⅰ)在图中画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.【解答】解:(Ⅰ)f(x)=,由分段函数的图象画法,可得f(x)的图象,如右:(Ⅱ)由|f(x)|>1,可得当x≤﹣1时,|x﹣4|>1,解得x>5或x<3,即有x≤﹣1;当﹣1<x<时,|3x﹣2|>1,解得x>1或x<,即有﹣1<x<或1<x<;当x≥时,|4﹣x|>1,解得x>5或x<3,即有x>5或≤x<3.综上可得,x<或1<x<3或x>5.则|f(x)|>1的解集为(﹣∞,)∪(1,3)∪(5,+∞).赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.ODABCEAODCB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
湖北省优质高中2016届高三联考试题数学(理工类)注意事项:答卷前,考生务必将姓名,准考证号等在答题卡和答题卷上真写清楚。
选择题答案用2B 铅笔直接填涂在答题卡上,非选择题用0.5mm 的黑色签字笔在每题对应的答题区域做答,答在试题卷上无效。
第Ⅰ卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求) 1.已知复数1z i =+(是虚数单位),则22z z-的共轭..复数是( ) A . 13i -+B . 13i +C .13i -D .13i --2.已知定义域为R 的函数()f x 不是奇函数,则下列命题一定为真命题的是( )A .()()x R f x f x ∀∈-≠-,B .()()x R f x f x ∀∈-=,C .000()()x R f x f x ∃∈-≠-,D .000()()x R f x f x ∃∈-=,3.若n 是2和8的等比中项,则圆锥曲线221y x n+=的离心率是( )A .B C 或 D 4.已知向量()()()3,1,1,3,,2a b c k ===- ,若()//a c b -,则向量a 与向量c 的夹角的余弦值是( )A B .15C .D .15-5.已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据,那么该棱锥外接球的体积是( )A .B .C .D .6.如右图所示,执行程序框图输出的结果是( )A . 111123411+++⋅⋅⋅+B . 111124622+++⋅⋅⋅+C . 111123410+++⋅⋅⋅+D . 111124620+++⋅⋅⋅+7.已知g (x )是R 上的奇函数,当x <0时,g (x )=-ln(1-x ),函数f (x )=⎩⎪⎨⎪⎧x 3 (x ≤0),g (x ) (x >0),若f (2-x 2)>f (x ),则实数x 的取值范围是( ) A .(-∞,1)∪(2,+∞) B .(-∞,-2)∪(1,+∞) C .(1,2) D .(-2,1)8.如下图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l ,n ∈N *)个点,相应的图案中总的点数记为n a ,( )A .20122013B .20132012 C .20142015D .201420139.要得到函数()sin 33f x x π⎛⎫=+⎪⎝⎭的导函数()'f x 的图象,只需将()f x 的图象( ) A .向右平移3π个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) B .向右平移6π个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) C .向左平移3π个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变)D .向左平移6π个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变)10. 在双曲线22221x y a b -= (a >0,b >0)中,222c a b =+,直线2a x c=-与双曲线的两条渐近线交于A ,B 两点,且左焦点在以AB 为直径的圆内,则该双曲线的离心率的取值范围为( )A .(0,2)B . (1,2) C. ⎝⎛⎭⎫22,1 D .(2,+∞)11.从重量分别为1,2,3,4,…,10,11克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为9克的方法总数为m , 下列各式的展开式中9x 的系数为m 的选项是( )A .2311(1)(1)(1)(1)x x x x ++++ B .(1)(12)(13)(111)x x x x ++++ C .2311(1)(12)(13)(111)x x x x ++++D .223211(1)(1)(1)(1)x x x x x x x x x ++++++++++ 12. 已知函数()g x 满足121()(1)(0)2x g x g e g x x -'=-+,且存在实数0x 使得不等式021()m g x -≥成立,则m 的取值范围为( )A.(],2-∞B. (],3-∞C. [)1,+∞D.[)0,+∞第Ⅱ卷(非选择题)本卷包括必考题和选考题两部分。
2016年黄冈市高三适应性考试数学答案(理科)一、BDDCA BCCCA CD二、13. 12- 14.2 1516. 32三、解答题(解答应写出文字说明、证明过程或演算步骤)17.解:(1)设等差数列{}n a 的首项为1a ,公差为d ,则21515411a a d a a d =+=⎧⎨=+=⎩∴132a d =⎧⎨=⎩∴3(1)22n a n n =+-⨯=+ …………(3分) ∴数列{}n b 的前n 项和221n S n n =++=2(1)n +当n =1时,114b S ==,当n ≥2时,221(1)21n n n b S S n n n -=-=+-=+,对1b =4不成立, 所以,数列{}n b 的通项公式为4,121,2n n b n n =⎧=⎨+⎩≥ …………6分(2)n =1时,1121120T b b ==, n ≥2时,111111(21)(23)22123n n b b n n n n +⎛⎫==-⎪++++⎝⎭, 所以 1111111111111161()()2025779212320252320101520(23)n n n T n n n n n --=+-+-++-=+-=+=+++++L n =1仍然适合上式, …………10分 综上,6120(23)n n T n -=+ ………… 12分18.解(Ⅰ)证明:Q 四边形ABCD 是菱形, BD AC ∴⊥.AE ⊥Q 平面ABCD ,BD ⊂平面ABCDBD AE ∴⊥.AC AE A =Q I ,∴BD ⊥平面ACFE . -------------------5分(Ⅱ)解:以O 为原点,OA ,OB 为x ,y 轴正向,z 轴过O 且平行于CF ,建立空间直角坐标系,则B,(0,D ,(1,0,2)E ,(1,0,)(0)F a a ->,()1,0,OF a =-uuu r---6分设平面EBD 的法向量为(,,)x y z =n ,则有00OB OE ⎧⋅=⎪⎨⋅=⎪⎩n n uu u ruu u r,即020x z ⎪⎩=+=令1z =,则(2,0,1)=-n -------------------8分由题意得||sin 45|cos ,|||||OF OF OF ⋅=<>===n n n o uuu r uuu r uuu r,解得3a =或13-.由0a >,得3a = -------------------10分(1,0,3),(1,2),cos ,OF BE OF BE =-===即所求的异面直线所成的角余弦值为 ---------------------12分 19K 2= 50×(30×6-9×5) 239×11×35×15= 40501001 = 4.046 > 3.841所以有95℅以上的把握认为被调查者喜欢头上长“草”的造型和自身喜欢动画片有关. -----------------6分 (Ⅱ)由频率分布直方图知抽到喜欢头上长“草”的频率为710,将频率视为概率,即从人群中抽取一名喜欢头上长“草”的概率为710.由题意知73,10X B ⎛⎫⎪⎝⎭~,从而X 的分布列为:-------------9分721()31010E X np ==⨯=, 7363()(1)31010100D X np p =-=⨯⨯=.-----------12分20.解:(Ⅰ)由题意,以椭圆C 的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为222)(a y c x =+-,∴圆心到直线01=++y x的距离d a ==(*)------------------------------------1分 ∵椭圆C 的两焦点与短轴的一个端点的连线构成等腰直角三角形,∴b c =,a =, 代入(*)式得1b c ==,∴a ==故所求椭圆方程为.1222=+y x……………………………………………………4分 (Ⅱ)由题意知直线l 的斜率存在,设直线l 方程为)2(-=x k y ,设()00,P x y ,将直线方程代入椭圆方程得:22228820(12)x k x k k -+-=+,∴422644(12)(82)0k k k ∆=-+->,解得212k <. 设11(),S x y ,22(),T x y ,则22121222882,1212k k x x x x k k -+==++, ----------------------6分 ∴121224(4)12x x ky y k k ++=-=-+ 由OS OT tOP +=uu r uu u r uu u r,得012012,tx x x ty y y =+=+当0t =时,直线l 为x 轴,则椭圆上任意一点P 满足OS OT tOP +=uu r uu u r uu u r,符合题意;当0≠t 时,20202812412k tx k k ty k ⎧=⎪⎪+⎨-⎪=⎪+⎩∴2021812k x t k =⋅+,021412ky t k -=⋅+.------------------------------------------------------------9分 将上式代入椭圆方程得:()()42222222321611212k k t k t k +=++,整理得: 2221612k t k =+=21612k +是2k 的递增函数, 由212k <知,204t <<,所以(2,0)(0,2)t ∈-U ,综上可得(2,2)t ∈-. ----------------------------------------------------------------12分 21.解:(Ⅰ) 由题意知:函数()f x 的定义域为(1,)-+∞,且2331(21)(1)2()(23)()1(1)(1)ax x ax x x x a f x x x x ++-+-+'=-=+++,①当231a --≤时,即1a ≤时若0x >,则()0f x '>;若10x -<<,则()0f x '<此时()f x 在区间(0,)+∞上单调递增,在区间 (1,0)-上单调递减. ②当1230a -<-<,即312a <<时若1230x a x -<<->或,则()0f x '>; 若230a x -<<,则()0f x '<,此时()f x 在区间(1,23)a --,(0,)+∞上单调递增,在区间(23,0)a -上单调递减.③当2a -3=0时32a =时,()0f x '≥,故此时()f x 在区间(1,)-+∞上单调递增.④当230a ->时,即322a <≤时 若1023x x a -<<>-或,则()0f x '>,若023x a <<-,则()0f x '<,所以,此时()f x 在区间(1,0)-,(23,)a -+∞上单调递增,在区间上(0,23)a -单调递减.-----------------------6分(Ⅱ)显然1()g x g x ⎛⎫= ⎪⎝⎭,设()1()ln ()ln(1)ln x g x x x x x x ϕ==++-,则1()()x x ϕϕ=,因此()x ϕ在(0,)+∞上的最大值等于其在(0,1]上的最大值. --------------------------7分2111()(1)ln(1)()ln 11x x x x x x x ϕ'=-+++⋅--+,设2111()(1)ln(1)()ln 11h x x x x x x x=-+++⋅--+,2223222(1)[ln(1)](1)()(1)x x x x x h x x x +++-+'=+,由(Ⅰ)知,当2a =时,()f x 在区间(0,1]单调递减,所以222()ln(1)(0)0(1)x x f x x f x +=+-<=+,()0,h x '<所以函数()h x 在区间(0,1]单调递减,于是()(1)0h x h =≥, 从而函数()x ϕ在区间(0,1]单调递增,进而()(1)2ln 2x ϕϕ=≤, 因为()ln ()x g x ϕ=所以函数()g x 的最大值等于4. --------------------------------------------12分请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号. 22.解析:(Ⅰ)连接,可得,∴ ..............3分 又,∴,又为半径,∴是圆的切线; ..............5分(Ⅱ)过作于点,连接,则有,...............7分设,则,∴ ...............8分 由可得,又由, 可得. ...............10分23.解析:(Ⅰ)由,,可得, ...............1分 所以曲线的普通方程为(或), ...............3分因为直线的参数方程为(为参数,),消去得直线的普通方程为; ...............5分 (Ⅱ)因为曲线是以为圆心,1为半径的圆,因为点在曲线上,所以可设点, ...............7分 所以点到直线的距离为, ...............8分因为,所以当时,,...............9分此时点的坐标为................10分24.解析:(Ⅰ)因为,当且仅当时等号成立,所以,解得;...............5分(Ⅱ)证明:要证,即证,只需证,即证,又,,所以,所以,故原不等式成立................10分1.【答案】B【解析】由于1|32A x x ⎧⎫=-⎨⎬⎩⎭≤≤,{}0,1,2A B =I ,所以A B I 中有3个元素,故选B .2.【答案】D【解析】因为复数2(1)(1)i z a a =-++为纯虚数,所以21010a a ⎧-=⎨+≠⎩,即a =1,所以2016i 1i a ++=20161i 112(1i)2(1i)1i 1i 1i (1i)(1i)2++--====-+++-,故选D . 3.【答案】D【解析】已知函数()f x 可导,则“0()0f x '=”是“0x 是函数()f x 极值点”的必要不充分条件,故选D . 4.【答案】C【解析】基本事件总数7299C C 36==因为这9个数的和为45,而且取出的7个数之和为35,所以平均数为5的事件个数相当于从1与9;2与8;3与7;4与6这4组数中去掉一组数的个数,即共4个基本事件个数,所以取出七个数的平均数是5的概率为41=369,故选C . 5.【答案】A【解析】1322BD AD AB AC CD AB AC AB AB AC AB =-=+-=--=-u u u r u u u r u u u r u u u r u u u r u u u r u u u ru uu r u u u r u u u r u u u r ,故选A . 6.【答案】B【解析】由题意知tan tan 63b a ππ<<,所以222222241,4,3c a b b e a a a +⎛⎫⎛⎫===+∈ ⎪ ⎪⎝⎭⎝⎭所以e ⎫∈⎪⎪⎝⎭,故选B . 7.【答案】C【解析】22cos sin 22()x x x f x π⎛⎫=-+ ⎪⎝⎭=⋅ab cos 222sin 26x x x π⎛⎫==+ ⎪⎝⎭,易知只有C 选项正确. 8.【答案】C【解析】作出不等式组1040x y x y y m -+⎧⎪+-⎨⎪⎩≥≤≥对应的平面区域如图:由z =2x +y 得2y x z =-+,平移直线2y x z =-+,由图象可知:当直线2y x z =-+经过点A 时,直线的截距最大,此时z 最大,由40x y y m +-=⎧⎨=⎩,解得4x m y m =-⎧⎨=⎩,即(4,)A m m -,此时2(4)8z m m m =-+=-,当直线2y x z =-+经过点B 时,直线的截距最小,此时z 最小,由10x y y m -+=⎧⎨=⎩,解得1x m y m =-⎧⎨=⎩,即(1,)B m m -,此时2(1)32z m m m =-+=-,因为目标函数z =2x +y 的最大值是最小值的差为2,所以8322m m --+=,即m =2.故选C . 9.【答案】C【解析】由于程序中根据k 的取值,产生的T 值也不同由题意知,在循环体中,当*2()k n n =∈N 时,T =n ;当4+1()k n n =∈N 时,T =-n -1;当4+3()k n n =∈N 时,T =n+1;故可将程序中的k 值从小到大,每四个分为一组,即(1,2,3,4),(5,6,7,8)而且每组的4个数中,偶数值乘以12累加至S ,但两个奇数对应的T 值相互抵消,即10)8642(21=+++=S ,故选C . 10.【答案】A 【解析】()ln 21f x x ax '=-+,若函数()(ln )f x x x ax =-有极值,则函数()ln 21f x x ax '=-+有零点,即方程ln 21x ax =-有解,从而函数ln y x =与21y ax =-图象有公共点,下考虑直线21y ax =-与曲线ln y x =相切的情况: 设切点00(,21)P x ax -,∴001|2x x y a x ='==,即012x a =,∴1,02P a ⎛⎫⎪⎝⎭代入曲线ln y x =中,解得12a =,结合图象可知,当12a =时,()0f x '=有唯一零点,且恒有(0)0f '≤,此时()f x无极值点;当12a<时,函数lny x=与21y ax=-图象有交公共点,且在公共点两侧()f x'异号,此时()f x有极值点,故选A11.【答案】C【解析】由题意可知几何体的形状是放倒的圆柱,底面半径为1,高为2,左侧与一个底面半径为1,高为1的半圆锥组成的组合体.几何体的表面积为:22111212+1+1+121=+12222ππ⋅⋅π⋅π⋅π⋅⋅⋅(,故选C12.【答案】D【解析】1()121xtf x+=-+①当10t+=,即1t=-时,()1f x=,此时(),(),()f a f b f c都为1,能构成一个正三角形的三边长,满足题意.②当10t+>,即1t>-时,()f x在R上单调递增,∴()1t f x-<<,由,()f x为“可构造三角形函数”得12112t t-⇒-<-≥≤.③当10t+<,即1t<-时,()f x在R上单调递减,∴1()f x t<<-,由()f x为“可构造三角形函数”得221t t-⇒-<-≥≤.综上,122t--≤≤,故选D.二、填空题(本大题共4小题,每小题5分,共20分)13.【答案】1-14.【答案】2【解析】54(1+)(12)ax x-展开式的通项可以写成5454C()C(2)C C(2)m m n nm n m n m nax x a x+⋅-=-,所以2x的系数为020*********545454C C(2)C C(2)C C(2)16a a a-+-+-=-,即210402416a a-+=-,解得2a=.15. 两边同时乘以AB,212AB AO AB∙=16.【答案】32【解析】∵M在抛物线y2=2px(p>0)上,M到抛物线焦点的距离为P.∴M点的坐标为,2pp⎛⎫⎪⎝⎭;2222122212132222AB y y bc a e k x x a a ---=====-。