下载文档原格式
《自抗扰控制器研究及其应用》篇一一、引言自抗扰控制器（Active Disturbance Rejection Control, ADRC）作为一种先进的控制算法，以其独特的控制策略和优异的性能在复杂系统和不确定环境下表现出色。
它以鲁棒性强、适应性强和快速响应等优势，广泛应用于航空、航天、机器人、电力系统和制造业等多个领域。
本文将就自抗扰控制器的原理、研究进展以及应用进行详细的探讨。
二、自抗扰控制器的原理自抗扰控制器是一种基于现代控制理论的非线性控制方法，其核心思想是通过实时观测和估计系统的状态和扰动，从而实现对系统精确的控制。
它主要由三个主要部分组成：跟踪微分器、非线性状态误差反馈和状态观测器。
首先，跟踪微分器负责为系统提供平滑的参考信号及其微分值。
这有助于系统在受到干扰时保持稳定。
其次，非线性状态误差反馈将估计的状态误差通过非线性状态反馈函数生成控制量，使系统状态尽快回到参考值。
最后，状态观测器用于实时观测系统的状态和扰动，为非线性状态误差反馈提供必要的反馈信息。
三、自抗扰控制器的研究进展近年来，自抗扰控制器在理论研究和应用方面取得了显著的进展。
在理论研究方面，学者们对自抗扰控制器的稳定性、鲁棒性和性能优化等方面进行了深入研究，提出了一系列改进的算法和策略。
这些研究为自抗扰控制器在复杂系统和不确定环境下的应用提供了坚实的理论基础。
在应用方面，自抗扰控制器已广泛应用于航空、航天、机器人、电力系统和制造业等多个领域。
例如，在航空航天领域，自抗扰控制器被用于飞行器的姿态控制和轨迹跟踪等任务；在机器人领域，自抗扰控制器被用于机器人的运动控制和路径规划等任务；在电力系统中，自抗扰控制器被用于提高电力系统的稳定性和可靠性等任务。
这些应用充分展示了自抗扰控制器的优越性能和广泛的应用前景。
四、自抗扰控制器的应用1. 航空航天领域：在航空航天领域，自抗扰控制器被广泛应用于飞行器的姿态控制和轨迹跟踪等任务。
由于航空航天系统的复杂性和不确定性，传统的控制方法往往难以满足要求。
基于LabVIEW与MATLAB混合编程的自抗扰控制系统设计与仿真李思远;谷海宇;徐大富;赵阳【摘要】Using DC torque motor as a control obj ect,to compensate the inadequacies of the classic PID control system,ADRC control system is built by MATLAB/Simulink,and it is imported LabVIEW through Simulation Interface Toolkit.Finally NI PXIe-8135 controller is used as the next crew for real-time simulation.The simulation results show that the ADRC control system which can compensate for deficiencies in the classic PID control system with rapidity,accuracy and disturbance resistance and other aspects,and the feasibility of the system.%以直流力矩电机作为控制对象,对经典PID控制系统进行改进,采用LabVIEW与MATLAB/Simulink的混合编程方法搭建了自抗扰控制系统,并通过仿真接口工具包将其导入LabVIEW,以NI PXIe-8135控制器为下位机进行实时仿真,验证了自抗扰控制系统相比经典PID控制系统提高了系统的快速性、精度及抗扰能力,同时验证了联合仿真的可行性.【期刊名称】《测试技术学报》【年(卷),期】2016(030)006【总页数】6页(P461-466)【关键词】PID控制;自抗扰控制;混合编程;实时仿真【作者】李思远;谷海宇;徐大富;赵阳【作者单位】哈尔滨工业大学航天学院,黑龙江哈尔滨 150001;哈尔滨工业大学航天学院,黑龙江哈尔滨 150001;上海宇航系统工程研究所,上海 201108;哈尔滨工业大学航天学院,黑龙江哈尔滨 150001【正文语种】中文【中图分类】TP273.2在目前工程控制领域中，经典PID控制仍然作为主要的过程控制方法，是因为其工作原理与结构简单易于实现，但是在工程实际应用中存在许多缺陷，例如，直接对给定信号和输出信号取误差常常会在系统初始的时候出现很大的超调；对误差信号、误差微分信号与误差积分信号的线性加和并不是最佳的组合方式；在扰动随时间变化的情况下，控制效果不理想等[1]. 自抗扰控制是韩京清研究员运用特殊非线性效应发展而来的一种不依赖于被控对象精确数学模型的新型实用的控制方法，可以很好地解决PID控制在工程中存在的缺陷[2,3].常用的编程语言MATLAB具有十分强大的计算、仿真、绘图等功能，但是它在界面开发、仪器连接控制和网络通讯等方面都不如LabVIEW，若将两者结合起来，则可以充分利用两种语言的优势，更好地解决各个领域的问题[4]. Simulink是MATLAB最重要的组件之一，是一种可视化的仿真工具，用于实现动态系统建模、仿真和综合分析. 本文采用LabVIEW与Simulink混合编程的方法，对以直流力矩电机为控制对象的自抗扰控制器进行设计与仿真，解决控制系统快速性、精度及抗扰能力，并提供简洁的操作界面.NI LabVIEW仿真接口工具包Simulation Interface Toolkit，是LabVIEW专门为调用MATLAB/Simulink的工具，用户可以利用LabVIEW丰富的界面作为Simulink的输入、输出，同时可以利用LabVIEW数据采集程序或其它测量程序连接Simulink[5]. LabVIEW仿真接口工具包的组件如下：1) Model. 一个以图形化形式、源代码形式或者编译过的形式仿真结构图，该模型包括数据的输入输出接口、控制参数和可见信号.2) Host VI. 包括前面板和程序框图，可使用前面板控制模型参数.3) SIT Server. 使用TCP/IP在Host VI和模型之间传输数据的服务器. 首先必须在运行仿真之前启动SIT Server，默认情况下在端口6011上运行.4) Host Computer. 运行Windows NT/2000/XP等操作系统的PC.5) Execution Computer. 运行MATLAB软件、 SIT Server和仿真的计算机.本文以NI PXIe-8135作为 Execution Computer. NI PXIe-8135是基于Intel Core i7-3610QE处理器的高性能嵌入式控制器，结合2.3 GHz基频、 3.3 GHz 四核处理器和双通道1 600 MHz DDR3内存，具有8 GB/s系统带宽和4 GB/s 插槽带宽，2个Super Speed USB端口、 4个高速USB端口、 2个千兆以太网端口、 GPIB、串口和其他外设. 工作流程如图 1 所示.首先，Host VI使用TCP/IP发送新的参数给SIT服务器，SIT服务器传送这些参数给Model模型. 然后由Model模型再使用这些新的参数去执行更新信号值，SIT服务器检测已建立映射的模型信号. 最后SIT Server传输新的信号值给Host VI更新前面板的指示器.2.1 直流电机系统模型本文以直流力矩电机为控制对象，对其进行建模[6]，直流力矩电机的电磁平衡方程与转矩方程为式中： Um为电枢电压； Tm为电磁转矩； Cm，Km为转矩常数； Im为电枢电流； Lm为电枢电感； Rm为电枢电阻. 电机额定运行存在摩擦，以及转子与负载具有一定的质量惯量，电机转矩平衡方程为式中： Tf为机械摩擦及其他损耗造成的阻转矩； TL为电机的负载转矩； TJ为由电机转子和负载的转动惯量产生的力矩； B为粘滞系数；ω为角速度. 由直流力矩点及的转矩平衡和电磁平衡的方程经过拉普拉斯变换可推导出传递函数式中： J为电机转动惯量； Ke为反电动势系数，可继续得出电机位置环的数学模型式中：θ为电机转角，其他符号含义与上面公式相同.2.2 自抗扰控制系统结构自抗扰控制器是在经典PID控制器的基础上发展得出的新控制理念，它继承了经典PID控制的精华，并将其控制缺陷进行了改进[7]. 自抗扰控制系统结构如图 2 所示.利用二阶最速开关系统构造出非线性跟踪微分器，采用离散形式，可以更好地跟踪不连续信号，并提取其近似的微分信号，其表达式为式中： v(k)是第k时刻的输入信号；δ是决定微分器跟踪速度的参数；fst(·)函数是最速控制综合函数式中：通过以上的设计可以使跟踪微分器的输出同时可以过滤噪声信号.扩张状态观测器的作用[8,9]是将控制对象尚未完全已知的系统模型，转化成含有未知扰动的积分串联环节，同时对其进行观测，其中所测得的信号当中就有对扰动的实时估计值. 本文采用二阶扩张状态观测器，其结构如式(8)状态空间表达式式中： y为系统输出； b0为系统控制输入的增益； f(x1,x2,t)为系统全部未知扰动的总和，并将其扩张，所以得出从而对其建立扩张状态观测器式中： z是扩张状态观测器的各输出状态； e1是扩张状态观测器对系统输出信号跟踪误差； z3则逼近系统的未知扰动f(x1,x2,t).2.3 自抗扰控制器控制律设计自抗扰控制器中的控制律设计在传统PD算法的基础上加以改进，保留其基本的误差反馈形式，在局部采用非线性算法，构成了非线性PD控制算法[10]，其表达式为式中：fal(·)函数是为了避免高频振荡，将幂函数|e|αsign(e)转化成在原点附近具有线性段的连续幂次函数，即饱和函数，δ为线性段的区间长度，其表达式为根据以上推导，若令x1=θ，x2=ω，由式(4)和式(5)，可得到电机位置环的状态方程再利用MATLAB/Simulink中的S函数将各个部分模块化[11]，连接，得到控制系统模块图，如图 3 所示，其中包含TD跟踪微分器输出与实际信号的对比，以及位置、位置误差、速度、扰动估计等输出量，并与经典PID算法进行对比. 3.1 系统仿真界面设计利用LabVIEW编辑界面，并将Simulink模型导入[12]后，得到控制面板如图 4 所示，而前面板界面可以对模型参数进行设置，对输出结果进行显示，如图 5 所示.3.2 系统仿真结果仿真实验采用的直流力矩电机型号为55LY54，额定电压27 V，电枢电阻8.5 Ω，电枢电感1.57 mH，堵转转矩0.126 N·m，转矩常数0.036 4 N·m/A，反电动势系数0.015 3 V·s/rad，转动惯量4.4×10-5 kg·m2，最大转速1 500 r/m. 自抗扰控制器扩张状态观测器参数为β1=300，β=4 000，β3=20 000，h=0.001，α图6 系统阶跃响应Fig.6 Step response of system1=0.25，α2=0.5，δ=0.002 5，非线性PD取值KP=40，KD=5，经典PID取值同样为Kp=40，Ki=1，Kd=5，仿真时间设为5 s. 系统在负载扰动为2sin(2t+30°) N·m的正弦量与3 s处突加幅值为2 N·m的混合扰动下的阶跃响应如图 6 所示，输出信号的误差如图 7 所示，扩张状态观测器对系统扰动的估计如图 8 所示.图 6 系统阶跃响应Fig.6 Step response of system通过，LabVIEW操作界面可修改期望值与扰动值，在仿真试验中可以看出自抗扰控制器在对突变信号的响应速度上，相较经典PID控制的快速性更好，能够更好地跟踪适应突变的信号，通过误差比较，可得到经典PID最大误差为0.004 rad，而自抗扰控制器输出的最大误差不到 0.001 rad，所以自抗扰控制得到的控制精度更高，且不需要积分调节，在突加扰动时只有少许波动，控制效果很好. 扩张状态观测器对负载扰动的观测基本与输入的扰动值相符，可以很好地补偿扰动. 同时，系统在LabVIEW软件调用下，运行稳定，可以方便地添加与实际设备的输入输出接口，有利于实际应用.本文采用LabVIEW与MATLAB/Simulink混合编程的方法搭建了自抗扰控制系统，通过仿真分析验证了系统的可行性与其良好的控制效果，LabVIEW具有简洁的操作界面，方便更改参数，并且可以进行实时仿真，同时仿真接口工具包含有与外界实物的接口，可将控制对象或控制器替换为实物，从而有针对性地解决实际应用问题.【相关文献】[1] 苏思贤. 自抗扰控制器及其应用研究[D]. 无锡：江南大学，2011.[2] 韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京：国防工业出版社，2009.[3] 黄一，薛文超. 自抗扰控制：思想、应用及理论分析[J]. 系统科学与数学，2012，32(10)： 1-21. Huang Yi, Xue Wenchao. ADRC control： ideology, application and theoretical analysis[J]. Journal of Systems Science and Mathematical Sciences, 2012, 32(10)： 1-21. (in Chinese)[4] 袁培铎. 基于LabVIEW与MATLAB混合编程的应用研究[J]. 机械制造与自动化，200(6)： 15-37. Yuan Peiduo. Application based on LabVIEW and MATLAB[J]. Machine Building, 200(6)：15-37. (in Chinese)[5] 吴成东，孙秋野，盛科. LabVIEW 虚拟仪器程序设计及应用[M]. 北京：人民邮电出版社，2008.[6] 叶恭宇. 基于自抗扰控制的机器人关节控制系统[D]. 浙江：浙江大学，2013.[7] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Trans. Ind.Electron，2009，56(3)： 900-906.[8] 黄一，韩京清. 非线性连续二阶扩张状态观测器的分析与设计[J]. 科学通报， 2000， 45(13)：1373-1378. Huang Yi, Han Jingqing. Analysis and design of second order nonlinear continuous ESO[J]. Science Bulletin, 2000, 45(13)： 1373-1378. (in Chinese)[9] 韩京清. 自抗扰控制技术[J]. 前沿科学，2007，1(1)： 24-31. Han Jingqing. ADRC control technology[J]. Frontier of Science, 2007, 1(1)： 24-31. (in Chinese)[10] 韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程，2002，9(3)： 13-18. Han Jingqing. From PID technology to “ADRC control”[J]. Scientific Journal of Control Engineering, 2002, 9(3)： 13-18. (in Chinese)[11] 王兵树，姜萍，林永君. Simulink中自抗扰控制技术自定义模块库的创建[J]. 系统仿真学报，2010，22(3)： 610-615. Wang Bingshu, Jiang Ping, Lin Yongjun. Simulink in disturbance rejection control technology to create a custom module library[J]. Journal of System Simulation, 2010, 22(3)： 610-615. (in Chinese)[12] 曲丽蓉，胡容，范寿康. LabVIEW、 MATLAB及其混合编程技术[M]. 北京：机械工业出版社，2011.。
基于Simulink的火炮伺服系统自抗扰控制仿真作者：郭婧杨刚杨军贾强来源：《现代电子技术》2014年第10期摘要：为了解决火炮伺服系统存在负载变化大、冲击扰动力矩强等问题，将自抗扰控制技术应用到火炮伺服系统位置控制器中。
该控制算法通过实时估计与补偿来弥补传统控制方法的不足。
通过在Simulink软件平台搭建了ADRC的火炮伺服系统三环模型，仿真结果对比传统PID控制。
对比结果表明，基于ADRC的系统超调小、响应速度较快、具有较强的鲁棒性。
关键词： Simulink；伺服系统；自抗扰；火炮中图分类号： TN964⁃34 文献标识码： A 文章编号： 1004⁃373X（2014）10⁃0120⁃03Abstract： An active disturbance rejection control （ADRC） technology is proposed for an artillery servo system with load disturbance and large disturbed moment. It is to be used in the location controller in the artillery servo system. The control method made up insufficient of the traditional control method by real⁃time estimation and compensation. Three⁃loop model （speed loop， location loop and current loop） of artillery servo system with closed⁃loop ADRC was established in the Simulink software. It was compared with the traditional PID mode control method. The simulation results show the system based on ADRC technology has the advantages ofhigh⁃speed response， less overshoot and strong robustness.Keywords： Simulink； servo system； ADRC； antillery0 引言某火炮伺服系统是一个具有冲击力矩强、负载变化大等特点的非线性系统。
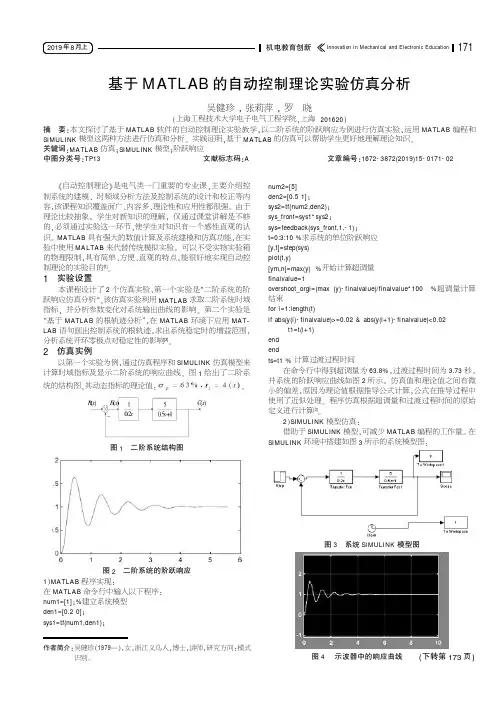
(下转第173页)《自动控制理论》是电气类一门重要的专业课,主要介绍控制系统的建模、时频域分析方法及控制系统的设计和校正等内容,该课程知识覆盖面广、内容多、理论性和应用性都很强。
由于理论比较抽象,学生对新知识的理解,仅通过课堂讲解是不够的,必须通过实验这一环节,使学生对知识有一个感性直观的认识。
MATLAB 具有强大的数值计算及系统建模和仿真功能,在实验中使用MALTAB 来代替传统模拟实验,可以不受实物实验箱的物理限制,具有简单、方便、直观的特点,能很好地实现自动控制理论的实验目的[1]。
1实验设置本课程设计了2个仿真实验,第一个实验是“二阶系统的阶跃响应仿真分析”,该仿真实验利用MATLAB 求取二阶系统时域指标,并分析参数变化对系统输出曲线的影响。
第二个实验是“基于MATLAB 的根轨迹分析”,在MATLAB 环境下应用MAT ⁃LAB 语句画出控制系统的根轨迹,求出系统稳定时的增益范围,分析系统开环零极点对稳定性的影响[2]。
2仿真实例以第一个实验为例,通过仿真程序和SIMULINK 仿真模型来计算时域指标及显示二阶系统的响应曲线。
图1给出了二阶系统的结构图,其动态指标的理论值:。
图1二阶系统结构图图2二阶系统的阶跃响应1)MATLAB 程序实现:在MATLAB 命令行中输入以下程序:num1=[1];%建立系统模型den1=[0.20];sys1=tf(num1,den1);num2=[5]den2=[0.51];sys2=tf(num2,den2);sys_front=sys1*sys2;sys=feedback(sys_front,1,-1);t=0:3:10%求系统的单位阶跃响应[y,t]=step(sys)plot(t,y)[ym,n]=max(y)%开始计算超调量finalvalue=1overshoot_orgi=(max (y)-finalvalue)/finalvalue*100%超调量计算结束for i=1:length(t)if abs(y(i)-finalvalue)>=0.02&abs(y(i+1)-finalvalue)<0.02t1=t(i+1)end endts=t1%计算过渡过程时间在命令行中得到超调量为63.8%,过渡过程时间为3.73秒,并系统的阶跃响应曲线如图2所示。
