集体备课稿三角恒等变换
- 格式:doc
- 大小:1.82 MB
- 文档页数:19

三角恒等变换备课教案备课教案:三角恒等变换一、引言三角恒等变换是高中数学中的重要内容,对于学生深入理解三角函数的性质和应用具有重要意义。
本教案将通过引导学生发现和探究三角恒等变换的规律,帮助学生理解和掌握相关的变换技巧。
二、知识背景1. 三角函数的基本关系:(1) 正弦函数:sinθ = 对边/斜边(2) 余弦函数:cosθ = 邻边/斜边(3) 正切函数:tanθ = 对边/邻边2. 三角函数的周期性:(1) 正弦函数、余弦函数的周期是2π(2) 正切函数的周期是π3. 三角函数的基本恒等式:(1) 余弦函数的平方与正弦函数的平方和为1:cos^2θ + sin^2θ = 1(2) 正切函数与余切函数的乘积始终等于1:tanθ · cotθ = 1(3) 正弦函数与余切函数、余弦函数与正切函数的关系:sinθ/cotθ = cosθcosθ/tanθ = sinθ三、教学过程1. 引入:通过提问的方式引导学生回顾三角函数的基本关系和周期性规律。
2. 发现:给出一个具体的三角函数等式,例如sinθ = cos(π/2 - θ),请学生尝试寻找与之相关的恒等式。
3. 探究:根据学生的发现,引导学生使用初等三角函数的定义和已知的三角函数恒等式,进行推导和证明,找出恒等式的变换规律。
4. 总结:整理学生的发现和推导过程,总结三角恒等变换的基本规律,并给出示例进行演示和讲解。
5. 练习:提供一些练习题,让学生运用所学的三角恒等变换规律,解决相关的三角函数等式和问题。
四、教学评价1. 通过观察学生的推导过程和解题思路,评价他们对三角恒等变换规律的理解和掌握情况。
2. 提供针对性的反馈和指导,帮助学生纠正错误和加深对知识点的理解。
3. 鼓励学生积极参与课堂讨论和解题过程,培养他们的合作和思考能力。
五、课后作业1. 题目一:证明sin(π/2 - θ) = cosθ。
2. 题目二:利用三角恒等变换,化简并求解tanθ + 1 = secθ的解。
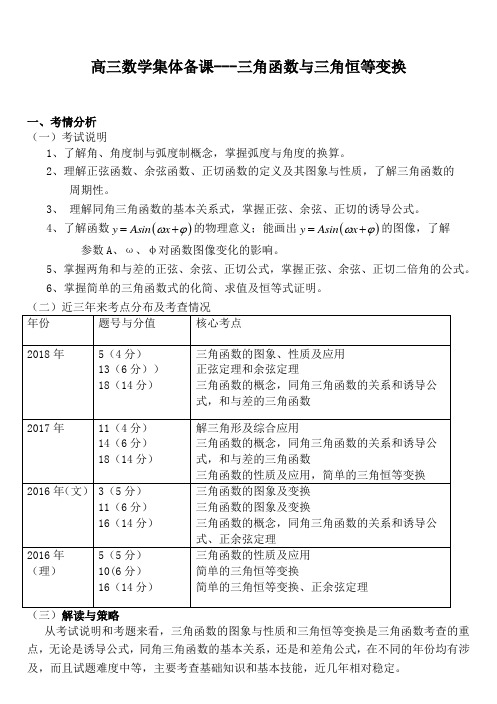
高三数学集体备课---三角函数与三角恒等变换一、考情分析 (一)考试说明1、了解角、角度制与弧度制概念,掌握弧度与角度的换算。
2、理解正弦函数、余弦函数、正切函数的定义及其图象与性质,了解三角函数的周期性。
3、 理解同角三角函数的基本关系式,掌握正弦、余弦、正切的诱导公式。
4、了解函数()y Asin x ωϕ=+的物理意义;能画出()y Asin x ωϕ=+的图像,了解参数A 、ω、φ对函数图像变化的影响。
5、掌握两角和与差的正弦、余弦、正切公式,掌握正弦、余弦、正切二倍角的公式。
6、掌握简单的三角函数式的化简、求值及恒等式证明。
从考试说明和考题来看,三角函数的图象与性质和三角恒等变换是三角函数考查的重点,无论是诱导公式,同角三角函数的基本关系,还是和差角公式,在不同的年份均有涉及,而且试题难度中等,主要考查基础知识和基本技能,近几年相对稳定。
三角解答题以往考查解三角形较多,因为解三角形的试题相对灵活,但文理不分科后,作为入门级的试题,合并三角变换的三角函数题会成为主流,当然也不排除考查简单的正余弦定理和面积公式,可以确定的是,一定不会用到太多技巧,容易入手,能得分,是应有之意。
二、真题回顾【2018浙江,18】已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P ().(Ⅰ)求sin (α+π)的值;(Ⅱ)若角β满足sin (α+β)=,求cos β的值.【2017浙江,18】已知函数()()22f x sin x cos x x R =--∈(I )求2f 3π⎛⎫⎪⎝⎭的值 (II )求()f x 的最小正周期及单调递增区间。
[2016年理](5)设函数2()sin sin f x x b x c =++,则()f x 的最小正周期( )A .与b 有关,且与c 有关B .与b 有关,但与c 无关C .与b 无关,且与c 无关D .与b 无关,但与c 有关 [2016年文] (3) 函数2sin y x =的图象是( )(10)已知22cos sin 2sin()(0)x x A x b A ωφ+=++>,则A =__ _,b =________.浙江三角函数高考的热点:(1)三角函数的概念、诱导公式及同角三角函数的基本关系(2) sin()y A x k ϖϕ=++图像(周期,单调性,对称轴,最值)体现了函数研究的惯例。

三角恒等变换教案一、教学目标1. 知识与技能:(1)理解三角恒等变换的概念和意义;(2)掌握三角恒等变换的基本公式;(3)能够运用三角恒等变换解决实际问题。
2. 过程与方法:(1)通过观察、分析、归纳三角恒等变换的规律;(2)培养学生的逻辑思维能力和运算能力。
3. 情感态度与价值观:(1)激发学生对数学的兴趣和探究欲望;(2)培养学生的团队合作意识和克服困难的勇气。
二、教学内容1. 三角恒等变换的概念和意义;2. 三角恒等变换的基本公式;3. 三角恒等变换的运用。
三、教学重点与难点1. 教学重点:(1)三角恒等变换的概念和意义;(2)三角恒等变换的基本公式;(3)三角恒等变换的运用。
2. 教学难点:(1)三角恒等变换公式的灵活运用;(2)解决实际问题时的变形和计算。
四、教学方法1. 采用问题驱动法,引导学生主动探究三角恒等变换的规律;2. 通过示例讲解,让学生掌握三角恒等变换的基本公式;3. 利用练习题和小组讨论,提高学生的实际应用能力和团队合作意识。
五、教学过程1. 导入新课:(1)复习相关三角函数知识;(2)提问:什么是三角恒等变换?为什么学习三角恒等变换?2. 知识讲解:(1)讲解三角恒等变换的概念和意义;(2)介绍三角恒等变换的基本公式;(3)示例讲解:如何运用三角恒等变换解决实际问题。
3. 课堂练习:(1)布置练习题,让学生独立完成;(2)选取部分学生的作业进行讲解和评价。
4. 小组讨论:(1)让学生分组讨论,分享解题心得和经验;5. 课堂小结:(1)回顾本节课所学内容;(2)强调三角恒等变换在数学和实际生活中的重要性。
6. 课后作业:(1)布置巩固练习题;(2)鼓励学生自主学习,深入探究三角恒等变换的运用。
六、教学评价1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答的正确性以及与同学的合作情况。
2. 练习作业评价:检查学生作业的完成质量,包括答案的正确性、解题方法的合理性以及书写的规范性。

简单的三角恒等变换(一)张掖中学 宋娟一、教学目标知识与技能:理解并掌握二倍角的正弦、余弦、正切公式,并会利用公式进行简单的恒等变形,体会三角恒等变形在数学中的应用;过程与方法:通过二倍角的变形公式推导半角的正弦、余弦、正切公式,体会化归、方程、逆向使用公式的数学思想,提高学生推理能力;情感、态度与价值观:通过例题的讲解,让学生体会化归、变形使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生推理能力. 二、教学重、难点教学重点:利用公式进行简单的恒等变换;教学难点:利用倍角公式推出半角公式,并利用变形的方法解决问题. 三、教学方法:探究式教学法. 四、教学类型:新授课. 五、教学内容复习引入(学生组织完成)问题1:和差角的正弦、余弦、正切公式(六个); 问题2:二倍角的正弦、余弦、正切公式(三个); 问题3:二倍角的变形公式(四个). 新课讲解思考1(学生组织完成):如何用cos α表示222sin cos tan 222ααα、、?分析:观察α与2α的关系是2倍的关系,所以我们要利用刚刚学过的二倍角的变形公式.解:α是2α的二倍角.在倍角公式2cos 212sin αα=-中,以α代替2α,以2α代替α,即得2cos 12sin 2αα=-,所以21cos sin 22αα-=; ①在倍角公式2cos 22cos 1αα=-中,以α代替2α,以2α代替α,即得2cos 2cos 12αα=-,所以21cos cos 22αα+=. ②将①②两个等式的左右两边分别相除,即得21cos tan 21cos ααα-=+.思考2:若已知cos α,如何计算sincos tan 222ααα、、?sincos tan 222ααα=== (半角公式) 强调:“±”号由2α所在象限决定. 例1:已知5sin 13α=,且2παπ<<,求tan 2α的值.解512sin cos 13213,tan24222tan tan 522πααπαππαπααπαα=<<∴=-<<∴<<∴>=====因为且又由公式例2 求证sin 1cos tan 21cos sin ααααα-==+ 证明22sin sin2cossin sin 222tan21cos cos cos 2cos 2cos 2222sin sin 2sin 2sin1cos 2222tan2sin sin coscos2sin222αααααααααααααααααααααα⋅====+⋅⋅-====⋅利用例2的结论,再做一下例1,比较两种方法.例3 已知3sin 25θ=,022πθ<<,求22cos sin 12)4θθπθ--+.分析:由降幂公式知22cos 1cos 2αα=+,故有cos sin cos sin θθθθ-=+原式 ﹡ 此处有两种处理方法:方法一、由已知求出cos sin θθ、的值,带入﹡式计算,即可得到结果; 方法二、由﹡继续变形,将半角化为倍角进行计算. 解法一22cos sin......cos sin020cos0,sin02434sin2,02cos2525cos212sin2cos1sin121010θθθθππθθθθπθθθθθθθθ-=*+<<∴<<∴>>=<<==-=-∴==**==原式由由得又带入式得解法二222cos sincos sin(cos sin)(cos sin)(cos sin)12sin cos1sin2......cos sin cos234sin2,02cos252532115544255θθθθθθθθθθθθθθθθπθθθ-=+-=+---==*-=<<=*-*==原式由得带入式得=小结:对于例3,我们从不同角度出发,解法一先利用倍角计算半角,再带入求值,解法二先利用半角化为倍角,再带入求值.在三角恒等变换中,正所谓“条条大路通罗马”.在以后的学习当中,此类问题是三角恒等变换中常见的问题.万丈高楼平地起,在此告诫同学们,基础知识的理解和必要的记忆是很重要的,所以在以后的学习中,不管题目如何变化,都有一个固定的解题理论,那就是我们的倍角公式,及其逆用,掌握好了基础的理论知识,不管题目如何变化,我们都能将他们各个击破.所谓“咬定青山不放松,任尔东南西北风”.下面我们来分小组讨论一下这一个问题:(练一练)化简22221sin sin cos cos cos2cos22αβαβαβ⋅+⋅-⋅.分析:1.从“角”入手,倍角化半角;2.从“幂”入手,利用降幂公式将次;3.从“形”入手,利用配方法.本题目至少有6种解法,请同学们讨论完成.课堂小结三个数学方法1.从“角”入手,倍角化半角(半角化倍角);2.从“幂”入手,利用降幂公式将次(利用升幂公式升次);3.从“形”入手,利用配方法(分母有理化、分子有理化).两个人生哲理1.条条大路通罗马;2.咬定青山不放松,任尔东南西北风.布置作业习题3.2A组1(1)、(2)、(4)、(5)课后反思。

高中数学教学备课教案三角恒等变换和解三角形高中数学教学备课教案三角恒等变换和解三角形一、引言数学是一门抽象的科学,对于高中数学教学备课教案的设计,对于学生的学习效果起着至关重要的作用。
本文将以三角恒等变换和解三角形为主题,探讨高中数学教学备课教案设计的相关内容。
二、三角恒等变换的基础概念1. 直角三角形的基础知识在教学备课的过程中,首先需要复习直角三角形的基本概念,如斜边、邻边、对边、正弦定理、余弦定理等。
2. 三角恒等变换的定义及相关恒等式通过引导学生回顾三角函数的定义及其各自的特点,帮助他们掌握三角恒等变换的几个重要恒等式,如正弦恒等式、余弦恒等式和正切恒等式。
三、教学备课教案的设计1. 知识目标的明确化在教学备课阶段,教师需要明确本次教学的主要目标,例如学生能够熟练掌握三角恒等变换的定义、掌握基本的恒等式,并能够应用到解决实际问题中。
2. 教学过程的设计为了提高教学效果,我们可以采用以下教学步骤:a. 播放相关视频或动画,引发学生的兴趣,激发他们对三角恒等变换的学习兴趣。
b. 通过教师讲解和示范,帮助学生理解三角恒等变换的意义和应用。
c. 以案例分析的方式,引导学生运用三角恒等变换恒等式解决具体问题。
d. 通过小组合作或课堂讨论的方式,让学生彼此交流,分享解题思路和方法,加深对三角恒等变换的理解和掌握。
3. 思考题的设计在备课过程中,我们可以设计一些思考题,以帮助学生提高解题能力和思维能力。
例如:a. "给定一个直角三角形,如果已知一个角的值和某一边的长度,如何求解其他两边的长度?请详细解答。
b. "如何通过正弦恒等式和余弦恒等式来解决实际问题?请提供一个具体的案例进行说明。
四、课堂实施与评估1. 有效的教学辅助工具在教学实施中,教师可以运用多媒体教学辅助工具,如投影仪、电子白板等,使学生更好地理解三角恒等变换的概念和应用。
2. 学习效果的评估根据教学备课教案的设计目标,我们可以采用以下方式对学生的学习效果进行评估:a. 给学生布置相关练习,检查他们对三角恒等变换的掌握情况。

三角恒等变换教案一、教学目标1. 知识与技能:(1)理解三角恒等变换的概念和意义;(2)掌握三角恒等变换的基本公式;(3)能够运用三角恒等变换解决实际问题。
2. 过程与方法:(1)通过观察和分析,培养学生的逻辑思维能力;(2)通过练习和应用,提高学生解决实际问题的能力。
3. 情感态度与价值观:(1)培养学生对数学学科的兴趣和好奇心;(2)培养学生的团队合作意识和解决问题的自信心。
二、教学内容1. 三角恒等变换的概念和意义(1)引入三角函数的定义和图像;(2)解释三角恒等变换的含义和作用。
2. 三角恒等变换的基本公式(1)sin(α±β)的公式;(2)cos(α±β)的公式;(3)tan(α±β)的公式。
三、教学过程1. 导入(1)复习相关三角函数的定义和图像;(2)提出问题,引导学生思考三角恒等变换的必要性。
2. 新课讲解(1)讲解三角恒等变换的概念和意义;(2)引导学生推导三角恒等变换的基本公式。
3. 练习与应用(1)布置相关的练习题,巩固学生对三角恒等变换的理解;(2)引导学生运用三角恒等变换解决实际问题。
四、教学评价1. 课堂讲解的评价:(1)观察学生在课堂上的参与度和理解程度;(2)通过提问和回答,检查学生对三角恒等变换的理解。
2. 练习题的评价:(1)检查学生完成练习题的情况和答案的正确性;(2)分析学生在解题过程中存在的问题和错误,及时进行反馈和指导。
五、教学资源1. 教学PPT:包含三角恒等变换的概念、意义和基本公式的讲解;2. 练习题:提供相关的练习题,供学生巩固和应用所学知识;3. 教学参考书:提供详细的三角恒等变换的讲解和例题。
六、教学策略1. 案例分析:通过分析具体的三角函数例子,让学生理解恒等变换的应用。
2. 小组讨论:让学生分组讨论三角恒等变换的性质,促进学生之间的交流和合作。
3. 问题解决:设计一些实际问题,让学生运用所学的三角恒等变换知识去解决,提高学生的应用能力。
教学计划:《三角恒等变换》一、教学目标知识与技能:学生能够理解并掌握三角恒等变换的基本公式,包括和差化积、积化和差、二倍角公式等。
学生能够熟练运用三角恒等变换公式进行化简、求值及证明。
培养学生的逻辑推理能力和代数运算能力。
过程与方法:通过观察、分析、归纳等数学活动,引导学生发现三角恒等变换的规律。
采用“公式推导—例题讲解—练习巩固”的教学模式,帮助学生逐步掌握三角恒等变换的方法。
鼓励学生自主探究,通过小组合作解决复杂问题,培养团队协作能力。
情感态度与价值观:激发学生对数学学习的兴趣,感受数学的美妙与和谐。
培养学生的耐心和细心,养成严谨的科学态度。
引导学生认识到数学在解决实际问题中的重要性,增强应用数学的意识。
二、教学重点和难点重点:三角恒等变换的基本公式及其推导过程;运用公式进行化简、求值及证明。
难点:灵活运用三角恒等变换公式解决复杂问题;理解并记忆众多公式的内在联系。
三、教学过程1. 导入新课(5分钟)情境引入:通过展示一些与三角恒等变换相关的实际问题(如天文学中的角度计算、物理学中的波动分析等),引导学生思考这些问题背后可能涉及的数学知识,从而引出三角恒等变换的主题。
复习旧知:简要回顾三角函数的基本性质、图像及诱导公式,为学习三角恒等变换做好铺垫。
明确目标:介绍本节课的学习目标,即掌握三角恒等变换的基本公式及其应用。
2. 公式推导(15分钟)和差化积公式推导:通过图形展示和代数运算相结合的方式,引导学生推导出和差化积公式。
强调公式的推导过程,帮助学生理解公式的来源和含义。
积化和差公式推导:类比和差化积公式的推导过程,引导学生自主推导积化和差公式。
鼓励学生提出疑问和见解,促进课堂互动。
二倍角公式推导:利用三角函数的倍角关系,引导学生推导出二倍角公式。
强调公式的记忆方法和应用技巧。
3. 例题讲解(10分钟)基础例题:选取具有代表性的基础例题进行讲解,如利用三角恒等变换公式化简表达式、求三角函数值等。
高中数学备课教案三角恒等变换的综合应用高中数学备课教案:三角恒等变换的综合应用导言:三角恒等变换是数学中的重要概念,它在各个数学领域都有广泛的应用。
本教案旨在帮助高中数学教师更好地教授三角恒等变换,并通过综合的应用案例,帮助学生提高解题能力和理解能力。
一、知识回顾1. 三角恒等变换的基本概念回顾(这部分可以罗列出三角恒等变换的基本公式、性质等)2. 三角函数的基本关系回顾(这部分可以涵盖正弦定理、余弦定理等)二、应用案例在实际问题中,三角恒等变换常常被用于解决各种几何、物理、工程等问题。
以下是几个常见的应用案例。
案例一:三角形面积计算题目描述:已知三角形ABC的边长分别为a、b、c,通过应用三角恒等变换,求解三角形ABC的面积。
解题思路:1. 根据海伦公式,可以利用三角恒等变换将面积计算问题转化为边长计算问题。
2. 具体求解步骤可参考以下算法:①计算半周长s=(a+b+c)/2;②计算面积S=s*(s-a)*(s-b)*(s-c)的平方根;③输出结果。
案例二:三角函数方程求解题目描述:已知三角函数方程sin(x)=cos(x),通过应用三角恒等变换,求解x的值。
解题思路:1. 利用三角恒等变换将sin(x)和cos(x)转化为同一种三角函数。
2. 具体求解步骤可参考以下算法:①利用tan(x)=sin(x)/cos(x)将sin(x)和cos(x)转化为tan(x);②将sin(x)=cos(x)代入tan(x)=sin(x)/cos(x),得到tan(x)=1;③求解tan(x)=1的解集,即x={π/4+kπ|k∈Z};④输出结果。
案例三:三角函数图像变换题目描述:已知函数y=sin(x),通过应用三角恒等变换,绘制函数y=sin(2x)的图像。
解题思路:1. 利用三角恒等变换将sin(2x)转化为sin(x)。
2. 具体绘图步骤可参考以下算法:①绘制函数y=sin(x)的基本图像;②沿x轴方向缩放两倍,即将x坐标缩小为原来的一半;③在新的坐标系下,绘制函数y=sin(x)的图像;④输出结果。
数学教案三角恒等变换数学教案:三角恒等变换引言:三角恒等变换是高中数学中的重要内容,它在解题过程中具有广泛的应用。
本教案将通过多种实例,引导学生理解三角恒等变换的概念、性质及应用,提高学生解决三角函数相关问题的能力。
一、知识导入:基本概念与性质(500字左右)1. 引入:提出实际中的三角形问题,引发学生思考三角形之间的关系。
2. 提出三角恒等变换的概念,并解释其意义和用途。
3. 结合基本三角函数的定义,介绍三角恒等变换的性质和基本公式。
二、基本恒等变换(500字左右)1. 说明三角恒等变换的基本形式,并给出示例。
2. 推导和解释基本恒等变换的推导过程,帮助学生理解其中的数学原理。
3. 针对不同类型的三角函数,列举相应的基本恒等变换公式。
三、应用实例一:解三角方程(500字左右)1. 提供一些实际问题,通过三角恒等变换的方法,将其转化为解方程的问题。
2. 引导学生通过恒等变换的方式,解决多种类型的三角方程。
3. 鼓励学生总结解题方法和技巧,帮助他们深入理解三角恒等变换的实际应用。
四、应用实例二:三角函数的求值与简化(500字左右)1. 提供一些实际问题,要求学生利用三角恒等变换简化复杂的三角函数式子。
2. 引导学生通过代入不同的角度值,比较不同的三角函数值,推导出恒等变换的结果。
3. 帮助学生发现并总结三角函数简化的一般规律。
五、综合应用:证明三角恒等式(500字左右)1. 提出一些已知的三角恒等式,要求学生通过恒等变换的方式来证明其正确性。
2. 指导学生进行恒等变换的证明过程,注重逻辑推理和数学推导的合理性。
3. 提供一些挑战性问题,鼓励学生运用恒等变换证明复杂的三角恒等式。
六、总结与拓展(200字左右)1. 总结三角恒等变换的基本思想和方法,强调其在解题中的重要性。
2. 提供一些额外的拓展问题,引导学生进一步思考和应用所学的三角恒等变换知识。
3. 引导学生关注数学以及实际生活中的三角形相关问题,并从中发现和解决问题的方法。
三角恒等变换【1】(A ,新课标I ,理2)sin 20cos10-cos160sin10=A.2-B.2C.12-D.12【2】(A ,重庆,文6)若11tan,tan()32,则tan = A.17 B.16 C.57 D.56【3】(C ,重庆,理9)若5tan 2tan πα=则=--)5sin()103cos(παπα A.1 B.2 C.3 D.4【4】(A ,四川,理12) 75sin 15sin +的值是___.【5】(B ,四川,文13)已知0cos 2sin =+αα,则ααα2cos cos sin 2-的值是 .【6】(B ,江苏,文理8)已知2tan -=α,71tan =+)(βα,则βtan 的值为 .【7】(A ,广东,文16)已知tan 2α=.(1)求tan()4πα+的值;(2)求2sin 2sin sin cos cos 21ααααα+--的值.解三角形【1】(A ,广东,文5)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若2a =,c =cos A =b c <,则b = A.3B. C.2【2】(A ,湖北,文15理13)如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75的方向上,仰角为30,则此山的高度CD = m.【3】(A ,广东,理11).设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c,若a = 1sin 2B =,6C π=,则b = .【4】(A ,福建,理12)若锐角ABC ∆的面积为,且5,8AB AC ==,则BC 等于 .【5】(B ,北京,文11)在ABC △中,3=a ,6=b ,3π2=∠A ,则=∠B .【6】(B ,北京,理12)在ABC ∆中,6,5,4===c b a 则=CA sin 2sin . 【7】(B ,天津,理13)在△ABC 中,内角C B A ,,所对的边分别为c b a ,,.已知△ABC 的面积为153,2=-c b ,41cos -=A ,则a 的值为 . 【8】(B ,重庆,文13)设ABC ∆的内角A ,B ,C 的对边分别为,,a b c ,且2a =,1cos 4C =-,3sin AAB第2题图2sin B =,则c = .【9】(B ,重庆,理13)在ABC ∆中,120B =AB =A 的角平分线,3=AD 则.____=AC【10】(B ,安徽,文12)在ABC ∆中,AB =,A ∠=75,B ∠=45,则=AC .【11】(B ,福建,文14)若ABC ∆中,AC 45A =,75C =,则BC = .【12】(C ,新课标I ,理16)在平面四边形ABCD 中,75A B C ∠=∠=∠=,2BC =,则AB 的取值范围是 .【13】(A ,新课标I ,文17)已知,,a b c 分别是ABC ∆内角,,A B C 的对边,2sin 2sin sin B A C =.(I)若a b =,求cos B ;(II)若90B =,且a = 求ABC ∆的面积. 【14】(A ,新课标Ⅱ,文17)△ABC 中,D 是BC 上的点,AD 平分BAC ∠,DC BD 2=.(I)求CB∠∠sin sin ;(II)若60BAC ∠=,求B ∠.【15】(A ,新课标Ⅱ,理17)△ABC 中,D 是BC 上的点,AD 平分BAC ∠,△ABD 面积是△ADC 面积的2倍. (I)求sin sin BC∠∠; (II)若1,,2AD DC ==求BD 和AC 的长. DCAB第14、15题图【16】(A ,天津,文16)△ABC 中,内角A ,B ,C 所对的边分别为,c ,b ,a 已知△ABC 的面积为 .cos41-,2==-A c b (I)求a 和C sin 的值; (II)求)cos(62πA +的值.【17】(A ,山东,文17)ABC ∆中,角C B A ,,所对的边分别为c b a ,,,且已知,33cos =B 32,96)sin(==+ac B A ,求A sin 和c 的值. 【18】(A ,江苏,文理15)在ABC ∆中,已知2=AB ,3=AC , 60=A .(1)求BC 的长; (2)求C 2sin 的值.【19】(A ,安徽,理16)在ABC ∆中,A ∠=34π,6AB =,AC =D 在BC 边上,BD AD =,求AD 的长.【20】(A ,湖南,理17)ABC ∆的内角C B A ,, 的对边分别为c b a ,,,A b a tan =,且B 为钝角.(I)证明:2π=-A B ;(II)求C A sin sin +的取值范围.【21】(A ,陕西,文17理17)ABC ∆的内角C B A ,,所对的边分别为c b a ,,.向量)3,(b a =与)sin ,(cos B A =平行.(I)求A ;(II)若2,7==b a ,求ABC ∆的面积.【22】(B ,上海,文21)如图,,,O P Q 三地有直道相通,3OP =千米,4PQ =千米,5OQ =千米.现甲、乙两警员同时从O 出发匀速前往Q 地,经过t 小时,他们之间的距离为()f t (单位:千米).甲的路线是OQ ,速度5千米/小时,乙的路线是OPQ ,速度是8千米/小时.乙到达Q 地后在原地等待.设1t t =时,乙到达P 地;2t t =时,乙到达Q 地.(1)求1t 与1()f t 的值;(2)已知警员的对讲机的有效通话距离是3千米.当12t t t ≤≤时,求()f t 的表达式,并判断()f t 在12[,]t t 上的最大值是否超过3?说明理由.【23】(B ,上海,理20)如图,,,A B C 三地有直道相通,5AB =千米,3AC =千米,4BC =千米.现甲、乙两警员同时从A 地出发匀速前往B 地,经过t 小时,他们之间的距离为()f t (单位:千米).甲的路线是AB ,速度为5千米/小时,乙的路线是ACB ,速度为8千米/小时.乙到达B 地后在原地等待.设1t t =时,乙到达C 地. (1)求1t 与1()f t 的值;(2)已知警员的对讲机的有效通话距离是3千米.当11t t ≤≤时,求()f t 的表达式,并判断()f t 在1[,1]t 上的最大值是否超过3?说明理由.【24】(B ,四川,文19)已知C B A ,,为ABC ∆的内角,B A tan ,tan 是关于x 的方程px x 32+)(01R p p ∈=+-的两个实根.PQO第22题图BCA第23题图(1)求C 的大小;(2)若6,3==AC AB ,求p 的值. 【25】(B ,四川,理19)如图,D C B A ,,,为平面四边形ABCD 的四个内角.(1)证明:AAA sin cos 12tan-=; (2)若,3,6,180===+BC AB C A ,4=CD 5=AD ,求2tan 2tan 2tan 2tanDC B A +++的值.【26】(B ,浙江,文16)在ABC ∆中,内角C B A ,,所对的边分别为c b a ,,.已知2)4tan(=+A π.(I)求AA A2cos 2sin 2sin +的值; (II)若3,4==a B π,求ABC ∆的面积.【27】(B ,浙江,理16)在△ABC 中,内角C B A ,,所对的边分别为c b a ,,.已知4π=A ,22212b ac -=.(I)求C tan 的值;(II)若△ABC 的面积为3,求b 的值.【28】(B ,湖南,文17)设ABC ∆的内角,,A B C 的对边分别为,,,tan a b c a b A =.(I)证明:sin cos B A =;BCDA第25题图(II)若3sin sin cos 4C A B -=,且B 为锐角,求,,A B C .三角恒等变换【1】(A ,新课标I ,理2)、D解析:原式sin 20cos10=+cos 0sin1021sin302==.错误!未找到引用源。
【2】(A ,重庆,文6)、A解析:)tan(tan a b a b -+= = 71tan )tan(1tan )tan(=++-+a b a a b a 1tan 7b ∴=.【3】(C ,重庆,理9)、C解析:=--)5sin()103cos(παπα5sincos 5cos sin 103sin sin 103cos cos παπαπαπα-+ 5sin 5cos tan 103sin tan 103cos ππαπαπ-+=5sin5cos 5tan 2103sin5tan 2103cos ππππππ-+=.35sin 5sin 3==ππ【4】(A ,四川,理12)、26解析:sin15sin 75sin15cos15+=+2660sin 2== . 【5】(B ,四川,文13)、1-解析:由0cos 2sin =+αα知2tan -=α,所以22sin cos cosααα-=2222sin cos cos sin cos αααα-+.11tan 1tan 22-=+-=αα【6】(B ,江苏,文理8)、3解析:法1 因为tan()αβ+tan tan 1tan tan αβαβ+=-17=,又2tan -=α,所以3tan =β. 法2 ])tan[(tan αβαβ-+=αβααβαtan )tan(1tan )tan(++-+= 3)2(711)2(71=-⨯+--=.【7】(A ,广东,文16)解析:(1)因为tan 2α=,所以321124tantan 14tantan )4tan(-=-+=-+=+παπαπα.2sin 22sin sin cos cos 21ααααα+--()1)1cos 2(cos sin sin cos sin 222---+=αααααα222sin cos sin sin cos 2cos αααααα=+-22tan tan tan 2ααα=+-41422==+-.解三角形【1】(A ,广东,文5)、C解析:由余弦定理得:A bc c b a cos 2222-+=,所以233221242⋅⋅-+=b b ,即0862=+-b b ,解得2=b 或4=b .因为c b <,所以2=b .【2】(A ,湖北,文15理13)、6100解析:由题意知图中⊥DC 面ABC ,DBC ∠=30,CAB ∠=30,ABC ∠=105,因而ACB ∠=45, 在ABC ∆中由正弦定理得sin 45sin 30AB BC=,其中600=AB m, 故2300=BC m ,610033==BC CD m. 【3】(A ,广东,理11)、1解析:因为1sin 2B =且(0,)B π∈, 所以6B π=或23A B C ππ=--=,又a = 由正弦定理sin sin a bA B=,可得1b =. 【4】(A ,福建,理12)、7【解析】:由已知得ABC ∆的面积为1sin 20sin 2AB AC A A ⋅==sin 2A =,(0,)2A π∈,所以3A π=.由余弦定理得2222cos BC AB AC AB AC A =+-⋅=49,7BC =.【5】(B ,北京,文11)、4π解析:由正弦定理,得sin sin a b A B ==sin B =,所以4π=∠B .【6】(B ,北京,理12)、1解析:436521636252cos 222=⨯⨯-+=-+=bc a c b A .132432cos 2sin cos sin 2sin 2sin =⨯⨯===A c a C A A C A . 【7】(B ,天津,理13)、8解析:415sin ,153sin 21===∆A A bc S ABC ,24=∴bc 222()252b c b c bc ∴+=-+=22212cos 5248644a b c bc A ∴=+-=+⨯=.8=∴a【8】(B ,重庆,文13)、4解析:由3sin 2sin AB 可得32a b =且2a =所以3b =,又因12,cos ,4a C代入余弦公式可解4c =. 【9】(B ,重庆,理13)、6解析:在ABD ∆中,由正弦定理得︒=∠120sin 3sin 2ADB ,所以,4π=∠ADB 故 ︒=∠15BAD ,又AD 平分角A ,则,30︒=∠BAC 由此可得ABC ∆是底角为︒30等腰三角形,所以在ABC ∆中易得.6=AC【10】(B ,安徽,文12)、2解析:如图所示,在ABC ∆中,由正弦定理可知:sin(1807545)AB--sin 45AC=,所以2=AC . 【11】(B ,福建,文14)解析:由题意得18060B A C =--=,由正弦定理得sin sin AC BCB A=,则sin sin AC ABCB=,所以BC ==【12】(C ,新课标I,理16)、解析:若D 与C 重合,此时AB 最小:2cos75AB BC =⋅⋅=.若D 与E 重合,此时,A与E 重合,AB 最大:CDEAB第12题图ABC第10题图1cos75AB====. 故AB的取值范围为. 【13】(A ,新课标I ,文17)解析:(I)由题设及正弦定理可得22b ac =. 又a b =,可得2a b c ==由余弦定理,得2221cos 24a cb B ac +-== (II)由(I)知22b ac =.因为B =o90,由勾股定理得222a cb +=.故222a c ac +=,得a c ==所以△ABC 的面积为1.【14】(A ,新课标Ⅱ,文17)解析:(I)由正弦定理得sin sin AD BDB BAD=∠∠,sin sin AD DC C CAD =∠∠, 因为AD 平分∠BAC , BD =2DC ,所以sin sin B C ∠∠DC BD =12=. (II)法1:因为180()C BAC B ∠=-∠+∠60,BAC ∠=所以sin C ∠sin()BAC B =∠+∠1cos sin 22B B =∠+∠, 由(I)知2sin B ∠ sin C =∠,所以tan B ∠=30B ∠=. 法2:由(I)可知AC AB 2=, 在ABC ∆中,由余弦定理可得222BC AB AC =+2cos60AB AC -⋅22242AC AC AC =+- 23AC =,所以AC BC 3=,由余弦定理得cos B ∠2222AB BC AC AB BC +-=⋅222=2=,因为0180B <<,所以30B ∠=. 【15】(A ,新课标Ⅱ,理17)解析:(I)法1:依题意2ABD ADC S S ∆∆=,BAD ∠CAD =∠. 因为1sin 2ABD S AB AD BAD ∆=⋅∠, ADC S ∆1sin 2AD AC CAD =⋅∠,所以2AB AC =.由正弦定理得sin 1sin 2B ABC AC ∠==∠. 法2:设ABC ∆的BC 边上的高为h , 由题设可得22121==⋅⋅=∆∆DC BD DC h BDh S S ADCABD, 由角平分线定理得DC BD AC AB =,由正弦定理得AC AB sin sin BC∠=∠, 所以21sin sin =∠∠C B (II)因为ABD S ∆:ADC S ∆=BD :DC,所以BD =在ABD ∆和ADC ∆中,由余弦定理知2222cos AB AD BD AD BD ADB =+-⋅∠,2AC 222cos AD DC AD DC ADC =+-⋅∠.故2AB22222326AC AD BD DC +=++=.由(I)知AB2AC =,所以1AC =.【16】(A ,天津,文16)解析:(I)在△ABC 中,由,41-=A cos可得sin 4A =由15321==A sin bc S ABC Δ. 得,bc 24=又由,c b 2=-解得.c ,b 46== 由,A cos bc c b a 2222-+=可得.a 8=由,Csin cA sin a =得.sin 815=C (II)626262πA πA πA sin sin cos cos )cos(-=+A A A cos sin )cos (⋅⨯--=22112232.163715-=【17】(A ,山东,文17)解析:在ABC ∆中,由33cos =B ,得 36sin =B 因为π=++C B A , 所以96)sin(sin =+=C B A . 因为B C sin sin <,所以B C <,可知C 为锐角, 所以935cos =C . 322sin cos cos sin )sin(sin =+=+=C B C B C B A 由CcA a sin sin =可得,c CAc a 32sin sin ==又32=ac ,所以1=c . 【18】(A ,江苏,文理15)解析:(1)由余弦定理知,222BC AB AC =+2cos AB AC A -⋅⋅72132294=⨯⨯⨯-+=, 所以7=BC ;(2)由正弦定理知,ABCC AB sin sin =, 所以721760sin 2sin sin ==⋅= A BC AB C . 因为BC AB <,所以C 为锐角, 则772731sin 1cos 2=-=-=C C .因此734cos sin 22sin =⋅=C C C . 【19】(A ,安徽,理16)解析:设ABC ∆的内角C B A ,,所对的边分别为c b a ,,,由余弦定理得:90cos 2222=-+=A bc c b a ,所以103=a .又由正弦定理得1010sin sin ==a Ab B , 由题设知40π<<B ,所以10103cos =B , 在ABD ∆中,由正弦定理得)2sin(sin B BAB AD -=πB B B cos sin 2sin 6=10cos 3==B.【20】(A ,湖南,理17)解析:(I)由A b a tan =及正弦定理,得B Ab a A A sin sin cos sin ==,所以A B cos sin =,即 )2sin(sin A B +=π. 又B 为钝角,),2(2πππ∈+A ,故A B +=2π,即2π=-A B . (II)由(I)知 022)(>-=+-=A B A C ππ, 所以)4,0(π∈A .于是)22sin(sin sin sin A A C A -+=+πA A 2cos sin +=2sin 12sin A A2192(sin )48A .因为40π<<A ,所以 22sin 0<<A ,因此8989)41(sin 2222≤+--<A . 由此可得C A sin sin +的取值范围是]89,22(. 【21】(A ,陕西,文17理17)解析:(I)因为n m //,所以-B a sin =A b cos 30,由正弦定理得0cos sin 3sin sin =-A B B A ,又0sin ≠B ,从而3tan =A ,由于π<<A 0,所以3π=A .(II)法1 由余弦定理得A bc c b a cos 2222-+=,而2,7==b a ,3π=A ,得c c 2472-+=,即0322=--c c ,因为0>c ,所以3=c .故ABC ∆的面积为233sin 21=A bc . 法2 由正弦定理得Bsin 23sin7=π,从而=B sin 721,又由b a >,知B A >,所以772cos =B ,)3sin()sin(sin π+=+=B B A C +=3cos sin πB 142133sin cos =πB .所以ABC ∆的面积为233sin 21=C ab . 【22】(B ,上海,文21)解析:(1)有已知138t =,设此时甲到A 地,则315588OA =⋅=. 在POA 中,222AP OP OA =+2cos OP OA POQ -⋅⋅⋅∠22151533693()2388564=+-⨯⨯⨯=.所以1()f t =(2)由已知278t =,当12[,]t t t ∈,即37[,]88t ∈时,甲位于A 地,乙位于B 地,则55,78QA t QB t =-=-,()f t AB =====max 3()() 3.88f t f ==<所以()f t 在12[,]t t 上的最大值不超过3. 【23】(B ,上海,理20)解析:(1)138t =,此时甲位于AB 之间与A 距离158千米处,又3cos 5A =,故13()()8f t f ===.(2)当78t =时,乙到达B 处,故当718t ≤≤时,()5(1)f t t =-; 当3788t ≤≤时,设甲位于P 处,乙位于Q 处,则55,78BP t BQ t =-=-,4cos 5B =,此时()f t =故37[,],88()755,(,1].8t f t t t ∈=⎨⎪-∈⎪⎩=故当37[,]88t∈时,3()()388f t f ≤=<;而7[,1]8t ∈时,()f t 单调递减,从而 75()() 3.88f t f <=<综上,()f t 在1[,1]t 上的最大值不超过3. 【24】(B ,四川,文19)解析:(1)由已知,方程0132=+-+p px x的判别式)1(4)3(2+--=p p ∆04432≥-+=p p ,所以2-≤p 或32≥p . 由韦达定理,有,3tan tan p B A -=+p B A -=1tan tan . 于是33tan tan 1tan tan )tan(-=-=-+=+ppB A B A B A .所以3)tan(tan =+-=B A C ,所以60=C .(2)由正弦定理,sin sin AC CB AB==22=,解得 45=B 或 135=B (舍去). 于是 75180=--=C B A . 则32)3045tan(75tan tan +=+== A . 所以)tan (tan 31B A p +-=31)132(31--=++-=.【25】(B ,四川,理19)解析:(1)2cos2sin 22sin 22cos 2sin2tan 2A A AA A A ==AAsin cos 1-=; (2)由题意,B D A C -=-=180,180,由(1)得2tan 2tan 2tan 2tan D C B A +++ 1cos 1cos 1cos(180)sin sin sin(180)A B A A B A ----=++-1cos(180)sin(180)B B --+-BA sin 2sin 2+= 连接BD ,在ABD ∆中,有222BD AB AD =+-A AD AB cos 2⋅,在BCD ∆中,有22BD BC =2CD +2cos BC CD C -⋅. 则)(2cos 2222CD BC AD AB CD BC AD AB A ⋅+⋅--+=73)4356(245362222=⨯+⨯--+=.于是7102cos 1sin 2=-=A A . BCDA第25题图连接AC ,同理可得)(2cos 2222CD AD BC AB CD AD BC AB B ⋅+⋅--+=191)4536(245362222=⨯+⨯--+=.于是19106cos 1sin 2=-=B B . 所以2tan 2tan 2tan 2tanD C B A +++ 310410619210272sin 2sin 2=⨯+⨯=+=B A . 【26】(B ,浙江,文16)解析:(I)由2)2π(t =+A an ,得31t =anA 所以2sin22tan 2sin 2cos 2tan 15A A A A A ==++. (II)由()π,,031t ∈=A anA ,得1010sin =A , 10103cos =A . 又由3,4==a B π及正弦定理BbA a sin sin =, 得53=b ,由)sin(sinB AC +=)4sin(π+=A 得552sin =C . 设ABC ∆的面积为S ,则9sin 21==C ab S . 【27】(B ,浙江,理16)解析:(I)由22221c a b =-及正弦定理得:B 2sin C 2sin 2121=-,所以C B 2sin 2cos =-.又由4π=A ,即π43=+C B ,得 ==-C B 2sin 2cos C C cos sin 2,解得2tan =C .(II)由tan 2C =,()0,C π∈得:552sin =C ,55cos =C .又因为)4sin()sin(sin C C A B +=+=π, 故有10103sin =B .由正弦定理得b c 322=,又因为4π=A ,3sin 21=A bc ,所以26=bc ,故3=b .【28】(B ,湖南,文17)解析:(I)由tan a b A =及正弦定理,得sin sin cos sin A a AA b B==,所以sin cos B A =. (II)sin sin cos C A B -=sin(180())A B -+sin cos A B -sin()sin cos A B A B =+-sin cos cos sin A B A B =+sin cos A B -cos sin A B =,3cos sin 4A B ∴=.由(I )知sin cos B A =,因此23sin 4B =,又B为钝角,所以sin B =,故120B =,由cos sin A B ==知30A =,从而180()30C A B =-+=. 综上所述,30A =,120B =,30C =.。