浙江省温州市鹿城区实验中学2020-2021学年九年级上学期期末数学试题

2021年浙江省温州市鹿城区中考数学一模试卷一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．（4分）3的相反数是（）A．3B．﹣3C．D．﹣2．（4分）截止2021年3月21日，电影《你好，李焕英》的票房已突破5310000000元，其中数据5310000000用科学记数法表示为（）A．53.1×108B．5.31×108C．0.531×109D．5.31×109 3．（4分）如图所示，某物体由4块立方体组成，它的主视图是（）A．B．C．D．4．（4分）一只不透明的盒子里装有9个只有颜色不同的球，其中红球4个、白球3个、黑球2个．从盒子里任意摸出1个球，是红球的概率为（）A．B．C．D．5．（4分）某校举办了一次“交通安全知识“测试，王老师从全校学生的答卷中随机地抽取了200名学生的答卷，并将测试成绩分为A，B，C，D四个等级，绘制成如图所示的条形统计图．若该校学生共有1000人，则该校成绩为A的学生人数估计为（）A．30B．75C．150D．2006．（4分）如图，小华在课外时间利用仪器测量红旗的高度，从点A处测得旗杆顶部B的仰角为α，并测得到旗杆的距离AC为l米，若AD为h米，则红旗的高度BE为（）A．（l tanα+h）米B．（）米C．l tanα米D．米7．（4分）一家工艺品厂按计件方式结算工资．小鹿去这家工艺品厂打工，第一天工资60元，第二天比第一天多做了5件，工资为75元．设小鹿第一天做了x件，根据题意可列出方程为（）A．＝B．＝C．＝D．＝+5 8．（4分）《几何原本》里有一个图形：在△ABC中，D，E是边AB上的两点（AD＜AE），且满足AD＝BE．过点D，E分别作BC的平行线，过点D作AC的平行线，它们将△ABC 分成如图的5个部分，其面积依次记为S1，S2，S3，S4，S5．若S2＝18，S3＝6，则S4的值为（）A．9B．18C．27D．549．（4分）在平面直角坐标系中，点M，N的坐标分别为（0，4），（3，4），若抛物线y＝a （x﹣2）2+3与线段MN有且只有一个交点，则a的值可以是（）A．B．C．1D．10．（4分）如图，E，F分别是正方形ABCD边AB，BC上的点，BE＝BF＝2．以DE，DF 为边作▱DEGF，连接GE并延长交AD于点H，连接HF．若HF⊥ED，则AE的长为（）A．B．C．2﹣2D．2﹣2二、填空题（本题有6小题，每小题5分，共30分）11．（5分）因式分解：a2﹣3a＝．12．（5分）不等式2x﹣1＞3的解集是．13．（5分）已知圆的半径为2cm，90°圆心角所对的弧长为cm．14．（5分）如图，点A（2，2）在反比例函数y＝（x＞0）的图象上，则△BCD的面积为．15．（5分）如图，直线l1：y＝x+3分别与x轴，y轴交于点A，B，直线l2：y＝﹣x+m分别与x轴，y轴交于点C，D，直线l1，l2相交于点E，将△ABO向右平移5个单位得到△A′B'O'，若点B′恰好落在直线l2上，则DE：B'C＝．16．（5分）某厂家设计一种双层长方体垃圾桶，AB＝70cm，BC＝25cm，CP＝30cm，侧面如图1所示，EG为隔板，等分上下两层．下方内桶BCGH绕底部轴（CP）旋转打开，若点H恰好能卡在原来点G的位置，则内桶边BH的长度应设计为cm；现将BH调整为25cm，打开最大角度时，点H卡在隔板上，如图2所示，可完全放入下方内桶的球体的直径不大于cm．三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）17．（5分）计算：2sin30°+﹣20210．18．（5分）化简：（a﹣1）2﹣a（a+2）．19．（8分）如图，在△ABC中，AB＝AC，点D，E在BC上（BD＜BE），BD＝CE．（1）求证：△ABD≌△ACE．（2）若∠ADE＝2∠B，BD＝2，求AE的长．20．（8分）某学校在一次广播操比赛中，901班，902班，903班的各项得分如表：班级服装统一动作整齐动作标准901班857085902班758580903班908595（1）若取三个项目的得分平均分作为该班成绩，分别求各班的成绩．（2）若学校认为三个项目的重要程度各不相同，从低到高依次为“服装统一”“动作整齐”“动作准确”，它们在总分中所占的比例分别为10%，a%，b%．请你设计一组符合要求的a，b值，并直接给出三个班级的排名顺序．21．（8分）如图，将一个长为8，宽为6的大矩形分割成如图所示24个全等的小长方形，它们的顶点称为格点．请按下列要求分别作出格点三角形和格点四边形．（1）在图1中画出一个等腰△PCD，使点A，B在△PCD内部（不包括在△PCD边上）．（2）在图2中画出一个矩形QEFG，使点A，B在矩形QEFG内部（不包括在矩形QEFG 边上）．22．（10分）如图，抛物线y＝﹣（x﹣m）2+9交x轴于A，B两点，点A在点B左侧，点C 的坐标为（6，0），AC＜BC，过点C作CD⊥x轴交抛物线于点D，过点D作DE⊥CD 交抛物线于点E．（1）若点A的坐标为（4，0），求DE的长．（2）当DE＝AB时，求m的值．23．（10分）如图，AB是⊙O的直径，点C为圆上一点，点D为的中点，连接AD，作DE⊥AB交BC的延长线于点E．（1）求证：DE＝EB．（2）连接DO并延长交BC于点F．若CF＝2CE，BD＝5，求⊙O的半径．24．（12分）下表是某奶茶店的一款奶茶近两天的销售情况．销售情况销售数量（单位：杯）销售收入（单位：元）小杯大杯第一天2030460第二天2525450（1）问这款奶茶小杯和大杯的销售单价各是多少元？（2）已知这款奶茶小杯成本4元/杯，大杯成本5元/杯，奶茶店每天只能供应80杯该款奶茶，其中小杯不少于10杯，求该款奶茶一天的最大利润．（销售利润＝销售收入﹣成本）（3）为了满足市场的需求，奶茶店推出每杯2元的加料服务，顾客在选完杯型后可以自主选择加料或者不加料．小明恰好用了208元购买该款奶茶，其中小杯不加料的数量是总杯数的，则小明这款奶茶大杯加料的买了杯．25．（14分）如图，在矩形ABCD中，BC＝1，AB＝2，过对角线BD上一点P作AB的垂线交AB于点F，交CD于点E，过点E作EG∥BD交BC于点G，连接FG交BD于点H，连接DF．（1）求的值．（2）当四边形DFGE有一组邻边相等时，求BG的长．（3）点B关于FG的对称点记为B'，若B'落在△EFG内部（不包含边界），求DP长度的取值范围．2021年浙江省温州市鹿城区中考数学一模试卷参考答案与试题解析一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．（4分）3的相反数是（）A．3B．﹣3C．D．﹣【解答】解：根据相反数的概念及意义可知：3的相反数是﹣3．故选：B．2．（4分）截止2021年3月21日，电影《你好，李焕英》的票房已突破5310000000元，其中数据5310000000用科学记数法表示为（）A．53.1×108B．5.31×108C．0.531×109D．5.31×109【解答】解：5310000000000＝5.31×109．故选：D．3．（4分）如图所示，某物体由4块立方体组成，它的主视图是（）A．B．C．D．【解答】解：从正面看易得底层有3个正方形，上层中间有一个正方形．故选：B．4．（4分）一只不透明的盒子里装有9个只有颜色不同的球，其中红球4个、白球3个、黑球2个．从盒子里任意摸出1个球，是红球的概率为（）A．B．C．D．【解答】解：袋子中球的总数为9，而红球有4个，则从中任摸一球，恰为红球的概率为．故选：D．5．（4分）某校举办了一次“交通安全知识“测试，王老师从全校学生的答卷中随机地抽取了200名学生的答卷，并将测试成绩分为A，B，C，D四个等级，绘制成如图所示的条形统计图．若该校学生共有1000人，则该校成绩为A的学生人数估计为（）A．30B．75C．150D．200【解答】解：1000×＝150（人），即该校成绩为A的学生人数估计为150人，故选：C．6．（4分）如图，小华在课外时间利用仪器测量红旗的高度，从点A处测得旗杆顶部B的仰角为α，并测得到旗杆的距离AC为l米，若AD为h米，则红旗的高度BE为（）A．（l tanα+h）米B．（）米C．l tanα米D．米【解答】解：如图，DE＝1米，∠BAC＝α，DE＝h米，四边形ADEC为矩形，则DE＝AC＝1米，AD＝CE＝h米，在Rt△ADC中，∵tan∠BAC＝，∴BC＝1tanα，∴BE＝BC+CE＝（1tanα+h）米．故选：A．7．（4分）一家工艺品厂按计件方式结算工资．小鹿去这家工艺品厂打工，第一天工资60元，第二天比第一天多做了5件，工资为75元．设小鹿第一天做了x件，根据题意可列出方程为（）A．＝B．＝C．＝D．＝+5【解答】解：设小鹿第一天做了x件，则第二天比第一天多做了（x+5）件，依题意得：＝．故选：A．8．（4分）《几何原本》里有一个图形：在△ABC中，D，E是边AB上的两点（AD＜AE），且满足AD＝BE．过点D，E分别作BC的平行线，过点D作AC的平行线，它们将△ABC 分成如图的5个部分，其面积依次记为S1，S2，S3，S4，S5．若S2＝18，S3＝6，则S4的值为（）A．9B．18C．27D．54【解答】解：如图，连接GF，∵AD＝BE，DG∥AC，EF∥BC，∴＝＝＝，∵∠DHE＝∠GHF，∴△DHE∽△GHF，∴＝（）2，∵S2＝18，S3＝6，∴＝，S△HGF＝S3，∴S△DHE＝（）2×3＝27，则S4的值为27．故选：C．9．（4分）在平面直角坐标系中，点M，N的坐标分别为（0，4），（3，4），若抛物线y＝a （x﹣2）2+3与线段MN有且只有一个交点，则a的值可以是（）A．B．C．1D．【解答】解：∵抛物线y＝a（x﹣2）2+3，∴该抛物线的顶点坐标为（2，3），∵点M，N的坐标分别为（0，4），（3，4），抛物线y＝a（x﹣2）2+3与线段MN有且只有一个交点，∴，解得≤a＜1，故选：B．10．（4分）如图，E，F分别是正方形ABCD边AB，BC上的点，BE＝BF＝2．以DE，DF为边作▱DEGF，连接GE并延长交AD于点H，连接HF．若HF⊥ED，则AE的长为（）A．B．C．2﹣2D．2﹣2【解答】解：如图，延长BC至Q，使得CQ＝AE，连接EF，∵四边形ABCD是正方形，∴∠A＝∠B＝∠ADC＝∠BCD＝90°，AB＝CD＝BC＝AD，AD∥BC，∵BE＝BF，∴AB﹣BE＝BC﹣BF，即AE＝CF，在△AED和△CFD中，，∴△AED≌△CFD（SAS），∴DE＝DF，∠1＝∠4，∵四边形DEGF是平行四边形，∴四边形DEGF是菱形，∴DE∥GF，DF＝FG，∵HF⊥ED，∴∠HFG＝90°，∴∠1+∠2＝90°，∠4+∠ADF＝90°，∴∠HDF＝∠2，∴HF＝DF，∴HF＝GF，∴△GFH是等腰直角三角形，∴∠G＝∠EDF＝45°，∠1＝∠4＝22.5°，在△AED与△CDQ中，，∴△AED≌△CDQ（SAS），∴DE＝DQ，∠1＝∠3＝22.5°，∴∠FDQ＝45°，在△EDF与△QDF中，，∴△EDF≌△QDF（SAS），∴EF＝FQ＝2AE，∵BE＝BF＝2，∴EF＝＝2，∴AE＝．故选：B．二、填空题（本题有6小题，每小题5分，共30分）11．（5分）因式分解：a2﹣3a＝a（a﹣3）．【解答】解：a2﹣3a＝a（a﹣3）．故答案为：a（a﹣3）．12．（5分）不等式2x﹣1＞3的解集是x＞2．【解答】解：2x﹣1＞3，移项得：2x＞3+1，合并同类项得：2x＞4，不等式的两边都除以2得：x＞2，故答案为：x＞2．13．（5分）已知圆的半径为2cm，90°圆心角所对的弧长为πcm．【解答】解：圆的半径为2cm，90°圆心角所对的弧长为：l＝＝π（cm），故答案为：π．14．（5分）如图，点A（2，2）在反比例函数y＝（x＞0）的图象上，则△BCD的面积为．【解答】解：将点A（2，2）代入y＝，得：2＝，∴k＝4，∴y＝，∴B（1，4），C（3，），∵D（3，4），∴BD＝2，CD＝4﹣＝，∴S△BCD＝BD•CD＝×2×＝，故答案为：．15．（5分）如图，直线l1：y＝x+3分别与x轴，y轴交于点A，B，直线l2：y＝﹣x+m分别与x轴，y轴交于点C，D，直线l1，l2相交于点E，将△ABO向右平移5个单位得到△A′B'O'，若点B′恰好落在直线l2上，则DE：B'C＝20：21．【解答】解：因为y＝x+3，所以B（0，3），将B向右平移5个单位后B′（5，3），因为B′在直线l2：y＝﹣x+m上，所以m＝8，所以l2：y＝﹣x+8，所以D（0，8），C（8，0），因为直线l1，l2相交于点E，所以x+3＝﹣x+8得x＝，所以y＝，所以E（），作EH⊥y轴于H，由△DHE∽△COB′得，，所以DE：B'C＝20：21，故答案为：20：21．16．（5分）某厂家设计一种双层长方体垃圾桶，AB＝70cm，BC＝25cm，CP＝30cm，侧面如图1所示，EG为隔板，等分上下两层．下方内桶BCGH绕底部轴（CP）旋转打开，若点H恰好能卡在原来点G的位置，则内桶边BH的长度应设计为10cm；现将BH调整为25cm，打开最大角度时，点H卡在隔板上，如图2所示，可完全放入下方内桶的球体的直径不大于21cm．【解答】解：如图1中，连接CH，过点H作HT⊥CG于T，z则四边形BCTH是矩形．∵CG＝CH＝CD＝35cm，HT＝BC＝25cm，∴BH＝CT＝＝＝10（cm），如图2中，连接CH，过点G作GJ⊥CG′于J，过点B′作B′M⊥GH于M交BC于N．∵∠HMB′＝∠B′NC＝∠CB′H＝90°，∴∠B′HM+∠HB′M＝90°，∠HB′M+∠CB′N＝90°，∴∠B′HM＝∠CB′N，在△B′MH和△CNB′中，，∴△B′MH≌△CNB′（AAS），∴MH＝NB′，MB′＝CN，∵CH＝25cm，CG＝35，∴HG＝＝＝5，设HM＝x，则CN＝MB′＝x+5，在Rt△MHB′中，则有x2+（x+5）2＝252，∴x＝15，∴CN＝20（cm），NB′＝15（cm），∴sin∠BCB′＝＝，∵∠B′CG′＝∠BCG＝90°，∴∠GCG′＝∠BCB′，∴sin∠GCG′＝，∴GJ＝C•sin∠GCG′＝35×＝21（cm），∴可完全放入下方内桶的球体的直径不大于21cm，故答案为：10，21．三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）17．（5分）计算：2sin30°+﹣20210．【解答】解：原式＝2×+3﹣1＝1+3﹣1＝3．18．（5分）化简：（a﹣1）2﹣a（a+2）．【解答】解：（a﹣1）2﹣a（a+2）＝a2﹣2a+1﹣a2﹣2a＝1﹣4a．19．（8分）如图，在△ABC中，AB＝AC，点D，E在BC上（BD＜BE），BD＝CE．（1）求证：△ABD≌△ACE．（2）若∠ADE＝2∠B，BD＝2，求AE的长．【解答】（1）证明：∵AB＝AC，∴∠B＝∠C，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵∠ADE＝2∠B，∴∠B＝∠BAD，∴BD＝AD＝2，∵△ABD≌△ACE，∴AE＝AD＝2．20．（8分）某学校在一次广播操比赛中，901班，902班，903班的各项得分如表：班级服装统一动作整齐动作标准901班857085902班758580903班908595（1）若取三个项目的得分平均分作为该班成绩，分别求各班的成绩．（2）若学校认为三个项目的重要程度各不相同，从低到高依次为“服装统一”“动作整齐”“动作准确”，它们在总分中所占的比例分别为10%，a%，b%．请你设计一组符合要求的a，b值，并直接给出三个班级的排名顺序．【解答】解：（1）901班平均成绩为（85+70+85）÷3＝80（分），902班平均成绩为（75+85+80）÷3＝80（分），903班平均成绩为（90+85+95）÷3＝90（分）；（2）取a＝40，b＝50，901班平均成绩为85×10%+70×40%+85×50%＝79（分），902班平均成绩为75×10%+85×40%+80×50%＝81.5（分），903班平均成绩为90×10%+85×40%+95×50%＝90.5（分），所以903第一名，902第二名，901第三名．21．（8分）如图，将一个长为8，宽为6的大矩形分割成如图所示24个全等的小长方形，它们的顶点称为格点．请按下列要求分别作出格点三角形和格点四边形．（1）在图1中画出一个等腰△PCD，使点A，B在△PCD内部（不包括在△PCD边上）．（2）在图2中画出一个矩形QEFG，使点A，B在矩形QEFG内部（不包括在矩形QEFG 边上）．【解答】解：（1）如图，△PCD即为所求作（答案不唯一）．（2）如图，矩形QEFG即为所求作（答案不唯一）．22．（10分）如图，抛物线y＝﹣（x﹣m）2+9交x轴于A，B两点，点A在点B左侧，点C 的坐标为（6，0），AC＜BC，过点C作CD⊥x轴交抛物线于点D，过点D作DE⊥CD 交抛物线于点E．（1）若点A的坐标为（4，0），求DE的长．（2）当DE＝AB时，求m的值．【解答】解：（1）把A（4，0）代入y＝﹣（x﹣m）2+9得﹣（4﹣m）2+9＝0，解得m＝1或m＝7，∵点A在点B左侧，∴m＝7，即抛物线的对称轴为直线x＝7，∵CD⊥x轴，DE⊥CD，∴点E与点D关于直线x＝7对称，而D点的横坐标为6，∴DE＝2×（7﹣6）＝2；（2）当y＝0时，﹣（x﹣m）2+9＝0，解得x1＝m﹣3，x2＝m+3，∴A（m﹣3，0），B（m+3，0），∴AB＝m+3﹣（m﹣3）＝6，∴DE＝AB＝3，∵D点的横坐标为6，∴2（m﹣6）＝3，∴m＝．23．（10分）如图，AB是⊙O的直径，点C为圆上一点，点D为的中点，连接AD，作DE⊥AB交BC的延长线于点E．（1）求证：DE＝EB．（2）连接DO并延长交BC于点F．若CF＝2CE，BD＝5，求⊙O的半径．【解答】（1）证明：∵点D为的中点，∴＝，∴∠DBC＝∠A，∵AB为直径，∴∠ADB＝90°，∵DE⊥AB，∴∠A+∠DBA＝∠EDB+∠DBA＝90°，∴∠A＝∠EDB，∴∠DBC＝∠EDB，∴DE＝EB；（2）如图：∵D为的中点，∴DF⊥BC，CF＝BF，∵CF＝2CE，设CE＝x，CF＝BF＝2x，则DE＝EB＝5x，DF＝4x，在Rt△DFB中，DF2+BF2＝BD2，即4x2+2x2＝52，解得：x＝，∴BF＝，DF＝2，，∵∠A＝∠EDB＝∠DBF，∴sin A＝sin，∴，∴．答：半径是．24．（12分）下表是某奶茶店的一款奶茶近两天的销售情况．销售情况销售数量（单位：杯）销售收入（单位：元）小杯大杯第一天2030460第二天2525450（1）问这款奶茶小杯和大杯的销售单价各是多少元？（2）已知这款奶茶小杯成本4元/杯，大杯成本5元/杯，奶茶店每天只能供应80杯该款奶茶，其中小杯不少于10杯，求该款奶茶一天的最大利润．（销售利润＝销售收入﹣成本）（3）为了满足市场的需求，奶茶店推出每杯2元的加料服务，顾客在选完杯型后可以自主选择加料或者不加料．小明恰好用了208元购买该款奶茶，其中小杯不加料的数量是总杯数的，则小明这款奶茶大杯加料的买了6杯．【解答】解：（1）设小杯奶茶销售单价为a元，大杯奶茶销售单价为b元，根据题意，得，解得，答：小杯奶茶销售单价为8元，大杯奶茶销售单价为10元；（2）设售出小杯奶茶m杯，总利润为w元，则w＝4m+5（80﹣m）＝﹣m+400，∵m≥10，k＝﹣1＜0，∴w随m的增大而减小，∴当m＝10时，w的最小值为390元；（3）设小杯不加料奶茶为p杯，其中小杯加料和大杯不加料共q杯，则大杯加料奶茶为（2p﹣q）杯，根据题意，得：8p+10q+12（2p﹣q）＝208，整理，得：16p﹣q＝104，解得，∴2p﹣q＝6，即小明这款奶茶大杯加料的买了6杯．故答案为：6．25．（14分）如图，在矩形ABCD中，BC＝1，AB＝2，过对角线BD上一点P作AB的垂线交AB于点F，交CD于点E，过点E作EG∥BD交BC于点G，连接FG交BD于点H，连接DF．（1）求的值．（2）当四边形DFGE有一组邻边相等时，求BG的长．（3）点B关于FG的对称点记为B'，若B'落在△EFG内部（不包含边界），求DP长度的取值范围．【解答】解：（1）如图1，∵四边形ABCD是矩形，∴∠ABC＝90°，∵EF⊥AB，∴∠AFE＝90°，∴∠ABC＝∠AFE，∴EF∥BC，∵EG∥BD，∴四边形EPBG是平行四边形，∴EP＝BG，∴tan∠EDP＝＝＝，∴＝2；（2）①如图1，当DE＝EG时，设BG＝x，则DE＝EG＝2x，CE＝2﹣2x，CG＝1﹣x，在Rt△CEG中，CE2+CG2＝EG2，∴（2﹣2x）2+（1﹣x）2＝（2x）2，解得：x＝5﹣2，∴BG＝5﹣2；②如图1，当EG＝GF时，∵CE＝BF，∠C＝∠ABC＝90°，∴Rt△ECG≌Rt△FBG（HL），∴BG＝CG＝CB＝，③如图1，当DF＝GF时，设BG＝x，则AF＝DE＝2x，∵DF2＝GF2，∴DA2+AF2+BG2+BF2，∴12+（2x）2＝（2﹣2x）2+x2，解得：x＝4±，∵BG＜1，∴BG＝4﹣；④∵∠DEF＝90°，∴DF＞DE，即DF＝DE不存在；综上所述，BG的长为：5﹣2或或4﹣；（3）当点B′落在边EG上时，如图2，设BG＝x，B′F＝BF＝CE＝2﹣2x，∵∠FB′G＝∠FBG＝90°，∴∠EFB′＝∠CEG＝∠CDB，∠C＝∠EB′F＝90°，∴△EFB′∽△BDC，∴＝，∴＝，解得：x＝1﹣，∴DP＝EP＝﹣1；当点B′落在边EF上，如图3，∵BG＝B′G＝CE，∴x＝2﹣2x，解得：x＝，∴DP＝x＝，综上所述，﹣1＜DP＜．。

2020-2021学年浙江省温州市高一（上）期末数学试卷（B卷）一、选择题（共8小题）.1．已知集合A＝{1，2，3}，B＝{2，4}，则A∪B＝（）A．{2}B．{2，3}C．{1，2，3}D．{1，2，3，4}2．下列函数既不是奇函数也不是偶函数的是（）A．y＝x3B．y＝x2C．y＝x D．3．已知函数，则f（x2）的定义域为（）A．（﹣∞，﹣1）∪（1，+∞）B．（﹣∞，0）∪（1，+∞）C．（﹣1，1）D．（0，1）4．在平面直角坐标系中,角α的顶点与原点重合,终边与单位圆的交点为,则sin(π-α)＝( ) A．B．C．D．5．已知a＝e0.3，b＝ln0.3，c＝0.3e，则（）A．a＞b＞c B．a＞c＞b C．c＞b＞a D．b＞c＞a6．已知a，b，c是实数，且a≠0，则“∀x∈R，ax2+bx+c＜0”是“b2﹣4ac＜0”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件7．已知a＞0，b＞0，a+b＝1，则下列等式可能成立的是（）A．a2+b2＝1B．ab＝1C．a2+b2＝D．a2﹣b2＝8．某工厂有如图1所示的三种钢板，其中长方形钢板共有100张，正方形钢板共有60张，正三角形钢板共有80张．用这些钢板制作如图2所示的甲、乙两种模型的产品，要求正方形钢板全部用完，则制成的甲模型的个数最少有（）A．10个B．15个C．20个D．25个二、多项选择题（共4小题）.9．已知函数y＝x2﹣2x+2的值域是[1，2]，则其定义域可能是（）A．[0，1]B．[1，2]C．[]D．[﹣1，1]10．已知，且tanθ＝m，则下列正确的有（）A．B．tan（π﹣θ）＝m C．D．11．已知函数f（x）＝2sin（ωx+φ）（ω＞0）的图象过两点，则ω的可能取值为（）A．1B．2C．3D．412．在同一直角坐标系中，函数f（x）＝log a（x﹣b），g（x）＝b x﹣a的图象可能是（）A B C D三、填空题：本题共4小题，每小题5分，共20分。

浙江省温州市鹿城区2023-2024学年九年级（上）期末科学能力检测提优卷亲爱的同学:欢迎参加考试!请你认真审题，积极思考,细心答题，发挥最佳水平。

答题时，请注意以几点:1.全卷共8页,有四大题，33小题。

全卷满分160分.考试时间120分钟。

2.答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上均无效。

3.答题前，认真阅读答题纸上的《注意事项》，按规定答题。

4.本卷中g 取10Nkg一.选择题(本题共15小题，每题只有一个选项符合题意，每小题3分，共45分)1.下列变化中属于化学变化的是()A．榨取果汁B．粉碎废纸C．切割玻璃D．燃放烟花2.《易经》记载：“泽中有火”“上火下泽”。

这是对甲烷气体在湖泊池沼水面上起火现象的描述。

下列有关甲烷的叙述，正确的是（）A．甲烷的化学式为C 2H 4B．甲烷属于有机物C．甲烷燃烧只生成水D．甲烷与空气的混合物遇火一定不会发生爆炸3.小金是一名发育正常的九年级学生，下面是与他有关的一些数据，你认为合理的是（）A.他走上楼梯的功率约为1000WB.他走上楼梯时对地面的压强约为1000PaC.他从1楼走到4楼教室的过程中克服重力做功1000JD.他把科学课本从地上捡起来放到桌上，对课本做功约为3J4.如图所示，对于图片中所描述的物理过程，下列分析中正确的是（）A.图甲，厚玻璃内的空气被压缩时，空气的内能减少B.图乙，瓶子内的空气推动塞子跳起时，空气的内能增大C.图丙，试管内的水蒸气推动塞子冲出时，水蒸气的内能减少D.图丁，汽缸内的气体推动活塞向下运动时，气体的内能增大5.小金将小球竖直向上抛出，小球先上升后下落，不计空气阻力。

小球从离开手后到落回手中之前，此过程中能量变化的分析，正确的是（）A.动能先增大后减小B.势能先减小后增大C.机械能先减小后增大D.机械能保持不变6.将过量盐酸加入一定质量的氢氧化钠溶液中，充分反应后得到溶液X。

下列现象或事实描述不合理．．．的是（）A.溶液X 显酸性B.向X 滴加少量硝酸银溶液无沉淀生成C.向X 滴加少量硫酸铜溶液无沉淀生成D.向X 加入锌粒有气体生成7.非洲旱季，常用Hippo roller（中间有转轴的塑料桶）运水。

浙江省温州市鹿城区温州市实验中学2025届英语九上期末学业水平测试试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

Ⅰ. 单项选择1、---QQ and Wechat have changed people’s life in many ways.--- _____. We can use them to keep in touch and communicate with others more easily.A．Completely B．Exactly C．Probably D．Possibly2、—Mom, _____ I hang out with my friends now?— Sure, but you _____ clean up your bedroom first.A．can; may B．may; have toC．must; need D．need; must3、Would you like to go to the museum with me?I’d love to, ______ I’m afraid I have no time.A．but B．and C．or D．so4、— Did you buy a new phone last Sunday?—No, I a folding smartphone next month.A．bought B．buy C．will buy5、My father wants me to____ doing my homework as soon as I come home from school.A．win the heart of B．take care ofC．get into the habit of D．stay in touch with6、— Do you know that China is one of countries in the world?—Y es, I do. It’s much than the US.A．oldest; older B．the oldest; the olderC．the oldest; older D．the older; older7、Miss Zhao is very friendly. We all like ________ .A．me B．you C．her D．him8、It that China _ its first homemade aircraft carrier (国产航空母舰) in the water in Dalian on April 26, 2017.A．was reported; put B．was reported; was putC．reported; put D．reported; was putA．was held B．will be held C．is held D．will hold10、---Look! Who's ______ boy talking with Jack over there?---Oh, he is my cousin, Bob. He is _____ honest boy.A．a; the B．the; an C．the; a D．a; anⅡ. 完形填空11、阅读下面短文，从各题所给的A、B、C和D四个选项中，选出可以填入空白处的最佳选项。

2020-2021学年九年级数学上册期末综合复习专题提优训练（人教版）专题05 二次函数的图象与性质【典型例题】1．（2020·福建省连江第三中学初三月考）在同一坐标系内，函数y ＝kx 2和y ＝kx ＋2（k ≠0）的图象大致如图（ ） A ． B ． C ． D ．【答案】D2．（2020·上海市静安区实验中学初三课时练习）抛物线()232y x =-+3可以看作把抛物线23y x =向_______平移_______个单位，向_______平移_______个单位得到． 【答案】右 2 上 33．（2020·湖南长沙·初三开学考试）已知一个二次函数的图象经过点()1,0A -、()3,0B 和()0,3C -三点. （1）求此二次函数的解析式；（2）求此二次函数的图象的对称轴和顶点坐标.【答案】（1）设二次函数解析式为()()13y a x x =+-，∵抛物线过点()0,3C -，∴()()30103a -=+-，解得1a =，∴()()21323y x x x x =+-=--.（2）由（1）可知：223y x x =--， ∵a =1,b =-2,c =-3, ∴对称轴是直线12b x a =-=，244ac ba -=-4,顶点坐标是()1,4-.4．（2020·浙江杭州外国语学校初三月考）已知一条抛物线分别过点(3,2)-和(0,1)，且它的对称轴为直线2x=，试求这条抛物线的解析式.【答案】解:∵抛物线的对称轴为2x =,∴可设抛物线的解析式为2(2)y a x b =-+把(3,2)-,(0,1)代入解析式得()()2232=202=1a b a b ⎧-+-⎪⎨-+⎪⎩， 解得1a =,3b =-,∴所求抛物线的解析式为2(2)3y x =-- 【专题训练】一、选择题1．（2020·竹溪县蒋家堰镇中心学校期末）函数()221y x ++＝-的顶点坐标是（） A ．(2,-1) B ．(-2,1) C ．(-2,-1) D ．(2,1)【答案】B2．（2020·江苏崇川·期末）抛物线y ＝x 2先向右平移1个单位，再向上平移3个单位，得到新的抛物线解析式是( ) A ．y ＝(x +1)2+3 B ．y ＝(x +1)2﹣3 C ．y ＝(x ﹣1)2﹣3 D ．y ＝(x ﹣1)2+3【答案】D3．（2020·福建省连江第三中学初三月考）二次函数y ＝﹣（x －2）2＋1的图象中，若y 随x 的增大而减小，则x 的取值范围是（ ）A ．x ＜2B ．x ＞2C ．x ＜﹣2D ．x ＞﹣2【答案】B4．（2020·竹溪县蒋家堰镇中心学校期末）若函数y ＝（a ﹣1）x 2﹣4x +2a 的图象与x 轴有且只有一个交点，则a 的值为（ ）． A ．-1 B ．2 C ．-1或2 D ．-1或2或1【答案】D5．（2021·福建学业考试）若二次函数2(0)y ax bx c a =++<的图像对称轴为直线12x =-经过不同的5点(),A p q ，()00,B y ，()12,C y ，)2D y ，()1,E p q --，则0y ，1y ，2y 的大小关系（ ）A ．012y y y >>B ．012y y y <<C ．021y y y >>D ．102y y y >>【答案】C6．（2020·竹溪县蒋家堰镇中心学校期末）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，给出以下结论：①a +b +c ＜0；②b 2﹣4ac ＞0；③b ＞0；④4a ﹣2b +c ＜0；⑤a +c ＜23，其中正确结论的个数是（ ）A ．②③④B ．①②⑤C ．①②④D ．②③⑤【答案】B7．（2020·台州市椒江区前所中学月考）关于x 的一元二次方程2102ax bx ++=有一个根是﹣1，若二次函数212y ax bx =++的图象的顶点在第一象限，设2t a b =+，则t 的取值范围是（ ）A．1142t<<B．114t-<≤C．1122t-≤<D．112t-<<【答案】D8．（2020·湖南长沙·初三开学考试）已知二次函数y＝﹣x2+mx+m（m为常数），当﹣2≤x≤4时，y的最大值是15，则m 的值是（）A．﹣19或315B．6或315或－10C．﹣19或6D．6或315或－19【答案】C9．（2020·湖南长沙·初三开学考试）二次函数y＝ax2+bx的图象如图所示，则一次函数y＝ax+b的图象大致是（）A．B．C．D．【答案】D10．（2020·浙江杭州外国语学校初三月考）已知直线x＝1是二次函数y＝ax2+bx+c（a，b，c是实数，且a≠0）的图象的对称轴，点A（x1，y1）和点B（x2，y2）为其图象上的两点，且y1<y2，（）A．若x1<x2，则x1+x2﹣2＜0B．若x1<x2，则x1+x2﹣2>0C．若x1＞x2，则a（x1+x2-2）＞0D．若x1＞x2，则a（x1+x2-2）<0【答案】D二、填空题11．（2020·湖南隆回·初三一模）二次函数243y x x =--+的最大值为_________.【答案】712．（2020·湖南广益实验中学开学考试）二次函数223y x x =-+-图象的顶点坐标是 ．【答案】（1，﹣2）．13．（2020·上海市静安区实验中学初三课时练习）抛物线(2)(3)y x x =+-的开口______，对称轴是_____________，顶点是_______． 【答案】向下 直线x =12 11(,6)2414．（2020·上海市静安区实验中学初三课时练习）已知抛物线22y x mx =+-的对称轴为x =1，则m =______． 【答案】-215．（2020·上海市静安区实验中学初三课时练习）某广告公司设计一幅周长为20米的矩形广告牌，设矩形的一边长为x 米，广告牌的面积为S 平方米，则S 与x 的函数关系式为________________．【答案】210S x x =-+16．（2020·浙江杭州外国语学校初三月考）抛物线y ＝ax 2+bx +c （a ≠0）的部分图象如图所示，其与x 轴的一个交点坐标为（﹣3，0），对称轴为x ＝﹣1，则当y ＜0时，x 的取值范围是_____．【答案】﹣3＜x ＜117．（2020·湖南广益实验中学开学考试）在平面直角坐标系中，若点P (a ，b )的坐标满足a ＝b ≠0，则称点P 为“对等点”．已知二次函数y ＝x 2+mx ﹣m 的图象上存在两个不同的“对等点”，且这两个“对等点”关于原点对称，则m 的值为_____．【答案】118．（2020·湖南长沙·初三开学考试）如图，二次函数2(0)y ax bx c a =++≠的图象经过点1(,0)2-，对称轴为直线1,x =下列5个结论：0abc <①；240a b c -+=②；20a b +>③；230c b -<④；()a b m am b +≤+⑤．其中正确的结论为_________________． (注：只填写正确结论的序号)【答案】②⑤三、解答题19．（2020·呼和浩特市敬业学校初二期末）直线33y x =-+与x 轴y 轴分别交于点A ,B ，抛物线2(2)y a x k =-+经过点A ,B ，并与x 轴交于另一点C ，其顶点为P , （1）求,a k 的值；（2）抛物线的对称轴上有一点Q ,使ABQ ∆是以AB 为底边的等腰三角形，求点Q 的坐标；【答案】解：（1）∵直线y=-3x+3与x轴、y轴分别交于点A、B，∴A（1，0），B（0，3）．又∵抛物线y=a（x-2）2+k经过点A（1，0），B（0，3），∴43a ka k+=⎧⎨+=⎩，解得11ak=⎧⎨=-⎩，故a，k的值分别为1，-1；（2）设Q点的坐标为（2，m），对称轴x=2交x轴于点F，过点B作BE垂直于直线x=2于点E．在Rt△AQF中，AQ2=AF2+QF2=1+m2，在Rt△BQE中，BQ2=BE2+EQ2=4+（3-m）2，∵AQ=BQ，∴1+m2=4+（3-m）2，∴m=2，∴Q点的坐标为（2，2）．20．（2020·云南昆明·初三学业考试）如图，抛物线y ＝ax 2+bx 过点P （﹣1，5），A （4，0）．（1）求抛物线的解析式；（2）在第一象限内的抛物线上有一点B ，当P A ⊥PB 时，求点B 的坐标．【答案】（1）由题意，把点(1,5),(4,0)P A -代入2y ax bx =+得51640a b a b -=⎧⎨+=⎩，解得14a b =⎧⎨=-⎩，则抛物线的解析式为24y x x =-；（2）如图，过P 点作PD x ⊥轴于D ，BE PD ⊥于E ， ∵(1,5),(4,0)P A -，∴5,1,4PD OD OA ===，∴145AD OD OA =+=+=，∴5PD AD ==， 45APD DAP ∴∠=∠=︒，设2(,4)B m m m -，则21,45BE m PE m m =-=+-，点B 在第一象限内的抛物线上，4m ∴>，∵PA PB ⊥，即90APB ∠=︒，∴18045BPE APD APB ∠=︒-∠-∠=︒，∴PBE △是等腰直角三角形，∴BE PE =，即2145m m m -+=-，整理得：2560m m --=，解得6m =或14m =-<（舍去），此时22464612m m --=⨯=，故点B 的坐标为(6,12)B ．21．（2020·上海市静安区实验中学初三课时练习）已知二次函数的图像过抛物线223y x x =++的顶点和坐标原点．(1)求二次函数的解析式(2)判断点A （-2，5）是否在这个二次函数的图像上 ．【答案】解：(1)2223(1)2y x x x =++=++，∴顶点坐标为（-1，2）设2(1)2(0)y a x a =++≠，代入（0，0）得，02a =+，解得，2a =-∴二次函数的解析式为22(1)2y x =-++(2)当x =-2时，y =0，∴点A （-2，5）不在这个二次函数的图像上22．（2020·江苏如东·初三二模）已知抛物线y =ax 2+bx +c （a ，b ，c 为常数，a >0）的对称轴为直线x =1，且与x 轴只有一个公共点．（1）试用含a 的式子表示b 和c ；（2）若（x 1，y 1），（3，y 2）是该抛物线上的两点，y 2<y 1，求x 1的取值范围；（3）若将该抛物线向上平移2个单位长度所得新抛物线经过点（3，6），且当p ≤x ≤q 时，新抛物线对应的函数有最小值2p ，最大值2q ，求p ﹣q 的值．【答案】（1）∵抛物线y =ax 2+bx +c （a ，b ，c 为常数，a ＞0）的对称轴为直线x =1， ∴﹣2b a=1， ∴b =﹣2a ，∵抛物线与x轴只有一个公共点．∴b2﹣4ac=0，即(﹣2a)2﹣4ac=0，∴c=a；（2）∵（x1，y1），（3，y2）是该抛物线上的两点，对称轴为x=1，∴（3，y2）关于对称轴的对称点为（﹣1，y2），∵a＞0，抛物线开口向上，∴y2＜y1时，x1的取值范围是x1＞3或x1＜﹣1；（3）由（1）知：抛物线y=ax2﹣2ax+a=a(x﹣1)2（a＞0），将该抛物线向上平移2个单位长度所得新抛物线为y=a(x﹣1)2+2，∵经过点（3，6），∴6=4a+2，解得a=1，∴新抛物线为y=(x﹣1)2+2，∴当x=1时，抛物线有最小值为2，∴2p=2，解得p=1，∴1≤x≤q，∵对称轴为x=1，∴当x=q时，在p≤x≤q范围内有最大值2q，∴2q=（q﹣1）2+2，解得q=3或1（舍去），∴p﹣q=1﹣3=﹣2．23．（2020·浙江金华·初三其他）已知：等腰△ABC的底边在x轴上，其中点C与平面直角坐标系原点重合，点A为（4，0），点B，点D是AB边的中点．抛物线y＝ax2+bx+c始终经过A，C两点，（1）当△ABC是正三角形时，点B在抛物线上（如图）．求抛物线的函数表达式；个单位后，发现抛物线经过点D，求n的值；（2）若将（1）中抛物线向下平移4（3）若将△ABC ABC n的值．【答案】解：（1）∵△ABC是正三角形，∴AC＝BC＝AB＝4，∴点B（2，），设抛物线y＝ax（x﹣4）且过（2，），∴＝2a （2﹣4），∴a∴抛物线的解析式为y ＝﹣2x 2+； （2）∵AB ＝AC ，点A 为（4，0），点C （0，0），∴点B （2 n ）， ∵点D 是AB 边的中点，∴点D （3n ），个单位，∴平移后的抛物线解析式为：y ＝﹣2x 2+﹣4， ∵平移后的抛物线经过点D ，∴2n ＝﹣2×9+3﹣4， ∴n ＝32；（3）∵△ABC 的重心坐标为（2），∴△ABC 向上平移3个单位后，重心坐标为（2，3 n +3），∵y2+x﹣2）2+∴顶点坐标为（2，，个单位，∵平移后△ABC的重心与抛物线顶点也相距3∴|∴n＝4或6．24．（2020·浙江杭州外国语学校初三月考）如图，抛物线y＝ax2+bx+c（a≠0）的图象经过A（1，0），B（3，0），C（0，6）三点．（1）求抛物线的解析式．（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D，直线BE交AD于点E，若直线BE将△ABD的面积分为1：2两部分，求点E的坐标．（3）P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P，使A、D、P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．【答案】解：（1）∵抛物线y ＝ax 2+bx +c （a ≠0）的图象经过A (1，0)，B (3，0)，∴设抛物线解析式为：y ＝a (x ﹣1)(x ﹣3)，∵抛物线y ＝a (x ﹣1)(x ﹣3)(a ≠0)的图象经过点C (0，6)，∴6＝a (0﹣1)(0﹣3)，∴a ＝2，∴抛物线解析式为：y ＝2(x ﹣1)(x ﹣3)＝2x 2﹣8x +6；（2）∵y ＝2x 2﹣8x +6＝2(x ﹣2)2﹣2，∴顶点M 的坐标为(2，﹣2)，∵抛物线的顶点M 与对称轴l 上的点N 关于x 轴对称，∴点N (2，2)，设直线AN 解析式为：y ＝kx +b ，由题意可得：022=+⎧⎨=+⎩k b k b ， 解得：22k b ==-⎧⎨⎩， ∴直线AN 解析式为：y ＝2x ﹣2，联立方程组得：222286=-⎧⎨=-+⎩y x y x x ， 解得：1110x y =⎧⎨=⎩，2246=⎧⎨=⎩x y ，∴点D （4，6），∴S △ABD ＝12×2×6＝6， 设点E (m ，2m ﹣2)，∵直线BE 将△ABD 的面积分为1：2两部分，∴S △ABE ＝13S △ABD ＝2或S △ABE ＝23S △ABD ＝4， ∴12×2×(2m ﹣2)＝2或12×2×(2m ﹣2)＝4， ∴m ＝2或3，∴点E (2，2)或(3，4)；（3）若AD 为平行四边形的边，∵以A 、D 、P 、Q 为顶点的四边形为平行四边形，∴AD ＝PQ ，∴x D ﹣x A ＝x P ﹣x Q 或x D ﹣x A ＝x Q ﹣x P ，∴x P ＝4﹣1+2＝5或x P ＝2﹣4+1＝﹣1，∴点P 坐标为(5，16)或(﹣1，16)；若AD 为平行四边形的对角线，∵以A 、D 、P 、Q 为顶点的四边形为平行四边形，∴AD 与PQ 互相平分， ∴22++=P Q A D x x x x ，∴x P ＝3，∴点P 坐标为(3，0)，综上所述：当点P 坐标为(5，16)或(﹣1，16)或(3，0)时，使A 、D 、P 、Q 为顶点的四边形为平行四边形．25．（2020·竹溪县蒋家堰镇中心学校期末）如图1，抛物线()21y x a x a -++＝与x 轴交于A ，B 两点（点A 位于点B的左侧），与y 轴负半轴交于点C ，若AB ＝4． （1）求抛物线的解析式；（2）如图2，E 是第三象限内抛物线上的动点，过点E 作EF ∥AC 交抛物线于点F ，过E 作EG ⊥x 轴交AC 于点M ，过F 作FH ⊥x 轴交AC 于点N ，当四边形EMNF 的周长最大值时，求点E 的横坐标；（3）在x 轴下方的抛物线上是否存在一点Q ，使得以Q 、C 、B 、O 为顶点的四边形被对角线分成面积相等的两部分？如果存在，求点Q 的坐标；如果不存在，请说明理由．【答案】解：（1）依题意得：()21x a x a ++-=0，则12121,x x a x x a +=+=，则AB 4==，解得：a ＝5或﹣3，抛物线与y 轴负半轴交于点C ，故a ＝5舍去，则a ＝﹣3，则抛物线的表达式为：223y x x +＝﹣…①；（2）由223y x x +＝﹣得：点A 、B 、C 的坐标分别为：()3,0-、()()1,00-3、，， 设点E ()2,23m m m +﹣，OA ＝OC ，故直线AC 的倾斜角为45°，EF ∥AC ，直线AC 的表达式为：y ＝﹣x ﹣3，则设直线EF 的表达式为：y ＝﹣x +b ，将点E 的坐标代入上式并解得：直线EF 的表达式为：y ＝﹣x +()233m m +﹣…②，联立①②并解得：x ＝m 或﹣3﹣m ，故点F ()23,4m m m --+，点M 、N 的坐标分别为：(),3m m --、()33m m --+，，则EF ))23F E x x m MN -=--=，四边形EMNF 的周长C ＝ME +MN +EF +FN ＝(226m m --+-∵﹣2＜0，故S 有最大值，此时m ＝32+-，故点E 的横坐标为：32+-； （3）①当点Q 在第三象限时，当QC 平分四边形面积时， 则1Q B x x ==，故点Q ()1,4--；当BQ 平分四边形面积时， 则1111,133222OBQ Q Q QCBO S y S x =⨯⨯=⨯⨯+⨯⨯四边形，则11121133222Q Q y x ⎛⎫⨯⨯=⨯⨯+⨯⨯ ⎪⎝⎭， 解得：32Q x =-，故点Q 315,24⎛⎫-- ⎪⎝⎭； ②当点Q 在第四象限时，同理可得：点Q ⎝⎭；综上，点Q 的坐标为：()1,4--或315,24⎛⎫-- ⎪⎝⎭或⎝⎭．。

浙教新版2020-2021学年九年级上册数学期末复习试题1 一．选择题（共10小题，满分40分，每小题4分）1．已知A（m，2020），B（m+n，2020）是抛物线y＝﹣（x﹣h）2+2036上两点，则正数n＝（）A．2B．4C．8D．162．如图所示的是正十二角形体，因为其独特的对称美，所以2019年在英国举办的第60界国际数学奥林匹克的会标，就选用了正十二角形体，若将它绕自身中心旋转一定角度后能与原图重合，则这个角度不可能是（）A．60°B．90°C．120°D．180°3．如图，AB是⊙O的直径，CD是弦，点C，D在直径AB的两侧．若∠AOC：∠AOD：∠DOB＝2：7：11，CD＝4，则的长为（）A．2πB．4πC．D．π4．把抛物线y＝﹣x2先向左平移1个单位，再向下平移2个单位，得到的抛物线的表达式是（）A．y＝﹣（x+1）2+2B．y＝﹣（x+1）2﹣2C．y＝﹣（x﹣1）2﹣2D．y＝（x+1）2﹣25．一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都随机选择一条路径，则它获得食物的概率是（）A．B．C．D．6．已知点（﹣1，y1），（，y2），（2，y3）在函数y＝ax2﹣2ax+a﹣2（a＞0）的图象上，则将y1、y2、y3按由大到小的顺序排列是（）A．y1＞y2＞y3B．y1＞y3＞y2C．y2＞y1＞y3D．y3＞y2＞y1 7．如图，在大小为4×4的正方形网格中，是相似三角形的是（）A．①②B．②③C．①③D．②④8．某厂计划加工180万个医用口罩，第一周按原计划的速度生产，一周后以原来速度的1.5倍生产，结果比原计划提前一周完成任务．若设原计划每周生产x万个口罩，则可列方程为（）A．＝+1B．＝﹣1C．＝+2D．＝﹣29．如图，△ABC的三个顶点坐标分别为A（1，2），B（4，2），C（4，4），若反比例函数y＝在第一象限内的图象与△ABC有交点，则实数k的取值范围是（）A．2≤k≤16B．2≤k≤8C．1≤k≤4D．8≤k≤16 10．如图，在矩形ABCD中，AB＝3，BC＝5，点E在对角线AC上，连接BE，作EF⊥BE，垂足为E，直线EF交线段DC于点F，则＝（）A．B．C．D．二．填空题（共6小题，满分30分，每小题5分）11．某学校食堂为了了解服务质量，随机调查了来食堂就餐的200名学生，调查的结果如图所示，根据图中给出的信息，这200名学生中对该食堂的服务质表示不满意的有人．12．若△ABC∽△A′B′C′，∠A＝50°，∠C＝110°，则∠B′的度数为．13．某市民广场有一个直径16米的圆形喷水池，喷水池的周边有一圈喷水头（喷水头高度忽略不计），各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合，水柱离中心3米处达最高5米，如图所示建立直角坐标系．王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的他站立时必须在离水池中心O米以内．14．一面墙上有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图，若矩形的高为2m，宽为m，则要打掉墙体的面积为m2．15．如图是一株美丽的勾股树．所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形边长为7cm，则正方形A、B、C、D的面积的和是．16．如图，平行四边形ABCD中，∠A＝60°，．以A为圆心，AB为半径画弧，交AD于点E，以D为圆心，DE为半径画弧，交CD于点F．若用扇形ABE围成一个圆维的侧面，记这个圆锥的底面半径为r1；若用扇形DEF围成另一个圆锥的侧面，记这个圆锥的底面半径为r2与，则的值为．三．解答题（共8小题，满分80分，每小题10分）17．（1）解方程：（x﹣2）x＝2x﹣1．（2）计算：|﹣|+×+（）﹣1﹣（﹣）0．18．如图，在▱ABCD中，AE、CF分别平分∠BAD、∠BCD．求证：（1）AE＝CF；（2）AE∥CF．19．目前中学生带手机进校园现象越来越受到社会关注，针对这种现象，某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度，在此次调查活动中，初三（1）班和初三（2）班各有2位家长对中学生带手机持反对态度，现从这4位家长中选2位家长参加学校组织的家校活动，用列表法或画树状图的方法求选出的2位家长来自相同班级的概率．温馨提示：初三（1）班两名家长用A1，A2表示；初三（2）班两名家长用B1，B2表示．20．如图，下列网格由小正方形组成，点A，B，C都在正方形网格的格点上．（1）在图1中画出一个以线段BC为边，且与△ABC面积相等但不全等的格点三角形；（2）在图2和图3中分别画出一个以线段AB为边，且与△ABC相似（但不全等）的格点三角形，并写出所画三角形与△ABC的相似比．（相同的相似比算一种）21．如图，Rt△ABC中，∠C＝90°，AB＝4，在BC上取一点D，连结AD，作△ACD 的外接圆⊙O，交A B于点E．张老师要求添加条件后，编制一道题目，并解答．（1）小明编制题目是：若AD＝BD，求证：AE＝BE．请你解答．（2）在小明添加条件的基础上请你再添加一条线段的长度，编制一个计算题（不标注新的字母），并直接给出答案．（根据编出的问题层次，给不同的得分）22．如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．（1）求二次函数的解析式；（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．23．阿静家在新建的楼房旁围成一个矩形花圃，花圃的一边利用20米长的院墙，另三边用总长为32米的离笆恰好围成．如图，设AB边的长为x米，矩形ABCD的面积为S平方米．（1）求S与x之间的函数关系式，并写出自变量x的取值范围．（2）当x为何值时，S有最大值？并求出最大值．24．问题提出（1）如图1，在Rt△ABC中，∠ACB＝90°，AC＞BC，∠ACB的平分线交AB于点D．过点D分别作DE⊥AC，DF⊥BC．垂足分别为E，F，则图1中与线段CE相等的线段是．问题探究（2）如图2，AB是半圆O的直径，AB＝8．P是上一点，且＝2，连接AP，BP．∠APB的平分线交AB于点C，过点C分别作CE⊥AP，CF⊥BP，垂足分别为E，F，求线段CF的长．问题解决（3）如图3，是某公园内“少儿活动中心”的设计示意图．已知⊙O的直径AB＝70m，点C在⊙O上，且CA＝CB．P为AB上一点，连接CP并延长，交⊙O于点D．连接AD，BD．过点P分别作PE⊥AD，PF⊥BD，垂足分别为E，F．按设计要求，四边形PEDF内部为室内活动区，阴影部分是户外活动区，圆内其余部分为绿化区．设AP的长为x（m），阴影部分的面积为y（m2）．①求y与x之间的函数关系式；②按照“少儿活动中心”的设计要求，发现当AP的长度为30m时，整体布局比较合理．试求当AP＝30m时．室内活动区（四边形PEDF）的面积．参考答案与试题解析一．选择题（共10小题，满分40分，每小题4分）1．解：∵A（m，2020），B（m+n，2020）是抛物线y＝﹣（x﹣h）2+2036上两点，∴2020＝﹣（x﹣h）2+2036，解得x1＝h﹣4，x2＝h+4，∴A（h﹣4，2020），B（h+4，2020），∵m＝h﹣4，m+n＝h+4，∴n＝8，故选：C．2．解：∵正十二角形体的中心角为30°，∴观察图象可知，旋转角是30°的偶数倍数时，可以与本身重合，故选：B．3．解：∵∠AOC：∠AOD：∠DOB＝2：7：11，∠AOD+∠DOB＝180°，∴∠AOD＝×180°＝70°，∠DOB＝110°，∠COA＝20°，∴∠COD＝∠COA+∠AOD＝90°，∵OD＝OC，CD＝4，∴2OD2＝42，∴OD＝2，∴的长是＝＝，故选：D．4．解：依题意可知，原抛物线顶点坐标为（0，0），平移后抛物线顶点坐标为（﹣1，﹣2），所以所得抛物线解析式为：y＝﹣（x+1）2﹣2．故选：B．5．解：由一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都会随机的选择一条路径，观察图可得：第一次选择，它有3种路径；第二次选择，每次又都有2种路径；两次共6种等可能结果，其中获得食物的有2种结果，∴获得食物的概率是＝，故选：C．6．解：∵y＝ax2﹣2ax+a﹣2＝a（x﹣1）2﹣2（a＞0），∴图象的开口向上，对称轴是直线x＝1，∵点（﹣1，y1）到对称轴的距离最大，点（，y2）到对称轴的距离最小，∴y1＞y3＞y2，故选：B．7．解：∵①中的三角形的三边分别是：2，，，②中的三角形的三边分别是：3，，，③中的三角形的三边分别是：2，2，2，④中的三角形的三边分别是：3，，4，∵①与③中的三角形的三边的比为：1：，∴①与③相似．故选：C．8．解：∵原计划每周生产x万个口罩，一周后以原来速度的1.5倍生产，∴一周后每周生产1.5x万个口罩，依题意，得：＝+1．故选：A．9．解：∵△ABC是直角三角形，∴当反比例函数y＝经过点A时k最小，经过点C时k最大，∴k最小＝1×2＝2，k最大＝4×4＝16，∴2≤k≤16．故选：A．10．解：如图，连接BF，取BF的中点O，连接OE，OC．∵四边形ABCD是矩形，EF⊥BE，∴∠BEF＝∠BCF＝90°，AB＝CD＝3，BC＝AD＝5，∵OB＝OF，∴OE＝OB＝OF＝OC，∴B，C，F，E四点共圆，∴∠EBF＝∠ECF，∴tan∠EBF＝tan∠ACD，∴＝＝，故选：B．二．填空题（共6小题，满分30分，每小题5分）11．解：因为200名学生中对该食堂的服务质量表示不满意占总体的百分比为：1﹣46%﹣38%﹣9%＝7%，所以200名学生中对该食堂的服务质量表示很满意有：200×7%＝14（人）．故答案为：14．12．解：∵∠A＝50°，∠C＝110°，∴∠B＝180°﹣50°﹣110°＝20°，∵△ABC∽△A′B′C′，∴∠B′＝∠B＝20°．故答案为20°．13．解：设OA右侧的抛物线的解析式为y＝a（x﹣3）2+5，∵某市民广场有一个直径16米的圆形喷水池，∴该抛物线过点（8，0），∴0＝a（8﹣3）2+5，得a＝﹣，∴OA 右侧的抛物线的解析式为y ＝﹣（x ﹣3）2+5＝x 2++，当y ＝1.8时，1.8＝﹣（x ﹣3）2+5，得x 1＝7，x 2＝﹣1，∵各方向喷出的水柱恰好在喷水池中心的装饰物OA 的顶端A 处汇合，点A 的坐标为（0，），∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心O 7米以内， 故答案为：7．14．解：如图，连结AD 、BC 交于O ，∵∠BDC ＝90°，∴BC 是直径，∴BC ＝＝＝， ∴OA ＝OB ＝AB ＝， ∴△AOB 是正三角形，∴∠AOB ＝60°，∠AOC ＝120°，∴S △AOB ＝，S △AOC ＝，∴S ＝2（S 扇形OAC ﹣S △AOC ）+S 扇形OAB ﹣S △AOB＝2[﹣]+[﹣]＝π﹣，∴打掉墙体面积为（π﹣）平方米， 故答案为：（π﹣）．15．解：∵所有的三角形都是直角三角形，所有的四边形都是正方形，∴正方形A的面积＝a2，正方形B的面积＝b2，正方形C的面积＝c2，正方形D的面积＝d2，又∵a2+b2＝x2，c2+d2＝y2，∴正方形A、B、C、D的面积和＝（a2+b2）+（c2+d2）＝x2+y2＝72＝49cm2．故答案为49cm2．16．解：设AD＝3k，AB＝2k，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A+∠D＝180°，∵∠A＝60°，∴∠D＝120°，∴的长＝＝＝2πr1，可得r1＝，∴的长＝＝＝2πr2，可得r2＝，∴＝1，故答案为1．三．解答题（共8小题，满分80分，每小题10分）17．解：（1）（x﹣2）x＝2x﹣1x2﹣2x﹣2x＝﹣1，则x2﹣4x＝﹣1，x2﹣4x+4＝3，（x﹣2）2＝3，则x﹣2＝±，解得：x1＝2+，x2＝2﹣；（2）|﹣|+×+（）﹣1﹣（﹣）0＝+2+2﹣1＝3+1．18．证明：（1）∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∠BAD＝∠DCB，∴∠ADE＝∠CBF，∵AE、CF分别平分∠BAD、∠BCD，∴∠DAE＝∠DAB，∠BCF＝∠DCB，∴∠DAE＝∠BCF，∴△ADE≌△CBF（ASA），∴AE＝CF．（2）∵△ADE≌△CBF，∴∠AED＝∠CFB，∴AE∥CF．19．解：画树状图如下：共有12种等可能结果，其中2人来自相同班级的共有4种，所以2人来自相同班级的概率为＝．20．解：（1）如图所示，△BCD即为所求．（2）如图所示，△ABE和△ABF即为所求，相似比；相似比．21．（1）证明：连结DE，∵∠C＝90°，∴AD为直径，∴DE⊥AB，∵AD＝BD，∴AE＝BE；（2）答案不唯一．①第一层次：若AC＝4，求BC的长．答案：BC＝8；②第二层次：若CD＝3，求BD的长．答案：BD＝5；③第三层次：若CD＝3，求AC的长．设BD＝x，∵∠B＝∠B，∠C＝∠DEB＝90°，∴△ABC～△DBE，∴＝，∴＝，∴x＝5，∴AD＝BD＝5，∴AC＝＝4．22．解：（1）用交点式函数表达式得：y＝（x﹣1）（x﹣3）＝x2﹣4x+3；故二次函数表达式为：y＝x2﹣4x+3；（2）①当AB为平行四边形一条边时，如图1，则AB＝PF＝2，则点P坐标为（4，3），当点P在对称轴左侧时，即点C的位置，点A、B、P、F为顶点的四边形为平行四边形，故：点P（4，3）或（0，3）；②当A B是四边形的对角线时，如图2，AB中点坐标为（2，0）设点P的横坐标为m，点F的横坐标为2，其中点坐标为：，即：＝2，解得：m＝2，故点P（2，﹣1）；故：点P（4，3）或（0，3）或（2，﹣1）；（3）直线BC的表达式为：y＝﹣x+3，设点E坐标为（x，x2﹣4x+3），则点D（x，﹣x+3），S＝AB（y D﹣y E）＝﹣x+3﹣x2+4x﹣3＝﹣x2+3x，四边形AEBD∵﹣1＜0，故四边形AEBD面积有最大值，当x＝，其最大值为，此时点E（，﹣）．23．解：（1）由题意可得，S＝x（32﹣2x）＝﹣2x2+32x，∵，解得，6≤x＜16，即S与x之间的函数关系式是S＝﹣2x2+32x（6≤x＜16）；（2）∵S＝﹣2x2+32x＝﹣2（x﹣8）2+128，∴当x＝8时，S有最大值，最大值是128平方米．24．解：（1）∵∠ACB＝90°，DE⊥AC，DF⊥BC，∴四边形CEDF是矩形，∵CD平分∠ACB，DE⊥AC，DF⊥BC，∴DE＝DF，∴四边形CEDF是正方形，∴CE＝CF＝DE＝DF，故答案为：CF、DE、DF；（2）连接OP，如图2所示：∵AB是半圆O的直径，＝2，∴∠APB＝90°，∠AOP＝×180°＝60°，∴∠ABP＝30°，同（1）得：四边形PECF是正方形，∴PF＝CF，在Rt△APB中，PB＝AB•cos∠ABP＝8×cos30°＝8×＝4，在Rt △CFB 中，BF ＝＝＝＝CF ， ∵PB ＝PF +BF ，∴PB ＝CF +BF ，即：4＝CF +CF ，解得：CF ＝6﹣2； （3）①∵AB 为⊙O 的直径，∴∠ACB ＝∠ADB ＝90°，∵CA ＝CB ，∴∠ADC ＝∠BDC ，同（1）得：四边形DEPF 是正方形，∴PE ＝PF ，∠APE +∠BPF ＝90°，∠PEA ＝∠PFB ＝90°，∴将△APE 绕点P 逆时针旋转90°，得到△A ′PF ，PA ′＝PA ，如图3所示： 则A ′、F 、B 三点共线，∠APE ＝∠A ′PF ，∴∠A ′PF +∠BPF ＝90°，即∠A ′PB ＝90°，∴S △PAE +S △PBF ＝S △PA ′B ＝PA ′•PB ＝x （70﹣x ），在Rt △ACB 中，AC ＝BC ＝AB ＝×70＝35， ∴S △ACB ＝AC 2＝×（35）2＝1225，∴y ＝S △PA ′B +S △ACB ＝x （70﹣x ）+1225＝﹣x 2+35x +1225；②当AP ＝30时，A ′P ＝30，PB ＝AB ﹣AP ＝70﹣30＝40，在Rt △A ′PB 中，由勾股定理得：A ′B ＝＝＝50，∵S △A ′PB ＝A ′B •PF ＝PB •A ′P ，∴×50×PF ＝×40×30，解得：PF ＝24，∴S 四边形PEDF ＝PF 2＝242＝576（m 2），∴当AP ＝30m 时．室内活动区（四边形PEDF ）的面积为576m 2．。

2020-2021学年九年级上册数学第 1章《二次函数》单元测试卷式是（）1. 卜列关于X 的函数一定为二次函数的是（ A . y=4xB , y= 5x2 - 3xC. y=ax 2+bx+cD , y=x 3-2x+12.将二次函数y= 2x 2+5的图象先向左平移 3个单位，再向下平移 1个单位，则平移后的函数关系A. y=2 (x+3) 2+6 B . y=2 (x+3) 2+4 C. y=2 (x- 3) 2+6D. y=2 (x-3) 2+43. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长） ,其余三边除大门外用栅栏围成，栅栏总长度为 50m,门宽为2m.若饲养室长为 xm,占地面积为ym 2,则关于x 的函数表达式为（:2+26x (2<x<52)B. C. -2 .y= - . x +50x (2w x< 52) y= - x 2+52x (2< x< 52) - 2 一 一 一 __________ y=一方x2+27x- 52 (2<x< 52)（aw0）在同一坐标系中的图象可能是（D .5.以下抛物线的顶点坐标为（2, 0）的是（10.如图，已知顶点为（-3, -6）的抛物线y=ax 2+bx+c 经过点（-1, -4）,则下列结论:-1;⑤若点（-2, m ） , （- 5, n ）在抛物线上，则 m>n,其中正确的个数共有（二.填空题⑥y= （ x+1 ） 2- x 2.这六个式子中，二次函数有12.把二次函数 y=x 2- 4x+5化为y=a （x —h ） 2+k 的形式，那么h+k=A . y= 3x 2+2B . y= 3x2 - 2C. y=3 (x — 2) 2D. y=3 (x+2) 26.二次函数y= ax 2+bx+c 的图象如图所示，其对称轴是x=-1, 卜列结论中正确的是（8.二次函数C. 2a+b=0D. a - b+c>2 (x-1) 2+b (aw0)的图象经过点(0, 2) a+b 的值是（ B. - 1C. 2D. 3 x 2- 2x+c 在-3< x< 2的范围内有最大值为一5, 则c 的值是（B. 3C. - 3D. - 69.二次函数 y=ax 2—2ax+b 中，当—1wxw 4 时，—2wyw3,贝U b — a 的值为( B. - 6或 7C. 3D. 3 或—2①b 2>4ac ；② ax 2+bx+c< - 6；③ 9a- 3b+c= - 6；④关于 x 的二次方程 ax 2+ bx+ c= - 4 的根为B. 2个C. 3个D. 4个11.观察：① y = 6x 2；② y=- 3x 2+5；③2 1y=200x 2+400x+200;④ y=x 3-2x;⑤ ¥二工 二.（只填序号）13. 一名男生参加抛实心球测试，已知球的高度 y （m ）与水平距离 x （m ）之间的关系是7.二次函数 y= a2B. 4ac< b -114 .已知抛物线的顶点坐标是(-2, 3),其图象是由抛物线 y=-8x 2+1平移得到的，则该抛物线的解析式为.15 .抛物线y=a (x- h) 2+k (a<0)经过(-1,3)、( 5, 3)两点，则关于 x 的不等式a (x- h -1) 2+k<3的解集为.16 .已知二次函数 y=ax 2+bx+c (aw0, a, b, c,为常数)，对称轴为直线 x=1,它的部分自变量x 与函数值y 的对应值如下表.请写出ax 2+bc+c= 0的一个正数解的近似值 (精确到0.1)x - 0.4 — 0.3 — 0.2 — 0.117 .若函数y=x 2+2x+m 的图象与x 轴没有交点，则 m 的取值范围是 .18 .已知二次函数 y=ax 2+ (a-1) x- 2a+1,当1vxv3时，y 随x 的增大而减小，则 a 的取值范围是.19 .如果二次函数y=a (x-1) 2(aw0)的图象在它的对称轴右侧部分是上升的，那么a 的取值范围是.20 .小甬是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线y=-/父2的性质时，将一个直角三角板的直角顶点置于平面直角坐标系的原点 O,两直角边与该抛物线交于A, B 两点 (如图)，对该抛物线，小甬将三角板绕点 O 旋转任意角度时惊奇地发现，交点A, B 的连线段总经过一个固定的点，则该点的坐标是三.解答题21 .已知二次函数 y=2x 2+4x- 6,(1)将二次函数的解析式化为y= a (x-h) 2+k 的形式.(2)写出二次函数图象的开口方向、对称轴、顶点坐标. 22 .已知二次函数(k 为常数)，求k 的值.__ 1 2 产12工m,则这名男生抛实心球的成绩是3m.y= ax 2+ bx+c0.920.38—0.12—0.5823.在平面直角坐标系xOy中，抛物线y= ax2+4ax+4a-4 (aw0)的顶点为A.(1)求顶点A的坐标；(2)过点(0, 5)且平行于x轴的直线1,与抛物线y=ax2+4ax+4-4 (aw 0)交于B、C两点.①当a=1时，求线段BC的长；②当线段BC的长不小于8时，直接写出a的取值范围.532 -11— I I E II」] ■ I J 、-5 一4 4-2 口, 1 2 3 4 5x-2~-3-4-5 _____________24.已知二次函数的图象y=- x2+bx+c如图所示，它与轴的交点坐标为(- 1,0), (3, 0)(1)求b, c的值；(2)根据图象，直接写出函数值y<0时，自变量x的取值范围.25.二次函数y=ax2+bx+c (aw0)与一次函数y=x+k (kw0)的图象如图所示，根据图象解答下列问题：(1)写出方程ax2+bx+c=0的两个根；(2)写出不等式ax2+bx+c- x- k< 0的解集；(3)写出二次函数值y随x的增大而减小的自变量x的取值范围；(4)若方程ax2+bx+c= m有两个不等的实数根，求m的取值范围;26.如图，一段长为45m的篱笆围成一个一边靠墙的矩形花园，墙长为27m,设花园的面积为sm2,平行于墙的边为xm.若x不小于17m,(1)求出s关于x的函数关系式;(2)求s的最大值与最小值.花园27.在平面直角坐标系xOy中，二次函数y = x2-2mx+1图象与y轴的交点为A,将点A向右平移4个单位长度，向上平移1个单位长度得到点B.(1)直接写出点A的坐标为，点B的坐标为;(2)若函数y=x2-2mx+1的图象与线段AB恰有一个公共点，求m的取值范围.参考答案与试题解析・选择题1.解：A、是一次函数，故此选项不符合题意；B、是二次函数，故此选项符合题意；C、当a=0时不是二次函数，故此选项不符合题意；D、不是二次函数，故此选项不符合题意；故选：B.2.解：根据“左加右减，上加下减”的法则可知，将抛物线y= 2x2+5向左平移3个单位，再向下平移1个单位，那么所得到抛物线的函数关系式是y=2 (x+3) 2+4.故选：B.3.解：y关于x的函数表达式为：y=g (50+2-x) x b-l= ---- x+26x (2W x<52).故选：A.4,解：①当a>0时，二次函数y= ax2-a的图象开口向上、对称轴为y轴、顶点在y轴负半轴，一次函数y= ax - a (aw0)的图象经过第一、三、四象限，且两个函数的图象交于y轴同一点；②当a<0时，二次函数y= ax2-a的图象开口向下、对称轴为y轴、顶点在y轴正半轴，一次函数y=ax-a (aw0)的图象经过第一、二、四象限，且两个函数的图象交于y轴同一点.对照四个选项可知D正确.故选：D.5.解：抛物线y= 3x2+2的顶点为(0, 2);抛物线y= 3x2-2的顶点为(0, - 2);抛物线y=3 (x-2) 2的顶点为(2, 0);抛物线y=3 (x+2) 2的顶点为(-2, 0);故选：C.6.解：A、由抛物线的开口向下知a<0,对称轴在y轴的左侧，a、b同号，即b<0,与y轴的交点为在y轴的正半轴上，. 0,因此abc>0,故错误;B、抛物线与x轴有两个交点，b2 - 4ac>0,即4acv b2,故正确;C、对称轴为x= ----- --= - 1,得2a = b,23.2a- b= 0,故错误；D、•.当x= - 1 时，y>0• -a- b+c>0,故错误.故选：B.7.解：二.二次函数y=a (x- 1) 2+b (aw0)的图象经过点(0, 2),a+b = 2.故选：C.8.解：把二次函数y= - x2-2x+c转化成顶点坐标式为y= - (x+1) 2+c+l,又知二次函数的开口向下，对称轴为x=- 1,故当x= - 1时，二次函数有最大值为- 5,故-1+2+c= - 5,故c= - 6.故选：D.2 29.解：:抛物线y=ax — 2ax+b=a (x—1) +b- a,「•顶点(1, b - a)当a>0 时，当-1WxW4 时，—2WyW3,函数有最小值，b - a= - 2,当a<0 时，当—1wxw4 时，—2wyw3,函数有最大值，b - a= 3,故选：D.10.解：二•抛物线与x轴有2个交点，•・△= b2- 4ac>0,即b2>4ac,所以①正确；•.•抛物线的顶点坐标为(-3, - 6),即x= - 3时，函数有最小值，•.ax2+bx+c> - 6,所以②错误；•.•抛物线的顶点坐标为(-3, - 6),•••9a-3b+c= - 6,所以③正确；•••抛物线y= ax2+bx+c 经过点(-1, - 4),而抛物线的对称轴为直线x= - 3,.二点(-1, - 4)关于直线x= - 3的对称点(-5, - 4)在抛物线上，••・关于x的一元二次方程ax2+bx+c= - 4的两根为-5和-1 ,所以④错误；•••抛物线开口向上，对称轴为直线x= - 3,而点(-2, m) , ( - 5, n)在抛物线上，: - 3 - ( - 5) > - 2 - ( - 3),m<n,所以⑤错误.故选：B.二.填空题11.解：这六个式子中，二次函数有：①y=6x2；②y=- 3x2+5；③y= 200x2+400x+200;故答案为：①②③.12.解：y=x —4x+5= ( x _ 2) 2+1,. .h=2, k= 1,h+k=2+1= 3.故答案为：3.13.解：•••一名男生参加抛实心球测试，已知球的高度y (m)与水平距离x (m)之间的关系是7T小亭卷i 2: 1・・・当y=0,则0 = - y；5-x2+Vx+—, _L 乙O R-J解得：x1= 10, x2= - 2,，这名男生抛实心球的成绩为10m,故答案为：10.14.解：,•,该抛物线是由抛物线y= - 8x2+1平移得到的，a= - 8,又•••抛物线的顶点坐标是(- 2, 3),该抛物线的解析式为y=- 8 (x+2) 2+3.故答案为：y=- 8 (x+2) 2+3.15.解：二.抛物线y=a (x-h) 2+k (a>0)经过(-1, 3) , ( 5, 3)两点,，大致图象如图所示：•1-y= a (x- h- 1) 2+k (a>0)经过(0, 3) , (6, 3)两点则关于x的不等式a (x-h-1) 2+kW3的解集为：x< 0或x>6.故答案为：*^0或*>6.16.解：由表可知，当x= - 0.2时，y的值最接近0, 所以，方程ax2+bx+c= 0一个解的近似值为-0.2, 设正数解的近似值为a,.•.对称轴为直线x=1,一+(一。

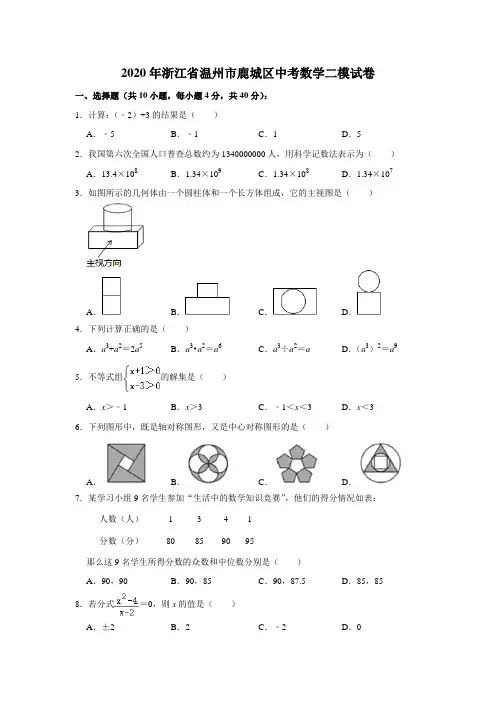
2020年浙江省温州市鹿城区中考数学二模试卷一、选择题（共10小题，每小题4分，共40分）：1．计算：（﹣2）+3的结果是（）A．﹣5B．﹣1C．1D．52．我国第六次全国人口普查总数约为1340000000人，用科学记数法表示为（）A．13.4×108B．1.34×109C．1.34×108D．1.34×107 3．如图所示的几何体由一个圆柱体和一个长方体组成，它的主视图是（）A．B．C．D．4．下列计算正确的是（）A．a3+a2＝2a5B．a3•a2＝a6C．a3÷a2＝a D．（a3）2＝a9 5．不等式组的解集是（）A．x＞﹣1B．x＞3C．﹣1＜x＜3D．x＜3 6．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．7．某学习小组9名学生参加“生活中的数学知识竞赛”，他们的得分情况如表：人数（人）1341分数（分）80859095那么这9名学生所得分数的众数和中位数分别是（）A．90，90B．90，85C．90，87.5D．85，85 8．若分式＝0，则x的值是（）A．±2B．2C．﹣2D．09．在我国古代数学著作《九章算术》“勾股”章中有一题：“今有开门去阃（kǔn）一尺，不合二寸，问门广几何？”大意是说：如图，推开双门（AD和BC），门边缘D，C两点到门槛AB的距离为1尺（1尺＝10寸），双门间的缝隙CD为2寸，那么门的宽度（两扇门的和）AB为（）A．103寸B．102寸C．101寸D．100寸10．如图，一个坡角为15°的看台横截面上看旗杆CD，在这横截面上进行测量得到以下数据：在点A和点B处测得旗杆顶端的仰角分别为60°和30°，点A离地面高度为1米，且测得点A到点B的距离为8米，则旗杆的高度为（）A．25米B．24米C．23米D．26米二、填空题（共6小题，每小题5分，共30分）：11．（5分）因式分解：x2﹣4x＝．12．（5分）一次函数y＝﹣x+2的图象与y轴的交点坐标为．13．（5分）若一个反比例函数的图象位于二、四象限，则它的解析式可能是（写出一个即可）．14．（5分）如图，将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置，若AB＝16cm，则图中阴影部分的面积为cm2．15．（5分）如图，四边形OABC是一张矩形纸片，将边BC折叠，使点B落在边OA的点D处．已知折痕CE＝5，且tan∠BCD＝，则CO＝．16．（5分）图1是一个高脚杯截面图，杯体CBD呈抛物线状（杯体厚度不计），点B是抛物线的顶点，AB＝9，EF＝2，点A是EF的中点，当高脚杯中装满液体时，液面CD ＝4，此时最大深度（液面到最低点的距离）为12，将高脚杯绕点F缓缓倾斜倒出部分液体，当∠EFH＝30°时停止，此时液面为GD，则液面GD到平面l的距离是；此时杯体内液体的最大深度为．三、解答题（共8小题，共80分）：17．（10分）（1）计算：；（2）先化简，再求值：（3﹣m）（3+m）+m（m﹣4）﹣7，其中．18．（10分）为关注学生出行安全，调查了某班学生出行方式，调查结果分为四类：A﹣骑自行车，B﹣步行，C﹣坐社区巴士，D﹣其它，并将调查结果绘制成以下两幅不完整的统计图．请你根据统计图，解答下列问题：（1）本次一共调查了多少名学生？（2）C类女生有名，D类男生有名，并将条形统计图补充完整．（3）若从被调查的A类和D类学生中分别随机选取一位同学进行进一步调查，请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率．19．（8分）如图，在四边形ABCD中，E是AB的中点，AD∥EC，∠AED＝∠B．（1）求证：△AED≌△EBC．（2）当AB＝6时，求CD的长．20．（8分）如图1、图2是两张形状、大小完全相同的5×5方格纸，方格纸中的每个小正方形的边长均为1，点A、B在小正方形的顶点上．（1）在图1中画出一个以点A、B为顶点的面积为3的平行四边形（要求所作的平行四边形且各顶点都在格点上）．（2）在图2中画出一个以点A、B为顶点的面积为8的的平行四边形（要求所作的平行四边形各顶点都在格点上）．21．（10分）如图，在平面直角坐标系中，抛物线y＝﹣x2+x+6与x轴交于点A，B两点，B点在点A的右边，与y轴交于点C，点P是x轴上方抛物线上的一点，点D坐标为（0，2）．（1）求线段AB的长度；（2）如图，以BD，BP为边作▱DBPE，当抛物线的对称轴恰好经过▱DBPE对称中心时，求点P的坐标，并说明此时点E是否在抛物线上．22．（10分）如图，Rt△ABC中，∠C＝90°，点O在边AB上，以O点为圆心、OB为半径作圆，分别与BC、AB相交于点D、E，连接AD，AD是⊙O的切线．（1）求证：∠CAD＝∠B；（2）若BC＝4，tan B＝，求⊙O半径．23．（10分）某校计划采购凳子，商场有A、B两种型号的凳子出售，并规定：对于A型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠a元；B型凳子的售价为40元/张．学校经测算，若购买300张A型凳子需要花费14250元；若购买500张A 型凳子需要花费21250元．（1）求a的值；（2）学校要采购A、B两种型号凳子共900张，且购买A型凳子不少于150张且不超过B型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？24．（14分）如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连接BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．（1）填空：B的坐标为；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；（3）设AD＝x，矩形BDEF的面积为y，求y关于x的函数关系式，并求出y的最小值．（4）如图2，若点E边OC上，EF与BC相交于点G，连接BE及DG，BE和DG相交于点H，若BH＝3HE，记△GEC的面积为S1，△BGF的面积为S2，请直接写出的值．2020年浙江省温州市鹿城区中考数学二模试卷参考答案与试题解析一、选择题（共10小题，每小题4分，共40分）：1．计算：（﹣2）+3的结果是（）A．﹣5B．﹣1C．1D．5【分析】根据有理数的加法法则：绝对值不等的异号两数相加，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0．【解答】解：（﹣2）+3＝3﹣2＝1故选：C．2．我国第六次全国人口普查总数约为1340000000人，用科学记数法表示为（）A．13.4×108B．1.34×109C．1.34×108D．1.34×107【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：1340000000＝1.34×109，故选：B．3．如图所示的几何体由一个圆柱体和一个长方体组成，它的主视图是（）A．B．C．D．【分析】根据主视图是从正面看得到的视图，可得答案．【解答】解：从正面看下面是一个比较长的矩形，上面是一个比较窄的矩形．故选：B．4．下列计算正确的是（）A．a3+a2＝2a5B．a3•a2＝a6C．a3÷a2＝a D．（a3）2＝a9【分析】根据合并同类项法则、同底数幂的乘法法则、同底数幂的除法法则、积的乘方法则计算，判定即可．【解答】解：a3与a2不是同类项，不能合并，A错误；a3•a2＝a5，B错误；a3÷a2＝a，C正确；（a3）2＝a6，D错误，故选：C．5．不等式组的解集是（）A．x＞﹣1B．x＞3C．﹣1＜x＜3D．x＜3【分析】利用不等式的性质，先求出两个不等式的解集，再求其公共解．【解答】解：，由①式得x＞﹣1；由②式得x＞3，所以不等式组的解集为x＞3．故选：B．6．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【分析】根据中心对称图形的定义判断，得到答案．【解答】解：A、不是轴对称图形，是中心对称图形；B、是轴对称图形，是中心对称图形；C、是轴对称图形，不是中心对称图形；D、是轴对称图形，不是中心对称图形；故选：B．7．某学习小组9名学生参加“生活中的数学知识竞赛”，他们的得分情况如表：人数（人）1341分数（分）80859095那么这9名学生所得分数的众数和中位数分别是（）A．90，90B．90，85C．90，87.5D．85，85【分析】众数是一组数据中出现次数最多的数据；找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；可得答案．【解答】解：在这一组数据中90是出现次数最多的，故众数是90；排序后处于中间位置的那个数是90，那么由中位数的定义可知，这组数据的中位数是90．故选：A．8．若分式＝0，则x的值是（）A．±2B．2C．﹣2D．0【分析】分式的值为0时，分子等于0且分母不等于0．【解答】解：依题意得：x2﹣4＝0且x﹣2≠0，解得x＝﹣2．故选：C．9．在我国古代数学著作《九章算术》“勾股”章中有一题：“今有开门去阃（kǔn）一尺，不合二寸，问门广几何？”大意是说：如图，推开双门（AD和BC），门边缘D，C两点到门槛AB的距离为1尺（1尺＝10寸），双门间的缝隙CD为2寸，那么门的宽度（两扇门的和）AB为（）A．103寸B．102寸C．101寸D．100寸【分析】画出直角三角形，根据勾股定理即可得到结论．【解答】解：设OA＝OB＝AD＝BC＝r，过D作DE⊥AB于E，则DE＝10，OE＝CD＝1，AE＝r﹣1．在Rt△ADE中，AE2+DE2＝AD2，即（r﹣1）2+102＝r2，解得2r＝101．故门的宽度（两扇门的和）AB为101寸．故选：C．10．如图，一个坡角为15°的看台横截面上看旗杆CD，在这横截面上进行测量得到以下数据：在点A和点B处测得旗杆顶端的仰角分别为60°和30°，点A离地面高度为1米，且测得点A到点B的距离为8米，则旗杆的高度为（）A．25米B．24米C．23米D．26米【分析】过A作AE⊥CD于E，AF⊥BC于点F，解直角三角形即可得到结论．【解答】解：过A作AE⊥CD于E，AF⊥BC于点F，∵∠BAC＝180°﹣15°﹣60°＝105°，∠ABC＝45°∴∠ACB＝30°，∵AB＝8，∴AF＝BF＝AB＝8，∴AC＝2AF＝16，∵∠AEC＝90°，∠ACE＝30°，∴CE＝AC＝24，∵DE＝1，∴CD＝24+1＝25（米），答：旗杆的高度为25米，故选：A．二、填空题（共6小题，每小题5分，共30分）：11．（5分）因式分解：x2﹣4x＝x（x﹣4）．【分析】直接提取公因式x，进而分解因式得出即可．【解答】解：x2﹣4x＝x（x﹣4）．故答案为：x（x﹣4）．12．（5分）一次函数y＝﹣x+2的图象与y轴的交点坐标为（0，2）．【分析】根据y轴上点的坐标特征把x＝0代入一次函数解析式，求出对应的函数值即可得到与y轴的交点坐标．【解答】解：把x＝0代入y＝﹣x+2得y＝2，所以一次函数y＝﹣x+2的图象与y轴的交点坐标为（0，2）．故答案为（0，2）．13．（5分）若一个反比例函数的图象位于二、四象限，则它的解析式可能是y＝﹣（写出一个即可）．【分析】根据反比例函数的性质可列式子．答案不唯一，要注意符合题意，只写一个即可．【解答】解：反比例函数的图象位于二、四象限，k＜0，则它的解析式可能是y＝﹣．14．（5分）如图，将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置，若AB＝16cm，则图中阴影部分的面积为32πcm2．【分析】由旋转的性质得：∠BAB'＝45°，四边形AB'C'D'≌四边形ABCD，图中阴影部分的面积＝四边形ABCD的面积+扇形ABB'的面积﹣四边形AB'C'D'的面积＝扇形ABB'的面积，代入扇形面积公式计算即可．【解答】解：由旋转的性质得：∠BAB'＝45°，四边形AB'C'D'≌四边形ABCD，则图中阴影部分的面积＝四边形ABCD的面积+扇形ABB'的面积﹣四边形AB'C'D'的面积＝扇形ABB'的面积＝＝32π；故答案为：32π．15．（5分）如图，四边形OABC是一张矩形纸片，将边BC折叠，使点B落在边OA的点D 处．已知折痕CE＝5，且tan∠BCD＝，则CO＝8．【分析】首先证明tan∠EDA＝，设AE＝3t，则AD＝4t，再根据勾股定理表示出DE＝5t，即BE＝5t，所以OC＝AB＝8t，再证明两个相似三角形，得到CD＝10t，从而在直角三角形CDE中，根据勾股定理列方程计算．【解答】解：∵四边形ABCD是矩形，∴∠B＝∠O＝∠A＝90°，OC＝AB，由翻折的性质可知，∠B＝∠CDE＝90°，BE＝DE，∴∠BCD+∠DEB＝180°，∵∠DEA+∠DEB＝180°，∴∠BCD＝∠DEA，∴tan∠DEA＝tan∠BCD＝＝，∴设AE＝3t，则AD＝4t，由勾股定理得DE＝5t，∴OC＝AB＝AE+EB＝AE+DE＝8t，∵∠CDO+∠EDA＝90°，∠EDA+∠AED＝90°，∴∠CDO＝∠AED，∴△OCD∽△ADE，∴＝，∴＝，∴CD＝10t，在△DCE中，∵CD2+DE2＝CE2，∴（10t）2+（5t）2＝（5）2，解得t＝1，∴OC＝8，故答案为8．16．（5分）图1是一个高脚杯截面图，杯体CBD呈抛物线状（杯体厚度不计），点B是抛物线的顶点，AB＝9，EF＝2，点A是EF的中点，当高脚杯中装满液体时，液面CD ＝4，此时最大深度（液面到最低点的距离）为12，将高脚杯绕点F缓缓倾斜倒出部分液体，当∠EFH＝30°时停止，此时液面为GD，则液面GD到平面l的距离是10；此时杯体内液体的最大深度为．【分析】以A为原点，直线EF为x轴，直线AB为y轴，建立平面直角坐标系，由待定系数法求得抛物线的解析式；将高脚杯绕点F倾斜后，仍以A为原点，直线EF为x轴，直线AB为y轴，建立平面直角坐标系，分别用待定系数法求得直线l的解析式和直线GD的解析式，过点M作MP⊥l于点P，用三角函数求得液面GD到平面l的距离；过抛物线最低点Q作QL∥l，再将QL的解析式与抛物线的解析式联立，得出关于x的一元二次方程，由判别式求得q，最后用三角函数求得答案．【解答】解：以A为原点，直线EF为x轴，直线AB为y轴，建立平面直角坐标系，如图：由题意得：A（0，0），B（0，9），C（﹣2，21），D（2，21），设抛物线的解析式为：y＝ax2+9，将D（2，21）代入得：21＝a×+9，解得：a＝1，∴y＝x2+9．将高脚杯绕点F倾斜后，仍以A为原点，直线EF为x轴，直线AB为y轴，建立平面直角坐标系，如图：由题意得：A（0，0），F（，0），E（﹣，0），B（0，9），C（﹣2，21），D（2，21），由题可知，直线l与x轴的夹角为30°，GD∥l，∵l经过点F（，0），且∠EFH＝30°，∴设直线l的解析式为：y＝x+b，将F（，0）代入，解得b＝﹣1，∴y＝x﹣1，又∵GD∥l，∴k GD＝k l＝，∴设直线GD的解析式为y＝x+p，将D（2，21）代入，解得p＝19，∴y＝x+19，∴M（0，19），N（0，﹣1），过点M作MP⊥l于点P，∵∠EFH＝30°，∠F AN＝90°，∴∠ANF＝60°，∴MP＝MN•sin60°＝[19﹣（﹣1）]×＝10．过抛物线最低点Q作QL∥l，L为QL于MP的交点，设直线QL的解析式为y＝x+q，由得：x2﹣x+9﹣q＝0，∵只有一个交点Q，∴△＝0，∴﹣4（9﹣q）＝0，∴q＝，∴ML＝（19﹣）×sin60°＝．故答案为：10，．三、解答题（共8小题，共80分）：17．（10分）（1）计算：；（2）先化简，再求值：（3﹣m）（3+m）+m（m﹣4）﹣7，其中．【分析】（1）直接利用二次根式的性质、特殊角的三角函数值和幂的性质分别化简得出答案；（2）原式首先利用平方差公式以及单项式乘以多项式法则计算，然后合并同类项，把m 的值代入计算即可求出值．【解答】解：（1）原式＝5+﹣（﹣1）＝5+1+1＝7．（2）原式＝9﹣m2+m2﹣4m﹣7＝﹣4m+2．当时，原式＝＝﹣1+2＝1．18．（10分）为关注学生出行安全，调查了某班学生出行方式，调查结果分为四类：A﹣骑自行车，B﹣步行，C﹣坐社区巴士，D﹣其它，并将调查结果绘制成以下两幅不完整的统计图．请你根据统计图，解答下列问题：（1）本次一共调查了多少名学生？（2）C类女生有3名，D类男生有1名，并将条形统计图补充完整．（3）若从被调查的A类和D类学生中分别随机选取一位同学进行进一步调查，请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率．【分析】（1）用步行的人数除以所占的百分比即可得出调出的总人数；（2）用调查的总人数乘以所占的百分比，即可求出C类和D类的人数，从而补全统计图；（3）根据题意先画出树状图得出所以等情况数和恰好是一位男同学和一位女同学的情况数，然后根据概率公式即可得出答案．【解答】解：（1）本次调查的学生数＝10÷50%＝20（名）；（2）C类女生数有20×25%﹣2＝3名；D类男生数有20×（1﹣50%﹣25%﹣15%）﹣1＝1名，条形统计图为：故答案为：3，1；（3）画树状图为：共有6种等可能的结果数，其中恰好是一位男同学和一位女同学的结果数为3种，所以所选A，D两类同学中恰好是一位男同学和一位女同学的概率是＝．19．（8分）如图，在四边形ABCD中，E是AB的中点，AD∥EC，∠AED＝∠B．（1）求证：△AED≌△EBC．（2）当AB＝6时，求CD的长．【分析】（1）利用ASA即可证明；（2）首先证明四边形AECD是平行四边形，推出CD＝AE＝AB即可解决问题；【解答】（1）证明：∵AD∥EC，∴∠A＝∠BEC，∵E是AB中点，∴AE＝EB，∵∠AED＝∠B，∴△AED≌△EBC．（2）解：∵△AED≌△EBC，∴AD＝EC，∵AD∥EC，∴四边形AECD是平行四边形，∴CD＝AE，∵AB＝6，∴CD＝AB＝3．20．（8分）如图1、图2是两张形状、大小完全相同的5×5方格纸，方格纸中的每个小正方形的边长均为1，点A、B在小正方形的顶点上．（1）在图1中画出一个以点A、B为顶点的面积为3的平行四边形（要求所作的平行四边形且各顶点都在格点上）．（2）在图2中画出一个以点A、B为顶点的面积为8的的平行四边形（要求所作的平行四边形各顶点都在格点上）．【分析】（1）构造底为1，高为3的平行四边形即可．（2）构造对角线分别为2，4的菱形即可．【解答】解：（1）如图1中，平行四边形ABCD即为所求．（2）如图2中，平行四边形ABCD即为所求．21．（10分）如图，在平面直角坐标系中，抛物线y＝﹣x2+x+6与x轴交于点A，B两点，B点在点A的右边，与y轴交于点C，点P是x轴上方抛物线上的一点，点D坐标为（0，2）．（1）求线段AB的长度；（2）如图，以BD，BP为边作▱DBPE，当抛物线的对称轴恰好经过▱DBPE对称中心时，求点P的坐标，并说明此时点E是否在抛物线上．【分析】（1）根据题意求出A、B两点坐标即可求出线段AB的长度；（2）根据抛物线的对称轴恰好经过▱DBPE对称中心即可求出点P的坐标，再根据平行四边形的性质即可求出点E的坐标，将E点横坐标代入y＝﹣x2+x+6即可判断此时点E是否在抛物线上．【解答】解：（1）令y＝0可得++6＝0，解得x1＝﹣3，x2＝4，∴A（﹣3，0），B（4，0），∴AB＝4﹣（﹣3）＝7；（2）由题可得y＝﹣x2+x+6抛物线的对称轴为x＝，∴设▱DBPE的对称中心为（，a），∴P（1，6），由平移的性质可得E的坐标为（﹣3，8），∵当x＝﹣3时，y＝0，∴此时点E不在抛物线上．22．（10分）如图，Rt△ABC中，∠C＝90°，点O在边AB上，以O点为圆心、OB为半径作圆，分别与BC、AB相交于点D、E，连接AD，AD是⊙O的切线．（1）求证：∠CAD＝∠B；（2）若BC＝4，tan B＝，求⊙O半径．【分析】（1）连接OD，由切线的性质以及圆的半径构成的等腰三角形即可证明∠CAD ＝∠B；（2）设圆的半径为r，利用锐角三角函数定义求出AB的长，再利用勾股定理列出关于r 的方程，求出方程的解即可得到结果．【解答】解：（1）证明：∵AD是⊙O的切线，∴OD⊥AD，∴∠ADO＝90°，∴∠ODB+∠ADC＝90°，∵∠C＝90°，∴∠ADC+∠DAC＝90°，∴∠DAC＝∠ODB，∵OD＝OB，∴∠B＝∠ODB，∴∠CAD＝∠B；（2）设圆O的半径为r，在Rt△ABC中，AC＝BC tan B＝2，根据勾股定理得：AB＝＝2，∴OA＝2﹣r，在Rt△ACD中，tan∠CAD＝tan B＝，∴CD＝AC tan∠CAD＝1，根据勾股定理得：AD2＝AC2+CD2＝4+1＝5，在Rt△ADO中，OA2＝OD2+AD2，即（2﹣r）2＝r2+5，解得：r＝，∴⊙O半径为．23．（10分）某校计划采购凳子，商场有A、B两种型号的凳子出售，并规定：对于A型凳子，采购数量若超过250张，则超出部分可在原价基础上每张优惠a元；B型凳子的售价为40元/张．学校经测算，若购买300张A型凳子需要花费14250元；若购买500张A 型凳子需要花费21250元．（1）求a的值；（2）学校要采购A、B两种型号凳子共900张，且购买A型凳子不少于150张且不超过B型凳子数量的2倍，请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少？最少是多少元？【分析】（1）设A型凳子的售价为x张，根据题意列方程组解答即可；（2）设购买A型凳子m张，则购买B型凳子（900﹣m）张，根据题意求出m的取值范围；设总采购费用为w元，根据题意得出w与m的函数关系式，再根据一次函数的性质解答即可．【解答】解：（1）设A型凳子的售价为x元/张，根据题意得，解得，答：a的值为15．（2）设购买A型凳子m张，则购买B型凳子（900﹣m）张，根据题意得，解得150≤m≤600，设总采购费用为w元，根据题意得当150≤m≤250时，w＝50m+40（900﹣m）＝10m+36000；当250＜m≤600时，w＝50×250+（50﹣15）×（m﹣250）+40（900﹣m）＝﹣5m+39750，∴，当150≤m≤250时，10＞0，w随m的增大而增大，m＝150时，w的最小值为37500；当250＜m≤600时，﹣5＜0，w随m的增大而减小，m＝600时，w的最小值为36750．∵37500＞36750，∴购买A型凳子600张，购买B型凳子300张时总采购费用最少，最少是36750元．24．（14分）如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连接BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．（1）填空：B的坐标为（2，2）；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；（3）设AD＝x，矩形BDEF的面积为y，求y关于x的函数关系式，并求出y的最小值．（4）如图2，若点E边OC上，EF与BC相交于点G，连接BE及DG，BE和DG相交于点H，若BH＝3HE，记△GEC的面积为S1，△BGF的面积为S2，请直接写出的值．【分析】（1）求出AB、BC的长即可得出结果；（2）先推出∠ACO＝30°，∠ACD＝60°由△DEC是等腰三角形，分两种情况：①当E 在线段CO上时，观察图象可知，只有ED＝EC，∠DCE＝∠EDC＝30°，推出∠DBC ＝∠BCD＝60°，可得△DBC是等边三角形，推出DC＝BC＝2，即可得出结果；②当E在OC的延长线上时，只有CD＝CE，∠DBC＝∠DEC＝∠CDE＝15°，得出∠ABD＝∠ADB＝75°即可得出结果；（3）①先表示出DN，BM，证出△BMD∽△DNE，即可得出结论；②作DH⊥AB于H，用x表示BD、DE的长，构建二次函数即可解决问题．【解答】解：（1）∵四边形AOCB是矩形，∴BC＝OA＝2，OC＝AB＝2，∠BCO＝∠BAO＝90°，∴B（2，2）．故答案为（2，2）．（2）存在；理由如下：∵OA＝2，OC＝2，∵tan∠ACO＝＝＝，∴∠ACO＝30°，∠ACB＝60°，分两种情况：①当E在线段CO上时，△DEC是等腰三角形，观察图象可知，只有ED＝EC，如图1所示：∴∠DCE＝∠EDC＝30°，∴∠DBC＝∠BCD＝60°，∴△DBC是等边三角形，∴DC＝BC＝2，在Rt△AOC中，∠ACO＝30°，OA＝2，∴AC＝2AO＝4，∴AD＝AC﹣CD＝4﹣2＝2，∴当AD＝2时，△DEC是等腰三角形；②当E在OC的延长线上时，△DCE是等腰三角形，只有CD＝CE，∠DBC＝∠DEC＝∠CDE＝15°，如图2所示：∴∠ABD＝∠ADB＝75°，∴AB＝AD＝2，综上所述，满足条件的AD的值为2或2．（3）过点D作MN⊥AB交AB于M，交OC于N，如图3所示：∵A（0，2）和C（2，0），∴直线AC的解析式为y＝﹣x+2，设D（a，﹣a+2），∴DN＝﹣a+2，BM＝2﹣a，∵∠BDE＝90°，∴∠BDM+∠NDE＝90°，∠BDM+∠DBM＝90°，∴∠DBM＝∠EDN，∵∠BMD＝∠DNE＝90°，∴△BMD∽△DNE，∴＝＝＝，在Rt△ADM中，∵AD＝x，∠DAM＝∠ACO＝30°，∴DM＝AD＝x，AM＝＝＝x，∴BM＝2﹣x，在Rt△BDM中，BD＝＝＝﹣6x+12，∴DE＝BD＝•，∴矩形BDEF的面积为y＝•（）2＝x2﹣2x+4，∴y＝（x﹣3）2+，∵＞0，∴x＝3时，y有最小值，即当点D运动到距A点的距离为3时，y有最小值．（4）如图4中，设，DE＝BF＝m，则BD＝EF＝m，∵EG∥BD，∴＝＝3，∴EG＝m，∴FG＝m，∴BG＝＝＝m，∵∠CGE＝∠BGF，∠ECG＝∠F＝90°，∴△ECG∽△BFG，∴＝（）2＝（）2＝．。

2020-2021学年温州市实验中学九年级上学期期中考科学试卷亲爱的考生：欢迎参加考试！请你认真审题，积极思考，仔细答题，发挥最佳水平。

答题时，请注意以下几点：1.全卷共8页，有4大题，32小题，满分180分，考试时间120分钟。

2.答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上无效。

3.本卷可能用到的相对原子质量：H-1;C-12;0-16;Ca-40;C1-35.5;Na-23;Mg-24;S-32; Zn-65祝你成功！卷Ⅰ一、选择题（本题有15小题，每小题4分，共60分。

每小题只有一个选项是正确的，不选、多选、错选均不给分）1 .在“电闪雷鸣”这一自然现象中，没有涉及到的能量形式是【A】电能【B】声能【C】光能【D】核能【答案】D【解答】通常涉及核能的有核裂变和核聚变2. 家庭厨房就是一个化学小世界，米、油、盐、醋，其主要成分属于无机物的是【A】米（淀粉）【B】油（脂肪）【C】盐（氯化钠）【D】醋（醋酸）【答案】C【解答】有机物是指含碳化合物（不包括碳的氧化物，碳酸以及碳酸盐），C项NaCl不含碳元素。

3 .下图是某些物品的近似pH,其中酸性最强的【A】猴桃pH=3.0【B】牛奶pH=6.5【C】醋pH=3.8【D】小苏打pH=9.1【答案】A【解答】pH越大，酸性越强。

pH越小，碱性越强。

4.由于新冠疫情，“地摊经济”曾风靡一时。

下列地摊活动中涉及化学变化的是【A】手工刺绣【B】西瓜切块【C】露天烧烤【D】捏制泥人【答案】C【解答】物质燃烧有涉及到化学反应5. 规范操作是实验成功的基本保证，下列实验操作规范的是【A】液体加热【B】稀释浓硫酸【C】胶头滴管加液【D】锌粒放入试管【答案】B【解答】A加热试管液体不超过1/3，C滴管不能深入到试管，D固体用纸槽送6. 乌牛茶味醇气香，是茶中珍品。

为了使茶树正常生长，茶农需要施加化肥（NH4)3PO4.这种化肥属于【A】氮肥【B】磷肥【C】钾肥【D】复合肥【答案】D【解答】N、P、K含其中两种元素或以上的称为复合肥，例如KNO37.下列选项中，物质的名称、俗名、化学式不完全一致的是【A】碳酸钠——纯碱——Na2CO3【B】氯化钠——食盐——NaCl【C】氢氧化钙——生石灰——Ca(OH)2【D】氢氧化钠——烧碱——NaOH【答案】C【解答】生石灰是氧化钙，记忆方法CaO+H2O==Ca(OH)2生石灰放入到水里“煮”一下（该反应能放出大量热），变成熟石灰。

2020-2021上学期人教版九年级数学期末试卷一．选择题（共12小题）1．如果一个数的绝对值小于另一个数，则这两个数的和是（）A．正数B．正数或零C．负数D．负数或零2．下列各数：1，，4.112134，0，，3.14，其中分数有（）A．6个B．3个C．4个D．5个3．x＝3是下列方程的解的有（）①﹣2x﹣6＝0；②|x+2|＝5；③（x﹣3）（x﹣1）＝0；④x＝x﹣2．A．1个B．2个C．3个D．4个4．等式就像平衡的天平，能与如图的事实具有相同性质的是（）A．如果a＝b，那么ac＝bc B．如果a＝b，那么＝（c≠0）C．如果a＝b，那么a+c＝b+c D．如果a＝b，那么a2＝b25．若M在第三象限，则M点的坐标可能是（）A．（1，2）B．（2，﹣3）C．（﹣5，﹣6）D．（﹣3，5）6．如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（，0），顶点D的坐标为（0，），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A₂，作正方形A2B2C2C1，…，按这样的规律进行下去，第2021个正方形的周长为（）A．（）2020B．（）2021C．4×（）2020D．4×（）2021 7．下列几何体，用一个平面去截，不能截得三角形截面的是（）A．圆柱B．圆锥C．三棱柱D．正方体8．已知正方形ABCD的边长为3cm，以直线AB为轴，将正方形旋转一周，所得几何体的体积是（）A．27cm3B．27πcm3C．18cm3D．18πcm39．如图是台球桌面示意图，阴影部分表示四个入球孔，小明按图中方向击球（球可以多次反弹），则球最后落入的球袋是（）A．1号袋B．2号袋C．3号袋D．4号袋10．如图，在等边△ABC中，点D和点B关于直线AC对称，过点D做DE⊥BC，交BC 的延长线于点E，若CE＝5，则BE的长为（）A．5B．10C．5D．1511．某市有9个区，为了解该市初中生的体重情况，有人设计了四种调查方案，你认为比较合理的是（）A．测试该市某一所中学初中生的体重B．测试该市某个区所有初中生的体重C．测试全市所有初中生的体重D．每区随机抽取5所初中，测试所抽学校初中生的体重12．﹣2和2对应的点将数轴分成3段，如果数轴上任意n个不同的点中至少有3个在其中之一段，那么n的最小值是（）A．5B．6C．7D．8二．填空题（共6小题）13．若向前进10米记为+10，那么向后退10米记为．14．方程（b﹣3）b+2015＝1的解是b＝．15．点P到x轴和y轴的距离分别为2和3，且点P在第四象限，则P点的坐标为．16．一个直棱柱一共有21条棱，那么这个棱柱的底面的形状是．17．如图，在矩形ABCD中，AB＝8，BC＝4，一发光电子开始置于AB边的点P处，并设定此时为发光电子第一次与矩形的边碰撞，将发光电子沿着PR方向发射，碰撞到矩形的边时均反射，每次反射的反射角和入射角都等于45°，当发光电子与矩形的边碰撞2020次后，它与AB边的碰撞次数是．18．为统计了解某市4万名学生平均每天读书的时间，有以下步骤：①得出结论，提出建议；②分析数据；③从4万名学生中随机抽取400名学生，调查他们平均每天读书的时间；④利用统计图表将收集的数据整理和表示，请您对以上步骤进行合理排序．（只填序号）三．解答题（共9小题）19．为全力迎接全国第十四届运动会，西安市将继续加快交通高质量发展，不断增强市民获得感和幸福感．某检修小组从O地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶记录如下，（单位：km）第一次第二次第三次第四次第五次第六次第七次﹣4+7﹣9+8+6﹣5﹣1（1）求收工时距O地多远？（2）在第几次记录时距O地最远？（3）若每千米耗油0.2升，问共耗油多少升？20．把下列各数填在相应的集合中：22，，0.81，﹣3，，﹣3.1，0，3.14，π，1.6整数集合{…}；负分数集合{…}．21．阅读理解题：下面是小明将等式x﹣4＝3x﹣4进行变形的过程：x﹣4+4＝3x﹣4+4，①x＝3x，②1＝3．③（1）小明①的依据是．（2）小明出错的步骤是，错误的原因是．（3）给出正确的解法．22．已知方程3x+2a﹣1＝0的解与方程x﹣2a＝0的解互为相反数，求a的值．23．已知点P（2x﹣6，3x+1）在y轴上，求P的坐标．24．计算下面圆锥的体积．25．国庆期间，广场上对一片花圃做了美化造型（如图所示），整个造型构成花的形状．造型平面呈轴对称，其正中间“花蕊”部分（区域①）摆放红花，两边“花瓣”部分（区域②）摆放黄花．（1）两边“花瓣”部分（区域②）的面积是．（用含a的代数式表示）（2）已知a＝2米，红花价格为220元/平方米，黄花价格为180元/平方米，求整个造型的造价（π取3）．26．2020年3月线上授课期间，小莹、小静和小新为了解所在学校九年级600名学生居家减压方式情况，对该校九年级部分学生居家减压方式进行抽样调查．将居家减压方式分为A（享受美食）、B（交流谈心）、C（室内体育活动）、D（听音乐）和E（其他方式）五类，要求每位被调查者选择一种自己最常用的减压方式．他们将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．表1：小莹抽取60名男生居家减压方式统计表（单位：人）减压方式A B C D E人数463785表2：小静随机抽取10名学生居家减压方式统计表（单位：人）减压方式A B C D E人数21331表3：小新随机抽取60名学生居家减压方式统计表（单位：人）减压方式A B C D E人数65261310根据以上材料，回答下列问题：（1）小莹、小静和小新三人中，哪一位同学抽样调查的数据能较好地反映出该校九年级学生居家减压方式情况，并简要说明其他两位同学抽样调查的不足之处．（2）根据三人中能较好地反映出该校九年级居家减压方式的调查结果，估计该校九年级600名学生中利用室内体育活动方式进行减压的人数．27．若干个人相聚，其中有些人彼此认识，已知：（1）如果某两个人有相等数目的熟人，则他两没有公共的熟人；（2）有一个人至少有56个熟人．证明：可找出一个聚会者，他恰好有56个熟人．2020-2021上学期人教版九年级数学期末试卷参考答案与试题解析一．选择题（共12小题）1．【分析】根据一个数的绝对值小于另一个数，可知另一个数是正数，并且另一个数的绝对值较大，根据有理数的加法法则即可确定答案．【解答】解：∵一个数的绝对值小于另一个数，∴另一个数是正数，并且另一个数的绝对值较大，∴这两个数的和一定是正数．故选：A．2．【分析】根据有理数的分类判断即可．【解答】解：在1，，4.112134，0，，3.14中，分数有4.112134，，3.14，共3个．故选：B．3．【分析】分别求出四个方程的解各是多少，判断出x＝3是所给方程的解的有多少个即可．【解答】解：①∵﹣2x﹣6＝0，∴x＝﹣3．②∵|x+2|＝5，∴x+2＝±5，解得x＝﹣7或3．③∵（x﹣3）（x﹣1）＝0，∴x＝3或1．④∵x＝x﹣2，∴x＝3，∴x＝3是所给方程的解的有3个：②、③、④．故选：C．4．【分析】利用等式的性质对每个等式进行变形即可找出答案．【解答】解：观察图形，是等式a＝b的两边都加c，得到a+c＝b+c，利用等式性质1，所以成立．故选：C．5．【分析】根据在第三象限的点的横坐标和纵坐标均为负数判断即可．【解答】解：A．点（1，2）在第一象限；B．（2，﹣3）在第四象限；C．（﹣5，﹣6）在第三象限，D．（﹣3，5）在第二象限，故选：C．6．【分析】根据相似三角形的判定定理，得出△AA1B∽△A1A2B1，继而得知∠BAA1＝∠B1A1A2；利用勾股定理计算出正方形的边长；最后利用正方形的周长公式计算三个正方形的周长，从中找出规律，问题也就迎刃而解了．【解答】解：设正方形的周长分别为C1，C2 (2021)根据题意，得：AD∥BC∥C1A2∥C2B2，∴∠BAA1＝∠B1A1A2＝∠B2A2x（两直线平行，同位角相等）．∵∠ABA1＝∠A1B1A2＝90°，∴△BAA1∽△B1A1A2，∵顶点A的坐标为（，0），顶点D的坐标为（0，），∴OA＝，OD＝，在直角△ADO中，根据勾股定理，得：AD＝＝1，∴AD＝AB＝1，∵cot∠DAO＝＝，∵tan∠BAA1＝＝cot∠DAO，∴BA1＝AB＝，∴CA1＝1+＝，同理，得：C1A2＝+＝＝（）2，由正方形的周长公式，得：C1＝4×（）0C2＝4×（）1，C3＝4×（）2，…由此，可得∁n＝4×（）n﹣1，∴C2021＝4×（）2020．故选：C．7．【分析】当截面的角度和方向不同时，圆柱，球的截面不相同，无论什么方向截取圆柱都不会截得三角形．【解答】解：用一个平面截一个几何体，不能截得三角形的截面的几何体有圆柱．故选：A．8．【分析】首先根据题意可得将正方形旋转一周可得圆柱体，圆柱的高为3cm，底面直径为6cm，再计算体积即可．【解答】解：直线AB为轴，将正方形旋转一周可得圆柱体，圆柱的高为3cm，底面直径为6cm，∴所得几何体的体积＝32•π•3＝27π（cm3），故选：B．9．【分析】利用轴对称画图可得答案．【解答】解：如图所示，，球最后落入的球袋是2号袋，故选：B．10．【分析】连接CD，构造含30°角的直角三角形DCE，根据BC＝DC进行计算即可．【解答】解：如图，连接CD，∵△ABC是等边三角形，点D和点B关于直线AC轴对称，∴BC＝DC，∠ACB＝∠ACD＝60°，∴∠DCE＝60°，∵DE⊥CE，CE＝5，∴∠CDE＝30°，∴CD＝2CE＝10，∴BC＝10．∴BE＝BC+CE＝10+5＝15．故选：D．11．【分析】利用抽样调查的中样本的代表性即可作出判断．【解答】解：某市有9个区，为了解该市初中生的体重情况，设计了四种调查方案．比较合理的是：每区随机抽取5所初中，测试所抽学校初中生的体重，故选：D．12．【分析】将数轴上的3段看成3个抽屉，先考虑相反的情况，得到的结果再取反即为答案．令每个抽屉最多有2个点，则最多有6个点，由此可得出结论．【解答】解：∵令每个抽屉最多有2个点，则最多有6个点，∴n≥7．故选：C．二．填空题（共6小题）13．【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．【解答】解：若向前进10米记为+10，那么向后退10米记为﹣10．故答案为：﹣10．14．【分析】根据零指数幂的性质得到b+2015＝0，右侧求得b的值．【解答】解：根据题意，得b+2015＝0，或b﹣3＝1．解得b＝﹣2015或b＝4故答案是：﹣2015或4．15．【分析】根据第四象限内点的横坐标是正数，纵坐标是负数，点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度解答即可．【解答】解：∵点P（x，y）在第四象限，P到x轴，y轴的距离分别等于2和3，∴点P的横坐标是3，纵坐标是﹣2，∴点P的坐标为（3，﹣2）．故答案为：（3，﹣2）．16．【分析】根据n棱柱有3n条棱可得答案．【解答】解：∵一个直n棱柱有3n条棱，∴21÷3＝7，故答案为：7．17．【分析】如图，以AB为x轴，AD为y轴，建立平面直角坐标系，根据反射角与入射角的定义可以在格点中作出图形，可以发现，在经过6次反射后，发光电子回到起始的位置，即可求解．【解答】解：如图以AB为x轴，AD为y轴，建立平面直角坐标系，根据图形可以得到：每6次反弹为一个循环组依次循环，经过6次反弹后动点回到出发点（6，0），且每次循环它与AB边的碰撞有2次，∵2020÷6＝336…4，当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹，点P的坐标为（2，0），∴它与AB边的碰撞次数是＝336×2+1＝673次，故答案为：673．18．【分析】根据调查的一般步骤，得出结论．【解答】解：调查的一般步骤：先随机抽样，再收集整理数据，然后分析数据，最后得出结论．故答案为：③④②①．三．解答题（共9小题）19．【分析】（1）首先把题目的已知数据相加，然后根据结果的正负即可确定相距O多少千米；（2）分别写出各次记录时距离O地的距离，然后判断即可；（3）首先把所给的数据的绝对值相加，然后乘以0.2升，即可求解．【解答】解：（1）﹣4+7+（﹣9）+8+6+（﹣5）+（﹣1）＝2（千米）．答：收工时检修小组在O地东面2千米处；（2）第一次距O地|﹣4|＝4千米；第二次：|﹣4+7|＝3（千米）；第三次：|3﹣9|＝|﹣6|＝6（千米）；第四次：|﹣6+8|＝2（千米）；第五次：|2+6|＝8（千米）；第六次：|8﹣5|＝3（千米）；第七次：|3﹣1|＝2（千米）．所以距O地最远的是第5次；（3）从出发到收工汽车行驶的总路程：|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣1|＝40；从出发到收工共耗油：40×0.2＝8（升）．答：从出发到收工共耗油8升．20．【分析】根据整数包括正整数、0和负整数，可得整数集合；根据小于0的分数为负分数，可得负分数集合．【解答】解：整数集合{22，﹣3，0…}；负分数集合{，﹣3.1…}．故答案为：22，﹣3，0；，﹣3.1．21．【分析】根据等式的性质解答即可．【解答】解：（1）小明①的依据是等式的两边都加（或减）同一个数（或整式），结果仍得等式；（2）小明出错的步骤是③，错误的原因是等式两边都除以0；（3）x﹣4＝3x﹣4，x﹣4+4＝3x﹣4+4，x＝3x，x﹣3x＝0，﹣2x＝0，x＝0．故答案为：等式的两边都加（或减）同一个数（或整式），结果仍得等式；③；等式两边都除以0．22．【分析】先求出每个方程的解，根据相反数得出关于a的方程，求出方程的解即可．【解答】解：解方程3x+2a﹣1＝0得：x＝，解方程x﹣2a＝0得：x＝2a，∵方程3x+2a﹣1＝0的解与方程x﹣2a＝0的解互为相反数，∴2a+（﹣）＝0，解得：a＝﹣．23．【分析】根据y轴上点的横坐标为0列方程求出x的值，再求解即可．【解答】解：∵点P（2x﹣6，3x+1）在y轴上，∴2x﹣6＝0，解得x＝3，所以，3x+1＝9+1＝10，故P（0，10）．24．【分析】根据圆锥的体积解答即可．【解答】解：圆锥的体积：＝（cm3）．25．【分析】（1）区域②的面积＝2个正方形的面积．（2）分别求出区域①，②的面积，再乘以单价即可．【解答】解：（1）区域②的面积＝2a2．故答案为：2a2．（2）整个造型的造价：220（2×22﹣×22）+180（2×22+•π•22）＝2960（元）．26．【分析】（1）根据抽取样本的原则，为使样本具有代表性、普遍性、可操作性的原则进行判断；（2）样本中“采取室内体育锻炼减缓压力”的占，因此估计总体600人的是采取室内体育锻炼减缓压力的人数．【解答】解：（1）小新同学抽样调查的数据能较好地反映出该校九年级学生居家减压方式情况，小莹同学调查的只是男生，不具有代表性，小静同学调查的人数偏少，具有片面性，对整体情况的反映容易造成偏差．（2）600×＝260（人），答：该校九年级600名学生中利用室内体育活动方式进行减压的大约有260人．27．【分析】考虑聚会中熟人最多的人（如果不止一个，则任取其中之一），记为A，设A认识了n个人，设为B1，B2，…，B n，由条件（1）知B i，B j熟人的数目不相等，于是B1，B2，…，B n，各人的熟人数互不相等，且均不超过n（根据的最大性），因此，必然是1，2，…，n，再根据条件（2）知n≥56，从而求解．【解答】解：考虑聚会中熟人最多的人（如果不止一个，则任取其中之一），记为A，设A认识了n个人，设为B1，B2，…，B n，由于任意两人B i，B j都以A为共同熟人，由条件（1）知B i，B j熟人的数目不相等，于是B1，B2，…，B n，各人的熟人数互不相等，且均不超过n（根据的最大性），因此，必然是1，2，…，n，再根据条件（2）知n≥56，因此1，2，…，n中包含着56，即B1，B2，…，B n中必有人恰好认识56人．。

2023年浙江省温州市鹿城区小升初模拟数学试卷一、选择（每题1分，每题只有一个正确答案，共10分）1．（1分）温州一季度实现国民生产总值2002.1亿元，增长5.2%，横线上的数是（）A．准确数B．近似数C．整数D．正整数2．（1分）小温期末复习整理了下面的图和算式，其中画框部分表示2×3的是（）A．B．C．D．3．（1分）小温在计算48÷1.6时，探索了下面几种算法，其中算法错误的是（）A．48÷8÷0.2B．（48×10）÷（1.6×10）C．48÷4÷0.4D．48÷8×0.24．（1分）小温用数字卡片1、2、5、8摆出了所有的三位数，其中最小的数是（）A．质数B．偶数C．5的倍数D．3的倍数5．（1分）如图，长方形的两条边分别长6cm和2cm，以它较短的边为轴旋转一周形成一个圆柱。

这个圆柱的（）A．高是6cm B．底面半径是3cmC．底面积是π×62cm2D．体积是π×33×2cm36．（1分）六年级举行小发明比赛，六（2）班同学交了35件作品，六（2）班比六（1）班多交14。

如果把六（1）班的作品看成4份，那么下面表示错误的是（）A．六（2）班交了5份B．两个班一共交了9份C ．六（1）班交了35x(1+14) 件D ．六（2）班和六（1）班作品数的比是5：47．（1分）下面各组中的两种量成正比例关系的是（ ）A ．小温看一本300页的书，平均每天看的页数与天数。

B ．杭州亚运会吉祥物的单价一定，总价与数量。

C ．龙舟比赛的路程一定，航行的速度与时间。

D ．新能源汽车的电量一定，消耗的电量和剩余电量。

8．（1分）一件衣服的销售价是300元，其中60%是成本，40%是利润。

现在要降价促销，如果要保证利润不低于60元。

那么下面的折扣比较合理的是（ ）A ．6折B ．7折C ．8折D ．95折 9．（1分）如图，中间是面积为16cm 2 的正方形，与这个正方形每一条边相连的都是圆心角为90° 的扇形。

浙江省温州市鹿城区第二十三中学2024-2025学年九年级数学第一学期开学统考试题题号一二三四五总分得分批阅人A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）如图，直线与相交于点，点的横坐标为，则关于的不等式的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．2、（4分）函数中自变量x 的取值范围是（ ）A ．x ＞3B ．x ＜3C ．x≤3D ．x≥﹣33、（4分）已知边长分别为a 、b 的长方形的周长为10，面积4，则ab 2+a 2b 的值为（ ）A ．10B ．20C ．40D ．804、（4分）如图所示，在直角坐标系内，原点O 恰好是▱ABCD 对角线的交点，若A 点坐标为(2，3)，则C 点坐标为( )A ．(－3，－2)B ．(－2，3)C ．(－2，－3)D ．(2，－3)1y x b =+21y kx =-P P 1-x 1x b kx +<-5、（4分）如图，点O 在ABC 内，且到三边的距离相等，若∠A=60°，则∠BOC 的大小为( )A ．135°B ．120°C ．90°D ．60°6、（4分）如图，矩形沿折叠，使点落在边上的点处，如果，那么的度数是（ ）A ．B ．C ．D ．7、（4分）下列不能判断是正方形的有（ ）A ．对角线互相垂直的矩形B ．对角线相等的矩形C ．对角线互相垂直且相等的平行四边形D ．对角线相等的菱形8、（4分）如图，将点P(-2，3)向右平移n 个单位后落在直线y=2x-1上的点P'处，则n 等于( )A ．4B ．5C ．6D ．7二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）计算：_________．10、（4分）等腰三角形的一个外角为100︒，则这个等腰三角形的顶角为_________.ABCD AE D BC F 30BFA ∠=︒CEF ∠60︒45︒30°20︒=11、（4分）某中学组织八年级学生进行“绿色出行，低碳生活”知识竞赛，为了了解本次竞赛的成绩，把学生成绩分成五个等级，并绘制如图所示的扇形统计图(不完整)统计成绩，则等级所在扇形的圆心角是_______º.12、（4分）如图，在菱形中，，菱形的面积为24，则菱形周长为________13、（4分）如图，在矩形中，，过矩形的对角线交点作直线分别交、于点，连接，若是等腰三角形，则____.三、解答题（本大题共5个小题，共48分）14、（12分）如图，直线y= x+b ，分别交x 轴，y 轴于点A 、C ，点P 是直线AC 与双曲线y=在第一象限内的交点，过点P 作PB⊥x 轴于点B ，若OB=2，PB=3.（1）填空：k= ；（2）求△ABC 的面积；（3）求在第一象限内，当x 取何值时，一次函数的值小于反比例函数的值？,,,,A B C D E C ABCD 4,6AB BC ==ABCD O AD BC E F 、AF AEF AE =12kx15、（8分）某工厂制作AB 两种型号的环保包装盒．已知用3米同样的材料分别制成A 型盒的个数比制成B 型盒的个数少1个，且制作一个A 型盒比制作一个B 型盒要多用20%的材料．求制作每个A ，B 型盒各用多少材料？16、（8分）甲、乙两名射击选示在10次射击训练中的成绩统计图（部分）如图所示：根据以上信息，请解答下面的问题；选手A 平均数中位数众数方差甲a 88c 乙7.5b 6和9 2.65（1）补全甲选手10次成绩频数分布图．（2）a ＝ ，b ＝ ，c ＝ ．（3）教练根据两名选手手的10次成绩，决定选甲选手参加射击比赛，教练的理由是什么？（至少从两个不同角度说明理由）．17、（10分）近年来，越来越多的人们加入到全民健身的热潮中来.“健步走”作为一项行走速度和运动量介于散步和竞走之间的步行运动，因其不易发生运动伤害，不受年龄、时间和场地限制的优点而受到人们的喜爱.随着信息技术的发展，很多手机可以记录人们每天健步走的步数，为大家的健身做好记录.小明的爸爸妈妈都是健步走爱好者，一般情况下，他们每天都会坚持健步走.小明为了给爸App爸妈妈颁发4月份的“运动达人”奖章，进行了抽样调查，过程如下，请补充完整.从4月份随机抽取10天，记录爸爸妈妈运动步数（千步）如下：爸爸12 10 11 15 14 13 14 11 14 12妈妈11 14 15 2 11 11 14 15 14 14根据以上信息，整理分析数据如下表所示：平均数中位数众数爸爸12.612.5妈妈1414（1）直接在下面空白处写出表格中，的值；（2）你认为小明会把4月份的“运动达人”奖章颁发给谁，并说明理由.18、（10分）如图，已知ABC 为等边三角形，点D 、E 分别在BC 、AC边上，且AE=CD ，AD 与BE 相交于点F ．（1）求证：BE=AD ；（2）求∠BFD 的度数．B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）利用因式分解计算：2012-1992=_________；20、（4分）若，则= ．21、（4分）不等式组的解集为x ＞2，则a 的取值范围是_____________.22、（4分）在菱形中，，为中点，为对角线上一动点，连结和，则的值最小为_______．b a a b 2y =++y x 2{x x a >>ABCD 460AB ABC =∠=︒，E AD P BD PA PE PA PE +23、（4分）已知：，代数式的值为_________.二、解答题（本大题共3个小题，共30分）24、（8分）解不等式组：25、（10分）如图所示，在□ABCD 中，点E ，F 在它的内部，且AE ＝CF ，BE ＝DF ，试指出AC 与EF 的关系，并说明理由．26、（12分）如图，四边形ABCD 和四边形ACED 都是平行四边形，点R 为DE 的中点，BR 分别交AC 、CD 于点P 、Q ．（1）求证：△PCQ ∽△RDQ ；（2）求BP ：PQ ：QR 的值．x =2y =-222x xy y -+2931213x x x +≥⎧⎪+⎨>-⎪⎩参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、C 【解析】由图像可知当x<-1时，，然后在数轴上表示出即可.【详解】由图像可知当x<-1时，，∴可在数轴上表示为：故选C.本题主要考查一次函数和一元一次不等式的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．函数y 1＞y 2时x 的范围是函数y 1的图象在y 2的图象上边时对应的未知数的范围，反之亦然．2、B 【解析】解：由题意得，1-x ＞0，解得x ＜1．故选：B ．本题考查函数自变量取值范围．3、B 【解析】直接利用矩形周长和面积公式得出ab ，a+b ，进而利用提取公因式法分解因式得出答案.【详解】解：由边长分别为a 、b 的长方形的周长为10，面积4，.则2（a+b ）=10，ab=4，则a+b=5，故ab 2+a 2b=ab （b+a ）=4×5=20.故选：B.本题主要考查了提取公因式法以及矩形的性质应用，正确分解因式是解题关键.4、C1x b kx +<-1x b kx +<-根据图像,利用中心对称即可解题.【详解】由题可知▱ABCD 关于点O 中心对称,∴点A 和点C 关于点O 中心对称,∵A(2，3)，∴C(－2，－3)故选C.本题考查了中心对称,属于简单题,熟悉中心对称的点的坐标变换是解题关键.5、B 【解析】由条件可知O 为三角形三个内角的角平分线的交点，则可知∠OBC+∠OCB=（∠ABC+∠ACB ）=（180°-∠A ），在△BOC 中利用三角形的内角和定理可求得∠BOC ．【详解】∵O 到三边的距离相等∴BO 平分∠ABC ，CO 平分∠ACB ∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°−∠A)∵∠A=60°∴∠OBC+∠OCB=60°∴∠BOC=180°−(∠OBC+∠OCB)=180°−60°=120°故选B.本题考查了角平分线的性质，熟练掌握角平分线把一个角分成两个相等的角是解题的关键．6、C【解析】先由矩形的性质折叠的性质得出∠AFE=∠D=90°，从而得出∠CFE=60°，在利用直角三角形的性质即可．12121212∵四边形ABCD是矩形，∴∠C=∠D=90°，由折叠得，∠AFE=∠D=90°，∴∠BFA+∠CFE=90°，∴∠CFE=90°-∠BFA=60°，∵∠C=90°，∴∠CEF=90°-∠CFE=30°，故选C．此题主要考查了矩形的性质，折叠的性质，直角三角形的性质，解本题的关键是求出∠CFE．7、B【解析】根据正方形的判定逐项判断即可．【详解】A、对角线互相垂直的矩形是正方形，此项不符题意B、对角线相等的矩形不一定是正方形，此项符合题意C、对角线互相垂直且相等的平行四边形是正方形，此项不符题意D、对角线相等的菱形是正方形，此项不符题意故选：B．本题考查了正方形的判定，熟记正方形的判定方法是解题关键．8、A【解析】由平移的性质得出P'的坐标，把P'点坐标代入直线y=2x-1上即可求出n的值；【详解】由题意得P'(-2+n,3)，则3=2(-2+n)-1，解得n=4.故答案为A.本题主要考查了一次函数的图象，平移的性质，掌握一次函数的图象，平移的性质是解题的关键.二、填空题（本大题共5个小题，每小题4分，共20分）9【解析】先计算二次根式的乘法，然后进行化简，最后合并即可.【详解】原式.故答案为本题考查了二次根式的混合运算，掌握各种知识点的运算法则是解答本题的关键.10、12.【解析】因为题中没有指明该外角是顶角的外角还是底角的外角，所以应该分两种情况进行讨论．【详解】解：当100°的角是顶角的外角时，顶角的度数为180°-100°=80°；当100°的角是底角的外角时，底角的度数为180°-100°=80°，所以顶角的度数为180°-2×80°=20°；∴顶角的度数为80°或20°．故答案为80°或20°．本题考查等腰三角形的性质，三角形内角和定理及三角形外角性质等知识；分情况进行讨论是解答问题的关键．11、72°【解析】根据扇形统计图计算出C 等级所在的扇形的圆心角，即可解答【详解】C 等级所在的扇形的圆心角=(1−25%−35%−8%−12%)⋅360°=72°，故答案为：72°此题考查扇形统计图，难度不大==-=12、20【解析】根据菱形面积公式可求BD 的长，根据勾股定理可求菱形边长，即可求周长．【详解】解：∵S 菱形ABCD =AC×BD ，∴24=×8×BD ，∴BD=6，∵ABCD 是菱形，∴AO=CO=4，BO=DO=3，AC ⊥BD ，∴，∴菱形ABCD 的周长为4×5=20.本题考查了菱形的性质，利用菱形的面积公式求BD 的长是本题的关键．13、或【解析】连接AC ，由矩形的性质得出∠B =90°，AD =BC =6，OA =OC ，AD ∥BC ，由ASA 证明△AOE ≌△COF ，得出AE =CF ，若△AEF 是等腰三角形，分三种情讨论：①当AE =AF 时，设AE =AF =CF =x ，则BF =6-x ，在Rt △ABF 中，由勾股定理得出方程，解方程即可；②当AF =EF 时，作FG ⊥AE 于G ，则AG =AE =BF ，设AE =CF =x ，则BF =6-x ，AG =x ，得出方程x =6-x ，解方程即可；③当AE =FE 时，作EH ⊥BC 于H ，设AE =FE =CF =x ，则BF =6-x ，CH =DE =6-x ，求出FH =CF -CH =2x -6，在Rt △EFH 中，由勾股定理得出方程，方程无解；即可得出答案．【详解】解：连接AC ，如图1所示：4133121212∵四边形ABCD 是矩形，∴∠B =90°，AD =BC =6，OA =OC ，AD ∥BC ，∴∠OAE =∠OCF ，在△AOE 和△COF 中， ，∴△AOE ≌△COF （ASA ），∴AE=CF ，若△AEF 是等腰三角形，分三种情讨论：①当AE =AF 时，如图1所示：设AE =AF =CF =x ，则BF =6-x ，在Rt △ABF 中，由勾股定理得：12+（6-x ）2=x 2，解得：x =，即AE=；②当AF =EF 时，作FG ⊥AE 于G ，如图2所示：则AG =AE =BF ，设AE =CF =x ，则BF =6-x ，AG =x ，OAE OCF OA OC AOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩1331331212所以x =6-x ，解得：x =1； ③当AE =FE 时，作EH ⊥BC 于H ，如图3所示：设AE =FE =CF =x ，则BF =6-x ，CH =DE =6-x ，∴FH =CF -CH =x -（6-x ）=2x -6，在Rt △EFH 中，由勾股定理得：12+（2x -6）2=x 2，整理得：3x 2-21x +52=0，∵△=（-21）2-1×3×52＜0，∴此方程无解；综上所述：△AEF 是等腰三角形，则AE 为或1；故答案为：或1．本题考查了矩形的性质、全等三角形的判定与性质、勾股定理、解方程、等腰三角形的性质、分类讨论等知识；根据勾股定理得出方程是解决问题的关键，注意分类讨论．三、解答题（本大题共5个小题，共48分）14、（1）6；（1）6；（3）0＜x ＜1【解析】（1）∵PB⊥x 轴于点B ，OB=1，PB=3，∴P（1，3），∵点P 是直线AC 与双曲线y=在第一象限内的交点，∴k=1×3=6，故答案为6；（1）∵直线y=x+b 经过点P （1，3），∴×1+b=3，12133133∴b=1，即y=x+1，令x=0，解得y=1，即C （0，1）；令y=0，解得x=﹣4，即A （﹣4，0）；∴AB=6，CO=1，∴S △ABC =×6×1=6；（3）由图象及点P 的横坐标为1，可知：在第一象限内，一次函数的值小于反比例函数的值时，x 的范围为0＜x ＜1．15、制作每个A 型盒用0.1米材料，制作每个B 型盒用0.5米材料．【解析】设制作每个B型盒用x 米材料，则制作每个A 型盒用（1+20%）x 米材料，根据数量＝材料总数÷每个环保包装盒所需材料结合用3米同样的材料分别制成A 型盒的个数比制成B 型盒的个数少1个，即可得出关于x 的分式方程，解方程并经检验后即可得出结论．【详解】设制作每个B 型盒用x 米材料，则制作每个A 型盒用（1+20%）x 米材料，依题意得：﹣＝1，解得：x ＝0.5，经检验，x ＝0.5是所列分式方程的解，且符合题意，∴（1+20%）x ＝0.1．答：制作每个A 型盒用0.1米材料，制作每个B 型盒用0.5米材料．本题考查分式方程的应用，正确得出题中等量关系是解题关键．16、（1）4；（2）8、1.2、7.5；（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的3x 3(120%)x方差小，说明甲的成绩稳定．【解析】（1）根据甲的成绩频数分布图及题意列出10﹣（1+2+2+1），计算即可得到答案；（2）根据平均数公式、中位数的求法和方差公式计算得到答案；（3）从平均数和方差进行分析即可得到答案.【详解】解：（1）甲选手命中8环的次数为10﹣（1+2+2+1）＝4，补全图形如下：（2）a＝＝8（环），c ＝×[（6﹣8）2+2×（7﹣8）2+4×（8﹣8）2+2×（9﹣8）2+（10﹣8）2]＝1.2，b ＝＝7.5，故答案为：8、1.2、7.5；（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的方差小，说明甲的成绩稳定．本题考查频数分布直方图、平均数、中位数和方差，解题的关键是读懂频数分布直方图，掌握平均数、中位数和方差的求法.17、 (1)；（2）详见解析.【解析】（1）根据平均数、众数的定义分别求出a ，b 的值；（2）根据平均数与中位数的意义说明即可.【详解】解：(1)由题意，可得a=（11+14+15+2+11+11+14+15+14+14）÷10=12.1，67284921010+⨯+⨯+⨯+110872+12.1,14a b ==10个数据中，14出现了3次，次数最多，所以b=14；∴； (2)答案不唯一，理由须支撑推断结论.例如：我认为小明会把4月份的“运动达人”奖章颁发给爸爸，因为从平均数的角度看，爸爸每天的平均运动步数比妈妈多.我认为小明会把4月份的“运动达人”奖章颁发给妈妈，因为从中位数的角度看，妈妈有超过5天的运动步数达到或超过了14千步，而爸爸没有，妈妈平均步数低于爸爸完全是受一个极端值的影响造成的，考虑到这一极端值很可能是由于某种特殊原因(例如生病等)造成的，可以排除此干扰.本题考查了中位数、众数和平均数的概念，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫伯这组数据的中位数；一组数据中出现次数最多的数据叫做众数；平均数是指在一组数据中所有数据之和再除以数据的个数.18、（1）见解析；（2）60°【解析】（1）根据等边三角形的性质可得AB=AC ，∠BAC=∠C=60°，然后根据SAS 可证△ABE ≌△CAD ，再根据全等三角形的性质即得结论；（2）由全等三角形的性质可得∠ABE=∠CAD ，然后根据三角形的外角性质和角的和差即可得出结果．【详解】解：（1）∵△ABC 是等边三角形，∴AB=AC ，∠BAC=∠C=60°，又∵AE=CD ，∴△ABE ≌△CAD （SAS ），∴BE=AD ；（2）∵△ABE ≌△CAD ，∴∠ABE=∠CAD ，∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°．本题考查了等边三角形的性质、三角形的外角性质以及全等三角形的判定和性质，属于常考题型，熟练掌握上述基本知识是解题的关键．12.1,14a b ==一、填空题（本大题共5个小题，每小题4分，共20分）19、800【解析】分析：先利用平方差公式分解因式，然后计算即可求解.详解：2012-1992=（201+199）（201-199）=800.故答案为800.点睛：本题考查了因式分解在进行有理数的乘法中的运用，涉及的是平方差公式的运用，使运算简便．20、1．【解析】试题分析：有意义，必须，，解得：x=3，代入得：y=0+0+2=2，∴==1．故答案为1．考点：二次根式有意义的条件．21、a≤2【解析】根据求一元一次不等式组解集的口诀，即可得到关于a 的不等式，解出即可.【详解】由题意得a ≤2.本题考查的是解一元一次不等式组，解答本题的关键是熟练掌握求一元一次不等式组解集的口诀：同大取大，同小取小，大小小大中间找，小小大大找不到（无解）.22、【解析】根据轴对称的性质，作点E′和E 关于BD 对称．则连接AE′交BD 于点P ，P 即为所求作的点．PE+PA 的最小值即为AE′的长．【详解】作点E′和E 关于BD 对称．则连接AE′交BD 于点P ，∵四边形ABCD 是菱形，AB=4，E 为AD 中点，2y =+30x -≥30x -≥y x 23∴点E′是CD的中点，∴DE′=DC=×4=2，AE′⊥DC ，∴．故答案为此题考查轴对称-最短路线问题，熟知“两点之间线段最短”是解题的关键．23、4【解析】根据完全平方公式计算即可求出答案．【详解】解：∵，，∴x−y ＝2，∴原式＝（x−y ）2＝4，故答案为：4本题考查二次根式的化简求值和完全平方公式，解题的关键是熟练运用完全平方公式，本题属于基础题型．二、解答题（本大题共3个小题，共30分）24、【解析】先求出每个不等式的解集，再求出不等式组的解集即可．【详解】解：解不等式①得，解不等式②得，1212==x =2y =-3 4.x -≤<2931213x xx +⎧⎪⎨+>-⎪⎩①②…x 3≥-x 4<∴原不等式组的解集是本题考查了解一元一次不等式组，能根据不等式的解集求出不等式组的解集是解此题的关键．25、AC 与EF 互相平分，见解析.【解析】由题意可证△ABE ≌△DCF ，可得∠BAE ＝∠DCF ，即可得∠CAE ＝∠ACF ，可证AE ∥CF 即可证AECF 是平行四边形，可得AC 与EF 的关系．【详解】AC 与EF 互相平分∵▱ABCD ∴AB ∥CD ，AB ＝CD ∴∠BAC ＝∠ACD ∵AB ＝CD ，AE ＝CF ，BE ＝DF ∴△ABE ≌△CDF ∴∠BAE ＝∠FCD 且∠BAC ＝∠ACD ∴∠EAC ＝∠FCA ∴CF ∥AE 且AE ＝CF ∴四边形AECF 是平行四边形∴AC 与EF 互相平分本题考查了平行四边形的性质，全等三角形的判定和性质，证AECF 是平行四边形是本题的关键．26、（1）见解析；（2）【解析】（1）根据平行线的性质可得，再根据，即可证明；（2）根据平行四边形的性质可得，，再根据相似三角形的性质可得，从而可得，再根据，即可求解．3x 4.-≤<::3:1:2BP PQ QR =PCQ RDQ ∠=∠PQC RQD ∠=∠PCQ RDQ △∽△PB PR =12PCRE =12PQPCPCQR DR RE ===2QR PQ =3BP PR PQ QR PQ ==+=【详解】解：（1）∵，∴．又∵．∴．（2）∵四边形和四边形都是平行四边形，∴，．∴，．又∵点是中点，∴．由（1）知，∴，∴．又∵，∴．本题考查了相似三角形的问题，掌握平行四边形的性质、相似三角形的性质以及判定定理是解题的关键．PC DR ∥PCQ RDQ ∠=∠PQC RQD ∠=∠PCQ RDQ △∽△ABCD ACED BC AD CE ==//AC DE PB PR =12PC RE =R DE DR RE =PCQ RDQ △∽△12PQ PC PC QR DR RE ===2QR PQ =3BP PR PQ QR PQ ==+=::3:1:2BP PQ QR =。