1长方体的长宽高都扩大为原来的3倍那么它的体积就扩大为倍

人教版五年级下册数学第三单元测试卷一、填空题1．一根长方体木料，长2m，宽0.5m，厚2dm，把它锯成4段，表面积最少增加( )dm2。

2．把一个长8dm、宽6dm、高4dm的长方体切成两个同样大小的长方体，表面积最少增加( )，最多增加( )。

3．把4个棱长是1分米的正方体拼成一个长方体，长方体的表面积可能是( )平方分米，也可能是( )平方分米。

4．用铁丝做一个棱长5分米的正方体框架，至少需要( )分米的铁丝，至少需要( )平方分米的铁皮才能把它围起来。

5．把一根长60厘米、宽5厘米、高8厘米的长方体木料锯成长都是30厘米的两段，表面积比原来增加( )平方厘米。

6．一个棱长为8厘米的正方体被切成3个大小形状相同的小长方体，则表面积比原来增加( )平方厘米。

7．有一个长方体长22厘米、宽15厘米、高3厘米，那么这个长方体的表面积是( )平方厘米。

8．一个长方体的棱长总和是48厘米，长、宽、高的和是( )厘米，若一个正方体和这个长方体的棱长总和相等，那么这个正方体的表面积是( )平方厘米。

9．一个正方体与一个长方体拼成一个新长方体，这个新长方体的表面积比原来的长方体表面积增加了64平方厘米，这个正方体的表面积是( )平方厘米。

10．在正方体的展开图中，“2”相对面的数字是( )。

二、判断题1．正方体的底面边长是5厘米，它的体积是125立方厘米。

( )2．一天，小明渴极了，一次喝了1m3的水。

( )3．长方体（不考虑正方体）最多有8条棱的长度相等。

( )4．表面积相等的两个长方体，体积不一定相等。

( )5．长方体中的三条棱长分别叫做长、宽、高。

( )三、选择题1．下列图形中，能折成正方体的是（）。

A．B．C．D．2．至少需要（）个同样的小正方体，才可以拼成一个稍大的正方体。

A．1 B．4 C．6 D．83．长方体的长、宽、高都扩大到原来的3倍，则它的体积扩大到原来的（）倍。

A．3 B．9 C．18 D．274．用棱长为1cm的正方体，依次摆出下面的长方体。

五年级下册数学第3单元练习题答案一、我会填１、10.2立方米＝立方分米 .5升=毫升9.8毫升＝立方厘米3.28立方分米＝升6.075立方米＝立方分米＝立方厘米2、在括号里填上适当的单位。

一块橡皮的体积约是一个柜子的体积约是22一瓶可乐300一个洗衣机的容积是7. 教室的占地面积是50一枝铅笔长203、用两个棱长都是5厘米的正方体拼成一个长方体，这个长方体的长是厘米，宽是厘米，高是厘米，棱长总和是，体积是。

4、一个喷雾器的药箱容积是13L，如果每分钟喷出药液650ml，喷完一箱药液需要用分钟。

5、把50升水倒入一个棱长是5分米的正方体容器里，水的高度是分米。

6、一个长方体的底面积是32平方米，高和宽都是4分米，这个长方体的表面积是平方分米。

7、一个正方体的棱长总和是12厘米，它的表面积是平方厘米，体积是立方厘米。

二、我会判断。

1、正方体是长、宽、高都相等的长方体2、一个粉笔盒的体积是1平方分米3、把一块下方体橡皮泥捏成一个长方体后，虽然它的形状变了，但是它所占有的空间大小不变4、把棱长是2m的石块放在地上，石块所占地面的面积是8m5、一个正方体的棱长是6dm，它的表面积和体积相等三、我会选择1、下面图可以折叠成正方体。

A、B、CD2、正方体的棱长扩大3倍，表面积扩大倍，体积扩大倍。

A、 B、9C、2D、543、把一个棱长是5分米的正方体木块，平均分成两个大小完全一样的长方体后，表面积，体积的长方体框架。

A、2cmB、3cmC、4cmD、5cm5、一个棱长是4分米的正方体，棱长总和是分米。

A、1B、2C、32D、486、一个正方体的棱长是4分米，把它锯成棱长是1分米的小正方体，可锯成个。

A、8B、32C、64D、无法确定7、一个正方体的底面积是25平方米，体积是125立方米，它的高是米。

A、3B、5C、D、。

）四、我会算1、求下面立体图形的表面积和体积。

五、我会解决问题1、一根长方体木料长5米，横截面的面积是0.06平方米。

周测培优卷4棱长和、表面积的能力检测卷一、我会填。

(每空2分，共20分)1．右图是由棱长1 cm的小正方体摆成的，它的棱长是()，棱长和是()。

2．用一根长72 cm的铁丝围成一个正方体框架，这个正方体框架的棱长是()cm。

3.聪聪用一些小棒和橡皮泥小球拼搭长方体框架，上图是他已经完成的一部分，如果要完成一个长方体框架：(1)还需要()个橡皮泥小球。

(2)还需要()根9 cm长的小棒、()根5 cm长的小棒和()根3 cm长的小棒。

(3)这个框架的表面积是()cm2。

4．正方体一个面的周长是32厘米，它的表面积是()平方厘米。

5．一个正方体的表面积是96 m2，一个面的面积是()dm2。

二、我会辨。

(对的画“√”，错的画“×”)(每题3分，共9分)1．长方体6个面都是长方形，正方体6个面都是正方形。

() 2．正方体的棱长扩大到原来的2倍，表面积也扩大到原来的2。

() 3．将一个长方体切成两个同样大小的长方体，每个小长方体的表面积是原长方体表面积的一半。

()三、我会选。

(每题3分，共9分)1．一个棱长总和是72 cm的长方体，长、宽、高的和是()cm。

A．12B．18C．36D．722．用7个小正方体拼成下面的图形，现在把画“×”的正方体拿走，它的表面积和原来比，()。

A．不变B．增加了C．减小了D．无法判断3．下图标出了一个房间(地面是长方形)的长、宽、高，这个房间的占地面积是()m2。

A．12 B．15 C．20 D．94四、我会按要求解答。

(共20分)1．下面哪些图形可以围成正方体？在括号里画“√”。

(每题2分，共8分)2．下图是用边长为2 cm的小正方体拼成的长方体。

右面的图形哪一个是这个长方体6个面中的一个？在图形上用“√”标出，并注明有几个这样的面。

(12分)五、走进生活，解决问题。

(每题7分，共42分)1．快递员想在长25 cm、宽15 cm、高12 cm的长方体邮件盒表面包一层塑料膜，至少需要多少平方厘米的塑料膜？2．做下面这样一个手提袋至少需要多少平方厘米的纸板？3．如下图，昆虫箱的前、后面是防蝇纱网，其余四个面是木板。

人教五年级下单元测试第3单元班级________姓名________一、判断题(共5题；共10分)1．棱长是2厘米的正方体，它的棱长总和是24平方厘米。

（）2．至少要8个小正方体才能拼成一个大正方体（）3．正方体的六个面一定是正方形，但长方体的六个面不一定都是长方形。

（）4．正方体的棱长扩大到原来的3倍，它的体积就扩大到原来的27倍。

（）5．把棱长1分米的正方体木块锯成棱长1厘米的正方体小木块，共可锯成100块。

（）二、填空题(共7题；共13分)6．在横线上填上适当的单位名称：一块橡皮的体积大约是8；一个教室大约占地48；一本数学书的体积约是150。

7．一个长方体，长10厘米，宽2厘米，高4.5厘米．它的表面积是平方厘米，体积是立方厘米．8．要做一个长6分米、宽4分米、高2分米的无盖玻璃鱼缸，用角钢做它的框架，至少需要角钢分米，把它放在桌面上，占平方分米.9．一个正方体钢块的棱长和是60厘米，如果每立方厘米的钢重7.8克，这个钢块重千克。

10．小卖部要用角铁做一个长250厘米，宽60厘米，高80厘米的长方体柜台，六面装玻璃，至少需要米角铁。

11．一个长方体和正方体的楼长总和相等。

长方体的长7cm，宽5cm，高3cm，这个正方体的棱长是cm。

12．两个完全相同的长方体，长5厘米，宽4厘米，高3厘米，拼成一个表面积最大的长方体后，表面积比原来减少了平方厘米．三、选择题(共5题；共10分)13．一个长方体的长、宽、高都扩大为原来的2倍，它的体积就扩大到原来的（）倍。

A．4B．6C．814．一个长方体的所有棱长之和是36厘米，则相交于一个顶点的所有棱长之和是（）。

A．9厘米B．12厘米C．18厘米D．3厘米15．生活中有许多长方体状物体。

有一样物体的长宽高分别是26cm、18cm、0.7cm，它可能是（）。

A．牙膏盒B．牛奶盒C．书柜D．数学书16．一根长方体木料，它的横截面积是10cm2，把它截成三段，表面积增加（）。

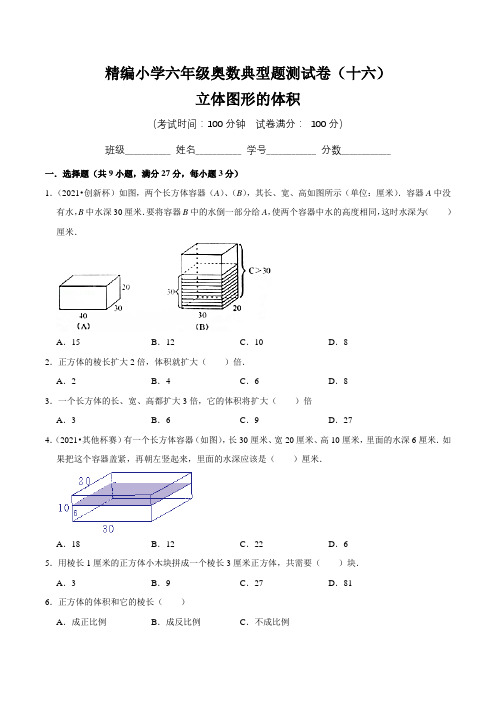
精编小学六年级奥数典型题测试卷（十六）立体图形的体积（考试时间：100分钟试卷满分：100分）班级___________ 姓名___________ 学号____________ 分数____________一．选择题（共9小题，满分27分，每小题3分）1．（2021•创新杯）如图，两个长方体容器（A）、（B），其长、宽、高如图所示（单位：厘米）．容器A中没有水，B中水深30厘米．要将容器B中的水倒一部分给A，使两个容器中水的高度相同，这时水深为（）厘米．A．15 B．12 C．10 D．82．正方体的棱长扩大2倍，体积就扩大（）倍．A．2 B．4 C．6 D．83．一个长方体的长、宽、高都扩大3倍，它的体积将扩大（）倍A．3 B．6 C．9 D．274．（2021•其他杯赛）有一个长方体容器（如图），长30厘米、宽20厘米、高10厘米，里面的水深6厘米．如果把这个容器盖紧，再朝左竖起来，里面的水深应该是（）厘米．A．18 B．12 C．22 D．65．用棱长1厘米的正方体小木块拼成一个棱长3厘米正方体，共需要（）块．A．3 B．9 C．27 D．816．正方体的体积和它的棱长（）A．成正比例B．成反比例C．不成比例7．一个长方体的铁皮水箱容量是400升，底面是边长为8分米的正方形，水箱深（）分米．A．50 B．6.25 C．12.5 D．258．一个长方体，上下两个面是正方形，表面积是14平方厘米，正好可以分成三个正方体，这个长方体的体积是（）立方厘米．A．1 B．3 C．9 D．149．一个正方体的棱长扩大3倍后，体积是162立方厘米，原正方体的体积是（）立方厘米．A．54 B．18 C．6 D．81二．填空题（共10小题，满分30分，每小题3分）10．（2021•学而思杯）如图，有一个棱长是10厘米的正方体木块，从它的上面、前面和左面的中心分别凿穿一个边长为4厘米的正方形孔，穿孔后，木块剩余部分的体积是立方厘米．11．（2021•希望杯）若一个长方体，长是宽的2倍，宽是高的2倍，所有棱长之和是56，则此长方体的体积是．12．（2021•其他模拟）一个长方体的表面积是33.66平方分米，其中一个面的长是2.3分米，宽是2.1分米，它的体积是立方分米．13．（2020•奥林匹克）把一个长方体的木条左右两端切去长度分别为5厘米的一段和4厘米的一段后，得到一个正方体．如果正方体的表面积比原长方体的表面积减少360平方厘米，那么，原长方体的体积是立方厘米．14．（2021•其他杯赛）有大、小两个正方体水池，它们的棱长分别是6米、3米．把一堆碎石完全沉没在大水池的水里，大水池的水面升高了3厘米．如果将这堆碎石完全沉浸在小水池的水里，小水池的水面升高了厘米．（注意：原来水池并没有装满，但有足够多的水，并且水从未溢出）15．（2021•学而思杯）如图，水深7米，那么此容器还能装立方米的水（π取3）．16．（2018•陈省身杯）把正方体用一个与它的一面平行的平面切开，分成A、B两个长方体．当A、B的表面积之比为3：5时，如果A长方体的体积为312cm3，那么B长方体的体积为cm3．17．（2018•陈省身杯）一个长方体的相邻两个面面积之和是77平方厘米，它的长、宽、高都是整数厘米，且都是质数．这个长方体的体积是立方厘米．18．（2020•春蕾杯）有一个长方体，它的正面和底面的面积之和是117，如果它的长、宽、高都是素数，那么它的体积是．19．（2020•希望杯）如图，将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，这根长方体木块原来的体积是立方分米．三．解答题（共9小题，满分43分）20．（4分）一块长方体钢板长2.2米，宽1.5米，厚0.01米．它的体积是多少立方分米？21．（4分）一个长方体沙坑的长是8米，宽是4.2米，深是0.6米，每立方米沙土重1.75吨，填平这个沙坑共要用沙土多少吨？22．（5分）如图，一块长方形铁皮，利用图中的阴影部分刚好能做一个圆柱形油桶（接头处不计），求这个油桶的容积？23．（5分）（2021•其他杯赛）如图是一个长方体，阴影部分的面积和是78平方厘米，这个长方体的体积是多少立方厘米？24．（5分）一个直角三角形，两条直角边分别是3厘米和4厘米，以直角边为轴旋转一周，可以得到一个圆锥体，这个圆锥体的体积最小是多少立方厘米？．（5分）小红想测量一个铁球的体积，于是把它放进一个底面长20厘米，宽15厘米的长方体容器中，铁球完全被水埋没，水面上升了4厘米，铁球的体积是多少立方厘米？26．（5分）（2018•其他杯赛）在一个长为16分米，宽为10分米的长方形玻璃鱼缸中，放进一块体积为800立方分米的假山石，鱼缸中的水正好上升到缸口，如果把这块假山石取出，水面高度为16分米，这个玻璃鱼缸的容积是多少升？27．（5分）（2020•华罗庚金杯模拟）有一个棱长是10厘米的正方体木块，在它的上、左、前三个面中心分别穿一个3厘米见方的孔，直至对面．求穿孔后木块的体积．（3厘米见方：边长3厘米的正方形）28．（5分）（2020•希望杯）某日是台风天气，雨一直均匀地下着，在雨地里放一个如图1所示的长方体容器，此容器装满雨水需要1小时．请问：雨水要下满如图2所示的三个不同的容器，各需要多长时间？参考答案一．选择题（共9小题，满分27分，每小题3分）1．（2021•创新杯）如图，两个长方体容器（A）、（B），其长、宽、高如图所示（单位：厘米）．容器A中没有水，B中水深30厘米．要将容器B中的水倒一部分给A，使两个容器中水的高度相同，这时水深为（）厘米．A．15 B．12 C．10 D．8【分析】在这个变化过程中水的体积没有变化，原来水的体积等于右边的底面积×高，现在水的体积就是两个底面积之和×高，抓住这个关系进行解题．【解答】解：设现在水的高度是a厘米30×40×a+30×20×a＝30×20×301800a＝18000a＝10故选：C．2．正方体的棱长扩大2倍，体积就扩大（）倍．A．2 B．4 C．6 D．8【分析】根据正方体的体积计算公式V＝a3，以及因数与积的变化规律，正方体棱长扩大2倍，体积扩大2的立方倍．由此解答．【解答】解：根据正方体的体积计算方法可知，正方体棱长扩大2倍，体积扩大2的立方倍，即扩大2×2×2＝8倍．故选：D．3．一个长方体的长、宽、高都扩大3倍，它的体积将扩大（）倍A．3 B．6 C．9 D．27【分析】可设原来长、宽、高分别为a、b、h，那么现在就分别为3a、3b、3h，分别表示出原来的与现在的体积，即可得出答案．【解答】解：设原来长为a，宽为b，高为h，则现在的长为3a，宽为3b，高为3h；原来的体积：abh，现在的体积：3a×3b×3c＝27abc，（27abc）÷（abc）＝27；答：体积扩大27倍．故选：D．4．（2021•其他杯赛）有一个长方体容器（如图），长30厘米、宽20厘米、高10厘米，里面的水深6厘米．如果把这个容器盖紧，再朝左竖起来，里面的水深应该是（）厘米．A．18 B．12 C．22 D．6【分析】先根据长方体的体积公式V＝abh，求出长方体玻璃箱内水的体积，由于玻璃箱内水的体积不变，把水箱的左面作为底面，所以用水的体积除以左面那个面的底面积就是水面的高度，然后即可解答．【解答】解：30×20×6÷（20×10）＝3600÷200＝18（厘米），故选：A．5．用棱长1厘米的正方体小木块拼成一个棱长3厘米正方体，共需要（）块．A．3 B．9 C．27 D．81【分析】用棱长1厘米的正方体小木块，拼成一个棱长3厘米的大正方体，每条棱长上至少需要3块小正方体，由此即可解答问题．【解答】解：用棱长1厘米的正方体小木块，拼成一个棱长3厘米的大正方体，每条棱长上至少需要3块小正方体，所以需要的小正方体的个数为：3×3×3＝27（块），故选：C．6．正方体的体积和它的棱长（）A．成正比例B．成反比例C．不成比例【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．【解答】解：因为，体积：棱长3＝1（一定），即体积与棱长的立方的比值一定，那么正方体的体积和它的棱长的立方成正比例；但是正方体的体积和它的棱长不成比例；故选：C．7．一个长方体的铁皮水箱容量是400升，底面是边长为8分米的正方形，水箱深（）分米．A．50 B．6.25 C．12.5 D．25【分析】长方体的体积＝底面积×高，由“一个长方体水箱容积是400升，这个水箱底面是一个边长为8分米的正方形”，可以先求出水箱底面的面积，进而求出水箱的高．【解答】解：400升＝400立方分米400÷（8×8）＝6.25（分米）故选：B．8．一个长方体，上下两个面是正方形，表面积是14平方厘米，正好可以分成三个正方体，这个长方体的体积是（）立方厘米．A．1 B．3 C．9 D．14【分析】一个长方体上下两个面是正方形，它的表面积是14平方厘米，正好切成三个相同的小正方体，则切开的截面应该是正方形，这个长方体表面上相当于共有14个这样的正方形，所以每个小正方形的面积为14÷14＝1平方厘米，因为1×1＝1，所以每个小正方体的棱长就是1厘米，再根据体积V＝a3，解答即可．【解答】解：切开的截面应该是正方形，这个长方体表面上相当于共有14个这样的正方形，14÷14＝1（平方厘米）因为1×1＝1，所以每个小正方体的棱长是1厘米，1×1×1×3＝3（立方厘米）故选：B．9．一个正方体的棱长扩大3倍后，体积是162立方厘米，原正方体的体积是（）立方厘米．A．54 B．18 C．6 D．81【分析】根据正方体的体积公式V＝a3，再根据因数与积的变化规律，积扩大的倍数等于因数扩大倍数的乘积，一个正方体的棱长扩大到原来的3倍后，体积是162立方厘米，也就是正方体的体积扩大了3×3×3＝27倍，把162缩小27即可求出原正方体的体积；由此解答．【解答】解：一个正方体的棱长扩大到原来的3倍后，也就是正方体的体积扩大了3×3×3＝27倍，162÷（3×3×3）＝162÷27＝6（立方厘米）故选：C．二．填空题（共10小题，满分30分，每小题3分）10．（2021•学而思杯）如图，有一个棱长是10厘米的正方体木块，从它的上面、前面和左面的中心分别凿穿一个边长为4厘米的正方形孔，穿孔后，木块剩余部分的体积是648立方厘米．【分析】根据题干可得，这个图形剩下的体积等于原正方体的体积减去3个长宽高分别是4厘米、4厘米、10厘米的小长方体的体积，因为最中间的边长为4厘米的小正方体被多减了2次，所以再加上2个边长4厘米的小正方体的体积，就是这个图形剩下的体积．【解答】解：由分析可知：木块剩余部分的体积是10×10×10﹣4×4×10×3+4×4×4×2＝1000﹣480+128＝648（立方厘米）故答案为648．11．（2021•希望杯）若一个长方体，长是宽的2倍，宽是高的2倍，所有棱长之和是56，则此长方体的体积是64．【分析】根据长方体的棱长总和公式：长方体的棱长总和＝（长+宽+高）×4，把高看作一份，则宽为2份，长为4份，首先用棱长总和除以4求出长、宽、高的和，进而求出长、宽、高．再根据长方体的体积公式：v＝abh，把数据代入公式解答即可．【解答】解：长方体的高是：56÷4÷（1+2+4），＝14÷7，＝2，宽是：2×2＝4，长是：4×2＝8，体积是：8×4×2＝64，答：这个长方体的体积是64．故答案为：64．12．（2021•其他模拟）一个长方体的表面积是33.66平方分米，其中一个面的长是2.3分米，宽是2.1分米，它的体积是13立方分米．【分析】因为V＝Sh，要求长方形的体积，必须先求出它的高．根据计算公式：h＝S侧面积÷C底面周长即可解决．【解答】解：侧面积：33.66﹣2.3×2.1×2＝33.66﹣9.66＝24（平方分米）；高：24÷[（2.3+2.1）×2]＝24÷[4.4×2]＝24÷8.8＝2（分米）；体积：2.3×＝＝13（立方分米）；答：它的体积是13立方分米．故答案为：13．13．（2020•奥林匹克）把一个长方体的木条左右两端切去长度分别为5厘米的一段和4厘米的一段后，得到一个正方体．如果正方体的表面积比原长方体的表面积减少360平方厘米，那么，原长方体的体积是1900立方厘米．【分析】设长方体的木条的宽为x厘米，则长为（x+9）厘米，高为x厘米，根据正方体的表面积比原长方体的表面积减少360平方厘米，得4x×9＝360，求出x，即可求出原长方体的体积．【解答】解：设长方体的木条的宽为x厘米，则长为（x+9）厘米，高为x厘米，∵正方体的表面积比原长方体的表面积减少360平方厘米，∴4x×9＝360，∴x＝10，∴原长方体的体积是x（x+9）x＝1900立方厘米，故答案为1900．14．（2021•其他杯赛）有大、小两个正方体水池，它们的棱长分别是6米、3米．把一堆碎石完全沉没在大水池的水里，大水池的水面升高了3厘米．如果将这堆碎石完全沉浸在小水池的水里，小水池的水面升高了12厘米．（注意：原来水池并没有装满，但有足够多的水，并且水从未溢出）【分析】水面升高的那部分水的体积就是这堆碎石的体积，根据长方体的体积公式即可求出；然后用这堆碎石的体积除以小正方形水池的底面积即可求出．【解答】解：6米＝600厘米、3米＝300厘米600×600×3＝1080000（立方厘米）1080000÷（300×300）＝12（厘米）故答案为：12．15．（2021•学而思杯）如图，水深7米，那么此容器还能装立方米的水（π取3）．【分析】此题圆锥与已装水（也是一个圆锥）的高度比是7：5，所以体积比是（7×7×7）：（5×5×5），由此再根据圆锥的体积，可以求出圆锥部分还可以装多少水．圆柱的容积直接运用公式求出．【解答】解：圆柱部分的容积4×4×3×3＝144（立方米）圆锥的容积4×4×3×7÷3＝112（立方米）圆锥的容积与水体积之比（7×7×7）：（5×5×5）＝343：125圆锥上面空的部分大小：343﹣125＝218112÷343×218＝（立方米）还能装的水144+＝（立方米）故填16．（2018•陈省身杯）把正方体用一个与它的一面平行的平面切开，分成A、B两个长方体．当A、B的表面积之比为3：5时，如果A长方体的体积为312cm3，那么B长方体的体积为936cm3．【分析】设原正方体的每个面的面积为S，则原正方体的表面积为6S，将其分成A、B两个长方体时，此时两个长方体的表面积之和是8S，根据表面积之比是3：5，求到A的表面积是3S，B的表面积是5S．这样可知A的上下前后四个面的面积和为3S﹣2S＝S，B的上下前后四个面的面积和是5S﹣2S＝3S，因此这两个长方体的宽之比是S：3S＝1：3，它们的长和高分别相等，所以体积比也就是1：3．【解答】解：设原正方体的每个面的面积为S．6S+2S＝8S8S÷（3+5）×3＝3S8S﹣3S＝5S（3S﹣2S）：（5S﹣2S）＝1：3312÷1×3＝936（平方厘米）故答案为：936．17．（2018•陈省身杯）一个长方体的相邻两个面面积之和是77平方厘米，它的长、宽、高都是整数厘米，且都是质数．这个长方体的体积是110立方厘米．【分析】设这个长方体的相邻两个面的公共棱为a，另外两条不同的棱为b和c，那么有a×（b+c）＝77，因为三个数都是质数，77＝7×11，所以a可能是7，也可能是11．当a＝7时，b+c＝11，找不到两个质数的和是11，因此a一定是11，那b和c分别是5和2，因此体积就是11×5×2＝110立方厘米．【解答】解：设这个长方体的相邻两个面的公共棱为a，另外两条不同的棱为b和c，那么有a×（b+c）＝77a×（b+c）＝7711×（5+2）＝7711×5×2＝110（立方厘米）故答案为：110．18．（2020•春蕾杯）有一个长方体，它的正面和底面的面积之和是117，如果它的长、宽、高都是素数，那么它的体积是222或182．【分析】正面和底面之和为117平方厘米，所以长×宽+长×高＝长×（宽+高）＝117，把117分解因数为：117＝3×3×13＝3×39＝9×13，又因为长、宽、高都是质数，故长＝3，宽+高＝39或长＝13，长+宽＝9，然后确定长、宽、高，由此可以解决问题．【解答】解：长×宽+长×高＝长×（宽+高）＝117，117＝3×3×13＝3×39＝9×13，又因为长、宽、高都是质数，故长＝3，宽+高＝39＝2+37，所以体积是3×2×37＝222；或长＝13，长+宽＝9＝2+7，所以体积13×2×7＝182；故答案为：222或182．19．（2020•希望杯）如图，将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，这根长方体木块原来的体积是1000立方分米．【分析】首先分析长方体木块锯成6段需要5次横截面增加10个面，求出一个横截面的面积再乘以长度即可．【解答】解：依题意可知：将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，变面积增加了10个面，那么每一个面的面积为100÷10＝10平方分米．10米＝100分米．体积为：10×100＝1000（立方分米）．故答案为：1000三．解答题（共9小题，满分43分）20．（4分）一块长方体钢板长2.2米，宽1.5米，厚0.01米．它的体积是多少立方分米？【分析】首先根据长方体的体积公式：V＝abh，解答即可．【解答】解：2.2×1.5×0.01＝0.033（立方米）＝33（立方分米）答：它的体积是33立方分米．21．（4分）一个长方体沙坑的长是8米，宽是4.2米，深是0.6米，每立方米沙土重1.75吨，填平这个沙坑共要用沙土多少吨？【分析】首先根据长方体的容积（体积）公式：V＝abh，求出沙的体积，然后用沙的体积乘每立方米沙的重量即可．【解答】解：8×4.2×0.6×1.75＝20.16×1.75＝35.28（吨）答：填平这个沙坑共要沙土35.28吨．22．（5分）如图，一块长方形铁皮，利用图中的阴影部分刚好能做一个圆柱形油桶（接头处不计），求这个油桶的容积？【分析】由题意可知，做成的这个油桶的底面周长加底面直径正好是8.28厘米，由于圆周长是直径的π倍，把底面直径看作“1”，则周长就是π，用8.28分米除以（1+π）就是底面直径，这个油桶的高是直面直径的2倍．再根据圆直径与半径的关系“r＝d÷2”、圆柱的体积计算公式“V＝πr2h”即可解答．【解答】解：8.28÷（1+3.14）＝8.28÷4.14＝2（dm）2÷2＝1（dm）3.14×12×（2+2）＝3.14×1×4＝12.56（dm3）答：这个油桶的容积是12.56dm3．23．（5分）（2021•其他杯赛）如图是一个长方体，阴影部分的面积和是78平方厘米，这个长方体的体积是多少立方厘米？【分析】设长方体的宽为a，则依据“阴影部分的面积和是180平方厘米”即可求出长方体的宽，进而利用长方体的体积公式即可求解．【解答】解：设长方体的宽为a，则10a+3a＝7813a＝78a＝66×10×3＝180（立方厘米）；答：这个长方体的体积是180立方厘米．24．（5分）一个直角三角形，两条直角边分别是3厘米和4厘米，以直角边为轴旋转一周，可以得到一个圆锥体，这个圆锥体的体积最小是多少立方厘米？【分析】直角三角形绕一条直角边旋转一周，得到的图形是一个圆椎体，由此可知：以4厘米的直角边为轴旋转，得到的是一个底面半径为3厘米（或4厘米），高为4厘米（或3厘米）的圆锥，由此利用圆锥的体积公式求出它们的体积即可．【解答】解：×3.14×32×4＝3.14×12＝37.68（立方厘米）×3.14×42×3＝3.14×16＝50.24（立方厘米）50.24＞37.68答：这个圆锥体的体积最小是37.68立方厘米．25．（5分）小红想测量一个铁球的体积，于是把它放进一个底面长20厘米，宽15厘米的长方体容器中，铁球完全被水埋没，水面上升了4厘米，铁球的体积是多少立方厘米？【分析】往盛水的长方体容器里放入一个铁球后，水面升高了，升高了的水的体积就是这铁球个的体积，升高的部分是一个长20厘米、宽15厘米，高4厘米的长方体，根据长方体的体积计算公式列式解答即可．【解答】解：20×15×4＝1200（立方厘米）答：这个铁球的体积是1200立方厘米．26．（5分）（2018•其他杯赛）在一个长为16分米，宽为10分米的长方形玻璃鱼缸中，放进一块体积为800立方分米的假山石，鱼缸中的水正好上升到缸口，如果把这块假山石取出，水面高度为16分米，这个玻璃鱼缸的容积是多少升？【分析】根据长方体的体积（容积）公式：V＝Sh，那么，h＝V÷S，用假石山的体积除以鱼缸的底面积求出现在水面距离缸口多少分米，进而求出鱼缸的高，然后把数据代入公式解答．【解答】解：800÷（16×10）＝5（分米）16×10×（16+5）＝3360（立方分米）3360立方分米＝3360升答：这个玻璃鱼缸的容积是3360升．27．（5分）（2020•华罗庚金杯模拟）有一个棱长是10厘米的正方体木块，在它的上、左、前三个面中心分别穿一个3厘米见方的孔，直至对面．求穿孔后木块的体积．（3厘米见方：边长3厘米的正方形）【分析】由题意可知，三个空交汇处可以看作一个棱长是3厘米的小正方体，只需要算一次，用一个孔的体积乘以3减去2个交汇处棱长是3厘米的小正方体的体积，则穿孔后木块的体积等于大正方体的体积﹣孔的体积即可．【解答】解：孔的体积是：3×3×10×3﹣3×3×3×2＝216（立方厘米）穿孔后木块的体积是：10×10×10﹣216＝784（立方厘米）答：穿孔后木块的体积是784立方厘米．28．（5分）（2020•希望杯）某日是台风天气，雨一直均匀地下着，在雨地里放一个如图1所示的长方体容器，此容器装满雨水需要1小时．请问：雨水要下满如图2所示的三个不同的容器，各需要多长时间？【分析】因为装雨水的单位面积的数量是一定，所以要根据图1所示的长方体容器求出每平方厘米每小时接水的体积，然后再根据图2所示的三个不同的容器的接水口的面积求各需要多长时间即可．【解答】解：图1所示的长方体容器的容积：10×10×30＝3000（立方厘米）接水口的面积为：10×30＝300（平方厘米）接水口每平方厘米每小时可接水：3000÷300÷1＝10（立方厘米）所以，图①需要：10×10×30÷（10×10×10）＝3（小时）图②需要：（10×10×20+10×10×10）÷（10×10×20）＝1.5（小时）图③需要：2÷2＝1（厘米）3.14×1×1×20÷（3.14×1×10）＝2（小时）答：容器①需要3小时，容器②需要1.5小时，容器③需要2小时．。

2021-2021学年苏教版六年级数学上册《长方体和正方体的体积》同步练习一．选择题（共8小题）1．梭长是90cm的正方体油箱的体积和容积相比（）A．容积大B．体积大C．一样大2．金龙鱼牌花生油油桶的标签上印有“净含量5升”的字样，“5升”指的是（）A．油桶的容积B．桶内花生油的体积C．油桶的体积D．油桶的表面积3．下面（）容器的容量比1升小．A．B．C．D．4．一个杯子能装水300ml，这个杯子的（）是300ml．A．体积B．容积C．质量5．长方体的长、宽、高都扩大为原来的3倍，它的体积扩大为原来的（）倍。

A．3B．9C．27D．66．把一个正方体木块切成两个完全相同的长方体，表面积增加了18平方分米，原来正方体的体积是（）立方分米。

A．27B．54C．729D．647．一个长6dm，宽5dm、高4dm的盒子，最多能放（）块棱长为2dm的正方体木块．A．10B．12C．158．一个长方体，它的正面、上面和左面的面积分别是35cm2、40cm2、56cm2，那么这个长方体的体积是（）cm3。

A．210B．262C．280D．300二．填空题（共10小题）9．军军过生日时，爸爸送给他一个圆锥形的陀螺，陀螺的底面直径是6厘米，高是4厘米，这个陀螺的体积是立方厘米．若用一个长方体盒子包装它，这个盒子的容积至少是立方厘米．10．一个长方体棱长的和是144厘米．已知它的长、宽、高恰好是三个连续偶数，则这个长方体的体积是立方厘米．（长方体体积＝长×宽×高）11．容器所能容纳物体的叫做容器的容积．12．有一个长方体的长、宽、高分别是6厘米、4厘米和3厘米。

现在把它的长缩短了2厘米，那么长方体的表面积减少了平方厘米，体积减少了立方厘米。

13．一个长方体，如果高增加2厘米，就变成一个棱长是5厘米的正方体。

原来这个长方体的体积是立方厘米。

14．如图的纸板可以折成一个长方体纸盒．（单位：cm）拼成的长方体的表面积是平方厘米，体积是立方厘米．15．小华在一个长方体玻璃容器中，摆了若干个体积为1立方厘米的小正方体。

期中测试（时间：60分钟满分：100分）一、我会填.（18分） 1．4.5L =（ ）mL35.09m =（ ）3dm =（ ）3cm 2220dm 7cm =（ ）2cm36080cm =（ ）3dm （ ）3cm2．477同时是2.3.5的倍数，这个四位数最小是（ ），最大是（ ）3．分母是8的最简真分数有（ ）.4．（1）30÷（ ） 1.25==（ ）（2）6=565=（ ）（ ）5．27的分子扩大到原来的4倍，要使分数的大小不变，分母应该加（ ）.6．一个长方体木箱（没有盖），长、宽、高分别是40cm ，30cm 和50cm ，如果想在它外面刷上绿色的油漆，那么涂油漆的面积是（ ）2dm .7．两个质数的和是10，积是21，它们分别是（ ）和（ ）.8．从一个长为124cm 、宽为10cm 、高为10cm 的长方体中锯最大的正方体，最多可以锯（ ）个.二、我会判.（正确的画“√”，错误的画“×”）（6分） 1．自然数除了质数就是合数.（ ） 2．分子比分母大的分数叫做假分数.（ ） 3．因为63=84，所以它们的分数单位也相同.（ ） 4．一个自然数如果没有因数2，一定是质数. （ ） 5．底面积大的长方体，体积一定大. （ ） 6．冰箱的容积小于它的体积.（ ）三、我会选.（12分）1．大于59而小于79的分数有（ ）个.A ．1B ．2C ．无数2．如果长方体的长、宽、高都扩大到原来的3倍，那么它的体积扩大到原来的（ ）倍. A ．3B ．9C ．273．61，要使这个三位数是3的倍数，里应填（ ）. A ．0，3，6，9B ．2，4，6，7，8C ．2，5，84．10g 盐溶入100g 水中，盐占盐水的（ ）.A ．110B ．111C ．195．一个长方体水箱容积是100L ，这个水箱底面是一个边长为5dm 的正方形，则水箱的高是（） A ．20dmB ．10dmC ．4dm6．五个连续的奇数，如果中间一个是c ，那么最小的一个是（）. A ．2a -B ．4a -C ．6a -四、计算下面立体图形的表面积和体积.（20分）1． 2．横截面是周长为20cm 的正方形，长为6dm .五、按要求做一做.（13分）1．把一个图形看作单位“1”，用分数表示下列各图中的阴影部分，填在括号里.（4分）2．下图是一个长方体的平面展开图，请分别测量长方体的长、宽、高.（3分）长（ ）cm宽（ ）cm高（ ）cm3．连一连.（6分）（1）（2）（3）六、组数游戏.（5分）在5，2，3，4中选三个数字按要求组成三位数.1．当它是2的倍数时，这个数最大是多少？最小是多少？2．当它是3的倍数时，最大是多少？最小是多少？3．当它是5的倍数时，最大是多少？最小是多少？七、我会解答.（25分）1．强强、伟伟、亮亮三位好朋友，他们的年龄是三个连续的自然数，三个数的和是24，猜猜他们三人各是多少岁？（4分）2．有一块花布长5m，正好可以做6条同样大小的童裤，每条童裤用这块布的几分之几？每条童裤用布几分之几米？（5分）3．一块长方形铁皮（如图），将它的四个角各切掉一个边长为5cm的正方形，然后做成无盖盒子,这个盒子用了多少铁皮？它的体积是多少？（10分）4．有一个长为5dm、宽为4dm、深为2dm的长方体玻璃缸，向缸中放入一个正方体铁块，然后注满水（此时水已淹没正方体铁块），当取出这个铁块后，水面下降了0.2dm，这个铁块的体积是多少？（6分）期中测试 答案一、1.【答案】4500 5090 5090000 2007 6 802.【答案】1470 74703.【答案】18 3858 784.【答案】25 6 36 55.【答案】216.【答案】827.【答案】3 78.【答案】12 二、 1.【答案】× 2.【答案】× 3.【答案】× 4.【答案】× 5.【答案】× 6.【答案】√ 三、 1.【答案】C 2.【答案】C 3.【答案】C 4.【答案】B 5.【答案】C 6.【答案】B 四、1.【答案】2420cm 3500cm2.【答案】31250cm 31500cm 五、1.【答案】34 45 84 322.【答案】略3.【答案】略 六、1.【答案】542 2342.【答案】543 2343.【答案】435 235 七、1.【答案】分别是7岁，8岁，9岁2.【答案】1166÷=,556()6m ÷= 3.【答案】铁皮：21100cm 体积：33000cm 4.【答案】3540.24(dm )⨯⨯=期中测试（时间：60分钟满分：100分）一、填一填.（21分）1.在1，11，19，27，53，87，97这些数中，（ ）是质数，（ ）是合数，（ ）既是奇数又是合数，（ ）既不是质数又不是合数.2.既是3的倍数，又是2，5的倍数中最大的两位数是（ ）.3把一根长为3m 的绳子平均分成4段，每段长为m （ ）（ ），每段占全长的（ ）（ ）. 4.37的分子加上9，要使分数的大小不变，分母应（ ） 5.分数单位是112的最小假分数是（ ）（ ），最大真分数是（ ）（ ），最小带分数是（ ）.6.33.75dm (= 3)cm35dm (= )(L = )ML .7.用铁丝做一个棱长为5cm 的正方体框架，至少需要（ ）cm 铁丝.8.一个正方体棱长总和为36dm ，它的表面积是（ ）2dm ，体积是（ ）3dm . 9.在79，14，77，65，1613，545中，真分数有（ ），假分数有（ ），把这些假分数化为带分数或整数分别为（ ）. 10.一个几何体，从上面看到的图形是，从正面看到的图形是，搭这样的一个几何体，最少需要（ ）个小正方体.二、判一判.（正确的画“√”，错误的画“×”.）（12分） 1.从不同的方向观察同一个物体，看到的形状可能相同. （ ） 2.一个数的因数一定小于它的倍数. （ ） 3.所有的偶数都是合数.（ ） 4.最简分数的分子和分母没有公因数. （ ） 5.两个质数的积一定是合数.（ ） 6.长方体和正方体都有6个面，8个顶点.（ ）三、选一选.（7分） 1.40的因数有（ ）个. A .6B .7C .82.甲、乙都是不为0的自然数，甲是乙的15倍，甲和乙的最小公倍数是（ ）. A .甲B .15C .乙D .甲×乙3.小明每小时做7道题，小红每小时做S 道题，平均做一道题（ ）. A .小红用的时间多B .小明用的时间多C.两人用的时间同样多4.一个正方体的棱长扩大到原来的3倍，它的表面积就扩大到原来的（）倍.A.3B.6C.95.（1）从正面看到的图形是，从左面看到的图形是的几何体是（）. （2）从正面看到的图形是，从左面看到的图形是的几何体是（）. （3）从正面看到的图形是.从上面看到的图形是的几何体是（）.四、计算.（32分）1.求出每组数的最大公因数与最小公倍数.（6分）24和3648和127和92.先把下面的分数约分，再把是假分数的化成整数或带分数.（6分）40 35513452133.比较下面各组分数的大小.（6分）4 5和815512和3859和474.把下面的小数化成分数，把分数化成小数（不能化成有限小数的保留三位小数.）（6分）0.050.260.125589501735.计算下面图形的表面积和体积.（8分）（1）（2）表面积：表面积：体积：体积：五、解决问题.（28分）1.家电商城开业第一周卖出75台电视机，35台洗衣机，卖出的电视机的台数是洗衣机的几分之几？洗衣机的台数是电视机的几分之几？（6分）2.有长为12cm，16cm，44cm的木棒各一根.要把它们截成同样长的小棒，不能有剩余，每根小棒最长是多少厘米？（5分）3.丽丽家准备做一个无盖长方体玻璃水缸，长为0.8m，宽为4dm，高为5m.至少需要多少平方分米的玻璃？它最多可以装水多少升？（玻璃的厚度忽略不计.）（6分）4．一个长方体容器，从里面量，长为20cm，宽为16cm，高为10cm，里面装了7cm深的水.往这个容器里放入一块石头，石头完全浸没在水中，水深变为9cm.这块石头的体积是多少立方厘米？（5分）15m，要粉刷教室的顶5.一间新教室长为9m，宽为6m，高为4m，其中门窗的面积和为2棚和四周墙壁（门窗除外），平均每平方米用涂料0.45kg，一共需涂料多少千克？（6分）期中测试答案一、1.【答案】11，19，53，9727，8727，8712.【答案】903.【答案】34144.【答案】乘4或加上215.【答案】1212111211126.【答案】3750550007.【答案】608.【答案】54279.【答案】79，1477，1316，65，5451，3113，115，410510.【答案】7二、1.【答案】√2.【答案】×3.【答案】×4.【答案】×5.【答案】√6.【答案】√三、1.【答案】C2.【答案】A3.【答案】B4.【答案】C5.【答案】（1）B（2）C（3）A四、1.【答案】12，7212，481，632.【答案】4081==13577 5131==13422 52=4133.【答案】48515＞ 53128＞ 5497＜4.【答案】10.05=20 130.26=50 10.125=8 5=0.6258 9=0.185017 5.6673≈5.【答案】（1）2174cm 3135cm （2）254dm 327dm 五、1.【答案】75157535==357÷ 3573575==7515÷ 2.【答案】4cm 3.【答案】0.8m 8dm = 2(8554)2841⨯+⨯⨯+⨯= 3845160(dm )160(L)⨯⨯==4.【答案】972(cm)-= 320162640(cm )⨯⨯=5.【答案】2(9464)29615159(m )⨯+⨯⨯+⨯-= 1590.4571.55(kg)⨯=期中测试一、填空.（每空2分，共34分） 1.33.02 m =（ ）3dm390 020 cm =（ ）L2.一个两位数既是3的倍数，又是5的倍数，而且是偶数，这个两位数最小是（ ），最大是（ ）.3.既是42的因数，又是7的倍数的数有（ ）.4.一个数只有（ ）和（ ）两个因数，这个数是质数.5.已知A=2335⨯⨯⨯，B=225⨯⨯，C=235⨯⨯，那么A ，B ，C 的最大公因数是（ ），最小公倍数是（ ）.6.20以内的质数有（ ）.7.在（ ）里填上合适的体积或容积单位.体积约是8（ ）. 容积约是60（ ）.体积约是1（ ）.容积约是10（ ）.8.一个长方体的长是5 cm ，宽和高都是4 cm ，它的棱长总和是（ ）cm ，它的表面积是（ ）cm 3，它的体积是（ ）cm 3. 二、判断.（每题2分，共10分） 1.和之间没有分数.（ ） 2.一个数的倍数一定大于这个数的因数.（ ） 3.两个分数的分数单位不同，分母大的分数单位就大. （ ） 4.一个物体的体积和容积的计算方法相同，意义也相同. （ ） 5.一个正方体的棱长之和是12 cm ，它的体积是1 cm 3.（ ）三、选择.（每题3分，共15分）1.下面各数中，既是奇数又是合数的是（ ）. A .19B .91C .90D .232.下面各数中，同时是2，3，5的倍数的数是（ ）. A .405B .340C .240D .803.一个立体图形，从正面看到的是，从上面看到的是，从左面看到的是，这个立体图形是由（ ）个小正方体组成的. A .3B .4C .5D .64.一个盒子有8个顶点，如下图所示沿对角线切成两半，如果分开摆放，那么这两半一共有（）个顶点.A.6B.8C.12D.165.东东早上喝了一杯牛奶，约240（）.A.LB.mLC.dm3D. m3四、实践与操作.（每题5分，共10分）1.下面是丁红画的一个长方体展开图的一部分，请你把没画的部分画出来.2.从下面4张数字卡片中选出3张，按要求组成三位数.（每小题至少写出2个）（1）奇数：（）（2）偶数：（）（3）3的倍数：（）（4）5的倍数：（）（5）既是2的倍数，又是5的倍数：（）五、分别计算下列图形的表面积和体积.（单位：cm）（每题6分，共12分）1.2.六、解决问题.（第1，2题每题6分，第3题7分，共19分）1.丁丁先用橡皮泥做了一个长12 cm、宽10 cm、高8 cm的长方体，然后在下面和上面各挖去一个棱长为3 cm的正方体，并把它们粘在长方体的两边（如下图），你能求出这个立体图形的表面积吗？2.下图是一个长方体容器，容器中的水有多少升？3.五（1）班男生有14人，女生有21人，现在要把男、女生分别排队，并且每排的人数相同，每排最多有多少人？这时男、女生各有多少排？期中测试 答案一、1.【答案】3020 90.022.【答案】30 903.【答案】7，14，21，424.【答案】1 它本身5.【答案】10 1806.【答案】2，3，5，7，11，13，17，197.【答案】3cm mL 3dm3m 8.【答案】52 112 80 二、 1.【答案】× 2.【答案】× 3.【答案】× 4.【答案】× 5.【答案】√ 三、 1.【答案】B 2.【答案】C 3.【答案】C 4.【答案】C 5.【答案】B 四、1.【答案】（画法不唯一）2.【答案】（1）561 165 （2）510 156 （3）165 516（4）160 165 （5）610 560 （答案不唯一） 五、1.【答案】表面积：522cm 体积：24 3cm2.【答案】表面积：542cm 体积：27 3cm 六、1.【答案】212101281082=592cm ⨯⨯⨯⨯（++）（） 23344592=736cm ⨯⨯⨯+（）2.34020202=8000cm ⨯⨯÷（）38000 cm =8 L答：容器中的水有8L. 3.每排最多有7人. 男生：147=2÷（排） 女生：217=3÷（排）答：每排最多有7人，这时男生有2排，女生有3排.。

五年级下册第3单元长方体与正方体单元检测卷-真题演练-人教版一．选择题（共8小题）1．比较体积相等的两个正方体的表面积,它们的大小（）A．不相等B．相等C．不一定相等D．无法比较2．（万柏林区期中）一个长方体长a厘米,宽b厘米,高h厘米,如果它的宽增加3厘米,则它的体积比原来增加（）立方厘米。

A．3ab B．3ahC．3bh D．以上均不正确3．（2022春•兴化市月考）把一个半径和高都是1分米的圆柱沿底面半径平均分成若干等份,切开拼成一个近似的长方体,表面积增加（）平方分米。

A．2 B．3.14 C．4 D．4.144．（2020•兰西县）长方体的长、宽、高都扩大为原来的3倍,它的体积扩大为原来的（）倍。

A．3 B．9 C．27 D．65．（集美区期中）一个正方体的棱长扩大为原来的2倍,表面积就扩大为原来的____倍,体积扩大为原来的____倍。

（）A．2、4 B．4、4 C．4、8 D．2、86．（鼓楼区期末）一个长方体形状的玻璃容器,从里面量长为50厘米,宽为40厘米,高为45厘米。

向容器里注水,当容器内的水体第1次出现正方形面时,容器里有水（）升。

A．90 B．100 C．80 D．817．（•叶县）一个长方体金鱼缸,长50cm,宽40cm,高35cm,它后面的玻璃打碎了,要重新配一块。

重新配上的玻璃是（）平方分米。

A．20 B．1750 C．17.5 D．13.58．（越秀区期末）用5个棱长3cm的小正方体拼成一个长方体,所拼成长方体的表面积比原来5个小正方体表面积之和减少（）cm2。

A．15 B．36 C．45 D．72二．填空题（共7小题）9．（淄博期末）42000cm2＝m2 2.06m3＝dm31.25L＝mL0.78dm3＝L＝mL3.6立方米＝立方米立方分米10．（2020•丰润区）将一个长是4厘米、宽是3厘米、高是2厘米的铁块,放入到一个装满水的圆柱型的量杯中,溢出的水有毫升．11．（玄武区期末）一个长方体纸盒,长15厘米,宽12厘米,高8厘米。