阿基米德定律

阿基米德原理的内容是什么阿基米德原理是描述浮力的一个重要定律，它是古希腊数学家阿基米德在公元前三世纪提出的。

根据阿基米德原理，一个物体浸没在液体中所受到的浮力等于它所排开的液体的重量，也就是说，浮力的大小与物体在液体中排开的液体的体积成正比。

这个原理在日常生活中有着广泛的应用，也在科学研究和工程设计中发挥着重要作用。

阿基米德原理的提出，对于我们理解物体在液体中的浮沉情况提供了重要的依据。

根据这个原理，我们可以得出一个结论，一个物体在液体中的浮沉情况取决于物体的密度和液体的密度。

如果物体的密度大于液体的密度，那么物体会下沉；如果物体的密度小于液体的密度，那么物体会浮起。

这一结论对于船只的设计和建造、潜水艇的浮潜、气球的飞行等都有着重要的指导意义。

除了在日常生活和工程设计中的应用，阿基米德原理在科学研究中也有着广泛的应用。

例如，在液体中测定物体的密度时，可以利用阿基米德原理来进行测量。

通过测量物体在空气中和在液体中的重量差，就可以计算出物体的密度。

这种方法在材料科学、地质学、生物学等领域都有着重要的应用。

阿基米德原理还可以帮助我们理解一些自然现象。

例如，为什么冰块会浮在水面上？这就是因为冰块的密度小于水的密度，根据阿基米德原理，冰块会受到浮力的作用而浮在水面上。

同样地，气球在空气中飞行也是利用了阿基米德原理，气球的密度小于空气的密度，所以会受到浮力的作用而飘浮在空中。

总的来说，阿基米德原理是描述浮力的一个重要定律，它对我们理解物体在液体中的浮沉情况、科学研究和工程设计都有着重要的意义。

通过对阿基米德原理的深入理解，我们可以更好地利用它来解决实际问题，推动科学技术的发展。

希望本文的介绍能够帮助读者更好地理解阿基米德原理，同时也能够引起更多人对科学原理的关注和研究。

阿基米德浮力定律物体浸在任何一种液体中时，该物体浸入的体积都等于所排出的液体的体积，因此，物体所受的液体浮力一定与所排开的液体重量相等。

它的发现者是古代著名的科学家阿基米德。

传说，当时叙拉古国王希罗想要制作一顶纯金的皇冠，就让大臣交给珠宝工匠一锭称过重量的金子。

珠宝工匠夜以继日，很快就制好了精美绝伦的皇冠。

国王看了十分高兴。

然而这个国王是个多疑之人，他担心工匠在皇冠中掺了假，盗走一部分黄金。

于是，命令左右大臣去调查此事。

阿基米德答应了国王的请求，回到家后就开始思考解决难题的办法。

他冥思苦想、茶饭不思。

日子一天一天地过去了，阿基米德还是一筹莫展，他几乎想放弃这项任务。

当他坐进浴盆时，突然发现了一个奇怪的现象：他坐进浴盆里，当水溢出盆外时，感到自己的身体略略往上漂浮，身体浸没在水中的部分越多，溢出的水就越多，身体就感到越轻，也就是说，水的托力就越大，当他跨出浴盆后，发现盆中的水少了很多。

这个司空见惯的现象却激发了阿基米德的灵感，促使他从中发现了一个极其重要的科学原理。

阿基米德在国王和大臣们面前进行了如下实验：他取来与皇冠一样重的一块白银和一块黄金，依次将白银、黄金和皇冠浸入一个盛满水的容器里，仔细观察在3种情况下溢出水的数量。

结果，浸入皇冠时所溢出的水的数量，介于黄金和白银所排溢的水的数量之间。

通过这种方法，阿基米德得知这顶皇冠不是纯金也不是纯银，而是金子和银子的混合物。

阿基米德立即告诉国王：皇冠一定掺了假，绝不是纯金制成的。

阿基米德作为一名科学家，并没有浅尝辄止，仅仅满足于皇冠问题的解决，经过反复实验，终于发现了伟大的浮力定律。

后来，人们为了纪念这位伟大的科学家，就将浮力定律命名为“阿基米德定律”。

阿基米德原理1. 简介阿基米德原理是古希腊科学家阿基米德发现的一个重要原理，它描述了浸入流体中的物体所受到的浮力大小与物体在流体中排除的液体体积成正比的关系。

阿基米德原理对理解浮力、浮力的应用以及物体在液体中的浮沉具有重要意义。

本文将详细介绍阿基米德原理的原理和应用。

2. 阿基米德原理的原理阿基米德原理的基本观点是：浸入流体中的物体所受到的浮力等于物体排除的液体的重量。

阿基米德原理可以用如下公式表示：F浮= ρ液体 × V排除 × g其中，F浮是物体所受到的浮力，ρ液体是液体的密度，V 排除是物体排除液体的体积，g是重力加速度。

3. 阿基米德原理的应用3.1 浮力与物体的浮沉根据阿基米德原理，当物体的密度小于液体的密度时，物体所受到的浮力大于物体的重力，物体将浮在液体表面。

相反，当物体的密度大于液体的密度时，物体所受到的浮力小于物体的重力，物体将沉入液体中。

3.2 水下物体的浮力阿基米德原理在水下物体的浮力计算中应用广泛。

例如，潜水艇的浮力调整主要通过控制进出水舱的液体体积来实现。

根据阿基米德原理，调整水舱内的液体体积，可以调整潜水艇所受到的浮力，从而控制潜水艇的上浮或下潜。

3.3 测量物体的密度利用阿基米德原理，我们可以测量物体的密度。

只需要将物体悬挂在空中，并浸入液体中，通过测量物体所受到的浮力，可以计算出物体排除液体的体积，从而计算出物体的密度。

4. 阿基米德原理的示例4.1 船只的浮力船只内部的空腔使其密度较小，从而使其能够浮在水面上。

根据阿基米德原理，船只所受到的浮力等于排除的水的重量，浮力恰好抵消船只自身和载货物的重力，从而保持平衡。

4.2 游泳时的浮力在水中游泳时，我们可以感受到浮力的存在。

由于人体的密度小于水的密度，根据阿基米德原理，我们所受到的浮力大于自身的重力，体重得到减轻，感觉轻松自在。

5.阿基米德原理是一个重要的物理原理，它描述了浸入流体中的物体所受到的浮力与物体排除的液体体积成正比的关系。

阿基米德的浮力定律阿基米德的浮力定律是描述物体在液体中所受浮力的规律，由古希腊物理学家阿基米德提出。

该定律认为，在一个静止的液体中，浸没在其中的物体所受到的浮力大小等于液体中所排斥的重量。

这个定律的形式化表述是：浮力等于物体排开液体的重量。

这个浮力的大小取决于液体的密度、物体的体积和受力对象所处的深度。

阿基米德的浮力定律是许多实际应用的基础，如船只的浮力，潜水员的浮力调节，漂浮在水面上的物体等。

下面，我将从实际生活中的例子来探讨阿基米德浮力定律的应用。

1. 船只的浮力船只的设计利用了阿基米德的浮力定律。

船只的体积较大，当它浸没在水中时，其所受到的浮力等于经水排开的重量。

根据阿基米德的定律，浮力大于船只自身的重量，船只就能浮在水面上。

这样，人们可以利用船只在水上航行，进行运输和旅行。

2. 潜水员的浮力调节潜水员在深水中进行工作或探索时，需要根据实际需求调节自身的浮力。

他们使用气瓶中的空气来调节浮力。

当潜水员需要上浮时，他们会往气瓶中注入更多的空气，增加所受到的浮力，从而上浮到水面；当潜水员需要下潜时，他们会释放部分空气，减少浮力，使自己能在水中保持稳定的深度。

3. 水上漂浮的物体阿基米德的浮力定律也可以解释为什么一些物体可以漂浮在水面上。

例如，一个木块会浮在水中，因为其密度小于水的密度。

根据阿基米德定律，木块所受到的浮力等于排开的水的重量，大于自身的重量，所以它能浮在水面上。

而相反，如果一个物体的密度大于水的密度，那么它将下沉到水底。

除了这些例子，阿基米德的浮力定律在许多其他领域也有广泛的应用。

例如，工程设计中需要考虑建筑物的浮力以确保其稳定性；研究水下潜艇的设计需要考虑浮力的调节；在油井开采过程中，需要考虑到地下液体的浮力等等。

总结起来，阿基米德的浮力定律是一个重要的物理定律，它描述了物体在液体中所受的浮力等于排斥液体的重量。

这个定律在船舶设计、潜水员操作以及物体漂浮等方面都有实际应用。

理解和应用这个定律，可以帮助我们更好地认识自然界中的现象，并在实际生活中做出合理的决策和设计。

阿基米德原理内容阿基米德原理，又称浮力定律，是古希腊数学家阿基米德在公元前3世纪提出的一个关于浮力的原理。

这一原理是指，在静止的液体中，物体受到的浮力等于其排开的液体的重量。

这一原理对于我们理解物体在液体中的浮沉现象以及设计制造浮力装置具有重要意义。

首先，我们来看一下阿基米德原理的具体内容。

在静止的液体中，当一个物体部分或全部浸没在液体中时，液体会对物体产生一个向上的浮力，这个浮力的大小等于物体排开的液体的重量。

这意味着，当物体受到的浮力大于或等于其自身的重力时，物体就会浮起来；当物体受到的浮力小于其自身的重力时，物体就会下沉。

这就是阿基米德原理的核心内容。

阿基米德原理的应用非常广泛。

首先，它对于我们理解物体在液体中的浮沉现象具有重要意义。

无论是船只在水中浮沉，还是气球在空气中飘浮，都可以通过阿基米德原理来解释。

其次，阿基米德原理也为我们设计制造浮力装置提供了理论依据。

例如，潜水艇和潜水器的浮潜原理，以及气球和飞艇的飞行原理，都与阿基米德原理密切相关。

除此之外，阿基米德原理还在我们的日常生活中发挥着重要作用。

比如，我们在洗澡时，身体会感觉轻盈是因为身体浸没在水中受到的浮力；而在游泳时，我们可以利用浮力来保持身体的浮起。

甚至在水中玩耍时，我们也可以感受到阿基米德原理的存在。

总的来说，阿基米德原理是一个非常重要的物理原理，它对我们理解物体在液体中的浮沉现象，设计制造浮力装置，以及日常生活中的一些现象都具有重要意义。

通过对阿基米德原理的深入理解，我们可以更好地利用浮力来解决实际问题，同时也能够更好地理解自然界中的一些现象。

希望大家能够加深对阿基米德原理的理解，从而更好地应用它在实际生活中。

阿基米德原理是指在液体中浸没的物体所受的浮力等于其排开液体的重力，即物体在液体中所受的浮力等于物体排开的液体的重量。

阿基米德原理是由古希腊数学家阿基米德在公元前三世纪提出的。

他通过一系列的实验发现，当一个物体浸没在液体中时，它所受的浮力等于排开的液体的重量。

这个原理在物理学中被广泛应用，对于理解物体的浮沉和浮力的作用具有重要意义。

根据阿基米德原理，一个物体在液体中浸没时受到的浮力等于物体排开的液体的重量。

浮力的大小等于液体的密度乘以排开液体的体积，公式为F=γVg，其中F代表浮力，γ代表液体的密度，V代表排开液体的体积，g代表重力加速度。

根据这个原理，我们可以解释物体浮力的大小和物体的浮沉现象。

当一个物体的密度大于液体的密度时，物体所受的浮力小于物体的重力，物体将下沉；当物体的密度小于液体的密度时，物体所受的浮力大于物体的重力，物体将浮起。

利用阿基米德原理，我们可以解释为什么物体在水中浮起，以及为什么一些物体可以漂浮在水上。

比如一艘船，在浸没在水中时，船体受到的浮力等于船体排开的水的重量，这个浮力正好抵消了船体的重力，所以船体就能够浮在水面上。

而一块密度小于水的木块也能浮在水上，是因为木块所受的浮力大于木块的重力，所以木块会浮起。

阿基米德原理的应用不仅仅局限于液体中，对于气体中的物体也是适用的。

在气体中，物体所受的浮力等于物体排开的气体的重力。

这个原理解释了为什么气球能够漂浮在空中。

除了浮力的应用，阿基米德原理还可以解释物体的测重现象。

当一个物体浸没在液体中时，液体会对物体施加一个向上的浮力，这个浮力的大小等于物体的重量。

所以，我们可以利用一个浸没在液体中的物体所受的浮力来测量物体的重量。

总之，阿基米德原理是物理学中一条重要的原理，它描述了浸没在液体中的物体所受的浮力等于物体排开的液体的重量。

这个原理对于解释浮沉现象、测重和理解物体的浮力起着重要作用。

我们在日常生活中可以通过阿基米德原理来理解许多现象，如船的浮力、气球的漂浮等。

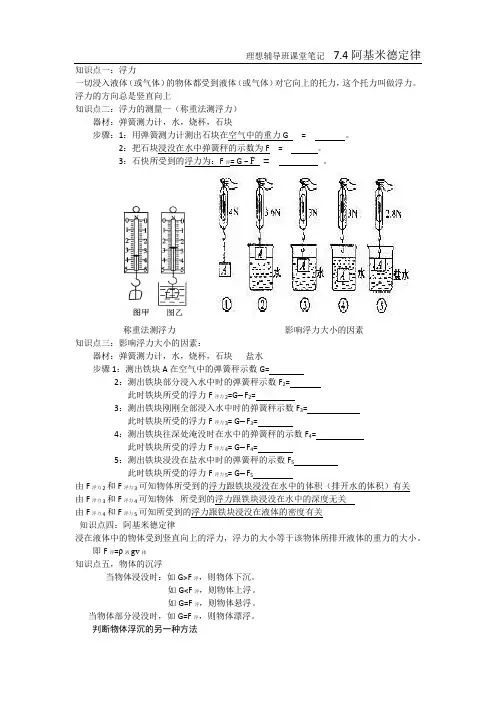
知识点一：浮力一切浸入液体（或气体）的物体都受到液体（或气体）对它向上的托力，这个托力叫做浮力。

浮力的方向总是竖直向上知识点二：浮力的测量一（称重法测浮力）器材：弹簧测力计，水，烧杯，石块步骤：1：用弹簧测力计测出石块在空气中的重力G = 。

2：把石块浸没在水中弹簧秤的示数为F = 。

3：石快所受到的浮力为：F浮= G – F = 。

称重法测浮力影响浮力大小的因素知识点三：影响浮力大小的因素：器材：弹簧测力计，水，烧杯，石块盐水步骤1：测出铁块A在空气中的弹簧秤示数G=2：测出铁块部分浸入水中时的弹簧秤示数F2=此时铁块所受的浮力F浮力2=G−F2=3：测出铁块刚刚全部浸入水中时的弹簧秤示数F3=此时铁块所受的浮力F浮力3= G−F3=4：测出铁块往深处淹没时在水中的弹簧秤的示数F4=此时铁块所受的浮力F浮力4= G−F4=5：测出铁块浸没在盐水中时的弹簧秤的示数F5此时铁块所受的浮力F浮力5= G−F5由F浮力2和F浮力3可知物体所受到的浮力跟铁块浸没在水中的体积（排开水的体积）有关由F浮力3和F浮力4可知物体所受到的浮力跟铁块浸没在水中的深度无关由F浮力4和F浮力5可知所受到的浮力跟铁块浸没在液体的密度有关知识点四：阿基米德定律浸在液体中的物体受到竖直向上的浮力，浮力的大小等于该物体所排开液体的重力的大小。

即F浮=ρ液gv排知识点五，物体的沉浮当物体浸没时：如G>F浮，则物体下沉。

如G<F浮，则物体上浮。

如G=F浮，则物体悬浮。

当物体部分浸没时，如G=F浮，则物体漂浮。

判断物体浮沉的另一种方法。

根据阿基米德原理可得：F浮=ρ液gV排对于浸没的物体而言：V物=V排①若ρ液<ρ物,则F浮<G，物体下沉。

②若ρ液=ρ物,则F浮=G,物体悬浮在液体中任何深度的地方。

③若ρ液>ρ物,则F浮>G，物体上浮。

④上浮稳定后处于漂浮状态，这时F浮=G可见判断物体的浮沉可用两种方法，比较物体的重力和浮力，比较物体的密度和液体的密度。

阿基米德原理及其应用一、阿基米德原理1.内容：浸在液体中的物体所受的浮力,大小等于 它排开的液体所受的重力 。

2。

公式：F 浮= G 排 = ρ液gV 排 。

3。

适用范围:适用于 液体 和 气体 。

二、决定浮力大小的因素物体所受浮力的大小跟 排开液体的体积 和 液体的密度有关 。

阿基米德原理的理解和应用1.“浸在”的含义，包括两种情况（1）物体完全浸没在液体中，此时V 排=V 物; (2)物体部分浸入液体中,此时V 排＜V 物。

2.阿基米德原理也适用于气体,在气体中受到的浮力F 浮= ρ气gV 排3。

有些有关浮力的计算题,要同时用到F 浮=G —F 和F 浮=G 排= ρ液gV 排两种方法.（1）若物体下部没有接触液体（如陷入河底的桥墩)，则不受浮力作用，不能用阿基米德原理计算浮力大小.（2）由阿基米德原理公式可知，浮力的大小只跟液体密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、在液体中是否运动等因素无关.（3）注意公式中物理量的单位，ρ液的单位是kg/m 3，V 排的单位是m 3。

【典例】（2010·常州中考)在第26次南极科学考察过程中,我国科考队员展开了多项科学探究。

科考队员在南极格罗夫山地区发现了新的陨石分布区,并找到上千块陨石.科考队员对编号为“cz20100603”的陨石进行密度测量:首先将陨石悬挂于弹簧测力计下，读出弹簧测力计的示数是3。

4 N ；然后将陨石全部浸没于水中，读出弹簧测力计的示数是2。

4 N 。

陨石的密度是多少？（g 取10 N ／kg)【思路点拨】本题综合性较强，主要涉及称重法求浮力、阿基米德原理、密度等知识的综合应用。

根据题干寻求已知量，再求未知量。

已知条件：G 和F →F 浮=G-F →【规范解答】陨石全部浸入水中时受到的浮力:F 浮=G-F=3。

4 N-2。

4 N=1.0 N根据阿基米德原理F 浮=ρ水gV 排得，陨石的体积V=V 排=1.0×10—4 m 3陨石的质量：F V V V g m V GG m g ⎫=→=⎪ρ⎪→ρ=⎬⎪→=⎪⎭浮排排水已知条件：3343F V g 1.0 N 1.010 kg /m 10 N /kg 1.010 m -=ρ=⨯⨯=⨯浮排水4333m 0.34 kg=V 1.010 m 3.410 kg /m -ρ=⨯=⨯G 3.4 N m 0.34 kgg 10 N /kg===陨石的密度：答案：陨石的密度是3.4×103 kg/m3 不能正确理解影响浮力大小的因素【典例】关于物体所受的浮力，下列说法中正确的是（ ） A.漂在水面上的物体比沉底的物体受到的浮力大 B 。

杠杆原理阿基米德
阿基米德(Archimedes)是古希腊著名的科学家，他在《几何原本》一书中提出了杠杆原理，并给出了其中的定律。

杠杆原理是指一个物体或质量在一个关节处的力量可以由另一
个关节处的力量来替代。

也就是说，一个物体的力量可以通过杠杆的支点来实现增强或减弱，这样就可以改变物体的力量大小，从而实现解决复杂的问题。

阿基米德的杠杆定律：
1.当两个力相等时，两者之间的杠杆距离也是相等的;
2.当两个力的杠杆距离不同时，力大的一侧的距离要比力小的一侧的距离长;
3.当两个力的杠杆距离相等时，力大的一侧的杠杆力和力小的一侧的杠杆力也是相等的;
4.当两个力的杠杆距离不同时，力大的一侧的杠杆力也比力小的一侧的杠杆力大;
由杠杆定律可以得出一个实用的结论：当把一个力应用到一个关节处，不管是增加还是减小力量，都可以由另一处的力来抵消，实现力量的均衡。

因此，杠杆原理对于解决复杂的力学问题非常有用，并且也使得许多工程界的技术发展成为可能。

- 1 -。

阿基米德定律阿基米德定律是指，浸在液体里的物体受到向上的浮力，浮力的大小等于物体排开的液体的重量。

阿基米德定律也适用于气体。

接下来为您简单介绍，希望对您有所帮助。

1.杠杆原理:阿基米德原理。

公式:动力×动力臂=阻力×阻力臂。

杠杆又扭轴费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称作杠杆平衡条件。

必须并使杠杆均衡，促进作用在杠杆上的两个力矩（力与力臂的乘积）大小必须成正比。

即为：动力×颤抖力臂=阻力×阻力臂，用代数式则表示为f1· l1=f2·l2。

式中，f1则表示动力，l1则表示颤抖力臂，f2则表示阻力，l2则表示阻力臂。

战国时代的墨子最早提出杠杆原理，在《墨子· 经下》中说衡而必正，说在得；衡，加重于其一旁，必捶，权重不相若也，相衡，则本短标长，两加焉，重相若，则标必下，标得权”。

这两条对杠杆的平衡说得很全面。

里面存有等臂的，存有左右臂的；存有发生改变两端重量并使它偏动的，也存有发生改变两臂长度并使它偏动的。

这里还要顺带提到的就是，古希腊科学家阿基米德存有这样一句流传好久的名言：“给我一个支点，我就能够砸开整个地球！”，这句话就是说道杠杆原理。

2.浮力定律:阿基米德定律。

公式:f浮=g排液=ρ液gv排液。

浮力就是由液体(或气体)对物体向上和向上压力差产生的。

灌入液体里的物体受向上的浮力，浮力的大小等同于它两边的液体受的重力。

f浮 = g排在=ρ液v排在g。

从公式中可以窥见：液体对物体的浮力与液体的密度和物体两边液体的体积有关，而与物体的质量、体积、重力、形状、浸的深度等均毫无关系。

3.求积原理:穷竭法。

阿基米德还有一个杰出发现是指出圆球的体积和表面积都是外切圆球的圆柱体体积和表面积的2/3。

阿基米德原理介绍1.阿基米德原理是什么1.1定义浸在静止流体(气体或液体)中的物体受到一个浮力，其大小等于该物体所排开的流体的重量，方向垂直向上，通过被排开流体的质心。

1.2公式1.公式F浮=G排=ρ涂·g·V排单位:F浮——Nρ涂——千克/米3g%%——牛顿/千克V排——米32.推导阿基米德原理：根据浮力产生原因，上下表而的压力差:以边长为a的正方形铁块为例，沉没水中时水深h。

上表面压强p1=ρg(h-a), 压强等于液体密度乘以g乘以深度，水总的深度是h，下表面压强p2=ρgh 水中正方体高a，正方体上表面距离水面h-aF浮=a^2 p2-a^2 p1 浮力等于下表面压力减去上表面压力，压力等于压强乘以受力面积=a^2[ρgh-ρg(h-a)] 正方体底面积是边长的平方a^2=a^2ρga=a^3ρg=Vρg铁块体积就是排开水的体积。

1.3浮力的有关因素浮力只与ρ液，V排有关；与ρ物(G物)，h深和V物无直接关系。

1.4阿基米德被发现的故事阿基米德发现的浮力原理奠定了流体静力学的基础。

传说海伦国王召见阿基米德，请他鉴定纯金王冠是否掺假。

他冥思苦想了很多天，在踏进浴缸洗澡的时候，从看到水上涨中获得灵感，有了关于浮体的重大发现，通过皇冠排出的水解决了国王的问题。

在著名的《论浮体》一书中，他按照各种固体的形状和比重的变化来确定其浮于水中的位置，并且详细阐述和总结了后来闻名于世的阿基米德原理：放在液体中的物体受到向上的浮力，其大小等于物体所排开的液体重量。

从此使人们对物体的沉浮有了科学的认识。

2.阿基米德原理的适用范围2.1适用范围适用于液体和气体。

阿基米德原理适用于全部或部分浸没在静态流体中的物体，要求物体的下表面必须与流体接触。

如果物体的下表面没有完全与流体接触，例如被水淹没的码头、插入海底的沉船、打入湖底的桩等。

，在这样的情况下，此时水的力不等于原理中规定的力。

如果相对于物体有明显的水流，这个原理就不适用。

阿基米德原理的内涵
阿基米德原理，又称浮力定律，是古希腊数学家阿基米德在公元前3世纪提出的一个关于物体浮沉的重要定律。

它表明，浸泡在流体中的物体受到的向上浮力大小等于所排开液体的重量，物体的浮沉取决于它的体积和密度。

首先，阿基米德原理揭示了物体在浸泡在流体中时受到的浮力并非与物体的质量有关，而是与物体所排开的液体的重量相等。

这一点对于我们理解浮力的本质非常重要。

根据原理，只要物体所受到的浮力大于物体自身的重力，它就能够浮起来。

这也解释了为什么轻的物体可以浮在水面上。

其次，阿基米德原理告诉我们物体的浮沉与其体积和密度有关。

物体越大，所排开的液体越多，浮力就越大。

而密度越小，浸泡在流体中时的浮力就越大。

这就是为什么空气中的气球可以悬浮在空中，因为气球的密度比空气小。

这个原理在工程设计中也非常重要，例如设计浮船、潜水艇等。

最后，阿基米德原理的内涵还涉及到物体的浸泡深度和浮力的大小之间的关系。

根据原理，物体在流体中的浸泡深度与所受到的浮力成正比。

也就是说，只要物体的一部分浸没在流体中，它所受到的浮力就会减小。

这个特点在我们日常生活中也有所体现，例如在水中把手臂伸入水中，感觉到的浮力就会减小。

综上所述，阿基米德原理揭示了物体浮沉的规律，其内涵包括浮力与排开液体的重量相等、浮沉取决于物体的体积和密度、浮力与浸泡深度成正比等。

这一重要原理在科学研究和工程设计中都有广泛的应用。

通过深入理解和应用阿基米德原理，我们能够更好地解释各种浮力现象，并为相关领域提供更准确的设计和研究基础。

阿基米德原理公式变形
阿基米德原理是描述物体在浸泡在液体中时受到浮力的原理。

该原理可以用以下公式表示：浮力（Fb）= 密度（ρ）×重力加速度（g）×体积（V），
其中，密度（ρ）表示液体的密度，重力加速度（g）表示重力加速度的大小，体积（V）表示物体浸泡在液体中的体积。

阿基米德原理的另一种常见变形形式是：
浸没物体所受到的浮力等于被该物体所排开的液体的重量。

这种变形形式强调了浸没物体所受到的浮力与其所排开的液体的重量相等。

阿基米德原理可以通过不同的形式和表达方式来描述和计算浮力。

当液体中有多个物体浸没时，每个物体所受到的浮力等于其排开的液体的重量之和。

这可以表示为：
浮力（Fb）= 液体密度（ρ液体）×浸没体积（V浸没）×重力加速度（g）。

其中，液体密度（ρ液体）表示液体的密度，浸没体积（V浸没）表示物体浸没在液体中的体积，重力加速度（g）表示重力加速度的大小。

这种形式的阿基米德原理适用于液体中存在多个浸没物体的情况，可以根据每个物体的体积和液体的密度来计算它们各自所受到的浮力。