人教版五年级数学下册阿基米德定律(优选)

阿基米德定理
阿基米德定理（Archimedes’Principle）是由古希腊数学家和发明家阿基米德第一次提出的，它给出了描述液体密度和浮力的一般定律。

它是浮力的一般原理，提供了计算物体浮力的基础，同时也提供了一种认识液体性质的基础。

它可以用来解释液体密度是多少、物体在液体中能做什么样的运动以及为什么物体能够悬浮在液体中。

阿基米德定理的核心即为：在某一圆柱形体的体积内所含的任何物体，其浮力等于其拥有重量的水体的体积，也就是说，浮力等于物体的重量乘以液体的密度。

浮力的大小取决于物体的大小和液体的密度。

密度指的是指水体的重量乘以体积，能够反映出液体的稠密程度，浮力是液体所产生的一种抗力，它能够抵消重力，使物体能够悬浮在液体中。

阿基米德定理的发现改变了人们对液体的认识，它使人们能够更深入地理解液体的性质，同时也为液体未来的研究提供了基础。

它的实用性已经被证明，它不仅被用于船舶设计，同时也被用于太空技术以及材料力学等领域。

阿基米德定理不仅能够用于学术研究，还能够用于日常实践，比如可以用来称重物体，计算液体的密度，以及计算物体在液体中的浮力等，都能够借助阿基米德定理进行计算。

阿基米德定理是研究浮力的一般原理，但是它也有一些局限性，比如它不能够解释物体的漂浮方式，或者物体与液体的相互作用等。

这些问题，只有深入研究才能够找到解决方案。

阿基米德定理的发现，标志着液体的研究迎来了新的发展，它不仅为研究浮力提供了实用的研究原理，也为液体未来的研究开拓了新的道路。

它为人们更深入地理解液体提供了可能，同时也为将来液体技术的发展开拓了广阔的新天地。

阿基米德定律
阿基米德有许多故事，其中最着名的要算发现阿基米德定律的那个洗澡的故事了。

国王做了一顶金王冠，他怀疑工匠用银子偷换了一部分金子，便要阿基米德鉴定它是不是纯金制的，且不能损坏王冠。

阿基米德捧着这顶王冠整天苦苦思索，有一天，阿基米德去浴室洗澡，他跨入浴桶，随着身子浸入浴桶，一部分水就从桶边溢出，阿基米德看到这个现象，头脑中像闪过一道闪电，“我找到了！”
阿基米德拿一块金块和一块重量相等的银块，分别放入一个盛满水的容器中，发现银块排出的水多得多。

于是阿基米德拿了与王冠重量相等的金块，放入盛满水的容器里，测出排出的水量；再把王冠放入盛满水的容器里，看看排出的水量是否一样，问题就解决了。

随着进一步研究，沿用至今的流体力学最重要基石——阿基米德定律诞生了。

阿基米德——由洗澡得出浮力定律阿基米德——由洗澡得出浮力定律——由洗澡得出浮力定律阿基米德（前287—前212），是希腊最伟大的数学家和物理学家。

其中浮力定律的发现却是由一件趣事引起的。

传说叙拉古国王亥厄洛命金匠打制一顶纯金的王冠。

新王冠做得十分精巧，纤细的金丝密密地织成了各种花样，大小也正合适，国王十分高兴。

但转念一想：我给了工匠15两黄金，会不会被他们私吞了几两呢？因此，马上叫人拿秤来称，结果不多不少正好15两。

但一位大臣说：“重量一样不等于黄金没有少，万一金匠在黄金中掺进了银子或其他东西，重量可以不变，但王冠已不是纯金的了。

”国王听后觉得很有道理，但有什么办法能既不损坏王冠又知道王冠是否掺了银子呢？国王把这个难题交给了阿基米德。

阿基米德欣然领命。

可是，不损伤王冠就不能取样跟纯金比较，也不能用试金石查检金的纯度。

从表面看，是无法看出金子纯度的，该怎样判定王冠的黄金纯度呢？阿基米德思来想去，一直想不出判定方法来。

一连几个星期，他茶饭不思。

阿基米德心力交瘁，觉得总这样也不是办法，还是先调节一下身心，再继续研究吧。

于是，他吩咐给自己准备洗澡水。

仆人这一次把浴盆里的水加得太满了。

阿基米德一条腿刚伸进去，水便溢出盆来，再伸进一条腿，水又漫出来一点，等到洗好澡，盆里的水已经少了一些。

这时候，他再把腿伸进盆去，那水却不再溢出来，即使全身都浸泡在盆里，水也没有溢出一点儿。

看到这种现象，阿基米德突然明朗起来。

物体进入水中，一定会排出与体积相等的水，那么，体积越大排开的水一定就越多了。

如果把与王冠等重的纯金浸入水中，它排出的水是一定的，如果王冠里掺了别的金属，那些金属的体积一定比纯金大，那么肯定会多排出一些水，两相对比，王冠里有没有假，不就很清楚了吗？想到这里，阿基米德跳出浴盆开始检验自己的设想。

他用各种金属放进水盆，计算溢出的水。

得出的结论跟自己的想法完全相同。

这时，他觉得解决王冠的问题已经成熟，便带着必要的仪器进了王宫，准备测试一下王冠是否真由纯金所制。

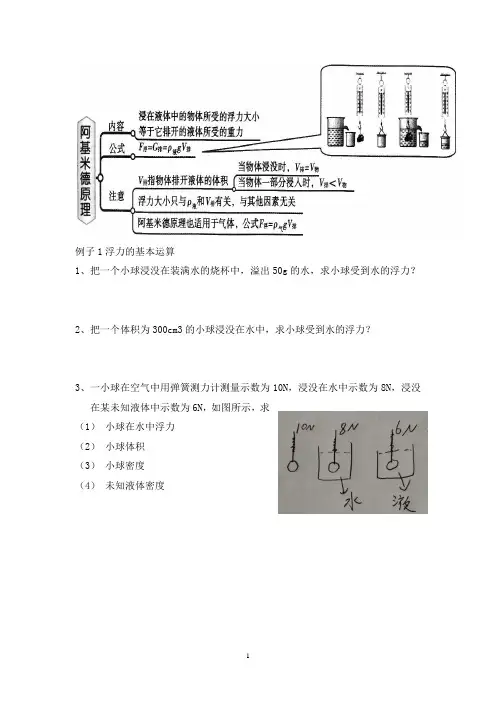
例子1浮力的基本运算1、把一个小球浸没在装满水的烧杯中，溢出50g的水，求小球受到水的浮力？2、把一个体积为300cm3的小球浸没在水中，求小球受到水的浮力？3、一小球在空气中用弹簧测力计测量示数为10N，浸没在水中示数为8N，浸没在某未知液体中示数为6N，如图所示，求（1）小球在水中浮力（2）小球体积（3）小球密度（4）未知液体密度4、体积为100 cm3的铝块(ρ=2.7×103kg／m3)，它的一半浸入水中，它受到的铝=0．8×103 kg／m3) 浮力是多少?当它浸没在酒精中受到的浮力是多少?(ρ酒5、如图所示，弹簧测力计下面悬挂一个重8 N的物体．当把物体浸没在水中时，弹簧测力计示数变为 6 N，此时圆柱形容器内水的高度为0．2 m(g取10 N／kg)．求：(1)物体受到水的浮力多大?(2)物体的体积为多大?(3)当物体浸没在水中时，水对容器底部的压强为多大?6、如图所示，将一块密度为2×103 kg／m3、体积为l00 cm3的石块，用细线系着浸没在装有水的容器中．(g＝10 N／kg，水的密度为l．0×103 kg／m3)求：(1)石块的重力．(2)石块所受浮力．7、一小球重力为8N，把烧杯中装一定量的水，放在称上，称的示数为20N，用弹簧测力计拉住小球，把小球放入烧杯中，水未溢出，此时弹簧测力计示数为3N，求此时称的示数？8、一个铝球，在空气中用弹簧测力计称量，示数为54N，完全浸没在水中称量示数为24N，问该铝球是否是空心的，如果是，求空心体积（铝的密度为2.7×103 kg／m3）例子2验证阿基米德原理小颖同学在探究“浮力的大小等于什么”时，用弹簧测力计、密度大于水的塑料块、烧杯、小桶等器材进行实验，如图a、b、c、d是四个步骤的示意图，a、b、c、d是四次弹簧测力计的示数分别为F1，F2，F3，F4，其中d测量空桶受到的____________，此实验操作的正确顺序是_____________，由a、b两图中弹簧测力计的读数可求出塑料块受到的浮力表达式_______；被排开液体受到的重力表达式为__________；如果关系式________成立，就可得到著名的阿基米德原理。

阿基米德定律的主要内容是什么
阿基米德定律指出浸入静止流体中的物体受到一个浮力，其大小等于该物体所排开的流体重量，方向竖直向上并通过所排开流体的形心。

用武力公式来表示为：F浮=G液排=m液排g=gV排ρ液（V排表述物体排开液体的体积）。

扩展资料
传说希伦王召见阿基米德，让他鉴定纯金王冠是否掺假。

他冥思苦想多日，在跨进澡盆洗澡时，从看见水面上升得到启示，作出了关于浮体问题的重大发现，并通过王冠排出的水量解决了国王的疑问。

在著名的《论浮体》一书中，他按照各种固体的'形状和比重的变化来确定其浮于水中的位置，并且详细阐述和总结了后来闻名于世的阿基米德原理：放在液体中的物体受到向上的浮力，其大小等于物体所排开的液体重量。

从此使人们对物体的沉浮有了科学的认识。

阿基米德定律阿基米德定律是指，浸在液体里的物体受到向上的浮力，浮力的大小等于物体排开的液体的重量。

阿基米德定律也适用于气体。

接下来为您简单介绍，希望对您有所帮助。

1.杠杆原理:阿基米德原理。

公式:动力×动力臂=阻力×阻力臂。

杠杆又扭轴费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称作杠杆平衡条件。

必须并使杠杆均衡，促进作用在杠杆上的两个力矩（力与力臂的乘积）大小必须成正比。

即为：动力×颤抖力臂=阻力×阻力臂，用代数式则表示为f1· l1=f2·l2。

式中，f1则表示动力，l1则表示颤抖力臂，f2则表示阻力，l2则表示阻力臂。

战国时代的墨子最早提出杠杆原理，在《墨子· 经下》中说衡而必正，说在得；衡，加重于其一旁，必捶，权重不相若也，相衡，则本短标长，两加焉，重相若，则标必下，标得权”。

这两条对杠杆的平衡说得很全面。

里面存有等臂的，存有左右臂的；存有发生改变两端重量并使它偏动的，也存有发生改变两臂长度并使它偏动的。

这里还要顺带提到的就是，古希腊科学家阿基米德存有这样一句流传好久的名言：“给我一个支点，我就能够砸开整个地球！”，这句话就是说道杠杆原理。

2.浮力定律:阿基米德定律。

公式:f浮=g排液=ρ液gv排液。

浮力就是由液体(或气体)对物体向上和向上压力差产生的。

灌入液体里的物体受向上的浮力，浮力的大小等同于它两边的液体受的重力。

f浮 = g排在=ρ液v排在g。

从公式中可以窥见：液体对物体的浮力与液体的密度和物体两边液体的体积有关，而与物体的质量、体积、重力、形状、浸的深度等均毫无关系。

3.求积原理:穷竭法。

阿基米德还有一个杰出发现是指出圆球的体积和表面积都是外切圆球的圆柱体体积和表面积的2/3。

阿基米德定理
阿基米德定理可以说是数学史上最杰出的定理之一，它是古希腊数学家阿基米德研究的结果，是整个数学史上第一个证明了正多边形内角和的定理。

阿基米德定理是数学史上最著名的定理之一，被为数学史上最强大的定理。

阿基米德定理由古希腊数学家阿基米德提出，并最终证明了它的真实性，其主要内容是：“在任何一个正多边形中，内角之和为180度。

”正多边形指的是四边以上都相等的多边形，其中包括三角形、四边形、五边形、六边形等等。

阿基米德定理最初由古希腊数学家阿基米德发现，他认为，在正多边形中，所有内角和为180度，这是他对正多边形的平行性的最初推论。

他发现，在每一边拐弯的地方，都有一个内角，并且总的内角数不能超过180度，他使用证明的方法旋转一个多边形，从而证明了这一定理。

阿基米德定理不仅可以用来解决一些特定的几何问题，而且可以用来证明其他几何理论，因此，在数学史上拥有重要地位。

它有重要的教学意义，因为它被用来解释一些数学概念，如弧度、多边形、空间几何等。

它还有着重要的实际意义，在很多领域都有应用，比如建筑，汽车工业等等，它可以帮助人们更好地构思和设计。

此外，阿基米德定理也影响到一些与数学有关的其他领域，比如物理、化学等，有些物理事件甚至是基于阿基米德定理，它也有助于理解和解释许多自然现象。

总之，阿基米德定理是一个关于正多边形内角和的定理，它是古希腊数学家阿基米德研究的结果，是数学史上第一个被证明的定理，它对数学的发展至关重要，也对其他一些理论及实践有重大影响。

阿基米德定律
阿基米德有许多故事，其中最着名的要算发现阿基米德定律的那个洗澡的故事了。

国王做了一顶金王冠，他怀疑工匠用银子偷换了一部分金子，便要阿基米德鉴定它是不是纯金制的，且不能损坏王冠。

阿基米德捧着这顶王冠整天苦苦思索，有一天，阿基米德去浴室洗澡，他跨入浴桶，随着身子浸入浴桶，一部分水就从桶边溢出，阿基米德看到这个现象，头脑中像闪过一道闪电，“我找到了！”
阿基米德拿一块金块和一块重量相等的银块，分别放入一个盛满水的容器中，发现银块排出的水多得多。

于是阿基米德拿了与王冠重量相等的金块，放入盛满水的容器里，测出排出的水量；再把王冠放入盛满水的容器里，看看排出的水量是否一样，问题就解决了。

随着进一步研究，沿用至今的流体力学最重要基石——阿基米德定律诞生了。

阿基米德与二次幂和公式阿基米德（、Aristotle），古希腊哲学家，曾经是学术界著名的思想家，他在数学和哲学方面有很深的研究，他的思想影响着西方文明后世的发展。

其中，他对于数学有重大的贡献，他对二次幂，也就是平方形式有重要的研究，提出了“阿基米德定律”，从而为数学研究提供了一种新的方法和抽象的范例。

二、阿基米德定律“阿基米德定律”就是说，一个变量的二次幂的函数是它的一次幂的函数的平方，通俗的说就是两个一次幂的函数的乘积等于它们的平方函数。

“阿基米德定律”的表述：如果x的一次幂是f，x的二次幂就是f2，这时，f2就是f的平方，而f的平方又等于f乘以f，也就是说f乘以f等于f2。

这实际上就是“阿基米德定律”，也就是说，x的一次幂f乘以它自己，等于它的二次幂f2。

三、阿基米德定律的公式X的二次幂函数定义为f2(x)，它等于X的一次幂函数f(x)的平方，那么，X的二次幂函数可以用如下的形式表示：f2（x）=f（x）f（x）这就是“阿基米德定律”的定义，用符号表示形式如下：f2（x）=f（x）四、阿基米德定律的应用阿基米德定律是一种对二次幂函数及其应用研究的重要贡献，它所涉及的函数可用于求解一元二次方程，它有以下几个重要的应用：（1）一元二次方程的求解：二次幂函数的特性在一元二次方程的解决中发挥了重要的作用，平方形式就是其中的一种，把一元二次方程换成阿基米德定律，就可以通过解二次方程来求解一元二次方程的解。

（2）曲线图表的绘制：二次幂函数的曲线，就是根据阿基米德定律绘制的，它可以用来表示物体不断加快或减慢的运动轨迹，如抛物线等。

（3）换根式：换根式是根据阿基米德定律把指数式变为平方形式的一种方法，它的步骤是：根据阿基米德定律把指数式分解成两部分（分解成相等的两个部分），然后解决它们，最后再把它们变回原来的指数式。

五、小结“阿基米德定律”是数学中一个重要的定理，其定义是，一个变量的二次幂的函数是它的一次幂的函数的平方，符号表示形式为f2（x）=f（x），这个定理是对多项式函数形式及应用的重要贡献，它可用来求解一元二次方程，以及绘制曲线，以及换根式的研究中。

阿基米德折弦定理阿基米德折弦定理，也称为阿基米德定理，是数学中的一个重要定理，与圆和三角函数有关。

该定理最早记载于公元前250年的古希腊数学家阿基米德的著作《圆的测量》中。

阿基米德折弦定理陈述如下：对于任意一条弧，该弧两端的弦的长度之积等于从弦中点引垂线得到的两条线段的长度之积。

即，在一个圆的内部任取一条弧，该弧的两个端点连成一条弦，然后在这条弦的中点处竖直一条线段，将弦分成两条线段，两条线段的长度之积等于从中点引垂线得到的两条线段的长度之积。

具体公式为：AB×CD=BC×DE其中，AB表示弦的长度，BC为弦的中点到圆的距离，CD和DE分别为弦的两边到圆的距离。

该定理可以用来推导出三角函数之间的关系，因此在三角函数的求解中也有着广泛的应用。

证明：如图，以弧AB所对的圆心为O，过弦AB中点C引一条竖直线段DE交弦AB于点F。

因为OF=CD=DE，所以FC=EF。

在ΔBOF中，根据勾股定理有：(BO)²=(OF)²+(BF)²由于OF=CD=DE，可以写成：(BO)²=(CD)²+(BF)²在ΔCFC'中，根据勾股定理有：(CF)²=(CC')²+(FC')²但是，因为CF=EF，且CC'为BC的中垂线，即CC'=BC/2，所以可写成：(CF)²=(BC/2)²+(FC')²又因为BC=2CF，所以可以简化成：(CF)²=(CF)²+(FC')²即，(FC')²=CF²-FC²在ΔDEF中，根据勾股定理有：(DF)²=(DE)²+(EF)²由于EF=FC，可以写成：(DF)²=(DE)²+(FC)²同理，在ΔCEF中，根据勾股定理有：(FC)²=(CE)²+(EF)²因为EF=FC，所以：(FC)²=(CE)²+(FC)²即，(CE)²=0这说明点E恰好位于圆的直径上。

阿基米德定理的内容阿基米德定理，又称为圆锥曲面积定理，是由古希腊数学家阿基米德在公元前3世纪提出的一个重要几何定理。

它描述了一个立体体积与一个相似但比例不同的立体体积之间的关系。

阿基米德定理的内容为：如果两个立体体积的底面积相等，且高度成比例，那么这两个立体体积的体积也成比例。

为了更好地理解阿基米德定理，我们可以通过一个具体的例子来说明。

假设我们有一个圆锥体A和一个相似但比例不同的圆锥体B。

设圆锥体A的底面半径为r，高度为h，体积为V。

而圆锥体B的底面半径为kr，高度为kh，体积为k^3V，其中k为比例系数。

根据阿基米德定理，圆锥体A和圆锥体B的底面积相等，即πr^2=π(kr)^2=k^2πr^2。

而且圆锥体A和圆锥体B的高度也成比例，即h:kh=1:k，即h=k^2h。

因此，根据阿基米德定理，圆锥体A和圆锥体B的体积也成比例，即V:k^3V=1:k^3，即V=k^3V。

这个例子清楚地展示了阿基米德定理的内容：两个立体体积的底面积相等，且高度成比例，那么这两个立体体积的体积也成比例。

这一定理在几何学和物理学中有着广泛的应用。

阿基米德定理的重要性在于它提供了一种简单而有效的方法来计算相似立体体积之间的比例关系。

通过比较底面积和高度的比例，我们可以得出体积的比例，并且不需要具体计算出底面积和高度的数值。

这在实际问题中具有很大的实用性。

比如，如果我们知道一个正方体的体积为V，而另一个正方体的底面积是前一个的2倍，高度是前一个的3倍，那么根据阿基米德定理，我们可以知道第二个正方体的体积是第一个的6倍，即6V。

除了圆锥体，阿基米德定理还可以应用于其他形状的立体，比如圆柱体、球体等。

只要满足底面积相等且高度成比例的条件，阿基米德定理都适用。

这为我们在实际问题中的计算提供了很大的便利。

总结起来，阿基米德定理是一条关于立体体积间比例关系的重要几何定理。

它通过比较底面积和高度的比例，给出了两个相似立体体积之间的比例关系。