第一节 动态规划的基本模型
多阶段决策过程的最优化问题
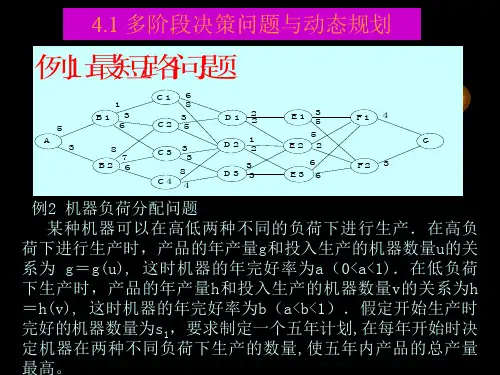
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若 干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达 到最好的活动效果。当然,各个阶段决策的选取不是任意确定的,它依赖于 当前面临的状态,又影响以后的发展,当各个阶段决策确定后,就组成一个 决策序列,因而也就确定了整个过程的一条活动路线,这种把一个问题看作 是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问 题就称为多阶段决策问题。如下图所示:
当x=N时,到达递归出口,如果Curr比Ans大,则把Ans更新为Curr;否则向下一行两个位置行走,即递归执行 Dfs(x+1,y,Curr+A[x+1][y])和Dfs(x+1,y+1,Curr+A[x+1][y+1])。 #include <iostream> using namespace std; const int MAXN = 1005; int A[MAXN][MAXN],F[MAXN][MAXN],N,Ans; void Dfs(int x,int y,int Curr) {
记忆化搜索需要对方法一中的搜索进行改装。由于需要记录从一个点开始到终 点的路径的最大权值和,因此我们重新定义递归函数Dfs。
定义Dfs(x,y)表示从(x,y)出发到终点的路径的最大权值和,答案就是Dfs(1,1)。 计算Dfs(x,y)时考虑第一步是向左还是向右,我们把所有路径分成两大类:
①第一步向左:那么从(x,y)出发到终点的这类路径就被分成两个部分,先从(x,y) 到(x+1,y)再从(x+1,y)到终点,第一部分固定权值就是A[x][y],要使得这种情况的路 径权值和最大,那么第二部分从(x+1,y)到终点的路径的权值和也要最大,这一部分 与前面的Dfs(x,y)的定义十分相似,仅仅是参数不同,因此这一部分可以表示成 Dfs(x+1,y)。综上,第一步向左的路径最大权值和为A[x][y]+Dfs(x+1,y);