河北省石家庄市2020届高三年级阶段性训练题数学(文科)试卷(word 版)答案
- 格式:pdf
- 大小:950.46 KB
- 文档页数:8

2020年河北省石家庄市藁城第三中学高三数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知且, 当时均有, 则实数的取值范围是( )A. B.C. D.参考答案:C略2. 已知F为椭圆的左焦点,A是椭圆的短轴的上顶点,点B在x轴上,且AF⊥AB,A,B,F三点确定的圆C恰好与直线x+my+3=0相切,则m的值为()A.±3 B.C.±D.3参考答案:C【考点】椭圆的简单性质.【分析】求得椭圆的焦点坐标,设B,则圆心C(,0),半径为r=,利用勾股定理求得x的值,利用点到直线的距离公式,即可求得m的值.【解答】解:由题意可知:椭圆+=1的左焦点(﹣1,0),设B(x,0),由AF⊥AB,且A,B,F三点确定的圆C,圆心C(,0),半径为r=,在△AOC中,由丨AO丨2+丨OC丨2=丨AC丨2=r2,即()2+()2=()2,解得:x=3,则C(1,0),半径为2,由题意可知:圆心到直线x+my+3=0距离d==2,解得:m=±,故选:C.【点评】本题考查椭圆的标准方程及简单几何性质,考查点到直线的距离公式,考查计算能力,属于中档题.3. 已知函数,则满足的实数的取值范围是()A. B.C. D.参考答案:A试题分析:令,则,因由可得因,即.又,故函数是偶函数,所以当时,,即函数是单调递增函数,故由可得,即,解之得,故应选A.考点:函数的单调性和奇偶性及不等式的解法等知识的综合运用.【易错点晴】本题以可导函数满足的不等式为背景,考查的是导函数的与函数的单调性之间的关系的应用问题.解答本题的关键是如何将不等式进行等价转化为.再依据题设条件先构造函数,将问题转化为证明函数是单调递增函数,从而将不等式化为,从而使得问题最终获解.4. 若二项式中所有项的系数之和为,所有项的系数的绝对值之和为,则的最小值为()参考答案:B5. 下面给出四个命题:①若平面//平面,是夹在间的线段,若//,则;②是异面直线,是异面直线,则一定是异面直线;③过空间任一点,可以做两条直线和已知平面垂直;④平面//平面,,//,则;其中正确的命题是()A.①② B.①②③ C.①②④ D.①④参考答案:D6. 已知集合,,则A. B. C. D.参考答案:C7. 在△ABC中,A=60°,AB=2,且△ABC的面积为,则BC的长为()A.B.C.2D.2参考答案:B【考点】余弦定理.【分析】利用三角形面积公式列出关系式,把AB,sinA,已知面积代入求出AC的长,再利用余弦定理即可求出BC的长.【解答】解:∵在△ABC中,A=60°,AB=2,且△ABC的面积为,∴AB?AC?sinA=,即×2×AC×=,解得:AC=1,由余弦定理得:BC2=AC2+AB2﹣2AC?AB?cosA=1+4﹣2=3,则BC=.故选:B.8. 是虚数单位,则复数在复平面内对应的点在().第一象限.第二象限.第三象限.第四象限参考答案:D,所以对应点位,在第四象限,选D.9. 在区间[0,1]上随机取两个数,则这两个数之和小于的概率是()A.B.C.D.参考答案:D【考点】CF:几何概型.【分析】设取出的两个数为x、y,则可得“0≤x≤1,0≤y≤1”表示的区域为纵横坐标都在[0,1]之间的正方形区域,易得其面积为1,而x+y<1.5表示的区域为直线x+y=1.5下方,且在0≤x≤1,0≤y≤1所表示区域内部的部分,分别计算其面积,由几何概型的计算公式可得答案.【解答】解:设取出的两个数为x、y,则有0≤x≤1,0≤y≤1,其表示的区域为纵横坐标都在[0,1]之间的正方形区域,易得其面积为1,而x+y<1.5表示的区域为直线x+y=1.5下方,且在0≤x≤1,0≤y≤1表示区域内部的部分,易得其面积为1﹣=,则两数之和小于1.5的概率是.故选:D.10. 曲线与直线有两个不同的交点,实数k的范围是()A. (,+∞)B. (,C. (0,)D. (,参考答案:B本试题主要是考查了直线与圆的位置关系的运用。

2020年河北省石家庄市高考数学综合训练试卷(文科)(二)一、选择题(本大题共12小题,共60.0分)1.已知集合A={0,1,2,3,4,5},B={x|x2−x−2≤0},则A∩B=()A. {1,2}B. {0,1,2}C. {−1,0,1}D. {0,1}2.已知复数z满足(1+i)z=(1−i)2,则z=()A. −1+iB. 1+iC. 1−iD. −1−i3.林管部门在每年植树节前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图所示.根据茎叶图,下列描述正确的是()A. 甲种树苗的高度的中位数大于乙种树苗的高度的中位数,且甲种树苗比乙种树苗长得整齐B. 甲种树苗的高度的中位数大于乙种树苗的高度的中位数,但乙种树苗比甲种树苗长得整齐C. 乙种树苗的高度的中位数大于甲种树苗的高度的中位数,且乙种树苗比甲种树苗长得整齐D. 乙种树苗的高度的中位数大于甲种树苗的高度的中位数,但甲种树苗比乙种树苗长得整齐4.已知A={a|关于x的不等式ax2+2ax−2<0的解集为R},B={a|−2<a<0},则x∈A是x∈B的()A. 既不充分也不必要条件B. 必要而不充分条件C. 充要条件D. 充分而不必要条件5.已知抛物线x2=2py的焦点是F,其上一点M(m,1),其中|MF|=3,则p=()A. 8B. 4C. 14D. 186.在△ABC中,4sinA+3cosB=5,4cosA+3sinB=2√3,则角C等于()A. 150∘或30∘B. 120∘或60∘C. 30∘D. 60∘7.若△ABC的内角A、B、C所对的边a、b、c,若角A、B、C依次成等差数列,且(a+c)2=12+b2,则△ABC的面积为()A. 6−3√3B. 6√3−9C. 2√3D. √38.已知平面α与平面β相交,直线m⊥α,则()A. β内必存在直线与m 平行,且存在直线与m 垂直B. β内不一定存在直线与m 平行,也不一定存在直线与m 垂直C. β内不一定存在直线与m 平行,但必存在直线与m 垂直D. β内必存在直线与m 平行,但不一定存在直线与m 垂直9. 已知函数f(x)={x −1,x ≤1lnx,x >1,则满足f(1−t)<f(1+t)的t 的取值范围是( ) A. (−∞,0) B. (−1,0) C. (0,+∞) D. (0,1)10. 已知x ,y 满足约束条件{y ≤1x +y +4≥0x −y ≤0,则z =x +2y 的最小值是( )A. −8B. −6C. −3D. 311. 已知三棱锥S −ABC 的所有顶点都在球O 的表面上,△ABC 是边长为1的正三角形,SC 为球O的直径,且SC =2,则此三棱锥的体积为( ) A. 14 B. √24 C. √26 D. √212 12. 如图,圆O 是半径为1的圆,OA =12,设B ,C 为圆上的任意2个点,则AC ⃗⃗⃗⃗⃗ ⋅BC⃗⃗⃗⃗⃗ 的取值范围是( )A. [−18,3]B. [−1,3]C. [−1,1]D. [−18,1]二、填空题(本大题共4小题,共20.0分)13. 已知等差数列{a n }中,a 3=9,a 9=−3,a 17= ______ .14. 小明随机播放A ,B ,C ,D ,E 五首歌曲中的两首,则A ,B 两首歌曲至少有一首被播放的概率是______.15. 设双曲线y 2a 2−x 2b 2=1(a >0,b >0)的离心率是3,则其渐近线的方程为______.16. 设函数f(x)=e x −e −x ,若对所有x ≥0都有f(x)≥ax ,则实数a 的取值范围为______.三、解答题(本大题共7小题,共82.0分)17. 已知数列{a n }中,a 1=1,a n+1=an 2a n +1(n ∈N ∗). (1)求证:数列{1a n }为等差数列;(2)求数列{a n}的通项公式a n;(3)设2b n =1a n+1,数列{b n b n+2}的前n项和T n,求证:T n<34.18.如图,在三棱锥P−ABC中,△ABC和△PAC都是正三角形,AC=2,E、F分别是AC、BC的中点,且PD⊥AB于D,平面PAC⊥平面ABC.(Ⅰ)证明:EF⊥ED;(Ⅱ)求点F到平面PAB的距离.19.为选派一名学生参加全市实践活动技能竞赛,A,B两名学生在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据如图所示(单位:mm):平均数方差完全符合要求的个数A200.0262B20s B25根据测试得到的有关数据,试解答下列问题:(1)考虑平均数与完全符合要求的个数,你认为_________学生的成绩好些;(2)计算出s B2的大小,考虑平均数与方差,说明谁的成绩好些;(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.20.已知椭圆C:x2a2+y2b2=1(a>0b>0)的离心率为12,点F1,F2分别是椭圆C的左,右焦点,以原点为圆心,椭圆C的短半轴为半径的圆与直线x−y+√6=0相切.(I)求椭圆C的方程;(Ⅱ)若过点F2的直线l与椭圆C相交于点M,N两点,求使△F l MN面积最大时直线l的方程.21.设函数f(x)=xe a−x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e−1)x+4.(1)求a,b的值;(2)求f(x)的单调区间.22.在直角坐标系xOy中,曲线C1的普通方程为x2+y2−2x=0,以原点O为极点,x轴正半轴为.极轴建立极坐标系,曲线C2的极坐标方程为ρ2=31+2sinθ(Ⅰ)求C1的参数方程与C2的直角坐标方程;(ρ≥0)与C1交于异于极点的点A,与C2的交点为B,求|AB|.(Ⅱ)射线θ=π323.已知函数f(x)=|2x−1|−a(a∈R).(1)若f(x)在[−1,2]上的最大值是最小值的2倍,解不等式f(x)≥5;f(x+1)成立,求实数a的取值范围.(2)若存在实数x使得f(x)<12-------- 答案与解析 --------1.答案:B解析:解:B={x|−1≤x≤2};∴A∩B={0,1,2}.故选:B.可求出集合B,然后进行交集的运算即可.本题考查交集的运算,属于基础题.2.答案:A解析:本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.把已知等式变形,再由复数代数形式的乘除运算化简求得z,则z−可求.解:由(1+i)z=(1−i)2=−2i,得z=−2i1+i =−2i(1−i)(1+i)(1−i)=−1−i,∴z−=−1+i.故选:A.3.答案:D解析:解:由茎叶图中的数据得,甲、乙两种树苗抽取的样本高度分别为:甲:19,20,21,23,25,29,31,32,33,37乙:10,10,14,26,27,30,44,46,46,47由已知得:甲的中位数是12×(25+29)=27,乙的中位数是12×(27+30)=28.5;且甲的数据分布比较集中,乙的数据分布较为分散,∴乙种树苗的中位数大于甲种树苗的中位数,甲种树苗比乙种树苗长得整齐.故选:D.由茎叶图中的数据求出甲、乙的中位数,根据数据的分布情况得出甲、乙树苗长得整齐情况. 本题考查了茎叶图与中位数、方差的应用问题,是基础题.4.答案:B解析:本题主要考查充分条件和必要条件的判断,结合不等式恒成立的条件求出A 的集合是解决本题的关键.难度不大.根据不等式恒成立,求出集合A 的等价条件,结合充分条件和必要条件的定义进行判断即可. 解:当a =0时,不等式ax 2+2ax −2<0等价为−2<0,此时不等式恒成立,满足条件;当a ≠0时,要使不等式ax 2+2ax −2<0的解集为R ,则{a <0△=4a 2+8a <0,得−2<a <0, 综上A ={a|关于x 的不等式ax 2+2ax −2<0的解集为R}={a|−2<a ≤0},∵B ={a|−2<a <0},∴B ⫋A ,即x ∈A 是x ∈B 的必要不充分条件,故选:B .5.答案:B解析:解:抛物线C :x 2=2py(p >0)的焦点为F ,抛物线C 上一点M(m,1)满足|MF|=3,可得:{m 2=2p m 2+(1−p 2)2=9, 解得:m 2=8,p =4,故选:B .利用点的抛物线上,推出m ,p 的方程,利用|MF|=3,列出方程,求出m 2,p 即可.本题考查直线与抛物线的位置关系的应用,考查方程思想的应用,是中档题.6.答案:C解析:本题考查三角函数的化简求值,属于中档题,注意角的范围的判断,是本题的易错点. 利用同角函数的关系式求出A ,B 的关系,可得C 的大小.解:由4sinA+3cosB=5,可得:16sin2A+9cos2B+24sinAcosB=25…①,由4cosA+3sinB=2√3,可得:16cos2A+9sin2B+24sinBcosA=12…②,用①+②可得:25+24(sinAcosB+sinBcosA)=37,∵sinAcosB+sinBcosA=sin(A+B)=sinC,∴24sinC=12,sinC=12,∴C=150∘或C=30∘.∵当C=5π6,即A+B=π6时,A<π6,∴cosA>cosπ6=√32,∴4cosA>4√32,∵sinB>0,∴3sinB>0,∴3sinB+4cosA>2√3,与题中的3sinB+4cosA=2√3矛盾.故选C.7.答案:D解析:由角A、B、C依次成等差数列,可求角B,由余弦定理及(a+c)2=12+b2,可求ac,再利用三角形面积公式可求答案.该题考查余弦定理、三角形面积公式,属于基础题.解:∵角A、B、C依次成等差数列,∴2B=A+C,又∵A+B+C=180°,∴B=60°,则由余弦定理得:b2=a2+c2−2accos60°,即b2=a2+c2−ac①,又∵(a+c)2=12+b2,②由①②可得ac=4,∴S△ABC=12acsin60°=√3,故选D.。
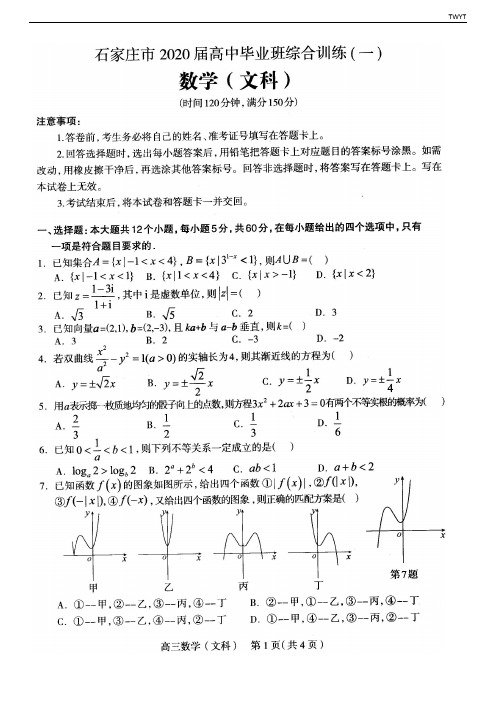

河北省石家庄市第三十五中学2020年高三数学文模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 在等差数列{a n}中,A.212B.188C.-212D. -188参考答案:D2. 已知函数,则的图象大致为()A. B.C. D.参考答案:A【分析】利用特殊值,对函数图像进行排除,由此得出正确选项. 【详解】由于,排除B选项.由于,,函数单调递减,排除C选项.由于,排除D选项.故选A.3. 右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.B.C.D.参考答案:D4.已知数列的前n项和为,,现从前m项:,,…,中抽出一项(不是,也不是),余下各项的算术平均数为37,则抽出的是()A.第6项B.第8项C.第12项 D.第15项参考答案:答案:B5. 有关命题的说法错误的是( )A.命题“若则”的逆否命题为:“若, 则”B.“”是“”的充分不必要条件C.对于命题:. 则:D.若为假命题,则、均为假命题参考答案:D6.如果复数(其中为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于A、B、 C、D、2参考答案:答案:C7. 如图,四棱锥P﹣ABCD中,△PAB与△PBC是正三角形,平面PAB⊥平面PBC,AC⊥BD,则下列结论不一定成立的是()A.PB⊥AC B.PD⊥平面ABCDC.AC⊥PD D.平面PBD⊥平面ABCD参考答案:【分析】在A中,取PB中点O,连结AO、CO,推导出PB⊥平面AOC,从而PB⊥AC;在B中,推导出PD与AC不垂直,从而PD与平面ABCD不垂直;在C中,推导出AC⊥PB,AC⊥BD,PB∩BD=B,从而AC⊥平面PBD,进而AC⊥PD;在D中,由AC⊥平面PBD,得到平面PBD⊥平面ABCD.【解答】解:在A中,取PB中点O,连结AO、CO,∵四棱锥P﹣ABCD中,△PAB与△PBC是正三角形,平面PAB⊥平面PBC,AC⊥BD,∴AO⊥PB,CO⊥PB,∵AO∩CO=O,∴PB⊥平面AOC,∵AC?平面AOC,∴PB⊥AC,故A成立;在B中,∵△PAB与△PBC是正三角形,∴PA=PC,AB=AC,设AC∩BD=M,连结PM,则PM⊥AC,∴PD与AC不垂直,∴PD与平面ABCD不垂直,故B不成立;在C中,∵PB⊥平面AOC,AC?平面AOC,∴AC⊥PB,∵AC⊥BD,PB∩BD=B,∴AC⊥平面PBD,∵PD?平面PBD,∴AC⊥PD,故C成立;在D中,∵AC⊥平面PBD,AC?平面ABCD,∴平面PBD⊥平面ABCD,故D成立.故选:B.【点评】本题考查命题真假的判断,考查线面、线线、面央间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.8. 已知某几何体的正视图和侧视图均为边长为1的正方形,则这个几何体的体积不可能是A. B. C. 1 D.参考答案:D9. 已知复数,则它的共轭复数等于( )A. B. C. D.参考答案:C略10. 函数y=的图像(A)关于原点对称(B)关于主线对称(C)关于轴对称(D)关于直线对称参考答案:A二、 填空题:本大题共7小题,每小题4分,共28分11. 若,则向量在向量方向上的投影为.参考答案:12. 若的展开式的常数项为84,则的值为 .参考答案:13. 将“杨辉三角”中的数从左到右、从上到下排 成一数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…, 右图所示程序框图用来输出此数列的前若干项并求其和,若输入m=4则相应最后的输出S 的值是__________.参考答案: 214. 已知正项等比数列中,,,若数列满足,则数列的前项和 .参考答案:因为,解得,所以,所以,所以,所以数列的前项和.15. 已知m ,n 是不重合的两条直线,α,β是不重合的两个平面.下列命题: ①若α⊥β,m⊥α,则m∥β; ②若m⊥α,m⊥β,则α∥β; ③若m∥α,m⊥n,则n⊥α; ④若m∥α,m β,则α∥β.其中所有真命题的序号是 .参考答案:16. 已知直线l 分别过函数y=a x ,(a >0且a ≠1)于函数y=log b x ,(b >0且b ≠1)的定点,第一象限的点P (x ,y )在直线l 上,则﹣﹣的最大值为 ﹣ .参考答案:故由截距式得到直线l 的方程为x+y=1,又由第一象限的点P (x,y )在直线l 上,则x+y=1,(x >0,y >0)则==(当且仅当即时,取“=”)故答案为.17. .复数z=(i 为复数的虚数单位)的模等于 .参考答案:略三、 解答题:本大题共5小题,共72分。

2020年河北省石家庄市东寺中学高三数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设,则()A、 B、 C、D、参考答案:C2. 已知函数是上的偶函数,若对于,都有,且当时,,则的值为A. B.C.D.参考答案:B3. 直线与曲线的公共点的个数为(A)1 (B)2 (C)3 (D)4参考答案:答案:D解析: 将代入得:,显然该关于的方程有两正解,即x有四解,所以交点有4个,故选择答案D。
4. .“”是“”的()A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件参考答案:A【分析】判断充分条件还是必要条件,就看由题设能否推出结论,和结论能否推出题设,本着这个原则,显然能推出,但是不一定能推出,有可能,所以可以判断“”是“”的充分不必要条件.【详解】因为由,由推不出,有可能,所以“”是“”的充分不必要条件,故本题选A.【点睛】本题考查了充分条件和必要条件的判定,解题的关键是理解掌握它们定义,对于本题正确求解不等式也很关键.5. 积分=()A. B. C. D.参考答案:B略6. 函数y= f(x)的图象上每一点的纵坐标伸长为原来的3倍,再将横坐标缩小为原来的,再将图象向右平移个单位,可得y=cosx,则原来的函数为()A y=cos()B y=cos()C y=3cos()D y=cos()参考答案:A略7. 下面程序框图运行后,如果输出的函数值在区间[-2,]内则输入的实数x的取值范围是()A. B.C. D.参考答案:D略8. 已知点F1、F2是双曲线C:﹣=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为()A.(1,+∞)B.[,+∞)C.(1,] D.(1,]参考答案:C【考点】双曲线的简单性质.【分析】由直角三角形的判定定理可得△PF1F2为直角三角形,且PF1⊥PF2,运用双曲线的定义,可得|PF1|﹣|PF2|=2a,又|PF1|≥3|PF2|,可得|PF2|≤a,再由勾股定理,即可得到c≤a,运用离心率公式,即可得到所求范围.【解答】解:由|F1F2|=2|OP|,可得|OP|=c,即有△PF1F2为直角三角形,且PF1⊥PF2,可得|PF1|2+|PF2|2=|F1F2|2,由双曲线定义可得|PF1|﹣|PF2|=2a,又|PF1|≥3|PF2|,可得|PF2|≤a,即有(|PF2|+2a)2+|PF2|2=4c2,化为(|PF2|+a)2=2c2﹣a2,即有2c2﹣a2≤4a2,可得c≤a,由e=可得1<e≤,故选:C.9. 定义在R上的偶函数满足:对任意有,则()(A)(B)(C)(D)参考答案:B10. 函数的值域为()A. B. C. D.参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.参考答案:76,40.【考点】由三视图求面积、体积.【分析】根据几何体的三视图得该几何体是一个底面为直角梯形的四棱柱,由三视图求出几何元素的长度,由梯形的面积公式、柱体的体积公式求出该几何体的体积,由四棱柱的各个面的长度求出几何体的表面积.【解答】解:根据几何体的三视图得:该几何体是一个底面为直角梯形的四棱柱,其底面是正视图中的直角梯形,上底为1cm,下底为4cm,高为4cm,由侧视图知四棱柱的高为4cm,所以该几何体的体积V==40(cm3),由正视图可知直角梯形斜腰是5,则该几何体的表面积S表面积=2×+(1+4+4+5)×4=76(cm2),故答案为:76,40.12. 若方程表示焦点在x轴上的椭圆,则实数a的取值范围是_____.参考答案:或.【分析】方程表示焦点在轴上的椭圆,可以得到不等式,解这个不等式,求出实数的取值范围.【详解】解:∵方程表示焦点在轴上的椭圆,∴,∴或.故答案为:或.【点睛】本题考查了焦点在横轴上椭圆方程的识别,考查了解不等式的能力.13. 在区间和上分别取一个数,记为和,则方程,表示焦点在y 轴上的椭圆的概率是 .参考答案:本题为几何概型概率,测度为面积,分母为矩形,面积为8,分子为直线在矩形中上方部分(直角梯形),因为面积直线正好平分矩形,所以所求概率为14. 复数z=1+4i(i为虚数单位),则|2z+|= .参考答案:5【考点】复数求模.【分析】由z=1+4i,得,然后代入化简,再由复数求模公式计算得答案.【解答】解:由z=1+4i,得.则,∴|2z+|=.故答案为:5.15. 已知直线与曲线(为参数)无公共点,则过点的直线与曲线的公共点的个数为 .参考答案:216. 复数;参考答案:17. 不等式的解集为 .参考答案:;试题分析:考点:分式不等式的解法.三、解答题:本大题共5小题,共72分。

2020年河北省石家庄市龙州中学高三数学文模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,且g(3)=0.则不等式的解集是A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)参考答案:2. 已知两个函数、的定义域和值域都是集合{1, 2, 3},且满足下表:则方程的解集为A. {1}B. {2}C. {3}D.参考答案:C3. 已知集合,,则()A. B. C. D.参考答案:B 4. 若是等差数列{}的前n项和,且则的值为__________.A.12 B.18 C.22 D.44参考答案:C略5. 椭圆与双曲线有相同的焦点,则实数的值是()A.B.1或C.1或D.1参考答案:D略6. 已知,i为虚数单位,若,则A.B.C.3 D.参考答案:D7. 集合A={-1,0,1},B={y|y=cosx,x∈A},则A B= ()A.{0} B.{1} C.{0,1} D.{-1,0,1}参考答案:B略8. 根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为, (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是()A.75,25 B.75,16x123f(x)231x123g(x)321C.60,25 D.60,16参考答案:D9. 已知定义域为的函数满足:(1)对任意,恒有成立;(2)当时,.给出以下结论:①对任意,有;②对任意,不等式恒成立;③存在,使得;④“函数在区间上单调递减”的充要条件是存在,使得.其中所有正确结论的序号为A.①②③B.②③④C.①②④D.①②③④参考答案:C略10. 在等差数列中,已知,则= ()A.10 B.18 C.20 D.28参考答案:C略二、填空题:本大题共7小题,每小题4分,共28分11. 在△ABC中,内角A,B,C的对边分别为a,b,c;若a2﹣c2=bc,sinB=2sinC,则角A=.参考答案:考点:正弦定理;余弦定理.专题:计算题;解三角形.分析:先利用正弦定理化简sinB=2sinC得b=2c,再由a2﹣c2=bc可得 a2=7c2 ,然后利用余弦定理表示出cosA,把表示出的关系式分别代入即可求出cosA的值,根据A的范围,利用特殊角的三角函数值即可求出A的值.解答:解:由sinB=2sinC及正弦定理可得b=2c,再由a2﹣c2=bc可得 a2=7c2 ,再由余弦定理可得 cosA===,∵0<A<π∴A=.故答案为:.点评:本题主要考查了正弦、余弦定理,及特殊角的三角函数值化简求值,属于中档题.12. 函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[a,b]?D,使f(x)在[a,b]上的值域为[﹣b,﹣a],那么y=f(x)叫做对称函数,现有f(x)=﹣k是对称函数,那么k的取值范围是.参考答案:【考点】函数单调性的判断与证明;函数的定义域及其求法;函数的值域.【专题】压轴题;新定义. 【分析】函数在定义域(﹣∞,2]上是减函数,由②可得 f (a )=﹣a ,f (b )=﹣b ,由此推出 a 和 b 是方程在(﹣∞,2]上的两个不同的实根.利用换元法,转化为∴k=﹣t 2+t+2=﹣(t ﹣)2+在[0,+∞)有两个不同实根,解此不等式求得 k 的范围即为所求. 【解答】解:由于在(﹣∞,2]上是减函数,故满足①,又f (x )在[a ,b]上的值域为[﹣b ,﹣a],∴所以a 和 b 是关于x 的方程在(﹣∞,2]上有两个不同实根.令t=,则x=2﹣t 2,t≥0,∴k=﹣t 2+t+2=﹣(t ﹣)2+, ∴k 的取值范围是,故答案为:.【点评】本题考查函数的单调性的应用,求函数的值域,体现了转化的数学思想,得到a 和 b 是方程在(﹣∞,2]上的两个根,是解题的难点,属中档题. 13. 已知,且,则的最大值等于_____________。
2020年河北省石家庄市北苏镇中学高三数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 曲线在点处的切线与坐标轴围成的三角形的面积为A.1 B.2 C.D.参考答案:C2. 已知函数的两个极值分别为和,若和分别在区间(0,1)与(1,2)内,则的取值范围为()(A)(B)(C)(D)参考答案:A因为,由题意可知:画出,满足的可行域,如图1中的阴影部分(不包括边界)所示,表示可行域内的点与点D(1,2)的连线的斜率,记为,观察图形可知,,而,,所以。
3. 定义域为的函数,满足,,则不等式的解集为(▲)A. B. C. D.参考答案:D略4. 设函数f(x)=在区间[0,e]上随机取一个实数x,则f(x)的值不小于常数e的概率是()A.B.1﹣C.D.参考答案:B【考点】几何概型.【分析】1≤x≤e,e≤f(x)≤1+e,以长度为测度,即可求出概率.【解答】解:由题意,0≤x<1,f(x)<e,1≤x≤e,e≤f(x)≤1+e,∵f(x)的值不小于常数e,∴1≤x≤e,∴所求概率为=1﹣,故选B.5. 已知函数,则下列结论不正确的是()A.最大值为2B.最小正周期为πC.把函数的图象向右平移个单位长度就得到f(x)的图像D.单调递增区间是,参考答案:C6. (6)下图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为(A)0.2 (B)0.4(C)0.5 (D)0.6参考答案:B.7. (2015春?黑龙江期末)已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)的部分图象如图,则函数f(x)的解析式为()A.f(x)=4sin(x﹣)B.f(x)=﹣4sin(x+)C.f(x)=﹣4sin(x﹣)D.f(x)=4sin(x+)参考答案:B考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:数形结合.分析:由图象先确定A,再由周期确定ω,再代值求φ,可得解析式.解答:解:由图象可得A=﹣4,==6﹣(﹣2),解得ω=,故函数的解析式可写作f(x)=﹣4sin(x+φ),代入点(6,0)可得0=﹣4sin(+φ),故+φ=kπ,k∈Z,即φ=kπ﹣,又|φ|<,故当k=1时,φ=,故选B点评:本题考查三角函数解析式的确定,先确定A,再由周期确定ω,再代值求φ,属中档题.8. 已知在各项为正数的等比数列中,与的等比中项为4,则当取最小值时,等于()A.32 B.16 C.8 D.4参考答案:B设各项为正数的等比数列的公比为∵与的等比中项为4∴∴∴当且仅当,即时取等号,此时故选A9. 已知全集U=R,A={x|x2﹣2x<0},B={x|x≥1},则A∪(?U B)=()A.(0,+∞)B.(﹣∞,1)C.(﹣∞,2)D.(0,1)参考答案:C【考点】1H:交、并、补集的混合运算.【分析】求出A中不等式的解集确定出A,根据全集R及B,求出B的补集,找出A与B 补集的并集即可.【解答】解:由A中的不等式解得:0<x<2,∴A=(0,2),∵全集U=R,B={x|x≥1},∴?U B=(﹣∞,1),则A∪(?U B)=(﹣∞.2),故选:C.10. 已知双曲线:的两条渐近线是,,点是双曲线上一点,若点到渐近线距离是3,则点到渐近线距离是()A.B.1 C.D.3参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数在处取得极值,若,则的最小值是________.参考答案:-13试题分析:令导函数当x=2时为0,列出方程求出a值;求出二次函数的最小值,利用导数求出f(m)的最小值,它们的和即为的最小值.求导数可得,∵函数在x=2处取得极值,∴-12+4a=0,解得a=3,∴,∴n∈ 时,,当n=-1时,最小,最小为-9,当m∈时,令得m=0,m=2,所以m=0时,f(m)最小为-4,故的最小值为-9+(-4)=-13.故答案为:-13.考点:导数在最大值、最小值问题中的应用;函数在某点取得极值的条件.【方法点睛】利用导数性质研究函数的最值问题属于平时练习和考试的常见题目,解决问题的方法主要是分类讨论,结合导函数的有关性质进行求解,涉及题型比较丰富,有一定难度.12. 已知△ABC的内角A,B,C的对边分别为a,b,c,若,则△ABC的面积为.参考答案:;13. d.参考答案:。