三角数阵 数列专题

我是这样解的
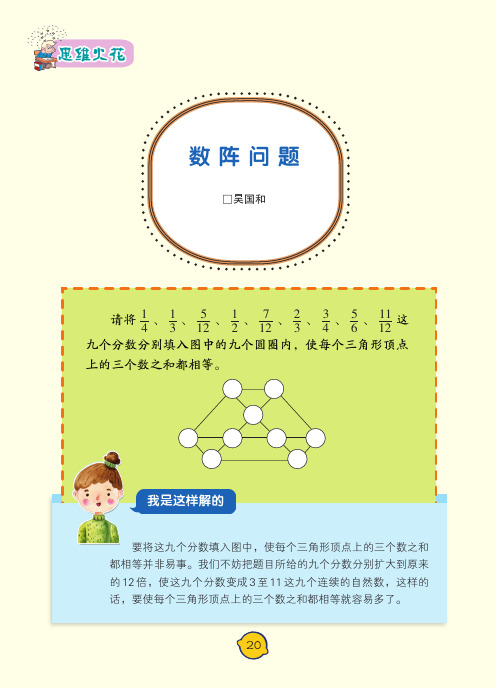
请将14、13、512、12、712、23、34、56、1112这九个分数分别填入图中的九个圆圈内，使每个三角形顶点上的三个数之和都相等。

数阵问题
□吴国和
要将这九个分数填入图中，使每个三角形顶点上的三个数之和都相等并非易事。

我们不妨把题目所给的九个分数分别扩大到原来的12倍，使这九个分数变成3至11这九个连续的自然数，这样的话，要使每个三角形顶点上的三个数之和都相等就容易多了。

从图中可知，外围三个小三角形顶点上九个数之和，正好就是3至11这九个连续自然数的和——63，所以每个三角形顶点上的三个数之和是63÷3＝21。

在3至11这九个连续自然数中，三个数之和为21的可能情形共有八种：3＋7＋11，3＋8＋10，4＋6＋11，4＋7＋10，4＋8＋9，5＋6＋10，5＋7＋9，6＋7＋8。

而处于图形中间小三角形上的每个数，都应在三个三角形中出现，也就是说，填在中间的三个数，必须在上面八组和中至少出现3次。

由上面排出的八种情况不难分析出，填在中间的三个数，只能从4、6、7、8、10这五个数中选取。

又因为这五个数中满足三数之和等于21，所以这三个数要么是4、7、10，要么是6、7、
8。

由此可以得到两个答案，然后把每个自然数缩小到原来的112，还原成原分数。

先放大，后缩小，是解决问题的关键。

121112137125614
51234231311121271223145123456（作者单位：江苏省海门市德胜小学）
4
31075
98116
114
6
3875
910。

数阵图练习题数阵图（Number Grid）是一种用数字组成的图形，在数学教学中常用来培养学生的逻辑思维和解题能力。

下面是一些数阵图练习题，帮助你巩固自己的数学知识和解题技巧。

1. 数阵图中的数列在数阵图中，每个数字都和相邻的数字有一定的关系。

观察下面的数阵图，并找出横向和纵向的数列规律。

```1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 2021 22 23 24 25```横向数列：1, 2, 3, 4, 5纵向数列：1, 6, 11, 16, 21根据观察，我们可以得出结论：横向数列的公差为1，纵向数列的公差为5。

2. 数阵图中的数学运算在数阵图中，数字之间的运算规律也是一种常见的题型。

观察下面的数阵图，并计算出横向和纵向数学运算的结果。

```1 4 9 16 252 6 12 20 303 8 15 24 354 10 18 28 405 12 21 32 45```横向数学运算：1^2, 2^2, 3^2, 4^2, 5^2 （平方）纵向数学运算：1^2, 2^2, 3^2, 4^2, 5^2 （平方）根据观察，我们可以得出结论：横向数学运算是计算每个数字的平方，纵向数学运算也是计算每个数字的平方。

3. 数阵图中的缺失数字在数阵图中，有时候会有一些数字缺失。

观察下面的数阵图，并找出其中的缺失数字。

```3 6 9 12 1518 ? 24 27 3033 36 39 42 4548 51 ? 57 6063 66 69 ? 75```根据观察，我们可以得出结论：缺失数字分别为21、54、72。

4. 数阵图中的数学规律在数阵图中，数字之间可能会存在一些数学规律。

观察下面的数阵图，并找出其中的数学规律。

```1 123 58 13 21 34 5589 144 233 377 610987 1597? 4181 6765 10946```根据观察，我们可以得出结论：这是一个斐波那契数列的数阵图。

1312*第06课时 数列之数阵问题【考点点悟】传道解惑，高屋建瓴数列之数阵是将一些数据按照一定的规律以图表或图阵的方式呈现出来的特殊数列. 数阵问题是能够检查学生数学直觉思维能力，它多是要求学生能够从已给的一些数据中，来观察数的变化规律,其特点是直观新颖，能较好地考察学生的观察与分析能力，以及归纳与想象能力等．是近几年高考中倍受青睐的一种新题型．探求数表型数列问题，关键是要能充分挖掘所给数表所提供的信息特征，把握数表所隐含的规律性，综合运用观察、分析、归纳和猜想的思想方法，发现和破译问题的知求关系，使问题顺利获解.【小题热身】明确考点，自省反思 1.能够在如右表所示的33⨯正方形的9个空格中填入正整数，使得每一行都成等差数列，每 一列都成等比数列，问必须填进标有*号的空格 的数是 .2.将全体正整数排成一个三角形数阵：12345678910按照以上排列的规律，第n 行(3)n ≥从左向右的第3个数为 ． 3.1934年，东印度（今孟加拉国）学者森德拉姆发现了“正方形筛子”（如图所示），该“正方形筛子”中位于第100行的第100个数是4.用n 个不同的实数1a ，2a ，…，n a 可得到个!n 个不同的排列，每个排列为一行写成一个!n 行的数阵．对第i 行1i a ，2i a ，…，in a ，记12323(1)ni i i i i n b a a a na =-+-++- ，1,2,3,,!i n = ．例如：用1，2，3可得数阵如图所示，由于此数阵中每一列各数之和都是12，所以，1261221231224b b b ++=-+⨯-⨯=- ，那么，在用1，2，3，4，5形成的数阵中，12120b b b ++= ___________．【考题点评】分析原因，醍醐灌顶例 1. 在如表所示的55⨯正方形的25个空格中填入正整数，使得每一行，每一列都成思路透析:（设出通项ij a 为从下到下第i 行，从左到右第j 列的空格中所填的数，根据其特征规律及等差数列的性质，将未知数据的关系式列出，求得方程组的解．设ij a 为从上到下第i 行，从左到右第j 列的空格中所填的数，则52a x =，41a y =．由第3行得3321862y a +=，由第3列得3321032a x =⨯-，所以2113x y +=．① 由第2行得232743a y =⨯-，由第3列得2333210331034a a x =-=⨯-， 所以148331034y x -=⨯-，整理得43161x y -=．②联立①②解得50x =，13y =．所以1555218621864172a a x =⨯-=⨯-=，1333532112a a a =-=，故1315141422a a a +==，故标有*号的空格应填142． 点评：高中新课标非常重视学生的探究能力，用数据阵形式给出的行列均成等差数列的“数据”表，其表格中的数据编制时关系不是非常明显，这也正是高考考查探究能力的重要形式．以数据表格、杨辉三角或数矩阵为载体的探究性试题已经成为高考的命题趋势．例2. 在一个有限的实数列中，任意七个连续项之和都是负数，而任意十一个连续项之和都是正数．试问：此数列最多能包含多少项？思路透析:（根据题目所给已知条件，可构造一个每横行七个数，每纵列十一个数的数阵如下：1714131211965438543274321 a a a a a a a a a a a a a a a a a a a a 考虑到每一横行为连续七项，其和小于0，每一纵列为连续十一项，其和大于0．于是得到矛盾，所以17<n ．另一方面有可以构造一个连续十六项的数列满足题目要求：6，6，-15，6，6，6，-16，6，6，-16，6，6，6，-15，6，6，故符合条件的数列最多有十六项．点评：对于这一类问题的设计，可使学生心态开放、主体性凸现，个性张扬，创造性得到释放．例3. 定义如下运算：11121311112131111213121222322122232212223231323333132333313233312312312n k k n k k n k k m m m mn n n n nk m m m x x x x y y y y z z z z x x x x y y y y z z z z x x x x y y y y z z z z x x x x y y y y z z z ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 3mk z ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ 其中112233.(1,1,,ij i j i j i j in nj z x y x y x y x y i m j n i j =++++∈ ≤≤≤≤N *）． 现有2n 个正数的数表A 排成行列如下：（这里用ij a 表示位于第i 行第j 列的一个正数，,i j ∈N *）111213121222323132333123n nn n n n nna a a a a a a a a a a a a a a a ，其中每横行的数成等差数列，每竖列的数成等比数列，且各个等比数列的公比相同，若241a =，4218a =，43316a =． （1）求ij a 的表达式（用i ，j 表示）；（2）若11121311112221222322122331323333132123121323333n n n n n n n nn n n a a a a b b a a a a b b a a a a b b a a a a b b n ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ，求1i b ，2i b （1i n ≤≤，用i ，n 表示）． 思路透析: （1）每一行的数成等差数列，∴42a ，43a ，44a 成等差数列．∴4342442a a a =+，∴4414a =，又每一列的数成等比数列， 故24424a a q = ，∵241a =，∴214q =，且0n a >，∴12q =．∴44243421(2)(2)()816j j a a j d j a a =+-=+--=，∴441()22i ij j i ja a -==．（2）11231232222i i i i i nb n =⨯+⨯+⨯++⨯222211(21)(1)(123)232i i n n n n +++=++++=⨯ ，23212333332222n i i i i i n b =⨯+⨯+⨯++⨯ ，① ∴2312121333332222n n i i i i i n n b +-=⨯+⨯++⨯+⨯ ，②②－①得2312112(333)33222n n i i i i n b +=-++++⨯-⨯21113313321322n n i i i n ++-=-⨯+⨯-⨯-111[(21)33]2n i n ++=-+∴1211[(21)33]2n i i b n ++=-+． 点评:新背景等比数列题型往往利用新定义或新概念将等比数列的知识点交汇于其中，该类题型是新高考命题的新动向．本题是等比数列与“行列式”相交汇的新背景题型，由于新型的定义式的出现，导致该题型又多了几分神秘的色彩，为我们接受新型问题开阔了眼界．例4. 64个正数排成8行8列，如下所示181211a a a 282221a a a…… ……888281a a a在符号ij a (1≤i ≤8，1≤j ≤8)中，i 表示该数所在的行数，j 表示该数所在的列数．已知每一行中的数依次都成等差数列，而每一列中的数依次都成等比数列（每列公比q 都相等），且.41,1,21322411===a a a （1）若131221,41a a a 和求=的值；（2）求ij a 的通项公式（注：用j i ,表示）；（3）记第n 行各项之和为n A (1≤n ≤8)数列{}n a ，{}n b ，{}n c 满足)(2,361n n n n n mb a mb A a +==+（m 为非零常数），n n nb c a =．求证{}n c 为等差数列． 思路透析: （1）41,212111==a a ，每一列成公比相等的等比数列， ∴其公比22132121111.,24a q a a q a ==== 又∴12 1.a =又每一行成等差数列，∴在第一行中有131112,2a a a +=∴133.2a = （2）设第一行的公差为d ，.41)(,1)3(21121232111424=+===+==q d a q a a q d a q a a 两式联立解得.21,21==q d 从而111111[(1)]().2i i i ij j a a q a j d q j --=⋅=+-=⋅∴1().2iij a j =⋅（3）181312111a a a a A ++++= 1187187188182222a d ⨯⨯=+⨯=⨯+⨯= ∴111128111218n n n n n n n A a a a a q a q a q ---=++=+++11111218136()()1822n n n q a a a --=+++=⨯=∴362.n n na A == 由12()n n n mb a mb +=+得，11222n n n n mb mb a ++-==． 两边同除以12n +得， .1)22(11=-++n n n n b b m 即为.1)22(11=-++nn n n b b m ∴11n n c c m +-=（常数）∴数列{}n c 成等差数列．点评:此题以数阵为载体，一改数列知识的单调、呆板的引入形式，使高考数学题充满活力和魅力！例5. 下表给出一个“三角形数阵”：14 12，14 34，38，316， …已知每一列的数成等差数列；从第三行起，每一行的数成等比数列，每一行的公比都相等．记第i 行第j 列的数为(,,ij a i j i j ∈≥N *）．（1）求83a ；（2）试写出ij a 关于i ，j 的表达式；（3）记第n 行的和为n A ，求数列{}n A 的前m 项和m B 的表达式． 思路透析: （1）由题知，1{}i a 为等差数列，因为，1114a =，2112a =，所以公差14d =，8111(81)244a =+-⨯=． 又各行成等比数列，公比都相等，3134a =，3238a =，所以每行的公比是12q =，所以283112()22a =⨯=．（2）由（1）知，111(1)444i i a i =+-= ，所以1111111()()()2422j j j ij i i a a i --+===． （3）211111[1()()]222n n n A a -=++++ 1111[2()]()4222n n n n n -+=-=-．11123(12)()222482m m m B m =+++-++++设1232482m m mT =++++ ． ①则11123248162m m mT +=++++ ． ② 由①－②，得1111111121122422222m m m m m m m m m T ++++=+++-=--=- ．所以，111(1)2(1)2(1)122242m m m m m m m m m B ++++++=--=+-． 点评：解决数阵问题的关键是抓住题目中所给出的各行与各列所构成数列的类型，再根据所给出的特殊项推出各行、各列的前几项，进而求出通项．例 6. 设｛a n ｝是集合{}Z t s t s st ∈<≤+，且,022中所有的数从小到大排列成的数列，即a 1＝3，a 2＝5，a 3＝6，a 4＝9，a 5＝10，a 6＝12，……将数列｛a n ｝各项按照上小下大，左小右大的原则写成如图11所示的三角形数表： （Ⅰ）写出这个三角形数表的第四行、第五行各数; （Ⅱ）求a 100．思路透析: 容易看出，按照如图所示的排法，第4行有4个数字，第5行有5个数字……。

数阵问题专项练习30题(有答案)ok数阵问题专项练习30题（有答案）1．如图：5个小三角形的顶点处有6个圆圈，如果在这些圆圈中分别填上6个质数，它们的和是20，而且每个小三角形三个顶点上的数之和相等，问这6个质数的积是多少？2．把1～9个数分别填入○中，使每条边上四个数的和相等．3．把1～8这8个数填入图中，使每边上的加、减、乘、除成立．4．把1～9，填入图中，使每条线段三个数和及四个顶点的和也相等．5．将1～8个数分别填入图中，使每个圆圈上五个数和分别为20，21，22．6．把1～12这十二个数，填入下图中的12个○内，使每条线段上四个数的和相等，两个同心圆上的数的和也相等．7．把1～11这11个数分别填入如下图11个○内，使每条虚线上三个○内数的和相等，一共有几种不同的和？8．将1﹣12这十二个数分别填入图中的十二个小圆圈里，使每条直线上的四个小圆圈中的数字之和26．9．把1～10填入图中，使五条边上三个○内的数的和相等．10．下图中有大、小六个正方形，将1～9九个数分别填入圈内，使每个正方形角上的四个数的和都相等．11．将1～11填入下图的各个圆圈内，使每条线段上三个圆圈内的数的和都等于18．12．将98～106九个数分别填入下图中的空圈内，使每条线上四个数的和都等于402．13．将1、2、3、4、5、6、7、8、9分别填入图中的9个圆圈内，使图中每条直线上所填数之和都等于K，问：K 的值是多少？（图中有7条直线）14．将1～10这十个数分别填入下图中的十个○内，使每条线段上四个○内数的和相等，每个三角形三个顶点上○内数的和也相等．15．利用猴子跳楼法，写出1﹣49的数字并且每一行一列对角线上的数字之和相等．16．将，，，，这九个数分别填入图中，使每一横行，每一竖行，两条对角线中三个数的和都相等．17．现将12枚棋子，放在图中的20个方格中，每格最多放1枚棋子．要求每行每列所放的棋子数的和都是偶数，应该怎样放，在图上表示出来．18．把2、3、4、5、6、7、8、9、10填下入面的空格里（三行三列的格子），使横行、竖行、斜行上三个数的和都是18．19．有大、中、小三个正方形，组成了8个三角形，现在先把1，2，3，4分别填在大正方形的4个顶点上，再把1，2，3，4分别填在中正方形的4个顶点上，最后把1，2，3，4分别填在小正方形的4个顶点上．请问：能否使8个三角形顶点上数字之和相等？如果能，请给出填数方法；如果不能，请说明理由．20．将1至6六个数填入下图所示球体的圈内，使球体的各个大圆上每四个数的和都相等．21．在右面□里填上1﹣8这8个数字，这8个数字使连线的两个□里的数字不相邻．22．将1至8八个数分别填入圈内，使每个大圆上五个数的和分别为20、21或22，一共各有几组填法？23．将1、4、7、10、13、16、19、22八个数分别填入圈内；如果正方形每条边上的三个数的和都相等，那么四个角上四个数的和最小是多少？24．将1～12填入下图的空格中，使每个圆内的四个数的和都等于25．25．把1﹣﹣7这七个自然数分别填入下圆圈里，使每条线上的三个数的和相等．26．将1～8八个数分别填入下图的圈内，使三个大圆上的四个数的和都相等．这个和最大可以是多少？最小必须是多少？27．10个连续的自然数中第三个的数是9，把这10个数填入图中的10个方格内，每格填一个数，要求图中3个2×2的正方形中4个数之和相等，那么这个和最小值是_________ ．28．把1～16这16个数，填入图中的16个○内，使五个正方形的四个顶点上○内数的和相等．29．如图中有大、中、小三个正方形，组成了八个三角形．现在把1，2，3，4分别填在大正方形的四个顶点上，再把1，2，3，4分别填在中正方形的四个顶点上，最后把1，2，3，4分别填在小正方形的四个顶点上．（1）能不能使八个三角形顶点上数字之和都相等？（如果能，请画草图填出；如不能，请说明理由）（2）能不能使八个三角形顶点上数字之和各不相同？（如果能，请画草图填出；如不能，请说明理由）30．10棵树栽5行，每行栽4棵，你能设计出怎样栽吗？（用△代表树画一画．）参考答案：1．分析：根据题意，每个小三角形三个顶点上的数之和相等，这6个质数都是一样的，但是没有6个相同的质数和是20；把中间的单独看作一个与其它5个质数不一样的质数；因为3×5+5=20；也就是20=3+3+3+3+3+5；然后再进一步解答即可．解答：解：根据题意可得：20=3+3+3+3+3+5；所以，可得：这6个质数的积是：3×3×3×3×3×5=1215．2．分析：首先设三个顶点处的三个数分别为a、b、c，在运算中都加了2次，所以1+2++3+4+5+6+7+8+9+a+b+c=45+a+b+c一定是3的倍数，进一步得出a+b+c也是3的倍数，三个数的和可以是6，9，12，15，18，由此进一步分析得出答案：①当a+b+c=6时，每一条边上的和为（45+6）÷3=17，答案如图①．②当a+b+c=9时，每一条边上的和为（45+9）÷3=18，经计算找不出结论．③当a+b+c=12时，每一条边上的和为（45+12）÷3=19，答案如图②．④当a+b+c=15时，每一条边上的和为（45+15）÷3=20，经计算找不出结论．⑤当a+b+c=18时，每一条边上的和为（45+18）÷3=21，答案如图③．解答：解：由以上分析可得，符合的有三种情况，答案如下：3．分析：由于将1、2、3、4、5、6、7、8分别填入图中8个空格内，由于左边的运算既有除法，也有乘法，又因为8和6的约数不止一个，所以可以确定左上角和右下角的数字一个应该是8和6，然后根据图中的运算即可确定其他数字．①从左上角为6开始，6﹣5=1，1+7=8，8=2×4，6÷3=2；②从左上角为8开始，8﹣7=1，1+5=6，6=3×2，8÷4=2．这样，就完成了填图．解答：解：根据分析答案如下图：4．分析：根据题意，先求出每条线段三个数和及四个顶点的和，再根据题意解答．解答：解：根据题意，1～9的和是：1+2+3+…+8+9=45，有两种配对方式，第一种是：（1、9），（2、8），（3、7），（4、6），5；（1、8），（2、7），（3、6），（4、5），9；根据配对，假设中间的数字是5，那么四个顶点的和是：（45﹣5）÷2=20，每条线段三个数和也为20，20﹣5=15，只有7+8=15，9+6=15，只有两组，与题意不符；假设中间的数字是9，那么四个顶点的和是：（45﹣9）÷2=18，每条线段三个数和也为18；根据配对，尝试可以得出答案：5．分析：1+2+3+4+5+6+7+8=36．①20+20﹣36=4，也就是公共部分两个数的和应该是4，所以中间的两个数应填1和3，左右两边三个数的和相等且为20﹣4=16，左面可填2、6、8，右面可填4、5、7；②21+21﹣36=6，也就是公共部分两个数的和应该，6，所以中间的两个数应填2和4或1和5，左右两边三个数的和相等且为21﹣6=15，中间的两个数填2和4时，左面可填1、6、8，右面可填3、5、7，中间的两个数填1和5时，左面可填3、4、8，右面可填2、6、7；③22+22﹣36=8，也就是公共部分两个数的和应该，8，所以中间的两个数应填1和7、2和6或3和5（有三种填法），左右两边三个数的和相等且为22﹣8=14，以中间的两个数填1和7为例，左面可填2、4、8，右面可填3、5、6．解答：解：根据分析，数字填法如下图：6．分析：1+2+3+…+12=78，使每条线段上四个数的和相等为78÷3=26，两个同心圆上的数的和也相等为78÷2=39，1+12+5+8=26，9+4+10+3=26，2+6+7+11=26，1+7+3+8+11+9=39，2+4+5+6+10+12=39，符合题意．解答：解：由分析答案如下：7．分析：假设中间○内填入的数是a，每条虚线上三个○内数的和是k，则有1+2+3+4+5+6+7+8+9+10+11+4a=5k，66+4a=5k：当a=1时，k=（66+4）÷5=14；当a=2、3、4、5、时，k不是整数，无解；当a=6时，k=（66+24）÷5=18；当a=7、8、9、10时，k不是整数，无解；当a=11时，k=（66+44）÷5=22；即可得解．一共有3种不同的和．解答：解：把1～11这11个数分别填入如下图11个○内，使每条虚线上三个○内数的和相等，一共有3种不同的和.14、18、22，如下图所示：8．数阵问题专项练习30题(有答案)ok分析：此图可看作由两个三角形组成，先看尖向上的三角形，把1、2和10写在顶点上．其中一条边，1+10=11，那么另外两个空的和为26﹣11=15，因为10用过了，所以只能填7和8；另一条边10+2=12，另外两个空的和为26﹣12=14，所以只能是9和5；再看底边，1+2=3，所以另外两个空只能是11+12=23．这样就还剩下尖向下的三角形三个顶点上的数字，先看底边，7+9=16，那么另外两个空为4和6，最后一个顶点就为3．解答：解：答案如图，9．分析：把1～10填入图中，使五条边上三个○内的数的和相等．五条边上三个○内的数的总和是1+2+3+4+5+6+7+8+9+10+（a+b+c+d+e）=55+（a+b+c+d+e），a、b、c、d、e是在五条边交点上，重复加两遍的数字，很明显，每条边上的数字和是11+＞11，所以，重复的数字应为大数，探究一下，把1、2、3、4、5放在中间，10放在1 所在边上，（6+7+8+9+10）÷5=40÷5=8，8也在1、10边上，相应其他边为（10、2、7），（7、3、9），（9、4、6，），（6、5、8）每条边上的和为19，如下图：解答：解：如图：10．分析：根据题意，可得1～9九个数的和是：1+2+3+…+8+9=45，根据图，最大的正方形与斜着的正方形再加上中间的圈的数的和是45，根据配对，可知5不能配对，（45﹣5）÷2=20，每个正方形角上的四个数的和是20，再根据题意解答即可．解答：解：根据题意，1～9九个数的和是：1+2+3+…+8+9=45，前后数配对可得，（1、9），（2、8），（3、7），（4、6），5由分析可得，每个正方形角上的四个数的和是：（45﹣5）÷2=20；根据配对，中间一个数字是5，经过尝试，可得如下答案：数阵问题专项练习30题(有答案)ok11．分析：根据题意，设中间的圆圈中的数是A，那么每条线段上三个圆圈内的数相加的和都等于18，也就是1+2+3+4+5+6+7+8+9+10+11+A+A+A+A=18×5，然后再进一步解答即可．解答：解：设中间的圆圈中的数是A；根据题意可得：1+2+3+4+5+6+7+8+9+10+11+A+A+A+A=18×5，66+4A=90，4A=24，A=6；那么每条线段剩下的两个数的和是：18﹣6=12；又因为，1+11=12，2+10=12，3+9=12，4+8=12，5+7=12；分别放到每条线段剩下的两个圆圈中；由以上可得：．12．分析：402﹣95﹣97=210，只有104+106=210，可以先确定这两个空，402﹣96﹣104=202，103+99=202；402﹣96﹣106=200，102+98=200；402﹣97﹣99=206，105+101=206；402﹣95﹣102﹣105=100；正好把98、99、100、101、102、103、104、105、106全部填入．解答：解：答案如图，13．分析：根据题干，可以看出有些圆圈处于三条直线上，而另一些圆圈处于两条直线上，还有一个圆圈处于一条直线上，要想利用“重数”的分析法，有很大的困难，通过分析不难看出有一个圆圈的位置特殊，即A圆圈，除去这个圆圈，剩下的8个圆圈正好组成3行，从它出发就能找到答案．数阵问题专项练习30题(有答案)ok解答：解：如下：除去A圆圈的数字，剩下的8个圆圈恰好组成三行，那么每条直线上所填数字之和为：1+2+3+4+5+6+7+8+9﹣A=3K，所以A一定是3的倍数，也就是说A一定是3或6或9，那么K的值可能是14或13或12，如果A=9，那么右下角圈内只能填1或2，此时右下角的数字至少为10，显然不符合题意．如果A=6，那么每条直线上圈内数之和K=13，而在下图中可以得出B=C+6（比较法），因此D+6+B=C+D+12=13，显然这是错误的．所以只要当A=3时可以得出正确答案如下图：所以K=14．答：K的值是14．14．分析：假设中间的数是a，每条线段上四个○内数的和相等为k，则有：1+2+3+…+10+2a=3k，55+2a=3k，当a=1时，k=57÷3=19，1+2+6+10=19，1+7+8+3=19，1+9+4+5=19，每个三角形三个顶点上○内数的和也相等，2+7+9=18，4+6+8=18，5+3+10=18．符合题意．解答：解：15．分析：把1﹣49这49个数字放入一个7×7的矩阵中，使每行、每列及对角线上的七个数字之和相等，即构造一个7阶幻方．对所有奇数阶幻方的构造，都可以采取“连续摆数法”（猴子跳楼），其法则如下：把“1”放在中间一列最上边的方格中，从它开始，按对角线方向（比如说按从左下到右上的方向）顺次把由小到大的各数放入各方格中，如果碰到顶，则折向底，如果到达右侧，则转向左侧，如果进行中轮到的方格中已有数或到达右上角，则退至前一格的下方．数阵问题专项练习30题(有答案)ok解答：解：这个幻方如下：16．分析：将，，，，，，九个数分别化为分母是12的分数，得到分子分别为6、4、3、2、8、9、1、5、7，而用这连续9个数组成的幻方是熟知的，如下图：再将图中的每个数除以12就是所求．解答：解：答案如下图：17．分析：每行每列的棋子总数是偶数，那么每行和每列的棋子数可能是2个或者4，一共有4行，那么每行的数量分别是：2、2、4、4；一共有5列，所以一列的数量分别是：2，2，2，2；先确定第一列的两个棋子的位置，然后根据每行和每列的棋子数填入方格中．解答：解：○代表棋子，可以这样填：答案不唯一．18．数阵问题专项练习30题(有答案)ok分析：我们可以利用两种方法解答：（1）幻和法：先根据幻和求出中心数：18÷3=6；剩余的每两个数的和是18﹣6=12；由12=2+10=3+9=4+8=5+6；调整每一对数的位置填入表格即可．（2）罗伯法：①居上行正中央，依次斜填切莫忘，上出框界往下写，右出框时左边放，重复便在下格填，出角重复一个样．②在第一行居中的方格内放2，依次向右上方填入3、4、5…；③如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；④如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；⑤如果右上方已有数字和出了对角线，则向下移一格继续填写． 3阶幻方不止这一种填法，只要将2（开始的数）放于四个边格的正中，向幻方外侧依次斜填其余数字；若出边，将数字另放一侧；若目标格已有数字或出角，回一步填写数字，再继续按一开始的相同方向依次斜填其余数字（详见下图按线放法）．解答：解：根据分析填图如下：19．分析：不能，我们把8个三角形顶点的数字加起来，假设相等是m，则8m=大正方形的数字和+3遍中正方形的数字和+2遍小正方形的顶点数字和，各个正方形的数字和都是1+2+3+4=10，代入，8m=60，60不能被8整除，因此得解．解答：解：假设三角形的顶点数字和相等是m，则有：8m=（1+2+3+4）×（1+3+2），8m=60，60不能被8整除，所以m不存在，假设错误．即不能使8个三角形顶点上数字之和相等．答：不能使8个三角形顶点上数字之和相等．20．分析：根据图，先求出各个大圆上每四个数的和，再根据题意进一步解答即可．解答：解：由图可知，这个球体由三个大圆，把这三个大圆的每四个数加起来，正好是1至6六个数加了两次，那么每个大圆四个数的和是：2×（1+2+3+4+5+6）÷3=14，将1到刘分为，（1、6）（2、5）（3、4）；根据尝试可以得出答案．21．分析：要使□里填上1﹣8这8个数字，这8个数字使连线的两个□里的数字不相邻，中间的两个“□”里必然填入两头的数，可把最中间的填入1，中间下面的填入8，“1”的左右分别填入3、4，“8”的左右分别填入5、6，最上面的填入7，这样就完成了填空．解答：解：根据分析填空如下图：22．分析：设两圈相交部分的两个数分别为a和b，每个圆上五数之和为k．根据题意，可得：1+2+3+…+8+a+b=2k，36+a+b=2k，把k=20、21或22代入，即可求出a+b的值，即可确定a、b的值．解答：解：设两圈相交部分的两个数分别为a和b，每个圆上五数之和为k．根据题意，可得：1+2+3++8+a+b=2k，36+a+b=2k；（1）如果k=20，则a+b=4，4=1+3，一组填法．（2）如果k=21，则a+b=6，6=1+5；6=2+4，两组填法．（3）如果k=22，则a+b=8，8=1+7；8=2+6；8=3+5，三组填法．23．分析：因为1+4+7+10+13+16+19+22=92，设正方形四个角上四个数分别为a、b、c、d．因为a、b、c、d被加了两次，所以可设92+a+b+c+d=4k．a+b+c+d取最小值为1+4+7+10=22，92+22=114，114不是4的倍数，又因为每两个数之间相差3，符合以上条件的最小值为120，则四个数的和就是120﹣92=28．解答：解：根据92+a+b+c+d=4k，a+b+c+d取最小值为1+4+7+10=22，92+22=114，114不是4的倍数，又因为每两个数之间相差3，符合以上条件的最小值为120，则四个数的和就是120﹣92=28，1+7+16+4=28．答案如下：24．分析：假设中间两圆交叉处的数是a、b、c、d，则有1+2+3+…+12+a+b+c+d=25×4，78+a+b+C+d=100，a+b+c+d=22，8+7+2+5=22，9+7+8+1=25，10+7+5+3=25，4+8+2+11=25，6+2+5+12=25；解答：解：答案如图，25．分析：假设中间的数字是a，每条直线上的三个数的和都相等是m，列出等式，凑数，即可得解．解答：解：1+2+3+4+5+6+7+2a=3m，28+2a=3m，m=（28+2a）÷3，a和m都必须是整数，把a从1～7这个代入，m是整数的即为解，a=1，m=10；2+7+1=3+6+1=4+5+1=10；a=4，m=12；4+7+1=2+4+6=3+4+5=12；a=7，m=14；1+6+7=2+5+7=3+4+7=14；如下图所示：26．分析：要使和最小，重复数字尽可能要小．因为：1+2+3+…+8+a+a+b+c=3k（a、b、c为重复的数字，k为大圆上的四个数的和），也就是36+2a+b+c=3k，所以2a+b+c的和应是3的倍数，且尽可能小，只有1+1+3+4=9能被3整除且最小，36+9=3k，k=45÷3=15；同样，要使和最大，则考虑重复数字尽可能大，只有8+8+7+4=27能被3整除且最大，36+27=3k，k=63÷3=21．解答：解：根据分析：这个和最大可以是21；最小必须是15．填法如下图：27．分析：10个连续的自然数中第三个的数是9，说明这10个数是7、8、9、10、11、12、13、14、15、16，假设中间的两个方格的数是a、b，3个2×2的正方形中4个数之和为k，则有：7+8+9+…+16+a+b=3k，115+a+b=3k，38+=k，a+b+1必须是3的倍数，当a+b+1=7+10+1=18，或者a+b+1=8+9+1=18时，k最小=38+6=44．解答：解：答案如图，28．数阵问题专项练习30题(有答案)ok分析：因为1+2+…+16=（1+16）×（16÷2）=136，136÷4=34，所以每个正方形内的数的和为34，然后组出4组和为34的4个数，再从每组选出一个能组成和为34的数填入中间的正方形，又因为1+16=17、2+15=17、3+14=17、4+13=17、5+12=17、6+11=17、7+10=17、8+9=17，所以可以把它们两两相组填入图中，同时注意中间的四个数的和为34即可．解答：解：根据分析答案如下图：29．分析：（1）不能，我们把8个三角形顶点的数字加起来，假设相等是m，则8m=大正方形的数字和+3遍中正方形的数字和+2遍小正方形的顶点数字和，各个正方形的数字和都是1+2+3+4=10，代入可得8m=60，60不能被8整除，因此得解．（2）由于每个三角形顶点上数字之和最小可能是1+1+2=4，最大可能是4+4+3=11，故可能使八个三角形顶点上数字之和各不相同．解答：解：（1）假设三角形的顶点数字和相等是m，则有：8m=（1+2+3+4）×（1+3+2），8m=60，60不能被8整除，所以m不存在，假设错误．即不能使8个三角形顶点上数字之和相等．答：不能使8个三角形顶点上数字之和相等．（2）如图所示：30．分析：10棵树栽5行，每行栽4棵，必然有几棵树会处在多行列中，再从10和5的角度出发，寻求突破．组成五星的线有5条，在5个角上各栽一棵树，交叉点各栽一棵树，就完成了设计．解答：解：如图：。

2、观察表一寻找规律（表二表三分别是从表一中选取的一部分）。

则a+b=＿＿＿。

表二表三3真分数：1/4, 2/4,3/4,1/5, 2/5 ,3/5, 4/5 …那么第1001个分数是＿＿＿。

4、先观察算式，找出规律，然后填数。

(11－2)÷9=1 (111－3)÷9=12 (1111－4)÷9=123(11111－ )÷9=1234(－ )÷9=123456 5、找规律填上合适的数。

6、根据数与数的规律，找出与其他3个圆内数的排列规律不同的一个圆。

( )7、1，1，4，2，7，3，10，1，13，2，16，3，19，1，22，2，25，3，……,100。

请观察上面数列的规律，问： （1） 这个数列一共有多少项？ （2） 这个数列所有数的总和是多少？数列、数阵练习题汇总1、观察下列各数：1, 1, 5/7, 7/15, 9/31,…按你发现的规律计算这列数的第7个数为＿＿＿。

8、观察下面两列数：5、9、13、17、21、25、29、……4、7、10、13、16、19、22、……它们中间第15对相同的数是9、在下面的一列数中,只有一个九位数,它是______.??????……10、把自然数按下表的规律排列,其中12在8的正下方,在88正下方的数是______.??????????? 1??????????? 2? 3??????????? 4? 5? 6??????????? 7? 8? 9? 10??????????? 11 12 13 14 15??????????? 16 ×××××??????????? ×××××××11、计算:1996+1995-1994-1993+1992+1991-1990-1989+…+4+3-2-1,结果是____.12、下面是一列有规律排列的数组:(1,1/2 ,1/3);(1/3,1/4 ,1/5),(1/5,1/6 ,1/7);……;第100个数组内三个分数分母的和是______.13、把所有的奇数依次一项,二项,三项,四项循环分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39, 41),(43),…,则第100个括号内的各数之和为______.14、有一串数,第100行的第四个数是______.1，23，4，5，67，8，9，10，11，1213，14，15，16，17，18，19，2015、下图是自然数列排成的数表，按照这个规律，1993在哪一列？A B C D E F1 2 36 5 47 8 912 11 1013 14 1518 17 1619………16、观察下面的三角形数阵：12 34 5 67 8 9 10………..第1000行第89个数是______________17、下面的算式是按规律排列的：5+1，3+4，1+7，5+10，3+13，1+16，…，请观察上面数列的规律。

2、观察表一寻找规律（表二表三分别是从表一中选取的一部分）。

则a+b=＿＿＿。

表一 表二 表三3、一列自然数0,1,2,3…,2005，… ，2024。

第一个数是0，从第二个数开始，每一个都比它前一个大1，最后一个是2004。

现在将这列自然数排成以下数表：⑴ 第10行第1个数是？⑵ 第1行第20个数是？ ⑶ 2005在第几行第几列？4、有一串真分数：1/2 ,1/3, 2/3, 1/4, 2/4, 3/4,1/5, 2/5 ,3/5, 4/5 …那么第1001个分数是＿＿＿。

5、把5，6，7，8，9填入图中的五个○中，每个○中的数互不相同，且每条直线上的三个○中的数的和相同，则共有多少种不同的填法？数列、数阵练习题1、观察下列各数：1, 1, 5/7, 7/15, 9/31,…按你发现的规律计算这列数的第7个数为＿＿＿。

6、如图是有名的“六角幻方”：将l到19这19个自然数填人图中的圆圈中，使得每一条直线上圆圈中的各数之和相等，美国数学爱好者阿当斯从l910年开始，到1962年，用了52年的时间才找到了解答．我们给大家填人了6个自然数，请你完成这个“六角幻方”．7、将1-12这12个数分别填入图中的12个小圆圈里，使每条直线上的四个小圆圈中的数字之和都相等，这个相等的和是多少？8、把5，6，7，8，9填入图中的五个○中，每个○中的数互不相同，且每条直线上的三个○中的数的和相同，则共有多少种不同的填法？9、观察下面的数列，找出其中的规律，并根据规律，在括号中填上合适的数.（1）1，1，2，3，5，8，（ ），21，34… （2）1，2，2，4，3，8，4，16，5，（ ） （3）2，1，4，3，6，9，8，27，10，（ ）.（4）下面数列的每一项由3个数组成的数组表示，它们依次是： （1， 3，5），（2，6，10），（3，9，15）…问：第100个数组内3个数的和是多少？10、先观察算式，找出规律，然后填数。