弦线上波的传播规律

弦线上波的传播规律实验报告
实验目的：
观察弦线上波的传播规律。

实验原理：
在弦线上产生的波是机械波，其传播是由弦线的振动引起的。

当弦线一侧受到外力的作用时，使得弦线在这一侧产生振动，振动沿着弦线传播，形成波。

弦线上波的特点：
1.波长：指在相邻两个波峰之间的距离，通常用λ表示。

2.振幅：指波形的高低程度，通常用A表示。

3.频率：指在单位时间内波峰的个数，通常用f表示。

4.周期：指波形重复的时间，通常用T表示。

5.速度：指波传播的速度，通常用v表示。

实验材料：
弦线、定滑轮、弹簧尺、蜡烛、打火机、振动发生器等。

实验步骤：
1.将弦线固定在两个定滑轮上。

2.将弦线的一端固定在支架上，另一端绑在定滑轮的中心位置。

3.在弦线的中央放置一个振动发生器，调整振动发生器的频率，使得弦线产生波。

4.用弹簧尺测量弦线上波的波长，再由波长计算出波的速度。

5.将蜡烛放在弦线下方，在弦线上产生驻波，观察波的反射、
折射等现象。

实验结果：
通过实验测量，我们得到了波长λ和频率f的数据，通过计算
得到波速v的值。

我们还观察到了弦线上波的反射、折射等现象，验证了波的传播规律。

实验结论：
通过实验，我们验证了弦线上波的传播规律，了解了波的特点和性质，学习了波的计算方法，为深入学习波的原理和应用打下了基础。

弦线驻波实验总结引言弦线驻波实验是物理学实验中非常经典的一种实验。

通过操纵绷紧的弦线，可以观察到产生的驻波现象，进而探究驻波的性质和规律。

本文将对弦线驻波实验进行总结，并探讨实验中所涉及到的一些重要概念和原理。

一、实验原理弦线驻波实验是基于波动学原理进行的，它基于弦线的振动过程，观察到驻波的现象。

在驻波实验中，弦线被固定在两端，并以一定的频率产生振动。

振动的波动会在弦线中产生前进波和反射波。

当两波相遇并满足一定条件时，它们会形成驻波现象，即波节和波腹的交替排列。

二、实验步骤1. 准备工作：将弦线绷紧，保持平直并固定在两端。

2. 激发振动：用手或其他装置在弦线上产生振动，保持一定的频率。

3. 观察驻波现象：通过观察弦线上形成的波节和波腹的排列来判断是否形成驻波。

4. 测量波长和频率：利用测量工具如尺子或测频仪等，测量驻波的波长和频率。

5. 分析数据：根据测量结果计算波速和其他相关参数。

三、实验中的观察与现象在实验中，我们可以观察到一些有趣的现象：1. 波节和波腹的交替出现：当驻波形成时，弦线上会出现交替排列的波节（振动幅度最小的位置）和波腹（振动幅度最大的位置）。

这种交替的出现是驻波现象的显著特征。

2. 波长的变化：根据实验中测得的波长数据，我们可以观察到驻波的波长会受到调节弦线长度和振动频率的影响。

当弦线长度固定时，增加振动频率会导致波长变短。

四、实验结果与讨论通过一系列实验操作和数据处理，我们可以得出一些结论和讨论：1. 波速与频率的关系：根据实验中测得的数据，我们可以进一步计算出驻波的波速。

根据波速的定义公式：波速 = 频率× 波长，我们可以发现波速与频率是成正比关系。

2. 波长与振动模式：根据实验中观察到的波长变化现象，我们可以推断出不同振动模式下的波长变化规律。

例如，在弦线长度固定的情况下，当振动频率为基频（最低频率）时，波长最长。

随着频率增加，波长逐渐减小。

五、实验意义和应用弦线驻波实验作为一种经典的物理实验，具有重要的学习和应用价值：1. 深化对波动学原理的理解：通过实际操作和观察驻波现象，我们可以更加深入地理解波动学原理，包括波的传播、波速、波长等概念与性质。

实验五 研究弦线上波的传播规律一、实验目的1.观察弦线上驻波的变化，了解并熟悉实验仪器的调整方法。

2.研究弦线振动时的振动频率与振幅变化对形成驻波的影响。

波长与张力的关系；3.在弦线张力不变时，研究弦线振动时驻波波长与振动频率的关系。

4.改变弦线张力后，研究弦线振动时驻波波长与振动频率的关系。

二、仪器和用具可调频率的数显机械振动源、弦线支撑平台、固定滑轮、可调滑轮、砝码盘、米尺、弦线、砝码、频闪灯、分析天平等。

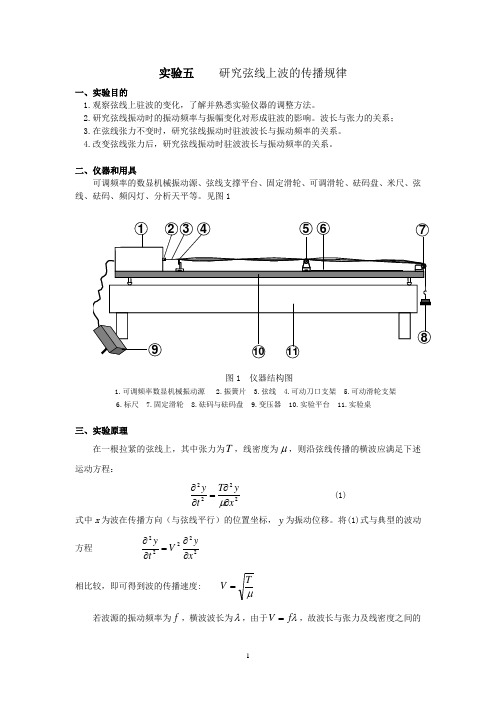
见图1图1 仪器结构图1.可调频率数显机械振动源2.振簧片3.弦线4.可动刀口支架5.可动滑轮支架6.标尺7.固定滑轮8.砝码与砝码盘9.变压器 10.实验平台 11.实验桌三、实验原理在一根拉紧的弦线上，其中张力为T ，线密度为μ，则沿弦线传播的横波应满足下述运动方程：2222xyT ty ∂∂=∂∂μ (1)式中x 为波在传播方向（与弦线平行）的位置坐标，y 为振动位移。

将(1)式与典型的波动方程22222xy Vty ∂∂=∂∂相比较，即可得到波的传播速度: μTV =若波源的振动频率为f ，横波波长为λ，由于λf V =，故波长与张力及线密度之间的关系为：μλTf1=(2)为了用实验证明公式(2)成立，将该式两边取对数，得：f T log log 21log 21log --=μλ若固定频率f 及线密度μ，而改变张力T ，并测出各相应波长λ，作log λ-log T 图，若得一直线，计算其斜率值（如为21），则证明了λ∝21T的关系成立。

同理，固定线密度μ及张力T ，改变振动频率f ，测出各相应波长λ，作log λ-log f 图，如得到斜率为-1的直线则验证了λ∝f-1。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波，一维驻波是波干涉中的一种特殊情形。

在弦线上出现许多静止点，称为驻波的波节，相邻两波节间的距离为半个波长。

实验弦振动的研究【实验目的】1.观察弦振动形成的驻波。

2.用两种方法测量弦线上横波的传播速度，比较两种方法测得结果的符合情况。

3.验证弦振动的基频与张力、弦长的关系。

【仪器用具】电振音叉（约100Hz），弦线，分析天平，滑轮，弹簧及尺，砝码，低压电源，米尺。

【实验原理】1.弦线上横波传播速度（一）如图1所示，将细弦线的一端固定在电振音叉上，另一端绕过滑轮挂在砝码或弹簧上，当音叉振动时，强迫弦线振动，弦振动频率应当和音叉的频率ν相等。

若适当调节砝码重量或弹簧拉力，可在弦上出现明显稳定的驻波，即弦与音叉共振，设驻波波长为λ，则弦线上横波传播速度V等于V=νλ(1)2.弦线上横波传播速度（二）=的微分段加以讨论（图2）。

设若横波在张紧的弦线上沿x轴正方向传播，我们取 AB dsρ。

在A、B处受到左右弦线的线密度（即单位长质量）为ρ，则此微分段弦线ds的质量为ds邻段的张力分别为1T 、2T ，其方向为沿弦线的切线方向与x 轴交成1α、2α角。

由于弦线上传播的横波在x 方向无振动，所以作用在微分段ds 上的张力的x 分量应该为零，即2211cos cos 0T T αα-= （2）又根据牛顿第二定律，在y 方向微分段的运动方程为：222112sin sin d y T T ds dtααρ-= (3) 对于小的振动，可取ds dx ，而1α、2α都很小，所以1cos 1α ，2cos 1α ，11sin tg αα ，22sin tg αα 。

又从导数的几何意义可知1xdx tg dy α⎛⎫= ⎪⎝⎭，2x dx dy tg dx α+⎛⎫= ⎪⎝⎭，式（2）将成为210T T -=，即21T T T ==表示张力不随时间和地点而变，为一定值。

式（3）将成为22x dx xdy dy d y T T dx dx dx dt ρ+⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭。

（4） 将x dxdy dx +⎛⎫ ⎪⎝⎭按泰勒级数展开并略去二级微量，得 22x d x x xd y d y d y dx dx dx dx +⎛⎫⎛⎫⎛⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭。

实验** 弦线上的驻波实验[引言]弦线上波的传播规律的研究是力学中的重要内容。

本实验重点在于观测弦线上形成的驻波，并用实验确定弦振动时，驻波波长与张力的关系，驻波波长与振动频率的关系，以及驻波波长与弦线密度的关系。

常用的实验方法有两种：一是采用振动频率固定的电动音叉，通过改变弦线长度或张力，形成稳定驻波；二是采用频率连续可调的振动体，改变弦长或张力，形成稳定驻波从而验证弦线上驻波的振动规律。

掌握驻波原理测量横波波长的方法。

这种方法不仅在力学中有重要应用，在声学、无线电学和光学等学科的实验中都有许多应用。

[预习提示]1． 波的叠加原理。

2． 驻波的形成原理。

3． 弦线的共振频率和波速与哪些条件有关？[实验目的]1. 了解波在弦线上的传播及弦波形成的条件。

2．测量拉紧弦不同弦长的共振频率。

3. 测量弦线的密度。

4. 测量弦振动时波的传播速度。

[实验仪器]DH4618型弦振动研究实验仪，DH4618型弦振动实验仪信号源，双踪示波器[实验原理]由波动理论知道，两列振幅和频率均相同、振动方向一致且传播方向相反的简谐波叠加后会产生驻波。

合成振幅为零的点称为波节，合成振幅最大的点称为波腹。

相邻两波节或波腹间的距离都是半个波长。

各种乐器，包括弦乐器、管乐器和打击乐器，都是由于产生驻波而发声。

在弦乐器中，沿弦线传播的行波在乐器一端被反射，反射波与入射波相互叠加，形成驻波，如图**-1所示。

图**-1 驻波示意图设沿x 轴正方向传播的波为入射波，沿x 轴负方向传播的波为反射波，则它们的波动方程可以写为1,2cos 2()Y A ft x πλ=±。

其中A 为简谐波的振幅，f 为频率，λ为波长，x 为弦线上质点的位置坐标。

两波叠加后的合成波为驻波，其方程为：122cos 2()cos 2Y Y A x ft πλπ+= （**-1）由此可见，入射波与反射波合成后，弦上各点都在以同一频率作简谐振动，它们的振幅为|2cos 2()|A x πλ，只与质点的位置x 有关，与时间无关。

弦线上波的传播规律实验报告实验报告：弦线上波的传播规律
摘要：
本实验通过实验在弦线上观察到波传播规律，初步了解波在弦
线上的传播原理。

实验结果表明，波动的传播速度与弦线拉紧程
度和弦线线密度有关。

引言：
波是指在某一介质中传播的一种物理现象，其传播过程中能量
和物质本身并不随之传播。

波动分为机械波和电磁波两种，本实
验主要探究机械波的传播规律。

弦线上的波动是一种纵波，通过
实验可以观察到弦线上纵波基本的传播规律，从而更好地理解波
的传播原理。

材料与实验方法：
所需材料有弦线、尺子、各式重物、台式振荡器等。

本实验的
具体步骤为：将弦线在横向方向上安装在固定装置上，再在两端
分别固定不同重量的小球，保持拉紧程度相等。

在一定的频率下，
开启台式振荡器，产生波动，逐一改变弦线的线密度和重物的种类、数量，记录下波动传播的速度和波的振幅变化。

实验结果与分析：
在本实验中，我们观察到了弦线上波动的传播规律。

实验结果
表明，弦线的拉紧程度越大、线密度越大，其传播速度也就越大，振幅也就越大。

此外，不同重量的小球对波形谱的影响也很明显，小球数量越多，波动的传播速度越快，振幅也相应变大。

因此，
可以得出结论：传播速度的大小取决于弦线的拉紧程度、线密度
和小球数量等因素。

结论：
通过本实验的观察和分析，我们初步了解了弦线上波动的传播
规律。

弦线上波的传播速度大小与弦线拉紧程度、线密度和小球
数量等因素有关。

了解波动传播规律对于深层次地理解波动现象
有着十分重要的意义。

弦线上波的传播规律实验报告弦线上波的传播规律实验报告引言：波是自然界中常见的现象，它们以各种形式存在，如声波、光波和水波等。

而弦线上的波动是一种常见而又有趣的现象，通过实验我们可以观察和研究弦线上波的传播规律。

本实验旨在通过实验观察和数据分析，探索弦线上波的传播规律。

实验目的：1. 观察弦线上波的传播过程；2. 研究波的传播速度与弦线张力、线密度以及波长的关系；3. 探究波的反射和干涉现象。

实验器材：1. 细弦：我们选择了一根细弦，用于模拟弦线上波的传播；2. 弦线固定装置：用于固定弦线，确保实验的稳定性；3. 频率发生器：用于产生不同频率的波；4. 动态示波器：用于观察和记录波动的波形；5. 质量块：用于改变弦线的张力。

实验步骤：1. 将细弦固定在两个固定装置上，保持弦线的水平状态；2. 调节频率发生器，产生特定频率的波；3. 将频率发生器连接到细弦的一端，使波从这一端传播；4. 使用动态示波器观察和记录波动的波形；5. 改变弦线的张力，观察波的传播速度的变化；6. 改变频率发生器的频率，观察波长对波的传播速度的影响；7. 在弦线上加入质量块，改变线密度，观察波的传播速度的变化；8. 观察波的反射和干涉现象。

实验结果与分析：1. 弦线上波的传播速度与张力成正比：通过改变弦线的张力，我们观察到波的传播速度随着张力的增加而增加，这是因为张力增加会导致弦线的劲度增大，波在弦线上传播的速度也随之增加。

2. 弦线上波的传播速度与线密度成反比：通过在弦线上加入质量块，我们观察到波的传播速度随着线密度的增加而减小，这是因为线密度的增加会导致弦线的质量增加，波在弦线上传播的速度也随之减小。

3. 弦线上波的传播速度与波长无关：通过改变频率发生器的频率，我们观察到波的传播速度并不会随着波长的变化而变化，这是因为波长只影响波的频率，而不会影响波的传播速度。

4. 弦线上波的反射和干涉现象：我们观察到当波遇到固定装置时会发生反射现象，反射波的形状和入射波相同；当两个波在弦线上相遇时会发生干涉现象，干涉波的形状由两个波的叠加决定。

实验题目：横波在弦线上的传播规律一、实验目的1.观察弦线上形成的驻波，用实验验证在频率一定时，驻波波长与张力的关系；2.在张力不变时，验证驻波波长与振动频率的关系；3.学习对数作图或最小二乘法进行数据处理；二、实验仪器可调频率的数显机械振动源、平台、固定滑轮、可调滑轮、砝码盘、米尺、弦线、砝码、电子秤等三、实验原理在一根拉紧的弦线上，沿弦线传播的横波满足运动方程：2222y T y t xμ∂∂=∂∂ （1）将该式与典型的波动方程22222y y v t x ∂∂=∂∂比较，可得波的传播速度：v =，其中T 为张力，μ线密度. 若波源的振动频率为f , 则横波的波长：λ=（2）两边取对数，得 11log log log log 22T f λμ=-- 若固定频率f 和线密度μ，改变张力T ，并测出各相应波长λ，作log log T λ-，若得一直线，计算其斜率值，（如为1/2），则证明1/2T λ∝的关系成立。

同理，固定线密度μ和张力T ，改变振动频率f ，测出相应波长λ，作log log f λ-，如得一斜率为-1的直线就验证了1f λ-∝。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波。

弦线上出现的静止点，称为波节，相邻两波节的距离为半个波长。

若观察到在长为L 的弦上有n 个驻波，则波长λ=2L/n 。

四、实验内容与步骤1. 验证频率一定时，横波波长与弦线上张力的关系选定一个波源振动频率并记录，改变砝码盘上所挂砝码的个数以改变张力（5次）。

每改变一次张力，均要移动可动滑轮的位置，使弦线上出现稳定且幅度比较大的驻波。

记录频率值，两支架间的距离L, L 上所形成的半波数的个数n ，以及砝码与砝码盘的总质量。

计算出波长（利用公式λ=2L/n ），张力（砝码与砝码盘所受的重力），作log λ- logT 图，计算其斜率，并于理论值比较。

2. 验证张力一定时，横波波长与波源频率的关系给砝码盘挂上一定数量砝码（一般三个）并记录，以保持张力一定。