浙江工业大学材料力学第7章答案
- 格式:doc
- 大小:561.00 KB
- 文档页数:14



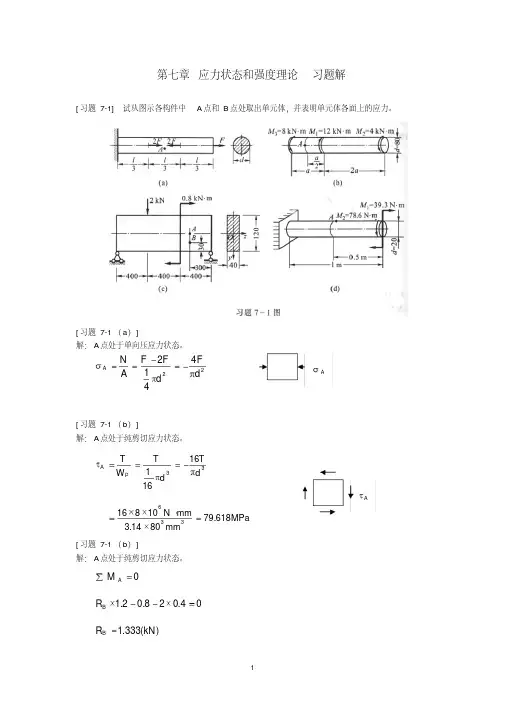
习题7-3图P F P F P F P F 0PF P -F P2F -P2FP2F -P2F 000P F P F P F P-F P -F P -F P F P F P F P F 0P F P -F P2F -P2FP2F -P2F00P F P F P F P -F P -F P-F 0习题7-3图 材料力学_高教第二版_范钦珊_第7章习题答案第7章 弹性平稳稳固性分析7-1 关于钢制细长压杆受力达到分叉载荷以后,还能不能继续承载,有如下四种答案,试判定哪一种是正确的。
(A )不能,因为载荷达到临界值时,屈曲位移将无穷制地增加; (B )能,压杆一直到折断时为止都有承载能力; (C )能,只要横截面上的最大应力不超过必然限度; (D )不能,因为超过度叉载荷后变形再也不是弹性的。
正确答案是 C 。
7-2 图示两头铰支圆截面细长压杆,在某一截面上开有一小孔。
关于这一小孔对压杆承载能力的阻碍,有以下四种论述,试判定哪一种是正确的。
(A )对强度和稳固承载能力都有较大减弱;(B )对强度和稳固承载能力都可不能减弱;(C )对强度无减弱,对稳固承载能力有较大减弱; (D )对强度有较大减弱,对稳固承载能力减弱极微。
正确答案是 D 。
7-3 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。
关于四桁架所能经受的最大外力F Pmax 有如下四种结论,试判定哪一种是正确的。
(A ))d ()b ()c ()a (max P max P max P max P F F F F =<=; (B ))d ()b ()c ()a (max P max P max P max P F F F F ===; (C ))c ()b ()d ()a (max P max P max P max P F F F F =<=;(D ))d ()c ()()a (max P max P max P max P F F b F F =<=。
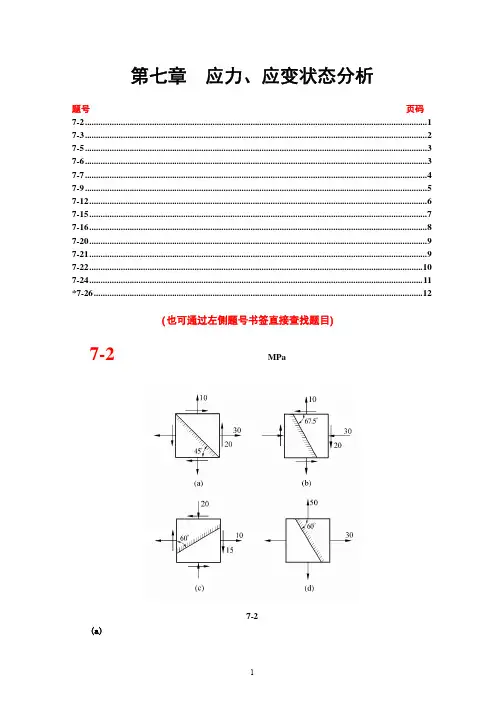



材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。

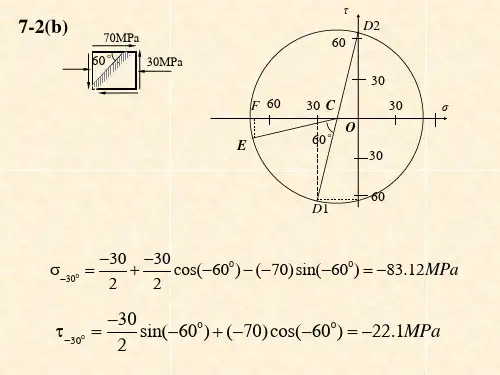
作业参考答案(7-10章)7-1 (a )已知:045201030=-===ατσσMPa MPaMPaxy y xMPa MPa xy yx xy yx yx 1045220452210302224045220452210302103022224545=︒⨯-︒⨯-=+-==︒⨯+︒⨯-++=--++=cos sin cos sin sin cos sin cos ατασστατασσσσσ (b )已知:05.67203010-=-=-==ατσσMPaMPa MPaxy y x567220567223010222343856722056722(-30)102(-30)102222=︒⨯--+︒⨯-+=+-=-=︒⨯-+︒⨯--++=--++=).cos()().sin(cos sin .).sin().cos(sin cos ατασστατασσσσσααxy y x xy yx y x MPa(d )已知:012003050-====ατσσxy y x MPaMPaMPa MPa xy yx xy yx yx 668240230502223524023050230502222..)sin(cos sin )cos(sin cos -=︒--=+-==︒--++=--++=ατασστατασσσσσαα7-2 (a )已知:MPa MPaMPaxy y x 202040===τσσ︒-=︒︒-=-=-⨯-=--====⎩⎨⎧=+⎪⎭⎫ ⎝⎛-±+=+⎪⎪⎭⎫ ⎝⎛-±+=⎩⎨⎧3587316116463222040202220647365264736522022040220402200003212222....tan ....min max αασστασσστσσσσσσyx xyxy y x y x xMPa MPa MPa MPa(a )7-3(a )解:MPaMPa MPaMPaMPa 6527060260703060311321=+=-===-===σστσσσσσmax max(b )解:给定应力状态中有一个主应力是已知的,即σz =30MPa 。
第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态,空间应力状态即三向应力状态。
(√)2、单元体中正应力为最大值的截面上,剪应力必定为零。
(√)3、单元体中剪应力为最大值的截面上,正应力必定为零。
(×) 原因:正应力一般不为零。
4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同,且均为应力轴 上的一个点。
(×) 原因:单向应力状态的应力圆不为一个点,而是一个圆。
三向等拉或等压倒是为一个点。
5、纯剪应力状态的单元体,最大正应力和最大剪应力值相等,且作用在同一平面上。
(×) 原因:最大正应力和最大剪应力值相等,但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。
(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。
(×)8、塑性材料制成的杆件,其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。
(×) 原因:塑性材料也会表现出脆性,比如三向受拉时,此时,就应用第一强度理论9、纯剪应力状态的单元体既在体积改变,又有形状改变。
(×) 原因:只形状改变,体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂,而管内的冰不会被破坏,只是因为冰的强度比铸铁的强度高。
(×) 原因:铸铁的强度显然高于冰,其破坏原因是受到复杂应力状态 11.圆杆受扭时,杆内阁点处于纯剪切状态。
(√)12.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)二、 选择题1、危险截面是( C )所在的截面。
A 最大面积B 最小面积C 最大应力D 最大内力2、关于用单元体表示一点处的应力状态,如下论述中正确的一种是( D )。
A 单元体的形状可以是任意的B 单元体的形状不是任意的,只能是六面体微元C 不一定是六面体,五面体也可以,其他形状则不行D 单元体的形状可以是任意的,但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件内任意一点,随着所截取截面方位不同,一般来说( D ) A 正应力相同,剪应力不同 B 正应力不同,剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时,轴表面各点处于( B )A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点,说法正确的是( B )。
浙江工业大学材料力学第7章答案7.1一实心圆杆1,在其外依次紧套空心圆管2和3。
设三杆的抗拉刚度分别为E 1A 1、E 2A 2及E 3A 3,此组合杆承受轴向拉力F ,三杆之间无相对摩擦。
试求组合杆的伸长量。
解:平衡方程:F F F F N N N =++321(1)变形协调方程:333222111A E lF A E l F A E l F N N N == (2)方程(1)和(2)联立求解,得到:332211111AE A E A E AFE F N ++=332211222A E A E A E A FE F N ++= 332211333A E A E A E A FE F N ++=组合杆的伸长量为:332211111A E A E A E FlA E l F l N ++==∆7.2 在温度为2︒C 时安装铁轨,两相邻段铁轨间预留的空隙为Δ=1.2mm 。
当夏天气温升为40︒C 时,铁轨内的温度应力为多少?已知:每根铁轨长度为12.5m ,E =200GPa ,线膨胀系数α=12.5×10-6 m /m ⋅︒C 。
解:没有约束情况下,铁轨自由热膨胀时的伸长量mm9375.5m 109375.55.12)240(105.1236=⨯=⨯-⨯⨯=⋅∆⋅=∆--l T l T α (1)温度应力引起的铁轨长度变形为mm 0625.010200105.1233σσσσ=⨯⨯⨯===∆E l EA l F l N(温度应力σ的单位为MP a ) (2)变形协调条件为∆=∆-∆σl l T(3)方程(1)、(2)和(3)联立求解,可得MPa8.75=σ(压应力)7.3图示结构中,①、②和③三杆材料与截面相同,弹性模量为E ,横截面面积为A ,横杆CD 为刚体。
求三杆所受的轴力。
解:平衡方程F F F F N N N =++321(1)31=⋅-⋅a F a F N N (2)FF N 1F N 2F N 3变形协调方程:312l l l ∆+∆=∆ (3)物理方程:EAlF l N 112∆ EA l F l N 22=∆ EAl F l N 33=∆代入方程(3),可得补充方程 31231222N N N N N N F F F EAlF EA l F EA l F +=⇒+= (4) FC①②③DllaaF∆l 1∆l 2∆l 3DC①②③联立补充方程和平衡方程并求解,可得F F N 721= F F N 732= F F N 723= 7.4图示螺栓通过螺母拧紧套筒。
螺栓的螺距为0.65mm ,螺栓直径d 1=20mm ;套筒内径d 2=22mm ,外径D 2=32mm ;两者材料相同,E =200GPa 。
若将螺帽按拧紧方向再旋转60°,试求螺栓横截面上的正应力增加多少?不考虑螺母和螺栓头的变形。
解:拧紧螺帽后,螺栓受拉且轴力为1N F ,套筒受压且轴力为2N F ,平衡方程为021=-N N F F (1)螺母旋进60度后,则总位移为mm 108.065.036060=⨯=∆;假设螺栓伸长1l ∆,套筒缩短2l ∆,因而变形协调方程(如图)为∆=∆+∆21l l (2)物理方程为:211211111441d E lF d E l F EA l F l N N N ππ=⋅==∆(3)()()2222222222222441d D E l F d D E lF EA l F l N N N -=-⋅==∆ππ(4)方程(1)、(2)、(3)和(4)联立求解,可得250mm 套筒螺栓螺母kN641.151=N F螺栓横截面上的正应力为MPa 8.4920115644211=⨯⨯==πσA F N7.5 图示的刚性梁由三根钢杆联接,它们的截面积均为2cm 0.2=A ,钢的弹性模量E =200GPa ,其中杆3由于制造误差,其长度比杆1和杆2短l 0005.0=δ。
试求装配后各杆的应力。
解:平衡方程为0321=++N N N F F F(1)31=⋅-⋅a F a F N N (2)F N 1F N 2N 3变形协调方程为:()2312l l l ∆=-∆+∆δ,即δ=∆-∆+∆2312l l l (3)物理方程为EA lF l N 11=∆ EAl F l N 22=∆ EAlF l N ⋅=∆33(4)方程(4)代入方程(3),得到补充方程为δ=-+EA l F EA l F EA l F N N N 2312,即lEAF F F N N N δ=-+2312 (5) 补充方程联立平衡方程求解,可得 l EAF F N N 631δ==,lEA F N 32δ-=各杆的应力为l a a 123δ∆l 1∆l 2∆3①②③MPa 7.1660005.020*******=⨯===lll E δσσ MPa 3.3330005.020000031-=⨯-=-=ll l E δσ7.6图示结构的三根杆用同一材料制成,弹性模量为E ,杆1和杆3的截面积A A A ==31,杆2的截面积A A 22=。
试求载荷F 作用下各杆的内力。
解:受力图如下: 故平衡方程为 (1) θcos 60cos 21F F F N N =︒+ θsin 30cos 23F F F N N =︒⋅+ (2)根据结构变形图,有()()⎪⎪⎭⎫ ⎝⎛-=+=∆=∆⎪⎪⎭⎫ ⎝⎛+=-=∆ββδβδβδββδβδsin 21cos 2330cos cos sin 23cos 2160cos 321οοl l l故,变形协调条件为:2312321l l l ∆=∆+∆ (3)物理方程为 EAlF l N 11=∆,EAlF A E l F l N N 33230cos 222=⋅︒=∆,EAlF lN 33=∆ (4)方程(4)代入方程(3),得到补充方程为23132333N N N F F F =+(5)FFN 1FN 2FN 3θ方程(1)、(2)和(5)联立求解,可得()()F F N 6322sin 33cos 9341+-+=θθ,()F F N 632sin 33cos 32++=θθ,()()F F N 6322cos 33sin 3343+-+=θθ7.7 钢管壁厚δ1=2mm ,直径d 1=50mm ,套在直径为d 2=25mm 的实心钢轴外,两端与刚性法兰盘焊接,如图所示。
焊接前,轴上加200N·m 的扭转力偶,并在焊接过程中保持该状态。
焊接完后解除扭转力偶,试求钢管横截面上的扭矩。
解:焊接前,实心钢轴右端相对于左端的扭转角为0ϕ,扭矩为0T 。
焊接完后解除初始力偶后,钢管右端相对于左端的扭转角为1ϕ,扭矩为1T ;实心钢轴右端相对于左端的扭转角为2ϕ,扭矩为2T 。
受力平衡方程为:21=-T T (1)变形协调方程为:21ϕϕϕ=+ (2)物理方程为:()324650441111-⋅==πϕG lT GI l T p ,322542222⋅⋅==πϕG lT GIl T p ,3225200004200⋅⋅==πϕG lGI l T p (3)方程(1)、(2)和(3)联立求解,可得m N 9.1631⋅=T7.8 图示两端固定的圆截面实心阶梯轴,承受扭转力偶作用,如图所示。
若材料的许用切应力MPa 50][=τ,试设计轴的直径D 2。
解:平衡方程为eBCABM T T =+ (1)变形协调方程为BCAB ϕϕ= (2)物理方程为3242D G l T ABAB AB πϕ⋅=,3241D G l T BCBC BCπϕ⋅=(3)BC 段的扭转强度条件:][1631τπτ≤=D T BCBC(4)方程(1)、(2)、(3)和(4)联立求解,可得:mm2.772≥D ,取mm782=D。
7.9EI 。
ABCqaalAABBBDCCFM eaFa al/2(a)(b)(c)(d)Al/2l/2题7.9图解:(a )一次超静定梁。
F BABB CqaaACqaa解除多余支座约束B ,应用支反力BF 代替,得到图示静定基。
由叠加法可以得到截面B 的挠度为EIa q EI a F w BB384)2(548)2(43-= 变形协调方程为 0=Bw 于是可得45qaF B= 由0=∑AM可得0245)2(212=⋅+⋅+-a F a qa a q C ,()↑=83qaFC由结构几何与载荷的对称性,可知()↑=83qa F A(b )一次超静定梁。
AB D CFaa aAB D CFaaaF B解除多余支座约束B ,应用支反力BF 代替,得到图示静定基。
由叠加法可以得到截面B 的挠度为[][]aEI a a a a Fa a EI a a a a a F w BB36)3(36)2()3(2222222⋅--⋅⋅-⋅--⋅⋅=变形协调方程为0=Bw于是可得F F B87= 由0=∑AM可得3287=⋅-⋅+-a F a F Fa C ,()↓=F FC41由竖直向的受力平衡方程,可得()↑=F F A 83(c )一次超静定梁。
lABl/2(c)lABl/2F B解除多余支座约束B ,应用支反力BF 代替,得到图示静定基。
由叠加法可以得到截面B 的挠度为()EIl l Fl EI l l l F w B B 62336322⎪⎭⎫ ⎝⎛-⋅⋅--⋅=变形协调方程为 0=Bw于是可得F F B47= 由0=∑AM可得02347=⋅-⋅+l F l F M A ,FlMA41-=由竖直向的受力平衡方程,可得F F A 43=(d )一次超静定梁。
BBAl/2l/2M Al/2l/2解除多余支座约束B ,应用支反力BF 代替,得到图示静定基。
有叠加法可以得到截面B 的挠度为l EI l M EI l M EI l F w e e B B 2121221323⋅⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=变形协调方程为 0=Bw于是可得lMF eB89= 由竖直向的受力平衡方程,可得lMF eA89= 由0=∑AM可得089=⋅+-l lM M M ee A ,eAM M 81-=7.10 图示悬臂梁AD 和BE ,通过钢杆CD 连接。
已知,kN 50=F ,梁AD 和BE 的抗弯刚度均为26m N 1024⋅⨯=EI ,CD 杆长m 5=l ,横截面面积24m 103-⨯=A ,弹性模量GPa 200=E 。
试求悬臂梁AD 在D 点的挠度。
解:一次超静定结构。
变形协调方程为CDD C l w w ∆=- (1)F C D AB 2m 2m E物理关系为EIa F w N D 33-=,()EIa F EI a a Fa w N C 36632+-⋅-=,EAlF l N CD=∆ (2)方程(1)和(2)联立求解,可得()kN454.45124533=+=EIlEAa EAFa F N 悬臂梁AD 在截面D 的挠度为mm05.51024320004545431233-=⨯⨯⨯-=-=EI a F w N D7.11 图示结构,AC 梁的EI 和CD 杆的EA 为已知,且a =l /2。