电网络理论习题解

格式：doc
大小：817.72 KB
文档页数：20

下载文档原格式

电网络理论1-66

1-7
网络的时不变性和时变性
v (t )
y (t )
时不变网络
u( t )
u( t )
0
(a)
t
性质：
dv( t ) ˆ (t ) v dt
u(t-T)
dy( t ) ˆ (t ) y dt
0 u(t-T ) 0 T
(a)
t
0
T
(b)
t
ˆ ( t ) v( t )dt v

t
ˆ ( t ) y( t )dt y

t
(b)
t
1-7
网络的时不变性和时变性
传统型时不变网络的定义：若一个网络中不含任何非源时变网络元件，则称该网络为时不变的。
结论:不含时变网络元件的网络是端口型时不变网络。
1-8
网络元件及网络的无源性和有源性
传统的无源网络：若一个网络仅由无源网络元件构成，则该网络是无源的。端口型无源网络：设 n 端口网络于 to 时刻贮存的能量为 W(to) ，在 to 至 t 时间内从电源传送至 n 端口网络的能量为 t W ( t o , t ) uT ( )i( )d 式中 u( t )、i( t ) W ( t o ，t ) ， t
o
分别为n端口网络的端口电压向量和端口电流向量。如果对所有的初始时刻to，对所有的 t t o ，以及对所有的容许信号向量偶 (u( t ), i( t )),均有
W ( t o ) W ( t o , t ) W ( t o ) uT ( )i( )d 0
to t
i +
1-6
网络的线性和非线性1 qFra biblioteku –

电力网络分析计算试题及答案可编辑

3．1 电网结构如图3—11所示，其额定电压为10KV 。

已知各节点的负荷功率及参数：MVA j S )2.03.0(2+=，MVA j S )3.05.0(3+=，MVA j S )15.02.0(4+=Ω+=)4.22.1(12j Z ，Ω+=)0.20.1(23j Z ，Ω+=)0.35.1(24j Z试求电压和功率分布。

解：（1）先假设各节点电压均为额定电压，求线路始端功率。

0068.00034.0)21(103.05.0)(22223232232323j j jX R U Q P S N +=++=++=∆0019.00009.0)35.1(1015.02.0)(22224242242424j j jX R U Q P S N +=++=++=∆则： 3068.05034.023323j S S S +=∆+=如图所示简单系统，额定电压为110KV 双回输电线路，长度为80km ，采用LGJ-150导线，其单位长度的参数为：r=Ω/km ，x=Ω/km,b=km S /106-⨯。

变电所中装有两台三相110/11kV 的变压器，每台的容量为15MVA,其参数为：5.3%,5.10%,128P 5.40K 0===∆=∆o K I U kW kW P 。

母线A的实际运行电压为117kV ，负荷功率：MVA j S MVA j S LDc LDb 1520,1230+=+=。

当变压器取主抽头时，求母线c 的电压。

解（1）计算参数并作出等值电路。

输电线路的等值电阻、电抗和电纳分别为由于线路电压未知，可用线路额定电压计算线路产生的充电功率，并将其等分为两部分，便得var65.2var 1101038.42121242M M U B Q N c B -=⨯⨯⨯-=-=∆-将B Q ∆分别接于节点A 和b ，作为节点负荷的一部分。

两台变压器并联运行时，它们的等值电阻、电抗及励磁功率分别为kVkV某一额定电压为10kV 的两端供电网，如图所示。

电力网络分析计算试题及答案可编辑

3．1 电网结构如图3—11所示，其额定电压为10KV 。

已知各节点的负荷功率及参数：MVA j S )2.03.0(2+=，MVA j S )3.05.0(3+=，MVA j S )15.02.0(4+=Ω+=)4.22.1(12j Z ，Ω+=)0.20.1(23j Z ，Ω+=)0.35.1(24j Z试求电压和功率分布。

解：（1）先假设各节点电压均为额定电压，求线路始端功率。

0068.00034.0)21(103.05.0)(22223232232323j j jX R U Q P S N +=++=++=∆0019.00009.0)35.1(1015.02.0)(22224242242424j j jX R U Q P S N +=++=++=∆则： 3068.05034.023323j S S S +=∆+=3.2 如图所示简单系统，额定电压为110KV 双回输电线路，长度为80km ，采用LGJ-150导线，其单位长度的参数为：r=0.21Ω/km ，x=0.416Ω/km,b=2.74km S /106-⨯。

变电所中装有两台三相110/11kV 的变压器，每台的容量为15MVA,其参数为：5.3%,5.10%,128P 5.40K 0===∆=∆o K I U kW kW P 。

母线A的实际运行电压为117kV ，负荷功率：MVA j S MVA j S LDc LDb 1520,1230+=+=。

当变压器取主抽头时，求母线c 的电压。

解（1）计算参数并作出等值电路。

输电线路的等值电阻、电抗和电纳分别为由于线路电压未知，可用线路额定电压计算线路产生的充电功率，并将其等分为两部分，便得var65.2var 1101038.42121242M M U B Q N c B -=⨯⨯⨯-=-=∆-将B Q ∆分别接于节点A 和b?，作为节点负荷的一部分。

两台变压器并联运行时，它们的等值电阻、电抗及励磁功率分别为kVkV3.3 某一额定电压为10kV 的两端供电网，如图所示。

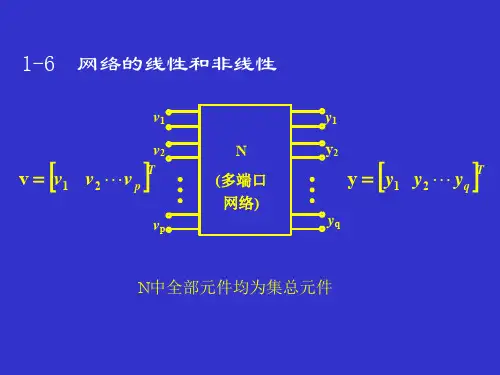
电网络理论1-66

i(
t
)

ic
(t
)

iL
(t
d
)
KVL u(t) ic (t) uc (t) dt q(t) u(t) uc (t) u(t) f (q(t))
u(t )、f
u(t) uL(t) iL(t)
d dt

(t
)

u(t
)

1
iL
(t
)
() 相同时，有 i(t) u(t)
1-7 网络的时不变性和时变性
v(t)
y(t)
时不变网络
u(t)
u(t)
性质：
0
(a)
t
vˆ (t) dv(t)
yˆ (t) dy(t)
0
(a)
t
dt
dt u(t-T
u(t-T)
t
vˆ (t) v(t)dt
t
)
yˆ (t) y(t)dt

0 T (b)
t
0 T (b)
W(to)，在to至t W(to，t) ，W (to
时
,t)
间内从电源
t uT ( )i( to
传送至n )d 式中
端口网络 u(t )、i(t )
的
能
量
为
分别为n端口网络的端口电压向量和端口电流向量。如果
对所有的初始时刻to，对所有的 t to，以及对所有的容许
信号向量偶(u(t), i(t)),均有
t
1-7 网络的时不变性和时变性
传统型时不变网络的定义：若一个网络中不含任何非源时变网络元件，则称该网络为时不变的。

国家电网考试之电网络分析理论：第二章补充内容

1 1 H I A ，P 1 ,2 1 1
1 1 x1 0 求 H X 0， 1 1 x1 0
T
B １，１
2019/4/22
25
x1 x2
0 -1 -1 0 H 0 ， 1 1 X 0 X B 0 1 1 0
的
解：①求特征根：
1 5 I A 2 3
I A 4 3 10
2
2 3
2
2
I A 0
1 2 j3 , 2 1
2019/4/22
6

②求特征量 i I A 0 1 5 I A 2 3
A 2 1 2
I A1 0
I A2 1
2019/4/22
28
1 对2×2阵 x2 x1 取 1 1 成立！？ I A2 1 1 12 1
1 1 x1 1 1 1 x 1 2
P AP J
1
2 1 I A 1 4
1 A1 ,2 1 ,2 0
AP PJ
1 2 3
A1, A2 1,1 2
A1 1
·
的相图
轾 2 过 Z (0) = 犏犏 2 臌
解：①求特征根
轾 l +1 - 2 [l I - A] = 犏犏 l - 1 臌5 l I - A = l - 1 + 10 = l + 9 l I- A = 0 l 1 = j3 l 2 = l 1

电网络理论习题解

Y33 = −Y31＋Y32
Y11 Y12 Yi Y21 Y22
Y31 Y32
Y13
Y23
Y33
(2) 将 VCVS 变换为 VCCS：i23 = −Ag3u43＝Ag3u34，原始不定导纳矩阵为
g1
0
Y i'
0
0
g1
g 2 g3 sC g3 g 2 sC
0 g 3 Ag 3 g3 Ag 3
本题中 LTiL(0−) = [0 0 0 0 L5iL5(0−) 0 0]T，uC(0−)/s = [0 0 0 0 0 uC6(0−)/s uC7(0−)/s]T
U1(s) 0 g U2 (s) g 0
U U
3 4
(s) (s)
g 1
g 0
U
5
(s)
0
1
U6 (s) 0 1
U7 (s) 1 0
.
阅前提示：以下习题答案仅供参考，未经仔细核实，定有不少谬误，如有发现，请及时指正，谢谢！
习题 1
1. 一个非线性电阻元件的电压、电流分别为：u(t) = cost，i(t) = cos4t(u、i 参考方向一致)。求该电阻元件的构成关系。
i(t) = cos4t = 8cos4t8cos2t+1 = 8u4(t)8u2(t)+1
2．二端元件的电压、电流分别为 u(t) = 2cost，i(t) = 0.5cost，试确定元件类型(即属于电阻、电感、电容等中的哪一类)，并论证其无源性。
i(t) = 0.5cost = 0.50.5u(t)
T
T
W(t0 , t)
u()i()d
0
2 cos(0.5 cos)d T 0

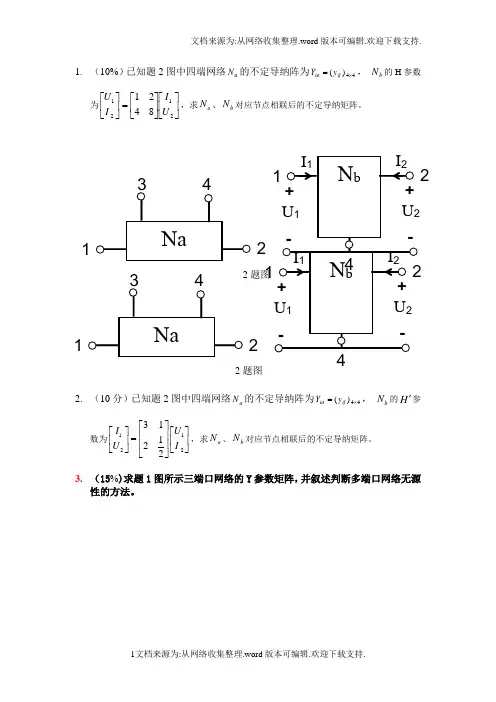
电网络分析理论第3、4章练习题(2)

1. （10%）已知题2图中四端网络a N 的不定导纳阵为44)(⨯=ij ia y Y ， b N 的H 参数为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡21218421U I I U ，求a N 、b N 对应节点相联后的不定导纳矩阵。

2. （10分）已知题2图中四端网络a N 的不定导纳阵为44)(⨯=ij ia y Y ， b N 的H '参数为112231122I U U I ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，求a N 、b N 对应节点相联后的不定导纳矩阵。

3. （15%)求题1图所示三端口网络的Y 参数矩阵，并叙述判断多端口网络无源性的方法。

222题图22题图题1图4. （15%）已知四端口网络Na 的不定导纳阵为44)(⨯=ij iay Y ，求增加C ，G后的不定导纳阵。

题2图5. （15%）图示两线性网络1N 和2N ，其节点方程（设均以大地为参考节点）分别为列出下列三种情况下的节点电压方程或改进节点电压方程（1）将节点对①－④，②－⑤用阻抗为零的导线联接；（7分）（2）将节点对①－④，②－⑤用联线联接，设每根联接线的阻抗为l Z ：（7分）（3）将节点对①－④，②－⑤下图所示的互感元件联接。

（6分）6. （15%）试列写题3图所示网络的改进节点方程。

题3图7. （20%）图（a ）为桥T 型网络，当在1、2端加上电导G 时，求1）改变后的网络图（b ）的不定导纳阵'i Y ；2）求图（c ）桥T 型二端口网络的短路导纳阵。

8. （15%）建立图示动态电路的s 域改进节点方程（MNA ）方程（设电路中动态元件的初始储能为零）9. （15%）列出图示电路的混合参数方程。

L 2142I 1 α U 110. （20%）图示两线性网络1N 和2N ，其节点方程（设均以大地为参考节点）分别为现将节点对①－④，②－⑤用联接线相联，问当：（1）忽略联接线的阻抗，（2）设每根联接线的阻抗为l Z 时，网络方程如何变化。

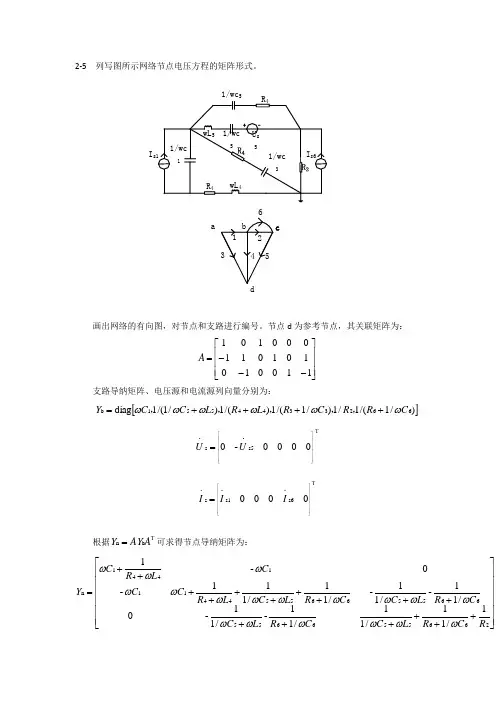
电网络理论

2-5 列写图所示网络节点电压方程的矩阵形式。

acI 1/wc画出网络的有向图，对节点和支路进行编号。

节点d 为参考节点，其关联矩阵为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=110010101011000101A支路导纳矩阵、电压源和电流源列向量分别为：[])/1/(1/1)/1/(1)/(1)/1/(1diag 6623344551b C R R C R L R L C C Y ωωωωωω++++=，，，，，T⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=0000.-0.s5s U UT⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=0.000..s6s1s I I I根据T=A AY Y b n 可求得节点导纳矩阵为：⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++++++=2665566556655665544111441n 1/11/11/11-/11-0/11-/11-/11/111-0-1R C R L C C R L C C R L C C R L C L R C C C L R C Y ωωωωωωωωωωωωωωωωωω根据s b .s .n .AY -U I A I =可求得节点等效电流源列向量为：⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++=s 55s6s 55s1s1.n ./11../11-.-.U L C I U L C I I I ωωωω所以节点电压方程的矩阵形式为：⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++++++s 55s6s 55s1s1c b a 2665566556655665544111441./11../11-.-....1/11/11/11-/11-0/11-/11-/11/111-0-1U L C I U L C I I U U U R C R L C C R L C C R L C C R L C L R C C C L R C ωωωωωωωωωωωωωωωωωωωωωω2-8 网络如图所示，参考方向已选定，如果选取支路4、5、6为树，且已知电源的角频率为ω，列写网络的割集方程的矩阵形式。

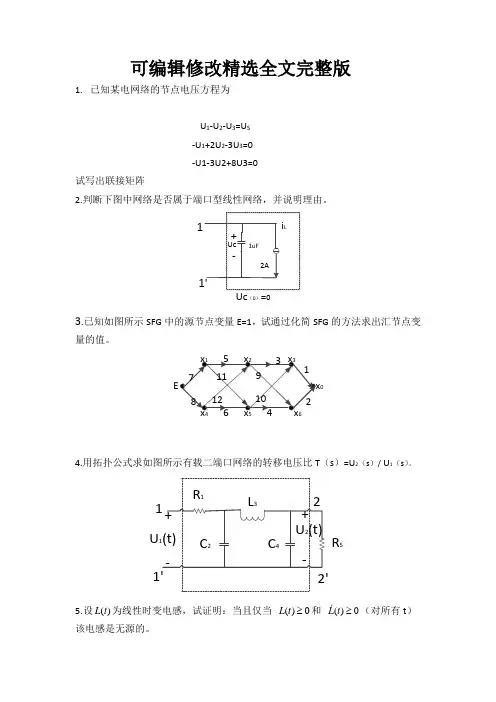
电网络理论试卷2精选全文

可编辑修改精选全文完整版1. 已知某电网络的节点电压方程为U 1-U 2-U 3=U S-U 1+2U 2-3U 3=0 -U1-3U2+8U3=0试写出联接矩阵2.判断下图中网络是否属于端口型线性网络，并说明理由。

1（0）03.已知如图所示SFG 中的源节点变量E=1，试通过化简SFG 的方法求出汇节点变量的值。

4.用拓扑公式求如图所示有载二端口网络的转移电压比T （s ）=U 2（s ）/ U 1（s ）。

R 1R 5C 2C 4L 3U 2(t)U 1(t)++--122'1'5.设()L t 为线性时变电感，试证明：当且仅当 ()0L t ≥和 ()0L t ≥（对所有t ）该电感是无源的。

6. 用Mason 公式求如图所示SFG 的图增益y T u。

d7.用灵敏度恒等式求下图所示网络的输入阻抗Zin 对各参数的灵敏度1inZ R S 。

答案： 1解：2解：1'12Ai L1uF（0）0U(t)i (t)+-Uc因为网路的端口型线性性质包括齐次性和可加性。

如图，()2dui t cdt=+ ，因为网路中含有独立的电流源，对输入输出有影响，所以端口网路不具备齐次性也不具备可加性，因此端口网路是端口型非线性网路。

3解：1.消去节点x1,x43131125x 0x 2x 3x 5x 61249102.消去节点x2,x53.消去节点x3,x6E4.解：电路拓扑图为：根据拓扑电路图，找出全部2-树（1,1’），2-树（12,1’）, 2-树（12’,1’），列出树枝编号如下：2-树（1,1’）：13 , 23,24,25,34,35 2-树（12,1’）:13 2-树（12’,1’）:无有载二端口网络的电压转移函数的拓扑公式为：2212,1'12',1'22'1212'21111,1'()()()()()T y T y U s U s T y ∑-∑-==∑ 得出结果：1322242413353531()11R SL T S C SC C S C C R SL L R L R SL =+++++5.解：220?0000:()1t ()()()[()]()()()21t ()()()2()(,)()()()()()ttt t t L t i t di W t u i d L i d L t i t d W t L t i t d t W t t u i d u t L t i t dtψττττττττψτττ-∞-∞===⋅=====+⎰⎰⎰0证明对于元件特性为()()()的线性时变电感，时刻电感元件的储能为：则时刻储能为：在[t ,t]时间区间，电源供给电感的能量为：其中02022200220000()()()()(),()(,)()()()()()111()()()()()()22211()(,)()()()()22()(,)0ttt t t t t t L t i t di t dL t i t L t dt dt W t t L i i d L i d L t i t L t i t L i d W t W t t L t i t L i d W t W t t τττττττττττττ===+=-++=++≥⎰⎰⎰⎰从而所以要该电感无源则成立即可故当且仅当00L t L t ≥≥（）和（）对所有的t 恒成立时，原命题成立得证6解：经分析可得图中回路有5个，不存在二阶回路，故1[d abc abe bcf ]1d abc bcf bdefbdef ∆=-----+=+++-前向路径有两条：11,1P abc =∆=22,1P d =∆=故11221P P y abc d T u d abc abe bcf bdef∆+∆+===∆+++++其回路如下:7. 解：由图可知：321321)(R R R R R R Z in +++=则321323211321323211)()(1)(32111321113211321132132111R R R R R R R R R S R R R R R S R R R R SSS S S S R R R R R R R R R R R R R R R R R R R R R R R R R Z R in+++=++-=++++++-+=-==++++++++。

电网络理论简答题总结

电网络理论考题总结（简答题）【1】N端口线性时变与非线性的电感元件、电容元件的定义，并举例。

线性时变电感：N端口元件满足关系，且为矩阵，与Ψ=L i(t)L(t)(N-1)×(N-1)磁链及电流无关。

线性时变电容：N端口元件满足关系，且为矩阵，与q=C v(t)C(t)(N-1)×(N-1)电荷及电压无关。

（电阻定义类似）☛☛☛一个不含时变元件的电路称为时不变电路，否则为时变电路。

若一个电容元件的库伏特性不是一条通过坐标原点的直线，该种电容就是非线性电容；电感的磁通链和电流间的函数关系为韦安特性，若电感元件的韦安特性不是一条过坐标原点的直线，则为非线性电感元件。

【2】N端口非线性电路的定义。

一是根据电路元件的特性来定义（含非线性元件即为非线性电路）；二是根据输入输出关系来定义（端口型定义，网络输入输出关系不同时存在可加性和齐次性时即为端口型非线性网络）。

【3】高阶有源滤波器的设计步骤。

（根据相应实例写步骤）一般：高阶：给出设计指标，根据设计指标选择逼近函数；确定阶数、找到对应的无源网络模型；选择实现方法（级联、多路反馈、无源模拟等）；参数退归一化；注意补偿、修正电路（直流通路）。

选取逼近函数类型；根据设计要求确定阶数；找到对应逼近函数的无源低通网络模型；选择实现方法（级联、多路反馈、无源模拟等）；根据要求的滤波器类型进行变换（如仿真电感、F D N R、L F等）；参数退归一化。

二阶：S a l l e n K e y---L P、H P、B P、高通、陷波或者双积分回路---K H NT T。

【4】高阶有源滤波器的分类。

按使用的器件：仿真电感、F D N R、C CⅡ、跨导电容、运放；按设计方法：级联法、多路反馈法、无源模拟法。

【5】高阶有源滤波器的设计方法，它们的共同点和特点。

❶级联法：级联滤波器易于调节和优化动态范围，但设计时各极、零点的搭配要慎重考虑，以实现较低灵敏度。

电力网络分析计算试题及答案版可编辑】P

答：中等长度输电线路的集中参数等值电路有型等值电路和型等值电路两种，电力系统分析计算中采用型等值电路。因为电力系统分析计算通常采用节点电压法，为减少独立节点的数目，所以采用型等值电路。
2、为什么要采用分裂导线？分裂导线对电晕临界电压有何影响？
答：采用分裂导线是为了减小线路的电抗，但分裂导线将使电晕临界电压降低，需要在线路设计中予以注意。
解：
1）变压器参数计算
①电阻计算
、、
②电抗计算
③电纳、电导计算
2）变压器等值电路
11、某电力系统，接线如图所示，各元件的技术参数标示于图中，不计变压器电阻、导纳和输电线路导纳，画出其等值电路，并计算
①按变压器额定变比归算到220KV侧的有名制参数
②按变压器平均额定变比归算到220KV侧的有名制参数
2、按变压器平均额定变比计算参数有名制
①输电线路
线路：
线路：
线路：
线路：
电缆线路：
②变压器
变电站B：
变电站C：
3、按变压器额定变比计算参数标幺制
①先将参数有名值按变压器额定变比归算到220KV侧，然后利用220KV侧基准值计算参数标幺制。
取220KV侧基准值、 ,则。利用前面按变压器额定变比求得的归算到220KV侧的参数有名制和选定的基准值，计算系统参数标幺值。
第一次作业参考答案
1、、电能生产的主要特点有哪些？
答：电能生产的主要特点可以归纳为以下三点。①电能生产的连续性特点；由于电能不能大量储存，电能的生产、输送和消费是同时完成的。②电能生产瞬时性的特点；这是因为电能的传输速度非常快（接近光速），电力系统中任何一点发生故障都马上影响到整个电力系统。③电能生产重要性的特点；电能清洁卫生、易于转换、便于实现自动控制，因此国民经济各部门绝大多数以电能作为能源，而电能又不能储存，所以电能供应的中断或减少将对国名经济产生重大影响。

电网络分析理论线性时变因果无源总结和例题

则：dy3(t) 3 df3(t)
dt
dt
dy1(t) 3 df1(t) , dy2 (t) 3 df2 (t)
dt
dt dt
dt
d[ay1(t)] 3 d[af1(t)] , d[by2 (t)] 3 d[bf2 (t)]
dt
dt
dt
dt
二式相加得： d[ay1(t) by2 (t)] 3 d[af1(t) bf2 (t)]
设 f3(t) af1(t) bf2(t) y3(t) 则：y3(t) 8sin[ f3(t)] 8sin[af1(t) bf2(t)]
y3(t) 8sin[af1(t) bf2 (t)] a{8sin[ f1(t)]} b{8sin[ f2 (t)]} y3(t) 8sin[ f3(t)] ay1(t) by2(t)
6.连续时间系统与离散时间系统
如果系统的输入和输出都是时间的连续函数，这个系统就称为连续时间系统；如果系统的输入和输出都是时间离散函数，这个系统就称为离散时间系统。
连续系统中传输和处理的是连续信号。
离散系统中传输和处理的是离散信号。在实际工作中系统中长将两系统组合使用，这种情况称为混合系统
满足（1）、（2）、（3）则系统为线性，
有一个不满足则系统为非线性。
2.时变系统与非时变系统
时不变特性是指系统的零输入状态输出波形仅取决于输入波形与系统特性而与输入信号接入系统的时间无关。设系统的输入 f (t) ，
输出为 y(t)
若 : f (t) y(t) f (t t0 ) y(t t0 ) t0为任意常数。
（2）可加性
若 : f1(t) y1(t) f2 (t) y2 (t) 则：f1(t) f2 (t) y1(t) y2 (t)

电网络理论习题

6.3 用梯形电路实现下列驱点函数(分别用 FosterⅠ、Ⅱ；CauerⅠ、Ⅱ这四种形式)：
(a)
Z ( s)
=
s4
s3 + 4s + 12s2 +
27
,
(b)
Z ( s)
=
(s2 + 1)(s2 + s(s2 + 2)
3)
.
6.4 试确定下列驱点函数能否用 RC 一端口来实现，能实现的实现之(FosterⅠⅡ、CauerⅠⅡ)。
1.5 一个二端电路元件的电压与电流的关系可写为 i = D d 2u dt 2
元件是有源的。
（D 为非零常数），证明该
1.6 图示二端口网络中，非线性电阻的特性为：
i1 1Ω
1Ω i2
+
+
+
(1) uR = iR2 ; (2) uR = iR3 . 试判断以上两种情况下此二端口是无源的还是有源的？
3.7 用直接法列写题 3.2(b)电路的改进节点方程。
4.1 求下列网络复杂性的阶数。
+
+
+
-
-
-
(a)
C4
+ r i1 -
i1 * L6
iS
+ u3-
R1
+
C3μ u3
L5 -
i5 *
M
R2 β i5
题图 3.6
+ -
+ (b)
++ u ku --
(c )
4.2 试写出图示电路的状态方程及输出方程。
式：
(a)
Zi d
=

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

阅前提示：以下习题答案仅供参考，未经仔细核实，定有不少谬误，如有发现，请及时指正，谢谢！习题11. 一个非线性电阻元件的电压、电流分别为：u(t) = cos ωt ，i(t) = cos4ωt(u 、i 参考方向一致)。

求该电阻元件的构成关系。

i(t) = cos4ωt = 8cos 4ωt -8cos 2ωt+1 = 8u 4(t)-8u 2(t)+12．二端元件的电压、电流分别为u(t) = 2cost ，i(t) = 0.5-cost ，试确定元件类型(即属于电阻、电感、电容等中的哪一类)，并论证其无源性。

i(t) = 0.5-cost = 0.5-0.5u(t)0T d )cos 5.0(cos 2d )(i )(u )t ,t (W TT0<-=ττ-τ=τττ=⎰⎰电阻，有源。

3．有两个二端元件，其电压、电流关系方程分别为dt)t (di )t (2i u(t) (2) dt du(t)2u(t)i(t) )1(2== 试确定各元件类型，并论证各元件的无源性。

（1）因为dt du dt dq i 2==，所以q = u 2+A ，A 为常数，电容元件。

)t (u 32d d du u 2u d )(i )(u )t (W 3t t =ττ⨯=τττ=⎰⎰∞-∞-，当u<0时，W(t)<0，有源。

（2）因为dtdi 32dt d u 3=ψ=，所以ψ = 32i 3+A ，电感元件。

0)t (i 21id d di i 2d )(i )(u )t (W 4t 2t ≥=τ⨯τ=τττ=⎰⎰∞-∞-，无源。

4．如题图1所示二端口电路，其中非线性电阻r 的构成关系为u r = i r 3。

此二端口是有源的还是无源的。

p = u 1i 1+u 2i 2 = i = (i 1R 1+u R )i 1+(i 2R 2+u R )i 2 = i 12R 1+i 22R 2+i R 4≥00pd d )()()t (W tt=≥τ=τττ=⎰⎰∞-∞-i u ，无源。

5．图1.23中对四种线性受控源给出了其一种零泛器模型。

证明各含零泛器电路与对应受控源间的等效性。

6．图1.16给出了用运放和电阻元件实现的CNIC 和VNIC 的电路。

试证明各含运放电路与对应的负阻抗变换器间的等效性。

题图1习题21. 对题图1所示有向图：(1)若以节点④为参考节点，写出关联矩阵A ；(2)若选树T(1，2，3，4，5)，写出基本割集矩阵Q f 和基本回路矩阵B f 。

⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------=1 1 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 11 10 9 8 7 6 5 4 3 2 1 A⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------=1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 1 1 1 0 0 0 11 10 9 8 7 6 5 4 3 2 1 f B⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----= 0 0 0 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 11 10 9 8 7 6 5 4 3 2 1 f Q2. 已知图G 对应于某一树的基本割集矩阵如下，(1)试写出对应于同一树的基本回路矩阵；(2)作出对应的有向图。

⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--------=0 1 1 0 0 0 1 0 0 0 00 0 1 1 1 0 0 1 0 0 01 1 0 1 1 0 0 0 1 0 00 0 0 1 1 1 0 0 0 1 01 0 0 0 0 1 0 0 0 0 1f Q ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------=-= 0 0 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 1 1 5 4 3 2 1 T l t Q B基本回路矩阵：B f = [B t 1l ]网络图如右所示，图中红线表示的是树枝。

3. 若考虑网络中电感和电容的初始值不为0，试写出矩阵表示的网络VCR 方程。

图2.11(a)电路中，电感、电容的初值分别为i L5(0−)、u C6(0−)和u C7(0−)，求支路电压向量U b (s)。

1③题图1 ①② ③ ⑤ ⑥设初值向量i L (0−)，u C (0−)，变换为s 域的电压源L T i L (0−)，u C (0−)/s ，L 为支路电感向量。

支路电压向量 U b (s) = Z b (s)[I b (s)+I s (s)]−U 's (s) 支路电流向量 I b (s) = Y b (s)[U b (s)+U 's (s)]−I s (s) 考虑初值时上式中 U 's (s) = U s (s)+L T i L (0−)−u C (0−)/s本题中L T i L (0−) = [0 0 0 0 L 5i L5(0−) 0 0]T ，u C (0−)/s = [0 0 0 0 0 u C6(0−)/s u C7(0−)/s]T⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----0 0 0 0 0 )0(i s 1)0(u C )0(u C )s (U G 1 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 0 0 0 G g g 0 C s /sL 1 0 0 0 g sC 0 0 G 0 g 0 )s (U )s (U )s (U )s (U )s (U )s (U )s (U 5L 6C 67C 7s 413657476543214. 用导纳矩阵法求题图2所示网络的支路电压向量。

作出网络图，以结点5为参考结点，取树(1、3、4、6、8)，列出矩阵。

⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡= 1- 0 0 1- 0 0 0 0 0 1- 0 0 0 0 0 1- 1 0 0 0 0 1- 1- 0 0 0 1- 0 1- 1 0 0 0 0 0 0 1 0 1 1 8 7 6 5 4 3 2 1 A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡= 0 1 1- 0 1 0 0 1-1- 0 1- 1 0 1- 0 0 0 0 0 0 1- 1- 1 0 87 6 5 4 3 2 1 f B ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1/R 1/R 1/R 1/sL 1/sL sC C s C s 87654321b Y0 0 (s)I s1题图2[]TC3C2s Ts8s1s 0 0 0 0 0 s )0(U s )0(U 0 (s)I - 0 0 0 0 0 0 I (s)⎥⎦⎤⎢⎣⎡--==--U I)s ( )s ( )s ()s ( )s ()s (s b 1f b s 1f b b U 0AY B AY I 0A B AY U ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=--5. 在题图3所示电路中，以I 5和I 2为直接求解的支路电流，列写改进结点方程。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----==0 1 0 0 0 1 10 1 1 0 1 0 0 1 0 1 1 0 0 1 ] [5 2 7 6 4 3 1 x E 0A A A A Y 0 = diag[G 1 G 2 G 4 G 6] Y x = diag[G 2 G 5]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+=31141610n G G 0 G 0 G 0 G 0 G G )s (Y ⎥⎦⎤⎢⎣⎡-=0 0 G G G 0 )s (522T x x A YI s (s) = [−I s1 0 0 0]T ，U s (s) = [U s1 0 0 −U s6]T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=1s 1s16s 61s 11s 0n U G I 0 U G U G I )s (I改进结点方程⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++--=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--+-----+0 0U U G I 0U G U G I I I I U U U 1 0 0 0 0 G 0 1 0 G G 0 0 0 0 0 1 1 0 1 0 G G 0 G 0 1 1 0 G 0 1 0 1 G 0 G G 7s 1s 1s16s 61s 11s 5273n 2n 1n 52231141616. 列写题图5所示网络以两条5Ω电阻支路为撕裂支路的撕裂结点方程。

题图3习题31．利用不定导纳矩阵计算题图1所示二端口网络的短路导纳矩阵。

图示电路原始不定导纳矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-----+---+=2122212222111111'i sC sC G G sC sC G G 0 0 sC 0 sC G G sC 0 G sC G Y 消除不可及端子4得三端网络不定导纳矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----+------+=442224422441244224422221442114412442114421211'i Y G G Y C s G Y C s G Y C s G Y C s sC G Y C s C s G Y C s G Y C s C s G Y C s sC G Y ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+-----+=442222144211442114421211i Y C s sC G Y C s C s G Y C s C s G Y C s sC G Y2．题图2所示网络，试求：(1) 根据不定导纳矩阵的定义求三端网络的不定导纳矩阵；(2) 用首先形成网络的原始不定导纳矩阵的方法，求三端网络的不定导纳矩阵。

210V题图5Ω6V 122'题图12(1) 将VCVS 变换为VCCS ，2、3端接地，1端接电源u 1，计算得sCg g )sC g (g Y 212111+++= sCg g )sC Ag g (g Y 2132121++++-=sCg g g Ag Y 213131++=1、3端接地，2端接电源u 2，计算得 Y 12 = −Y 11311131122g Y g Ag Y Y +-= 3111332g Y g Ag Y -=矩阵第3列可由1、2列相加取负可得 Y 13 = 0 Y 23 = Y 21＋Y 22 Y 33 = −Y 31＋Y 32⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211i Y Y Y Y Y Y Y Y Y Y (2) 将VCVS 变换为VCCS ：i 23 = −Ag 3u 43＝Ag 3u 34，原始不定导纳矩阵为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++---+-----+-++-=sC g g 0 sC g g Ag Ag g g 0 sC Ag g Ag g sC g g 0 g 0 0 g 2121333332333211'i Y 消除不可及端子4可得三端网络不定导纳矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-++-+-+++-++++-+--=3344233443133443223244321442144211i Ag g Y )sC g (Ag g Y g Ag Ag g Y )sC Ag g )(sC g (sC g g Y )sC Ag g (g 0 Y )sC g (g Y g g Y3．题图3所示一个不含独立源的线性三端网络，其输出端3开路。

电网络理论习题解

页数:20
重大电网络理论习题解

页数:9
电网络理论习题解

页数:20
电网络理论与分析滤波器的电抗设计

页数:28
电网络理论

页数:117
电网络理论第三章五节撕裂法

页数:44
电网络分析选论梁贵书

页数:182
电网络理论图论方程综合习题答案作者周庭阳

页数:4
同等学力申硕《电气工程学科综合水平全国统一考试》章节题库(电网络理论与电磁场数值分析)

页数:11
重大电网络理论习题解

页数:9

电网络理论习题解

合集下载

电网络理论1-66

电力网络分析计算试题及答案可编辑

最新【精选资料】电网络理论课后题答案讲学课件

电力网络分析计算试题及答案可编辑

电网络理论1-66

国家电网考试之电网络分析理论：第二章补充内容

电网络理论习题解

电网络分析理论第3、4章练习题(2)

电网络理论

电网络理论试卷2精选全文

电网络理论简答题总结

电力网络分析计算试题及答案版可编辑】P

电网络分析理论线性时变因果无源总结和例题

电网络理论习题

文档推荐

最新文档

电网络理论习题解

合集下载

电网络理论1-66

电力网络分析计算试题及答案 可编辑

最新【精选资料】电网络理论课后题答案讲学课件

电力网络分析计算试题及答案可编辑

电网络理论1-66

国家电网考试之电网络分析理论：第二章补充内容

电网络理论习题解

电网络分析理论第3、4章练习题(2)

电网络理论

电网络理论试卷2精选全文

电网络理论简答题总结

电力网络分析计算试题及答案版可编辑】P

电网络分析理论线性时变因果无源总结和例题

电网络理论习题

文档推荐

最新文档

电力网络分析计算试题及答案可编辑