DP问题不完全总结
- 格式:doc
- 大小:25.50 KB
- 文档页数:12

一、故障现象分析处理1、只要送电就偶尔报通讯故障,各子站随机出现通讯故障。
粗略检测回路电阻,阻值为112Ω左右,阻值在正常范围内。
对故障1,首先检查接线顺序问题,通讯DP头A、B端子的电缆是否有接反现象,其次看接线是否有不良现象,然后测量总线上的回路电阻值,理论上电阻值在110Ω左右就没有问题;偶尔报通讯故障一般就是信号衰减的问题,主要有接线和通讯头两方面原因。
2、各子站随机出现通讯故障。
粗略检测回路电阻,阻值为85Ω,阻值不在正常范围内。
对故障2,检查两端的DP通讯头,发现末尾的DP通讯头阻值异常,应该是220Ω,却只有140Ω左右,更换正常DP通讯头后,恢复正常。
3、运行时偶尔22~25子站报通讯故障,不运行时没有问题。
粗略测量阻值为112Ω,阻值在正常范围内。
对故障3,接线和通讯头均正常,测量阻值为112Ω,阻值在正常范围内,电缆也没有新增。
但是运行时报故障,判断是设备运行导致故障的发生,应是电磁干扰、变频电机在运行时影响通讯所致。
在电缆隧道中,通讯电缆与电机的动力电缆是在一起的。
为证实这一判断把这4个子站所带的电机全部停下,然后试车,发现不再报通讯故障。
因此,故障原因就是电磁干扰。
这种情况需重新敷设,避免通讯电缆和动力电缆同隧道。
二、问题分析1、单个从站故障现场总线控制系统中的从站基本都是安装在现场的设备,而现场环境比较恶劣,灰尘、雨水、振动等会影响现场设备的使用寿命。
当某个从站故障时,它会通过总线向主站发出大量的故障信息,如果总线中某处数据传输存在瓶颈,就有可能造成网络堵塞,导致所有从站与主站失去通信。
在闭冷水系统中,水的压力高、流速快,管道会有较大的振动,造成个别电动门频繁故障,故障电动门通过总线向DCS卡件发送大量报警信息。
而这个系统中光电转换器就是一个瓶颈,报警信息足够多时会使光电转换器出现数据堵塞而中断网络。
网络一旦中断,所有现场总线电动门就无法在DCS中操控。
只有处理好故障电动门,同时清空光电转换器数据,才能使网络恢复正常。

dp通讯故障快速处理方法
1.初步检查:首先检查网络线路是否接触良好,是否有过长的线路导致信号衰减。
同时,查看网络负载是否过大,因为过大的负载也可能导致通讯不稳定。
2.硬件检查:检查所有硬件的基本接线及通信原理,确保PLC、触摸屏、ET200等主要硬件设备工作正常。
特别注意检查M12通信及电源接头是否接触良好。
3.使用DP网络寻找故障点:采用逐一加站原则,先甩开所有从站,从DP网路离CPU最近的第一个DP站开始诊断。
如果全线只有某一个站报警,直接判断该站为通讯故障位置。
如果全线只有末站或末段报警,在故障段继续采用逐一加站原则进行诊断。
如果全线报警,则直接采用逐一加站原则进行诊断。
4.软件诊断:使用相关的诊断软件(如ProfiTrace)对网络进行诊断,查看网络拓扑结构,以便更好地定位故障点。
5.增加抗干扰设备:对于干扰严重的区域,可以尝试增加抗干扰设备,以提高通讯的稳定性。
6.替换法:如果通过以上方法仍无法确定故障点,可以尝试使用替换法,逐一替换可能存在问题的硬件设备,以便快速找到故障点。


Dp状态设计与方程总结1. 不完全状态记录 (2)<1>青蛙过河问题: (2)<2>利用区间dp (3)2.背包类问题 (4)<1> 0-1背包,经典问题 (4)<2>无限背包,经典问题 (4)<3>判定性背包问题 (4)<4>带附属关系的背包问题 (5)<5> + -1背包问题 (5)<6>双背包求最优值 (7)<7>构造三角形问题 (9)<8>带上下界限制的背包问题 (10)3.线性的动态规划问题 (13)<1>积木游戏问题 (13)<2>决斗(判定性问题) (13)<3>圆的最大多边形问题 (14)<4>统计单词个数问题 (14)<5>棋盘分割 (14)<6>日程安排问题 (15)<7>最小逼近问题(求出两数之比最接近某数/两数之和等于某数等等) (15)<8>方块消除游戏(某区间可以连续消去求最大效益) (15)<9>资源分配问题 (15)<10>数字三角形问题 (16)<11>漂亮的打印 (16)<12>邮局问题与构造答案 (17)<12>最高积木问题 (19)<13>两段连续和最大 (19)<14>2次幂和问题 (20)<15>N个数的最大M段子段和 (20)<16>交叉最大数问题 (20)4.判定性问题的dp(如判定整除、判定可达性等) (22)<1>模K问题的dp (22)<2>特殊的模K问题,求最大(最小)模K的数 (22)<3>变换数问题 (24)5.单调性优化的动态规划 (25)<1>1-SUM问题 (25)<2>2-SUM问题 (26)<3>序列划分问题(单调队列优化) (27)6.剖分问题(多边形剖分/石子合并/圆的剖分/乘积最大) (28)<1>凸多边形的三角剖分问题 (28)<2>乘积最大问题 (28)<3>多边形游戏(多边形边上是操作符,顶点有权值) (29)<4>石子合并(N^3/N^2/NLogN各种优化) (29)7.贪心的动态规划 (31)8.状态dp (33)<1>牛仔射击问题(博弈类) (33)<2>哈密顿路径的状态dp (35)<3>两支点天平平衡问题 (35)<4>一个有向图的最接近二部图 (36)9.树型dp (38)<1>完美服务器问题(每个节点有3种状态) (38)<2>小胖守皇宫问题 (40)<4>树中漫游问题 (41)<5>树上的博弈 (42)<6>树的最大独立集问题 (42)<7>树的最大平衡值问题 (42)<8>树的限制节点数坎边问题 (43)1.不完全状态记录<1>青蛙过河问题:由于河的长度十分长,达到10^9,所以不可能用dp[i]表示在坐标i时踩到的最少石头数,需要换种状态记录方式来压缩。
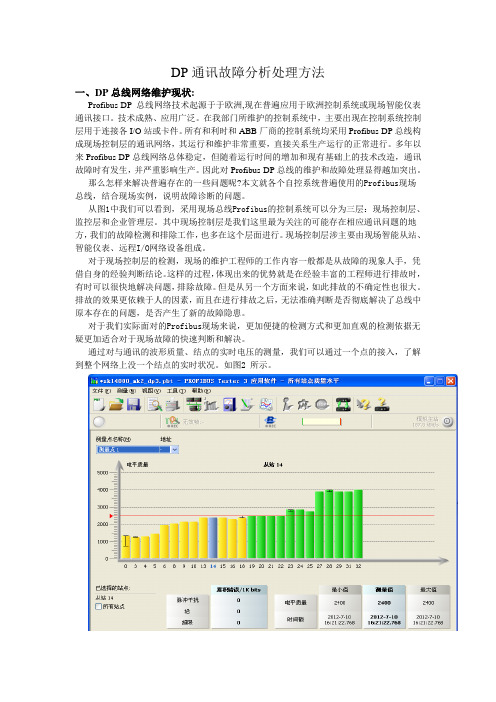
DP通讯故障分析处理方法一、DP总线网络维护现状:Profibus-DP总线网络技术起源于于欧洲,现在普遍应用于欧洲控制系统或现场智能仪表通讯接口。
技术成熟、应用广泛。
在我部门所维护的控制系统中,主要出现在控制系统控制层用于连接各I/O站或卡件。
所有和利时和ABB厂商的控制系统均采用Profibus-DP总线构成现场控制层的通讯网络,其运行和维护非常重要,直接关系生产运行的正常进行。
多年以来Profibus-DP总线网络总体稳定,但随着运行时间的增加和现有基础上的技术改造,通讯故障时有发生,并严重影响生产。
因此对Profibus-DP总线的维护和故障处理显得越加突出。
那么怎样来解决普遍存在的一些问题呢?本文就各个自控系统普遍使用的Profibus现场总线,结合现场实例,说明故障诊断的问题。
从图1中我们可以看到,采用现场总线Profibus的控制系统可以分为三层:现场控制层、监控层和企业管理层。
其中现场控制层是我们这里最为关注的可能存在相应通讯问题的地方,我们的故障检测和排除工作,也多在这个层面进行。
现场控制层涉主要由现场智能从站、智能仪表、远程I/O网络设备组成。
对于现场控制层的检测,现场的维护工程师的工作内容一般都是从故障的现象人手,凭借自身的经验判断结论。
这样的过程,体现出来的优势就是在经验丰富的工程师进行排故时,有时可以很快地解决问题,排除故障。
但是从另一个方面来说,如此排故的不确定性也很大。
排故的效果更依赖于人的因素,而且在进行排故之后,无法准确判断是否彻底解决了总线中原本存在的问题,是否产生了新的故障隐患。
对于我们实际面对的Profibus现场来说,更加便捷的检测方式和更加直观的检测依据无疑更加适合对于现场故障的快速判断和解决。
通过对与通讯的波形质量、结点的实时电压的测量,我们可以通过一个点的接入,了解到整个网络上没一个结点的实时状况。
如图2 所示。
通过以上的手段,我们能够在现场实际连接了检测工具之后,快速地检测出同一网段上每个结点的实时状态。

动态规划总结----By fj 动态规划,一种神奇的算法。
搞了这么久的dp,我们从初识它,到理解它,到运用它,她那神秘的面纱逐渐被揭下。
对它的理解:一种特殊的递推,一种剪枝的搜索。
它分多阶段,状态转移只受前一状态影响。
这期间,考了许多次考试,虽然考得不是很理想,但收获还是多多的。
以下是部分题目的解法及心得体会……Stone(2.11上午)完成这题后,感触颇多!1.解法的多样性。
法1)转移:f[i,j]表示将第i堆到第j堆石子合并所需要的最少代价;f[i,j]=f[i,k]+f[k+1,j]+w[i,j]; W[I,j]表示将这两部分石子合并的费用(实为i到j的每堆石子的代价和,可预先处理g[i]表示从第1个到第i堆石子的代价和,则w[I,j] = g[j] – g[i-1])边界:f[I,i+1] = g[i+1]-g[i-1]目标:f[1,n]复杂度:O(n^3)显然对于数据范围而言是出不来的。
法2)算法:从第一堆石子往后找,直到找到某堆石子的前堆石子数小于或等于其后堆石子数,将这堆石子与前堆石子合并,得到新堆;从新堆处往前找,直到某堆石子数大于新堆石子数,将新堆石子插入到这堆石子后面;重复以上操作直到只剩下一堆。
预处理:c[0]:=maxlongint;c[n+1]:=maxlongint;数据结构:链表(记录+指针);2.建立指针链接时,思路要清晰。
建立指针链接时,没开发的域为空;例:new(p);q:=p^.next;则q=nil。
故不能进行如下操作:p^.ne:=p^.next^.last;而应:new(pp);pp^.last:=p;p^.next:=pp.brush(2.11上午)看了解题报告后,其优化还是不懂,就选了未优化的算法。
但是10000*10000的数组空间不够,我真是个傻子,此处可以轻易将第二维压缩,通过罗雨屏的指点,空间立刻压缩到10000*100!真神!罗雨屏咋就那么聪明呢?Brike(2.11下午)开始没做出来,看了孟来俊的总结(知识点\杂新建文件夹(2)\常用算法\动态规划\动态规划-孟来俊)和王准轩的程序后发现他们的算法有点不同,弄得我迷迷糊糊。
总结做的……不是令人满意的结果,历时一个月,靠,大梁半个月……关键子工程(project.c/cpp/pas)在大型工程的施工前,我们把整个工程划分为若干个子工程,并把这些子工程编号为1、2、……、N;这样划分之后,子工程之间就会有一些依赖关系,即一些子工程必须在某些子工程完成之后才能施工。
由于子工程之间有相互依赖关系,因此有两个任务需要我们去完成:首先,我们需要计算整个工程最少的完成时间;同时,由于一些不可预测的客观因素会使某些子工程延期,因此我们必须知道哪些子工程的延期会影响整个工程的延期,我们把有这种特征的子工程称为关键子工程,因此第二个任务就是找出所有的关键子工程,以便集中精力管理好这些子工程,尽量避免这些子工程延期,达到用最快的速度完成整个工程。
为了便于编程,现在我们假设:(1)根据预算,每一个子工程都有一个完成时间。
(2)子工程之间的依赖关系是:部分子工程必须在一些子工程完成之后才开工。
(3)只要满足子工程间的依赖关系,在任何时刻可以有任何多个子工程同时在施工,也既同时施工的子工程个数不受限制。
(4)整个工程的完成是指:所有子工程的完成。
例如,有五个子工程的工程规划表五个子工完成时间子工程1 子工程2 子工程3 子工程4 子工程5程的工程规划表:序号子工程1 5 0 0 0子工程2 4 0 0 0子工程3 12 0 0 0子工程4 7 1 1 0 0子工程5 2 1 1 1其中,表格中第I+1行J+2列的值如为0表示“子工程I”可以在“子工程J”没完成前施工,为1表示“子工程I”必须在“子工程J”完成后才能施工。
上述工程最快完成时间为14天,其中子工程1、3、4、5为关键子工程。
输入数据:第1行为N,N是子工程的总个数,N≤200。
第2行为N个正整数,分别代表子工程1、2、……、N的完成时间。
第3行到N+2行,每行有N-1个0或1。
其中的第I+2行的这些0,1,分别表示“子工程I”与子工程1、2、…、I-1、I+1、…N的依赖关系,(I=1、2、……、N)。
DP 单调性问题总结罗梓璋单调性:单调性,意思是保持同样的趋向,单调递增或者单调递减。
在DP 中,很多情况下,本来是没有单调性的,但是删去不可能的决策之后,剩下的决策会呈现单调性。
具有单调性的决策是有序的,最优决策可能直接在头或者尾O(1)得到,也可以二分查找O(logn)得到,总体比O(n)寻找最有决策的时间要少很多。
所以单调性可以解决的问题是:保留可能决策,快速寻找最优决策。
单调队列:单调队列的本质是双端队列,单调队列的内部是单调的,新元素从队尾加入,如果新元素加入后不满足单调性,那么令原来队尾的元素出队,直到新元素加入后满足单调性或者队列空了。
如单调递减队列原来是5 2 1,加入一个元素3,则队列为:5 3。
单调队列的开头元素在不满足条件时出队。
(另外一种加入元素的可能是,二分查找合适的位置,代替原来的元素,但是不能直接插入元素,在某些题目可能有。
例如上面的例子为:5 3 1或3 2 1,视具体情况。
)单调队列是最简单的处理单调性问题的数据结构,最大的用处是:维护区间最值。
维护区间最值的要求是,区间的移动方向固定。
(要保证队首不加入元素。
)既然区间移动方向固定,那么可以区间每移动一个单位,那么多了一个新的元素,少了一个旧的元素。
新的元素一定在最后,旧的元素一定在最前。
如果队首的元素已经离开了区间,那么让它出队。
我们考虑两个元素A 和B ,B 比A 优,而且B 在A 的后面,因为A 比B 先离开区间,所以有B 在A 永远也不可能是最值了。
所以新的元素加入队列后,如果队列队尾的元素不如新的元素优,那么就可以删除掉队尾原来的元素,直到队尾的元素比新元素优,才把新的元素加入队尾。
我们发现这样的队列和单调队列完全符合,队列中前一个元素一定比后一个优,满足单调性,而且模型也一样。
这样区间最值一定是队首的元素,可以O(1)求出区间最值。
能用单调队列解决的问题有一个特性:两个元素哪个比较优是可以只用它们本身就可以判断的,如果判断哪个比较优与当前状态有关,那么如果随着状态改变两个元素的优劣颠倒了, 单调队列就失去了作用。
1. 资源问题1-----机器分配问题f[i,j]:=max(f[i-1,k]+w[i,j-k]);2. 资源问题2------01背包问题f[i,j]:=max(f[i-1,j-v[i]]+w[i],f[i-1,j]);3. 线性动态规划1-----朴素最长非降子序列f[i]:=max{f[j]+1}4. 剖分问题1-----石子合并f[i,j]:=min(f[i,k]+f[k+1,j]+sum[i,j]);5. 剖分问题2-----多边形剖分f[i,j]:=min(f[i,k]+f[k,j]+a[k]*a[j]*a[i]);6. 剖分问题3------乘积最大f[i,j]:=max(f[k,j-1]*mult[k,i]);7. 资源问题3-----系统可靠性(完全背包)f[i,j]:=max{f[i-1,j-c[i]*k]*P[I,x]};8. 贪心的动态规划1-----快餐问题f[i,j,k]:=max{f[i-1,j',k']+(T[i]-(j-j')*p1-(k-k')*p2) div p3};9. 贪心的动态规划2-----过河f[i]=min{{f(i-k)} (not stone[i]){f(i-k)}+1} (stone[i]); +贪心压缩状态10. 剖分问题4-----多边形-讨论的动态规划F[i,j]:=max{正正f[I,k]*f[k+1,j];负负g[I,k]*f[k+1,j];正负g[I,k]*f[k+1,j];负正f[I,k]*g[k+1,j];} g为min11. 树型动态规划1-----加分二叉树(从两侧到根结点模型)F[i,j]:=max{f[i,k-1]*f[k+1,j]+c[k]};12. 树型动态规划2-----选课(多叉树转二叉树,自顶向下模型)f[i,j]表示以i为根节点选j门功课得到的最大学分f[i,j]:=max{f[t[i].l,k]+f[t[i].r,j-k-1]+c[i]};13. 计数问题1-----砝码称重f[f[0]+1]=f[j]+k*w[j];(1<=i<=n; 1<=j<=f[0]; 1<=k<=a[i];)14. 递推天地1------核电站问题f[-1]:=1; f[0]:=1;f[i]:=2*f[i-1]-f[i-1-m];15. 递推天地2------数的划分f[i,j]:=f[i-j,j]+f[i-1,j-1];16. 最大子矩阵1-----一最大01子矩阵f[i,j]:=min(f[i-1,j],v[i,j-1],v[i-1,j-1])+1;ans:=maxvalue(f);17. 判定性问题1-----能否被4整除g[1,0]:=true; g[1,1]:=false; g[1,2]:=false; g[1,3]:=false; g[i,j]:=g[i-1,k] and ((k+a[i,p]) mod 4 = j)18. 判定性问题2-----能否被k整除f[i,j±n[i] mod k]:=f[i-1,j]; -k<=j<=k; 1<=i<=n20. 线型动态规划2-----方块消除游戏f[i,i-1,0]:=0f[i,j,k]:=max{f[i,j-1,0]+sqr(len(j)+k), //dof[i,p,k+len[j]]+f[p+1,j-1,0] //not do}; ans:=f[1,m,0];21. 线型动态规划3-----最长公共子串,LCS问题f[i,j]=0 (i=0)&(j=0);f[i-1,j-1]+1 (i>0,j>0,x[i]=y[j]);max{f[i,j-1]+f[i-1,j]}} (i>0,j>0,x[i]<>y[j]);22. 最大子矩阵2-----最大带权01子矩阵O(n^2*m)枚举行的起始,压缩进数列,求最大字段和,遇0则清零23. 资源问题4-----装箱问题(判定性01背包)f[j]:=(f[j] or f[j-v[i]]);24. 数字三角形1-----朴素の数字三角形f[i,j]:=max(f[i+1,j]+a[I,j],f[i+1,j+1]+a[i,j]);25. 数字三角形2-----晴天小猪历险记之Hill同一阶段上暴力动态规划f[i,j]:=min(f[i,j-1],f[i,j+1],f[i-1,j],f[i-1,j-1])+a[i,j];26. 双向动态规划1数字三角形3-----小胖办证f[i,j]:=max(f[i-1,j]+a[i,j],f[i,j-1]+a[i,j],f[i,j+1]+a[i,j]);27. 数字三角形4-----过河卒//边界初始化f[i,j]:=f[i-1,j]+f[i,j-1];28. 数字三角形5-----朴素的打砖块f[i,j,k]:=max(f[i-1,j-k,p]+sum[i,k],f[i,j,k]);29. 数字三角形6-----优化的打砖块f[i,j,k]:=max{g[i-1,j-k,k-1]+sum[i,k]};30. 线性动态规划3-----打鼹鼠’f[i]:=f[j]+1;(abs(x[i]-x[j])+abs(y[i]-y[j])<=t[i]-t[j]);31. 树形动态规划3-----贪吃的九头龙f[i,j,k]:=min(f[x1,j1,1]+f[x2,j-j1-1,k]+d[k,1]*cost[i,fa[i]]] {Small Head}, f[x1,j1,0]+f[x2,j-j1,k]+d[k,0]*cost[i,fa[i]] {Big Head});f[0,0,k]:=0; f[0,j,k]:=max(j>0)d[i,j]:=1 if (i=1) and (j=1)1 if (i=0) and (j=0) and (M=2)0 else32. 状态压缩动态规划1-----炮兵阵地Max(f[Q*(r+1)+k],g[j]+num[k]);If (map[i] and plan[k]=0) and((plan[P] or plan[q]) and plan[k]=0);33. 递推天地3-----情书抄写员f[i]:=f[i-1]+k*f[i-2];34. 递推天地4-----错位排列f[i]:=(i-1)(f[i-2]+f[i-1]);f[n]:=n*f[n-1]+(-1)^(n-2);35. 递推天地5-----直线分平面最大区域数f[n]:=f[n-1]+n:=n*(n+1) div 2 + 1;36. 递推天地6-----折线分平面最大区域数f[n]:=(n-1)(2*n-1)+2*n;37. 递推天地7-----封闭曲线分平面最大区域数f[n]:=f[n-1]+2*(n-1);:=sqr(n)-n+2;38 递推天地8-----凸多边形分三角形方法数f[n]:=C(2*n-2,n-1) div n;对于k边形f[k]:=C(2*k-4,k-2) div (k-1); //(k>=3)39 递推天地9-----Catalan数列一般形式1,1,2,5,14,42,132f[n]:=C(2k,k) div (k+1);40 递推天地10-----彩灯布置排列组合中的环形染色问题f[n]:=f[n-1]*(m-2)+f[n-2]*(m-1); (f[1]:=m; f[2]:=m(m-1);41 线性动态规划4-----找数线性扫描sum:=f[i]+g[j];(if sum=Aim then getout; if sum<Aim then inc(i) else inc(j);)42 线性动态规划5-----隐形的翅膀min:=min{abs(w[i]/w[j]-gold)};if w[i]/w[j]<gold then inc(i) else inc(j);43 剖分问题5-----最大奖励f[i]:=max(f[i],f[j]+(sum[j]-sum[i])*i-t;44 最短路1-----Floydf[i,j]:=max(f[i,j],f[i,k]+f[k,j]);ans[q[i,j,k]]:=ans[q[i,j,k]]+s[i,q[i,j,k]]*s[q[i,j,k],j]/s[i,j];45 剖分问题6-----小H的小屋F[l,m,n]:=f[l-x,m-1,n-k]+S(x,k);46 计数问题2-----陨石的秘密(排列组合中的计数问题)Ans[l1,l2,l3,D]:=f[l1+1,l2,l3,D+1]-f[l1+1,l2,l3,D];F[l1,l2,l3,D]:=Sigma(f[o,p,q,d-1]*f[l1-o,l2-p,l3-q,d]);47 线性动态规划------合唱队形两次F[i]:=max{f[j]+1}+枚举中央结点48 资源问题------明明的预算方案:加花的动态规划f[i,j]:=max(f[i,j],f[l,j-v[i]-v[fb[i]]-v[fa[i]]]+v[i]*p[i]+v[fb[i]]*p[fb[i]]+v[fa[i]]*p[fa[i]]);49 资源问题-----化工场装箱员50 树形动态规划-----聚会的快乐f[i,2]:=max(f[i,0],f[i,1]);f[i,1]:=sigma(f[t[i]^.son,0]);f[i,0]:=sigma(f[t[i]^.son,3]);51 树形动态规划-----皇宫看守f[i,2]:=max(f[i,0],f[i,1]);f[i,1]:=sigma(f[t[i]^.son,0]);f[i,0]:=sigma(f[t[i]^.son,2]);52 递推天地-----盒子与球f[i,1]:=1;f[i,j]:=j*(f[i-1,j-1]+f[i-1,j]);53 双重动态规划-----有限的基因序列f[i]:=min{f[j]+1}g[c,i,j]:=(g[a,i,j] and g[b,i,j]) or (g[c,i,j]);54 最大子矩阵问题-----居住空间f[i,j,k]:=min(min(min(f[i-1,j,k],f[i,j-1,k]),min(f[i,j,k-1],f[i-1,j-1,k])),min(min(f[i-1,j,k-1],f[i,j-1,k-1] ),f[i-1,j-1,k-1]))+1;55 线性动态规划------日程安排f[i]:=max{f[j]}+P[I]; (e[j]<s[i])56 递推天地------组合数C[i,j]:=C[i-1,j]+C[i-1,j-1];C[i,0]:=157 树形动态规划-----有向树k中值问题F[I,r,k]:=max{max{f[l[i],I,j]+f[r[i],I,k-j-1]},f[f[l[i],r,j]+f[r[i],r,k-j]+w[I,r]]};58 树形动态规划-----CTSC 2001选课F[I,j]:=w[i](if i∈P)+f[l[i],k]+f[r[i],m-k](0≤k≤m)(if l[i]<>0);59 线性动态规划-----多重历史f[i,j]:=sigma{f[i-k,j-1]}(if checked);60 背包问题(+-1背包问题+回溯)-----CEOI1998 Substractf[i,j]:=f[i-1,j-a[i]] or f[i-1,j+a[i]];61 线性动态规划(字符串)-----NOI 2000 古城之谜f[i,1,1]:=min{f[i+length(s),2,1], f[i+length(s),1,1]+1};f[i,1,2]:=min{f[i+length(s),1,2]+words[s],f[i+length(s),1,2]+words[s]};62 线性动态规划-----最少单词个数f[i,j]:=max{f[i,j],f[u-1,j-1]+l};63 线型动态规划-----APIO2007 数据备份状态压缩+剪掉每个阶段j前j*2个状态和j*2+200后的状态贪心动态规划f[i]:=min(g[i-2]+s[i],f[i-1]);64 树形动态规划-----APIO2007 风铃f[i]:=f[l]+f[r]+{1 (if c[l]<c[r])};g[i]:=1(d[l]<>d[r]) 0(d[l]=d[r]);g[l]=g[r]=1 then Halt;65 地图动态规划-----NOI 2005 adv19910F[t,i,j]:=max{f[t-1,i-dx[d[[t]],j-dy[d[k]]]+1],f[t-1,i,j];66 地图动态规划-----优化的NOI 2005 adv19910F[k,i,j]:=max{f[k-1,i,p]+1} j-b[k]<=p<=j;67 目标动态规划-----CEOI98 subtraF[I,j]:=f[I-1,j+a[i]] or f[i-1,j-a[i]];68 目标动态规划----- Vijos 1037搭建双塔问题F[value,delta]:=g[value+a[i],delta+a[i]] or g[value,delta-a[i]];69 树形动态规划-----有线电视网f[i,p]:=max(f[i,p],f[i,p-q]+f[j,q]-map[i,j]);leaves[i]>=p>=l, 1<=q<=p;70 地图动态规划-----vijos某题F[i,j]:=min(f[i-1,j-1],f[i,j-1],f[i-1,j]);71 最大子矩阵问题-----最大字段和问题f[i]:=max(f[i-1]+b[i],b[i]); f[1]:=b[1];72 最大子矩阵问题-----最大子立方体问题枚举一组边i的起始,压缩进矩阵B[I,j]+=a[x,I,j];枚举另外一组边的其实,做最大子矩阵73 括号序列-----线型动态规划f[i,j]:=min(f[i,j],f[i+1,j-1] (s[i]s[j]=”()”or(”[]”)),f[i+1,j+1]+1 (s[j]=”(”or”[” ) , f[i,j-1]+1(s[j]=”)”or”]”);74 棋盘切割-----线型动态规划f[k,x1,y1,x2,y2]=min{min{f[k-1,x1,y1,a,y2]+s[a+1,y1,x2,y2],f[k-1,a+1,y1,x2,y2]+s[x1,y1,a,y2]};75 概率动态规划-----聪聪和可可(NOI2005)x:=p[p[i,j],j];f[I,j]:=(f[x,b[j,k]]+f[x,j])/(l[j]+1)+1;f[I,i]=0;f[x,j]=1;76 概率动态规划-----血缘关系F[A, B]=(f[A0, B]+P[A1, B])/2;f[i,i]=1;f[i,j]=0;(i,j无相同基因)77 线性动态规划-----决斗F[i,j]=(f[i,j] and f[k,j]) and (e[i,k] or e[j,k]); (i<k<j)78 线性动态规划-----舞蹈家F[x,y,k]=min(f[a[k],y,k+1]+w[x,a[k]],f[x,a[k],k+1]+w[y,a[k]]);79 线性动态规划-----积木游戏F[i,a,b,k]=max(f[a+1,b,k],f[i+1,a+1,a+1,k],f[i,a+1,a+1,k]);80 树形动态规划(双次记录)-----NOI2003 逃学的小孩朴素的话枚举节点i和离其最远的两个节点j,k O(n^2)每个节点记录最大的两个值,并记录这最大值分别是从哪个相邻节点传过来的。
DP问题不完全总结1.按状态类型分写在前面:从状态类型分,并不表示一题只从属于一类。
其实一类只是一种状态的表示方法。
可以好几种方法组合成一个状态,来解决问题。
1.1.编号(长度)动态规划共性总结本类的状态是基础的基础,大部分的动态规划都要用到它,成为一个维。
一般来说,有两种编号的状态:状态(i)表示前i个元素决策组成的一个状态。
状态(i)表示用到了第i个元素,和其他在1到i-1间的元素,决策组成有的一个状态。
题库a)最长不下降子序列以一元组(i)作为状态,表示第i个作为序列的最后一个点的时候的最长序列。
于是很容易想到O(n2)得算法。
但本题可合理组织状态,引入一个单调的辅助数组,利用单调性二分查找,优化到O(nlogn)。
关于优化详见优化章。
一些问题可将数据有序化,转化成本题。
应用:拦截导弹(NOIP99 Advance 1)就是原题。
Beautiful People(sgu199),要将数据有序化:其中一个权作为第一关键字不下降排列,另一个权作为第二关键字不上升。
Segment(ural 1078),将线段的左端点有序化就可以了。
b)LCS状态(i,j),表示第1个字符串的第i位,与第2个字符串的第j位匹配,得到的最长的串。
若有多个串要LCS,则加维,即几个串就几个维。
我也将此题归入路径问题。
c)花店橱窗布置(IOI99)见路径问题。
1.2.区间动态规划共性总结本类问题与下一章的划分问题的决策的分割点无序交集比较大(占本类问题的30%)。
题库a)石子合并见划分问题b)模版匹配(CEOI01,Patten)这题特殊的地方是状态的值是一个集合而不是一个数。
c)不可分解的编码(ACM World Final 2002)d)Electric Path(ural1143)e)邮局(IOI2000 Day2 1)若状态表示的思路从第i个村庄可以从属于哪个邮局,无最优子结构。
转变一个方向:第k个邮局可以"控制"一个区间的村庄[i,j]。
于是方程就显然了:f(k,i,j)=min{f(k-1,p,i-1)+w(i,j)}(k-1=p=i-1)S(i)为村庄i到原点的距离。
w(i,j)=min{k|Sum{|S(k)-S(p)|}(i=p=j)}(i=k=j)找到[i,j]间最好的一个邮局点。
不过可以发现Sum{|S(k)-S(p)|是单调的,所以取中位数就可以了。
即上式中k的取值范围只有floor((i+j)/2),ceil((i+j)/2)两个。
Floor是下取整。
Ceil是上取整。
这样每次转移时间降到O(1)。
注意到是区间连续的,即(p,i-1)和(i,j)中的i-1,i是连续的,所以空间可以降维:f(i,j)表示放前i个邮局到前j个村庄的最优值。
f(i,j)=min{f(i-1,p-1)+w(p,j)}(i-1=p=j-1}e(i,j)为当f(i,j)到达最优值时的p.通过证明四边形不等式,得到e(i,j)=e(i,j+1)=e(i+1,j+1)决策数量又少了一个数量级。
1.3.坐标动态规划共性总结之后的一些问题,状态是由坐标维与其他的维组成。
本类与划分问题(是2维或多维的坐标系的划分)与路径问题的交集占本类问题中大多数。
题库a)棋盘分割(NOI99 4)主要是将公式变形,变形后的公式很容易看出方程。
状态是由2个坐标组成的4元组(x1,y1)(x2,y2),表示一个子棋盘。
这有点像之前的区间动态规划,只不过是将1维转2维。
后见路径问题。
1.4.数轴动态规划共性总结题库a)01背包应用:装箱问题(NOIP01 Trade 4)就是原题。
值币分割可利用方程的性质,空间降1维。
币值可重复的值币分割(pku1742,Problem FLouTianCheng's Contest in POJ)使用左右法在定位上加速。
另给状态加一个属性last,记录上一次剩下的可用的同币值硬币数(利用了当前转移是唯一前驱的特点)。
b)取火柴问题(sgu153 Playing with matches)c)Stone Pile(ural1005 Stone Pile)d)公路巡逻(CTSC2000)1.5.5.树型动态规划共性总结1)动态规划的顺序一般按照后序遍历的顺序,即处理完儿子再处理当前节点,才符合树的子结构的性质。
2)多叉树转换为二叉树由于要分配附加维到各个节点,而分配附加维是个划分问题,若还是按当前节点到各个儿子节点分配,则成了一个整数划分问题,O(n2)。
所以要把多叉树转换为二叉树,这样才能按动态规划的方式只决策当前点的分配问题,O(n)。
3)加当前点的选或不选的常数维加此维解决的是后效性问题。
…4)在将边信息转成树时的技巧将读入的边分裂成2条边,将这2条边关联起来(就是找到一条边,另一条边的编号就知道)。
用前向星表示法表示边(按起点有序),以后用边的时候,用了一条边打不可用标志,也将关联边打不可用标志。
这样可以保证O(n)的时间完成信息处理,而且在父节点找儿子的过程中带来很大的方便。
5)复杂度树型动态规划复杂度基本上是O(n);若有附加维m,则是O(nm)。
题库a)选课(CTSC97-3)由于要分配课程数,所以要多叉树转换为二叉树。
b)贪吃的九头龙(NOI02-3)若小头数大于1的话,则让不同的小头吃一段树枝的2个端点。
这样就把问题转化成:附加维是大头吃的个数,当前点由不由大头吃的常数维的动态规划。
由于涉及划分问题,所以要多叉树转换为二叉树。
c)求树的质心(sgu134 Centroid)给出一棵边不带权的树,求点,使得去掉此点后,剩下的最大的连通子图的顶点数最小.d)求树中的点最远距离最近。
给出一棵边带权的树,求树中的点,使得此点到树中的其他结点的最远距离最近。
Computer Network(sgu149)Computer Net(ural1056)1.6.集合动态规划(状态压缩)共性总结1)数据特殊性给出的数据在某一个或几个维度上一般具有比较小的范围(可以枚举一类的状态)。
一个枚举的状态是一个集合。
2)编码由于集合中元素个数的不定性或范围大,直接开数组存,不好索引数组(编程复杂度太高),所以要将集合编码。
利用数据的可枚举性,将枚举的状态(集合)编码。
一般来说码值的范围要很小(尽量排除无用的码值,如炮兵:当前格和上格存在炮兵的情况是非法的,可以排除)。
规定编码的码值代表的意思,要尽量规定好维护的码值。
(如炮兵:当前格存在炮兵的用2,上格存在炮兵用1。
这样下一层的规划时,只要码值-1即可)。
有时候可以直接利用编码的顺序动态规划,因为这时编码已经是拓补有序。
如TSP问题当前已选点集合的状态的前驱的编码的值一定比当前的编码的值小。
3)状态压缩对有限阶段的放置情况,行走情况编码(其实质也是放置的集合或行走路线的集合),这样的编码,也有人谓之:"状态压缩"。
此类题以"炮兵阵地"为典型,进行扩展。
题库a)购物(IOI95-2)可将每种物品按5进制编码。
(5为每种物品数的上限)由于物品数的上限为5,比较小,也可直接开数组存。
b)Roger游戏任务一(CTSC98 Day2 4)一个正方体在一个方格内的状态只有24种,而且可以通过顶面和前面来表示,这样用3维的状态(x,y,p)就可以解决,p为1到24种状态中的一种。
c)TSP问题观察一下TSP的搜索过程:for(x in未选点)TSP(x)即当前路的最后一个节点为x,现在要选择下一个节点y,而y要在未选点的集合中。
若未选点或已选点的集合已确定,则后效性消除。
可以DP。
状态为令X为当前路的已选点的集合(含i),当前路的最后一个节点为i。
2元组(X,i)为经过已选点的集合X到节点i的最短长度。
将X编码即可。
注意:并没有因为动态规划将问题从NP类带到P类。
应用:DNA Laboratory(Problem B,TU-Darmstadt Programming Contest 2004)将每个串的交迭部分求出,就可以将问题专成TSP但要输出字典序最小的,则需要注意DP顺序。
有具体的报告。
d)炮兵阵地十分经典,详见报告。
应用:Another Chocolate Maniac(sgu132)类似炮兵的做法的最值,只不过是求最小值,麻烦点。
Hardwood floor(sgu131)类似炮兵的做法的统计Little Knights(sgu225)类似炮兵的做法的统计,数据量太大要const Little Kings(sgu223)类似炮兵的做法的统计Bugs公司(CEOI 2002)类似炮兵的做法的最值1.7.利用动态规划思想求最值,编号(循环变量)的迭代共性总结要利用上次的一些运算"剩下"的循环变量作当前循环的边界,主要在于找出一种决策顺序,使之成立。
题库a)奶牛浴场b)Communication System将数据有序化,从大到小枚举带宽,每次可利用上次处理的结果Min,来决策当前状态。
称作迭代,或就是一种动态规划。
(zju1409,Problem CTehran 2002 Iran Nationwide Internet Programming Contest)1.8.记忆化搜索题库a)Magic Trick(Problem G,TU-Darmstadt Programming Contest 2004)2.按转移方式分2.1.存在性递推1)01统计(CTSC99 1)2)卡特兰数circle(sgu130)3)鹰蛋2.2.求一系列的分割(合并)点(划分问题)2.2.1.决策的分割点有序共性总结a)有序性每次决策的点的编号是有序的,即要按决策的顺序输出分割点的编号的话,编号是有序的,满足分割点的编号按升序排列。
b)方程一般形式f(n,m)=optimize{f(k,m-1)+w(k+1,n)}(n,m)表示从1到n个点中划分为m个部分的最优值;k为决策的分割点,即第m个部分为k+1到n;这里optimize可以为max,min。
题库a)整数划分常应用在将一个权分配给一定的小分割块,如:将大堆的石子分成一定的小堆,小堆可为空,大堆要分完。
有时应用在树型动态规划(二叉转多叉)中。
b)乘积最大(NOIP00 Advance 2)就是按上面的一般式的方程做。
2.2.2.决策的分割点无序共性总结a)无序性每次决策的点的编号是无序的,即要按决策的递归顺序输出分割点的编号的话,编号是无序的。
b)方程一般形式f(i,j)=optimize{f(i,k-1)+f(k+1,j)}+w(i,j)(i,j)表示从i到j的范围内选取一个分割点k的最优值,子问题是分割点左边(i,k-1)和右边(k+1,j)的点的范围的最优值;这里optimize可以为max,min。