高考文科数学双向细目表

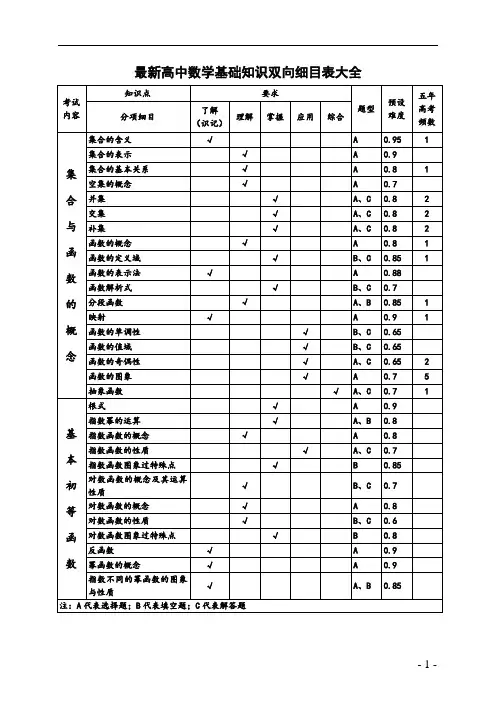
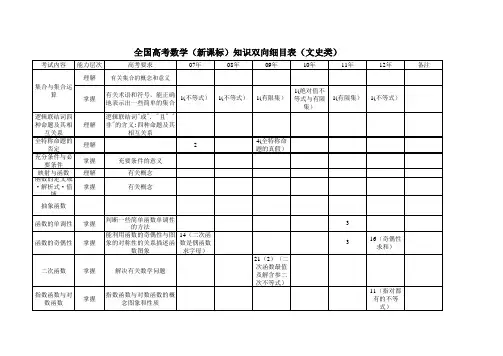
考试内容能力层次高考要求07年08年09年10年11年12年备注理解有关集合的概念和意义逻辑联结词四种命题及其相互关系理解逻辑联结词"或". "且" "非"的含义;四种命题及其相互关系全特称命题的否定理解24(全特称命题的真假）充分条件与必要条件掌握充要条件的意义映射与函数理解有关概念抽象函数函数的单调性掌握判断一些简单函数单调性的方法3二次函数掌握解决有关数学问题21（2）（二次函数最值及解含参二次不等式）指数函数与对数函数掌握指数函数与对数函数的概念图象和性质11（指对都有的不等式）全国高考数学（新课标）知识双向细目表（文史类）1(不等式）16（奇偶性求和）1(有限集）31(绝对值不等式与有限集）1(有限集）1(不等式）1(不等式）14（二次函数是偶函数求字母）有关术语和符号，能正确地表示出一些简单的集合有关概念能利用函数的奇偶性与图象的对称性的关系描述函数图象掌握掌握掌握集合与集合运算函数的定义域·解析式·值域函数的奇偶性函数的图象理解有关概念,利用特值、单调、周期、奇偶判断12（画图象求最值）12（综合周期、奇偶绝对值画图求交点个数）11（指对都有的不等式）零点与方程理解有关概念，会求零点区间、个数10（求零点区间）利用函数知识解应用题掌握应用函数知识解决实际难度问题18（1）函数的综合问题掌握综合运用函数知识解决数学问题9（奇偶与指数不等式结合）12（图象与对数运算结合）推理与证明数列的概念理解数列、通项公式的概念等比数列掌握等比数列的通项公式，前n 项和公式6（等比性质）8（和与项的比）1517（1）14（由和求公比）掌握差比裂项求和17（2）12（求和）17（求完通项、和后求和最值）8（性质应用）13（通项应用）16（基本量求d ）有关概念及解决实际问题由Sn求an的公式等差数列的通项公式，前n 项和公式掌握掌握掌握等差数列数列的综合应用三角函数概念公式掌握任意角的正弦、余弦、正切的定义，用三角函数线表示正弦、余弦和正切;同角三角函数的基本关系式;正弦、余弦的诱导公式7（用到定义）和差倍公式掌握通过公式的推导，了解它们的内在联系，从而培养逻辑推理能力9（二倍角、和差公式约分，含π/4的）11（二倍角化为二次函数求最值）17（1）107、11（用到）17（1）求值图象与性质掌握会用三角函数线画正弦函数，正切函数的图象，由诱导公式画余弦函数的图象;理解它们的性质; 会用"五点法"3(一个半周期闭区间上图象）6（由定义得解析式并判断图象）11（单调区间、对称轴）用"五点法"画函数y=Asin(ωx+Φ)的简图9（由图象求ω、Φ）16（由图象求ω、Φ进而求值）A 、ω、Φ的物理意义理解掌握y=Asin(ωx+Φ)的图象图象变换掌握利用三角知识求范围最值掌握运用所学三角知识解决实际问题了解共线向量，平面向量基本定理理解向量，向量共线的充要条件，平面向量的坐标9（共线条件）掌握向量的几何表示，实数与向量的积，向量加法与减法，平面向量的坐标运算4（线性运算的坐标表示）了解用平面向量的数量积可以处理有关长度、角度和垂直等问题2（用数量积坐标运算求夹角）掌握平面向量的数量积及其几何意义;向量垂直的条件5（由垂直求字母）7（由垂直求字母）13（由垂直求字母，非坐标）向量综合掌握综合不等式的概念性质理解不等式的性质不等式证明分析法、综合法、比较法证明简单的不等式均值不等式掌握并会简单的应用;17（2）15（解三角形后求面积）16（解三角形求线段长）17（实际测量求值）17（2）17（实际测量，用字母表示）正弦定理、余弦定理，并能运用它们解斜三角形掌握掌握ωx+Φ)的图象三角最值及综合应用正余弦定理向量、向量的加法与减法、实数与向量的积数量积解不等式掌握二次不等式、简单的分式不等式的解法7（二次不等式解法，三个范围公共解）21（2）（讨论解含参二次不等式）掌握简单的绝对值不等式的解法直线方程及位置关系理解直线的倾斜角和斜率20（斜率取值范围，化为不等式问题）掌握两点斜率公式:一点和斜率求出直线方程的方法;点斜式、两点式和一般式，熟练求出直线方程.两条直线平行与垂直的条件，两条直线成的角、点到直线的距离公式，两条直线的位直关系了解简单的线性规划问题，线性规划的意义掌握二元一次不等式表示平面区域，简单线性规划问题10（线段点到原点距离）611145圆与圆理解16（外切）20（1）（结合抛物线条件求圆的方20（1）（由三点定方程）13（求圆的方程）5（求关于直线对称的圆）20（1）（1次比2次型不不等式|a+b|≤|a|+|b|有关概念圆的标准方程和一般方程掌握理解灵活运用不等式的应用线性规化圆的方程绝对值不等式直线与圆掌握直线与圆的位置关系21（交点个数，结合向量共线类似椭圆问题）20（2）（分成弧的比）20（2）（结合OA、OB垂直类似椭圆问题）掌握椭圆的标准方程及其几何性质20（1）由定义性质求方程20（1）椭圆定义4(离心率）4理解椭圆的定义、概念双曲线了解双曲线的标准方程及其几何性质13（几何性质应用求离心率）2(直接求焦距）5（渐近线求离心率）10抛物线了解抛物线的标准方程及其几何性质7（从坐标考抛物线定义)14（弦中点求抛物线方程）4（知切点求切线）9（定义应用求距离）10(用到）20（2）（切线方程）轨迹方程了解20（2）代入法求轨迹并讨论什么曲线直线与圆锥曲线掌握综合16（求交点与原点组成三角形面积）20（2）（弦长问题）综合应用熟练掌握综合线面、面面平行12（平行垂直判断）18椭圆线面、面面垂直18（面面垂直化为线面垂直，存在问题）12（平行垂直判断）18（线线垂直与线面垂直、面面垂直转化，求体积）18（1）1819（1）三视图掌握三视图8（体积）1811（三视图求全面积）1587（三视图求体积）体积计算了解会求几何体的表面积、体积，会处理几何体的侧面展开图问题8,111818（2）19（2）了解球的概念11（球内接三棱锥）掌握球的性质、表面积、体积公式，球面距离14（球内接正六棱柱求球的体积）7（知内接长方体求表面积）16（球中直角三角形）综合18（由直观图得三视图计算体积，证线面平行）9（平行、垂直，体积计算）算法初步掌握程序框图5（求和）6（三数输出最大）10（条件结构）56（图的含义）古典概型掌握计算等可能性事件的概率，会用互斥事件的概率加法公式和相互独立事件的概率乘法公式计算一些事件的概率20（1）19（2）14（估计古典概型）618（2）几何概型了解计算几何概型概率20（2）球了解独立性检验19（2）了解线性回归的方法简单应用3（散点图观察正负相关）3(相关系数的理解）了解茎叶图16（说明直观含义）掌握频率分布直方图19（2）（画图并由图估计平均数）抽样19（1）（分层抽样人数）19（1）（估计比例）（3）（用分层更好）导数概念运算掌握函数在一点处的导数的定义和导数的几何意义；基本导数公式；和、差、积、商的求导法则；会求某些简单函数的导数；4掌握导数求切线1021（切线求字母，切线与定直线围成面积）1321（1）（切线求字母）13（知切点求切线）19（1）12平均数与方差计算掌握统计掌握会求一些实际问题的最大值和最小值19掌握导数证明不等式、恒成立21（2）（有特点）21（2）（有特点，用上了分析法）了解复数的有关概念及复数的代数表示和几何意义掌握运算法则，能进行复数代数形式的加法、减法、乘法、除法运算153（除法）2（除法）3（乘除）2（除法）2（除法）说明21题必考有选修选考有选修选考有选修选考，有选修选考，有选修选考，19是频率估计概率，数学期望21（1）（单调区间）21（1）（2）（恒成立求字母范围）21（1）（求极值）19可导函数的单调性与其导数的关系；可导函数在某点取得极值的必要条件和充分条件了解导数应用复数。

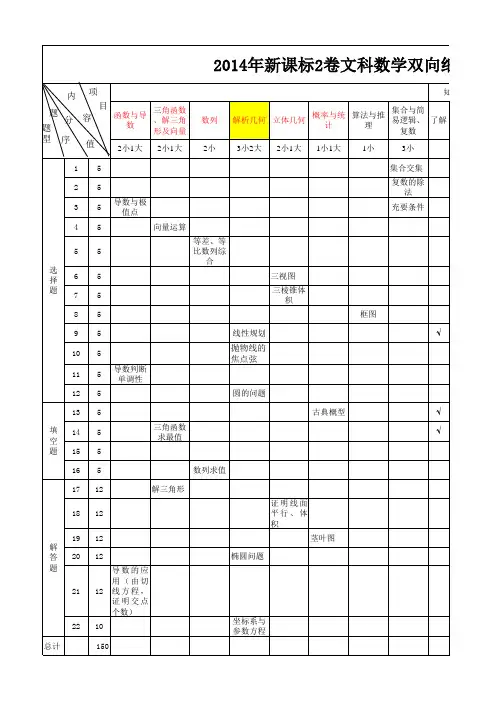
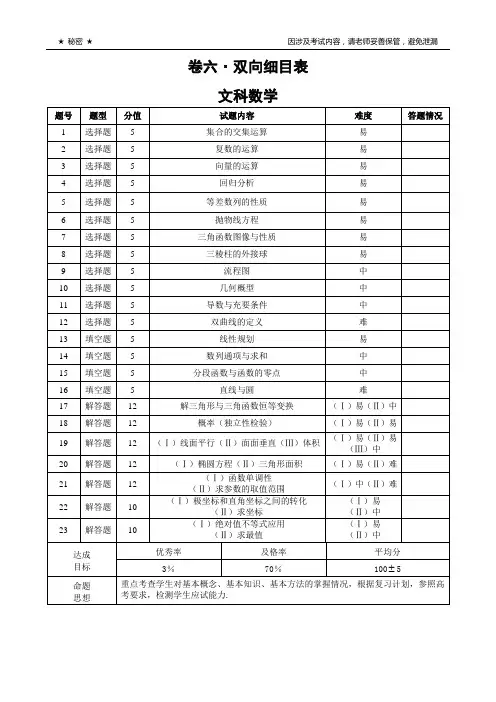
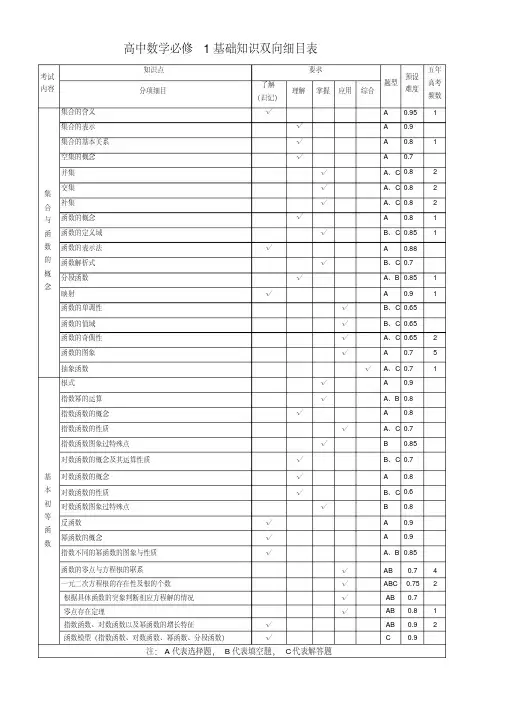
高中数学必修1基础知识双向细目表考试内容知识点要求题型预设难度五年高考频数分项细目了解（识记）理解掌握应用综合集合与函数的概念集合的含义√ A 0.95 1 集合的表示√ A 0.9集合的基本关系√ A 0.8 1 空集的概念√ A 0.7并集√A、C 0.8 2 交集√A、C 0.8 2 补集√A、C 0.8 2 函数的概念√ A 0.8 1 函数的定义域√B、C 0.85 1 函数的表示法√ A 0.88函数解析式√B、C 0.7分段函数√A、B 0.85 1 映射√ A 0.9 1 函数的单调性√B、C 0.65函数的值域√B、C 0.65函数的奇偶性√A、C 0.65 2 函数的图象√ A 0.7 5 抽象函数√A、C 0.7 1基本初等函数根式√ A 0.9指数幂的运算√A、B 0.8指数函数的概念√ A 0.8指数函数的性质√A、C 0.7指数函数图象过特殊点√ B 0.85对数函数的概念及其运算性质√B、C 0.7对数函数的概念√ A 0.8对数函数的性质√B、C 0.6对数函数图象过特殊点√ B 0.8反函数√ A 0.9幂函数的概念√ A 0.9指数不同的幂函数的图象与性质√A、B 0.85函数的零点与方程根的联系√AB 0.7 4 一元二次方程根的存在性及根的个数√ABC0.752根据具体函数的突象判断相应方程解的情况√AB0.7零点存在定理√AB0.81指数函数、对数函数以及幂函数的增长特征√AB0.92函数模型（指数函数、对数函数、幂函数、分段函数）√C0.9注：A代表选择题，B代表填空题，C代表解答题高中数学必修4基础知识双向细目表考试内容知识点要求题型预设难度五年高考频数分项细目了解（识记）理解掌握应用综合三角函数任意角√ A 0.95象限角的表示√AB 0.8扇形的弧长与扇形面积√AB 0.85三角函数的定义√AB 0.85三角函数线√AB 0.8同角基本关系式√BC 0.72 1 诱导公式1—4 √AC 0.87诱导公式5、6 √ A 0.95正弦、余弦函数图象√AB 0.87正弦、余弦函数的周期性、奇偶性√ABC 0.85 1 正弦、余弦函数的单调性与最值√ABC 0.85 3 正切函数的图像与性质√AB 0.8函数sin()y A x的图象√BC 0.7 2 三角函数模型的简单应用√AB 0.82三角恒等变换两角和与差的余弦公式√A、B、C0.95 3 两角和与差的正弦公式√A、B、C0.9 5 两角和与差的正切公式√A、B、C0.9二倍角的正弦公式√A、B、C0.9 2二倍角的余弦公式√A、B、C0.9 2二倍角的正切公式√A、B、C0.9三角恒等变换√A、B、C0.75 5注：A代表选择题，B代表填空题，C代表解答题。

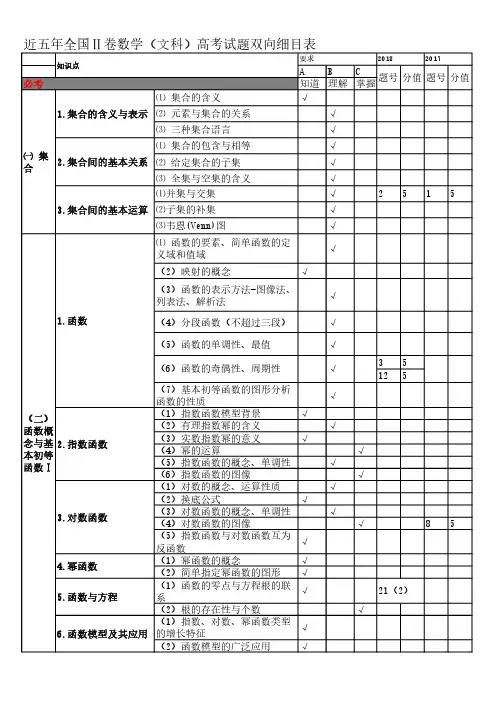
高考数学知识点双向细目表在高中阶段，数学是学生们的重要学科之一，也是高考必考科目之一。

为了顺利备战高考，了解数学知识点是非常重要的。

本文将为大家提供一份高考数学知识点双向细目表，以帮助同学们更好地了解数学知识体系和复习规划。

首先，我们来了解一下高考数学知识点的分类。

数学高考知识点主要包括代数、几何、三角学、概率与统计以及数学思维能力等五个方面。

每个方面又包含了具体的知识点。

下面将以这五个方面进行详细介绍。

代数部分是数学中的基础内容，主要包括函数、方程与不等式、数列与数学归纳法、概率与统计等几个知识点。

其中函数是代数部分的核心，包括一次函数、二次函数、指数函数、对数函数等。

函数的性质、图像与应用都是需要掌握的内容。

方程与不等式也是非常重要的知识点，包括一元一次方程、二元一次方程、二次方程、绝对值不等式以及分式方程等。

此外，数列与数学归纳法是代数部分的另一重点，需要了解等差数列与等比数列的概念与性质，以及如何利用数学归纳法证明数学命题。

最后，概率与统计是数学中的实际应用部分，需要了解基本的概率与统计方法，如频率、概率、条件概率、正态分布等。

几何部分是数学中的空间内容，主要包括平面几何、立体几何和空间解析几何。

平面几何包括了直线、曲线、多边形、圆等基本图形的性质与应用。

立体几何则需要了解体积、表面积等概念，要掌握球、圆锥、棱柱、棱台等几何体的性质。

空间解析几何是几何部分的进阶内容，需要掌握平面与直线的表示方法、位置关系与求交点的方法。

三角学是数学中的三角函数部分，主要包括三角函数的定义与性质、三角函数的图像与变换、三角恒等式与解三角方程等。

在此部分，还涉及到向量的概念与性质，包括向量的表示方法、运算法则、点积与叉积等。

概率与统计部分是数学中的实际应用部分，需要了解概率的基本概念与性质，条件概率、事件独立性的判定与计算方法等。

统计部分则包括数据的收集与整理、频数分析与频率分析、正态分布与抽样调查等内容。

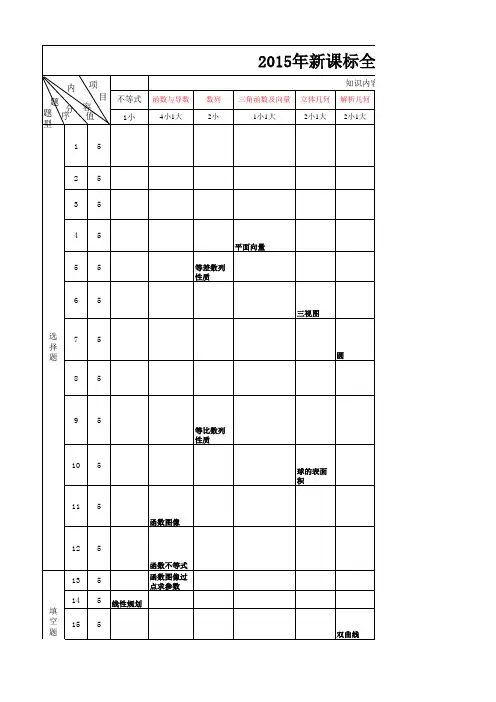
2023年数学新高考2卷双细目表1. 代数与函数1.1. 一元二次方程及一元二次不等式1.1.1 解一元二次方程：通过因式分解、配方法、公式法等方法解一元二次方程，包括真分式方程的解法。

1.1.2 解一元二次不等式：通过因式分解、配方法、开平方法等方法解一元二次不等式，建立二次函数与一元二次不等式之间的通联。

1.2. 参数方程1.2.1 理解参数方程的概念与性质，掌握参数方程与直角坐标系之间的相互转换。

1.2.2 利用参数方程解曲线的方程，求参数方程的参数范围等。

2. 解析几何2.1. 直线与圆2.1.1 直线方程：掌握点斜式、斜截式、两点式等直线方程的表示与相互转换。

2.1.2 圆的方程：掌握标准方程、一般方程等圆的方程，并能够在坐标系中画出对应的图形。

2.2. 平面向量2.2.1 理解平面向量的概念与性质，掌握平面向量的加减、数量积、夹角等运算法则。

2.2.2 应用平面向量解决几何问题，包括线性运动、平面图形的性质等。

3. 概率论3.1. 随机事件与概率3.1.1 随机事件的定义与性质，包括基本事件、必然事件、互斥事件、对立事件等。

3.1.2 概率的定义与性质，包括样本空间、事件的概率等概念。

3.2. 条件概率与独立性3.2.1 条件概率的概念与性质，包括条件概率的计算、全概率公式、贝叶斯公式等。

3.2.2 独立事件与互不独立事件的概念与应用。

4. 数学模型4.1. 建立数学模型的基本方法4.1.1 复杂问题抽象为数学问题，建立数学模型的基本思想与方法。

4.1.2 通过实际问题建立具体的数学模型，求解数学模型的参数与条件。

4.2. 数学建模的实际应用4.2.1 运用数学模型解决实际问题，包括人口增长、经济发展、资源分配等领域。

4.2.2 分析数学模型的合理性与局限性，提出改进与优化方案。

5. 综合应用5.1. 数学知识的交叉应用5.1.1 将不同数学知识相互通联，解决具体问题。

5.1.2 利用数学模型、概率统计等方法分析解决现实问题。

2023年数学学科高考双向细目表第一部分：知识与技能
1.1 数与代数
- 数的性质和运算
- 同类项与合并
- 一元一次方程与不等式
- 二元一次方程组与不等式组
- 函数与图像
- 幂指对数
- 平面向量
1.2 几何与形状
- 二维平面几何
- 三维空间几何
- 点、直线与面的位置关系
- 图形的性质与计算
- 圆的性质与计算
- 空间中的平面与直线
1.3 数据、统计与概率
- 数据的收集与整理
- 数据的分析与解释
- 概率的基本概念
- 概率计算与应用
- 统计与统计图表
第二部分：解决问题与实践应用
2.1 数学问题解决
- 解决实际问题的数学建模
- 利用数学工具解决问题
- 数学推理与论证方法
2.2 数学实践应用
- 应用数学知识解决实际问题
- 利用数学工具进行实际操作
- 数学思维与计算能力的培养
第三部分：学科素养与拓展
- 数学史和数学文化
- 数学与其他学科的关系
- 数学研究方法和论文写作
以上为2023年数学学科高考双向细目表，包含了数学学科的知识与技能、解决问题与实践应用以及学科素养与拓展三个部分。

详细列出了各个部分的具体内容，旨在指导学生备考高考并培养数学思维与计算能力。

选择题填空题解答题51210基础题稍难题难题1集合的基本概念2集合间的基本关系3集合的基本运算4命题的关系及命题真假判断5充分条件与必要条件的判断6充分条件与必要条件的应用7判断含有逻辑联结词的命题的真假8全（特）称命题的否定9利用命题的真假求参数的取值10求函数的定义域11求函数的解析式12分段函数求值13确定函数单调性或单调区间14函数的最值(值域)15函数的单调性的应用16函数奇偶性的判断及应用17函数的周期性18函数的奇偶性、周期性与单调性19幂函数20二次函数的图像与性质21二次函数的综合应用22指数幂的化简与求值23指数函数的图像及应用24指数函数的性质及应用25对数的应用26对数函数的图像与及应用高三数学（文）命题双向细目表知识章节集合与常用逻辑用语函数、导数及其运用命题及其关系、充分条件与必要条件简单的逻辑联结词、全称量词与存在量词函数及其表示函数的单调性与最值函数的奇偶性与周期性幂函数与二次函数指数函数(指数)对数与对数函数难度题型分值集合的概念与运算知识内容编号知识点27对数函数的性质及应用28作函数的图像29识图与辩图30函数的图像与应用31函数零点的判断与求解32二次函数的零点33函数零点的应用34导数的运算35导数的几何意义36求函数的单调区间37由函数的单调性求参数的取值范围38求函数的极值与最值39导数在不等式中的应用40终边相同的角41三角函数的定义42弧长与扇形的面积43同角三角函数基本关系的应用44诱导公式化简三角函数式45三角函数的定义域、值域46三角函数的单调性47三角函数的对称性与奇偶性、周期性48函数y=Asin(wx+﹠)的图像画法与变换49根据图像确定函数解析式50三角函数式的化简51三角函数式的求值52三角函数的综合应用53利用正、余弦定理解三角形54判断三角形的形状55三角形的面积问题三角函数、解三角形函数的图像函数与方程任意角、弧度制及任意角的三角函数同角三角函数基本关系与诱导公式三角函数的图像与性质函数y=Asin(wx+﹠)的图像及简单三角恒等变换正弦定理与余弦定理导数的概念及运算导数的应用正余弦定理的应用举例56测量距离、高度、角度问题57平面向量的有关概念58平面向量的线性运算59平面向量基本定理的应用60向量的坐标运算61平面向量数量积的运算62向量的模与夹角63复数的概念64复数的代数运算、几何意义65利用观察法求数列的通项公式66利用Sn与an的关系求通项67由递推关系求通项公式68等差数列的基本运算，判定与证明69等差数列的性质70等差数列前n项和的最值问题71等比数列的基本运算72等比数列的性质及应用73等比数列的判定与证明74分组转化法求和75裂项相消法求和76错位相减法求和77不等式的性质、比较大小78根据不等式性质求范围79一元二次不等式的解法80含参数的一元二次不等式解法81一元二次不等式恒成立问题82利用基本不等式求最值83利用基本不等式证明不等式等比数列数列求和平面向量、数系的扩充与复数引入数列平面向量的概念及线性运算平面向量基本定理及坐标表示平面向量的数量积及应用数系的扩充与复数的引入数列的概念与简单表示法等差数列不等式、推理与证明不等式与不等关系一元二次不等式及其解法基本不等式及其应用84二元一次不等式(组)表示的平面区域85求线性目标函数的最值86线性规划的实际应用87合情推理与演绎推理88直接证明与间接证明视图89三视图和直观图90空间几何体的表面积和体积91球与空间几何体的接、切问题92空间两条直线的位置关系93异面直线的所成的角94有关线面、面面平行的命题真假判断95线面平行、面面平行的判定与性质96直线与平面、平面与平面垂直的判定和性质97直线的斜率与倾斜角98直线方程的求法99直线方程的综合应用100两条直线的位置关系、点到直线的距离101求圆的方程102与圆有关的最值问题103与圆有关的轨迹问题104直线与圆的位置关系105圆的切线、弦长问题106圆与圆的位置关系107椭圆的定义及其标准方程108椭圆的几何性质109直线与椭圆的位置关系110双曲线的定义及其标准方程111双曲线的几何性质112直线与双曲线的综合问题113抛物线的定义立体几何平面解析几何简单推理平面的基本性质空间几何体的表面积和体积与证明二元一次不等式(组)与简单的线性规划问题双曲乡圆的方程直线的倾斜角与斜率、直线方程椭圆直线与圆、圆与圆的位置关系114抛物线的标准方程及其几何性质115直线与抛物线的位置关系116随机抽样117用样本估计总体118变量相关关系与统计案例119算法初步概率120随机事件概率、古典概型、几何概型参数方程、极坐标121参数方程、极坐标、122绝对值不等式123证明不等式的基本方法极坐标参数方程、不概率与统计不等式选讲统计、算法初步抛物线。

试卷命题双向细目表知识内容选择题填空题解答题考 查 内 容总 分 值难度 系数题 次分 值 题 次 分 值 题 次 分 值 集合、简易逻辑简易逻辑 1，3 8 集合的运算集合的运算 充分必要条件充分必要条件8 0.9+0.7 不等式不等式 6 4 13 6 基本不等式基本不等式 线性规划线性规划10 0.7+0.6 函数与方程函数与方程 5 4 17 4 函数图像性质、函数图像性质、 零点、恒成立零点、恒成立8 0.75+0.6 导数及应用导数及应用 10 4 20 15 4导数及应用导数及应用 23 0.6+0.7 三角函数三角函数4 4 18 14 图像与性质图像与性质 解三角形解三角形18 0.6+0.7 平面向量平面向量 9 4 基向量思想基向量思想 向量几何意义向量几何意义4 0.5 数列数列 15 6 22 15 等比等差数列等比等差数列 数列求和数列求和21 0.7+0.6 立体几何立体几何 7 4 14 6 19 15 线面位置、三视图、线面角、面面角25 0.7+0.7 +0.6 解析几何解析几何 8 4 11 4 21 15 双曲线离心率双曲线离心率 直线与圆锥曲线直线与圆锥曲线23 0.6+ 0.6+0.6 计数原理与古典概率、二项式定理定理 12 16 10 概率，离散型随机变量及其分布列变量及其分布列10 0.8+0.6 复数复数 2 4 复数概念复数概念 4 0.95 小结小结 10题 40分 7题 36分 5题 74分高中数学高中数学150 0.65 2018年高考模拟卷数学卷考试时间120分钟 满分150分本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至3页，非选择题部分3至4页。

页。

考生注意：考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。

卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。