下载文档原格式
数学试题双向细目表I. 整数与有理数A. 基本概念1. 整数的定义及性质2. 有理数的定义及性质B. 整数与有理数的运算1. 加法与减法2. 乘法与除法3. 混合运算C. 整数与有理数的应用1. 温度计算2. 货币兑换问题II. 代数表达式与方程式A. 代数表达式1. 变量与常数2. 四则运算3. 代数表达式化简B. 方程式1. 一元一次方程式2. 一元二次方程式3. 解方程应用题III. 几何A. 基本概念1. 点、线、面的定义2. 角的定义与性质B. 图形的性质与分类1. 三角形2. 四边形3. 圆与圆的构造C. 坐标系与向量1. 平面直角坐标系2. 向量的定义与运算IV. 概率与统计A. 概率1. 随机事件与样本空间2. 概率的计算3. 事件的复合与互斥B. 统计1. 数据的收集与整理2. 平均数与中位数3. 概率统计应用题V. 函数与图像A. 函数概念与性质1. 函数的定义2. 函数的图像与性质B. 常见函数类型1. 线性函数与非线性函数2. 幂函数与指数函数3. 对数函数与三角函数C. 函数的运算与应用1. 函数的加减与乘除2. 函数的复合与反函数VI. 三角函数A. 基本概念与性质1. 弧度与角度的换算2. 三角函数的定义B. 三角函数的图像与周期性1. 正弦函数与余弦函数2. 正切函数与余切函数C. 三角函数的应用1. 三角函数方程的解法2. 三角函数在几何中的应用VII. 数列与数学归纳法A. 数列的概念与性质1. 等差数列与等比数列2. 通项公式与求和公式B. 数学归纳法1. 数学归纳法的原理2. 数学归纳法的应用VIII. 解析几何A. 平面解析几何1. 平面直角坐标系2. 点、线、圆的方程B. 空间解析几何1. 空间直角坐标系2. 直线与平面的方程3. 空间图形的分类IX. 近似计算A. 有效数字与误差1. 有效数字的定义2. 误差的计算与表示B. 近似计算方法1. 数的四舍五入2. 数的科学记数法3. 近似计算的应用X. 排列组合与概率A. 排列与组合1. 排列的定义与计算2. 组合的定义与计算B. 概率统计1. 事件的概率计算2. 投掷与抽取问题的概率XI. 三角函数与复数A. 三角函数的复数表示1. 克莱布斯-戴维（C-D）公式2. 欧拉公式与复数表示B. 复数的运算与性质1. 复数的加减与乘除2. 复数的共轭与模XII. 微积分基础A. 导数的定义与性质1. 导数的定义2. 导数的性质与计算B. 函数的极值与应用1. 函数的极大值与极小值2. 函数的应用问题XIII. 平面向量A. 向量的概念与性质1. 向量的定义与表示2. 向量的性质与运算B. 向量的应用1. 向量的坐标表示2. 向量运算在几何中的应用XIV. 几何证明A. 平面几何证明1. 各种基本几何定理的证明2. 几何图形性质的证明B. 空间几何证明1. 空间几何定理的证明2. 空间图形性质的证明XV. 指数与对数函数A. 指数函数与对数函数的性质1. 指数函数的定义与性质2. 对数函数的定义与性质B. 指数与对数函数的应用1. 指数增长问题2. 对数衰减问题。
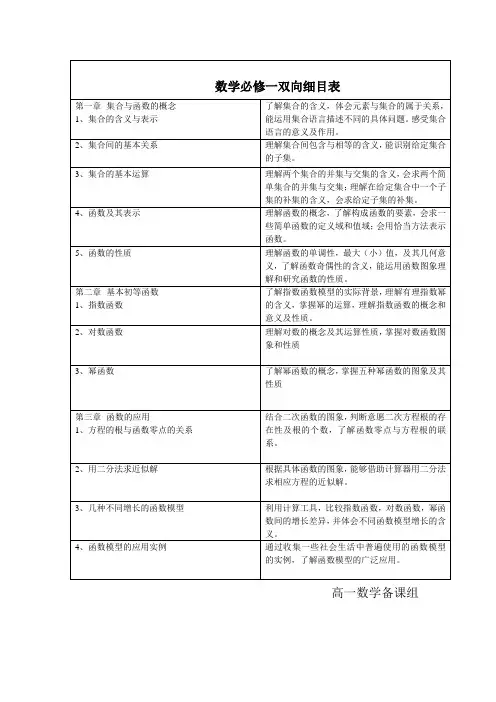
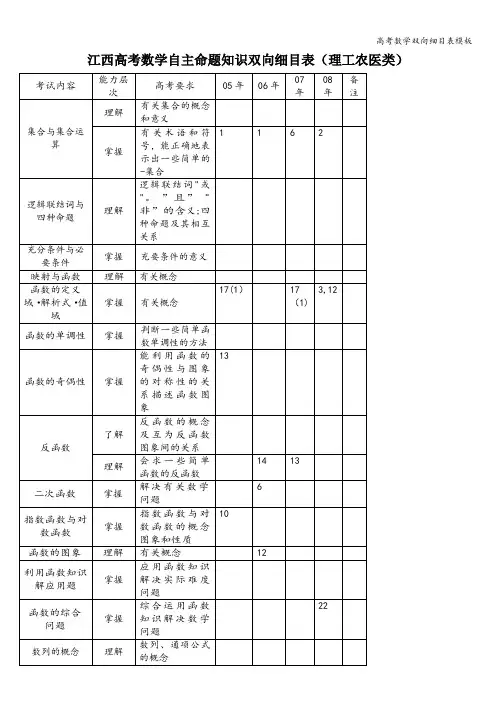
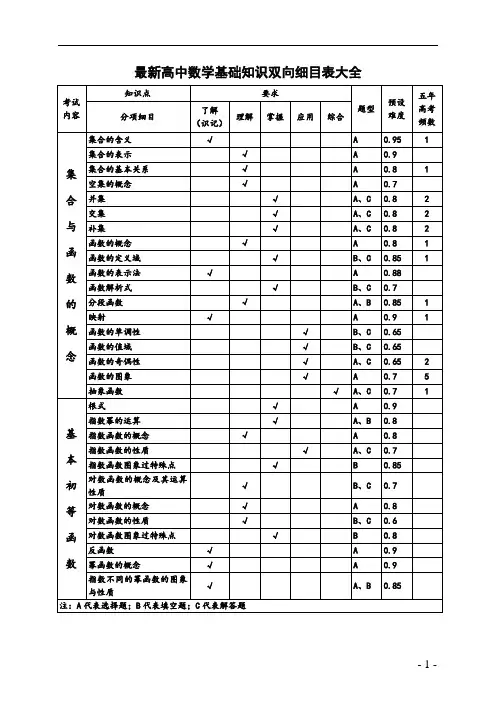
最新推荐高中数学基础知识双向细目表(定稿)最新的高中数学基础知识双向细目表包括集合的含义、表示和基本关系、空集的概念、并集、交集、补集、函数的概念、定义域、表示法、解析式、分段函数、映射、单调性、值域、奇偶性、图象、抽象函数、根式、指数幂的运算等知识点。
要求掌握这些知识点的应用、综合和理解，包括识记、填空和解答题型。
五年的高考考试频数为0.7至1，难度在0.6至0.95之间。
基本初等函数包括指数函数、对数函数和幂函数，要掌握它们的概念、性质、图象以及特殊点等内容。
此外，还要了解函数的零点与方程根的联系、一元二次方程根的存在性及根的个数，以及根据具体函数的突象判断相应方程解的情况。
对于几何学，要了解棱柱、棱锥、棱台、圆柱、圆锥、圆台、球和简单组合体的结构特征。
空间几何体的投影研究空间几何体的投影，包括中心投影和平行投影。
掌握三视图的画法，能够根据给定的图形画出其三视图。
理解主观图的画法，能够根据给定的图形画出其主观图。
了解平面图与直观图面积的关系，能够根据给定的图形计算其面积。
掌握棱柱、棱锥、棱台的表面积和体积的计算方法，能够根据给定的图形计算其表面积和体积。
理解球的表面积和体积的计算方法，能够根据给定的半径计算其表面积和体积。
了解几何体内切球和外接球的问题，能够根据给定的图形计算其内切球和外接球的半径。
空间几何体的投影是几何学中的重要内容，包括中心投影和平行投影。
掌握三视图的画法，可以根据给定的图形画出其三视图。
此外，理解主观图的画法，能够根据给定的图形画出其主观图。
在计算面积方面，需要了解平面图与直观图面积的关系，并能够根据给定的图形计算其面积。
在计算体积和表面积方面，需要掌握棱柱、棱锥、棱台的计算方法，以及球的表面积和体积的计算方法。
此外，需要了解几何体内切球和外接球的问题，能够根据给定的图形计算其内切球和外接球的半径。
本文介绍了数学必修三中的两个知识点：圆的方程和算法概念，以及一个统计学知识点。
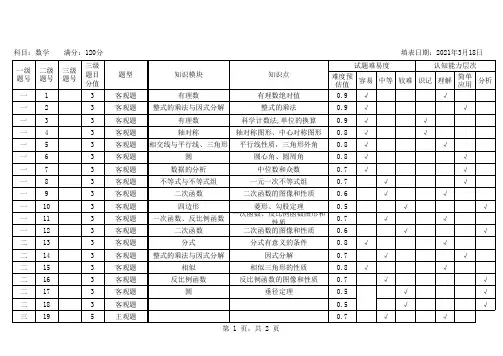
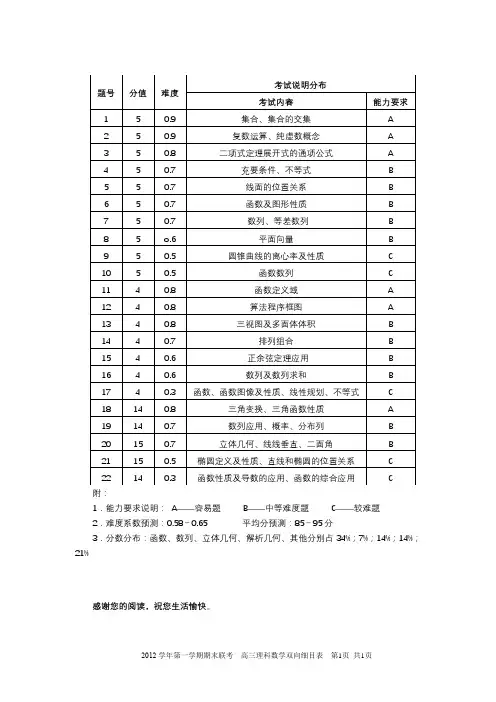
2023新课标全国2卷数学双向细目表一、概述随着时代的发展和教育体制的不断改革，教育教学内容也在不断更新。
在教育领域，新课标的推出是一个重要的事件，它对学生的学习内容和学习方法，以及教师的教学内容和教学方法都有着重要的指导作用。
本文根据2023年新课标全国2卷数学的双向细目表，进行了详细解读和分析，旨在帮助教师和学生更好地了解新课标的要求，有效指导教学实践。
二、2023新课标全国2卷数学双向细目表解读1. 教材选择根据新课标的要求，教材的选择应当注重贴近学生的生活和实际应用，提倡多角度、立体化的教学。
2. 学习目标新课标强调培养学生的数学思维能力和解决问题的能力，要求学生在学习数学的过程中，不仅要掌握数学的基本知识，更要具备数学的思维方式和解决问题的能力。
3. 教学内容在教学内容方面，新课标重视数学知识的系统性和整合性，提倡数学知识的跨学科性和综合性。
教学内容涵盖了数学的基本概念、基本原理和基本方法，同时还包括了一些前沿的数学知识和数学应用。
4. 学习方法新课标要求教师在教学中注重培养学生的自主学习能力，引导学生学会提出问题、探究问题和解决问题的方法，注重培养学生的团队合作精神和交流能力。
5. 教学评价新课标提倡多样化的教学评价方式，不再仅仅依靠考试成绩来评价学生的学习水平，而是要注重以课堂表现、作业与项目、综合评价等多种方式来全面评价学生的学习情况。
三、教学实践与有效策略1. 加强课堂教学的互动性在教学实践中，教师应该注重通过提问、讨论、案例分析等方式，激发学生的学习兴趣，提高学生的学习积极性，培养学生的自主学习能力。
2. 组织丰富多样的教学活动除了传统的讲授和练习，教师还应该开展更多的实验、探究、研究性学习等活动，让学生在实践中掌握知识，提高解决问题的能力。
3. 引导学生进行综合性实践活动教师应该引导学生参与数学建模、数学应用等综合性实践活动，让学生将所学知识应用到实际中去，提高数学知识的实际运用能力。
最新高考理科数学双向细目表
模块知识点考查内容知识要求2017 分
值2018 分
值
2019 分
值
备注
了解理
解
掌握
集合集合的含义与
表示集合的含义、元素与集合的
属于关系
√
列举法、描述法√
集合间的基本关系包含与相等的含义√识别给定集合子集√
全集与空集√
集合的基本运算并集与交集含义与运算√补集含义与运算√韦恩图表达集合的关系与运
算
√
函数概念与基本初等函数I 函数简单定义域值域，了解映射√
图像法、列表法、解析法表
示函数
√
分段函数√
函数单调性、最值及几何意
义
√
函数奇偶性√
函数图像研究函数性质√指数函数指数函数模型背景√
有理、实数指数幂、幂的运
算
√
指数函数概念、单调性√
指数函数图像过定点√对数函数对数的概念及其运算√
换底公式、自然对数、常用
对数
√
对数函数的概念、单调性√
对数函数图像过定点√
指数函数与对数函数互为反
函数
√
幂函数幂函数概念√
幂函数图像√
函数与方程二次函数、零点与方程根√
一元二次方程根的存在性及
根的个数
√
结合图像，用二分法求近似
解
√
函数模型及应用指、对、幂的增长特征√函数模型的应用√
立体几何初步空间几何体柱锥台的结构特征√
三视图√
斜二测画出直观图√
平行、中心投影√
会画视图和直观图√球柱锥台的表面积和体积公
式
√
点线面位置关系线面位置关系定义√
线面平行判定√
面面平行判定√
线面垂直判定√
面面垂直判定√
线面平行性质√
面面平行性质√
线面垂直性质√
面面垂直性质√
用已获结论证明空间图形的
位置关系
√
平面解析几何初步直线与方程结合图形，确定直线位置的
几何要素
√
直线倾斜角和斜率√
过两点的直线斜率计算公式√
判定直线平行或垂直√
点斜式、两点式、一般式√
斜截式与一次函数的关系√
两条相交直线的交点坐标√
两点间距离公式√
点到直线距离公式√
两条平行直线间距离√
圆与方程圆的几何要素，标准方程和
一般方程
√
判断直线与圆的位置关系√
判断两圆的位置关系√
应用直线与圆的方程√
代数方法处理几何问题的思
想
√
空间直角坐标系空间直角坐标表示点的位置√空间两点间距离公式√
算法初步算法的含义、
程序框图
算法的含义和思想√
顺序、条件分支、循环逻辑
结构
√
基本算法语句输入、输出、赋值、条件、
循环语句
√
统计随机抽样会用简单随机抽样从总体中
抽取样本
√
分层抽样和系统抽样√
用样本估计总体频率分布表、频率分布直方
图、折线图
√茎叶图√数据标准差意义和作用√平均数和标准差√用样本估计总体思想√
变量的相关性会画散点图，并认识变量间
的相关关系
√
最小二乘法，线性回归方程√
概率事件与概率频率与概率的意义√
互斥事件的概率加法公式√古典概型古典概型计算公式√
随机事件所含的基本事件数
及发生概率
√几何概型随机数的意义，运用模拟方
法估计概率
√
几何概型的意义√
基本初等函数II 任意角的概
念、弧度制
任意角的概念√
弧度制的概念、弧度与角度
的互化
√
三角函数理解正弦、余弦、正切的定
义
√
单位圆的三角函数线√
诱导公式√
会画三角函数图像√
三角函数周期性√
正余弦单调性、最值与X轴
交点等性质
√
正切函数性质√
同角三角函数的基本关系式√
正弦型函数参数对图像变化
的影响
√
平面向量平面向量的实
际背景及基本
概念
向量的实际背景√
平面向量的概念√
两个向量相等√
向量的几何表示√
向量的线性运
算
加法、减法、几何意义√
数乘的运算、几何意义√
两个向量共线的含义√
线性运算的性质和几何意义√
平面向量基本
定理和坐标表
示
平面向量基本定理及意义√
正交分解及坐标表示√
加法、减法、数乘坐标运算√
用坐标表示平面向量共线的
条件
√
平面向量的数
量积
平面向量的数量积含义与物
理意义
√
平面向量的数量积与向量投
影关系
√
数量积坐标表达式与运算√
用数量积表示夹角√
用数量积判断两个向量的垂
直关系
√向量的应用解决平面几何问题√
解决实际问题√
三角恒等变换和与差的三角
函数公式
两角和与差的余弦、正弦、
正切公式
√
二倍角公式√三角恒等变换积化和差、和差化积√
半角公式√
解三角形正弦定理余弦
定理
正弦定理√
余弦定理√应用三角形度量问题√
数列数列的概念与
简单表示法数列的概念√列表、图像、通项公式表示
方法
√数列是自变量为正整数的函
数
√
等差数列、等比数列等差数列概念√
等差数列通项公式和求和公
式
√等比数列概念√
等比数列通项公式和求和公
式
√等差数列与一次函数√
等比数列与指数函数√
不等式不等关系实际背景√一元二次不等实际情景中抽象√
式与二次函数、一元二次方程
联系
√
会解一元二次不等式，设计
程序框图
√
二元一次不等式组与简单的线性规划问题实际情景抽象出二元一次不
等式组
√
二元一次不等式组表示平面
区域
√二元线性规划问题√
基本不等式了解证明过程√
解决最值问题√
常用基本逻辑用语命题及其关系命题的概念√
四种命题及其关系√
充分、必要、充要条件√
简单的逻辑联
结词
或、且、非√
全称量词与存
在量词
全称量词√
存在量词√
含有量词命题的否定√
圆锥曲线与方程圆锥曲线实际背景√
椭圆定义几何图形标准方
程、简单性质
√
抛物线定义几何图形标准方
程简单性质
√
双曲线定义几何图形标准方
程简单性质
√
简单应用、数形结合思想√
曲线与方程方程的曲线与曲线的方程√
空间向量与立体几何空间向量及其
运算
空间向量概念、基本定理、
坐标
√
空间向量线性运算√
空间向量数量积√
用空间向量数量积表示共线
与垂直
√
空间向量的应
用
直线方向向量与平面的法向
量
√
线线、线面、面面平行关系√
线线、线面、面面垂直关系√
三垂线定理√
线线、线面、面面夹角计算√
导数及其应用导数概念及几
何意义
导数概念实际背景√
导数的几何意义√
导数的运算求导运算法则√
基本初等函数导数公式√在研究函数中
应用
单调性与导数关系√
函数取极值的必要条件和充
分条件
√
会求函数的极值√
会求闭区间上的最值√生活中的优化
问题
实际问题√
定积分与微积分定积分概念、实际背景、思
想
√微积分基本定理√
推理与证明合情推理与演
绎推理
归纳和类比推理√
演绎推理的基本模式√
联系和差异√直接证明与间
接证明
分析法与综合法√
反证法√数学归纳法数学归纳法√
数系的扩充与复数的引入复数的概念复数的概念√
复数相等的充要条件√
复数代数表示法与几何意义√
复数的四则运
算
四则运算√
加减法运算的几何意义√
计数原理分类加法、分
步乘法
分类加法√
分步乘法√排列与组合排列概念与公式√
组合概念与公式√二项式定理证明二项式定理√
展开式有关问题√
概率与离散型随机变量与分布列√
统计概率超几何分布√
条件概率√
两个事件相互独立√
N次独立重复试验与二项分布√
均值、方差√
正态分布曲线特点及意义√统计案例独立性检验√
回归分析√
坐标系与参数方程坐标系用极坐标表示点的位置√
极坐标与直角坐标互化√
简单图形的方程√
柱坐标系、球坐标系表示空
间中点位置
√
参数方程参数方程和参数的意义√
直线、圆、圆锥曲线的参数
方程
√
平摆线与渐开线√
不等式选讲含绝对值不等
式
几何意义√
绝对值三角不等式√柯西不等式不同形式√
几何意义√
柯西不等式一
般情
参数配方法√
排序不等式向量递归法√
伯努利不等式数学归纳法√均值不等式求极值√
证明不等式方法比较、综合、分析、反证、
放缩
√。
