点的运动轨迹

七年级几何动点知识点
几何学中，动点是指在空间中不断移动的点，与静态点相比，它具有更加丰富的几何性质。

在七年级几何学习中，了解动点的概念及特性是非常重要的。

本文将为您介绍七年级几何动点知识点。

一、动点的定义
动点是指在空间中不断移动的点。

它不同于静态点，它可以沿直线或曲线做任意运动。

二、动点的特性
1. 动点的轨迹：动点按照一定轨迹运动，其轨迹可以是一条直线、一条曲线或者是一些点的集合。

2. 动点的运动方向：动点的运动方向可以是直线或曲线，也可以是退化成点。

3. 动点的运动速度：动点可以以任意速度进行运动。

4. 动点的终止条件：动点可以在任意时刻停止运动。

三、动点的应用
动点不仅仅是一个几何概念，它还具有广泛的应用。

下面将为
您介绍动点在几何学中的应用。

1. 动点应用于轨迹绘制：几何学中的轨迹绘制就是一个动点的
概念，可以通过动点的运动绘制出轨迹来，如绘制圆、椭圆、双
曲线等等。

2. 动点应用于自由曲面绘制：在几何学中，自由曲面是由两个
动点所生成的曲面，其中每个动点的运动轨迹与另一个动点平行。

3. 动点应用于轴对称图形的绘制：轴对称图形是通过一个动点
的轨迹复制生成的图形，这种图形在几何学中应用广泛。

4. 动点应用于直线交叉产生角度：几何学中的角度定义是两条
直线交叉所产生的角度，这个概念就是通过动点来生成的。

综上所述，动点是在几何学中不可或缺的概念，掌握了动点的应用，可以更好地理解几何学中的概念，更好地解决问题。

希望本文能对您有所帮助。

求点的轨迹方程的六种常见方法点的轨迹方程是描述点在运动过程中所经过的路径的数学方程。

在数学和物理等领域，有许多方法可以推导和描述点的轨迹方程。

下面介绍六种常见的方法。

一、直角坐标系方法直角坐标系方法是最常见的一种方法，通常用于平面分析。

在直角坐标系下，点的位置可以用横坐标x和纵坐标y来表示。

如果已知点的坐标与时间的关系，可以通过方程联立或者曲线拟合的方法得到点的轨迹方程。

二、参数方程方法参数方程方法是一种将点的位置用参数表示的方法。

通过引入参数t，点的坐标可以用关于t的函数表示，如x=f(t)和y=g(t)，这样就可以得到点的轨迹方程。

参数方程方法适用于描述直线、圆和其他曲线的方程。

三、极坐标系方法极坐标系方法是一种将点的位置用极径r和极角θ来表示的方法。

通过引入极径和极角的关系表达式，可以得到点的轨迹方程。

例如，对于圆的方程可以表示为r=f(θ)，其中f(θ)是关于极角θ的函数。

四、矢量方程方法矢量方程方法是一种用矢量表示点的位置的方法。

通过引入位置矢量r(t)，可以得到点的轨迹方程。

位置矢量r(t)通常用分量表示，如r=(x,y,z)。

矢量方程方法适用于描述曲线在三维空间中的轨迹。

五、微分方程方法微分方程方法是一种通过点的运动规律和动力学方程来推导轨迹方程的方法。

通过对点的位置向量或者其分量进行微分，并代入运动规律方程，可以得到点的轨迹方程。

微分方程方法适用于描述受力作用下点的运动。

六、变分原理方法变分原理方法是一种通过极小化或者极大化一些物理量来推导轨迹方程的方法。

通过对点的位置或路径的泛函进行变分，可以得到使泛函取得极值的轨迹方程。

变分原理方法适用于描述光的传播、质点在介质中的传播等问题。

综上所述，点的轨迹方程可以通过直角坐标系方法、参数方程方法、极坐标系方法、矢量方程方法、微分方程方法和变分原理方法等六种常见方法推导和描述。

不同的方法适用于不同的情况和问题，选择合适的方法可以更方便地求解轨迹方程。

描述点的运动轨迹的三种方法描述点的运动轨迹是数学和物理中一个基本而又重要的概念。

以下是描述点的运动轨迹的三种主要方法：1. 参数方程法参数方程法是一种常见的方法，它通过选取合适的参数来描述点的运动轨迹。

这种方法特别适用于描述具有特定规律的点的运动，例如圆周运动或周期性运动。

参数方程的一般形式为：(x = f(t))(y = g(t))其中(x) 和(y) 是点的坐标，(t) 是参数（通常是时间）。

通过改变参数(t) 的值，我们可以得到一系列的点，这些点连在一起就形成了点的运动轨迹。

2. 直角坐标法直角坐标法是在二维平面上描述点的运动轨迹的一种直观方法。

我们可以在平面上选择一个固定点作为原点，然后建立两个互相垂直的坐标轴（通常是x轴和y轴），通过描述点在这两个坐标轴上的坐标值来描述其运动轨迹。

这种方法特别适用于描述直线运动或简单的曲线运动。

例如，如果一个点沿着直线做匀速直线运动，那么它的坐标(x) 和(y) 可以表示为：(x = x_0 + v_x t)(y = y_0 + v_y t)其中(x_0) 和(y_0) 是初始坐标，(v_x) 和(v_y) 是沿着x轴和y轴的速度，(t) 是时间。

3. 极坐标法极坐标法是在二维平面上描述点的运动轨迹的一种有效方法。

与直角坐标法不同，极坐标法使用距离原点的距离（径向坐标，通常表示为(r)）和点与x轴之间的夹角（角度，通常表示为(\theta) 或(\phi)\）作为描述点的运动的参数。

这种方法特别适用于描述曲线运动，尤其是旋转或螺旋式的运动。

对于做曲线运动的点，其极坐标可以表示为：(r = r(t))(\theta = \theta(t))通过改变时间(t)，我们可以得到一系列的点，这些点连在一起就形成了点的运动轨迹。

几何动点运动轨迹及最值一、动点运动轨迹——直线型（动点轨迹为一条直线，利用“垂线段最短”）Ⅰ．当一个点的坐标以某个字母的代数式表示，若可化为一次函数，则点的轨迹是直线； 1．在平面直角坐标系中，点P 的坐标为（0，2），点M 的坐标为39(1,)44m m −−−(其中m 为实数)，当PM 的长最小时，m 的值为__________．2．如图，在平面直角坐标系中，A (1，4)，B (3，2)，C (m ，－4m ＋20)，若OC 恰好平分四边形．．．OACB ．．．．的面积，求点C 的坐标．Ⅱ．当某一动点到某条直线的距离不变时，该动点的轨迹为直线；3．如图，矩形ABCD 中，AB ＝6，AD ＝8，点E 在边AD 上，且AE ：ED ＝1：3．动点P 从点A 出发，沿AB 运动到点B 停止．过点E 作EF ⊥PE 交射线BC 于点F ，设M 是线段EF 的中点，则在点P 运动的整个过程中，点M 运动路线的长为_________.【变式1】如图，矩形ABCD 中，AB ＝6，AD ＝8，点E 在边AD 上，且AE ：ED ＝1：3．动点P 从点A 出发，沿AB 运动到点B 停止．过点E 作EF ⊥PE 交边BC 或CD 于点F ，设M 是线段EF 的中点，则在点P 运动的整个过程中，点M 运动路线的长为___________.ABDCEFPM ABDCEFPM yxBAO【变式2】如图，在矩形ABCD 中，点P 在AD 上，AB ＝2，AP ＝1，E 是AB 上的一个动点，连接PE ，过点P 作PE 的垂线，交BC 于点F ，连接EF ，设EF 的中点为G ，当点E 从点B 运动到点A 时，点G 移动的路径的长是_________.【变式3】在矩形ABCD 中，AB ＝4，AD ＝6，P 是AD 边的中点，点E 在AB 边上，EP 的延长线交射线CD于F 点，过点P 作PQ ⊥EF ，与射线BC 相交于点Q ．（1）如图1，当点Q 在点C 时，试求AE 的长； （2）如图2，点G 为FQ 的中点，连结PG ． ①当AE ＝1时，求PG 的长；②当点E 从点A 运动到点B 时，试直接写出线段PG 扫过的面积． 变式3图14．如图，C 、D 是线段AB 上两点，且AC ＝BD ＝16AB ＝1，点P 是线段CD 上一个动点，在AB 同侧分别作等边△P AE 和等边△PBF ，M 为线段EF 的中点。

动点轨迹为直线的判定
从几何学角度来看，一个动点的轨迹如果是直线，那么它满足
以下条件：
1. 任意两点之间的距离是恒定的。

2. 任意三点共线。

首先，我们可以通过观察动点的运动轨迹来判断它是否为直线。

如果我们观察到动点在相同时间间隔内移动相同的距离，并且在同
一直线上移动，那么可以初步判定其轨迹为直线。

另外，我们也可
以利用数学工具，如坐标系和方程式来分析动点的运动轨迹，如果
动点的坐标满足直线方程式，那么可以确定其轨迹为直线。

从物理学角度来看，如果动点在运动过程中受到的外力平衡，
且速度保持恒定，那么它的轨迹也可能是直线。

这符合牛顿运动定
律中的惯性定律，即物体在受到外力作用时会保持匀速直线运动的
状态。

此外，我们还可以利用数学方法来判断动点轨迹是否为直线，
比如利用微积分中的导数和曲率来分析动点轨迹的变化情况，从而判断其是否为直线。

另外，我们也可以利用工程测量方法，比如通过测量动点在不同时间点的位置来确定其轨迹是否为直线。

综上所述，判定动点轨迹是否为直线需要综合运用几何学、物理学和数学等知识，通过观察、分析和实验来得出结论。

第二部分 运动学第六章点的运动学一、基本要求1．掌握描述点的运动的矢量法、直角坐标法和自然法（弧坐标法）。

2．了解描述点的运动的极坐标法。

3．能求点的运动轨迹。

4．能熟练地应用直角坐标法和自然法求解与点的速度和加速度有关的问题。

二、理论要点1．描述点的运动的三种基本方法（1）矢量法z 运动方程点的运动方程为动点在空间的几何位置随时间变化的规律。

以矢量形式表示的点的运动方程为)(t r r =z 轨迹轨迹为动点在空间运动时所经过的一条连续曲线。

在矢量法中，矢径r 的矢端曲线即为点的运动轨迹。

z 速度点的速度是个矢量，它等于矢径对时间的一阶导数，即dtd r v = z 加速度点的加速度也是个矢量，它等于速度矢对时间的一阶导数，或等于矢径对时间的二阶导数，即2dtd dt d 2r v a == （2）直角坐标法z 运动方程)()()(321t f z t f y t f x ===z 轨迹从上面点的运动方程中消去时间t 即可得轨迹方程。

如：),(0),(21==z y F y x Fz 速度 k j i v z y x v v v ++=dtdz v dt dy v dtdx v z y x ===即速度在各坐标轴上的投影等于动点的各对应坐标对时间的一阶导数。

由此可求得速度的大小和方向余弦。

z 加速度k j i a z y x a a a ++=222222dtz d dt dv a dty d dt dv a dtx d dt dv a z z y y x x ====== 即加速度在各坐标轴上的投影等于动点的各对应坐标对时间的二阶导数。

由此可求得加速度的大小和方向余弦。

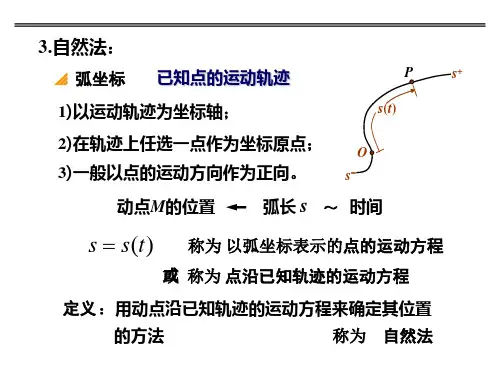
（3）自然法（弧坐标法）利用点的运动轨迹建立弧坐标及自然轴系，并用它们来描述和分析点的运动的方法称为自然法。

z 运动方程)(t f s =z 速度ττv dtds v == z 加速度 n τa a a n τn τa a +=+=22dt s d dt dv a τ== ρ2v a n =式中，ρ为曲率半径。

母题若X +1二3,y -5二t ，则y 与x点的运动轨迹符合一定条件的动点所形成的图形，或者说，符合一定条件的点的全体所组成的集合,叫做满足该条件的点的轨迹.“动点路径"是一个比较抽象的问题，但在高中解析几何中的学习是非常有用的，也是非常重要的。

在研究动点问题时，可以在运动中寻找不变的量，即不变的数量关系或位置关系．如果动点的轨迹是一条线段，那么其中不变的量便是该动点到某条直线的距离始终保持不变；如果动点的轨迹是一段圆弧，那么其中不变的量便是该动点到某个定点的距离始终保持不变．因此，解决此类动点轨迹问题便可转化为寻找变量与不变的关系。

常用的基本轨迹：1、如图，已知AB=10,P 是线段AB 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等边AACP 和厶PDB ，连接CD ，设CD 的中点为G ，当点P 从点A 运动到点B 时，则点G 移动路径的长是■ 变式1、(2010XX)如图：已知AB=10，点C 、D 在线段AB 上且AC=DB=2；P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等ffl^AEP 和等边APFB ，连接EF,设EF 的中点为G ；当点P 从点C 运动到点D 时，则点G 移动路径的长是.变式2、如图：已知AB=10，点C 、D 在线段AB 上且AC=DB=2；P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作正方形APEF 和正方形PBGH ，点0!和°?是这两个正方形的中心连接0%设°卩2的中点为Q ;当点P 从点C运动到点D 时，则点Q 移动路径的长是. 2、如图，已知线段AB=10,AC=BD=2，点P 是CD 上—动点，分别以AP 、PB 为边向上、向下作正方形APEF 和PHKB ，设正方形对角线的交点分别为°1、°2，当点P 从点C 运动到点D 时，线段0102中点G 的运动路径的长是.3、如图1，在RtAABC 中，乙C=90°,开始沿边AC 向点C 以1个单位长度的速度运动，动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动，过点P 作PD 〃BC ，交AB 于点D,连接PQ 分别从点A 、C 同时岀发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t 秒(tMO).(1)直接用含t 的代数式分别表示：QB=,PD=.(2)是否存在t 的值,A使四边形PDBQ为菱形？若存在，求岀t的值；若不存在，说明理由•并探究如何改变Q的速度(匀速运动)，使四边形PDBQ在某一时刻为菱形，求点Q的速度；(3)如图2,在整个运动过程中，求岀线段PQ 中点M所经过的路径长.变式1：如图，在平面直角坐标系中，矩形0ABC的两边OA、0C分别在x轴、y轴的正半轴上,0A=4,0C=2•点P从点0岀发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒•将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动，连接DP、DA.变式2：如图，边长为4的等边三角形AOB的顶点0在坐标原点，点A在x轴正半轴上，点B在第一象限•一动点P沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒•将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA,过点P作PD丄0B于点D.(1)填空：PD的长为用含t的代数式表示)；(2)求点C的坐标(用含t的代数式表示)；(3)在点P从0向A运动的过程中，A PCA能否成为直角三角形？求上的值•若不能，说理由；(4)填空：在点P从0向人运动的过程中，点C运动路线的长为.4、在矩形ABCD中，点P在AD上，AB=•：,AP=1。

点的运动轨迹符合一定条件的动点所形成的图形,或者说,符合一定条件的点的全体所组成的集合,叫做满足该条件的点的轨迹.“动点路径”就是一个比较抽象的问题,但在高中解析几何中的学习就是非常有用的,也就是非常重要的。

在研究动点问题时,可以在运动中寻找不变的量,即不变的数量关系或位置关系.如果动点的轨迹就是一条线段,那么其中不变的量便就是该动点到某条直线的距离始终保持不变;如果动点的轨迹就是一段圆弧,那么其中不变的量便就是该动点到某个定点的距离始终保持不变.因此,解决此类动点轨迹问题便可转化为寻找变量与不变的关系。

常用的基本轨迹: 1、如图,已知AB=10,P 就是线段AB 上的动点,分别以AP 、PB 为边在线段AB 的同侧作等边△ACP 与△PDB,连接CD,设CD 的中点为G,当点P 从点A 运动到点B 时,则点G 移动路径的长就是______.变式1、(2010桂林)如图:已知AB=10,点C 、D 在线段AB 上且AC=DB=2;P 就是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 与等边△PFB,连接EF,设EF 的中点为G;当点P 从点C 运动到点D 时,则点G 移动路径的长就是______.变式2、如图:已知AB=10,点C 、D 在线段AB 上且AC=DB=2;P 就是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作正方形APEF 与正方形PBGH,点O 1与O 2就是这两个正方形的中心,连接O 1O 2,设O 1O 2的中点为Q;当点P 从点C 运动到点D 时,则点Q 移动路径的长就是______.2、如图,已知线段AB=10,AC=BD=2,点P 就是CD 上一动点,分别以AP 、PB 为边向上、向下作正方形APEF 与PHKB,设正方形对角线的交点分别为O1、O2,当点P 从点C 运动到点D 时,线段O1O2中点G 的运动路径的长就是_____.母题:若3x t +=,5y t -=,则y 与x 之间的关系就是 _________ .3、如图1,在Rt △ABC 中,∠C=90°,AC=6,BC=8,动点P 从点A 开始沿边AC 向点C 以1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD ∥BC,交AB 于点D,连接PQ 分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(t ≥0).(1)直接用含t 的代数式分别表示:QB= _________ ,PD= _________ .(2)就是否存在t 的值,使四边形PDBQ 为菱形？若存在,求出t 的值;若不存在,说明理由.并探究如何改变Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度;(3)如图2,在整个运动过程中,求出线段PQ 中点M 所经过的路径长.变式1:如图,在平面直角坐标系中,矩形OABC 的两边OA 、OC 分别在x 轴、y 轴的正半轴上,OA ＝4,OC ＝2.点P 从点O 出发,沿x 轴以每秒1个单位长的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间就是t 秒.将线段CP 的中点绕点P 按顺时针方向旋转90°得点D ,点D 随点P 的运动而运动,连接DP 、DA .(1)请用含t 的代数式表示出点D 的坐标;(2)请直接写出随着点P 的运动,点D 运动路线的长、变式2:如图,边长为4的等边三角形AOB 的顶点O 在坐标原点,点A 在x 轴正半轴上,点B 在第一象限.一动点P 沿x 轴以每秒1个单位长的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间就是t 秒.将线段BP 的中点绕点P 按顺时针方向旋转60°得点C ,点C 随点P 的运动而运动,连接CP 、CA ,过点P 作PD ⊥OB 于点D .(1)填空:PD 的长为 用含t 的代数式表示);(2)求点C 的坐标(用含t 的代数式表示);(3)在点P 从O 向A 运动的过程中,△PCA 能否成为直角三角形？求t 的值.若不能,说理由;(4)填空:在点P 从O 向A 运动的过程中,点C 运动路线的长为 、4、在矩形ABCD 中,点P 在AD 上,AB= ,AP=1。

点的轨迹问题知识点总结一、点的轨迹的定义点的轨迹是指一个点在一定条件下所形成的路径。

在平面几何中，点的轨迹通常是在笛卡尔坐标系中表示的，可以用数学方程或者参数方程来描述。

点的轨迹是几何图形的一种，也可以看作是某个特定点的位置，随着某种变化而移动的结果。

二、点的轨迹的性质1. 封闭性：点的轨迹通常是封闭的，即当点按照一定条件运动时所形成的轨迹是一个封闭的曲线或者封闭的图形。

2. 对称性：点的轨迹通常具有某种对称性，可以是轴对称、中心对称或者其他特定的对称性。

这也是对称轨迹问题中常见的研究内容。

3. 交点性：点的轨迹通常会与其他几何图形相交，这时可以要求求出这些交点的坐标或者其他相关的性质。

4. 方程性质：点的轨迹通常可以用某种数学方程或者参数方程来描述，这种描述方法可以帮助我们更好地理解轨迹的性质。

5. 运动性质：点的轨迹通常是描述某个点随着时间的变化而形成的路径，因此轨迹的运动性质也是我们关注的重点。

三、常见的点的轨迹类型1. 直线：当一个点在平面上以一定的速度和方向直线运动时，它形成的轨迹是一条直线。

2. 圆：当一个点与固定点之间的距离保持不变，且这个固定点位于平面上的一固定圆周上时，这个点形成的路径是一个圆。

3. 抛物线：当一个点在平面上沿着一定的方向和速度运动时，它的轨迹是一个抛物线。

4. 椭圆：当一个点在平面上相对于两个固定点的距离之和保持不变时，这个点的轨迹是一个椭圆。

5. 双曲线：当一个点在平面上相对于两个固定点的距离之差保持不变时，这个点的轨迹是一个双曲线。

6. 渐开线：当一个点在平面上的距离与一个固定点之比保持不变时，这个点的轨迹是一个渐开线。

以上是一些常见的点的轨迹类型，当然还有其他更为复杂的轨迹类型，如三角形轨迹、四边形轨迹等。

四、点的轨迹问题的解题方法1. 分析法：通过对问题的条件进行分析，逐步推导出点的轨迹的数学表达式。

2. 参数法：引入一个参数，通过表示点的位置的数学表达式与参数的关系来描述点的轨迹。

点的运动轨迹在日常生活中，我们经常看到各种不同的点在空间中运动，它们的运动轨迹各不相同，引起了我们的好奇心。

本文将以点的运动轨迹为题，介绍几种常见的运动轨迹。

一、直线运动直线运动是最简单的一种运动轨迹，也是我们最常见的一种运动形式。

当一个点沿着一条直线运动时，它的轨迹就是一条直线。

比如我们在马路上看到的汽车行驶的轨迹，就是一条直线。

此外，我们还可以通过绘制两点之间的连线来模拟点的直线运动轨迹。

二、圆周运动圆周运动是另一种常见的运动轨迹。

当一个点围绕着一个固定的中心点做匀速圆周运动时，它的轨迹就是一个圆。

比如地球绕太阳运动的轨迹就是一个近似的圆。

此外，我们还可以通过绘制一系列等距离的点来模拟点的圆周运动轨迹。

三、抛物线运动抛物线运动是一种曲线运动，它的轨迹形状像一个抛物线。

当一个点在重力的作用下，以一个初始速度在水平方向上做抛体运动时，它的轨迹就是一个抛物线。

比如我们在体育课上投掷实验中看到的抛物线运动，就是一个典型的例子。

此外，我们还可以通过绘制一系列位置随时间变化的点来模拟点的抛物线运动轨迹。

四、椭圆运动椭圆运动是一种更加复杂的曲线运动，它的轨迹形状像一个椭圆。

当一个点围绕着两个焦点之间的直线做匀速运动时，它的轨迹就是一个椭圆。

比如地球绕太阳运动的轨迹就是一个近似的椭圆。

此外，我们还可以通过绘制一系列位置随时间变化的点来模拟点的椭圆运动轨迹。

五、螺旋运动螺旋运动是一种非常有趣的运动形式，它的轨迹形状像一个螺旋。

当一个点同时绕着一个中心点做圆周运动，并且沿着轴向移动时，它的轨迹就是一个螺旋。

比如我们在螺旋桨上看到的螺旋运动，就是一个典型的例子。

此外，我们还可以通过绘制一系列位置随时间变化的点来模拟点的螺旋运动轨迹。

六、随机运动除了以上几种规则的运动轨迹外，我们还可以遇到一些无规则的运动轨迹，这种运动被称为随机运动。

当一个点在空间中没有任何规律地运动时，它的轨迹就是一个随机的路径。

比如我们看到的飞蛾在夜晚灯光下的飞行轨迹，就是一个典型的随机运动。

第五章点的运动学本章将研究点的运动，包括点的运动方程、运动轨迹、速度、加速度等。

点的运动学也是研究刚体运动的基础。

第一节点的运动方程点在取定的坐标系中位置坐标随时间连续变化的规律称为点的运动方程。

点在空间运动的路径称为轨迹。

在某一参考体上建立不同的参考系，点的运动方程有不同的形式。

一、矢量法设点作空间曲线运动，在某一瞬时t ，动点为M，如图5-1所示。

选取参考体上某固定点O为坐标原点，自点O向动点M作矢量r，称r为点M相对于原点O的矢径。

当动点M运动时，矢径r随时间而变化，并且是时间的单值连续函数，即(5-1)上式称为矢量形式表示的点的运动方程。

显然，矢径r的矢端曲线就是动点的运动轨迹。

图5-1二、直角坐标法过点O建立固定的直角坐标系Oxyz，则动点M在任意瞬时的空间位置也可以用它的三个直角坐标x , y , z表示，如图5-1所示。

由于矢径的原点和直角坐标系的原点重合，矢径r可表为(5-2)式中i , j , k 分别为沿三根坐标轴的单位矢量。

坐标x , y , z也是时间的单值连续函数，即(5-3)式(5-3)称为点的直角坐标形式的运动方程，也是点的轨迹的参数方程。

三、自然法当动点相对于所选的参考系的轨迹已知时，可以沿此轨迹确定动点的位置。

在轨迹上任取固定点O 作为原点，选定沿轨迹量取弧长的正负方向，则动点的位置可用弧坐标s 来确定。

如图5-2所示。

动点沿轨迹运动时，弧长s 是时间的单值连续函数(5-4)上式称为点用自然法描述的运动方程。

图5-2以上三种形式的运动方程在使用上各有所侧重。

矢量形式的运动方程常用于公式推导；直角坐标形式的运动方程常用于轨迹未知或轨迹较复杂的情况；当轨迹已知为圆或圆弧时，用自然法则较为方便。

第二节点的速度和加速度动点运动的快慢和方向用速度表示，速度的变化情况则用加速度表示。

下面给出在各坐标系下，速度、加速度的数学表达式。

一、用矢量法表示点的速度和加速度如动点矢量形式的运动方程为r=r(t) ，则动点的速度定义为（5-5）即动点的速度等于动点的矢径r对时间的一阶导数。

盘点动点轨迹问题的基本图形动点轨迹问题是中考的重要压轴点.受学生解析几何知识的局限和思维能力的束缚，该压轴点往往成为学生在中考中的一个坎，致使该压轴点成为学生在中考中失分的一个黑洞.掌握该压轴点的基本图形，构建问题解决的一般思路，是中考专题复习的一个重要途径。

本文就动点轨迹问题的基本图形作一详述，动点轨迹基本类型为直线型和圆弧型.归纳一下，动点轨迹为直线型的有:①平面内到定直线的距离等于定长的点的轨迹是直线(线段);②平面内与定直线的夹角为定角的点的轨迹是直线(线段).动点轨迹是圆弧型的有:①平面内到一定点的距离为定长的点的轨迹是圆(圆弧);②平面内与两定点的张角是定角的点的轨迹是圆一、直线型类型一例1 如图1，已知半圆⊙O 的半径为2，初始位置与直线l 相切于点C ，直径AB 与直线l 平行，将半圆⊙O 在直线l 上无滑动地滚动至直径AB 与直线l 垂直，求圆心O 在此过程中形成的轨迹的长.简解 ∵在滚动过程中⊙O 与直线l 相切，∴圆心O 与直线l 的距离为半径长2，∴圆心O 的轨迹是一线段，长度为14圆弧长， 即弧长122 4BC ππ=⨯⨯=. 小结 此例因动点O 到定直线l 的距离为定长，所以基本图形为直线型类型一.这是动点轨迹入门级题目.例2 如图2，已知线段6AB =，P 为线段AB 上一动点，分别以AP 、BP 为边在线段AB 的同侧作等边APC ∆和等边BPD ∆，连结CD ，取CD 得中点Q ，在点P 从A 点到B 点运动的过程中，求点Q 运动路径的长.简解 过点C 作CM AB ⊥于M 点，过点D 作DN AB ⊥于N 点;过点Q 作QG AB ⊥于G 点，则////QG CM DN .则四边形CMND 是梯形，且QG 是中位线， ∴1()2QG CM DN =+1)2AP =)AP BP =+6QG ==(定值). ∴点Q 运动路径是AB 上侧与AB 平行的一条线段.通过点P 分别与点A 、点B 重合，运用极端法可知点Q 运动路径是以AB 为边的等边三角形的中位线，∴Q 点轨迹的长度为132AB =. 小结 此例因动点Q 到定直线AB 的距离为定长，所以基本图形为直线型类型一因动点较多，需抓住主动点P 对从动点Q 的制约作用以确定动点Q 的轨迹，继而运用极端法求得轨迹的长度.二、直线型类型二例3 如图3，已知ABC ∆是边长为6的等边三角形，角平分线AD 交BC 于D 点，P 是直线AD 上一动点，连结CP ，以CP 为边向下作等边三角形PCQ ∆，连结DQ ，求DQ 长度的最小值.简解 连结BQ ，过点D 作DH BQ ⊥于H 点.∵60ACB PCQ ∠=∠=︒，∴ACP BCQ ∠=∠.又∵CA CB =，CP CQ =，∴ACP BCQ ∆≅∆，∴30CBQ CAP ∠=∠=︒，即点Q 的轨迹为过B 点且与BC 成30°角的直线.∴当DH BQ ⊥时的垂线段DH 即为所求的DQ 长度的最小，∴在Rt BDH ∆中求得min 1322DQ DH BD ===. 小结 此例因动点Q 与定直线BC 的夹角为定角，所以基本图形为直线型类型二.须知当动点轨迹为直线时，定点与动点连线的最短距离为垂线段的长度.例4 如图4，已知Rt ABC ∆中点P 是边AC 所在直线上一动点，连结BP ，以BP 为斜边作等腰直角BPQ ∆，点F 为边AC 上一定点且2CF =，连结FQ ，求FQ 长度的最小值.简解 过点Q 作直线AC 的垂线，交AC 延长线于点N ，过点B 作BM NQ ⊥于点M .易证得QMB PNQ ∆≅∆，∴BM NQ CN ==.连结CQ ，则45QCN ∠=︒即点Q 的轨迹为过C 点且与CN 成45°角的直线，∴当FH CQ ⊥时的FH 的长度即为所求FQ 最小值，即min 22FQ FH ===. 小结 此例因动点Q 与定直线AC 的夹角为定角，所以基本图形为直线型类型二.须知图形中有等腰直角三角形存在时可运用构造全等三角形转移等量这一基本方法.三、圆弧形类型一例5 如图5，已知正方形ABCD 的边长为4，P 、Q 分别是边AB 、BC 上的动点，且4PQ =，M 是PQ 的中点，求DM 的最小值.简解 连结BM . ∵114222BM PQ ==⨯=(定值)， ∴M 在以B 为圆心2BM =为半径的圆上， ∴当,,B M D 三点共线时DM 取最小值，即最小值为2DM BD BM =-=.小结 此例因动点M 与定点B 的距离为定长，所以基本图形为圆弧型类型一.须知圆外一点与圆上动点的最大距离为d r +，最小距离为d r -.例6 如图6，正六边形ABCDEF 的边长为2，两顶点,A B 分别在x 轴和y 轴上运动.求顶点D 到原点O 的距离的最大值和最小值.简解 取AB 中点P ，连结OP ，DP . ∵112OP AB ==(定值)， ∴点P 是在以O 为圆心，112r AB ==为半径的圆上.又由Rt DBP ∆，求得PD ==(定值)，∴PD OP OD PD OP -≤≤+.①当,,O P D 三点共线且P 在线段OD 上时，OD PD OP =+1;②当,,O P D 三点共线且P 在线段DO 延长线上时，OD PD OP =-1. 小结 此例因动点P 与定点O 的距离为定长，所以基本图形为圆弧型类型一.须知两定长线段在共线时可求得折线最大长度为12d d +，最小值为12d d -.四、圆弧型类型二例7 如图，E 、F 是正方形ABCD 的边AD 上的两个动点，且满足AE DF =，连结CF 交BD 于点G ，连结BE 交AG 于点H .若正方形的边长为2，求线段DH 长度的最小值.简解 易证得BAE CDF ∆≅∆，∴ABE DCF ∠=∠.又GAD GCD ∆≅∆，∴GAD DCF ∠=∠，∴ABE GAD ∠=∠.∵90GAD BAH ∠+∠=︒，∴90ABE BAH ∠+∠=︒，即90BHA ∠=︒(定角)，∴点H 在以AB 的中点(设为O )为圆心，AB 为半径的圆(四分之一圆弧)上. 连结OD ，交⊙O 于P 点，当点H 运动到点P 时，DH 取得最小值1OD OP -=.小结 此例因动点H 与两定点A 、B 的张角为定角，所以基本图形为圆弧型类型二.由例5的方法可求得圆外一点与圆上动点的最小距离.例8 如图8，以(0,1)G 为圆心，半径为2的圆与x 轴交于A 、B 两点，与y 轴交于C 、D 两点，点E 为⊙G 上一动点，CF AE ⊥于点F ，求当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长.简解 ∵90AFC ∠=︒ (定角)，∴点F 在以AC 的中点(设为M )为圆心，12AC 为半径的圆上. 当点E 在B 点时，点F 在O 点; 当点E 在D 点时，点F 在A 点，∴点F 所经过的路径为弧OA .∵在Rt AOC ∆中30ACO ∠=︒，∴260AMO ACO ∠=∠=︒，∴弧长602360OA π=⨯=. 小结 此例因动点F 与两定点A 、C 的张角为定角，所以基本图形为圆弧型类型二.由例2的极端法确定圆弧的起点和终点，从而求得路径圆弧长.结束语构建基本图形形成解决问题的思维模式是初中几何教学的重要方法.本文就动点轨迹的基本图形作了比较系统的分类，为学生解决此类问题提供了一个可行的途径.但在实际教学中要注意防止过于固化而禁锢学生的思维，阻碍学生创造性思维、发散性思维的形成.。