动点问题中的最值、最短路径问题(解析版)

二次函数与几何的动点及最值、存在性问题目录题型01平行y轴动线段最大值与最小值问题题型02抛物线上的点到某一直线的距离问题题型03已知点关于直线对称点问题题型04特殊角度存在性问题题型05将军饮马模型解决存在性问题题型06二次函数中面积存在性问题题型07二次函数中等腰三角形存在性问题题型08二次函数中直角三角形存在性问题题型09二次函数中全等三角形存在性问题题型10二次函数中相似三角形存在性问题题型11二次函数中平行四边形存在性问题题型12二次函数中矩形存在性问题题型13二次函数中菱形存在性问题题型14二次函数中正方形存在性问题二次函数常见存在性问题：(1)等线段问题：将动点坐标用函数解析式以“一母式”的结构表示出来，再利用点到点或点到直线的距离公式列出方程或方程组，然后解出参数的值，即可以将线段表示出来.【说明】在平面直角坐标系中该点在某一函数图像上，设该点的横坐标为m，则可用含m字母的函数解析式来表示该点的纵坐标，简称“设横表纵”或“一母式”.(2)平行y轴动线段最大值与最小值问题：将动点坐标用函数解析式以“一母式”的结构表示出来，再用纵坐标的较大值减去较小值，再利用二次函数的性质求出动线段的最大值或最小值.(3)求已知点关于直线对称点问题：先求出直线解析式，再利用两直线垂直的性质(两直线垂直，斜率之积等于-1)求出已知点所在直线的斜率及解析式，最后用中点坐标公式即可求出对称点的坐标.(4)“抛物线上是否存在一点，使其到某一直线的距离为最值”的问题：常常利用直线方程与二次函数解析式联立方程组，求出切点坐标，运用点到直线的距离公式进行求解.(5)二次函数与一次函数、特殊图形、旋转及特殊角度综合：图形或一次函数与x 轴的角度特殊化，利用与角度有关知识点求解函数图像上的点，结合动点的活动范围，求已知点与动点是否构成新的特殊图形.2.二次函数与三角形综合(1)将军饮马问题:本考点主要分为两类：①在定直线上是否存在点到两定点的距离之和最小;②三角形周长最小或最大的问题，主要运用的就是二次函数具有对称性.(2)不规则三角形面积最大或最小值问题:利用割补法将不规则三角形分割成两个或以上的三角形或四边形，在利用“一母式”将动点坐标表示出来，作线段差，用线段差来表示三角形的底或高，用面积公式求出各部分面积，各部分面积之和就是所求三角形的面积.将三角形的面积用二次函数的结构表示出来，再利用二次函数的性质求出面积的最值及动点坐标.(3)与等腰三角形、直角三角形的综合问题:对于此类问题，我们可以利用两圆一线或两线一圆的基本模型来进行计算.问题分情况找点画图解法等腰三角形已知点A ，B 和直线l ，在l 上求点P ，使△PAB 为等腰三角形以AB为腰分别以点A ，B 为圆心，以AB 长为半径画圆，与已知直线的交点P 1，P 2，P 4，P 5即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB =AP ；②AB =BP ；③BP =AP 列方程解出坐标以AB 为底作线段AB 的垂直平分线，与已知直线的交点P 3即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB =AP ；②AB =BP ；③BP =AP 列方程解出坐标问题分情况找点画图解法直角三角形已知点A ，B 和直线l ，在l 上求点P ，使△PAB 为直角三角形以AB为直角边分别过点A ，B 作AB 的垂线，与已知直线的交点P 1，P 4即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB 2=BP 2+AP 2；②BP 2=AB 2+AP 2；③AP 2=AB 2+BP 2列方程解出坐标以AB 为斜边以AB 的中点Q 为圆心，QA 为半径作圆，与已知直线的交点P 2，P 3即为所求注：其他常见解题思路有：①作垂直，构造“三垂直”模型，利用相似列比例关系得方程求解；②平移垂线法：若以AB 为直角边，且AB 的一条垂线的解析式易求(通常为过原点O 与AB 垂直的直线)，可将这条直线分别平移至过点A 或点B 得到相应解析式，再联立方程求解．(4)与全等三角形、相似三角形的综合问题:在没有指定对应点的情况下，理论上有六种情况需要讨论，但在实际情况中，通常不会超过四种，要注意边角关系，积极分类讨论来进行计算.情况一探究三角形相似的存在性问题的一般思路：解答三角形相似的存在性问题时，要具备分类讨论思想及数形结合思想，要先找出三角形相似的分类标准，一般涉及动态问题要以静制动，动中求静，具体如下：①假设结论成立，分情况讨论．探究三角形相似时，往往没有明确指出两个三角形的对应点(尤其是以文字形式出现求证两个三角形相似的题目)，或者涉及动点问题，因动点问题中点的位置的不确定，此时应考虑不同的对应关系，分情况讨论；②确定分类标准．在分类时，先要找出分类的标准，看两个相似三角形是否有对应相等的角，若有，找出对应相等的角后，再根据其他角进行分类讨论来确定相似三角形成立的条件；若没有，则分别按三种角对应来分类讨论；③建立关系式，并计算．由相似三角形列出相应的比例式，将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理运算)，整理可得一元一次方程或者一元二次方程，解方程可得字母的值，再通过计算得出相应的点的坐标．情况二探究全等三角形的存在性问题的思路与探究相似三角形的存在性问题类似，但是除了要找角相等外，还至少要找一组对应边相等．3.二次函数与四边形的综合问题特殊四边形的探究问题解题步骤如下：①先假设结论成立；②设出点坐标，求边长；③建立关系式，并计算．若四边形的四个顶点位置已确定，则直接利用四边形边的性质进行计算；若四边形的四个顶点位置不确定，需分情况讨论：a.探究平行四边形：①以已知边为平行四边形的某条边，画出所有的符合条件的图形后，利用平行四边形的对边相等进行计算；②以已知边为平行四边形的对角线，画出所有的符合条件的图形后，利用平行四边形对角线互相平分的性质进行计算；③若平行四边形的各顶点位置不确定，需分情况讨论，常以已知的一边作为一边或对角线分情况讨论．b.探究菱形：①已知三个定点去求未知点坐标；②已知两个定点去求未知点坐标，一般会用到菱形的对角线互相垂直平分、四边相等的性质列关系式．c.探究正方形：利用正方形对角线互相垂直平分且相等的性质进行计算，一般是分别计算出两条对角线的长度，令其相等，得到方程再求解．d.探究矩形：利用矩形对边相等、对角线相等列等量关系式求解；或根据邻边垂直，利用勾股定理列关系式求解.题型01平行y轴动线段最大值与最小值问题1(2023·广东东莞·一模)如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，OA=OC =3，顶点为D．(1)求此函数的关系式；(2)在AC 下方的抛物线上有一点N ，过点N 作直线l ∥y 轴，交AC 与点M ，当点N 坐标为多少时，线段MN 的长度最大？最大是多少？(3)在对称轴上有一点K ，在抛物线上有一点L ，若使A ，B ，K ，L 为顶点形成平行四边形，求出K ，L 点的坐标．(4)在y 轴上是否存在一点E ，使△ADE 为直角三角形，若存在，直接写出点E 的坐标；若不存在，说明理由．【答案】(1)y =x 2+2x -3(2)当N 的坐标为-32,-154 ，MN 有最大值94(3)K -1，4 ，L -1，-4 或K -1，12 ，L -5，12 或K -1，12 ，L 3，12(4)存在，点E 的坐标为0,32 或0,-72或0,-1 或0,-3【分析】(1)由OA =OC =3求得A -3,0 ,C 0，-3 ,再分别代入抛物线解析式y =x 2+bx +c ，得到以b ，c 为未知数的二元一次方程组，求出b ，c 的值即可；(2)求出直线AC 的解析式，再设出M 、N 的坐标，把MN 表示成二次函数，配方即可；(3)根据平行四边形的性质，以AB 为边，以AB 为对角线，分类讨论即可；(4)设出E 的坐标，分别表示出△ADE 的平分，再分每一条都可能为斜边，分类讨论即可．【详解】(1)∵抛物线y =x 2+bx +c 经过点A ，点C ，且OA =OC =3,∴A -3,0 ,C 0，-3 ,∴将其分别代入抛物线解析式，得c =-39-3b +c =0，解得b =2c =-3 ．故此抛物线的函数表达式为：y =x 2+2x -3；(2)设直线AC 的解析式为y =kx +t ，将A -3,0 ,C 0，-3 代入，得t =-3-3k +t =0 ，解得k =-1t =-3 ，∴直线AC 的解析式为y =-x -3，设N 的坐标为n ，n 2+2n -3 ，则M n ，-n -3 ，∴MN =-n -3-n 2+2n -3 =-n 2-3n =-n +32 +94，∵-1<0，∴当n =-32时，MN 有最大值，为94，把n =-32代入抛物线得，N 的坐标为-32,-154，当N 的坐标为-32,-154 ，MN 有最大值94；(3)①当以AB 为对角线时，根据平行四边形对角线互相平分，∴KL 必过-1,0 ，∴L 必在抛物线上的顶点D 处，∵y =x 2+2x -3=x +1 2-4，∴K -1，4 ，L -1，-4②当以AB 为边时，AB =KL =4，∵K 在对称轴上x =-1，∴L 的横坐标为3或-5，代入抛物线得L -5,12 或L 3,12 ，此时K 都为-1，12 ，综上，K -1，4 ，L -1，-4 或K -1，12 ，L -5，12 或K -1，12 ，L 3，12 ；(4)存在，由y =x 2+2x -3=x +1 2-4，得抛物线顶点坐标为D -1,-4 ∵A -3，0 ，∴AD 2=-3+1 2+0+4 2=20，设E 0，m ，则AE 2=-3-0 2+0-m 2=9+m 2，DE 2=-1-0 2+-4-m 2=17+m 2+8m ，①AE 为斜边，由AE 2=AD 2+DE 2得：9+m 2=20+17+m 2+8m ，解得：m =-72，②DE 为斜边，由DE 2=AD 2+AE 2得：9+m 2+20=17+m 2+8m ，解得：m =32，③AD 为斜边，由AD 2=ED 2+AE 2得：20=17+m 2+8m +9+m 2，解得：m =-1或-3，∴点E 的坐标为0,32 或0,-72或0,-1 或0,-3 ．【点睛】本题主要考查待定系数法求二次函数解析式，二次函数图象与性质，平行四边形的判定与性质以及勾股定理等知识，会运用待定系数法列方程组，两点间距离公式求MN 的长，由平行四边形的性质判定边相等，运用勾股定理列方程．2(2023·河南南阳·统考一模)如图，抛物线与x 轴相交于点A 、B (点A 在点B 的左侧)，与y 轴的交于点C 0，-4 ，点P 是第三象限内抛物线上的一个动点，设点P 的横坐标为m ，过点P 作直线PD ⊥x 轴于点D ，作直线AC 交PD 于点E ．已知抛物线的顶点P 坐标为-3，-254．(1)求抛物线的解析式；(2)求点A 、B 的坐标和直线AC 的解析式；(3)求当线段CP =CE 时m 的值；(4)连接BC ，过点P 作直线l ∥BC 交y 轴于点F ，试探究：在点P 运动过程中是否存在m ，使得CE =DF ，若存在直接写出m 的值；若不存在，请说明理由．【答案】(1)y =14x 2+32x -4(2)A -8，0 ，B 2，0 ，y =-12x -4(3)-4(4)存在，m =2-25或m =-4【分析】(1)运用待定系数法即可求得抛物线的解析式；(2)令y =0，解方程即可求得点A 、B 的坐标，再运用待定系数法即可求得直线AC 的解析式；(3)过点C 作CF ⊥PE 于点F ，根据等腰三角形的性质可得点F 是PE 的中点，设P m ,14m 2+32m -4 ，则E m ，-12m -4 ，可得F m ，18m 2+12m -4 ，再由点F 与点C 的纵坐标相同建立方程求解即可；(4)过C 作CH ⊥PD 于H ，设P m ,14m 2+32m -4 ，由PF ∥BC ，可得直线PF 解析式为y =2x +14m 2-12m -4，进而可得OF =14m 2-12m -4 ，再证得Rt △CHE ≅Rt △DOF HL ，得出∠HCE =∠FDO ，进而推出∠FDO =∠CAO ，即tan ∠FDO =tan ∠CAO ，据此建立方程求解即可．【详解】(1)解：∵抛物线的顶点坐标为-3，-254∴设抛物线的解析式为y =a x +3 2-254，把点C 0，-4 代入，得：-4=9a -254，解得：a =14，∴y =14x +3 2-254=14x 2+32x -4，∴该抛物线的解析式为y =14x 2+32x -4．(2)解：令y =0，得14x 2+32x -4=0，解得：x 1=-8，x 2=2，∴A -8，0 ，B 2，0 ，，设直线AC 的解析式为y =kx +b ，则-8k +b =0b =-4 ，解得：k =-12b =-4 ，∴直线AC 的解析式为y =-12x -4．(3)解：如图，过点C 作CF ⊥PE 于点F ，∵CP =CE ，∴EF =PF ，即点F 是PE 的中点，设P m ,14m 2+32m -4 ，则E m ，-12m -4 ，∴F m ，18m 2+12m -4 ，∵PE ∥y 轴，CF ⊥PE ，∴CF ∥x 轴，∴18m 2+12m -4=-4，解得：m =-4或m =0(不符合题意，舍去)，∴m =-4．(4)解：存在m ，使得CE =DF ，理由如下：如图：过C 作CH ⊥PD 于H ，设P m,14m2+32m-4，由B2，0，C0，-4，由待定系数法可得直线BC解析式为y=2x-4，根据PF∥BC，设直线PF解析式为y=2x+c，将P m,14m2+32m-4代入得：1 4m2+32m-4=2m+c，∴c=14m2-12m-4，∴直线PF解析式为y=2x+14m2-12m-4，令x=0得y=14m2-12m-4，∴F0,14m2-12m-4，∴OF=14m2-12m-4，∵∠CHD=∠PDO=∠COD=90°，∴四边形CODH是矩形，∴CH=OD，∵CE=DF，∴Rt△CHE≅Rt△DOF HL，∴∠HCE=∠FDO，∵∠HCE=∠CAO，∴∠FDO=∠CAO，∴tan∠FDO=tan∠CAO，∴OF OD =OCOA，即14m2-12m-4-m=48=12，∴1 4m2-12m-4=-12m或14m2-12m-4=12m，解得：m=-4或m=4或m=2-25或m=2+25，∵P在第三象限，∴m=2-25或m=-4．【点睛】本题属于二次函数综合题，主要考查了待定系数法求函数解析式、二次函数综合应用、等腰三角形性质、矩形判定及性质、相似三角形判定及性质、解直角三角形等知识点，解题的关键是用含m的代数式表示相关点坐标和相关线段的长度．3(2023·山东聊城·统考三模)抛物线y=-x2+bx+c与x轴交于点A3,0，与y轴交于点C0,3，点P 为抛物线上的动点．(2)若P 为直线AC 上方抛物线上的动点，作PH ∥x 轴交直线AC 于点H ，求PH 的最大值；(3)点N 为抛物线对称轴上的动点，是否存在点N ，使直线AC 垂直平分线段PN ？若存在，请直接写出点N 的纵坐标；若不存在，请说明理由．【答案】(1)b =2，c =3(2)PH 取得最大值为94(3)存在，2-2或2+2【分析】(1)将坐标代入解析式，构建方程求解；(2)设PH 交y 轴于点M ，P m ,-m 2+2m +3 ，则PM =m ；待定系数法确定直线AC 的解析式为y =-x +3，从而确定PH =m -m 2-2m =-m 2+3m =-m -32 2+94，解得PH 最大值为94；(3)如图，设PN 与AC 交于点G ，可设直线PN 的解析式为y =x +p ，设点N (1,n )，求得y =x +(n -1)；联立y =-x +3y =x +(n -1) ，解得x =-n 2+2y =n 2+1，所以点P 的横坐标为2×-n 2+2 -1=-n +3，纵坐标为2×n2+1 -n =2，由二次函数解析式构建方程-(-n +3)2+2(-n +3)+3=2，解得n =2±2；【详解】(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A 3,0 ，与y 轴交于点C 0,3 ，∴-9+3b +c =0c =3，解得：b =2c =3 ，∴b =2，c =3；(2)设PH 交y 轴于点M ，P m ,-m 2+2m +3 ，∴PM =m ，∵PH ∥x 轴，∴点H 的纵坐标为-m 2+2m +3，设直线AC 的解析式为y =kx +n ，∴3k +n =0n =3 ，解得：k =-1n =3 ，∴直线AC 的解析式为y =-x +3．∴-m 2+2m +3=-x +3，∴x =m 2-2m ，∴H m 2-2m ,-m 2+2m +3 ，∴PH =m -m 2-2m =-m 2+3m =-m -322+94，∴当m =32时，PH 取得最大值为94(3)存在点N ，使直线AC 垂直平分线段PN ，点N 的纵坐标为2-2或2+2如图，设PN 与AC 交于点G ，∵AC 垂直平分PN ，直线AC 的解析式为y =-x +3∴可设直线PN 的解析式为y =x +p 设点N (1,n )，则n =1+p ∴p =n -1，∴y =x +(n -1)联立y =-x +3y =x +(n -1) ，解得x =-n 2+2y =n 2+1∴点P 的横坐标为2×-n 2+2 -1=-n +3，纵坐标为2×n 2+1 -n =2∴-(-n +3)2+2(-n +3)+3=2，解得n =2±2∴点N 的纵坐标为2-2或2+2．【点睛】本题考查利用二次函数解析式及点坐标求待定参数、待定系数法确定函数解析式、二次函数极值及其它二次函数综合问题，利用直线间的位置关系、点线间的位置关系，融合方程的知识求解坐标是解题的关键．题型02抛物线上的点到某一直线的距离问题1(2023·广东梅州·统考二模)探究求新：已知抛物线G 1:y =14x 2+3x -2，将抛物线G 1平移可得到抛物线G 2:y =14x 2．(1)求抛物线G 1平移得到抛物线G 2的平移路径；(2)设T 0,t ，直线l ：y =-t ，是否存在这样的t ，使得抛物线G 2上任意一点到T 的距离等于到直线l 的距离？若存在，求出t 的值；若不存在，试说明理由；(3)设H 0,1 ，Q 1,8 ，M 为抛物线G 2上一动点，试求QM +MH 的最小值．参考公式：若点M x 1,y 1 ，N x 2,y 2 为平面上两点，则有MN =x 1-x 22+y 1-y 2 2．【答案】(1)将G 1向左平移-6个单位，向上平移11个单位(2)存在，1(3)9【分析】(1)设G 1向左平移a 个单位，向上平移b 个单位得到函数G 2，列方程组即可求解；(2)设P x 0,x 204为抛物线G 2上的一点，根据题意列方程即可；(3)点H 坐标与(2)中t =1时的T 点重合，过点M 作MA ⊥l ，垂足为A ，如图所示，则有MH =MA ，当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值．【详解】(1).解：设G 1向左平移a 个单位，向上平移b 个单位得到函数G 2，由平移法则可知14(x +a )2+3(x +a )-2+b =14x 2，整理可得14x 2+3+12a x +14a 2+3a -2+b =14x 2，可得方程组3+12a =014a 2+3a -2+b =0，解得a =-6b =11 ；∴平移路径为将G 1向左平移-6个单位，向上平移11个单位；(2)解：存在这样的t ，且t =1时满足条件，设P x 0,x 204为抛物线G 2上的一点，则点P 到直线l 的距离为x 204+t ，点P 到点T 距离为(x 0-0)2+x 204-t2，联立可得：x 204+t =(x 0-0)2+x 204-t2，两边同时平方合并同类项后可得x 20-x 20t =0解得：t =1；(3)解：点H 坐标与(2)中t =1时的T 点重合，作直线l ：y =-1，过点M 作MA ⊥直线l ，垂足为A ，如图所示，则有MH =MA ，此时QM +MH =QM +MA ，当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值即QM +MA =QA =8-(-1)=9∴QM +MH 的最小值为9；【点睛】本题考查二次函数综合题，涉及到线段最小值、平移性质等，灵活运用所学知识是关键．2(2023·湖北宜昌·统考一模)如图，已知：点P 是直线l ：y =x -2上的一动点，其横坐标为m (m 是常数)，点M 是抛物线C ：y =x 2+2mx -2m +2的顶点．(1)求点M 的坐标；(用含m 的式子表示)(2)当点P 在直线l 运动时，抛物线C 始终经过一个定点N ，求点N 的坐标，并判断点N 是否是点M 的最高位置？(3)当点P 在直线l 运动时，点M 也随之运动，此时直线l 与抛物线C 有两个交点A ，B (A ，B 可以重合)，A ，B 两点到y 轴的距离之和为d ．①求m 的取值范围；②求d 的最小值．【答案】(1)M -m ,-m 2-2m +2(2)N (1,3)，点N 是点M 的最高位置(3)①m ≤-52或m ≥32；②d 取得最小值为2【分析】(1)将抛物线解析式写成顶点式即可求解；(2)根据解析式含有m 项的系数为0，得出当x =1时，y =3，即N (1,3)，根据二次函数的性质得出-m 2-2m +2=-m +1 2+3的最大值为3，即可得出点N 是点M 的最高位置；(3)①根据直线与抛物线有交点，联立方程，根据一元二次方程根的判别式大于等于0，求得m 的范围，即可求解；②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ，其中x 1<x 2，由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根，根据x 1+x 2=-2m +1，分情况讨论，求得d 是m 的一次函数，进而根据一次函数的性质即可求解．【详解】(1)解：y =x 2+2mx -2m +2=x +m 2-m 2-2m +2，∴顶点M -m ,-m 2-2m +2 ，(2)解：∵y =x 2+2mx -2m +2=x 2+2+2m x -1 ，∴当x =1时，y =3，抛物线C 始终经过一个定点1,3 ，即N (1,3)；∵M -m ,-m 2-2m +2 ，-m 2-2m +2=-m +1 2+3，∴M 的纵坐标最大值为3，∴点N 是点M 的最高位置；(3)解：①联立y =x -2y =x 2+2mx -2m +2 ，得x 2+2mx -x -2m +4=0，∵直线l 与抛物线C 有两个交点A ，B (A ，B 可以重合)，∴Δ=b 2-4ac =2m -1 2-4-2m +4 ，=4m 2+4m -15≥0，∵4m 2+4m -15=0，解得m 1=-52,m 2=32，∴当4m 2+4m -15≥0时，m ≤-52或m ≥32，②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ，其中x 1<x 2，由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根，∴x1+x 2=-2m +1，当m =-3时，如图所示，y A =0，当-3≤m ≤-52时，y 1≥0,y 2≥0，则d =x 1+x 2 =-2m +1 ，∵-2<0，∴当m =-52时，d 取得最小值为-2×-52 +1=5+1=6，当m ≥32时，d =-x 1+x 2 =--2m +1 =2m -1，∴当m =32时，d 取得最小值为2×32-1=2，综上所述，d 取得最小值为2．【点睛】本题考查了二次函数的性质，一元二次方程与二次函数的关系，熟练掌握二次函数的性质是解题的关键．3(2023·云南楚雄·统考一模)抛物线y =x 2-2x -3交x 轴于A ，B 两点(A 在B 的左边)，C 是第一象限抛物线上一点，直线AC 交y 轴于点P ．(1)直接写出A ，B 两点的坐标；(2)如图①，当OP =OA 时，在抛物线上存在点D (异于点B )，使B ，D 两点到AC 的距离相等，求出所有满足条件的点D 的横坐标；(3)如图②，直线BP 交抛物线于另一点E ，连接CE 交y 轴于点F ，点C 的横坐标为m ，求FP OP 的值(用含m 的式子表示)．【答案】(1)A (-1,0)，B (3,0)(2)0或3-41或3+41(3)13m 【分析】(1)令y =0，解方程可得结论；(2)分两种情形：①若点D 在AC 的下方时，过点B 作AC 的平行线与抛物线交点即为D 1．②若点D 在AC 的上方时，点D 1关于点P 的对称点G (0,5)，过点G 作AC 的平行线交抛物线于点D 2，D 3，D 2，D 3符合条件．构建方程组分别求解即可；(3)设E 点的横坐标为n ，过点P 的直线的解析式为y =kx +b ，由y =kx +b y =x 2-2x -3 ，可得x 2-(2+k )x -3-b =0，设x 1，x 2是方程x 2-(2+k )x -3-b =0的两根，则x 1x 2=-3-b ，推出x A ⋅x C =x B ⋅x E =-3-b 可得n =-1-b 3，设直线CE 的解析式为y =px +q ，同法可得mn =-3-q 推出q =-mn -3，推出q =-(3+b )-1-b 3 -3=13b 2+2b ，推出OF =13b 2+b ，可得结论．【详解】(1)解：令y =0，得x 2-2x -3=0，解得：x =3或-1，∴A (-1,0)，B (3,0)；(2)∵OP =OA =1，∴P (0,1)，∴直线AC 的解析式为y =x +1．①若点D 在AC 的下方时，过点B 作AC 的平行线与抛物线交点即为D 1．∵B (3,0)，BD 1∥AC ，∴直线BD 1的解析式为y =x -3，由y =x -3y =x 2-2x -3，解得x =3y =0 或x =0y =-3 ，∴D 1(0,-3)，∴D 1的横坐标为0．②若点D 在AC 的上方时，点D 1关于点P 的对称点G (0,5)，过点G 作AC 的平行线l 交抛物线于点D 2，D 3，D 2，D 3符合条件．直线l 的解析式为y =x +5，由y =x +5y =x 2-2x -3 ，可得x 2-3x -8=0，解得：x =3-412或3+412，∴D 2，D 3的横坐标为3-412，3+412，综上所述，满足条件的点D 的横坐标为0，3-412，3+412．(3)设E 点的横坐标为n ，过点P 的直线的解析式为y =kx +b ，由y =kx +b y =x 2-2x -3，可得x 2-(2+k )x -3-b =0，设x 1，x 2是方程x 2-(2+k )x -3-b =0的两根，则x 1x 2=-3-b ，∴x A ⋅x C =x B ⋅x E =-3-b∵x A =-1，∴x C =3+b ，∴m =3+b ，∵x B =3，∴x E =-1-b 3，∴n =-1-b 3，设直线CE 的解析式为y =px +q ，同法可得mn =-3-q∴q =-mn -3，∴q =-(3+b )-1-b 3 -3=13b 2+2b ，∴OF =13b 2+2b ，∴FP OP=13b +1=13(m -3)+1=13m ．【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，一元二次方程的根与系数的关系等知识，解题的关键是学会构建一次函数，构建方程组确定交点坐标，学会利用参数解决问题，属于中考压轴题．题型03已知点关于直线对称点问题1(2023·辽宁阜新·统考中考真题)如图，在平面直角坐标系中，二次函数y =-x 2+bx -c 的图象与x 轴交于点A (-3,0)和点B (1,0)，与y 轴交于点C ．(1)求这个二次函数的表达式．(2)如图1，二次函数图象的对称轴与直线AC :y =x +3交于点D ，若点M 是直线AC 上方抛物线上的一个动点，求△MCD 面积的最大值．(3)如图2，点P 是直线AC 上的一个动点，过点P 的直线l 与BC 平行，则在直线l 上是否存在点Q ，使点B 与点P 关于直线CQ 对称？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【答案】(1)y =-x 2-2x +3；(2)S △MCD 最大=98；(3)Q 1-5，-5 或1+5，5 ．【分析】(1)根据抛物线的交点式直接得出结果；(2)作MQ ⊥AC 于Q ，作ME ⊥AB 于F ，交AC 于E ，先求出抛物线的对称轴，进而求得C ，D 坐标及CD 的长，从而得出过M 的直线y =x +m 与抛物线相切时，△MCD 的面积最大，根据x +m =-x 2-2x +3的△=0求得m 的值，进而求得M 的坐标，进一步求得CD 上的高MQ 的值，进一步得出结果；(3)分两种情形：当点P 在线段AC 上时，连接BP ，交CQ 于R ，设P (t ，t +3)，根据CP =CB 求得t 的值，可推出四边形BCPQ 是平行四边形，进而求得Q 点坐标；当点P 在AC 的延长线上时，同样方法得出结果．【详解】(1)解：由题意得，y =-(x +3)(x -1)=-x 2-2x +3；(2)解：如图1，作MQ ⊥AC 于Q ，作ME ⊥AB 于F ，交AC 于E ，∵OA =OC =3，∠AOC =90°，∴∠CAO =∠ACO =45°，∴∠MEQ =∠AEF =90°-∠CAO =45°，抛物线的对称轴是直线：x =-3+12=-1，∴y =x +3=-1+3=2，∴D (1,2)，∵C (0,3)，∴CD =2，故只需△MCD 的边CD 上的高最大时，△MCD 的面积最大，设过点M 与AC 平行的直线的解析式为：y =x +m ，当直线y =x +m 与抛物线相切时，△MCD 的面积最大，由x +m =-x 2-2x +3得，x 2+3x +(m -3)=0，由△=0得，32-4(m -3)=0得，m -3=94，∴x 2+3x +94=0，∴x 1=x 2=-32，∴y =--32 2-2×-32 +3=154，y =x +3=-32+3=32，∴ME =154-32=94，∴MQ =ME ⋅sin ∠MEQ =ME ⋅sin45°=94×22=928，∴S △MCD 最大=12×2×928=98；(3)解：如图2，当点P 在线段AC 上时，连接BP ，交CQ 于R ，∵点B 和点Q 关于CQ 对称，∴CP =CB ，设P (t ，t +3)，由CP 2=CB 2得，2t 2=10，∴t 1=-5，t 2=5(舍去)，∴P -5，3-5 ，∵PQ ∥BC ，∴CR =BR =1，∴CR =QR ，∴四边形BCPQ 是平行四边形，∵1+(-5)-0=1-5，0+(3-5)-3=-5，∴Q 1-5，-5 ；如图3，当点P 在AC 的延长线上时，由上可知：P 5，3+5 ，同理可得：Q 1+5，5 ，综上所述：Q 1-5，-5 或1+5，5 ．【点睛】本题考查了二次函数及其图象的性质，一元二次方程的解法，平行四边形的判定和性质，轴对称的性质等知识，解决问题的关键是分类讨论．2(2023·四川甘孜·统考中考真题)已知抛物线y =x 2+bx +c 与x 轴相交于A -1，0 ，B 两点，与y 轴相交于点C 0，-3 ．(1)求b ，c 的值；(2)P 为第一象限抛物线上一点，△PBC 的面积与△ABC 的面积相等，求直线AP 的解析式；(3)在(2)的条件下，设E 是直线BC 上一点，点P 关于AE 的对称点为点P ，试探究，是否存在满足条件的点E ，使得点P 恰好落在直线BC 上，如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】(1)b =-2,c =-3.(2)y =x +1(3)存在，点P 的坐标为1+21,-2+21 或1-21,-2-21【分析】(1)由待定系数法即可求解；(2)S △PBC =S △ABC 得到AP ∥BC ，即可求解；(3)由题意的：∠AEP =∠AEP ,P E =PE ，即可求解．【详解】(1)由题意，得1-b +c =0,c =-3.∴b =-2,c =-3.(2)由(1)得抛物线的解析式为y =x 2-2x -3．令y =0，则x 2-2x -3=0，得x 1=-1，x 2=3．∴B 点的坐标为3，0 ．∵S △PBC =S △ABC ，∴AP ∥BC ．∵B 3，0，C 0，-3 ，∵AP∥BC，∴可设直线AP的解析式为y=x+m．∵A(-1，0)在直线AP上，∴0=-1+m．∴m=1．∴直线AP的解析式为y=x+1．(3)设P点坐标为m，n．∵点P在直线y=x+1和抛物线y=x2-2x-3上，∴n=m+1，n=m2-2m-3．∴m+1=m2-2m-3．解得m1=4，m2=-1(舍去)．∴点P的坐标为4，5．由翻折，得∠AEP=∠AEP ,P E=PE．∵AP∥BC，∴∠PAE=∠AEP '．∴∠PAE=∠PEA．∴PE=PA=4+12=52．2+5-0设点E的坐标为t，t-3，则PE2=t-42．2+t-3-52=52∴t=6±21．当t=6+21时，点E的坐标为6+21,3+21．设P (s,s-3),由P E=AP，P E=PE=52得：s-6-212，2=522+s-3-3-21解得：s=1+21，则点P 的坐标为1+21,-2+21．当t=6-21时，同理可得，点P 的坐标为1-21,-2-21．综上所述，点P 的坐标为1+21,-2+21．或1-21,-2-21【点睛】本题是二次函数的综合题，主要考查了用待定系数法求一次函数、二次函数的解析式，二次函数的性质，此题题型较好，综合性比较强，用的数学思想是分类讨论和数形结合的思想．3(2023·江苏连云港·连云港市新海实验中学校考二模)如图，“爱心”图案是由抛物线y=-x2+m的一部分及其关于直线y=-x的对称图形组成，点E、F是“爱心”图案与其对称轴的两个交点，点A、B、C、D是该图案与坐标轴的交点，且点D的坐标为6,0．(1)求m 的值及AC 的长；(2)求EF 的长；(3)若点P 是该图案上的一动点，点P 、点Q 关于直线y =-x 对称，连接PQ ，求PQ 的最大值及此时Q 点的坐标．【答案】(1)m =6，AC =6+6(2)52(3)2542，Q -234,-12【分析】(1)用待定系数法求得m 与抛物线的解析式，再求出抛物线与坐标轴的交点坐标，进而求得A 的坐标，根据对称性质求得B ，C 的坐标，即可求得结果；(2)将抛物线的解析式与直线EF 的解析式联立方程组进行求解，得到E ，F 的坐标，即可求得结果；(3)设P (m ,-m 2+6)，则Q (m 2-6,-m )，可得PQ =2×m -12 2-252 ，即求m -12 2-252的最值，根据二次函数的最值，即可得到m 的值，即可求得．【详解】(1)把D 6,0 代入y =-x 2+m 得0=-6+m解得m =6∴抛物线的解析式为：y =-x 2+6∴A 0,6根据对称性可得B -6,0 ，C 0,-6∴AC =AO +OC =6+6(2)联立y =-x y =-x 2+6解得x =3y =-3 或x =-2y =2 ∴E -2,2 ，F 3,-3∴EF =-2-3 2+2+3 2=52(3)设P (m ,-m 2+6)，则Q (m 2-6,-m )∴PQ =m -m 2-6 2+-m 2+6--m 2整理得PQ =2×m -12 2-254 ∵m -12 2≥0∴当m -12 2=0时，即m =12时，m -12 2-254 有最大值为254∴PQ 的最大值为2542∴12 2-6=-234故Q -234,-12【点睛】本题考查二次函数综合应用，涉及待定系数法求函数解析式，两点间的距离公式，求抛物线与一次函数的交点坐标，二次函数的最值等知识，解题的关键是掌握关于直线y =-x 对称的点坐标的关系．题型04特殊角度存在性问题1(2023·山西忻州·统考模拟预测)如图，抛物线y =18x 2+34x -2与x 轴交于A ，B 两点，与y 轴交于点C ．P 是直线AC 下方抛物线上一个动点，过点P 作直线l ∥BC ，交AC 于点D ，过点P 作PE ⊥x 轴，垂足为E ，PE 交AC 于点F ．(1)直接写出A ，B ，C 三点的坐标，并求出直线AC 的函数表达式；(2)当线段PF 取最大值时，求△DPF 的面积；(3)试探究在拋物线的对称轴上是否存在点Q ，使得∠CAQ =45°？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【答案】(1)A -8,0 ，B 2,0 ，C 0,-2 ．y =-14x -2(2)85(3)存在，-3,3 或-3,-253【分析】(1)对于直线y =18x 2+34x -2，当x =0时，y =-2，即点C 0,-2 ，令18x 2+34x -2=0，则x =2或-8，则点A ，B 的坐标分别为-8,0 ，2,0 即求出三个点的坐标，设直线AC 的表达式为y =kx +b ，利用待定系数法求解即可；(2)设点P 的横坐标为m ，则P m ,18m 2+34m -2 ，F m ,-14m -2 ，表示出PF =-18m 2-m ，求出PF max =2，再表示出点D 到直线PF 的距离d =85，利用S △DPF =12⋅PF ⋅d 进行求解即可；(3)由抛物线的表达式知，其对称轴为x =-3，当点Q 在x 轴上方时，设抛物线的对称轴交x 轴于点N ，交AC 于H ，故点Q 作QT ⊥AC 于点T ，在△AQH 中,∠CAQ =45°，tan ∠QHA =4，用解直角三角形的方法求出QH =174，即可求出Q 点坐标，当点Q Q 在x 轴上方时，直线AQ 的表达式为y =35x +8 ，当∠CAQ =45°时，AQ ⊥AQ ，即可求解．【详解】(1)解：对于抛物线y =18x 2+34x -2，当x =0时，y =-2，即点C 0,-2 ，令18x 2+34x -2=0，则x =2或-8，则点A ，B 的坐标分别为-8,0 ，2,0 ，即点A ，B ，C 三点的坐标分别为-8,0 ，2,0 ，0,-2 ，设直线AC 的表达式为y =kx +b ，则-8k +b =0b =-2 ，解得k =-14b =-2 ，∴直线AC 的函数表达式为y =-14x -2；(2)设点P 的横坐标为m ，则P m ,18m 2+34m -2 ，F m ,-14m -2 ，PF =-14m -2 -18m 2+34m -2 =-18m 2-m ，当m =--12×-18 =-4时，PF 最大，PF max =-18×(-4)2--4 =2，此时，P -4,-3 ，由B 2,0 ，C 0,-2 ，可得直线BC 的函数表达式为y =x -2，设直线l 的函数表达式为y =x +p ，将P -4,-3 代入可得p =1，∴直线l 的函数表达式为y =x +1，由y =-14x -2y =x +1 ，解得x =-125y =-75，∴D -125,-75 ，点D 到直线PF 的距离d =-125--4 =85，∴S △DPF =12⋅PF ⋅d =12×2×85=85．(3)存在，理由：由抛物线的表达式知，其对称轴为x =-3，当点Q 在x 轴上方时，如下图：设抛物线的对称轴交x 轴于点N ，交AC 于H ，故点Q 作QT ⊥AC 于点T ，则∠ACO =∠QHA ，则tan ∠ACO =tan ∠QHA =4，当x =3时，y =-14x -2=-54，则点H -3,-54 ，由点A ，H 的坐标得，AH =5174，在△AQH 中，∠CAQ =45°，tan ∠QHA =4，设TH =x ，则QT =4x ，则QH =17x ，则AH =AT +TH =5x =5174，则x =174，则QH =17x =174，则174-54=3，则点Q -3,3 ；当点Q Q 在x 轴上方时，直线AQ 的表达式为y =35x +8 ，当∠CAQ =45°时，AQ ⊥AQ ，则直线AQ 的表达式为y =-53x +8 ，当x =-3时，y =-5x +8 =-25，。

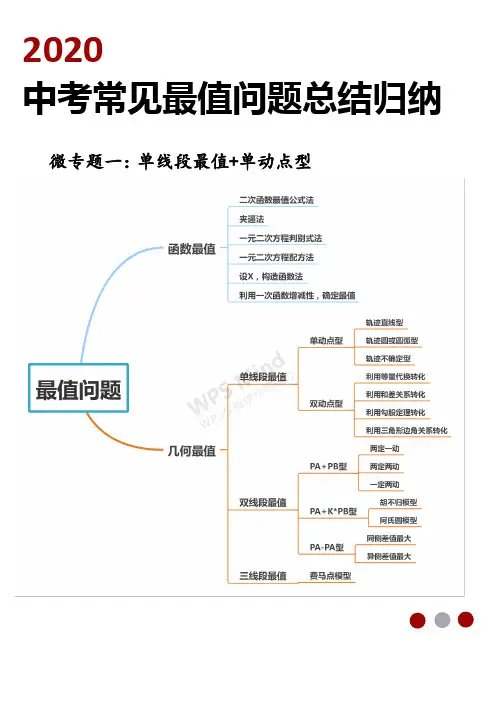
2020中考常见最值问题总结归纳微专题一：单线段最值+单动点型WORKINGPLAN微专题一：单线段最值+单动点型类型一：动点轨迹--直线型考法指导动点轨迹为一条直线时，利用“垂线段最短”求最值。

（1）当动点轨迹确定时可直接运用垂线段最短求最值（2）当动点轨迹不易确定是直线时，可通过以下三种方法进行确定①观察动点运动到特殊位置时，如中点，端点等位置时是否存在动点与定直线的端点连接后的角度不变，若存在该动点的轨迹为直线。

②当某动点到某条直线的距离不变时，该动点的轨迹为直线。

③当一个点的坐标以某个字母的代数式表示时，若可化为一次函数，则点的轨迹为直线。

【典例精析】例题1．（2020·全国初三单元测试）如图，矩形ABCD 中，4AB =，6BC =，点P 是矩形ABCD 内一动点，且∆∆=PAB PCD S S ，则PC PD +的最小值为_____．【答案】【详解】 ABCD 为矩形，AB DC ∴=又=PAB PCD S S∴点P 到AB 的距离与到CD 的距离相等，即点P 线段AD 垂直平分线MN 上，连接AC ，交MN 与点P ，此时PC PD +的值最小，且PC PD AC +====故答案为：【针对训练】1．（2018·湖北中考真题）如图，等腰Rt △ABC 中，斜边AB 的长为2，O 为AB 的中点，P 为AC 边上的动点，OQ ⊥OP 交BC 于点Q，M 为PQ 的中点，当点P 从点A 运动到点C 时，点M 所经过的路线长为（ ）A．4 B．2 C ．1 D ．2【答案】C【详解】连接OC ，作PE ⊥AB 于E，MH ⊥AB 于H，QF ⊥AB 于F ，如图，∵△ACB 为到等腰直角三角形，∴AC=BC=2，∠A=∠B=45°， ∵O 为AB 的中点，∴OC ⊥AB，OC 平分∠ACB，OC=OA=OB=1，∴∠OCB=45°，∵∠POQ=90°，∠COA=90°，∴∠AOP=∠COQ，在Rt △AOP 和△COQ 中A OCQ AO COAOP COQ ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴Rt △AOP ≌△COQ，∴AP=CQ，易得△APE 和△BFQ 都为等腰直角三角形，∴∴PE+QF=2，CQ+BQ，=2BC=2 ∵M 点为PQ 的中点，∴MH 为梯形PEFQ 的中位线，∴MH=12，PE+QF，=12， 即点M 到AB 的距离为12， 而CO=1，∴点M 的运动路线为△ABC 的中位线，∴当点P 从点A 运动到点C 时，点M 所经过的路线长=12AB=1， 故选C，2．（2017·江苏中考真题）如图，在平面内，线段AB=6，P为线段AB上的动点，三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P，且满足PC=PA．若点P沿AB方向从点A运动到点B，则点E运动的路径长为______，【答案】【详解】解：如图，由题意可知点C运动的路径为线段AC′，点E运动的路径为EE′，由平移的性质可知AC′=EE′，在Rt，ABC′中，易知AB=BC′=6，，ABC′=90°，，EE′=AC故答案为：3．如图，等边三角形ABC的边长为4，点D是直线AB上一点．将线段CD绕点D顺时针旋转60°得到线段DE，连结BE．（1）若点D在AB边上（不与A，B重合）请依题意补全图并证明AD=BE；（2）连接AE，当AE的长最小时，求CD的长．【答案】（1）见解析；（2）【详解】解：（1）补全图形如图1所示，AD=BE，理由如下：∵∵ABC是等边三角形，∵AB=BC=AC，∵A=∵B=60°，由旋转的性质得：∵ACB=∵DCE=60°，CD=CE，∵∵ACD=∵BCE，∵∵ACD∵∵BCE（SAS），∵AD=BE．（2）如图2，过点A作AF∵EB交EB延长线于点F．∵∵ACD∵∵BCE，∵∵CBE=∵A=60°，∵点E的运动轨迹是直线BE，根据垂线段最短可知：当点E与F重合时，AE的值最小，此时CD=CE=CF，∵∵ACB=∵CBE=60°，∵AC∵EF，∵AF∵BE，∵AF∵AC，在Rt∵ACF中，，∵CD=CF=类型二：动点轨迹--圆或圆弧型考法指导动点的轨迹为定圆时，可利用：“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和，最小值为定点到圆心的距离与半径之差”的性质求解。

A动点问题最值最值问题有四种情形：定点到动点的最值，动点在圆上或直线上，就是点到圆的最近距离，和点到直线的最近距离；三角形两边之和大于第三边的问题，当两边成一直线最大；几条线段之和构成一条线段最小；还有就是对称点最小问题。

一、定点到动点所在圆的最大或最小值，动点在一个定圆上运动，其实质是圆外一点到圆的最大或最小距离，就是定点与圆心所在直线与圆的交点的两个距离。

方法：证明动点在圆上或者去找不变的特殊三角形，证明两个三角形相似，求出某些边的值。

1．如图，△ABC 、△EFG 均是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长的最小值是〔〕 A ．32-B ．13+C ．2D ．13-提示：点M 在以AC 为直径的圆上2．〔2015•XX 〕如图，已知正方形ABCD 的边长为2，E 是边BC 上的动点，BF ⊥AE 交CD 于点F ，垂足为G ，连结CG ．下列说法：①AG ＞GE ；②AE =BF ；③点G 运动的路径长为π；④CG 的最小值为﹣1．其中正确的说法是②③．〔把你认为正确的说法的序号都填上〕提示：G 在以AB 为直径的圆上：正确答案是：②④3、如图，正方形ABCD 的边长为4cm,正方形AEFG 的边长为1cm ，如果正方形AEFG 绕点A旋转，那么C 、F 两点之间的最小距离为ABC4、如图，在边长为2的菱形ABCD中，∠A=60°,M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是5、如图，等腰直角△ACB，AC=BC=5，等腰直角△CDP，且PB=2，将△CDP绕C点旋转. 〔1〕求证：AD=PB〔2〕若∠CPB=135°，求BD；〔3〕∠PBC=时，BD∠PBC=时，BD有最小值，并画图说明.分析：在△ABD中有：BD≤AB+AD，当BD=AB+AD时BD最大，此时AB与AD在一条直线上，且AD在BA的延长线上，又△ACB是等腰直角三角形，∠CAB=45°，由〔1〕知∠PBC=∠CAD=180°-45°=135°BD≥AB-AD，当BD=AB-AD时BD最小，此时，AB与AD在一条直线上，且AD在线段AB上，此时∠CAD=45°，所以∠PBC=∠CAD=45°6、如图，△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°,∠BAE=135°,AD=1，，F为BE中点.〔1〕求CF的长〔2〕将△ADE绕A旋转一周，求点F运动的路径长；〔3〕△ADE绕点A旋转一周，求线段CF的X围.A BAACCAGDAGDA提示：本题根据中点构造三角形相似，△BOF∽△BAE,且12OF AE==7、如图，AB=4，O为AB中点，⊙O的半径为1，点P是⊙O上一动点，以点P为直角顶点的等腰△PBC〔点P，B，C按逆时针方向排列〕则线段AC的取值X提示：发现定等腰直角△AOC与等腰直角△OBE，从而得到相似。

动点产生的几何最值问题
1.线段上的最短路径问题：给定两个固定点A和B，求在连接A和B的线段上距离点A的最短路径。

2.圆上的最大面积问题：给定一个固定半径的圆，求在圆上的点中，以其中一点为圆心的圆所围成的面积的最大值。

3.圆外的最短路径问题：给定一个固定的圆和一个固定圆心外的点P，求从P点到圆上的一点之间的最短路径。

4.抛物线上的最大值问题：给定一条抛物线，求在给定区间上的点中，使得这些点到抛物线的距离的平方和最小。

5.曲线上的最大斜率问题：给定一条曲线，求在给定区间上的点中，使得这些点切线的斜率的绝对值最大。

这些问题可以通过不同的数学方法来解决，如微积分、向量分析、几何推理等。

根据具体问题的特点，选择最适合的方法进行求解。

通过建立数学模型，运用最优化理论和几何性质，可以得到问题的最优解。

专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点，它贯穿于整个初中数学，自数轴起始，至几何图形的存在性、几何图形的长度及面积的最值，函数的综合类题目，无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变，而其中又有一些技巧性很强的数学思想（转化思想），本专题以几个基本的知识点为经，以历年来中考真题为纬，由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间，线段最短；2. 垂线段最短；3. 若A、B是平面直角坐标系内两定点，P是某直线上一动点，当P、A、B在一条直线上时，PA PB 最大，最大值为线段AB的长（如下图所示）；（1）单动点模型作图方法：作已知点关于动点所在直线的对称点，连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示，P是x轴上一动点，求PA+PB的最小值的作图.P是∠AOB内一点，M、N分别是边OA、OB上动点，求作△PMN周长最小值.作图方法：作已知点P关于动点所在直线OA、OB的对称点P’、P’’，连接P’P’’与动点所在直、N即为所求.线的交点M5. 二次函数的最大（小）值()2y a x h k=-+，当a>0时，y有最小值k；当a<0时，y有最大值k.二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. （详见精品例题解析）三、精品例题解析例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为例2. （2019·凉山州）如图，已知A 、B 两点的坐标分别为（8,0），（0,8）. 点C 、F 分别是直线x =－5和x 轴上的动点，CF =10，点D 是线段CF 的中点，连接AD 交y 轴于点E ，当△ABE 面积取最小值时，tan ∠BAD =（ ）A .817 B . 717 C . 49 D . 59例3. （2019·南充）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是 （填写序号）.例4. （2019·天津）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点，若点Q （1,2Q b y +2QM +时，求b 的值.例5. （2019·舟山）如图，一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上，边AC 与EF 重合，12AC cm =．当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动．当点E 从点A 滑动到点C 时，点D 运动的路径长为 cm ；连接BD ，则△ABD 的面积最大值为2cm ．例6. （2019·巴中）如图，在菱形ABCD中，连接BD、AC交于点O，过点O作OH⊥BC于点H，以O为圆心，OH为半径的半圆交AC于点M.（1）求证：DC是圆O的切线；（2）若AC=4MC，且AC=8，求图中阴影部分面积；（3）在（2）的前提下，P是线段BD上的一动点，当PD为何值时，PH+PM的值最小，并求出最小值.B D专题01 动点问题中的最值、最短路径问题（解析）例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为【答案】4.【解析】解：∵PQ⊥EP，∴∠EPQ=90°，即∠EPB+∠QPC=90°，∵四边形ABCD是正方形，∴∠B=∠C=90°，∠EPB+∠BEP=90°，∴∠BEP=∠QPC，∴△BEP∽△CPQ，∴BE BP CP CQ=，∵AB=12，AE=3，∴BE=9，设CQ=y，BP=x，CP=12－x，（0<x<12）∴912xx y=-，即()()21216499x xy x-==--+，∴当x=6时，y有最大值为4，即CQ的最大值为4.【点睛】此题为“一线三直角模型”，解题方法为相似三角形性质求解，综合利用二次函数的性质求解最值问题.例2.（2019·自贡）如图，已知A、B两点的坐标分别为（8,0），（0,8）. 点C、F分别是直线x=－5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取最小值时，tan∠BAD=（）A.817B.717C.49D.59【答案】B.【解析】解：S△ABE=142BE OA BE ⨯⨯=,当BE取最小值时，△ABE面积为最小值.设x=－5与x轴交于点G，连接DG，因为D为CF中点，△CFG为直角三角形，所以DG=15 2CD=,∴D点的运动轨迹为以G为圆心，以5半径的圆上，如图所示由图可知：当AD与圆G相切时，BE的长度最小，如下图，过点E作EH⊥AB于H，∵OG=5，OA=8，DG=5，在Rt△ADG中，由勾股定理得：AD=12，△AOE∽△ADG，∴AO AD OE DG=,求得：OE=103，由OB=OA=8，得：BE=143，∠B=45°，AB=∴EH=BH=23BE=,AH=AB-BH=3，∴tan ∠BAD=717EH AH ==, 故答案为B .【点睛】此题解题的关键是找到△ABE 面积最小时即是AD 与D 的远动轨迹圆相切的时刻. 进而构造以∠BAD 为内角的直角三角形，利用勾股定理求出边长，代入三角函数定义求解.例3. （2019·南充）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是 （填写序号）.【答案】②③.【解析】解：根据题意可知：OE =12AB =12, 即E 的轨迹为以O 为圆心以12为半径的四分之一圆（第一象限的部分），根据弧长公式，得点E 的路径长为：9012180π⨯⨯=6π，故①错误； 因为AB =24,当斜边AB 上的高取最大值时，△OAB 的面积取最大值，点O 在以AB 为直径的圆上（圆心为E ），当OE ⊥AB 时，斜边AB 上的高最大， 所以△OAB 的面积取最大值为：124122⨯⨯=144，故②正确； 连接OE 、DE ，得：OD ≤OE +DE ，当O 、E 、D 三点共线时取等号，即OD 的最大值为25，如图，过点D 作DF ⊥y 轴于F ，过点E 作EG ⊥y 轴于G ,可得：25DF OD ==, 即：1225EG DF =， 512AF AD EG AE ==, 即：51125AF EG DF ==, 设DF =x ，在Rt △ADF 中，由勾股定理得：221255x x ⎛⎫+= ⎪⎝⎭，解得：x =26， 在Rt △ODF 中，由勾股定理得：OF =26即点D 的坐标为)2626125,262625(，故③正确. 综上所述，答案为：②③.例4. （2019·天津）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点.若点Q （1,2Q b y +2QM +时，求b 的值.【答案】见解析. 【解析】解：∵2y x bx c =-+经过点A (－1,0)， ∴1+b +c =0，即21y x bx b =--- ∵点Q （1,2Q b y +）在抛物线2y x bx c =-+上， ∴324Q b y =--， 即13,224b Q b ⎛⎫+-- ⎪⎝⎭， ∵b >0，∴Q 点在第四象限，222QM AM QM ⎛⎫+=+ ⎪⎝⎭所以只要构造出AM QM ⎫+⎪⎝⎭2QM +的最小值取N （1,0），连接AN ，过M 作MG ⊥AN 于G ，连接QM ，如图所示，△AGM 为等腰直角三角形，GM =2AM ，即当G 、M 、Q 三点共线时，GM +MQ 2QM +取最小值， 此时△MQH 为等腰直角三角形，∴QM 324b ⎫+⎪⎭，GM =2AM =)12m +()322=2122244b QM AM QM m ⎛⎫⎤⎫+=++++= ⎪⎥⎪⎭⎝⎭⎣⎦① ∵QH =MH ，∴324b +=12b m +-，解得：m =124b - ② 联立①②得：m =74，b =4.2QM +的最小值为4时，b =4.2QM +转化为22AM QM ⎛⎫+ ⎪⎝⎭，进而根据两点之间线段最短及等腰三角形性质求解.例5. （2019·舟山）如图，一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上，边AC 与EF 重合，12AC cm =．当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动．当点E 从点A 滑动到点C 时，点D 运动的路径长为 cm ；连接BD ，则△ABD 的面积最大值为2cm ．【答案】- 【解析】解：如图1所示，当E 运动至E ’，F 滑动到F ’时，图1过D ’作D ’G ⊥AC 于G ，D ’H ⊥BC 交BC 延长线于点H ，可得∠E ’D ’G =∠F ’D ’H ，D ’E ’=D ’F ’，∴Rt △E ’D ’G ≌Rt △F ’D ’H ，∴D ’G =G ’H ,∴D ’在∠ACH 的角平分线上，即C ，D ，D ’三点共线.通过分析可知，当D ’E ’⊥AC 时，DD ’的长度最大，随后返回初始D 点，如图2所示，D 点的运动路径为D →D ’→D ，行走路线长度为2DD ’；D '图2∵∠BAC =30°，AC =12，DE =CD∴BC=CD =DE=，由图知：四边形E ’CF ’D ’为正方形，CD ’=EF =12，∴DD ’=CD ’-CD=12-,D 点运动路程为2DD ’=24-图3如图3所示，当点D 运动至D ’时，△ABD ’的面积最大，最大面积为：'''''''ABC AE D BD F E CF D S S S S ++-△△△正方形=(((211112222⨯+⨯--⨯⨯=【点睛】准确利用全等、角平分线判定得到D 点的运动轨迹是关键，利用三角函数及勾股定理求解，计算较为繁琐，尤其是利用割补法求解三角形的面积时对学生计算能力要求较高，此题难度较大，新颖不BD'BD'失难度.例6. （2019·巴中）如图，在菱形ABCD 中，连接BD 、AC 交于点O ，过点O 作OH ⊥BC 于点H ，以O 为圆心，OH 为半径的半圆交AC 于点M .（1）求证：DC 是圆O 的切线；（2）若AC =4MC ，且AC =8，求图中阴影部分面积；（3）在（2）的前提下，P 是线段BD 上的一动点，当PD 为何值时，PH +PM 的值最小，并求出最小值.【答案】见解析.【解析】（1）证明：过点O 作ON ⊥CD 于N ， AC 是菱形ABCD 的对角线，∴AC 平分∠BCD ，∵OH ⊥BC ，ON ⊥CD ，∴OH =ON ，又OH 为圆O 的半径，BD∴ON 为圆O 的半径，即CD 是圆O 的切线.（2）由题意知：OC =2MC =4，MC =OM =2，即OH =2，在Rt △OHC 中，OC =2OH ，可得：∠OCH =30°，∠COH =60°，由勾股定理得：CH==23OCH OMHS S S π-=△阴影扇形（3）作点M 关于直线BD 的对称点M ’，连接M ’H 交BD 于点P ， 可知：PM =PM ’即PH +PM =PH +PM ’=HM ’，由两点之间线段最短，知此时PH +PM 最小， ∵OM ’=OM =OH ，∠MOH =60°，∴∠MM ’H =30°=∠HCM ，∴HM ’=HC=即PH +PM的最小值为在Rt △M ’PO 及Rt △COD 中，OP =OM ’ tan 30°，OD =OC tan 30°， 即PD =OP +OD=B D。

专题09 二次函数中动点引起的最短路径及图形存在性问题·最短路径思路点拨：1. 两点之间，线段最短；（1）单动点模型作图方法：作已知点关于动点所在直线的对称点，连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示，P 是x 轴上一动点，求P A +PB 的最小值的作图.OA 、OB 上动点，求作△PMN 周长最小值.作图方法：作已知点P 关于动点所在直线OA 、OB 的对称点P ’、P ’’，连接P ’P ’’与动点所在直线的交点M 、N 即为所求.2. 垂线段最短；3. 若A 、B 是平面直角坐标系内两定点，P 是某直线上一动点，当P 、A 、B 在一条直线上时，PA PB 最大，最大值为线段AB 的长（如下图所示）；O利用三角形面积计算方法（铅垂高水平宽法或底乘高法或割补法等）列出方程求解.·平行四边形存在性问题题型一、单动点周长最短及面积存在性问题（2019·四川凉山州中考）如图，抛物线y ＝ax 2+bx +c 的图象过点A （﹣1，0）、B （3，0）、C （0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P ，使得△P AC 的周长最小，若存在，请求出点P 的坐标及△P AC 的周长；若不存在，请说明理由；（3）在（2）的条件下，在x 轴上方的抛物线上是否存在点M （不与C 点重合），使得S △P AM ＝S △P AC ？若存在，请求出点M 的坐标；若不存在，请说明理由．【答案】见解析.【解析】解：（1）∵抛物线y＝ax2+bx+c的图象过点A（﹣1，0）、B（3，0）、C（0，3），∴3930a b cca b c-+=⎧⎪=⎨⎪++=⎩，解得：123abc=-⎧⎪=⎨⎪=⎩∴抛物线解析式为y＝﹣x2+2x+3.（2）如图，连接PB、BC∵点P在抛物线对称轴直线x＝1上，点A、B关于对称轴对称，P A＝PB，∴C△P AC＝AC+PC+P A＝AC+PC+PB∴当C、P、B在同一直线上时，PC+PB＝CB最小，由勾股定理得：ACBC＝，∴C△P AC设直线BC解析式为y＝kx+3把点B代入得：3k+3＝0，解得：k＝﹣1∴直线BC的解析式为：y＝﹣x+3，∴y P＝﹣1+3＝2∴点P（1，2）使△P AC（3）存在满足条件的点M，使得S△P AM＝S△P AC．∵S△P AM＝S△P AC∴点C和点M到直线P A距离相等∴CM∥P A，∵A（﹣1，0），P（1，2），可得直线AP的解析式为：y＝x+1，∴可得过点M 与直线AP 平行的直线解析式为：y ＝x +3或y =x －1，联立2323y x y x x =+⎧⎨=-++⎩，解得：03x y =⎧⎨=⎩（即点C ），14x y =⎧⎨=⎩∴点M 坐标为（1，4）.或联立2123y x y x x =-⎧⎨=-++⎩，解得：x y ⎧=⎪⎪⎨⎪=⎪⎩（在x 轴下方，舍去），x y ⎧=⎪⎪⎨⎪=⎪⎩ 综上所述，点M 的坐标为：（1，4）. 2. （2019·四川达州中考）如图，抛物线y ＝﹣x 2+2x +m +1（m 为常数）交y 轴于点A ，与x 轴的一个交点在2和3之间，顶点为B ．①抛物线y ＝﹣x 2+2x +m +1与直线y ＝m +2有且只有一个交点；②若点M （﹣2，y 1）、点N （12，y 2）、点P （2，y 3）在该函数图象上，则y 1＜y 2＜y 3； ③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y ＝﹣（x +1）2+m ； ④点A 关于直线x ＝1的对称点为C ，点D 、E 分别在x 轴和y 轴上，当m ＝1时，四边形BCDE 周长+其中正确判断的序号是 ．【答案】①③④．【解析】解：①把y ＝m +2代入y ＝﹣x 2+2x +m +1中，得x 2﹣2x +1＝0，∵△＝4﹣4＝0，∴此方程两个相等的实数根，则抛物线y ＝﹣x 2+2x +m +1与直线y ＝m +2有且只有一个交点，所以①正确；②∵抛物线的对称轴为x ＝1，∴点P（2，y3）关于x＝1的对称点为P′（0，y3），∵a＝﹣1＜0，∴当x＜1时，y随x增大而减小，∵﹣2＜0＜12，点M（﹣2，y1）、点N（12，y2）、点P′（0，y3）在该函数图象上，∴y2＜y3＜y1，所以②错误；③将该抛物线向左平移2个单位，再向下平移2个单位，抛物线的解析式为：y＝﹣（x+2）2+2（x+2）x+m+1﹣2，即y＝﹣（x+1）2+m，所以③正确；④当m＝1时，抛物线的解析式为：y＝﹣x2+2x+2，∴A（0，2），C（2，2），B（1，3），作点B关于y轴的对称点B′（﹣1，3），作C点关于x轴的对称点C′（2，﹣2），连接B′C′，与x轴、y轴分别交于D、E点，如图，则BE+ED+CD+BC＝B′E+ED+C′D+BC＝B′C′+BC，根据两点之间线段最短，知B′C′最短，而BC的长度一定，∴此时，四边形BCDE周长＝B′C′+BC=所以④正确；故答案为：①③④．3. （2019·山东潍坊中考）如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△P AB的周长最小时，S△P AB＝．【答案】125. 【解析】解：联立2145y x y x x =+⎧⎨=-+⎩， 解得，12x y =⎧⎨=⎩或45x y =⎧⎨=⎩， ∴点A 的坐标为（1，2），点B 的坐标为（4，5），∴AB ＝，作点A 关于y 轴的对称点A ′，连接A ′B 与y 轴的交于P ，则此时△P AB 的周长最小，点A ′的坐标为（﹣1，2），点B 的坐标为（4，5），设直线A ′B 的函数解析式为y ＝kx +b ，245k b k b -+=⎧⎨+=⎩，得35135k b ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线A ′B 的函数解析式为y ＝35x +135， 当x ＝0时，y ＝135， 即点P 的坐标为（0，135），将x ＝0代入直线y ＝x +1中，得y ＝1，∵直线y ＝x +1与y 轴的夹角是45°，∴点P 到直线AB 的距离是：（135﹣1）×sin 45°，∴△P AB 的面积是：112255⨯， 故答案为：125． 题型二、利用特殊角将线段转化求解最短路径4. （2019·天津中考）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点.（1）当b =2时，求抛物线的顶点坐标；（2）点D （b ，y D ）在抛物线上，当AM =AD ，m =5时，求b 的值；（3）点Q （1,2Q b y +2QM +的最小值为4时，求b 的值. 【答案】见解析.【解析】解：(1)∵2y x bx c =-+经过点A (－1,0)，∴1+b +c =0，即21y x bx b =---∵b =2，∴()2223=14y x x x =---- 即抛物线顶点坐标为（1，－4）.（2）∵点D （b ，y D ）在抛物线21y x bx b =---上，∴y D =－b －1，由b >0，知－b －1<0，∴点D 在第四象限，且在对称轴x =2b 的右侧， 过D 作DE ⊥x 轴于E ，E (b ,0)，∴AE =b +1，BE =b +1，即AE =BE ，∴∠ADE =∠DAE =45°，∴AD AE ，由AM =AD ，m =5，得：5－（－1）（b +1），解得：b －1.（3）∵点Q （1,2Q b y +）在抛物线2y x bx c =-+上， ∴324Q b y =--， 即13,224b Q b ⎛⎫+-- ⎪⎝⎭， ∵b >0，∴Q 点在第四象限，222QM AM QM ⎛⎫+=+ ⎪ ⎪⎝⎭所以只要构造出AM QM ⎫+⎪⎝⎭2QM +的最小值取N （1,0），连接AN ，过M 作MG ⊥AN 于G ，连接QM ，如图所示，△AGM 为等腰直角三角形，GM AM ，即当G 、M 、Q 三点共线时，GM +MQ 2QM +取最小值， 此时△MQH 为等腰直角三角形，∴QM 324b ⎫+⎪⎭，GM AM )1m +)322=2124b QM AM QM m ⎫⎤⎫+=++++=⎪⎥⎪⎪⎭⎝⎭⎣⎦ ① ∵QH =MH ，∴324b +=12b m +-，解得：m =124b - ② 联立①②得：m =74，b =4.2QM +时，b =4. 题型三、最短路径与平行四边形存在性问题5. （2019·湖北荆州中考）如图，在平面直角坐标系中，平行四边形OABC 的顶点A ，C 的坐标分别为（6，0），(4，3)，经过B ，C 两点的抛物线与x 轴的一个交点D 的坐标为(1，0).(1)求该抛物线的解析式；(2)若∠AOC 的平分线交BC 于点E ，交抛物线的对称轴于点F ，点P 是x 轴上一动点，当PE ＋PF 的值最小时，求点P 的坐标；(3)在(2)的条件下，过点A 作OE 的垂线交BC 于点H ，点M ，N 分别为抛物线及其对称轴上的动点，是否存在这样的点M ，N ，使得以点M ，N ，H ，E 为顶点的四边形为平行边形？若存在，直接写出点M 的坐标，若不存在，说明理由.【答案】见解析.【解析】解：（1）∵平行四边形OABC 中，A （6，0），C （4，3）∴BC ＝OA ＝6，BC ∥x 轴∴x B＝x C+6＝10，y B＝y C＝3，即B（10，3）设抛物线y＝ax2+bx+c经过点B、C、D（1，0）∴1001031643a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩，解得：19149139abc⎧=-⎪⎪⎪=⎨⎪⎪=-⎪⎩∴抛物线解析式为y＝19-x2+149x139-.（2）如图，作点E关于x轴的对称点E'，连接E'F交x轴于点P，∵C（4，3）由勾股定理得：OC＝5，∵BC∥OA∴∠OEC＝∠AOE∵OE平分∠AOC∴∠AOE＝∠COE∴∠OEC＝∠COE∴CE＝OC＝5∴x E＝x C+5＝9，即E（9，3）∴直线OE解析式为y＝1 3 x∵直线OE交抛物线对称轴于点F，对称轴为直线：x＝7，∴F（7，73）∵点E与点E'关于x轴对称，点P在x轴上∴E'（9，﹣3），PE＝PE'∴当点F、P、E'在同一直线上时，PE+PF＝PE'+PF＝FE'最小设直线E'F解析式为y＝mx+n，∴93773m nm n+=-⎧⎪⎨+=⎪⎩，解得：8321mn⎧=-⎪⎨⎪=⎩∴直线E'F：y＝83-x+21，当83-x+21＝0时，解得：x＝638，∴当PE+PF的值最小时，点P坐标为（638，0）．（3）存在满足条件的点M，N，使得以点M，N，H，E为顶点的四边形为平行四边形．设AH与OE相交于点G（t，13t），如图所示，∵AH⊥OE于点G，A（6，0）∴∠AGO＝90°∴AG2+OG2＝OA2∴（6﹣t）2+（13t）2+t2+（13t）2＝62∴解得：t1＝0（舍去），t2＝275，∴G（275，95），设直线AG解析式为y＝dx+e可得：直线AG：y＝﹣3x+18，当y＝3时，﹣3x+18＝3，解得：x＝5∴H（5，3），E（9，3）设M(x，y)，N(7,s)，①当四边形HEMN为平行四边形时，有：5+x =9+7,解得：x =11，y =209； ②当四边形HENM 为平行四边形时，有：5+7=9+x ,解得：x =3，y =209； ③当四边形HNEM 为平行四边形时，有：5+9=x +7，解得：x =7，y =4，综上所述，点M 的坐标为：（11，209），（3，209），（7，4）. 题型四、面积最值问题及周长最值问题6. （2019·山东东营中考）已知抛物线y =ax 2+bx －4经过点A (2,0)，B (－4,0)与y 轴交于点C ，（1）求这条抛物线的解析式；（2）如图1，点P 是第三象限内抛物线上的一个动点，当四边形ABPC 的面积最大时，求点P 的坐标；（3）如图2，线段AC 的垂直平分线交x 轴于点E ，垂直为D ，M 为抛物线的顶点，在直线DE 上是否存在一点G ，△CMG 的周长最小？若存在，求出点G 的坐标，若不存在，请说明理由.图1 图2【答案】见解析.【解析】解：（1）将A 、B 两点坐标代入y =ax 2+bx －4得：424016440a b a b +-=⎧⎨--=⎩，解得：121a b ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式为：2142y x x =+-. （2）连接BC ，过点P 作PD ⊥x 轴交BC 于点D ，如图，由题意知，AB =6，OC =4，设直线BC 的解析式为y =kx +m ，得：404k m m -+=⎧⎨=-⎩，解得：14k m =-⎧⎨=-⎩， 即直线BC 的解析式为：y =－x －4，设P (n ，2142n n +-)，则D (n ，－n －4)， S 四边形ABPC =S △ABC +S △BCP =12×AB ×OC +12×PD ×OB =12×6×4+12×[－n －4－（2142n n +-）]×4 =()2216n -++，∵－4<n <0，-1<0，∴当n =－2时，S 四边形ABPC 取最大值，最大值为：16，此时P 点坐标为（－2，－4）.（3）存在，如图，连接AM ，交DE 于点G ，此时△CMG 的周长最小，∵DE 是线段AC 的垂直平分线，∴C与点A关于直线DE对称，∴GC=GA，即GC+GM=GA+GM，根据两点之间线段最短的原则，当A、G、M共线时最短，由题意知，A(2，0)，C(0，－4)，∴D(1，－2)，AE=CE，设E（e，0），则AE=2－e，CE2=16+e2∴(2－e)2=16+e2解得：e=－3，即E（－3,0）可得：直线DE的解析式为：y=12-x－32，由A(2,0)，M（－1，92-）得直线AM的解析式为：y=32x－3，联立：y=12-x－32，y=32x－3得：x=34，y=158-，即G点坐标为：（34，158-）.。

动点最值问题通常涉及在给定条件下寻找动点的位置，以使得某个特定的函数或表达式达到最大值或最小值。

下面给出一个经典的动点最值问题例题：
例题：在直角坐标系中，点A的坐标为(0,4)，点B的坐标为(4,0)。

动点P在线段AB上运动，求线段OP（O为坐标原点）长度的最小值。

解：线段AB的长度可以根据勾股定理求出，为4√2。

由于点P在线段AB上运动，因此线段OP的长度最小值为O到AB的距离。

为了找到这个距离，可以过O作AB的垂线，交AB于点C。

由于△AOB是等腰直角三角形，所以OC = AC = BC = 2√2。

因此，线段OP的最小值为2√2。

这个问题考察了动点最值问题的基本思路和方法，即通过寻找动点的位置来使得某个特定的函数或表达式达到最大值或最小值。

同时，这个问题也涉及到了几何、代数和三角函数等多个数学知识点，需要综合运用这些知识点来解决问题。

初中数学动点产生的最值问题专项讲解一、如图1,在直线l上找到一点P,使得PA+PB最短.做法如图2,连接A、B与l的交点即为所求.图1 图2 图3 图4二、如图3,在直线l上找到一点P,使得PA+PB最短.做法如图4,做点B关于直线l 的对称点B/,连接AB/与l的交点即为点P.因为A、B两点是固定的,所以当题目要求找到一点P使得△PAB的周长最小时,做法也是一样的.三、如图5,在直线l上找到两点EF(点E在点F的左侧),EF的距离是定值,使得AE+EF+FB最小.做法如图6,过A做AA'∥l且AA'=EF,做B关于直线l的对称点B′,连接A'B'与直线l的交点即为F,过A做A'F的平行线与直线l的交点即为点E 同样地,因为AB两点是固定的,所以当题目要求使得四边形AEFB周长最小时,也是用同样的方法图5 图6 图7 图8四、如图7,直线a与直线b平行,在直线a上找到一点A,过点A作直线b的垂线交于点B,如何确定点A的位置可以使PA+AB+BQ最短.做法如图8,做PD垂直直线b交直线a于点C,交直线b于点D,在PD上截取PECD,连接EQ,EQ与直线b的交点即为点B,过点B做直线a的垂线,交点即为点A,连接PA即可.这种方法在实际生活中的应用就是著名的修桥问题.五、如图9,在直线l上找到一点M,使得|MA-MB|最小;直线l上找到一点N,使|NA-NB|最大.做法如图10,做AB 的中垂线与直线l 相交,交点即为M 、此时|MA-MB|有最小值0.如图11,延长BA 与直线l 相交,交点即为N 、此时|NA-NB|有最大值为AB.图9 图10 图11六、如图12,点P 是∠AOB 内部一点,在OA 上找到一点M 、OB 上找到一点N 使三角形PMN 的周长最小.做法如图13,分别作点P 关于QA 、OB 的对称点P1、P2,连接P1P2、与OA 的交点即为M,与OB 的交点即为N.此时,三角形PMN 的周长最短.图12 图13 图14 图15七、如图14,点P 是∠AOB 内部一点,在OA 上找到一点M 、过点M 作AMN 垂直OB 交OB 于点N,使得PM+MN 的最小.做法如图15,作点P 关于OA 的对称点Q,做QN 垂直OB 于N 、则QN 与OA 的交点为M.八、如图16,在三角形ABC 中找到一点P,使得PA+PB+PC 最小.做法如图17,分别以AB 、BC 、AC 为边向外做等边三角形,连接AD 、BE 、CF 的交点就是符合条件的点P.lABlP2OOO图16 图17 图18 图19九、如图18,三角形ABC 是等腰直角三角形,C 是直角顶点、以C 为圆心,21AB 长为半径作圆,在⊙C 上找到一点P,使得PA+22PB 最短. 做法如图19,取BC 的中点D,连接AD,则AD 与⊙C 的交点即为P. 注:在⊙C 上任取一点P,连接PC,PB,∵CP CD =CB CP =22,且∠PCD=∠BCP ∴△PCD ∽△BCP ， ∴PD =22PB学思路铺垫已知:二次函数y=-2x 2+3x-23与直线y=x 交于A 、B 两点,点A 在点B 的左侧. (1)A 、B 两点的坐标分别是__________、(2)在y 轴上找到一点C,使得三角形ABC 的周长最小,则点C 的的坐标为_______ (3)若以M 为圆心的圆经过AB 两点,且圆心角AMB 是直角,请写出M 的坐标_____;若以M 为圆心,以2为半径作圆,在此圆上找到一个点P,使PA+22PB 最小,则此最小值为_____________，_____________ 思路：①两定点在定直线同侧,作对称；②先转化22PB,取MB 的中点Q,连接AQ, 则AQ 的长度即为所求. 压轴题(山东滨州中考)如图2-4-20,已知直线y=kx+b(k 、b 为常数)分别与x 轴、y 轴交于点A(-4,0)、B(0,3),抛物线y=-x 2+2x+1与y 轴交于点C. (1)求直线y=kx+b 的函数解析式；(2)若点P(x,y)是抛物线y=-x 2+2x+1上的任意一点,设点P 到直线AB 的距离为d,求d 关于x 的函数解析式,并求d 取最小值时点P 的坐标;(3)若点E 在抛物线y=-x 2+2x+1的对称轴上移动,点F 在直线AB 上移动,求CE+EF 的最小值提能力1.(山东烟合中考)如图2-4-21,抛物线y=ax 2+bx+2与x 轴交于A 、B 两点,与y 轴交于C,AB=4,矩形OBDC 的边CD=1,延长DC 交抛物线于点E (1)抛物线的解析式为________;(2)如图2-4-22,点P 是直线EO 上方抛物线上的一个动点,过点P 作y 轴的平行线交直EO 于点G,作PH ⊥EO,垂足为H.设PH 的长为l,点P 的横坐标为m,求L 与m 的函解析式(不必写出m 的取值范围),并求出l 的最大值.2.(山东东营中考)如图2-4-23,直线y=33x+3分别与x 轴、y 轴交于B 、C 两点,点A 在x 轴上,∠ACB=90°,抛物线y=ax 2+bx+3经过A,B 两点.(1)A 、B 两点的坐标分别为_____________;抛物线的解析式为____________ (2)点M 是直线BC 上方抛物线上的一点,过点M 作MH ⊥BC 于点H,作MD ∥y 轴交BC 于点D,求△DMH 周长的最大值.3.(湖南岳阳中考)如图2-4-24,抛物线y=32x 2+bx+c 经过点B(3,0),C(0,-2),直线l:y=-32x-32交y 轴于点E,且与抛物线交于A,D 两点,P 为抛物线上一动点(不与A,D 重合.(1)抛物线的解析式为________;(2)当点P 在直线l 下方时,过点P 作PM ∥x 轴交l 于点M,PN ∥y 轴交l 于点N,求PM+PN 的最大值4.(天津中考)已知抛物线y= x 2+bx-3(b 是常数)经过点A(-1,0). (1)该抛物线的解析式和顶点坐标分别为________;(2)P(m,t)为抛物线上的一个动点,P 关于原点的对称点为P /.当点P /落在第二象限内,并且P /A 2取得最小值时,求m 的值.5.(湖南怀化中考)如图2-4-25,在平面直角坐标系中,已知抛物线y=ax 2+bx-5与x 轴交于点A(-1,0),B(5,0),与y 轴交于点C. (1)抛物线的函数表达式为________;(2)若点K 为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x 轴,y 轴上分别找点P,Q,使四边形PQKM 的周长最小,求出点P,Q 的坐标6.(甘肃兰州中考)如图2-4-26,抛物线y=-x 2+bx+c 与直线AB 交于A(-4,-4),B(0,4)两点,直线AC:y=-21x-6交y 轴于点C.点E 是直线AB 上的动点,过点E 作EF ⊥x 轴交AC 于点F,交抛物线于点G.(1)抛物线y=-x 2+bx+c 的表达式为________;(2)已知E(-2,0),H(0,-1)以点E 为圆心,EH 长为半径作圆,点M 为⊙E 上一动点,求21AM+CM 的最小值.。

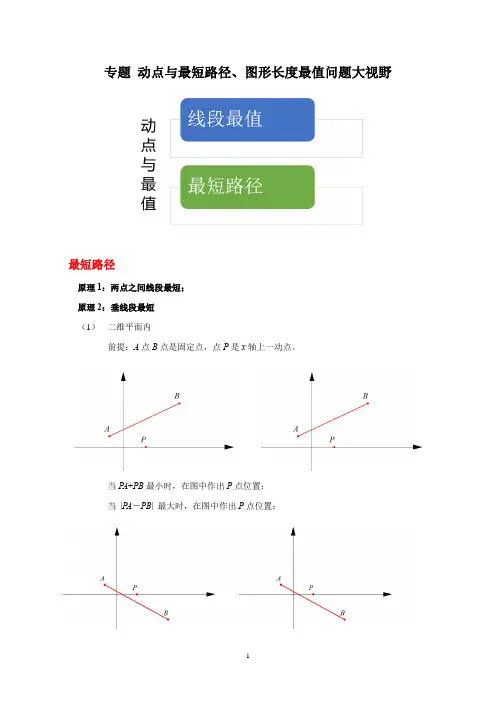
专题动点与最短路径、图形长度最值问题大视野最短路径原理1：两点之间线段最短；原理2：垂线段最短（1）二维平面内前提：A点B点是固定点，点P是x轴上一动点。

当P A+PB最小时，在图中作出P点位置；当|P A－PB| 最大时，在图中作出P点位置；当P A+PB最小时，在图中作出P点位置；当|P A－PB| 最大时，在图中作出P点位置；（2）立体图形中常见的有立方体、长方体、楼梯、树木绕绳问题解决方法：将立体图形曲面展开成平面图形，标出起始位置，借助勾股定理求解。

题型一、线段最值问题例1. 【2019·福州市晋安区期末】如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，点E是AB上的点，以AC为对角线的平行四边形AECF，则EF的最小值是（）A．5B．4C．1.5D．3【答案】D．【解析】解：∵在Rt△ABC中，∠B＝90°，∴BC⊥AB，∵四边形AECF是平行四边形，∴OE＝OF，OA＝OC，∴当OE取最小值时，线段EF最短，此时OE⊥AB，即OE是△ABC的中位线，∴OE＝12BC＝1.5，∴EF＝2OE＝3，即EF的最小值是3．故答案为：D．例2. 【2019·宿迁市期末】在△ABC中，AB=6cm，AC=8cm，BC=10cm，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，连接EF，则EF的最小值为______cm．【答案】24 5.【解析】解：∵AB=6，AC=8，BC=10，∴AB2+AC2=BC2，∴△ABC为直角三角形，∠A=90°，∵PE⊥AB于E，PF⊥AC于F，∴∠AEP=∠AFP=90°，∴四边形AEPF为矩形，连接AP，如图，EF=AP，当AP⊥BC时，AP的值最小，此时AP=245，∴EF的最小值为245．例3. 【2019·宜昌市期中】如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是（）A．2B．6C．﹣2D．4【答案】A．【解析】解：由题意知，点B’的轨迹是以E为圆心，BE的长为半径的圆弧，当B’、E、D共线时，B’D的值最小，最小值为：DE-BE2，故答案为：A.例4. 【2109·福州市期中】如图，平面内三点A、B、C，AB＝4，AC＝3，以BC 为对角线作正方形BDCE，连接AD，则AD的最大值是.【答案】2【解析】解：将△BAD绕点D顺时针旋转90°，得到△DCM，易证，△ADM是等腰直角三角形，AD=AM，2当A、C、M共线时，且C在A、M之间时，AM的长度最大，最大为7，∴AD.例5. 【2019·厦门大学附中期末】如图，在平面直角坐标系中，已知A（2，0），B（5，0），点P为线段AB外一动点，且P A＝2，以PB为边作等边△PBM，则线段AM的最大值为（）A．3B．5C．7D【答案】B.【解析】解：如图，点P 的轨迹为以A 为圆心，以OA 为半径的圆，点M 的轨迹为以点O ’为圆心以EF 的长为直径的圆，∴O ′（72）， ∴AO ′＝3，当点M 在AO ′的延长线上时，AM 的值最大，最大值为3+2＝5，故答案为：B ．题型二、最短路径问题例1.【2019·十堰市外国语期末】如图，在菱形ABCD 中，对角线AC =8，BD =6，点E ，F 分别是边AB ，BC 的中点，点P 在AC 上运动，在运动过程中，存在PE +PF 的最小值，则这个最小值是（ ）A .3B .4C .5D .6【答案】C .【解析】解：设AC 交BD 于O ，作E 关于AC 的对称点N ，连接NF ，交AC 于P ，则此时EP +FP 的值最小，∴PN =PE ，∵四边形ABCD是菱形，∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，∵E为AB的中点，∴N在AD上，且N为AD的中点，∵AD∥CB，∴∠ANP=∠CFP，∠NAP=∠FCP，∵AD=BC，N为AD中点，F为BC中点，∴AN=CF，∴△ANP≌△CFP，∴AP=CP，即P为AC中点，∵O为AC中点，∴P、O重合，即NF过O点，∵AN∥BF，AN=BF，∴四边形ANFB是平行四边形，∴NF=AB，∵AC⊥BD，OA=12AC=4，BO=12BD=3，由勾股定理得：AB=2+BO2=5，故答案为：C．例2. 【2019·厦门市期中】如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P满足S△P AB=13S矩形ABCD，则点P到A、B两点之间的距离之和P A+PB的最小值是【答案】【解析】解：设△ABP边BA上的高为h，∵S△P AB=13S矩形ABCD，∴h=2，即动点P的运动轨迹是与AB平行，且与AB距离为2的直线，不妨设这条直线为l，作A点关于直线l的对称点E，连接AE，BE，则BE的长度即为所求的最短距离，由勾股定理，得：BE=即P A+PB的最小值是故答案为：例3. 【2019·遵义市期中】如图，已知圆柱底面的周长为6cm，圆柱高为3cm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为（）cm．A．B．C D．6【答案】B．【解析】解：如图，把圆柱的侧面展开，得到矩形，这圈金属丝的周长最小为2AC的长度．由题意得：AB＝3cm，BC＝BC′＝3cm，∴AC＝cm，这圈金属丝的周长最小值为：2AC＝cm．故答案为：B．例4. 【2019·北京101中学期末】如图，在△ABC中，AB=BC=4，S△ABC=P、Q、K分别为线段AB、BC、AC上任意一点，则PK+QK的最小值为______．【答案】【解析】解：命题：在直角三角形中，若一条直角边是斜边长的一半，则该直角边所对的角为30°（证明略）；如图，过点A作AH⊥BC交CB的延长线于H，∵AB=CB=4，S△ABC=，∴AH=，∴∠HAB=30°，∠ABH=60°，∴∠ABC=120°，∵∠BAC=∠C=30°，作点P关于直线AC的对称点P′，过P′作P′Q⊥BC于Q交AC于K，则P′Q的长度=PK+QK的最小值，∴∠P′AK=∠BAC=30°，∴∠HAP′=90°，∴∠H=∠HAP′=∠P′QH=90°，∴四边形AP′QH是矩形，∴P′Q=AH=即PK+QK的最小值为，故答案为：【刻意练习】1. 【2019·抚顺市期中】如图，在矩形ABCD中，AD＝3，CD＝4，点P是AC上一个动点（点P与点A，C不重合），过点P分别作PE⊥BC于点E，PF∥BC交AB于点F，连接EF，则EF的最小值为．【答案】125．【解析】连接BP∵∠B＝∠D＝90°，AD＝3，CD＝4，∴AC＝5，∵PE⊥BC于点E，PF∥BC，∠B＝90°，∴四边形PEBF是矩形；∴EF＝BP，由垂线段最短可得BP⊥AC时，线段EF的值最小，1 2BC•AB＝12AC•CP，即12×4×3＝12×5•CP，CP＝125．故答案为：125．2. 【2019·鞍山市期末】如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）A．B．25C．+5D．35【答案】B．【解析】解：将长方体展开，连接A、B，根据两点之间线段最短，（1）如图，BD＝10+5＝15，AD＝20，由勾股定理得：AB＝25．（2）如图，BC＝5，AC＝20+10＝30，由勾股定理得，AB＝（3）如图：BD＝CD+BC＝20+5＝25，AD＝10，由勾股定理得：AB＝由于25＜故答案为：B．3. 【2019·临洮县期中】如图所示，在边长为2的菱形ABCD中，∠DAB＝60°，点E为AB中点，点F 是AC上一动点，则EF+BF的最小值为．【解析】解：连接DB，DE，设DE交AC于M，连接MB，DF，∵四边形ABCD是菱形，∴AC，BD互相垂直平分，∴点B关于AC的对称点为D，∴FD＝FB，∴FE+FB＝FE+FD≥DE，所以当点F运动到点M时，取等号，△ABD是等边三角形，E为AB的中点，∴DE⊥AB，∴AE ＝12AD ＝1，DE∴EF +BF4. 【2019·成都市期末】如图，△ABC ，△ADE 均为等腰直角三角形，∠BAC =∠DAE =90°，将△ADE 绕点A 在平面内自由旋转，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点，若AD =3，AB =7，则线段MN 的取值范围是______．【答案】MN ≤≤【解析】解：∵点P ，M 分别是CD ，DE 的中点，∴PM =12CE ，PM ∥CE ，同理，PN =12BD ，PN ∥BD ，∵△ABC ，△ADE 均为等腰直角三角形，∴AB =AC ，AD =AE ，∠BAC =∠DAE =90°，∴∠BAD =∠CAE ，∴△ABD ≌△ACE （SAS ），∴BD =CE ，∴PM =PN ，∴△PMN 是等腰三角形，∵PM ∥CE ，PN ∥BD ，∴∠DPM =∠DCE ，∠PNC =∠DBC ，∵∠DPN =∠DCB +∠PNC =∠DCB +∠DBC ，∴∠MPN =∠DPM +∠DPN=∠DCE +∠DCB +∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC=90°，∴△PMN是等腰直角三角形，∴PM=PN=12 BD，∴MN=2BD，∴点D在线段AB上时，BD最小，最小值为4，MN的最小值点D在BA延长线上时，BD最大，最大值为10，MN的最大值为，故答案为：MN≤≤5. 【2019·武汉市期末】如图，在菱形ABCD中，E为AB中点，P是BD上一个动点，则下列线段的长度等于P A+PE最小值的是（）A.BCB.CEC.DED.AC【答案】B.【解析】解：在菱形ABCD中，A与C关于直线BD对称，连接EC，与BD交于点P，此时P A+PE=CP+EP=CE值最小，故答案为：B．6. 【2019·固始县期末】如图所示，圆柱的高AB=3，底面直径BC=3，现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食，则它爬行的最短距离是（）A.3√1+πB.3√2D.3√1+π2C.3√4+π22【答案】C.【解析】解：（1）蚂蚁可以沿A-B-C的路线爬行，AB+BC=6，（2）把圆柱侧面展开，展开图如图所示，在Rt△ADC中，∠ADC=90°，CD=AB=3，AD=1.5π，AC=√AD2+CD2=3√4+π2＜6，2故答案为：C．7. 【2019·黄石期中】如图，在平面直角坐标系中，已知正方形ABCO，A（0，3），点D为x轴上一动点，以AD为边在AD的右侧作等腰Rt△ADE，∠ADE=90°，连接OE，则OE的最小值为（）B.√2C.2√2D.3√2A.2【答案】A.【解析】解：如图，作EH⊥x轴于H，连接CE，∵∠AOD=∠ADE=∠EHD=90°，∴∠ADO+∠EDH=90°，∠EDH+∠DEH=90°，∴∠ADO=∠DEH，∵AD=DE，∴△ADO≌△DEH（AAS），∴OA=DH=OC，OD=EH，∴OD=CH=EH，∴∠ECH=45°，过点O作OE′⊥CE，则△OCE′是等腰直角三角形，∵OC=3，∴OE′=由垂线段最短，知OE故答案为：A．8.【2019·广州市番禺区期末】如图一个圆柱，底圆周长10cm，高4cm，一只蚂蚁沿外壁爬行，要从A点爬到B点，则最少要爬行______cm．【解析】解：将圆柱展开，侧面为矩形，如图所示：∵底面圆的周长为10cm，∴AC=5cm，∵高BC=4cm，∴AB=√AC2+BC2=√41cm．故答案为：√41．9. 【2019·桑植县期末】如图1，在平面直角坐标系中，直线AB与x轴交于点A，与y轴交于点B，与直线OC：y=x交于点C．（1）若直线AB解析式为y=-2x+12，①求点C的坐标；②求△OAC的面积．（2）如图2，作∠AOC的平分线ON，若AB⊥ON，垂足为E，△OAC的面积为6，且OA=4，P、Q分别为线段OA、OE上的动点，连接AQ与PQ，试探索AQ+PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．【答案】见解析.【解析】解：（1）①联立y=-2x+12，y=x，解得：x=y=4，即点C的坐标为（4，4）；②在y=-2x+12中，当x=0时，y=12，当y=0时，-2x+12=0，x=6，∴点B（0，12），A（6，0），则△OAC的面积为：12×6×4=12；（2）∵ON平分∠AOC，AB⊥ON，∴ON是线段AC的垂直平分线，∴AQ=CQ，∴AQ+PQ=CQ+PQ，当C、Q、P共线，且CP⊥OA时，AQ+PQ取最小值，最小值为△OAC边OA上的高，∵△OAC的面积为6，OA=4，∴△OAC边OA上的高=2×6÷4=3.∴AQ+PQ存在最小值，最小值为3．10.【2019·泉州市期末】已知：AC是菱形ABCD的对角线，且AC=BC．（1）如图①，点P是△ABC的一个动点，将△ABP绕着点B旋转得到△CBE．①求证：△PBE是等边三角形；②若BC=5，CE=4，PC=3，求∠PCE的度数；（2）连结BD交AC于点O，点E在OD上且DE=3，AD=4，点G是△ADE内的一个动点如图②，连结AG，EG，DG，求AG+EG+DG的最小值．【答案】见解析.【解析】解：（1）①∵四边形ABCD是菱形∴AB=BC，∵AC=BC，∴AB=BC=AC，∴△ABC等边三角形，∴∠ABC=60°，由旋转知BP=BE，∠PBE=∠ABC=60°，∴△PBE是等边三角形；②由①知AB=BC=5，由旋转知△ABP≌△CBE，∴AP=CE=4，∠APB=∠BEC，∵AP2+PC2=42+32=25=AC2，∴△ACP是直角三角形，∴∠APC=90°，∴∠APB+∠BPC=270°，∵∠APB=∠CEB，∴∠CEB+∠BPC=270°，∴∠PBE+∠PCE=90°，∵∠PBE=∠ABC=60°，∴∠PCE=90°-60°=30°；（2）如图，将△ADG绕着点D顺时针旋转60°得到△A'DG'，由旋转知△ADG≌△A'DG'，∴A'D=AD=4，G'D=GD，A'G'=AG，∵∠G'DG=60°，G'D=GD，∴△G'DG是等边三角形，∴GG'=DG，∴AG+EG+DG=A'G'+EG+GG'∵当A'、G'、G、E四点共线时，A'G'+EG+G'G的值最小，即AG+EG+DG的值最小，∵∠A'DA=60°，∠ADE=12∠ADC=30°，∴∠A'DE=90°，∴AG+EG+DG=A'G'+EG+G'G=A'E=5，∴AG+EG+DG的最小值为5．11.【2019·宿迁市期末】如图，在边长为1个单位长度的小正方形组成的格点图中，点A、B、C都是格点．（1）点A坐标为______；点B坐标为______；点C坐标为______；（2）画出△ABC关于原点对称的△A1B1C1；（3）已知M（1，4），在x轴上找一点P，使|PM-PB|的值最大（写出过程，保留作图痕迹），并写出点P 的坐标______．【答案】（1）（-1，0）；（-2，-2）；（-4，-1）；（2）见解析；（3）（-5，0）.【解析】解：（1）由图象可知点A（-1，0），点B（-2，-2），点C（-4，-1）；（2）如图所示：（3）作点B关于x轴的对称点F（-2，2），连接MF交x轴于P，点P就是所求的点，理由：在x轴上任意取一点P1，∵|P1M-P1B|=|P1M-P1F|≤FM，∴|PM-PB|的最大值为线段FM的长度，设直线FM解析式为：y=kx+b，把F、M两点坐标代入，得：k+b=1，-2k+b=2，解得：23103kb⎧=⎪⎪⎨⎪=⎪⎩，即直线FM解析式为：y=210 33x+，当y=0时，x=-5，即点P坐标为（-5，0）．故答案为:（-5，0）．。

2022中考压轴：最短路径及最值问题（一）
【分析】（1）①根据要求画出图形即可；②首先证明∠ECF＝90°，设AE＝CF＝x，EF2＝y，则EC＝4−x，在Rt△ECF中，利用勾股定理即可解决问题；（2）如图2中，将△ABE绕点A顺时针旋转60°得到△AFG，连接EG，DF．作FH⊥AD于H．根据两点之间线段最短可得DF≤FG＋EG＋DE，BE＝FG，推出AE＋BE＋DE的最小值为线段DF 的长；
【点睛】本题考查作图−旋转变换，正方形的性质，勾股定理，两点之间线段最短等知识，解题的关键是学会构建二次函数解决最值问题，学会利用旋转法添加辅助线，学会用转化的思想思考问题，属于中考常考题型．
【点睛】本题考查圆与动点的综合问题，切线判定掌握两条原则，即是半径、是直角；涉及动点问题常需要分类讨论，解题时首先选取特殊情况求解，借此观察一般情况下动点运动规律；线段和最值问题通常利用对称性质做辅助线解答，可与将军饮马模型进行对比练习．【点睛】本题考查等边三角形与动点的综合问题，难度主要在于辅助线的构造，核心思想是将不在同一条直线上的各线段通过对称性，利用线段等量替换将问题转化到同一条直线，线段和最值另一典型题型为将军饮马，可对比练习．
【点睛】本题是四边形的综合问题，考查了待定系数法求函数解析式以及利用轴对称求最短路线和勾股定理等知识，掌握根据对称转化为两点之间的距离的问题是解题的关键．。

初中几何动点最值问题难题集锦初中几何动点最值问题是初中数学中的一道难题类型。

动点最值问题考察动点在几何形状内运动时，某一量的最大值或最小值的求解方法。

下面是一些初中几何动点最值问题的难题集锦。

1.【问题描述】在一个矩形ABCD中，点P动态地沿着矩形的边移动，求线段AP的最长长度。

【解答】假设矩形ABCD的边长为a和b（a<b），点P动态地沿着矩形的边移动。

我们可以观察到，当点P处于矩形的顶点A或D时，线段AP的长度为a；当点P处于矩形的顶点B或C时，线段AP的长度为b。

因此，线段AP的最长长度为b。

2.【问题描述】在一个圆形O内，点P动态地沿着圆的周长移动，求线段OP的最长长度。

【解答】设圆的半径为r，点P动态地沿着圆的周长移动。

根据三角形的性质，可以知道线段OP的长度最长时，点P应该位于圆的周长上的与点O相对的点，即直径上的点。

因此，线段OP的最长长度为2r。

3.【问题描述】在一个正方形ABCD内，点P动态地沿着正方形的边移动，求线段BP的最长长度。

【解答】设正方形ABCD的边长为a，点P动态地沿着正方形的边移动。

由于线段BP的长度等于点P距离B点的距离，所以线段BP的最长长度为正方形的对角线长度，即√2a。

4.【问题描述】在一个等腰直角三角形ABC中，点P动态地沿着三角形的边移动，求线段AP的最长长度。

【解答】设等腰直角三角形ABC的等腰边长为a，点P动态地沿着三角形的边移动。

可以观察到，当点P处于顶点B或C 时，线段AP的长度为a；当点P处于顶点A时，线段AP的长度为0。

因此，线段AP的最长长度为a。

5.【问题描述】在一个梯形ABCD中，点P动态地沿着梯形的边移动，求线段CP的最长长度。

【解答】设梯形ABCD的上底长为a，下底长为b（a>b），点P动态地沿着梯形的边移动。

可以观察到，当点P处于梯形的底端点C或顶端点D时，线段CP的长度为0；当点P处于梯形的上底端点A时，线段CP的长度为ab。

例6.（2019·绵阳）在平面直角坐标系中，将二次函数y =ax 2（a ＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x 轴交于点A 、B （点A 在点B 的左侧），OA =1，经过点A 的一次函数y =kx +b （k ≠0）的图象与y 轴正半轴交于点C ，且与抛物线的另一个交点为D ，△ABD 的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E 在一次函数的图象下方，求△ACE 面积的最大值，并求出此时点E 的坐标；（3）若点P 为x 轴上任意一点，在（2）的结论下，求PE +35P A 的最小值．【答案】见解析.【解析】解：（1）由平移知，平移后得到的抛物线解析式为y =a （x -1）2-2，∵OA =1，∴点A 的坐标为（-1，0），代入抛物线的解析式得，4a -2=0，得：a =12， ∴抛物线的解析式为()21122y x =--，即21322y x x =--． 令y =0，解得x 1=-1，x 2=3，∴B （3，0），∴AB =OA +OB =4，∵△ABD 的面积为5，∴S △ABD =12AB ·y D =5 ∴y D =52，2513222x x =--，解得x 1=-2，x 2=4， ∴D （4，52）， 设直线AD 的解析式为y =kx +b ， ∴5420k b k b ⎧+=⎪⎨⎪-+=⎩，解得：1212k b ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线AD 的解析式为：y =12x +12. （2）过点E 作EM ∥y 轴交AD 于M ，如下图所示，设E （a ，12a 2－a －32），M （a ，12a +12），∴ME =－12a 2+32a +2， ∴S △ACE =S △AME －S △CME =－14（a 2－3a －4）=－14（a －32）2+2516， ∴当a =32时，△ACE 的面积有最大值，最大值是2516，此时E 点坐标为（32，158-）． （3）作E 关于x 轴的对称点F ，连接EF 交x 轴于点G ，过点F 作FH ⊥AE 于点H ，交轴于点P ，∴AG=52，EG=158，∴43 AGEG=,∵∠AGE=∠AHP=90°∴sin∠EAG=35 PH EGAP AE==，∴PH=35 AP，∵E、F关于x轴对称，∴PE=PF，∴PE+35AP=FP+HP=FH，此时FH最小，∵EF=154，∠AEG=∠HEF，∴sin∠AEG=sin∠HEF=45 AG FHAE AE==∴FH=3．即PE+35PA的最小值是3．例7.（2019·潍坊）如图，在平面直角坐标系xoy中，O为坐标原点，点A（4，0），点B （0，4），△ABO的中线AC与y轴交于点C，且⊙M经过O，A，C三点．（1）求圆心M的坐标；（2）若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；（3）在过点B且以圆心M为顶点的抛物线上有一动点P，过点P作PE∥y轴，交直线AD于点E．若以PE为半径的⊙P与直线AD相交于另一点F．当EF＝P的坐标．【答案】见解析．【解答】解：（1）∵AC 为△ABO 的中线，点B （0，4）， ∴点C （0，2），∵点A （4，0），点M 为线段AC 的中点，即M （2，1）；（2）∵⊙P 与直线AD ，则∠CAD ＝90°，设∠CAO ＝α，则∠CAO ＝∠ODA ＝∠PEH ＝α，tan ∠CAO ＝12OC OA =＝tan α，则sin αcos α，AC CD ＝sin AC α＝10， 则D （0，﹣8），设直线AD 的解析式为：y ＝mx +n ：得：840b k b =-⎧⎨+=⎩，解得：k =2，b =－8， 直线AD 的表达式为：y ＝2x ﹣8；（3）抛物线的表达式为：y ＝a （x ﹣2）2+1，将点B 坐标代入上式并解得：a ＝34， 故抛物线的表达式为：y ＝34x 2﹣3x +4，过点P 作PH ⊥EF ，则EH ＝12EF ＝cos ∠PEH ＝cos EH PE α== 得：PE ＝5，设点P （x ，34x 2﹣3x +4），则点E （x ，2x ﹣8）， 则PE ＝34x 2﹣3x +4﹣2x +8＝5， 解得x ＝143或2（舍）， 则点P （143，193）．。

在几何教学中，求线段长度的最小值问题是学生的一大难点，学生往往不知如何入手，在教学中，教师只需进行归类总结，建立模型，使学生掌握相关模型，触类旁通，就不难解决，解决这类问题的基本依据就是：利用两点之间线段最短或点线之间垂线段最短。

一、构建模型
模型1、一个动点，一个定点+一条定直线且动点在直线或部分直线（线段或射线）上运动。

如图：P是直线L外一点，O是直线L上的一个动点，求线段PO长度的最小值。

问题解决：利用直线外一点到直线上所有点的连线中，垂线段最短（点线之间垂线段最短）。

过P作PO垂直于L，垂足为O。

则点P与直线L上的所有点连线中垂线段PO的长度最短。

.
模型2：两个定点，一个动点，动点在圆或部分圆（弧）上运动。

如图：P是⊙O外一点，点A在⊙O上运动，求线段PA的最小值，
问题解决：运用两点之间线段最短
连接PO交⊙O于A，这里O点、P点是定点，A点是动点，当P、A、O三点共线且P在OA之间时，OA+PA最小，而OA是⊙O的半径，长度不变，所以此时PA最小。

模型3：两个定点，一个动点+一条定直线，动点在直线上或部分直线上（射线或线段）运动。

1。

GFD ABCEA'MCDABNPCB动点问题最值最值问题有四种情形：定点到动点得最值，动点在圆上或直线上，就就是点到圆得最近距离，与点到直线得最近距离；三角形两边之与大于第三边得问题，当两边成一直线最大；几条线段之与构成一条线段最小；还有就就是对称点最小问题。

一、定点到动点所在圆得最大或最小值，动点在一个定圆上运动，其实质就是圆外一点到圆得最大或最小距离，就就是定点与圆心所在直线与圆得交点得两个距离。

方法：证明动点在圆上或者去找不变得特殊三角形，证明两个三角形相似，求出某些边得值。

1．如图，△ABC 、△EFG 均就是边长为2得等边三角形，点D 就是边BC 、EF 得中点，直线AG 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长得最小值就是（ ） A ．32-B ．13+C ．2D ．13-提示：点M 在以AC 为直径得圆上2．（2015•咸宁）如图，已知正方形ABCD 得边长为2，E 就是边BC 上得动点，BF ⊥AE 交CD 于点F ，垂足为G ，连结CG ．下列说法：①AG ＞GE ；②AE =BF ；③点G 运动得路径长为π；④CG 得最小值为﹣1．其中正确得说法就是 ②③ ．（把您认为正确得说法得序号都填上）提示：G 在以AB 为直径得圆上：正确答案就是：②④3、如图，正方形ABCD 得边长为4cm,正方形AEFG 得边长为1cm ，如果正方形AEFG 绕点A旋转，那么C 、F 两点之间得最小距离为 4、如图，在边长为2得菱形ABCD 中，∠A=60°,M 就是AD 边得中点，N 就是AB 边上一动点，将△AMN 沿MN 所在直线翻折得到△A ′MN ，连接A ′C ，则A ′C 长度得最小值就是5、如图，等腰直角△ACB ，AC=BC=5，等腰直角△CDP ，且PB=2，将△CDP 绕C 点旋转、CABAAA GDDA E（1）求证：AD=PB（2）若∠CPB=135°，求BD ；（3）∠PBC= 时，BD 有最大值，并画图说明； ∠PBC= 时，BD 有最小值，并画图说明、PBC=∠AB 上，6、如图，△ABC 与△ADE °,AD=1，，F 为BE 中点、（1）求CF 得长（2）将△ADE 绕A 旋转一周，求点F 运动得路径长； （3）△ADE 绕点A 旋转一周，求线段CF 得范围、提示：本题根据中点构造三角形相似，△BOF ∽△BAE,且7、如图，AB=4，O 为AB 中点，⊙O 得半径为1，点P 得等腰△PBC （点P ，B ，C 按逆时针方向排列）则线段AC AOC 中，AE-CE ≤AC AE ∥BC 交⊙O 于E ADE9、AB=4，E 为形外一点，且∠点，求BF 连AC,取DC 中点中点H ，则△FGH ∽△∴12GH AD ==∠DEA=90°，∴点F 在以GH 小距离。

在几何教学中，求线段长度的最小值问题是学生的一大难点，学生往往不知如何入手，在教学中，教师只需进行归类总结，建立模型，使学生掌握相关模型，触类旁通，就不难解决，解决这类问题的基本依据就是：利用两点之间线段最短或点线之间垂线段最短。

一、构建模型
模型1、一个动点，一个定点+—条定直线且动点在直线或部分直线（线段或射线）上运动。

如图：P是直线L外一点，0是直线L上的一个动点，求线段PO长度的最小值。

问题解决：利用直线外一点到直线上所有点的连线中，垂线段最短（点线之间垂线段最短）。

过P作P0垂直于L,垂足为0。

则点P与直线L上的所有点连线中垂线段P0的长度最短。

.
模型2:两个定点，一个动点，动点在圆或部分圆（弧）上运动。

如图：P是。

0外一点，点A在。

0上运动，求线段PA的最小值，
问题解决：运用两点之间线段最短
连接P0交。

0于A，这里0点、P点是定点，A点是动点，当P、A、0三点共线且P在0A 之间时，0A+PA最小，而0A是。

0的半径，长度不变，所以此时PA最小。

模型3:两个定点，一个动点+—条定直线，动点在直线上或部分直线上（射线或线段）运动
1。