珠心算的乘法运算

四年级珠心算珠心算是一种古老的计算方法，它源于中国古代。

在四年级的数学课上，我第一次接触到了珠心算，深深地被它的魅力所吸引。

下面我将向大家介绍一下四年级珠心算的学习内容和技巧。

珠心算主要包括加法、减法、乘法和除法四种运算。

在学习珠心算之前，我们需要先了解一下珠子的排列和表示方法。

珠子一般由五种颜色组成，分别代表个位、十位、百位、千位和万位。

每种颜色的珠子有不同的数量，比如个位有9颗珠子，十位有5颗珠子，百位有3颗珠子，以此类推。

通过珠子的排列和颜色，我们可以表示出一个数。

在进行珠心算计算时，我们首先需要将题目中的数字用珠子表示出来。

比如，如果计算32+17，我们可以用3颗白珠子表示30，2颗绿珠子表示2，1颗红珠子表示10，7颗蓝珠子表示7。

然后，我们将珠子按照对应的颜色排列好，就可以开始计算了。

加法是珠心算最基本的运算之一。

我们可以通过移动珠子的位置来实现加法运算。

比如，如果计算32+17，我们首先将两个数的珠子排列好，然后将绿珠子和蓝珠子相加得到9，将9颗珠子放在个位上；然后将白珠子和红珠子相加得到4，将4颗珠子放在十位上。

最后，我们得到的结果是49。

减法也是珠心算中常见的运算。

与加法类似，我们同样可以通过移动珠子的位置来实现减法运算。

比如，如果计算54-27，我们首先将两个数的珠子排列好，然后将白珠子和蓝珠子相减得到2，将2颗珠子放在个位上；然后将绿珠子和红珠子相减得到2，将2颗珠子放在十位上。

最后，我们得到的结果是27。

乘法是珠心算中稍微复杂一些的运算。

在进行乘法运算时，我们需要通过珠子的位置和数量来表示乘数和被乘数。

比如，如果计算32×4，我们可以用3颗白珠子和2颗绿珠子表示32，用4颗黄珠子表示4。

然后，我们将3颗白珠子和2颗绿珠子分别乘以4颗黄珠子，得到12颗黄珠子和8颗蓝珠子。

最后，我们将珠子按照对应的颜色和位置排列好，得到的结果是128。

除法是珠心算中最复杂的运算之一。

练习连续“一笔清”：
372×2×2 428×2×2
1,645×2×2×2 4,916×2×2×2
综合训练
写出2乘下列各数的积，并求和。
三位数
125
316
245
437
308
积 四位数
积 六位数
积 合计
4,376
3,518
9,675
2,458
9,821
142,857 285,714 428,571 571,428 857,142
综合训练
三位数
写出下列各数的积，并求和。 621×3 589 ×3 168 ×3
793 ×3
452 ×3
积 四位数
3097 ×3 5278 ×3 9845 ×3 6034 ×3 8519 ×3
积 六位数
571428
285714
428571
857142
714285
×3×2×5 ×4×5×3 ×4×3×5 ×3×5×4 ×2×4×3
×6×2×9 ×6×4×3 ×6×3×5 ×6×2×3
×4×9
积
合计
（七）乘数是“8”的一口清
8
的本个数、进位数对应关系如下：
• 被乘数：1 2 3 4 5 6 7 8 9 • 本个数：8 6 4 2 0 8 6 4 2 • 进位数：0 1 2 3 4 4 5 6 7
• 本个规律：
进位规律： 补数倍数
142,857 ×2×5
285,714 ×2×5
428,571 ×2×5
571,428 ×2×5
714,285 ×2×5
（三）乘数是“4”的一口清
4
的本个数、进位数对应关系如下：
• 被乘数：1 2 3 4 5 6 7 8 9 • 本个数：4 8 2 6 0 4 8 2 6 • 进位数：0 0 1 1 2 2 2 3 3

算盘乘除法口诀表可以参考如下：
* 算盘除法：
1. 定位原则：先上后下、先内后外。

2. 定位数珠位的珠确定后，将被除数也定在定位珠的上下方。

3. 除数与被除数上下对齐，除数放在右边档上，被除数放在左边档上。

4. 除数的档位是几，用几档的档位上就写一个商。

5. 用被除数档位的珠去乘商，得到的就是下一个商。

6. 直到被除数的档位用完，再倒过来除余数。

* 算盘乘法：
1. 定位原则：先上后下、先内后外。

2. 定位数珠位的珠确定后，将被乘数也定在定位珠的上下方。

3. 按位相乘（下珠动），个位数与1相乘的结果在小，9的进位（左手指在下向上用空拨），为高位；同样原理可得两位数的乘积；为不拨重复下面只需在上面一排数框下方写出相应的积作下一阶进位；两积之和便是被乘数在下方。

4. 进位的原理在上面与下面皆相同；两个算式就是四个结果即为最后的乘积（注意满五进位的下拨一个珠得0）加减十位便可。

关于算盘除法及乘法，使用前务必做好相关的技巧演练工作，若仍有问题可咨询计算机相关专业人士。

第二单元：两位数乘两位数
（二）教材说明和教学建议
【教材说明】 本单元主要教学两位数乘两位数珠算乘法。这部分内容是 在学生已经掌握了三位数乘一位数珠算乘法和二位数乘一位数 心算乘法的基础上进行教学的。这部分内容是学习多位数乘法 的起始部分和关键部分，学会了这部分内容，对于计算乘数是 更多位数的乘法也容易类推了。根据省实验要求，这部分内容 作为选修内容，可根据所教班级实际情况，确定是否选修。两 位数乘两位数乘法的算法是：从高位算起，乘数的十位和个位 上数分别与被乘数相乘，两次算出的积进行错位递加。 【教学建议】 1、可以用4课时教学，分别是两位数乘整十数、两位数乘两 位数（1）、两位数乘两位数（2）、两位数乘两位数（3）。
一、教材分析
2.基本方法： 三位数×一位数 （1）整百数×一位数 例4：200×3 300×2＋120
①3+1=4，从第四档千位开始拨起； ②记住第二个乘数3，和第一个乘数的最高 位百位上的2相乘，2×3=06，口诀：二 三06。从第四档千位拨入。
• 及时增加例题300×2＋120，也是为了及时 强化位值概念，以及为三位数乘一位数打下基 础。
分析：第1题：第一次相乘单积不满十，第二、第三次相乘的单积都 满十；单积相加时十位满十向百位进一，百位又满十向千位进一； 第2题：三次相乘的单积都满十，单积相加时没有进位。
一、教材分析
2.基本方法： 三位数×一位数 练习四
对以上三种题型的三位数×一位数进行多种形式练习
一、教材分析
2.基本方法： 三位数×一位数 （5）三位数×一位数4（乘数中间或末尾有0） 例8：102×4 120×4
一、教材分析
2.基本方法： 两位数×一位数 （1）整十数×一位数 试一试：20×7、5×20、 70×8+48

珠心算加减乘除口诀珠心算是中国古代的一种算术技巧，通过珠子的排列和移动来进行计算，具有高效、准确的特点。

在珠心算中，加减乘除是基本的运算法则，下面是珠心算加减乘除口诀的详细介绍。

一、加法口诀珠心算的加法口诀主要基于进位的概念，下面是具体的口诀表达方式：1+1=2，小珠两颗；2+2=4，中珠两颗；4+4=8，大珠两颗；8+8=16，小珠在左边；6+6=12，小珠在右边；9+9=18，十位加珠。

二、减法口诀珠心算的减法口诀同样依托于进位的原理，下面是减法口诀的表述方式：2-1=1，小珠剩一颗；4-2=2，中珠剩一颗；16-8=8，小珠在左边；12-6=6，小珠在右边；18-9=9，十位少一珠。

三、乘法口诀珠心算的乘法口诀是通过珠子的排列和组合来进行计算，以下是具体的表达方式：2×1=2，小珠两颗；2×2=4，中珠两颗；2×3=6，小珠在右边；2×4=8，大珠两颗；2×5=10，小珠在左边；2×6=12，小珠在右边。

四、除法口诀珠心算的除法口诀同样利用珠子的排列和移动来进行计算，下面是具体的表述方式：4÷2=2，中珠拿起来；6÷2=3，小珠在右边；10÷2=5，小珠在左边；12÷2=6，小珠在右边。

结语珠心算加减乘除口诀是中国古代算术技巧中的一种，通过珠子的排列和移动来进行计算。

这些口诀灵活高效，能够帮助人们在心算过程中快速准确地完成各种基本的运算。

虽然随着科技的发展，计算器等工具的普及，珠心算逐渐淡出了人们的视线，但其作为中国古代数学宝库中的一颗明珠，仍然值得我们学习和珍惜。

通过掌握珠心算加减乘除口诀，不仅可以提升计算能力，还可以感受到古代智慧的独特魅力。

珠心算的口诀传承和推广，让我们更好地了解和传承中华民族的数学文化遗产。

乘数 42 17 48 62 15 23 64 85 47 89 65 42 13 68 59 84 75
珠心算乘法练习题
乘数 653 257 823 457 360 236 928 465 2463 522 619 654 478 968 358 504 752
乘数 15 26 35 41 25 36 28 26 96 54 52 41 63 20 17 82 62
乘数 26 54 78 51 96 57 81 24 63 52 82 45 85 65 54 82 41
珠心算乘法练习题
乘数 954 289 364 247 651 753 987 325 626 368 205 451 546 285 754 692 769
乘数 60 24 56 92 21 42 60 15 63 25 96 32 58 54 15 28 30
珠心算乘法练习题
乘数 840 105 802 601 501 410 520 360 920 150 860 241 542 163 201 204 562
乘数 17 53 26 30 50 45 82 33 20 14 50 26 30 25 23 58 48
珠心算乘法练习题
乘数 183 369 241 562 148 685 471 263 214 562 186 293 521 462 158 153 624
乘数 26 35 28 26 24 15 36 25 86 24 15 63 24 15 67 48 59
珠心算乘法练习题
乘数 854 263 241 586 923 541 563 265 485 624 152 365 485 624 152 241 563
乘数 58 90 17 20 80 40 14 90 30 60 50 41 80 25 21 25 82

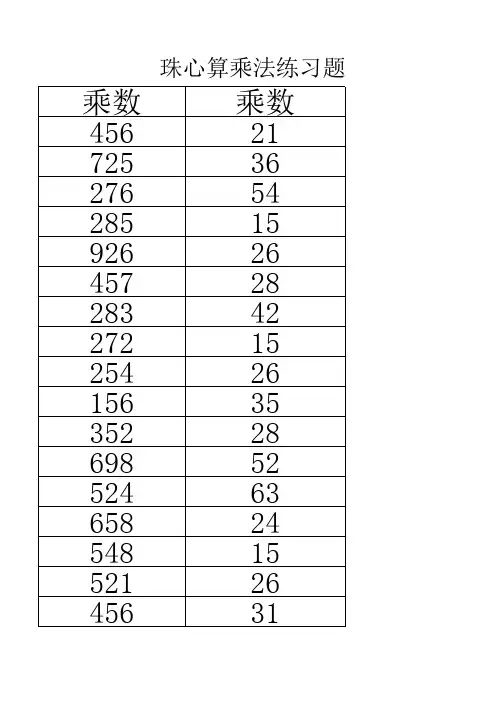
珠心算乘法题练习题免费可打印珠心算是一种通过心算进行计算的技巧，以快速而准确地解决数学问题而闻名。

在珠心算中，乘法是一个重要的部分。

为了帮助学生提升他们的珠心算乘法能力，以下是一些免费可打印的练习题，供大家使用。

练习题一：两位数乘以一位数1. 26 × 3 =2. 47 × 5 =3. 54 × 4 =4. 38 × 2 =5. 69 × 7 =6. 85 × 9 =7. 73 × 6 =练习题二：两位数乘以两位数1. 63 × 12 =2. 28 × 35 =3. 47 × 18 =4. 52 × 31 =5. 79 × 27 =7. 93 × 63 =练习题三：三位数乘以一位数1. 345 × 7 =2. 476 × 4 =3. 589 × 3 =4. 724 × 6 =5. 635 × 9 =6. 857 × 2 =7. 963 × 8 =练习题四：三位数乘以两位数1. 476 × 23 =2. 589 × 45 =3. 724 × 31 =4. 635 × 27 =5. 857 × 56 =6. 963 × 74 =7. 582 × 38 =练习题五：四位数乘以一位数2. 4761 × 4 =3. 5893 × 3 =4. 7246 × 6 =5. 6359 × 9 =6. 8572 × 2 =7. 9635 × 8 =练习题六：四位数乘以两位数1. 3458 × 23 =2. 5893 × 45 =3. 7246 × 31 =4. 6359 × 27 =5. 8572 × 56 =6. 9635 × 74 =7. 5823 × 38 =这些练习题可以帮助学生熟悉各种乘法运算的方法和步骤，并且提高他们的珠心算技能。

珠心算两位乘法练习题可打印一、题目练习：1. 28 × 34 = _______2. 53 × 46 = _______3. 79 × 52 = _______4. 65 × 37 = _______5. 42 × 58 = _______6. 87 × 29 = _______7. 36 × 71 = _______8. 51 × 93 = _______9. 72 × 86 = _______10. 94 × 67 = _______11. 69 × 44 = _______12. 57 × 83 = _______13. 39 × 61 = _______14. 86 × 23 = _______15. 45 × 75 = _______二、题目解析：以上是一组珠心算两位乘法练习题，每个题目需要进行两个数字的乘法运算。

通过解答这些练习题，可以提高孩子们的珠心算能力，加深对乘法的理解，并锻炼他们的计算思维能力。

三、如何使用可打印练习题：1. 打印出练习题：将上述练习题内容复制到文档中，并使用打印功能将其打印出来。

可以设置合适的页面布局和字体大小，以确保打印的练习题清晰可见。

2. 给孩子解答：将打印好的练习题交给孩子，让他们按照一题一行的方式进行解答。

鼓励他们使用珠心算的方法进行计算，而非依赖计算器或其他工具。

3. 检查答案：完成解答后，可以使用计算器或者标准的乘法计算方法来检查答案的准确性。

对于有错误的题目，可以帮助孩子找出错误并纠正。

4. 提供反馈和奖励：根据孩子的解答情况，给予积极的反馈和奖励。

对于正确率较高的题目，可以表扬孩子的努力和成绩，鼓励他们继续保持好的学习状态。

四、练习题的好处：1. 提高珠心算能力：通过大量练习珠心算乘法，孩子们的计算速度和准确性会逐渐提高。

珠算的一般公式法珠心算的公式是大家更好的了解珠心算的方法，那么珠心算公式是什么呢？珠心算公式为将简捷乘算法统一于十字相乘公式之中,进而运用多种方法,简化运算过程,提高计算速度。

下面就来看看吧！前面提到，如：27×964、1998×778、999992应怎样计算，才会更为快捷、方便。

根据以上原理，笔者研究出补数乘法的一般公式法，暂定为魏氏公式法：(1)设被乘数的最末一位数的补数为a，乘数的补数为b，那么在被乘数的末位的下位加a×b(a×b有进位者，要进到本位);(2)设被乘数去掉尾数后的数为n，那么应从被乘数首位的下位减去(n+1)×b。

注意(n+1)×b有进位，从首位减，b前有0位，有几个零应移档向后几位再减，就是：先从尾后加a×b，再在次档减(n+1)×b，这就是补数乘法的一般公式法。

利用此公式可以解决以下类别的数乘以任意数的快速计算问题：1、被乘数是两位数的例题;2、被乘数是两位以上的数时，n+1等于齐数或强数的例题。

如：例1：27×964=26028(补数036)(1)先在被乘数个位7的下位加上(a×b)，即3×036=108，得27.108;(2)再从被乘数的次高档7的本位减去(n+1)×b，即(2+1)×036，得26028，即是积数。

例2：19998×778=15558444(补数222)(1)先在被乘数个位8的下位加上(a×b)即2×222，得19998.444;(2)再从被乘数的次高档减去(n+1)×b即(1999+1)×222，得15558444，即得积。

注：实际上，(n+1)×b比原数少了10倍，把(n+1)再扩大10倍后，就是实际需要减的数。

如例2：第1步尾下加上444后，可看作19998444;达到千万位;(1999+1)×222×10=4440000，达到百万位;从19998444中减去4440000=15558444。

珠心算练习题加减乘除混合珠心算是一种古老而神奇的计算术，通过掌握特定的技巧和方法，能够在脑海中进行高速精确的计算。

本文将为大家提供一系列珠心算练习题，涵盖加法、减法、乘法和除法。

一、加法题1. 348 + 176 = ?2. 482 + 695 = ?3. 721 + 934 = ?4. 563 + 827 = ?5. 926 + 481 = ?二、减法题1. 829 - 315 = ?2. 673 - 218 = ?3. 957 - 642 = ?4. 584 - 219 = ?5. 748 - 426 = ?三、乘法题1. 18 × 6 = ?2. 37 × 9 = ?3. 52 × 7 = ?4. 63 × 4 = ?5. 41 × 8 = ?四、除法题1. 144 ÷ 12 = ?2. 315 ÷ 15 = ?3. 432 ÷ 18 = ?4. 648 ÷ 27 = ?5. 972 ÷ 36 = ?解答：一、加法题1. 348 + 176 = 5242. 482 + 695 = 11773. 721 + 934 = 16554. 563 + 827 = 13905. 926 + 481 = 1407二、减法题1. 829 - 315 = 5142. 673 - 218 = 4553. 957 - 642 = 3154. 584 - 219 = 3655. 748 - 426 = 322三、乘法题1. 18 × 6 = 1082. 37 × 9 = 3333. 52 × 7 = 3644. 63 × 4 = 2525. 41 × 8 = 328四、除法题1. 144 ÷ 12 = 122. 315 ÷ 15 = 213. 432 ÷ 18 = 244. 648 ÷ 27 = 245. 972 ÷ 36 = 27珠心算练习题加减乘除混合为提升珠心算能力提供了丰富的练习。

浅谈珠心算乘法教学的策略[宝典] 浅谈珠心算乘法教学的策略提纲一、多位数乘心算的基本原理1、乘法分配律(作图)2、乘心算应具备的三个技能: ?单积一口清多位数加减珠心算能力快速看数写数清盘的能力二、珠算、心算大九九口诀教学 1、大九九口诀教学优点:意义明确、比慢混淆、易于入盘、试商准又快读法:“丢十补0”法熟练程度:脱口而出、滚瓜烂熟。

2、大九九口诀教学模式3、空盘前乘法:优点:意义明确、比慢混淆、易于入盘、试商准又快读法:“丢十补0”法熟练程度:脱口而出、滚瓜烂熟。

三、多位数乘以一位数的珠算、心算教学1、空盘前乘法:优点:意义明确、比慢混淆、易于入盘、试商准又快珠算、心算方法:熟练程度:脱口而出、一口清、一眼成。

2、一位数乘多位数一位数乘两位数。

一位数乘三位数。

一位数乘四位数。

一位数与五位数和六位数。

四、多位数的乘珠算和心算1、两位数的乘珠算和心算。

2、两位数与三位数的乘珠算和心算。

3、两位数与四位数的乘珠算和心算。

4、三位数的乘珠算和心算。

5、三位数与四位数的乘珠算和心算。

五、小数乘珠算和心算。

一位数乘两位数。

一位数乘三位数。

一位数乘四位数。

一位数与五位数和六位数。

?两位数的乘珠算和心算。

两位数与三位数的乘珠算和心算。

?两位数与四位数的乘珠算和心算。

三位数的乘珠算和心算。

三位数与四位数的乘珠算和心算。

内容提要:关键词:正文:珠心算乘法是指在脑中按照珠算乘法的模型进行运算，简称乘心算。

珠心算乘法与口算乘法的运算顺序一致，均是由高位向低位依次运算。

珠心算乘法由于计算过程复杂，是教学中的难点之一。

笔者从事珠心算教学17年，对珠心算乘法进行多次探索和研究，总结出一套简单易学、行之有效的方法，并取得了较好的效果。

现与同行们一起探究如下:一、多位数乘心算的基本原理1、基本原理:多位数乘心算时是运用乘法分配律的过程进行运算的。

如教学467×5=,时，我们先将其转化成(400+60+7)×5，运用乘法分配律。

空盘前乘法的计算过程：
①例1 324×6=
公式定位法
⑴定位：两乘数位数相加得出积的位 数。这题为3+1=4，积为四位数。
⑵眼看前乘数324，脑记后乘数6，先 由前乘数第一位数3乘起，3×6=18， 把首积18从盘上对应的1档拨入。
⑶再用前乘数的第二位数2与乘数6 相乘，2×6=12，从盘上对应的2档 拨入。
（积末尾有0的特别要注意）。
固定个位法
▪ 在算盘上先定出个位档，然后按法、实的位数， 确定实首在盘上所置的档次，以得出积的位数。
▪ 在算前先将算盘编上档序号：选择任一记位点的 档为个位档(即正1位档)，向左依次为正2位档、 正3位档、正4位档……，向右依次为0位档、负 1位档、负2位档、负3位档……。
一、珠心算乘法概述
2.珠算乘法的分类：
珠算乘法从总的分类说，有基本乘法和其它乘法；
按计算的顺序分类，则可分为前乘法和后乘法；
以置积的位置分类，可分为隔位乘法和不隔位乘法；
按盘上置数与否又可分为两不摆、实法均摆盘或实法只
置其一于盘等。
空盘乘法
置数乘法
一、珠心算乘法概述
2.珠心算乘法的分类：
按计算方式可分为珠算乘法和心算乘法；
987654321×2=1975308642 987654321×3=2962962963 987654321×4=3950617284 987654321×5=4938271605 987654321×6=5925925926 987654321×7=6913580247 987654321×8=7901234568 987654321×9=8888888889
一、珠心算乘法概述
2.珠心算乘法的分类：
按乘数位数的多少分为表内乘法（一位数乘一位数）、 一位数乘法（其中一个乘数是一位数）和多位数乘法。 （例：726×3是一位数乘法，726×83是多位数乘法）。

珠心算的乘法运算学习目标：掌握珠算乘法的乘算原理，了解不同类型乘法的基本乘算方法，熟练掌握空盘前乘法学习内容：珠算乘法的算理算法一位数和多位数的空盘前乘法小数乘法1、珠算乘法是在加法的基础上，根据乘法口诀进行的运算，乘法是加法的简便运算。

2、珠算乘法的种类很多，按不同的分类方法，可有置数乘法、空盘乘法、前乘法、后乘法、隔位乘法、不隔位乘法等等，在这些方法中，最简便、最容易掌握的还是空盘前乘法，我们要学习的也是这种方法。

3、空盘前乘法：“空盘”是指被乘数和乘数均不置在算盘上，而将两者的乘积直接拨在算盘上；“前乘”是指乘数首先同被乘数的首位相乘，随后自左向右逐位相乘，直至乘完为止。

4、空盘前乘法的优点是：乘数和被乘数事先均不步入算盘，节约了拨珠布数的时间，尤其在求多笔乘积之和的算题时，可边乘边加，不必把各个乘积算得后再相加，节约了运算时间，提高了运算速度。

5、要学习空盘前乘法，需要有一些预备知识：（1）必须使用大九九口诀大九九口诀：大数在前小数在后，如：9×2=18 8×7=56小九九口诀：小数在前大数在后，如：2×9=18 7×8=56大九九口诀一律四字一句，有利于避免错位，提高计算速度。

（2）每个单积必须使用两位数记积法“单积”：两个1位数相乘所得的积即单积，如：3×5=15，15即为单积。

“两位数记积法”：每两个1位数相乘的积必须是两位数，没有数都要用0补齐。

如：6×4=24 1×5=05 3×0=00多位数乘法多位数乘法是指乘数和被乘数都在二位或二位以上的数字相乘的乘法。

空盘前乘的多位数乘法方法是：用乘数的首位数从左向右去乘被乘数的各位，把各单积依次退位叠加，结果为“第一分积”；再用乘数的次字位从左向右遍乘被乘数的各位，从第一分积的第二位起依次退位叠加，结果为“第一、第二分积”之和；若乘数还有第三位，方法同上，第一个单积从一、二分积之和的第三位起退位叠加即可。

珠心算技巧珠心算技巧-------------------------------------------------------------------------------- 告诉朋友来自状园培训网2010-04-20 被关注了220次珠心算一、一种做多位乘法不用竖式的方法。

我们都可以口算1X1 10X1,但是,11X12 12X13 12X14呢？这时候,大家一般都会用竖式，通过竖式计算,得数是132、156、168。

其中有趣的规律：积个位上的数字正好是两个因数个位数字的积。

十位上的数字是两个数字个位上的和。

百位上的数字是两个因数十位数字的积。

例如：12X14=168 1=1X1 6=2+4 8=2X4如果有进位怎么办呢？这个定律对有进位的情况同样适用，在竖式时只要~满几时，就向下一位进几。

~例如：14X16=224 4=4X6的个位2=2+4+6 2=1+1X1试着做做看下面的题：12X15= 11X13= 15X18= 17X19=二、几十一乘以几十一的速算方法例如：21×61＝41×91＝41×91= 51×61= 81×91= 41×51= 41×81= 71×81=这些算式有什么特点呢？是“几十一乘以几十一”的乘法算式，我们可以用：先写十位积，再写十位和（和满10 进1），后写个位积。

“先写十位积，再写十位和（和满10 进1），后写个位积”就是一见到几十一乘以几十一的乘法算式，如果十位数的和是一位数，我们先直接写十位数的积，再接着写十位数的和，最后写上1 就一定正确；如果十位数的和是两位数，我们先直接写十位数的积加1 的和，再接着写十位数的和的个位数，最后写一个 1 就一定正确。

我们来看两个算式：21×61＝41×91＝用“先写十位积，再写十位和（和满10 进1），后写个位积”这种速算方法直接写得数时的思维过程。

九九下九三、乘法九退一还一九退一还（五去四）24-9大九九口诀表一一01二二04三三09四四16五五25六六36七七49八八64九九81方法首积满十：被乘数位数+乘数位数48X63=，首位数积是4X6=24>10，就是首积满10，积为4位首积不够十：被乘数位数+乘数位数-1，48X10=，首位数积是4X1=04<10，就是首积满10，积为3位764X2=三、除法商（结果）的位数商位数=被除数位数-除数位数（如果被除数位数的首位小于除数的首位）商位数=被除数位数-除数位数+1（如果被除数位数的首位大于除数的首位）特殊：如果首位比较不出来，则比较下一位。

珠算除法有归除法和商除法两种.一二02二三06三四12四五20五六30六七42七八56八九72一三03 二四08三五15四六24五七35六八48七九63九一09一四04 二五10三六18四七28五八40六九54八一08九二18一五05二六12三七21四八32五九45七一07八二16九三27一六06二七14三八24四九36六一06七二14八三24九四36一七07二八16三九27五一05六二12七三21八四32九五45一八08二九18四一04五二10六三18七四28八五40九六54一九09三一03四二08五三15六四24七五35八六48九七63二一02三二06四三12五四20六五30七六42八七56九八72归除法用口诀进行计算，有九归口诀，退商口诀和商九口诀.九归口诀共61句：一归（用1除）：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九.二归（用2除）：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五.三归（用3除）：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二.四归（用4除）：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二.五归（用5除）：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八.六归（用6除）：逢六进一，逢十二进二，六三添作五，六一下加四，六二三余二，六四六余四，六五八余二.七归（用7除）：逢七进一，逢十四进二，七一下加三，七二下加六，七三四余二，七四五余五，七五七余一，七六八余四.八归（用8除）：逢八进一，八四添作五，八一下加二，八二下加四，八三下加六，八五六余二，八六七余四，八七八余六.九归（用9除）：逢九进一，九一下加一，九二下加二，九三下加三，九四下加四，九五下加五，九六下加六，九七下加七，九八下加八.退商口诀共9句：无除退一下还一，无除退一下还二，无除退一下还三，无除退一下还四，无除退一下还五，无除退一下还六，无除退一下还七，无除退一下还八，无除退一下还九，商九口诀共9句：见一无除作九一，见二无除作九二，见三无除作九三，见四无除作九四，见五无除作九五，见六无除作九六，见七无除作九七，见八无除作九八，见九无除作九九.除数是一位数的除法叫“单归”；除数是两位或两位以上的除法叫“归除”，除数的首位叫“归”，以下各位叫“除”.如，除数是534的归除，叫“五归三四除”.即用五归口诀求商后，再用34除。

四年级珠心算
珠心算是一种通过计算器来快速计算的技巧，主要训练人的心算能力。

四年级的珠心算主要包括以下内容：
1. 加法：计算两个数的和，例如：23 + 17 = ?
2. 减法：计算两个数的差，例如：58 - 32 = ?
3. 乘法：计算两个数的积，例如：6 x 9 = ?
4. 除法：计算两个数的商，例如：36 ÷ 4 = ?
5. 大数运算：计算较大的数的加减乘除，例如：234 + 567 = ?
在四年级学习珠心算时，学生会逐步提高计算速度和准确度，同时也会学习一些技巧和方法来简化计算过程。

四年级的珠心算训练也可以包括一些应用题，让学生能够将珠心算运用到实际生活中。

除了四则运算，珠心算还可以包括一些其他的计算技巧，例如快速计算平方数、立方数等。

珠心算不仅可以提高计算能力，还可以培养学生的注意力、观察力和逻辑思维能力。