重庆一中09月考-二模考试

重庆一中中考数学二模试卷一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号在答题卡中对应的方框涂黑．1．﹣2、0、1、﹣3四个数中，最小的数是（）A．﹣2 B．0 C．1 D．﹣32．下列图形是中心对称图形的是（）A．B． C．D．3．下列计算中，结果正确的是（）A．a2•a3=a6 B．（2a）•（3a）=6a C．（a2）3=a6D．a6÷a2=a34．函数y=的自变量取值范围是（）A．x≠3 B．x≠0 C．x≠3且x≠0 D．x＜35．我校2016级2198名考生在2016年中考体育考试中取得了优异成绩，为了考察他们的中考体育成绩，从中抽取了550名考生的中考体育成绩进行统计，下列说法正确的是（）A．本次调查属于普查B．每名考生的中考体育成绩是个体C．550名考生是总体的一个样本D．2198名考生是总体6．如图，直线AB∥CD，直线EF与直线AB相交于点M，MN平分∠AME，若∠1=50°，则∠2的度数为（）A．50°B．80°C．85°D．100°7．已知x﹣2y=3，则7﹣2x+4y的值为（）A．﹣1 B．0 C．1 D．28．如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=25°，则∠D=（）A．40°B．50°C．55°D．60°9．下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有1个空心小圆圈，第②个图形中一共有6个空心小圆圈，第③个图形中一共有13个空心小圆圈，…，按此规律排列，则第⑦个图形中空心圆圈的个数为（）A．61 B．63 C．76 D．7810．数学活动课，老师和同学一起去测量校内某处的大树AB的高度，如图，老师测得大树前斜坡DE的坡度i=1：4，一学生站在离斜坡顶端E的水平距离DF为8m处的D点，测得大树顶端A的仰角为α，已知sinα=，BE=1.6m，此学生身高CD=1.6m，则大树高度AB为（）m．A．7.4 B．7.2 C．7 D．6.811．在矩形ABCD中，AB=，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（）A．﹣B．﹣C．π﹣D．π﹣12．能使分式方程+2=有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的所有整数k的积为（）A．﹣20 B．20 C．﹣60 D．60二、填空题：（本题共6小题，每小题4分，共24分）请把下列各题的正确答案填写在答题卡中对应的横线上．13．2016年重庆高考报名人数近250000人，数据250000用科学记数法表示为．14．计算：（）﹣2+（π﹣3）0﹣= ．15．如图，在△ABC中， =，DE∥AC，则DE：AC= ．16．“2016重庆国际马拉松”的赛事共有三项：A、“全程马拉松”、B、“半程马拉松”、C、“迷你马拉松”．小明和小刚参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到以上三个项目组，则小明和小刚被分配到不同项目组的概率是．17．甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快．设甲、乙之间的距离为y米，乙行驶的时间为x秒，y 与x之间的关系如图所示．若丙也从甲出发的地方沿相同的方向骑自行车行驶，且与甲的速度相同，当甲追上乙后45秒时，丙也追上乙，则丙比甲晚出发秒．18．在正方形ABCD中，点E为BC边上一点且CE=2BE，点F为对角线BD上一点且BF=2DF，连接AE交BD于点G，过点F作FH⊥AE于点H，连结CH、CF，若HG=2cm，则△CHF的面积是cm2．三、解答题：（本大题共2个小题，每小题7分，共14分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．19．已知如图，点F、A、E、B在一条直线上，∠C=∠F，BC∥DE，AB=DE求证：AC=DF．20．为了掌握某次数学模拟考试卷的命题质量与难度系数，命题教师选取一个水平相当的初三年级进行调研，命题教师将随机抽取的部分学生成绩分为5组：第一组75～90；第二组90～105；第三组105～120；第四组120～135；第五组135～150．统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图．观察图形的信息，回答下列问题：请将频数分布直方图补充完整；若老师找到第五组中一个学生的语文、数学、英语三科成绩，如表．老师将语文、数学、英语成绩按照3：5：2的比例给出这位同学的综合分数．求此同学的综合分数．科目语文数学英语得分120146140四、解答题：（本大题共4个小题，每小题10分，共40分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．21．计算：（1）x（x+2y）﹣（x﹣y）2+y2（2）（﹣x+3）÷．22．如图，一次函数y1=ax+b（a≠0）的图象与反比例函数y2=（k≠0）的图象交于A、B两点，与x轴、y轴分别交于C、D两点．已知：OA=，tanAOC=，点B的坐标为（，m）（1）求该反比例函数的解析式和点D的坐标；（2）点M在射线CA上，且MA=2AC，求△MOB的面积．23．2016年5月29日，中超十一轮，重庆力帆将主场迎战河北华夏幸福，重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威．“铁血巴渝”球迷协会计划购买甲、乙两种球票共500张，并且甲票的数量不少于乙票的3倍．（1）求“铁血巴渝”球迷协会至少购买多少张甲票；（2）“铁血巴渝”球迷协会从售票处得知，售票处将给予球迷协会一定的优惠，本场比赛球票以统一价格（m+20）元出售给该协会，因此协会决定购买的票数将在原计划的基础上增加（m+10）%，购票后总共用去56000元，求m的值．24．把一个自然数所有数位上的数字先平方再求和得到一个新数，叫做第一次运算，再把所得新数所有数位上的数字先平方再求和又将得到一个新数，叫做第二次运算，…如此重复下去，若最终结果为1，我们把具有这种特征的自然数称为“快乐数”．例如：32→32+22=13→12+32=10→12+02=1，70→72+02=49→42+92=97→92+72=130→12+32+02=10→12+02=1，所以32和70都是“快乐数”．（1）写出最小的两位“快乐数”；判断19是不是“快乐数”；请证明任意一个“快乐数”经过若干次运算后都不可能得到4；（2）若一个三位“快乐数”经过两次运算后结果为1，把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2，求出这个“快乐数”．五、解答题：（本大题共2个小题，每小题12分，共24分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．25．在△ABC中，以AB为斜边，作直角△ABD，使点D落在△ABC内，∠ADB=90°．（1）如图1，若AB=AC，∠BAD=30°，AD=6，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；（2）如图2，若AB=AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP=CP（3）如图3，若AD=BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE=EC，请直接写出线段BF、FC、AD之间的关系（不需要证明）．26．已知如图1，抛物线y=﹣x2﹣x+3与x轴交于A和B两点（点A在点B的左侧），与y 轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC（1）求出直线AD的解析式；（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．重庆一中中考数学二模试卷参考答案与试题解析一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号在答题卡中对应的方框涂黑．1．﹣2、0、1、﹣3四个数中，最小的数是（）A．﹣2 B．0 C．1 D．﹣3【考点】有理数大小比较．【分析】根据有理数的大小比较法则（正数都大于0，负数都小于0，正数大于一切负数，两个负数，其绝对值大的反而小）比较即可．【解答】解：﹣2、0、1、﹣3四个数中，最小的数是﹣3；故选D．2．下列图形是中心对称图形的是（）A．B． C．D．【考点】中心对称图形．【分析】根据中心对称图形的概念和各图的性质求解．【解答】解：A、是轴对称图形，故此选项错误；B、是中心对称图形，故此选项正确；C、不是中心对称图形，故此选项错误；D、不是中心对称图形，故此选项错误．故选：B．3．下列计算中，结果正确的是（）A．a2•a3=a6 B．（2a）•（3a）=6a C．（a2）3=a6D．a6÷a2=a3【考点】同底数幂的除法；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式．【分析】分别根据同底数幂的乘法的性质，单项式乘单项式的法则，幂的乘方的性质，同底数幂的除法的法则，对各选项分析判断后利用排除法求解．【解答】解：A、应为a2•a3=a2+3=a5，故A错误B、应为（2a）•（3a）=6a2，故B错误C、（a2）3=a2×3=a6，故C正确；D、应为a6÷a2=a6﹣2=a4．故D错误故选：C．4．函数y=的自变量取值范围是（）A．x≠3 B．x≠0 C．x≠3且x≠0 D．x＜3【考点】函数自变量的取值范围．【分析】根据分母不等于0即可列不等式求解．【解答】解：根据题意得3﹣x≠0，解得：x≠3．故选A．5．我校2016级2198名考生在2016年中考体育考试中取得了优异成绩，为了考察他们的中考体育成绩，从中抽取了550名考生的中考体育成绩进行统计，下列说法正确的是（）A．本次调查属于普查B．每名考生的中考体育成绩是个体C．550名考生是总体的一个样本D．2198名考生是总体【考点】总体、个体、样本、样本容量．【分析】根据样本、总体、个体、样本容量的定义进行解答即可．【解答】解：样本是：从中抽取的550名考生的中考体育成绩，个体：每名考生的中考体育成绩是个体，总体：我校2016级2198名考生的中考体育成绩的全体，故选B．6．如图，直线AB∥CD，直线EF与直线AB相交于点M，MN平分∠AME，若∠1=50°，则∠2的度数为（）A．50°B．80°C．85°D．100°【考点】平行线的性质．【分析】由MN平分∠AME，得到∠AME=2∠1=100°，根据平行线的性质即可得到结论．【解答】解：∵MN平分∠AME，若∠1=50°，∴∠AME=2∠1=100°，∴∠BMF=∠AME=100°，∵直线AB∥CD，∴∠2=180°﹣∠BMF=80°，故选B．7．已知x﹣2y=3，则7﹣2x+4y的值为（）A．﹣1 B．0 C．1 D．2【考点】代数式求值．【分析】先求得2x﹣4y的值，然后整体代入即可．【解答】解：∵x﹣2y=3，∴2x﹣4y=6．∴7﹣2x+4y=7﹣（2x﹣4y）=7﹣6=1．故选：C．8．如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=25°，则∠D=（）A．40°B．50°C．55°D．60°【考点】切线的性质．【分析】连接OC，先根据圆周角定理得∠DOC=2∠A=50°，再根据切线的性质定理得∠OCD=90°，则此题易解．【解答】解：连接OC，∵OA=OC，∴∠A=∠OCA=25°，∴∠DOC=2∠A=50°，∵过点D作⊙O的切线，切点为C，∴∠OCD=90°，∴∠D=40°．故选：A．9．下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有1个空心小圆圈，第②个图形中一共有6个空心小圆圈，第③个图形中一共有13个空心小圆圈，…，按此规律排列，则第⑦个图形中空心圆圈的个数为（）A．61 B．63 C．76 D．78【考点】规律型：图形的变化类．【分析】由已知图形中空心小圆圈个数，知第n个图形中空心小圆圈个数为4n﹣（n+2）+n（n ﹣1），据此可得答案．【解答】解：∵第①个图形中空心小圆圈个数为：4×1﹣3+1×0=1个；第②个图形中空心小圆圈个数为：4×2﹣4+2×1=6个；第③个图形中空心小圆圈个数为：4×3﹣5+3×2=13个；…∴第⑦个图形中空心圆圈的个数为：4×7﹣9+7×6=61个；故选：A．10．数学活动课，老师和同学一起去测量校内某处的大树AB的高度，如图，老师测得大树前斜坡DE的坡度i=1：4，一学生站在离斜坡顶端E的水平距离DF为8m处的D点，测得大树顶端A的仰角为α，已知sinα=，BE=1.6m，此学生身高CD=1.6m，则大树高度AB为（）m．A．7.4 B．7.2 C．7 D．6.8【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．【分析】根据题意结合坡度的定义得出C到AB的距离，进而利用锐角三角函数关系得出AB的长．【解答】解：如图所示：过点C作CG⊥AB延长线于点G，交EF于点N，由题意可得： ==，解得：EF=2，∵DC=1.6m，∴FN=1.6m，∴BG=EN=0.4m，∵sinα==，∴设AG=3x，则AC=5x，故BC=4x，即8+1.6=4x，解得：x=2.4，故AG=2.4×3=7.2m，则AB=AG﹣BG=7.2﹣0.4=6.8（m），答：大树高度AB为6.8m．故选：D．11．在矩形ABCD中，AB=，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（）A．﹣B．﹣C．π﹣D．π﹣【考点】扇形面积的计算；矩形的性质．【分析】连接AE，根据勾股定理求出BE的长，进而可得出∠BAE的度数，由余角的定义求出∠DAE的度数，根据S阴影=S扇形DAE﹣S△DAE即可得出结论．【解答】解：连接AE，∵在矩形ABCD中，AB=，BC=2，∴AE=AD=BC=2．在Rt△ABE中，∵BE===，∴△ABE是等腰直角三角形，∴∠BAE=45°，∴∠DAE=45°，∴S阴影=S扇形DAE﹣S△DAE=﹣×2×=﹣．故选A．12．能使分式方程+2=有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的所有整数k的积为（）A．﹣20 B．20 C．﹣60 D．60【考点】抛物线与x轴的交点；分式方程的解．【分析】①解分式方程，使x≥0且x≠1，求出k的取值；②因为二次函数y=x2+2x﹣k﹣1的图象与x轴无交点，所以△＜0，列不等式，求出k的取值；③综合①②求公共解并求其整数解，再相乘．【解答】解： +2=，去分母，方程两边同时乘以x﹣1，﹣k+2（x﹣1）=3，x=≥0，∴k≥﹣5①，∵x≠1，∴k≠﹣3②，由y=x2+2x﹣k﹣1的图象与x轴无交点，则4﹣4（﹣k﹣1）＜0，k＜﹣2③，由①②③得：﹣5≤k＜﹣2且k≠﹣3，∴k的整数解为：﹣5、﹣4，乘积是20；故选B．二、填空题：（本题共6小题，每小题4分，共24分）请把下列各题的正确答案填写在答题卡中对应的横线上．13．2016年重庆高考报名人数近250000人，数据250000用科学记数法表示为 2.5×105．【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：250000=2.5×105，故答案为：2.5×105．14．计算：（）﹣2+（π﹣3）0﹣= 2 ．【考点】实数的运算；零指数幂；负整数指数幂．【分析】原式利用零指数幂、负整数指数幂法则，以及算术平方根定义计算即可得到结果．【解答】解：原式=4+1﹣3=2，故答案为：215．如图，在△ABC中， =，DE∥AC，则DE：AC= 5：8 ．【考点】相似三角形的判定与性质．【分析】由比例的性质得出=，由平行线得出△BDE∽△BAC，得出比例式，即可得出结果．【解答】解：∵=，∴=，∵DE∥AC，∴△BDE∽△BAC，∴=，故答案为：5：8．16．“2016重庆国际马拉松”的赛事共有三项：A、“全程马拉松”、B、“半程马拉松”、C、“迷你马拉松”．小明和小刚参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到以上三个项目组，则小明和小刚被分配到不同项目组的概率是．【考点】列表法与树状图法．【分析】先画树状图展示所有9种等可能的结果数，再找出其中小明和小刚被分配到不同项目组的结果数，然后根据概率公式计算．【解答】解：画树状图为：共有9种等可能的结果数，其中小明和小刚被分配到不同项目组的结果数为6，所以小明和小刚被分配到不同项目组的概率==．故答案为．17．甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快．设甲、乙之间的距离为y米，乙行驶的时间为x秒，y 与x之间的关系如图所示．若丙也从甲出发的地方沿相同的方向骑自行车行驶，且与甲的速度相同，当甲追上乙后45秒时，丙也追上乙，则丙比甲晚出发15 秒．【考点】函数的图象．【分析】①先根据图形信息可知：300秒时，乙到达目的地，由出发去距离甲1300米的目的地，得甲到目的地是1300米，而乙在甲前面100米处，所以乙距离目的地1200米，由此计算出乙的速度；②设甲的速度为x米/秒，根据50秒时，甲追上乙列方程求出甲的速度；③丙出发95秒追上乙，且丙比乙不是同时出发，可设丙比甲晚出发a秒，列方程求出a的值．【解答】解：由图可知：①50秒时，甲追上乙，②300秒时，乙到达目的地，∴乙的速度为： =4，设甲的速度为x米/秒，则50x﹣50×4=100，x=6，设丙比甲晚出发a秒，则（50+45﹣a）×6=（50+45）×4+100，a=15，则丙比甲晚出发15秒；故答案为：15．18．在正方形ABCD中，点E为BC边上一点且CE=2BE，点F为对角线BD上一点且BF=2DF，连接AE交BD于点G，过点F作FH⊥AE于点H，连结CH、CF，若HG=2cm，则△CHF的面积是cm2．【考点】相似三角形的判定与性质；正方形的性质．【分析】如图，过F作FI⊥BC于I，连接FE，FA，得到FI∥CD，设BE=EI=IC=a，CE=FI=2a，AB=3a，由勾股定理得到FE=FC=FA=a，推出HE=AE=，根据正方形的性得到BG平分∠ABC，由三角形角平分线定理得到=，求得HG=AE=a=2，于是得到结论．【解答】解：如图，过F作FI⊥BC于I，连接FE，FA，∴FI∥CD，∵CE=2BE，BF=2DF，∴设BE=EI=IC=a，CE=FI=2a，AB=3a，∴则FE=FC=FA=a，∴H为AE的中点，∴HE=AE=，∵四边形ABCD是正方形，∴BG平分∠ABC，∴=，∴HG=AE=a=2，∴a=，∴S△CHF =S△HEF+S△CEF﹣S△CEH=（a）2+•2a•2a﹣•2a•a=a2=，故答案为：．三、解答题：（本大题共2个小题，每小题7分，共14分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．19．已知如图，点F、A、E、B在一条直线上，∠C=∠F，BC∥DE，AB=DE求证：AC=DF．【考点】全等三角形的判定与性质；平行线的性质．【分析】根据平行线的性质可得∠B=∠DEF，再利用AAS判定△DEF≌△ABC，进而可得AC=DF．【解答】证明：∵BC∥DE，∴∠B=∠DEF，在△ABC和△DEF中，∴△DEF≌△ABC（AAS），∴AC=DF．20．为了掌握某次数学模拟考试卷的命题质量与难度系数，命题教师选取一个水平相当的初三年级进行调研，命题教师将随机抽取的部分学生成绩分为5组：第一组75～90；第二组90～105；第三组105～120；第四组120～135；第五组135～150．统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图．观察图形的信息，回答下列问题：请将频数分布直方图补充完整；若老师找到第五组中一个学生的语文、数学、英语三科成绩，如表．老师将语文、数学、英语成绩按照3：5：2的比例给出这位同学的综合分数．求此同学的综合分数．科目语文数学英语得分120146140【考点】频数（率）分布直方图；统计表；扇形统计图；加权平均数．【分析】（1）根据第三组的频数是20，对应的百分比是40%，据此即可求得调研的总分人数，然后利用总人数减去其他组的人数即可求得第五组的人数，从而补全直方图；（2）利用加权平均数公式即可求解．【解答】解：（1）调研的总人数是20÷40%=50（人），则第五组的人数少50﹣6﹣8﹣20﹣14=2．；（2）综合分数是=137（分）．答：这位同学的综合得分是137分．四、解答题：（本大题共4个小题，每小题10分，共40分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．21．计算：（1）x（x+2y）﹣（x﹣y）2+y2（2）（﹣x+3）÷．【考点】分式的混合运算；单项式乘多项式；完全平方公式．【分析】（1）先去括号，再合并同类项即可解答本题；（2）先化简括号内的式子，再根据分式的除法即可解答本题．【解答】解：（1）x（x+2y）﹣（x﹣y）2+y2=x2+2xy﹣x2+2xy﹣y2+y2=4xy；（2）（﹣x+3）÷====．22．如图，一次函数y1=ax+b（a≠0）的图象与反比例函数y2=（k≠0）的图象交于A、B两点，与x轴、y轴分别交于C、D两点．已知：OA=，tanAOC=，点B的坐标为（，m）（1）求该反比例函数的解析式和点D的坐标；（2）点M在射线CA上，且MA=2AC，求△MOB的面积．【考点】反比例函数与一次函数的交点问题；解直角三角形．【分析】（1）过A作AE⊥x轴于点E，在Rt△AOE中，可根据OA的长求得A点坐标，代入反比例函数解析式可求反比例函数解析式，进一步可求得B点坐标，利用待定系数法可求得直线AB的解析式，则可求得D点坐标；（2）过M作MF⊥x轴于点F，可证得△MFC∽△AEC，可求得MF的长，代入直线AB解析式可求得M点坐标，进一步可求得△MOB的面积．【解答】解：（1）如图1，过A作AE⊥x轴于E，在Rt△AOE中，tan∠AOC==，设AE=a，则OE=3a，∴OA==a，∵OA=，∴a=1，∴AE=1，OE=3，∴A点坐标为（﹣3，1），=（k≠0）的图象过A点，∵反比例函数y2∴k=﹣3，∴反比例函数解析式为y2=﹣，∵反比例函数y2=﹣的图象过B（，m），∴m=﹣3，解得m=﹣2，∴B点坐标为（，﹣2），设直线AB解析式为y=nx+b，把A、B两点坐标代入可得，解得，∴直线AB的解析式为y=﹣x﹣1，令x=1，可得y=﹣1，∴D点坐标为（0，﹣1）；（2）由（1）可得AE=1，∵MA=2AC，∴=，如图2，过M作MF⊥x轴于点F，则△CAE∽△CMF，∴==，∴MF=3，即M点的纵坐标为3，代入直线AB解析式可得3=﹣x﹣1，解得x=﹣6，∴M点坐标为（﹣6，3），∴S△MOB =OD•（xB﹣xM）=×1×（+6）=，即△MOB的面积为．23．2016年5月29日，中超十一轮，重庆力帆将主场迎战河北华夏幸福，重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威．“铁血巴渝”球迷协会计划购买甲、乙两种球票共500张，并且甲票的数量不少于乙票的3倍．（1）求“铁血巴渝”球迷协会至少购买多少张甲票；（2）“铁血巴渝”球迷协会从售票处得知，售票处将给予球迷协会一定的优惠，本场比赛球票以统一价格（m+20）元出售给该协会，因此协会决定购买的票数将在原计划的基础上增加（m+10）%，购票后总共用去56000元，求m的值．【考点】一元二次方程的应用；一元一次不等式的应用．【分析】（1）购买甲票x张，则购买乙票张，根据题意列出不等式解答即可；（2）根据题意列出方程解答即可．【解答】解：（1）设：购买甲票x张，则购买乙票张．由条件得：x≥3∴x≥375，故：“铁血巴渝”球迷协会至少购买375张甲票．（2）由条件得：500[1+（m+10）%]（m+20）=56000∴m2+130m﹣9000=0∴m1=50，m2=﹣180＜0（舍）故：m的值为50．24．把一个自然数所有数位上的数字先平方再求和得到一个新数，叫做第一次运算，再把所得新数所有数位上的数字先平方再求和又将得到一个新数，叫做第二次运算，…如此重复下去，若最终结果为1，我们把具有这种特征的自然数称为“快乐数”．例如：32→32+22=13→12+32=10→12+02=1，70→72+02=49→42+92=97→92+72=130→12+32+02=10→12+02=1，所以32和70都是“快乐数”．（1）写出最小的两位“快乐数”；判断19是不是“快乐数”；请证明任意一个“快乐数”经过若干次运算后都不可能得到4；（2）若一个三位“快乐数”经过两次运算后结果为1，把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2，求出这个“快乐数”．【考点】因式分解的应用．【分析】（1）根据“快乐数”的定义计算即可；（2）设三位“快乐数”为100a+10b+c，根据“快乐数”的定义计算．【解答】解：（1）∵12+02=1，∴最小的两位“快乐数”10，∵19→12+92=82→82+22=68→62+82=100→12+02+02=1，∴19是快乐数；证明：∵4→37→58=68→89→125→30→9→81→65→61→37，37出现两次，所以后面将重复出现，永远不会出现1，所以任意一个“快乐数”经过若干次运算后都不可能得到4．（2）设三位“快乐数”为100a+10b+c，由题意，经过两次运算后结果为1，所以第一次运算后结果一定是10或者100，则a2+b2+c2=10或100，∵a、b、c为整数，且a≠0，∴当a2+b2+c2=10时，12+32+02=10，①当a=1，b=3或0，c=0或3时，三位“快乐数”为130，103，②当a=2时，无解；③当a=3，b=1或0，c=0或1时，三位“快乐数”为310，301，同理当a2+b2+c2=100时，62+82+02=100，所以三位“快乐数”有680，608，806，860．综上一共有130，103，310，301，680，608，806，860八个，又因为三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2，所以只有310和860满足已知条件．五、解答题：（本大题共2个小题，每小题12分，共24分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤．25．在△ABC中，以AB为斜边，作直角△ABD，使点D落在△ABC内，∠ADB=90°．（1）如图1，若AB=AC，∠BAD=30°，AD=6，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；（2）如图2，若AB=AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP=CP（3）如图3，若AD=BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE=EC，请直接写出线段BF、FC、AD之间的关系（不需要证明）．【考点】三角形综合题．【分析】（1）在直角三角形中，利用锐角三角函数求出AB，即可；（2）先利用互余判断出，∠BDP=∠PEC，得到△BDP和△CEQ，再用三角形的外角得到∠EPC=∠PQC，即可；（3）利用线段垂直平分线上的点到两端点的距离相等，判断出∠AFB=90°即可．【解答】（1）解：∵∠ADB=90°，∠BAD=30°，AD=6，∴cos∠BAD=，∴AB===12，∴AC=AB=12，∵点P、M分别为BC、AB边的中点，∴PM=AC=6，（2）如图2，在ED上截取EQ=PD，∴∠BDP+∠ADE=90°，∵AD=AE，∴∠ADE=∠AED，∵把△ABD绕点A逆时针旋转一定角度，得到△ACE，∴∠AEC=∠ADB=90°∵∠AED+∠PEC=90°，∴∠BDP=∠PEC，在△BDP和△CEQ中，，∴△BDP≌△CEQ，∴BP=CQ，∠DBP=∠QCE，∵∠CPE=∠BDP+∠DBP，∠PQC=∠PEC+∠QCE，∴∠EPC=∠PQC，∴PC=CQ，∴BP=CP（3）BF2+FC2=2AD2，理由：如图3，连接AF，∵EF⊥AC，且AE=EC，∴FA=FC，∠FAC=∠FCA，∵EF⊥AC，且AE=EC，∴∠DAC=∠DCA，DA=DC，∵AD=BD，∴BD=DC，∵∠FAC=∠FCA，∠DAC=∠DCA，∴∠DAF=∠DCB，∴∠DAF=∠DBC，∴∠AFB=∠ADB=90°，在RT△ADB中，DA=DB，∴AB2=2AD2，在RT△ABB中，BF2+FA2=AB2=2AD2，∵FA=FC∴BF2+FC2=2AD2．26．已知如图1，抛物线y=﹣x2﹣x+3与x轴交于A和B两点（点A在点B的左侧），与y 轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC（1）求出直线AD的解析式；（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP 的值．【考点】二次函数综合题．【分析】（1）先求出点A，B坐标，再用待定系数法求出直线AD解析式；（2）先建立S△ADF=﹣（m+）2+，进而求出F点的坐标，再确定出点M的位置，进而求出点A1，A2坐标，即可确定出A2F的解析式为y=﹣x﹣①，和直线BD解析式为y=﹣x﹣1②，联立方程组即可确定出结论；（3）分四种情况讨论计算，利用锐角三角函数和勾股定理表示出线段，用相似三角形的性质即可求出PC的值．【解答】解：（1）∵抛物线y=﹣x2﹣x+3与x轴交于A和B两点，∴0=﹣x2﹣x+3，∴x=2或x=﹣4，∴A（﹣4，0），B（2，0），∵D（0，﹣1），∴直线AD解析式为y=﹣x﹣1；（2）如图1，过点F作FH⊥x轴，交AD于H，设F（m，﹣m2﹣m+3），H（m，﹣m﹣1），∴FH=﹣m2﹣m+3﹣（﹣m﹣1）=﹣m2﹣m+4，∴S△ADF =S△AFH+S△DFH=FH×|yD﹣yA|=2FH=2（﹣m2﹣m+4）=﹣m2﹣m+8=﹣（m+）2+，当m=﹣时，S△ADF最大，∴F（﹣，）如图2，作点A关于直线BD的对称点A1，把A1沿平行直线BD方向平移到A2，且A1A2=，连接A2F，交直线BD于点N，把点N沿直线BD向左平移得点M，此时四边形AMNF的周长最小．∵OB=2，OD=1，∴tan∠OBD=，∵AB=6，∴AK=，∴AA1=2AK=，..在Rt△ABK中，AH=，A1H=，∴OH=OA﹣AH=，∴A1（﹣，﹣），过A2作A2P⊥A2H，∴∠A1A2P=∠ABK，∵A1A2=，∴A2P=2，A1P=1，∴A2（﹣，﹣）∵F（﹣，）∴A2F的解析式为y=﹣x﹣①，∵B（2，0），D（0，﹣1），∴直线BD解析式为y=﹣x﹣1②，联立①②得，x=﹣，∴N点的横坐标为：﹣．（3）∵C（0，3），B（2，0），D（0，﹣1）∴CD=4，BC=，OB=2，BC边上的高为DH，根据等面积法得， BC×DH=CD×OB，∴DH==，∵A（﹣4，0），C（0，3），∴OA=4，OC=3，∴tan∠ACD=，①当PC=PQ时，简图如图1，..过点P作PG⊥CD，过点D作DH⊥PQ，∵tan∠ACD=∴设CG=3a，则QG=3a，PG=4a，PQ=PC=5a，∴DQ=CD﹣CQ=4﹣6a∵△PGQ∽△DHQ，∴，∴，∴a=，∴PC=5a=；②当PC=CQ时，简图如图2，过点P作PG⊥CD，∵tan∠ACD=∴设CG=3a，则PG=4a，∴CQ=PC=5a，∴QG=CQ﹣CG=2a，∴PQ=2a，.. ∴DQ=CD﹣CQ=4﹣5a∵△PGQ∽△DHQ，同①的方法得出，PC=4﹣，③当QC=PQ时，简图如图1过点Q作QG⊥PC，过点C作CN⊥PQ，设CG=3a，则QG=4a，PQ=CQ=5a，∴PG=3a，∴PC=6a∴DQ=CD﹣CQ=4﹣5a，利用等面积法得，CN×PQ=PC×QG，∴CN=a，∵△CQN∽△DQH同①的方法得出PC=④当PC=CQ时，简图如图4，过点P作PG⊥CD，过H作HD⊥PQ，设CG=3a，则PG=4a，CQ=PC=5a，∴QD=4+5a，PQ=4，..∵△QPG∽△QDH，同①方法得出．CP=综上所述，PC的值为：；4﹣，，=．。

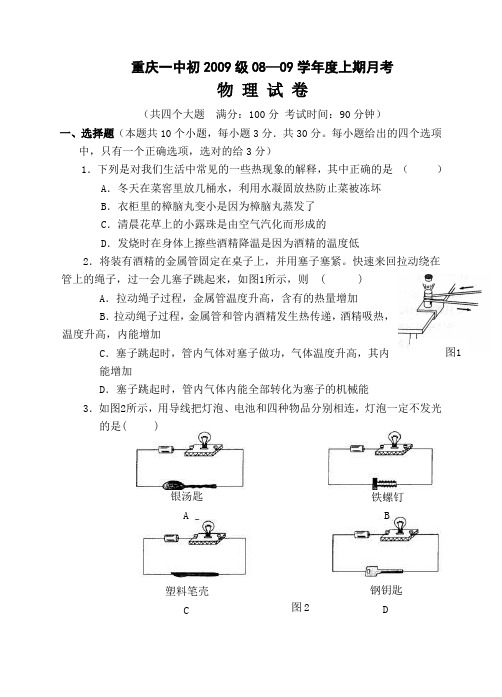
重庆一中初2009级08—09学年度上期月考物 理 试 卷（共四个大题 满分：100分 考试时间：90分钟）一、选择题（本题共10个小题，每小题3分．共30分。

每小题给出的四个选项中，只有一个正确选项，选对的给3分）1．下列是对我们生活中常见的一些热现象的解释，其中正确的是 （ ）A ．冬天在菜窖里放几桶水，利用水凝固放热防止菜被冻坏B ．衣柜里的樟脑丸变小是因为樟脑丸蒸发了C ．清晨花草上的小露珠是由空气汽化而形成的D ．发烧时在身体上擦些酒精降温是因为酒精的温度低2．将装有酒精的金属管固定在桌子上，并用塞子塞紧。

快速来回拉动绕在管上的绳子，过一会儿塞子跳起来，如图1所示，则 ( )A ．拉动绳子过程，金属管温度升高，含有的热量增加B ．拉动绳子过程，金属管和管内酒精发生热传递，酒精吸热，温度升高，内能增加C ．塞子跳起时，管内气体对塞子做功，气体温度升高，其内能增加D ．塞子跳起时，管内气体内能全部转化为塞子的机械能3．如图2所示，用导线把灯泡、电池和四种物品分别相连，灯泡一定不发光的是( )图1图2银汤匙A 铁螺钉B钢钥匙D塑料笔壳C4．有R1和R2两个电阻，且R1＞R2，将它们分别接到同一电源两端，要使电路中的总电流最大，连接方法应该是( )A．只接入R1 B．只接入R2C．R1和R2串联后接入 D．R1和R2并联后接入5. 如图3所示电路中，电源电压保持不变，闭合开关S1、S2，两灯都发光，当把开关S2断开时，灯泡L1的亮度及电流表示数的变化情况是（）A.L1亮度不变，电流表示数变小B.L1亮度不变，电流表示数不变C.L1亮度增大，电流表示数不变D.L1亮度减小，电流表示数变小6．下面几位同学的说法中正确的是( )A. 电功的单位与电能的单位不相同，在国际单位制中电功是“J”，而电能是“Kw·h”B. 电流做功的过程就是电能转化为其他形式的能的过程C. 电能表测量的是电能表在某一段时间内消耗的电能D. 电吹风通电时把电能全部转化成热能7．如图4所示电路，电源电压恒定不变。

2024年重庆一中中考物理二模试卷一、单选题：本大题共8小题，共24分。

1.对下列物理量的估测中，最接近实际的是( )A. 一个篮球的直径约为25cmB. 重庆夏天的平均气温约为45℃C. 体考用实心球每个的质量约为200gD. 教室内1台电风扇的电功率约为1000W2.唐朝诗人白居易在《暮江吟》中写道“一道残阳铺水中，半江瑟瑟半江红”，描绘出了夕阳下的江面上奇特的光色变化景象，涉及到了光的反射现象。

下列图中的光现象与反射现象原理相同的是( )A. 墙上手影B. 照镜子C. 雨后彩虹D. 林下光斑3.如图所示，是由物态变化形成的美丽的自然景观，以下分析正确的是( )A. 图甲，缥缈的平流雾是汽化现象B. 图乙，壮观的雾凇是凝固形成的C. 图丙，春天河冰化水是熔化现象D. 图丁，晶莹的露珠是凝华形成的4.下列有关电学知识的说法正确的是( )A. 毛皮摩擦过的橡胶棒失去电子带正电B. 带金属外壳的用电器在使用时要接地C. 负电荷定向移动的方向就是电流方向D. 使用测电笔时要用手接触笔尖金属体5.2024年3月31日，中国乒乓球运动员孙颖莎和梁靖崑在WTT仁川冠军赛决赛中分别获得女单和男单冠军。

如图所示，是运动员击球和手握奖杯站立静止时的照片。

备受鼓舞的小杰同学在观看比赛时有了很多关于力与运动方面的思考，下列说法正确的是( )A. 图甲，击飞的乒乓球在空中运动时不受力的作用B. 图甲，乒乓球能继续向前运动是受到惯性的作用C. 图乙，运动员的右手给奖杯的摩擦力方向是沿奖杯向上的D. 图乙，运动员的重力和运动员对地面的压力是一对平衡力6.如图所示，是小艾同学看见建筑工人用滑轮提升重物后画的草图。

已知每个滑轮重为50N，若将重为750N的重物在10s内提升3m，不计绳重及轮与轴间的摩擦，下列说法正确的是( )A. 重物上移的速度为0.6m/sB. 人对绳子施加的力为250NC. 人对绳子做功的功率为120WD. 该滑轮组的机械效率为93.75%7.如图甲所示，是一种测力装置的结构示意图。

word班次 某某 顺序号 考号— — — — — — — —密— — — — — — — — — — —封 — — — — — — — — — —线— — — — — — — — — — — —某某一中初2009级初三（上）月考试题数 学 试 题 2008．10考生注意：本试题共28小题，满分150分，考试时间120分钟一、选择题：（每小题只有一个正确答案，请将答案填入括号内。

本大题共10个小题，每小题4分，共40分。

） 1．随机掷一枚均匀的硬币两次，两次都是反面朝上的概率是（ ）．A ．41 B ．21 C ．43D ．1 2．在抛一枚均匀硬币的实验中，若没有硬币，则下列可作替代物实验的是（ ）．A ．一颗均匀的骰子B ．可乐瓶盖C ．图钉D ．除颜色外，大小、形状相同的两个小球 3．下列四幅图形中，表示两棵小树在同一时刻阳光下的影子的图形可能是（ ）．4．某种商品零售价经过两次降价后的价格为降价前的81％，则平均每次降价（ ）． A ．9.5％ B ．10％ C ．19％ D ．20％ 5．已知某种品牌电脑的显示器的寿命大约为4210⨯小时，这种显示器工作的天数为d （天），平均每天工作的时间为t （小时），那么能正确表示d 与t 之间的函数关系的图象是（ ）．6．等腰三角形的底和腰的长是方程0862=+-x x 的两根，则这个三角形的周长为（ ）． A ．8或10 B ．8C ．10D ．不能确定7．如图，在□ABCD 中，E 是BC 的中点，下列结论不正确．．．的是( )． A ．BF=21DF B ．S △FAD =2S △FBEC ．S 四边形FECD =5S △FBE D ．S △FAB =2S △FBE8．小刚身高7.1m ，测得他站立在阳光下的影子长为85.0m ，紧接着他把手臂竖直举起，测得影子长为1.1m ，那么小刚举起的手臂超出头顶（ ）．A ．B ．C ．D ．A BCF （第7题）A ．5.0mB ．55.0mC ．6.0mD ．2.2m初三数学试卷 共8页 第1页9．如图，在△ABC 中，D 、E 、F 分别为BC 、AC 、AB 的中点， AH ⊥BC 于点H ，FD=8cm ，则HE 的值为（ ）． A ．20 cm B ．16 cm C ．12 cm D ．8 cm 10．如图，A 、B 是反比例函数xy 2=的图象上的两点，AC 、都垂直于x 轴，垂足分别为C 、D ，AB 的延长线交x 轴于点若C 、D 的坐标分别为（1，0）、（4，0），则△BDE 的面积与 △ACE 的面积的比值是（ ）．A ．21 B ．41 C ．81 D ．161二、填空题：（请将答案填写在横线上。

秘密★启用前2022年重庆一中高2023届9月月考数学试题卷注意事项：1.答卷前,考生务必将自己的姓名、准考证号码填写在答题卡上．2.作答时,务必将答案写在答题卡上．写在试卷及草稿纸上无效．3.考试结束后,将答题卡交回．一、选择题：本题共8个小题,每小题5分,共40分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．设集合{|ln(1)}A y y x ==-，{|B y y ==，则A B = （）A ．[0,2)B ．(0,2)C ．[0,2]D ．[0,1)2．命题“x ∀∈R ，e 20x +>”的否定是（）A ．0x ∃∈R ，0e 20x +≤B ．x ∀∈R ，e 20x +≤C ．0x ∃∈R ，0e 20x +>D ．0x ∀∈R ，0e 20x +<3．下列函数中，既是偶函数又在()0,+∞上单调递增的是（）A ．12xy ⎛⎫= ⎪⎝⎭B ．2y x x=-C ．1y x =-D ．1y x x=-4．根据分类变量x 与y 的观察数据，计算得到2 3.174K =，依据下表给出的2K 独立性检验中的小概率值和相应的临界值，作出下列判断，正确的是（）()2P K k ≥0.10.050.010.0050.001k2.7063.8416.6357.87910.828A ．有95%的把握认为变量x 与y 独立B ．有95%的把握认为变量x 与y 不独立C ．变量x 与y 独立，这个结论犯错误的概率不超过10%D ．变量x 与y 不独立，这个结论犯错误的概率不超过10%5．已知()31sin 2,cos ,,43αββαβ+==为锐角，则()sin αβ+的值为()A.372212- B.321412- C.372212+ D.321412+6．已知抛物线21:4C y x =，圆222(2):2C x y -+=，直线():1l y k x =-与1C 交于A 、B 两点，与2C 交于M 、N 两点，若8AB =，则MN =（）AB C ．2D ．27．甲，乙，丙，丁四支足球队进行单循环比赛（每两个球队都要比赛一场），每场比赛的计分方法是:胜者得3分，负者得0分，平局两队各得1分,全部比赛结束后，四队的得分为：甲6分，乙5分，丙4分，丁1分，则（）A ．甲胜乙B ．乙胜丙C ．乙平丁D ．丙平丁8.若124,1()(2)2,1x ax a e x f x x a x a x -⎧+->=⎨+--≤⎩，且()0f x ≤的解集为[)2-+∞，，则a 的取值范围是（）A.(1,2)B.[]1,2C.[]2,4D.(]1,4二、选择题：本题共4个小题,每小题5分,共20分．在每小题给出的四个选项中,有多项符合题目要求．全部选对的得5分,有选错的得0分,部分选对的得2分．9．设函数op =UU +B +，给出的四个说法正确的是()A.=0时有()()f x f x -=-成立 B.=0且>0时，方程op =0有唯一实根C.=op 的图象关于点(0,p 对称 D.方程op =0恰有两个实根10．下列大小关系正确的有（）A ． 2.122 2.1>B ． 3.922 3.9<C ．1ln 2ln 22<D ．58log 3log 5<11．已知随机变量X 服从正态分布(0,1)N ，定义函数()f x 为X 取值不超过x 的概率，即()()f x P X x =≤。

重庆一中初2023届2022-2023学年度上期阶段性消化作业（二）物理试题(全卷共四个大题满分80分考试时间与化学共用120分钟)注意事项：1．试题的答案书写在答题卡上，不得在试题卷上直接作答。

2．作答前认真阅读答题卡上的注意事项。

3．考试结束，由监考人员将试题卷和答题卡一并收回。

一、选择题（每小题只有一个选项符合题意，每小题3分，共24分）1.下列对常见物理量的估测符合实际的是（）A.重庆12月的平均气温约为30℃B.家用电饭煲的额定功率约为1kWC.教室里的吊扇正常工作时的电流约为10AD.对人体的安全电压为不高于220V2.关于热学知识，下列说法正确的是（）A.物体吸收热量温度一定升高B.热值大的燃料，完全燃烧时放出的热量一定多C.热量可以从内能小的物体传递给内能大的物体D.物体吸收热量越多，比热容越大3.如图1所示，关于家庭电路和安全用电，下列说法正确的是（）A ．在电线上晒湿衣服B ．用电器金属外壳接地C ．使用试电笔时，手握住金属杆D ．电灯的开关应串联接在电灯与零线之间4.下列电学知识中，说法正确的是（）A.电功率越大的用电器，消耗的电能越多B.导体的电阻，与导体两端的电压成正比，与通过导体的电流成反比C.电视机和电烙铁分别在家庭电路中工作消耗相同电能时，电烙铁产生的热量较多D .两盏白炽灯并联接入同一家庭电路中工作时，电阻较大的灯实际功率较大5.城市里共享电动车方便快捷，已经成为大家近距离出行的首选交通工具。

使用时首先用手机相关APP 扫描车头或车尾的二维码即可解锁（S 1闭合）。

乘车人上车坐好后右手转动把手（S 2闭合），共享电动车即可启动行驶。

手动开关S 3和光控开关S 4都可控制车头灯（手动开关S 3闭合，车头灯可发光；若S 3断开，光线较暗时光控开关S 4自动闭合，车头灯也可发光）。

则下列图2中模拟电路符合上述要求的是（）图1火线零线地线图26.重庆一中物理兴趣小组的小勇同学为快递公司设计了分拣计数装置，其简化电路如图3所示。

班次 姓名 顺序号 考号— — — — — — — — — — — — —密— — — — — — — — — — —封 — — — — — — — — — —线— — — — — — — — — — — —重庆一中初2009级08—09学年度第二次模拟考试历史试卷 2009、6（开卷 本卷五个大题 满分50分 与政治合堂共用150分钟 ）一、选择题：本大题共15小题，每小题1分，共15分。

在备选答案中只有一项是符合题目A ．秦B ．赵C ．周D ．晋 2．我国历史上第一次大规模农民起义爆发于（ ）A ．咸阳B ．渔阳C ．巨鹿D ．大泽乡 3．“新疆是个好地方，地肥水美遍地牛羊”。

标志着今天新疆天山南北地区正式归属中央政府管辖的事件是（ ） A ．公元前221年，秦统一六国 B ．公元前60年，西域都护设立C ．西汉末年东汉初年，佛教经西域传入内地D ．1884年，清政府设立新疆行省4．某历史兴趣小组在排练历史剧《商鞅变法》，请帮他们找出剧本中的错误（ ） A ．商鞅不是秦国本地人，变法之余思念家乡 B ．秦孝公任用商鞅变法C ．秦国人纷纷放弃耕田织布，经营小商品买卖D ．一名士兵由于战功显赫，被封官赐爵，赏给土地房宅5．为响应国家关于开展“青少年阳光体育运动”的号召，在每天锻炼一小时的活动中，某校 把汉朝著名的民间医生华佗介绍给了同学们，其最主要的原因是（ ）A ．他最早编制了强身健体的五禽戏B ．他最早采用全身麻醉手术法C ．他奠定了中医治疗学的基础D ．他四处游历，撰写出《水经注》一书 6．殷商博物馆中要求选出最能体现商朝青铜器典型风格的文物，最应该当选的是（ ）A ．B ．C ．D ．7．“优秀流行歌曲创作大赛”在让观众一饱耳福的同时，还促进了精神文明建设。

音乐是古老不变的主题，至今能演奏出悠扬清脆曲目的最引人注目的战国编钟出土于（ ） A ．湖南长沙 B ．陕西西安 C ．湖北随州 D ．河南信阳 8．小青要到北京首都博物馆参观“甲骨文展”（①区）、“《九章算术》展”(②区)、“都江堰水 利工程模拟展”(③区)和“顾恺之绘画展”(④区)，如必须按历史事件先后顺序参观的话，那她应该按下面哪种顺序参观：（ ）A ．③①②④B ．④①②③C ．①③②④D ．①②③④ 9．抗战时期大后方工业区中，唯一门类齐全的综合性工业区是（ ）A ．贵阳B ．重庆C ．成都D ．昆明 10．1938年1月11日，《新华日报》创刊于（ ）A ．上海B ．重庆C ．延安D ．武汉 11．被重庆地下党和进步群众誉为“小《新华日报》”的是（ ）A 、《渝报》B 、《新蜀报》C 、《民报》D 、《挺进报》 12．1945年10月10日，国共双方代表签署《双十协定》的地点在（ )A ．桂园B ．特园C ．曾家岩50号D ．红岩村13号13．红岩精神是革命烈士对共产主义信念执著追求的高度概括，有一首《黑牢诗篇》正是其中的代表，它的作者是（ ）A ．B ．C ．D ．14．下列各项所示的前后历史事件，不存在因果关系的是（ ）A ．张骞出使西域——匈奴被打败B ．巴黎和会——五四运动C ．罗斯福新政——美国摆脱经济危机D ．反法西斯同盟形成——第二次世界大战胜利 15．下列历史事件，按发生时间先后顺序排列正确的是（ ）①齐桓公称霸 ②重庆解放 ③凡尔登战役 ④台儿庄战役 A ．①②③④ B ．①③④② C ．②④①③ D ．①③②④二、判断题：本大题共5个小题，每个1分，共5分。

来源于：回渊阁教育网2008—2009学年度下期一中初2009级摸底考试英语试卷2009. 2第I卷(100分)I. 听力测试。

(共30分)第一节. 情景反应。

(每小题1分，共6分)听一遍。

根据你所听到的句子，从A、B、C三个选项中选出最恰当的答语，并把答题卡上对应题目的答案标号涂黑。

1. A. Good idea B. Yes, I think so. C. Let’s go for a walk.2. A. Have a good time B. It’s cloudy. C. It’s Monday.3. A. I think it’s his. B. It’s broken, I’m afraid. C. I’ve got a bad cold.4. A. See you later. B. Excuse me. C. Yes, please.5. A. Good luck. B. It’s great. C. I’ll try it.6. A. I’m sorry to hear that. B. That’s OK. C. It doesn’t matter.第二节. 对话理解。

(每小题1分，共6分)听一遍。

根据你所听到的对话和问题，从A、B、C三个选项中选出正确答案，并把答题卡上对应题目的答案标号涂黑。

7. A. About 3 kilometers. B. About 4 kilometers. C. About 5 kilometers.8. A. At home. B. In a bookstore. C. In a zoo.9. A. Alice’s sister. B. Mary’s sister. C. Mary’s mother.10. A. A singer. B. A player. C. A nurse.11. A. Tea with sugar. B. Milk with sugar. C. Tea without sugar.12. A. On Monday. B. On Tuesday. C. On Wednesday.第三节. 短文理解。

2019-2020学年重庆一中九年级（上）第二次月考化学试卷一、选择题（本大题包括16小题，每题2分，共32分，每小题只有一个选项符合题意．）1．（2分）下列描述主要涉及物质化学性质的是（）A．金钢石用来做装饰品B．活性炭用来除冰箱异味C．分离液态空气制“液氧”D．进入久未开启的菜窑，需要做灯火实验2．（2分）“轻轨电车”是近年来新兴的交通工具（如图所示），具有无污染的优点。

当轻轨电车开动时，在轻轨电车跟架空电线的接触点上，由于高速摩擦会产生高温，因此接触点上的材料应该具有耐高温、有润滑性、不易氧化、能导电的性质。

你认为该接触点上材料的选用较为合适的是（）A．金刚石B．铝C．石墨D．铜3．（2分）下列事件的处理方式正确的是（）A．煤气中毒，给患者喝水溶解有毒气体B．油锅着火，立即用湿手巾捂住口鼻距离现场C．煤气泄漏，马上开灯检查D．森林着火，砍掉大火蔓延路线树木4．（2分）图中与另外三支蜡烛燃烧情况明显不同的蜡烛是（）A．B．C．D．5．（2分）CO2和O2是自然界中生命活动不可缺少的两种气体，它们的相同点是（）A．都能灭火B．都能供给呼吸C．都是无毒D．都是光合作用的原料6．（2分）关于化学方程式：4P+5O22P2O5，下列说法正确的是（）A．每4份质量的磷和5份质量的氧气在点燃条件下反应生成2份质量的五氧化二磷B．红磷和氧气在点燃条件下反应生成五氧化二磷C．每4个磷原子加5个氧分子在点燃条件下反应等于2个五氧化二磷分子D．每31份质量的红磷完全反应能生成284份质量的五氧化二磷7．（2分）agH2在bgO2中充分燃烧后，生成水的质量一定（）A．等于（a+b）g B．大于（a+b）gC．小于或等于（a+b）g D．大于或等于（a+b）g8．（2分）下列现象或事实，用相关知识加以解释，其中不正确的是（）A．A B．B C．C D．D9．（2分）下列化学方程式书写正确的是（）A．H2O2H2↑+O2↑B．CO+CuO Cu+CO2↑C．CO+O2CO2D．3Fe+2O2Fe3O410．（2分）如图探究CO2性质的实验中，结论表述不正确的是（）A．CO2能溶于水B．CO2能使紫色石蕊试液变红C．CO2能与氢氧化钠反应D．CO2密度大于空气11．（2分）小军设计了以下三组实验验证质量守恒定律：①无气体参与②有气体参加③有气体生成，如图：下列关于这组验证实验的说法错误的是（）A．①中铁钉在称量前需要进行打磨，目的是除去表面氧化膜B．②装置打开止水夹后，观察到注射器活塞往下移动C．③中烧杯反应后，烧杯内剩余物质有3种可能情况D．从微观的角度分析，这三个反应都遵循质量守恒定律是因为反应前后分子、原子都不变12．（2分）除去下列各物质中的少量杂质（括号内为杂质），所选用的试剂或方法正确的是（）A．CuO（C）：氧气流中灼烧B．CO（CO2）：灼热的氧化铜C．NaCl（CaCO3）：稀盐酸D．CO2（CO）：点燃13．（2分）碳与碳的化合物之间有如图所示转换关系。

2020-2021学年重庆一中九年级（上）第二次月考物理试卷一、选择题（每小题只有一个选项符合题意，每小题3分，共24分）1．（3分）下列数据最符合实际情况的是（）A．普通壁挂式空调正常工作的功率约为1000WB．洗澡时感觉最舒适的热水温度是70℃C．人体的安全电压为220VD．日光灯管的电流约为10A2．（3分）下列关于物态变化现象说法正确的是（）A．烧水时壶嘴冒出“白气“是液化现象，需要吸收热量B．用铁水浇铸工件是凝固现象，要放出热量C．“窗花“是水蒸气在寒冷的玻璃上凝固形成的，要放出热D．冰块液化为水，需要吸收热量3．（3分）关于温度、热量和内能，下列说法正确的是（）A．物体吸收热量，温度一定升高B．温度越高的物体含有的热量一定越多C．物体的内能增加，一定是从外界吸收了热量D．热量总是从温度高的物体传递给温度低的物体4．（3分）下列关于电学知识说法正确的是（）A．验电器的工作原理是异种电荷相互排斥B．金属导电时，电子定向移动的方向与电流方向相反C．在电压一定时，电阻与电流成反比D．电能表是测量用电器消耗电功率的仪表5．（3分）如图所示的电路中，电源电压保持不变，R1为定值电阻，闭合开关S，当滑动变阻器R2的滑片P向右移动时，下列说法中（）①电流表A的示数变小②电压表V的示数变大③电压表V与电流表A1的比值变小④滑动变阻器R2消耗的电功率变小A．只有①④正确B．只有②③正确C．只有①③正确D．只有②④正确6．（3分）智能安防已经进入百姓家里，在实体店体验房间里，出门时，在智能锁里设置外出模式相当于开关S闭合。

如果红外线传感器（相当于闭合S1）探测到人，窗户传感器（相当于闭合S2）探测到窗户的打开或烟雾传感器（相当于闭合S3）探测到烟雾，相应的开关都会闭合。

这时屋内的警报电铃会响起，同时视频监控拍摄图象给屋主发送报警信息。

报警铃和监控器的额定电压都是220V。

下列模拟安防电路符合以上描述的是（）A．B．C．D．7．（3分）如图所示，电源电压保持6V不变，R1＝10Ω。