北航卡尔曼滤波课程-捷联惯导静基座初始对准实验

惯性导航技术综合实验实验五惯性基组合导航及应用技术实验惯性/卫星组合导航系统车载实验一、实验目的①掌握捷联惯导/GPS组合导航系统的构成和基本工作原理；②掌握采用卡尔曼滤波方法进行捷联惯导/GPS组合的基本原理；③掌握捷联惯导 /GPS组合导航系统静态性能；④掌握动态情况下捷联惯导 /GPS组合导航系统的性能。

二、实验内容①复习卡尔曼滤波的基本原理（参考《卡尔曼滤波与组合导航原理》第二、五章）；②复习捷联惯导/GPS组合导航系统的基本工作原理（参考以光衢编著的《惯性导航原理》第七章）；三、实验系统组成①捷联惯导/GPS组合导航实验系统一套；②监控计算机一台。

③差分GPS接收机一套；④实验车一辆；⑤车载大理石平台；⑥车载电源系统。

四、实验内容1）实验准备①将IMU紧固在车载大理石减振平台上，确认IMU的安装基准面紧靠实验平台；②将IMU与导航计算机、导航计算机与车载电源、导航计算机与监控计算机、GPS 接收机与导航计算机、GPS 天线与GPS 接收机、GPS 接收机与GPS 电池之间的连接线正确连接；③ 打开GPS 接收机电源，确认可以接收到4颗以上卫星； ④ 打开电源，启动实验系统。

2） 捷联惯导/GPS 组合导航实验① 进入捷联惯导初始对准状态，记录IMU 的原始输出，注意5分钟内严禁移动实验车和IMU ；② 实验系统经过5分钟初始对准之后，进入导航状态； ③ 移动实验车，按设计实验路线行驶；④ 利用监控计算机中的导航软件进行导航解算，并显示导航结果。

五、 实验结果及分析(一)理论推导捷联惯导短时段（1分钟）位置误差，并用1分钟惯导实验数据验证。

1、一分钟惯导位置误差理论推导：短时段内（t<5min ），忽略地球自转0ie ω=，运动轨迹近似为平面1/0R =，此时的位置误差分析可简化为：（1） 加速度计零偏∇引起的位置误差：210.88022t x δ∇==m （2） 失准角0φ引起的误差：202 0.92182g t x φδ==m （3） 陀螺漂移ε引起的误差：330.01376g t x εδ==m 可得1min 后的位置误差值123 1.8157m x x x x δδδδ=++= 2、一分钟惯导实验数据验证结果：（1）纯惯导解算1min 的位置及位置误差图：lat0.01s 度lon0.01s度北向位移误差0.01sm 东向位移误差0.01sm（2）纯惯导解算1min 的速度及速度误差图：-100-50050Vx0.01s m /s020406080Vy0.01sm /s100020003000400050006000-0.4-0.3-0.2-0.10Vx 误差0.01s m /s100020003000400050006000-0.1-0.0500.050.1Vy 误差0.01sm /s实验结果分析：纯惯导解算短时间内精度很高，1min 的惯导解算的北向最大位移误差，东向最大位移误差，可见实验数据所得位置误差与理论推导的位置误差在同一数量级，结果不完全相同是因为理论推导时做了大量简化，而且实验时视GPS 为真实值也会带来误差；另外，可见1min 内纯惯导解算的东向速度最大误差s ，北向速度最大误差s 。

卡尔曼滤波实验报告2014 年 4 月GPS 静/动态滤波实验一、实验要求1、分别建立GPS 静态及动态卡尔曼滤波模型，编写程序对静态和动态GPS 数据进行Kalman 滤波。

2、对比滤波前后导航轨迹图。

3、画出滤波过程中估计均方差(P 阵对角线元素开根号)的变化趋势。

4、思考：① 简述动态模型与静态模型的区别与联系；② R 阵、Q 阵，P0阵的选取对滤波精度及收敛速度有何影响，取值时应注意什么；③ 本滤波问题是否可以用最小二乘方法解决，如果可以，请阐述最小二乘方法与Kalman 滤波方法的优劣对比。

二、实验原理2.1 GPS 静态滤波选取系统的状态变量为[ ]TL h λ=X ,其中L 为纬度(deg),λ为经度(deg)，h 为高度(m)。

设()w t 为零均值高斯白噪声，则系统的状态方程为：310()w t ⨯=+X(1)所以离散化的状态模型为：,111k k k k k W ---=+X X Φ(2)式中，,1k k -Φ为33⨯单位阵，k W 为系统噪声序列。

测量数据包括：纬度静态量测值、经度静态量测值和高度构成31⨯矩阵Z ，量测方程可以表示为：k k k Z HX V =+(3)式中，H 为33⨯单位阵，k V 为量测噪声序列。

系统的状态模型是十分准确的，所以系统模型噪声方差阵可以取得十分小，取Q 阵零矩阵。

系统测量噪声方差阵R 由测量确定，由于位置量测精度为5m ，采用克拉索夫斯基地球椭球模型，长半径e R 为6378245m ，短半径p R 为6356863m 。

所以R 阵为：2225180()005180()0cos()005p e R R L ππ⨯⎛⎫ ⎪⨯ ⎪ ⎪⨯= ⎪⨯⨯ ⎪ ⎪ ⎪⎝⎭R (4)2.2 GPS 动态滤波动态滤波基于当前统计模型，在地球坐标系下解算。

选取系统的状态变量为Tx x x y y y z z z X x v a y v a z v a εεε⎡⎤=⎣⎦,其中,,,x x x x v a ε依次为地球坐标系下x轴上的位置、速度、加速度和位置误差分量，,y z 轴同理。

3.5.3 捷联惯导系统快速初始对准方法(可能删除)（1）由系统的可观测性分析结果可知，在静基座对准过程中，两个水平失准角收敛速度较快，方位失准角收敛速度很慢，由于系统的可观测性无法提高，因此不能从方位失准角的可观测度上改进加快方位失准角的收敛速度，而直接利用两个水平失准角的快速收敛结果对方位失准角进行估计是一种加快方位角收敛速度的方法，进而提高系统的静基座对准的速度。

根据误差方程式可得捷联惯导系统静基座初始对准误差模型的方程式：2s i n E i e N N E L V g V δωδϕ∙=-+∇ 2sin N ie E E N L V g V δωδϕ∙=-++∇ sin cos sin cos E N U N ie U ie E E ie N E ie U L L L L ϕωϕωξϕϕωξϕϕωξϕ∙∙∙=-+=-+=+利用卡尔曼滤波器对准过程的状态估计，可得E ϕ、N ϕ、U ϕ的稳态误差为E N g δϕ∇=N E g δϕ∇=-cos cos tan E E E D L Lg L ξξδϕ∇=+≈ΩΩ 根据稳态误差方程可知，影响水平失准角误差的主要因素为加速度计的精度，影响方位角误差的主要因素为陀螺的精度，由于目前加速度计器件相较于陀螺发展较快，所以，在初始对准过程中，水平失准角要比方位失准角精度高。

假如用E ϕ、N ϕ的稳态估计值直接估计D ϕ，当E ϕ、N ϕ收敛时，D ϕ一定也会收敛，E ξ不可观测，cos EL ξΩ为稳态误差，由误差第三个式子可得快速初始对准时的方位角误差方程为1()D D N E Nϕϕϕ=Ω+Ω，初始对准过程首先应用卡尔曼滤波器进行系统状态变量的最优估计，由于E ϕ、N ϕ收敛较快会迅速进入稳态，将E ϕ转换到低通数字滤波器后用1()D D N E Nϕϕϕ=Ω+Ω方程对方位角D ϕ进行估计。

（2）快速对准仿真实验分析设置IMU 的相关参数为：加速度计零偏为100ug，随机游走为10ug 陀螺零偏为0.01/h ，随机游走为0.01/h ，假设经过粗对准后提供的姿态初始失准角为[1° 1° 1°]，所处地理纬度为北纬34°，仿真开始后对东向失准角进行低通滤波处理，在70s 后用快速精对准公式对方位角进行估计，此时水平失准角已经趋于稳定，仿真实验结果如下图所示，由图可知方位对准精度为30秒左右。

北航惯性导航综合实验三实验报告惯性导航技术综合实验实验三惯性导航综合实验实验3.1 初始对准实验一、实验目的结合已经采集并标定好的惯性传感器数据进行粗对准，了解实现对准的过程；通过比较不同传感器数据的对准结果，进一步认识惯性传感器性能在导航系统中的重要地位。

为在实际工程设计中针对不同应用需求下采取相应的导航系统方案提供依据。

二、实验内容利用加速度计输出计算得到系统的初始姿态，利用陀螺输出信号计算航向角。

对比利用不同的惯性传感器数据计算所得的不同结果。

三、实验系统组成MEMS IMU（或其他类型IMU）、稳压电源、数据采集系统与分析系统。

四、实验原理惯导系统在开始进行导航解算之前需要进行初始对准，水平对准的本质是将重力加速度作为对准基准，其对准精度主要取决于两个水平加速度计的精度，加速度计的零位输出将会造成水平对准误差；方位对准最常用的方位是罗经对准，其本质是以地球自转角速度作为对准基准，影响对准精度的主要因素是等效东向陀螺漂移。

(1) 其中，分别为当前时刻的俯仰角和横滚角计算值。

水平对准误差和方位对准误差如下所示：，(2) 五、实验步骤及结果1、实验步骤：采集静止状态下水平加速度计输出，按下式计算其平均值。

(3) 其中，为前n个加计输出均值；为前n-1个加计输出均值；为当前时刻加计输出值。

利用加计平均值来计算系统初始俯仰角和横滚角(4) 其中，分别为当前时刻的俯仰角和横滚角计算值。

2、实验结果与分析：2.1、用MIMS IMU的加速度计信息计算（1）俯仰角和横滚角图：（2）失准角：2.2、实验结果分析以上计算是基于MIMS IMU静止时data2进行的初始对准，与data2给定的初始姿态角相差不大。

六、源程序clear clc g = 9.__14; a=load(＇E:＼郭凤玲＼chushiduizhun＼data2.txt＇); ax=a(:,4)＇; ay=a(:,5)＇; az=a(:,6)＇; %初始值ax0(1)=ax(1)/1000*g; %%%%转化单位，由mg转化为m/s^2 ay0(1)=ay(1)/1000*g; az0(1)=az(1)/1000*g; theta(1)=asin(ay(1)/az(1)); gama(1)=-asin(ax(1)/az(1)); for i=2:__ ax0(i)=ax0(i-1)+(ax(i)-ax0(i-1))/i; ay0(i)=ay0(i-1)+(ay(i)-ay0(i-1))/i; az0(i)=az0(i-1)+(az(i)-az0(i-1))/i; theta(i)=asin(ay0(i)/az0(i));gama(i)=-asin(ax0(i)/az0(i)); end detfaix=mean(ay0)/g; detfaiy=mean(-ax0)/g; t=1:__; plot(t,theta,＇r＇,t,gama,＇b＇) title(＇俯仰角和横滚角＇);ylabel(＇弧度（rad）＇); legend(＇俯仰角＇,＇横滚角＇) 实验3.2 惯性导航静态实验一、实验目的1、掌握捷联惯导系统基本工作原理2、掌握捷联惯导系统捷联解算方法3、了解捷联惯导系统误差传递规律和方程二、实验原理捷联惯性导航系统（SINS）的导航解算流程如图1所示。

惯性导航技术综合实验实验五惯性基组合导航及应用技术实验惯性/卫星组合导航系统车载实验一、实验目的①掌握捷联惯导/GPS组合导航系统的构成和基本工作原理；②掌握采用卡尔曼滤波方法进行捷联惯导/GPS组合的基本原理；③掌握捷联惯导/GPS组合导航系统静态性能；④掌握动态情况下捷联惯导/GPS组合导航系统的性能。

二、实验内容①复习卡尔曼滤波的基本原理（参考《卡尔曼滤波与组合导航原理》第二、五章）；②复习捷联惯导/GPS组合导航系统的基本工作原理（参考以光衢编著的《惯性导航原理》第七章）；三、实验系统组成①捷联惯导/GPS组合导航实验系统一套；②监控计算机一台。

③差分GPS接收机一套；④实验车一辆；⑤车载大理石平台；⑥车载电源系统。

四、实验内容1）实验准备①将IMU紧固在车载大理石减振平台上，确认IMU的安装基准面紧靠实验平台；②将IMU与导航计算机、导航计算机与车载电源、导航计算机与监控计算机、GPS接收机与导航计算机、GPS天线与GPS接收机、GPS接收机与GPS电池之间的连接线正确连接；③ 打开GPS 接收机电源，确认可以接收到4颗以上卫星； ④ 打开电源，启动实验系统。

2） 捷联惯导/GPS 组合导航实验① 进入捷联惯导初始对准状态，记录IMU 的原始输出，注意5分钟内严禁移动实验车和IMU ；② 实验系统经过5分钟初始对准之后，进入导航状态； ③ 移动实验车，按设计实验路线行驶；④ 利用监控计算机中的导航软件进行导航解算，并显示导航结果。

五、 实验结果及分析(一) 理论推导捷联惯导短时段（1分钟）位置误差，并用1分钟惯导实验数据验证。

1、一分钟惯导位置误差理论推导：短时段内（t<5min ），忽略地球自转0ie ω=，运动轨迹近似为平面1/0R =，此时的位置误差分析可简化为：（1） 加速度计零偏∇引起的位置误差：210.88022t x δ∇==m （2） 失准角0φ引起的误差：202 0.92182g t x φδ==m （3） 陀螺漂移ε引起的误差：330.01376g t x εδ==m 可得1min 后的位置误差值123 1.8157m x x x x δδδδ=++= 2、一分钟惯导实验数据验证结果：（1）纯惯导解算1min 的位置及位置误差图：lat0.01s 度lon0.01s度北向位移误差0.01sm 东向位移误差0.01sm（2）纯惯导解算1min 的速度及速度误差图：-100-50050Vx0.01s m /s020406080Vy0.01sm /s100020003000400050006000-0.4-0.3-0.2-0.10Vx 误差0.01s m /s100020003000400050006000-0.1-0.0500.050.1Vy 误差0.01sm /s实验结果分析：纯惯导解算短时间内精度很高，1min 的惯导解算的北向最大位移误差-2.668m ，东向最大位移误差-8.231m ，可见实验数据所得位置误差与理论推导的位置误差在同一数量级，结果不完全相同是因为理论推导时做了大量简化，而且实验时视GPS 为真实值也会带来误差；另外，可见1min 内纯惯导解算的东向速度最大误差-0.2754m/s ，北向速度最大误差-0.08027m/s 。

惯性导航技术综合实验实验五惯性基组合导航及应用技术实验惯性/卫星组合导航系统车载实验一、实验目的①掌握捷联惯导/GPS组合导航系统的构成和基本工作原理：②掌握采用卡尔曼波波方法进行捷联惯导/GPS组合的基本原理：③掌握捷联惯导/GPS组合导航系统静态性能：④掌握动态情况下捷联惯导/GPS组合导航系统的性能。

二、实验内容①复习卡尔曼滤波的基本原理（参考《卡尔曼滤波与组合导航原理》第二、五章）；②复习捷联惯导/GPS组合导航系统的基本工作原理（参考以光衢编著的《惯性导航原理》第七章）；三、实验系统组成①捷联惯导/GPS组合导航实验系统一套：②监控计算机一台。

③差分GPS接收机一套：④实验车一辆：⑤车载大理石平台：⑥车载电源系统。

四、实验内容D实验准备①将IMU紧固在车载大理石减振平台上，确认IMU的安装基准面紧靠实验平台；②将IMU与导航计算机、导航计算机与车载电源、导航计算机与监控计算机、GPS接收机与导航计算机、GPS天线与GPS接收机、GPS接收机与GPS电池之间的连接线正确连接；③打开GPS接收机电源，确认可以接收到4颗以上卫星；④打开电源，启动实验系统。

2）捷联惯导/GPS组合导航实验①进入捷联惯导初始对准状态，记录IMU的原始输出，注意5分钟内严禁移动实验车和IMU；②实验系统经过5分钟初始对准之后，进入导航状态；③移动实验车，按设计实验路线行驶；④利用监控计算机中的导航软件进行导航解算，并显示导航结果。

五、实验结果及分析（一）理论推导捷联惯导短时段（1分钟）位置误差，并用1分钟惯导实验数据验证。

1、一分钟惯导位置误差理论推导：短时段内（t<5min）,忽略地球自转绍。

=0,运动轨迹近似为平面1/R = O,此时的位置误差分析可简化为：Vr2（1）加速度计零偏V引起的位置误差：Jx,= —= 0.8802 m2（2）失准角我引起的误差：3X2=^-= 0.9218m（3）陀螺漂移£引起的误差：= 0.0137 m6可得1min后的位置误差值5x =+ J.r2 + 5x. = 1.8157m2、一分钟惯导实验数据验证结果：（1）纯惯导解算1min的位置及位置误差图：（2）纯惯导解算1min的速度及速度误差图：vy 8060| 40200 1000 2000 3000 4000 5000 60000.01s实验结果分析：纯惯导解算短时间内精度很高，1min的惯导解算的北向最大位移误差-2.668m,东向最大位移误差-8.231m,可见实验数据所得位置误差与理论推导的位置误差在同一数量级，结果不完全相同是因为理论推导时做了大量简化，而且实验时视GPS为真实值也会带来误差；另外，可见1min内纯惯导解算的东向速度最大误差-0.2754m/s，北向速度最大误差-0.08027m/So(-)选取IMU前5分钟数据进行对准实验。

卡尔曼滤波实验报告捷联惯导静基座初始对准实验一、实验目的①掌握捷联惯导的构成和基本工作原理；②掌握捷联惯导静基座对准的基本工作原理；③了解捷联惯导静基座对准时的每个系统状态的可观测性；④了解双位置对准时系统状态的可观测性的变化。

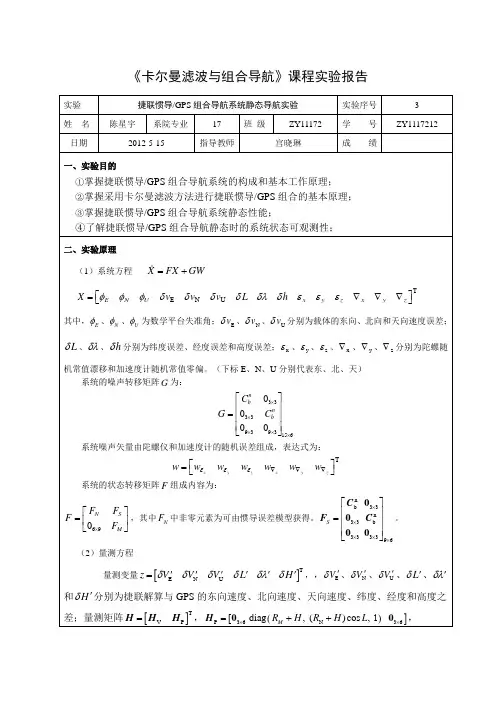
二、实验原理选取状态变量为：X = [6匕5匕+E+N乎U v x \ e X£y£J，其中导航坐标系选为东北天坐标系，5V 为东向速度误差，5V 为北向速度误差，乎 为东 向姿态误差角，*, 为北向姿态误差角,乎〃为天向姿态误差角,V ,为北向加速度偏置，£x 为东向陀螺漂移，8,为北向陀螺漂移，£Z为天向陀螺漂移。

则 系统的状态模型为：X = AX + W(1)其中0 2。

sin L0 - g 0 C C 00 0 1112-2。

sin L0 g 0 0 C C 0 021 22 00 0。

sin L -。

cos L 0 0 C C C 1112 13 0 0 -。

sin L 0 00 0 C C C 21 22 230 0 。

cos L 0 0 0 0 C C C A =31 32330 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0_0 _W = [W W W W W 0 0 0 0 0]T ，W ……W 为零均值高斯55* + 45乎白噪声，分别为加速度计误差和陀螺漂移的噪声成分，。

为地球自转角速度，C 为姿态矩阵C 中的元素，L 为当地纬度。

量测量选取两个水平速度误差：Z = [5V 5V ]叽 则量测方程为: E N即 Z = HX +n斯白噪声。

要利用基本卡尔曼滤波方程进行状态估计，需要将状态方程和量测方程进行离散化。

系统转移矩阵为:工 T 2 , T 3 ,① =I + TA + — A 2 + — A 3 + ♦…k / k -1k -1 2! k -13! k -1V x 为东向加速度偏置，5 V ]E5 V0 0 1000 0000 00(2)其中，H 为量测矩阵，“=%丑N 》为量测方程的随机噪声状态矢量，为零均值高« Tn/ =工——A k -1其中，T为采样间隔。