课时跟踪检测(七十二) 相似三角形的判定及有关性质
- 格式:doc
- 大小:263.50 KB
- 文档页数:9
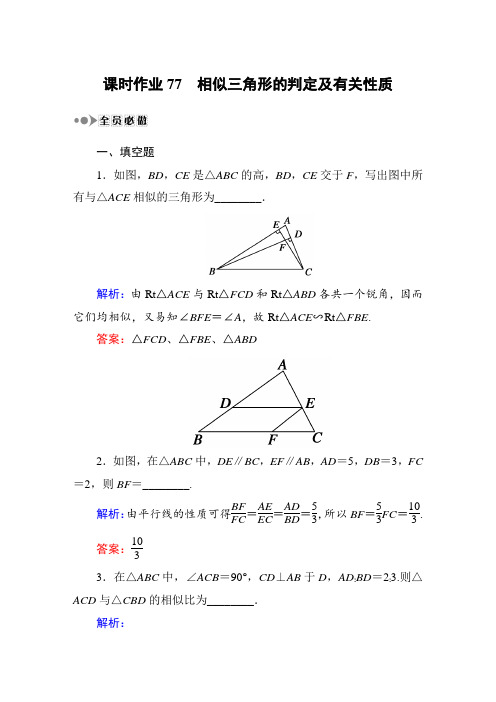
课时作业77 相似三角形的判定及有关性质一、填空题1.如图,BD ,CE 是△ABC 的高,BD ,CE 交于F ,写出图中所有与△ACE 相似的三角形为________.解析:由Rt △ACE 与Rt △FCD 和Rt △ABD 各共一个锐角,因而它们均相似,又易知∠BFE =∠A ,故Rt △ACE ∽Rt △FBE .答案:△FCD 、△FBE 、△ABD2.如图,在△ABC 中,DE ∥BC ,EF ∥AB ,AD =5,DB =3,FC =2,则BF =________.解析:由平行线的性质可得BF FC =AE EC =AD BD =53,所以BF =53FC =103. 答案:1033.在△ABC 中,∠ACB =90°,CD ⊥AB 于D ,AD BD =23.则△ACD 与△CBD 的相似比为________.解析:如图所示,在Rt △ACB 中,CD ⊥AB ,由射影定理得:CD 2=AD ·BD , 又∵AD :BD =2:3,令AD =2x , BD =3x (x >0),∴CD 2=6x 2,∴CD =6x .又∵∠ADC =∠BDC =90°,∠A =∠BCD . ∴△ACD ∽△CBD .易知△ACD 与△CBD 的相似比为AD CD =2x 6x =63.即相似比为6:3. 答案:6:3 4.如图,已知AB ∥EF ∥CD ,若AB =4,CD =12,则EF =__________. 解析:∵AB ∥CD ∥EF , ∴AB EF =BC CF ,BC BF =CD EF ,∴4EF =BC BC -BF ,BC BF =12EF ,∴4(BC -BF )=12BF , ∴BC =4BF , ∴BC BF =4=12EF , ∴EF =3. 答案:35.如图,在梯形ABCD 中,AD ∥BC ,BD 与AC 相交于O ,过O 的直线分别交AB 、CD 于E 、F ,且EF ∥BC ,若AD =12,BC =20,则EF =________.解析:∵EF ∥AD ∥BC ,∴△OAD ∽△OCB , OA :OC =AD :BC =12:20,△OAE ∽△CAB ,OE :BC =OA :CA =12:32, ∴EF =2×1232×20=15. 答案:156.如图,在圆O 中,直径AB 与弦CD 垂直,垂足为E ,EF ⊥DB ,垂足为F ,若AB =6,AE =1,则DF ·DB =________.解析:连接AD ,由射影定理可知ED 2=AE ·EB =1×5=5,又易知△EBD 与△FED 相似,得DF ·DB =ED 2=5.答案:57.如图,等边三角形DEF 内接于△ABC ,且DE ∥BC ,已知AH ⊥BC 于点H ,BC =4,AH =3,则△DEF 的边长为________.解析:设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DE BC =AM AH =AH -MH AH ,∴x 4=3-32x3=2-x 2,解得x =43. 答案:43 8.如图,在梯形ABCD 中,AB ∥CD ,且AB =2CD ,E 、F 分别是AB 、BC 的中点,EF 与BD 相交于点M .若DB =9,则BM =________.解析:∵E 是AB 的中点, ∴AB =2EB .∵AB =2CD ,∴CD =EB .又AB ∥CD ,∴四边形CBED 是平行四边形.∴CB ∥DE ,∴⎩⎪⎨⎪⎧∠DEM =∠BFM ,∠EDM =∠FBM ,∴△EDM ∽△FBM .∴DM BM =DEBF . ∵F 是BC 的中点,∴DE =2BF . ∴DM =2BM . ∴BM =13DB =3. 答案:3 9.如图,圆O 的半径为1,A ,B ,C 是圆周上的三点,满足∠ABC=30°,过点A做圆O的切线与OC的延长线交于点P,则P A=________.解析:连接AO,AC,因为∠ABC=30°,所以∠CAP=30°,∠AOC=60°,△AOC为等边三角形,则∠ACP=120°,∴∠APC=30°,∴△ACP为等腰三角形,且AC=CP=1,∴P A=2×1×sin60°= 3.答案: 3二、解答题10.已知△ABC中,BF⊥AC于点F,CE⊥AB于点E,BF和CE 相交于点P,求证:(1)△BPE∽△CPF;(2)△EFP∽△BCP.证明:(1)∵BF⊥AC于点F,CE⊥AB于点E,∴∠BFC=∠CEB.又∵∠CPF=∠BPE,∴△CPF∽△BPE.(2)由(1)得△CPF∽△BPE,∴EPFP=BPCP.又∵∠EPF=∠BPC,∴△EFP∽△BCP.11.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB于E,求证:(1)AB ·AC =BC ·AD ; (2)AD 3=BC ·CF ·BE .证明:(1)在Rt △ABC 中,AD ⊥BC , ∴S △ABC =12AB ·AC =12BC ·AD . ∴AB ·AC =BC ·AD .(2)Rt △ADB 中,DE ⊥AB ,由射影定理可得 BD 2=BE ·AB ,同理CD 2=CF ·AC , ∴BD 2·CD 2=BE ·AB ·CF ·AC .又在Rt △BAC 中,AD ⊥BC ,∴AD 2=BD ·DC , ∴AD 4=BE ·AB ·CF ·AC ,又AB ·AC =BC ·AD .即AD 3=BC ·CF ·BE .1.如图,在△ABC 中,D 为BC 边的中点,E 为AD 上的一点,延长BE 交AC 于点F .若AE AD =14,求AFAC 的值.解:如图,过点A 作AG ∥BC , 交BF 的延长线于点G . ∵AE AD =14,∴AE ED =13. 又∵△AGE ∽△DBE , ∴AG BD =AE ED =13.∵D 为BC 中点,BC =2BD , ∴AG BC =16.∵△AGF ∽△CBF ,∴AF FC =AG BC =16,∴AF AC =17.2.如图,AB 为⊙O 的直径,直线CD 与⊙O 相切于E ,AD 垂直CD 于D ,BC 垂直CD 于C ,EF 垂直AB 于F ,连接AE ,BE .求证:(1)∠FEB =∠CEB ; (2)EF 2=AD ·BC .证明:(1)由直线CD与⊙O相切,得∠CEB=∠EAB.由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=π2;又EF⊥AB,得∠FEB+∠EBF=π2.从而∠FEB=∠EAB.故∠FEB=∠CEB.(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,得Rt△BCE≌Rt△BFE,所以BC=BF.同理可证Rt△ADE≌Rt△AFE,得AD=AF.又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,所以EF2=AD·BC.。

相似三角形的判定与性质相似三角形是初中数学中重要的概念之一,它们具有相同的形状但是大小不同。
在初中数学学习中,我们需要学会如何判定两个三角形是否相似,以及相似三角形具有哪些性质。
本文将对相似三角形的判定方法与性质进行详细介绍。
一、相似三角形的判定要判定两个三角形是否相似,有三种常用的方法:AA判定法、SAS判定法和SSS判定法。
1. AA判定法:如果两个三角形的两个角分别相等,则这两个三角形相似。
具体而言,如果两个三角形中的两个角分别相等,即对应角相等,那么这两个三角形就是相似的。
2. SAS判定法:如果两个三角形中,一个角相等,并且两个边的比值相等,那么这两个三角形相似。
具体而言,如果两个三角形中,某个角相等,并且两边之比也相等,那么这两个三角形就是相似的。
3. SSS判定法:如果两个三角形的三边之比相等,则这两个三角形相似。
具体而言,如果两个三角形的对应边的比值相等,那么这两个三角形就是相似的。
以上三种判定法是判断相似三角形最常用的方法,通过使用其中的任意一种判定法,我们可以准确地判断两个三角形是否相似。
二、相似三角形的性质相似三角形有一些重要的性质,包括比例关系、角度关系和面积关系。
1. 边的比例关系:相似三角形的对应边之比相等。
如果两个三角形相似,那么它们的对应边的比值是相等的。
例如,若两个相似三角形的两个边的比值分别为a:b,c:d,那么它们的第三边的比值也是相等的,即比值为a/c=b/d。
2. 角度关系:相似三角形的对应角相等。
如果两个三角形相似,那么它们的对应角是相等的。
具体而言,如果一个角分别相等,则这两个三角形的对应角也相等。
3. 面积关系:相似三角形的面积比等于边长比的平方。
如果两个三角形相似,那么它们的面积比等于边长比的平方。
具体而言,若两个相似三角形的对应边的长度比为a:b,那么它们的面积比为a^2:b^2。
相似三角形的性质在数学中应用广泛。
例如,在测量中,我们可以利用相似三角形的边长比关系求取难以测量的长度。

相似三角形的判定与性质相似三角形是数学几何中的一个重要概念,它在解决实际问题和证明定理时起着关键作用。
相似三角形的判定是基于其边比和角相等的条件,而相似三角形的性质则涉及到各个角的对应关系和边的比例关系。
本文将详细介绍相似三角形的判定方法和性质。
一、相似三角形的判定方法在确定两个三角形是否相似时,常用的判定方法有以下几种:1. AA判定法(角-角判定法):如果两个三角形的两个角分别相等,那么它们是相似三角形。
具体来说,如果两个三角形的一个角相等,且对应边的夹角也相等,那么它们是相似的。
2. SSS判定法(边-边-边判定法):如果两个三角形的三边分别成比例,那么它们是相似三角形。
具体来说,如果两个三角形的对应边的长度之比相等,那么它们是相似的。
3. SAS判定法(边-角-边判定法):如果两个三角形的一个角相等,且两个角的对边成比例,那么它们是相似三角形。
这些判定方法是相似三角形性质的基础,通过判定可以确定两个三角形是否相似。
二、相似三角形的性质1. 两个相似三角形的对应角相等,即相应的角相等。
这是相似三角形定义的直接性质,对应角相等是相似三角形的必要条件。
2. 两个相似三角形的对应边成比例。
如果两个三角形相似,则它们的对应边的长度之比等于任意两个对应边的长度之比。
具体来说,设两个相似三角形的对应边分别为AB和A'B'、AC和A'C'、BC和B'C',则有AB/A'B' = AC/A'C' = BC/B'C'。
3. 两个相似三角形的高线成比例。
如果两个相似三角形的高线分别为h和h',那么h/h'等于相应的边的长度之比。
4. 两个相似三角形的面积之比等于对应边长度之比的平方。
设两个相似三角形的面积分别为S和S',对应边的长度之比为k,则有S/S' = k^2。
5. 两个相似三角形的周长之比等于对应边长度之比。

相似三角形的性质和判定知识点相似三角形是初中数学中的重要概念,它在几何学中具有广泛的应用。
相似三角形的性质和判定是学习和解题的基础,本文将详细介绍相似三角形的性质和判定的知识点。
一、相似三角形的定义相似三角形是指具有相同形状但不同大小的三角形。
两个三角形相似的条件是它们对应角相等,即对应边的比例相等。
二、相似三角形的性质相似三角形有一些重要的性质,如下:1. 对应角相等性质:如果两个三角形相似,它们的对应角相等。
2. 对应边成比例性质:如果两个三角形相似,它们的对应边成比例,即对于第一个三角形的一条边与第二个三角形的相应边的比等于第一个三角形的另一条边与第二个三角形的相应边的比。
3. 半角性质:如果两个三角形相似,它们的角的一半也相等。
4. 高线成比例性质:如果两个三角形相似,它们的高线与底边之比等于相应边之比。
5. 中线成比例性质:如果两个三角形相似,它们的中线与底边之比等于相应边之比。
这些性质对于判断和解决相似三角形的问题非常有用。
三、相似三角形的判定判定两个三角形是否相似有几个常用的方法,如下:1. AAA相似判定:如果两个三角形的对应角相等,则它们相似。
2. AA相似判定:如果两个三角形的一个角相等,并且两个角分别对应两个角相等,则它们相似。
3. SSS相似判定:如果两个三角形的对应边成比例,则它们相似。
4. SAS相似判定:如果两个三角形的一个角相等,并且两个角的相邻边的比相等,则它们相似。
这些判定方法能够帮助我们快速确定两个三角形是否相似,从而解决相关问题。
四、相似三角形的实际应用相似三角形的概念和性质在几何学中有广泛的应用。
下面介绍一些实际应用的例子:1. 相似三角形的测量:通过测量一个三角形的边长和角度,可以利用相似三角形的性质计算出其他三角形的边长和角度。
2. 地图比例尺:地图上的比例尺是通过相似三角形的性质确定的。
通过观察地图上的两个相似三角形,可以计算出地图上的实际距离。
3. 光学测距:在实际测量中,通过利用相似三角形的性质可以测量较远距离的物体高度、距离等。

相似三角形的性质及判定方法相似三角形是指具有相同形状但可能不同大小的两个或多个三角形。
在几何学中,相似三角形具有一些特定的性质和判定方法。
本文将探讨相似三角形的性质以及如何判定两个三角形是否相似。
一、相似三角形的性质1. 对应角相等性质:如果两个三角形的对应角相等,那么它们是相似的。
具体而言,如果两个三角形的对应角分别相等,则它们是相似的。
记为AA相似性质。
2. 对应边的比例性质:如果两个三角形的两对对应边的比例相等,那么它们是相似的。
具体而言,如果两个三角形的对应边所对应的长度比例相等,则它们是相似的。
记为SSS相似性质。
3. 角和对边的比例性质:如果两个三角形的对应角相等且对应边的长度比例相等,那么它们是相似的。
具体而言,如果两个三角形的对应角相等且对应边的长度比例相等,则它们是相似的。
记为SAS相似性质。
二、相似三角形的判定方法1. AA判定法:如果两个三角形的两个角分别相等,则它们一定是相似的。
即,如果两个三角形的两个角分别相等,则它们的第三个角也必然相等,从而满足AA相似性质。
2. SSS判定法:如果两个三角形的三对对应边的长度比例相等,则它们一定是相似的。
即,如果两个三角形的三对对应边的长度比例相等,则它们满足SSS相似性质。
3. SAS判定法:如果两个三角形的一个对应角相等,且对应边的长度比例相等,则它们一定是相似的。
即,如果两个三角形的一个对应角相等,且对应边的长度比例相等,则它们满足SAS相似性质。
三、实例分析为了更好地理解相似三角形的判定方法,我们来看一个实例。
已知三角形ABC和三角形DEF,已知∠A=∠D,∠B=∠E,且AB/DE = BC/EF = CA/FD,我们需要判定这两个三角形是否相似。
根据给定条件可知,∠A=∠D,∠B=∠E,且BC/EF = CA/FD。
根据SAS判定法,如果对应角相等且对应边的长度比例相等,则两个三角形相似。
由此得出结论,三角形ABC和三角形DEF是相似的。

相似三角形的判定与性质一、知识回顾1、相似三角形的判定:(1)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(2)平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似。
(3)如果两个三角形的两组对应边的比相等,且相应的夹角相等,那么这两个三角形相似(4)如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
2、相似三角形的性质(1)对应边的比相等,对应角相等。
(2)相似三角形的周长比等于相似比。
(3)相似三角形的面积比等于相似比的平方。
(4)相似三角形的对应边上的高、中线、角平分线的比等于相似比。
二、典型例题例 1:如图,已知直线 AB: y=4/3 x+b 交 x 轴于点 A( -3 , 0),交 y 轴于点 B,过点 B 作BC⊥AB 交 x 轴于点 C.(1)试证明:△ ABC∽△ AOB;( 2)求△ ABC 的周长.例 2:如图,一次函数y=kx+b 的图象经过点A( -1 ,0)和点( 1,4)交 y 轴于点 B.( 1)求一次函数解析式和 B 点坐标.( 2)过 B 点的另一直线 1 与直线 AB垂直,且交X轴正半轴于点P,求点 P 的坐标.(3)点 M( 0,a)为 y 轴正半轴上的动点,点N( b,O)为 X 轴正半轴上的动点,当直线MN⊥直线 AB时,求 a: b 的值.例 3:( 2000·陕西)如图,在矩形ABCD 中, EF 是 BD 的垂直平分线,已知 BD=20, EF=15,求矩形 ABCD 的周长.例 4:( 2010·攀枝花)如图所示,在△ ABC 中, BC > AC ,点 D 在 BC 上,且 DC=AC ,∠ ACB 的平分线 CF 交 AD 于点 F .点 E 是 AB 的中点,连接 EF .( 1)求证: EF ∥BC ;( 2)若△ ABD 的面积是 6,求四边形 BDFE 的面积.例题(1) 两个相似三角形的面积比为 s 1 : s 2 ,与它们对应高之比h 1 : h 2 之间的关系为 _______(2) 如图,已知 D E ∥ BC , CD 和 BE 相交于 O ,若 SABC:SCOB9 :16 ,则 AD:DB=_________AABADD ’DEODEEFFGA A ’CC ’OCB B ’BCDBC(2)题图(3) 题图(4) 题图(5) 题图(3)如图,已知 AB ∥CD,BO:OC=1:4, 点 E、 F 分别是 OC, OD的中点,则 EF:AB 的值为(4) 如图,已知DE∥FG∥ BC,且 AD:FD:FB=1:2:3, 则S ABC: S四边形DFGE: S四边形FBCG()A.1:9:36B.1:4:9C.1:8:27D.1:8:36(5)如图,把正方形 ABCD 沿着对角线 AC 的方向移动到正方形 A’B ’C’D ’的位置,它们的重叠部分的面积是原正方形面积的一半,若AC= 2 ,则正方形移动的距离 AA ’是(6) 梯形 ABCD中, AD∥BC,( AD<BC), AC、 BD交于点 O,若S OAB6S ABCD,则△AOD与△BOC的周长25之比为 __________ 。
相似三角形的性质与判定相似三角形在几何学中是一个重要的概念,它们具有一些特殊的性质和判定条件。
本文将介绍相似三角形的性质和判定方法。
一、相似三角形的性质相似三角形是指具有相同形状但可能不同大小的三角形。
相似三角形的性质有以下几个方面:1. 对应角相等:如果两个三角形的对应角相等,那么它们一定是相似的。
具体来说,如果两个三角形的三个内角两两相等,那么它们是相似的。
2. 对应边成比例:如果两个三角形的对应边成比例,那么它们一定是相似的。
具体来说,如果两个三角形的三条边各自成比例,那么它们是相似的。
3. 高度比例相等:如果两个相似三角形之间的高度比例相等,那么它们的面积比例也相等。
换句话说,如果两个三角形的高度比例相等,那么它们的面积比例也相等。
二、相似三角形的判定方法判定两个三角形是否相似有以下几种方法:1. AA判定法:如果两个三角形的两个对应角分别相等,那么它们是相似的。
这是相似三角形的基本判定法。
2. AAA判定法:如果两个三角形的三个内角两两相等,那么它们是相似的。
这是相似三角形的充要条件,也是最常用的判定法。
3. SSS判定法:如果两个三角形的三条边各自成比例,那么它们是相似的。
这是相似三角形的另一种判定法。
4. SAS判定法:如果两个三角形的两个对应边成比例,且夹角也相等,那么它们是相似的。
三、应用示例下面通过一个具体的示例来说明相似三角形的性质和判定方法。
假设有两个三角形ABC和XYZ,已知∠A = ∠X,∠B = ∠Y,且AB/XY = BC/YZ。
根据AA判定法可知,∠A = ∠X 和∠B = ∠Y,所以三角形ABC 与三角形XYZ相似。
根据对应边成比例可知,AB/XY = BC/YZ,所以三角形ABC与三角形XYZ相似。
因此,根据相似三角形的性质和判定方法,可以得出三角形ABC 与三角形XYZ是相似的。
结论:相似三角形具有相同形状但可能不同大小的特点。
判定两个三角形是否相似可以使用AA判定法、AAA判定法、SSS判定法和SAS判定法。
【高中数学】高中数学知识点:相似三角形的判定及有关性质相似三角形的定义:两个三角形具有相等的对应角和成比例的对应边,称为相似三角形。
相似三角形对应边的比值称为相似比(或相似系数)。
预备定理:平行于三角形一侧的直线与其他两侧(或两侧的延长线)相交,形成类似三角形的三角形判定定理1:对于任意两个三角形,如果一个三角形的两个角等于另一个三角形的两个角,则这两个三角形是相似的。
简要描述如下:两个角相等,两个三角形相似。
判定定理2:对于任意两个三角形,如果一个三角形的两侧与另一个三角形的两侧成正比,且夹角相等,则两个三角形是相似的。
简单的描述是:两边成比例,夹角相等,两个三角形相似。
判定定理3:对于任意两个三角形,如果一个三角形的三条边与另一个三角形的三条边成正比,则两个三角形是相似的。
简单的描述是:三条边成比例,两个三角形相似。
引理:如果直线与通过切割三角形两侧(或两侧的延长线)获得的相应线段成比例,则直线平行于三角形的第三条边。
直角三角形相似定理:(1)如果两个直角三角形有一个锐角对应于同一个直角三角形,那么它们是相似的;(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似。
(3)如果直角三角形的斜边和一个直角边与另一个三角形的斜边和直角边成正比,那么这两个直角三角形是相似的。
相似三角形的性质:(1)相似三角形的高度、中心线和角平分线之比等于相似比;(2)相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方;(3)相似三角形的对应角相等,对应边成比例;(4)相似三角形外接圆或内切圆的直径比、周长比等于相似比,外接圆或内切圆的面积等于相似比的平方。
相似三角形的判定方法:由于从定义出发判断两个三角形是否相似,需考虑6个元素,即三组对应角是否分别相等,三组对应边是否分别成比例,显然比较麻烦。
所以我们曾经给出过如下几个判定两个三角形相似的简单方法:(1)如果一个三角形的两侧与另一个三角形的两侧成正比,且夹角相等,则两个三角形相似;(2)如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似;(3)如果一个三角形的两个角等于另一个三角形的两个角,那么这两个三角形是相似的。
相似三角形的判定与性质相似三角形是指有着对应角度相等、对应边比例相等的两个三角形。
在解决几何问题中,判定两个三角形是否相似是非常重要的,因为相似三角形的性质可以帮助我们得到许多有用的结论。
本文将讨论相似三角形的判定方法以及其性质。
一、相似三角形的判定方法1. AA相似判定法:当两个三角形的两个对应角相等时,这两个三角形是相似的。
例如:若∠A1 = ∠A2且∠B1 = ∠B2,则△A1B1C1~△A2B2C2。
2. SSS相似判定法:当两个三角形的三边对应成比例时,这两个三角形是相似的。
例如:若A1B1/A2B2 = B1C1/B2C2 = C1A1/C2A2,则△A1B1C1~△A2B2C2。
3. SAS相似判定法:当两个三角形的两边成比例,且夹角对应相等时,这两个三角形是相似的。
例如:若A1B1/A2B2 = B1C1/B2C2且∠A1 = ∠A2,则△A1B1C1~△A2B2C2。
二、相似三角形性质1. 边比例性质:若△ABC~△A'B'C',则AB/A'B' = BC/B'C' = AC/A'C'。
也就是说,相似三角形的边长之比保持不变。
2. 高比例性质:若△ABC~△A'B'C',则AA'为两个三角形的对应边之比,BB'为对应边之比,CC'为对应边之比。
也就是说,相似三角形的高线段之比与对应边之比相等。
3. 角度性质:若△ABC~△A'B'C',则∠A = ∠A',∠B = ∠B',∠C = ∠C'。
也就是说,相似三角形的对应角度相等。
4. 面积比例性质:若△ABC~△A'B'C',则△ABC的面积与△A'B'C'的面积之比等于对应边的平方之比。
也就是说,相似三角形的面积之比等于对应边的平方之比。
相似三角形的判定与性质相似三角形是指具有相同形状但不一定相同大小的两个三角形。
在几何学中,相似三角形是一种重要的概念,它帮助我们理解和解决很多与三角形相关的问题。
本文将介绍相似三角形的判定方法以及它们的性质。
一、相似三角形的判定方法1. AAA判定法:如果两个三角形的对应角度相等,则这两个三角形相似。
即如果两个三角形的各个内角对应相等(即对应角相等),那么它们是相似的。
2. AA判定法:如果两个三角形的两个内角分别相等,并且它们的对应边成比例,则这两个三角形相似。
即如果两个三角形的两个角对应相等,并且对应边成比例,那么它们是相似的。
3. SAS判定法:如果两个三角形的一组对边成比例,并且其中一组对边夹角相等,则这两个三角形相似。
即如果两个三角形的两组对边成比例,并且夹角对应相等,那么它们是相似的。
二、相似三角形的性质1. 边长比:在相似三角形中,任意两对对应边的比值相等。
换句话说,如果两个三角形相似,那么它们的三条边的比值是相等的。
2. 高度比:在相似三角形中,任意两对对应高度的比值相等。
两个相似三角形的高度比等于对应边长比的倒数。
3. 面积比:在相似三角形中,任意两对对应面积的比值等于边长比的平方。
4. 角度比:在相似三角形中,任意一对对应角的比值相等。
换句话说,如果两个三角形相似,那么它们的三个角的比值是相等的。
5. 相似三角形的角平分线三等分:在相似三角形中,若一个角的两边与另一个角的两边成比例,则这两个角的角平分线相互平行。
6. 重心的性质:在相似三角形中,两个相似三角形的重心在同一直线上。
7. 相似三角形的垂心:在相似三角形中,两个相似三角形的垂心在同一直线上。
8. 相似三角形的外心:在相似三角形中,两个相似三角形的外心在同一直线上。
三、应用举例1. 比例问题:利用相似三角形的性质可以解决很多比例问题。
例如,已知一座塔的阴影与杆子的阴影的比值等于塔的高度与杆子高度的比值,通过相似三角形的比例关系可以求解塔的高度。
课时跟踪检测(七十二) 相似三角形的判定及有关性质1.如图所示,已知DE ∥BC ,BF ∶EF =3∶2,则AC ∶AE =________,AD ∶DB =________.2.如图,在直角梯形ABCD 中,DC ∥AB ,CB ⊥AB ,AB =AD =a ,CD =a2,点E ,F 分别为线段AB ,AD 的中点,则EF =________.3.(2012·广东高考)如图所示,直线PB 与圆O 相切于点B ,D 是弦AC 上的点,∠PBA =∠DBA .若AD =m ,AC =n ,则AB =________.4.(2012·湖北三校联考)如图,矩形ABCD 中,E 是BC 上的点,AE ⊥DE ,BE =4,EC =1,则AB 的长为________.5.在△ABC 中,∠ACB =90°,CD ⊥AB 于D ,AD ∶BD =2∶3.则△ACD 与△CBD 的相似比为________.6.(2012·西安二检)如图是某高速公路一个隧道的横截面,若它的形状是以O 为圆心的圆的一部分,路面AB =10米,净高CD =7米,则此圆的半径OA =________米.7.如图,CD 是Rt △ABC 斜边AB 上的高,将△BCD 沿CD 折叠,B 点恰好落在AB 的中点E 处,则∠A 等于________.8.将三角形纸片ABC 按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′、F 、C 为顶点的三角形与△ABC 相似,则BF =________.9.如图,在▱ABCD 中,E 是DC 边的中点,AE 交BD 于O ,S △DOE =9 cm 2,S △AOB =________.10.如图,在△ABC 中,AC =BC ,F 为底边AB 上的一点,BF AF =mn (m ,n >0),取CF 的中点D ,连接AD 并延长交BC 于点E .则BEEC=________.11.Rt △ABC 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD = 1∶9,则tan ∠BCD =________.12.如图△ABC 中,DE ∥BC ,BE 与CD 相交于点O ,AO 与DE 交于N ,AO 的延长线与BC 交于M ,若DN ∶MC =1∶4,则NE ∶BM =________,AE ∶EC =________.13.如图,在△ABC 中,AD 是BC 边上的高,DE ∥AC ,EF ⊥BC ,BE EA =32,BD =6,则FC =________.14.在△ABC 中,点D 是AC 的中点,点E 是BD 的中点,AE 交BC 于点F ,则BFFC的值为________.15.如图所示,在△ABC 中,∠ACB =90°,CD ⊥AB 于D ,AC =6,DB =5,则AD 的长为________.16.如图,在△ABC 中,DE ∥BC ,DF ∥AC ,AE ∶AC =3∶5,DE =6,则BF =________.17.(2012·茂名模拟)如图,在△ABC 中,D 是AC 的中点,E 是BD 的三等分点,AE 的延长线交BC 于F ,则S △BEFS 四边形DEFC=________.18.如图所示,在△ABC 和△DBE 中,已知AB BD =BC BE =AC DE =53.若△ABC 与△DBE 的周长差为10 cm ,则△ABC 的周长为________.19.(2012·潮州模拟)如图,AB 是⊙O 的直径,弦BD 、CA 的延长线相交于点E ,EF 垂直BA ,交BA 的延长线于点F .若∠EBA =30°,EF =3,EA =2AC ,则AF 的长为________.20.如图所示,在平行四边形ABCD 中,BC =24,E 、F 为BD 的三等分点,则BM =________,DN =________.21.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,BC =100,则EF =________.22.如图,PC 、DA 为⊙O 的切线,A 、C 为切点,AB 为⊙O 的直径,若DA =2,CD DP =12,则AB =________.答 案课时跟踪检测(七十二)1.解析:∵DE ∥BC ,∴AE AC =DE BC =EFBF .∵BF ∶EF =3∶2,∴AE AC =EF BF =23.∴AC ∶AE =3∶2.同理DE ∥BC ,得AB ∶AD =3∶2,即AB AD =32.∴AD AB =23,则AD AB -AD =23-2=2. 即ADBD=2.∴AD ∶BD =2∶1. 答案:3∶2 2∶12.解析:连接DE 和BD ,依题知,EB ∥DC ,EB =DC =a2,∴EBCD 为平行四边形,∵CB ⊥AB ,∴DE ⊥AB ,又E 是AB 的中点,故AD =DB =a , ∵E ,F 分别是AD ,AB 的中点,∴EF =12DB =12a .答案:a23.解析:因为直线PB 是圆的切线,所以∠ABP =∠C ,又因为∠ABP =∠ABD ,所以∠ABD =∠C ,又因为∠A =∠A ,所以△ABD ∽△ACB ,所以AD AB =ABAC ,所以AB =AD ·AC =mn .答案:mn4.解析:根据题意可以判断Rt △ABE ∽Rt △ECD , 则有AB BE =ECCD ,可得AB =2.答案:25.解析:如图所示,在Rt △ACB 中,CD ⊥AB ,由射影定理得:CD 2=AD ·BD ,又∵AD ∶BD =2∶3,令AD =2x , BD =3x (x >0),∴CD 2=6x 2,∴CD =6x . 又∵∠ADC =∠BDC =90°, ∴△ACD ∽△CBD .易知△ACD 与△CBD 的相似比为AD CD =2x 6x =63.即相似比为6∶3. 答案:6∶36.解析:设半径为x =AO =OC ,由题知AB =10,CD =7,在Rt △AOD 中,x 2=52+(7-x )2,解得x =377.答案:3777.解析:由题意知:BC =EC ,又∵E 为AB 的中点,∠ACB =90°, ∴EC =12AB .即BC =12AB .∴∠A =30°.答案:30°8.解析:设BF =x . 若△CFB ′∽△CBA , 则CF CB =B ′FAB ,即4-x 4=x 3. ∴12-3x =4x ,∴x =127.若△CFB ′∽△CAB ,则CF CA =B ′FAB ,即4-x 3=x3,得x =2. 即BF =2或127.答案:2或1279.解析:∵在▱ABCD 中 ,AB ∥DE , ∴△AOB ∽△EOD ,∴S △AOB S △DOE =⎝⎛⎭⎫AB DE 2.∵E 是CD 的中点, ∴DE =12CD =12AB ,则ABDE =2,∴S △AOB S △DOE=22=4, ∴S △AOB =4S △DOE =4×9=36(cm)2. 答案:36 cm 210.解析:如图,作FG ∥BC 交AE 于点G ,则FG CE =FD DC =1,BE FG =AB AF =m +n n .两式相乘即得BE EC =m +nn.答案:m +n n11.解析:由射影定理得CD 2=AD ·BD , 又BD ∶AD =1∶9,令BD =x , 则AD =9x (x >0). ∴CD 2=9x 2,∴CD =3x .Rt △CDB 中,tan ∠BCD =BD CD =x 3x =13.答案:1312.解析:∵OD OC =DN MC =14,OD OC =ON OM =14,∴NE BM =ON OM =14,即NE ∶BM =1∶4. ∵DE BC =AE AC =ON OM =14, ∴AE EC =13,即AE ∶EC =1∶3. 答案:1∶4 1∶313.解析:由DE ∥AC ,BE EA =BD OC =32,BD =6知DC =4.又EF ∥AD ,故6-FD FD =BE EA =32,解得FD =125,故FC =FD +DC =325.答案:32514.解析:过点D 作DM ∥AF 交BC 于点M .∵点E 是BD 的中点,∴在△BDM 中,BF =FM .又点D 是AC 的中点,∴ 在△CAF 中,CM =MF ,∴BF FC =BF FM +MC =12. 答案:1215.解析:在Rt △ABC 中,∠ACB =90°, CD ⊥AB , ∴AC 2=AD ·AB ,设AD =x ,则AB =x +5,又AC =6, ∴62=x (x +5),即x 2+5x -36=0, 解得x =4.∴AD =4. 答案:416.解析:DE BC =AE AC ⇒6BC =35⇒BC =10,故BF =10-6=4. 答案:417.解析:过D 点作DM ∥AF 交BC 于M , 因为DM ∥AF ,所以BF BM =BE BD =13,因为EF ∥DM ,所以S △BEF S △BDM =19,即S △BDM =9S △BEF . ∵S △BDM =12BM ·h ,S △MDC =12MC ·h ,BM MC =32,∴S △DMC S △BDM =23. 即S △DMC =23S △BDM =6S △BEF ,所以S 四边形DEFC =14S △BEF , 因此S △BEF S 四边形DEFC =114.答案:11418.解析:∵AB BD =BC BE =AC DE =53,∴△ABC ∽△DBE . ∴△ABC 的周长△BED 的周长=53.设△ABC 的周长为5k cm , 则△BED 的周长为3k cm , ∵5k -3k =10,即2k =10.∴k =5. ∴△ABC 的周长为25 cm. 答案:25 cm19.解析:在Rt △EF A 和Rt △BCA 中, ∠EAF =∠CAB ,所以△EF A ∽△BCA ,故EA AB =AFAC .设AF =a ,又EF =3,∠EBA =30°, 所以BF =3,则AB =3-a ,AE 2=AF 2+EF 2=a 2+3. 所以a ·(3-a )=12(3+a 2),解得a =1.所以AF 的长为1. 答案:120.解析:∵AD ∥BC ,∴△AED ∽△MEB ,△DFN ∽△BFM . ∴BM AD =BE ED =12,DN BM =DF FB =12. ∴BM =12AD =12,DN =12BM =6.答案:12 621.解析:∵AB ∥EF ∥CD ,∴EF AB =CF BC ,EF CD =BFBC .∴EF AB +EF CD =CF +BF BC =1, 即EF 20+EF 80=1. ∴EF =16. 答案:1622.解析:由DC =DA =2,CD DP =12,得DP =4. 设AB =2x ,则由Rt △OPC ∽Rt △DP A , 得x 6=223=33, 所以AB =2x =4 3. 答案:4 3。