6第六章 将军饮马

专题06.将军饮马模型将军饮马模型在考试中，无论是解答题，还是选择、填空题，都是学生感觉有困难的地方，也恰是学生能力区分度最重要的地方，主要考查转化与化归等的数学思想。

在各类考试中都以中高档题为主。

在解决几何最值问题主要依据是：①两点之间，线段最短；②垂线段最短，涉及的基本方法还有：利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等。

希望通过本专题的讲解让大家对这类问题有比较清晰的认识。

将军饮马模型在上学期（北师大版七年级下册）已经涉及，但是由于缺乏计算工具（勾股定理），所以只能是作出相关图形，很难进行相关最值的计算。

模型1、将军饮马--两定一动求线段和的最小值【模型探究】A，B为定点，m为定直线，P为直线m上的一个动点，求AP+BP的最小。

（1）如图1，点A、B在直线m两侧：辅助线：连接AB交直线m于点P，则AP+BP的最小值为AB.（2）如图2，点A、B在直线同侧：辅助线：过点A作关于定直线m的对称点A’，连接A’B交直线m于点P，则AP+BP的最小值为A’B.图1图2例1．（2022·江苏·八年级专题练习）要在街道旁修建一个奶站，向居民区A、B提供牛奶，小聪根据实际情况，以街道旁为x轴，测得A点的坐标为(0，3)，B点的坐标为(6，5)，则从A、B两点到奶站距离之和的最小值是____．【答案】10【分析】作A点关于x轴的对称点A'，连接A'B与x轴交于点P，连接AP，则A'B即为所求．【详解】解：作A点关于x轴的对称点A'，连接A'B与x轴交于点P，连接AP，∵AP ＝A 'P ，∴AP +BP ∵A （0，3），∴A '（0∴P 点到A 、B 的距离最小值为【点睛】本题考查轴对称求最短距离，熟练掌握轴对称求最短距离的方法，会根据两点坐标求两点间距离例2．（2023·河南南阳·八年级阶段练习）如图，等边ABC ∆的边长为4，点E 是AC 边的中点，点P 是ABC ∆的中线AD 上的动点，则EP CP +的最小值是_____．∵△ABC 是等边三角形，AD 是∴AD 是BC 的垂直平分线，∴点∵△ABC 是等边三角形，E 是例4．（2022·湖北江夏初二月考）在平面直角坐标系中，Rt △OAB 的顶点A 在x 轴上，点A 的坐标为（4，0），∠AOB =30°，点E 的坐标为（1，0），点P 为斜边OB 上的一个动点，则PA+PE 的最小值为_____．【分析】作A 关于OB 的对称点D ，连接ED 交OB 于P ，连接AP ，过D 作DN ⊥OA 于N ，则此时PA+PC 的值最小，求出AM 和AD ，再求出DN 、EN ，根据勾股定理求出ED ，即可得出答案．【解析】作A 关于OB 的对称点D ，连接ED 交OB 于P ，连接AP ，过D 作DN ⊥OA 于N ，则此时PA+PC 的值最小，∵DP =PA ，∴PA+PE =PD+PE =ED ，∵点A 的坐标为（4，0），∠AOB =30°，∴OA =4，∴AM =12OA =2，∴AD =2×2=4，∵∠AMB =90°，∠B =60°，∴∠BAM =30°，∵∠DNO =∠OAB =90°，∴DN ∥AB ，∴∠NDA =∠BAM =30°，∴AN =12AD =2，由勾股定理得：DN =，∵E （1，0），∴EN =4﹣1﹣2=1，在Rt △DNE 中，由勾股定理得：DE =，即PA+PC 【点睛】本题考查了轴对称确定最短路线问题，坐标与图形性质，含30度角的直角三角形的性质，勾股定理的应用，熟练掌握最短路径的确定方法找出点P 的位置以及表示PA+PE 的最小值的线段是解题的关键．例4.（2023·广东·八年级期中）如图，在△ABC 中，∠C ＝90°，CB ＝CA ＝4，∠A 的平分线交BC 于点D ，若点P 、Q 分别是AC 和AD 上的动点，则CQ +PQ 的最小值是．【解答】解：如图，作点P 关于直线AD 的对称点P ′，连接CP ′交AD 于点Q ，则CQ +PQ ＝CQ +P ′Q ＝CP ′．∵根据对称的性质知△APQ ≌△AP ′Q ，∴∠PAQ ＝∠P ′AQ ．又∵AD 是∠A 的平分线，点P 在AC 边上，点Q 在直线AD 上，∴∠PAQ ＝∠BAQ ，∴∠P ′AQ ＝∠BAQ ，∴点P ′在边AB 上．∵当CP ′⊥AB 时，线段CP ′最短．∵在△ABC 中，∠C ＝90°，CB ＝CA ＝4，∴AB＝4，且当点P ′是斜边AB 的中点时，CP ′⊥AB ，此时CP ′＝AB ＝2，即CQ +PQ 的最小值是2．故填：2．例5．（2023·江阴市八年级月考）某班级在探究“将军饮马问题”时抽象出数学模型：直线l 同旁有两个定点A 、B ，在直线l 上存在点P ，使得PA PB +的值最小．解法：如图1，作点A 关于直线l 的对称点A '，连接A B '，则A B '与直线l 的交点即为P ，且PA PB +的最小值为A B '．请利用上述模型解决下列问题：（1）几何应用：如图2，ABC ∆中，90C ∠=︒，2AC BC ==，E 是AB 的中点，P 是BC 边上的一动点，则PA PE +的最小值为；（2）几何拓展：如图3，ABC ∆中，2AC =，30A ∠=︒，若在AB 、AC 上各取一点M 、N 使CM MN +的值最小，画出图形，求最小值并简要说明理由．【答案】（1；（2【分析】（1）作点A 关于BC 的对称点A′，连接A′E 交BC 于P ，此时PA+PE 的值最小．连接BA′，先根据勾股定理求出BA′的长，再判断出∠A′BA=90°，根据勾股定理即可得出结论；（2）作点C 关于直线AB 的对称点C′，作C′N ⊥AC 于N 交AB 于M ，连接AC′，根据等边三角形的性质解答．【详解】解：（1）如图2所示，作点A 关于BC 的对称点A′，连接A′E 交BC 于P ，此时PA+PE 的值最小．连接BA′．由勾股定理得，，∵E 是AB 的中点，∴BE=12，∵90C ∠=︒，2AC BC ==，∴∠A′BC=∠ABC=45°，∴∠A′BA=90°，∴PA+PE 的最小值=A′E=；（2）如图3，作点C 关于直线AB 的对称点C′，作C′N ⊥AC 于N 交AB 于M ，连接AC′，则C′A=CA=2，∠C′AB=∠CAB=30°，∴△C′AC 为等边三角形，∴∠AC′N=30°，∴AN=12C′A=1，∴CM+MN 的最小值为．【点睛】本题考查的是轴对称--最短路线问题、勾股定理、等边三角形的判定和性质、含30°角的直角三角形的性质、垂线段最短，解这类问题的关键是将所给问题抽象或转化为数学模型，把两条线段的和转化为一条线段．模型2、将军饮马--两动一定求线段和的最小值【模型探究】已知定点A 位于定直线m ,n 的内侧,在直线m 、n 分别上求点P 、Q 点PA +PQ +QA 周长最短.辅助线：过点A 作关于定直线m 、n 的对称点A’、A’’，连接A’A’’交直线m 、n 于点P 、Q ，则PA +PQ +QA 的最小值为A’A’’.例1．（2022·上虞市初二月考）如图，点P 是∠AOB 内任意一点，OP =6cm ，点M 和点N 分别是射线OA 和射线OB 上的动点，若△PMN 周长的最小值是6cm ，则∠AOB 的度数是（）A．15B．30C．45D．60【答案】B【分析】分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，由对称的性质得出PM=DM，OP=OC，∠COA=∠POA；PN=DN，OP=OD，∠DOB=∠POB，得出∠AOB=12∠COD，证出△OCD是等边三角形，得出∠COD=60°，即可得出结果．【解析】分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：∵点P关于OA的对称点为D，关于OB的对称点为C，∴PM=DM，OP=OD，∠DOA=∠POA；∵点P关于OB的对称点为C，∴PN=CN，OP=OC，∠COB=∠POB，∴OC=OP=OD，∠AOB=12∠COD，∵△PMN周长的最小值是6cm，∴PM+PN+MN=6，∴DM+CN+MN=6，即CD=6=OP，∴OC=OD=CD，即△OCD是等边三角形，∴∠COD=60°，∴∠AOB=30°，故选：B．【点睛】此题考查轴对称的性质，最短路线问题，等边三角形的判定与性质，熟练掌握轴对称的性质，证明三角形是等边三角形是解题的关键．例2．（2022·江苏九年级一模）如图，Rt△ABC中，∠C=90°，AC=3，BC=4，D，E，F分别是AB，BC，AC边上的动点，则△DEF的周长的最小值是（）A．2.5B．3.5C．4.8D．6【答案】C【分析】如图作D关于直线AC的对称点M，作D关于直线BC的对称点N，连接CM，CN，CD，EN，FM，DN，DM．由∠MCA=∠DCA，∠BCN=∠BCD，∠ACD+∠BCD=90°，推出∠MCD+∠NCD=180°，可得M、B、N 共线，由DF+DE+EF=FM+EN+EF，FM+EN+EF≥MN，可知当M、F、E、N共线时，且CD⊥AB时，DE+EF+FD的值最小，最小值=2CD，求出CD的值即可解决问题．【详解】解：如图，作D关于直线AC的对称点M，作D关于直线BC的对称点N，连接CM，CN，CD，EN，FM，DN，DM．∴DF=FM，DE=EN，CD=CM，CD=CN，∴CD=CM=CN，∵∠MCA=∠DCA，∠BCN=∠BCD，∠ACD+∠BCD=90°，∴∠MCD+∠NCD=180°，∴M、C、N共线，∵DF+DE+EF=FM+EN+EF，∵FM+EN+EF≥MN，∴当M、F、E、N共线时，且CD⊥AB时，DE+EF+FD的值最小，最小值为MN=2CD，∵CD⊥AB，∴12•AB•CD=12•AB•AC，∴CD=•AB ACAB=125=2.4，∴DE+EF+FD的最小值为4.8．故选：C．【点睛】本题考查了轴对称-最短问题、两点之间线段最短、垂线段最短等知识，解题的关键是灵活运用轴对称以及垂线段最短解决最短问题，属于中考选择题中的压轴题．例3.（2023.山东八年级期末）如图所示，在四边形ABCD中，∠A＝90º，∠C＝90º，∠D＝60º，AD＝3，AB＝，若点M、N分别为边CD，AD上的动点，则△BMN的周长最小值为（）A. B. C.6 D.3【答案】C【解析】作点B关于CD、AD的对称点分别为点B'和点B''，连接B'B''交DC和AD于点M和点N，连接MB、NB；再DC和AD上分别取一动点M’和N’（不同于点M和N），连接M'B，M'B'，N’B和N'B''，如图1所示：∵B'B''＜M'B'＋M'N'＋N'B"，B'M'＝BM'，B"N'＝BN'，∴BM'＋M'N'＋BN'＞B'B"，又∵B'B"＝B'M＋MN＋NB"，MB＝MB'，NB＝NB''，∴NB＋NM＋BM＜BM'＋M’N'＋BN'NB＋NM＋BM时周长最小；连接DB，过点B'作B'H⊥DB''于B’’D的延长线于点H，如图示2所示：在Rt△ABD中，AD＝3，AB＝，，∴∠2＝30º，∴∠5＝30º，DB＝DB''，又∵∠ADC＝∠1＋∠2＝60º，∴∠1＝30º，∴∠7＝30º，DB'＝DB，∴∠B'DB''＝∠1＋∠2＋∠5＋∠7＝120º，DB'＝DB''＝DB，又∵∠B'DB"＋∠6＝180º，∴∠6＝60º，∴HD＝，HB'＝3，在Rt△B'HB''中，由勾股定理得：B'B"＝，NB＋NM＋BM＝6，故选C.模型3、将军饮马--两动两定求线段和的最小值【模型探究】A，B为定点，在定直线m、n上分别找两点P、Q，使PA+PQ+QB最小。

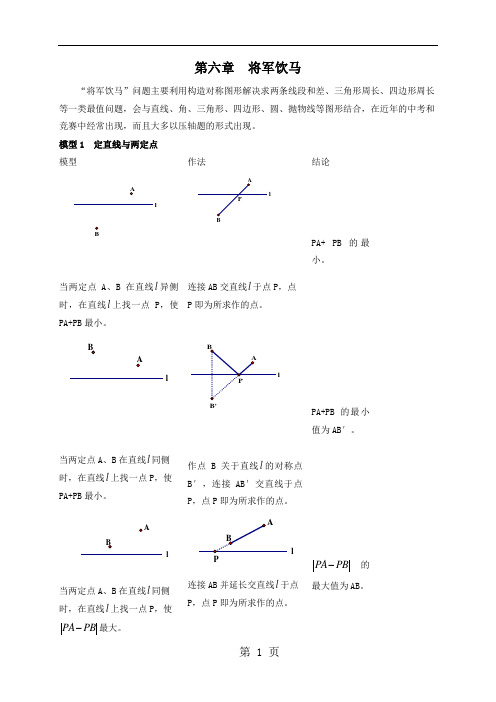
初中数学将军饮马第六章将军饮马“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

模型1定直线与两定点模型作法结论当两定点A、B在直线异侧时，在直线上找一点P，使PA+PB最小。

连接AB交直线于点P，点P即为所求作的点。

PA+ PB的最小。

当两定点A、B在直线同侧时，在直线上找一点P，使PA+PB 最小。

作点B关于直线的对称点B′，连接AB′交直线于点P，点P 即为所求作的点。

PA+PB的最小值为AB′。

当两定点A、B在直线同侧时，在直线上找一点P，使最大。

连接AB并延长交直线于点P，点P即为所求作的点。

的最大值为AB。

当两定点A、B在直线同侧时，在直线上找一点P，使最大。

作点B关于直线的对称点B′，连接AB′并延长交直线于点P，点P即为所求作的点。

的最大值为AB′。

当两定点A、B在直线同侧时，在直线上找一点P，使最小。

连接AB，作AB的垂直平分线交直线于点P，点P即为所求作的点。

的最小值为0。

模型实例例1．如图，正方形ABCD的面积是12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，则PD+PE的最小值为。

例2．如图，已知△ABC为等腰直角三角形，AC=BC=4，∠BCD=15°，P为CD上的动点，则的最大值是多少？热搜精练1．如图，在△ABC中，AC=BC=2，∠ACB-90°，D是BC边的中点，E是AB边上一动点，则EC+ED的最小值是。

2．如图，点C的坐标为（3，），当△ABC的周长最短时，求的值。

3．如图，正方形ABCD中，AB-7，M是DC上的一点，且DM-3，N是AC上的一动点，求的最小值与最大值。

模型2 角到定点模型作法结论点P在∠AOB的内部，在OB上找点D，在OA上找点C，使得△PCD周长最小。

lAlBAB'llBAlP第六章 将军饮马“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

模型1 定直线与两定点 模型 作法 结论当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使PA+PB 最小。

连接AB 交直线l 于点P ，点P 即为所求作的点。

PA+ PB 的最小。

当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA+PB 最小。

作点B 关于直线l 的对称点B ′，连接AB ′交直线于点P ，点P 即为所求作的点。

PA+PB 的最小值为AB ′。

当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA PB -最大。

连接AB 并延长交直线l 于点P ，点P 即为所求作的点。

PA PB-的最大值为AB 。

llAPDCBA当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA PB -最大。

作点B 关于直线l 的对称点B ′，连接AB ′并延长交直线于点P ，点P 即为所求作的点。

PA PB-的最大值为AB ′。

例1．如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，则PD+PE 的最小值为 。

例2．如图，已知△ABC 为等腰直角三角形，AC=BC=4，∠BCD=15°，P 为CD 上的动点，则PA PB -的最大值是多少？热搜精练1．如图，在△ABC 中，AC=BC=2，∠ACB-90°，D 是BC 边的中点，E是AB 边上一动点，则EC+ED 的最小值是 。

2．如图，点C 的坐标为（3，y ），当△ABC 的周长最短时，求y 的值。

3．如图，正方形ABCD 中，AB-7，M 是DC 上的一点，且DM-3，N 是AC 上的一 动点，求DN MN -的最小值与最大值。

将军饮马方法总结将军饮马是一种古代将领在战前饮酒开宴，观察酒杯中马的动作来预测战争胜负的方法。

这种方法源于古代中国的兵法典籍《孙子兵法》中的一种策略，被誉为战争智慧的体现。

本文将对将军饮马方法以及其背后的原理进行总结和探讨。

一、将军饮马的由来将军饮马这个词汇最早出现在《孙子兵法》中，其中记载了古代将领在战前用饮酒观察马的动作来预测战争胜负的做法。

将军在战前会将马放入大碗中，并倒入一碗酒，观察马在酒中的动作来判断战争的结果。

这种方法被认为是一种通过观察细微变化来预测未来的智慧，对于战争策略有着深远的影响。

二、将军饮马的原理将军饮马的原理在于通过观察马在酒中的动作来预测战争胜负。

马的动作往往可以反映出一些隐藏的信息，将军通过观察这些细微的变化来判断未来战争的结果。

1.马的姿态：将军观察马在酒中的姿态，如是否直立、是否有力地站立，可以了解到战争的开展情况。

如果马能够保持直立且有力地站立，那么说明战争将会顺利进行，并获得胜利的机会更大。

2.马的动作：将军还会观察马在酒中的动作，如是否舒展四肢、是否昂首挺胸。

如果马能够舒展四肢且昂首挺胸，那么说明战争将会迅速展开，并且取得较好的战果。

3.马的平衡：将军还会留意马在酒中的平衡状态，如是否保持稳定、是否有摇摆。

如果马能够保持稳定且不摇摆，那么说明战争将会有序进行，并且战局可能较为稳定。

通过观察这些细节，将军可以据此做出相应的战略决策，以尽可能地获得战争的胜利。

三、将军饮马的局限性虽然将军饮马方法在古代曾被广泛运用，但其并非百分百可靠，存在一定的局限性。

1.主观因素：将军饮马方法的判断结果往往受到将军主观意识的影响，将军可能会根据自己的喜好和想象来做出判断，导致结果不准确。

这是因为马在酒中的动作可以有多种解释，不同的人可能会给出不同的答案。

2.随机因素：马在酒中的动作往往是有一定随机性的，因此将军饮马方法并不能完全准确地预测战争的胜负。

即使马的动作符合理想状态，战争的结果也受到其他因素的影响，如战术、策略等。

将军饮马解题方法嘿，朋友们！今天咱来聊聊将军饮马问题，这可是个相当有趣又实用的解题方法呢！想象一下啊，有个将军骑着马在河边，他要去河对岸的一个地方，那怎么才能让马走的路程最短呢？这就是将军饮马问题的核心啦！咱先来看一个简单的例子。

比如说有一条河，河这边有个 A 点，河对岸有个 B 点，将军要从 A 点到 B 点。

那直接走直线过去不就好了吗？嘿嘿，可没那么简单哦！如果在河这边还有个 C 点，将军要先到 C 点办点事儿，然后再去 B 点，那这时候怎么走最短呢？这时候就得动动脑筋啦！我们可以先把 B 点关于河这条线对称过去，得到一个 B'点，然后连接 A 点和 B'点，这条线与河的交点就是将军饮马的最佳位置啦！你说神奇不神奇？为啥这样就是最短呢？这就好比你要去一个地方，中间有条河挡着，你总不能傻乎乎地直接游过去吧，得找个最省力的办法呀！将军饮马问题就是帮我们找到这个最省力的路径。

再举个例子，有一个三角形 ABC，在 AB 边上有个 D 点，将军要从 D 点出发，先到 AC 边上的某个点，再到 BC 边上的某个点，最后回到 D 点。

这时候咋办呢？还是用对称的方法呀！把那些要去的点都对称过去，然后连线，就能找到最短路径啦！这就好像你在走迷宫，得找到那根最快捷的线，才能最快地走出去呀！将军饮马问题不就是帮我们在数学的迷宫里找到那条最优路线嘛！你想想，生活中是不是也有很多类似的情况呀？比如说你要去几个地方办事，怎么安排路线才能最省时间最省力呢？这不就和将军饮马问题很像嘛！这种解题方法真的是太有用啦！它能让我们在面对复杂问题的时候，快速找到最优解。

就像有了一把钥匙，能打开难题的大门。

所以啊，大家可千万别小看了这将军饮马问题哦！它就像一个隐藏的宝藏，等你去发现它的神奇之处呢！以后遇到类似的问题，就可以试着用这种方法去解决，说不定一下子就豁然开朗啦！怎么样，是不是觉得很有意思呢？快去试试吧！。

将军饮马知识点总结
嘿，朋友们！今天咱来唠唠将军饮马这个有趣的知识点呀！
你们想啊，将军要去河边饮马，那他得找个最短的路吧，不然走冤枉路多累呀！这就好比咱出门，肯定也想找最近最省事儿的路嘛。

将军饮马问题呀，其实就是要在一个图形中找到一条最短的路线。

就像咱去超市买东西，得规划一下怎么走能最快买到所有需要的，还不绕路。

比如说，给你一条河，河这边有个点 A，河那边有个点 B，将军在 A 点，马在B 点，那将军咋走才能最快到马那呢？
这时候就得动点小脑筋啦！咱得把河看成一面镜子，然后把 B 点对称过去，得到一个对称点 B'，这时候将军直接去 B'点不就成啦？嘿嘿，是不是挺有意思的。

再举个例子呀，要是有个三角形 ABC，P 是三角形里面的一个点，那将军要从 A 点出发，经过 P 点再到 B 点，怎样最短呢？这也不难呀，还是用那招，把 B 点对称过来，然后连线，那路线不就出来啦！
你说这将军饮马问题多实用啊！生活中咱也经常能碰到类似的呢。

比如你要去几个地方办事，怎么安排路线最省时间，这不就是将军饮马嘛！
还有啊，这将军饮马问题还能变着花样考呢！有时候会给你多个点，让你找最短路线；有时候会把图形变复杂，让你去思考。

但咱只要抓住本质，就不怕它变。

咱学知识不就是为了用嘛，学会了将军饮马，以后遇到这种找最短路线的问题，咱就能轻松搞定啦！就像将军找到了最快去饮马的路一样，咱也能在各种问题中找到最快捷的解决办法呀！你们说是不是这个理儿？反正我觉得这将军饮马问题特别有意思，也特别有用，咱可得好好掌握它呀！这样以后不管碰到啥情况，咱都能像将军一样，聪明地找到最短路径，轻松应对各种挑战呢！。

将军饮马黯然销魂者，唐将饮马回秦(qín)都将军饮马，远行归来，身披战袍，英姿飒爽。

四方之事，皆已了，唯有马蹄声，还在耳旁。

伤心无敌者，唐将饮马回秦都。

汗血浸透，铁马寒霜，胸膛满是勇猛。

上阵杀敌，昔日身姿，如今行走于塞外烽（fēng）烟。

十个兄弟，只剩下一个，首领饮马回秦都。

故国战乱，纷争不已，百姓如蝼蚁。

将军睥睨，困境不惧，铁蹄踏过敌疆。

舌剑腾飞，敌血气锋芒，心中策略，威震四方。

王者之姿，尽展跃兵之材，回首看一看，英勇饮马回秦都。

俄然举杯，与将士同饮，悲喜交集，难忘今夜。

望人生，浩气长存，焚尽了昨日的忧愁。

胸怀壮志，腾云驾雾，将军欲翻身，金戈铁马。

风霜劲松，都成为过往，唯有深情，饮马回秦都。

莫问将军，今后归处，善用利剑，御前尽显纵横。

战争之地，乱世为凭，随意折腰语，也成笑谈。

将军为将，将略非凡，逐风追逐月，无人敌敌。

黯然销魂者，唐将饮马回秦都。

将军饮马，这是一幅关于将军勇猛归来的场景描写。

将军胸怀壮志，经历了千难万险的战斗，现在他饮马回到了秦都。

这个将军是唐朝的英雄，他身披战袍，英姿飒爽。

他的身上沾满了汗血，铁马寒霜，但他的气势依然无敌。

他上阵杀敌时的身姿，已经留存在塞外的烽烟之中。

十个兄弟中，已经只剩下他一个，他是伤心无敌的将军。

故国战乱，纷争不已，百姓如蝼蚁。

但将军睥睨这困境，战胜了一切困难，铁蹄踏过敌疆，舌剑腾飞。

他的心中有着无敌的策略，他的威名震动四方。

他展现了王者之姿，他是跃兵之材。

尽管回首看一看，他仍然是英勇的将军，饮马回秦都。

俄然举杯，将军与将士同饮。

他们共同感受到悲喜交集的情感，难忘今夜。

将军望着人生，他的浩气依然长存，他烧尽了昨日的忧愁。

心中充满着壮志，他希望能够腾云驾雾，重塑金戈铁马的辉煌。

风霜劲松已经成为过往，但将军的深情却依然在他饮马回秦都的时刻流淌。

将军的归处，不再重要。

他将会善用利剑，尽显纵横。

战争之地是他的舞台，乱世为他提供了施展才华的机会。

将军随意折腰语，也成为了笑谈。

第六章将军饮马“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现．PE D C B A PDA例题：例1．如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，则PD +PE 的最小值为 ．练习：1.如图，AB 是一条东西走向的公路，D ，E 是公路同一侧的两个村庄，若D ，E 到公路的距离分别是2和3公里，点E 在点D 的正西方向5公里，若在公路上建一个收购站点C ，求D ，E 两村到点C 距离之和的最小值．2. 如图，在边长为1的菱形ABCD 中，∠B ＝60°，点N 是对角线AC 上的一个动点，求MD +MN 的最小值．例2．如图，已知△ABC 为等腰直角三角形，AC =BC =4，∠BCD =15°，P 为CD 上的动点，则PA PB 的最大值是多少？ABE DCB AA （3MND CBA热搜精练1．如图，在△ABC 中，AC =BC =2，∠ACB ＝90°，D 是BC 边的中点，E 是AB 边 上一动点，则EC +ED 的最小值是 ．2．如图，点C 的坐标为（3，y ），当△ABC 的周长最短时，求y 的值．3．如图，正方形ABCD 中，AB ＝7，M 是DC 上的一点，且DM ＝3，N 是AC 上的一 动点，求DN MN 的最小值与最大值．4.如图，在△ABC中，AC=2，∠ACB＝90°，∠A＝60°，点D，E分别是AB和BC 边上的动点，求CD+DE的最小值．C B模型2 角到定点O CD M NB A 模型实例例1．如图，∠AOB =30°，∠AOB 内有一定点P ，且OP =10，在OA 上有一 点Q ，OB 上有一点R ．若△PQR 周长最小，则最小周长是多少？热搜精练1．如图，∠MON =40°，P 为∠MON 内一定点，A 为OM 上的点，B 为ON 上的点， 当△PAB 的周长取最小值时：（1）找到A 、B 点，保留作图痕迹；（2）求此时∠APB 等于多少度．如果∠MON = ，∠APB 又等于多少度？2．如图，四边形ABCD 中，∠BAD =110°，∠B =∠D =90°，在BC 、CD 上分别找一点M 、N ，使△AMN 周长最小，并求此时∠AMN +∠ANM 的度数．O NONB3．如图，在x 轴上找一点C ，在y 轴上找一点D ，使AD +CD +BC 最小，并 求直线CD 的解析式及点C 、D 的坐标．4．如图∠MON =20°，A 、B 分别为射线OM 、ON 上两定点，且OA =2，OB =4， 点P 、Q 分别为射线OM 、ON 上两动点，当P 、Q 运动时，线段 AQ+PQ+PB 的最小值是多少？模型3 两定点一定长C D O yx EBA模型实例例1．在平面直角坐标系中，矩形OABC如图所示，点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=2．当四边形BDEF的周长最小时，求点E的坐标．FC D O y x BA 21B A 热搜精练1．在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在， x 轴、y 轴的正半轴上，A （3，0），B （0，4），D 为边OB 的中点． （1）若E 为边OA 上的一个动点，求△CDE 的周长最小值；（2）若E 、F 为边OA 上的两个动点，且EF =1，当四边形CDEF 的周长最小时，求点E 、F 的坐标．2．村庄A 和村庄B 位于一条小何的两侧，若河岸彼此平行，要架设一座与河岸垂直的桥，桥址应如何选择，才使A 与B 之间的距离最短？3. 如图，已知点A (-4，8)和点B (2，n )在抛物线上．(1) 求a 的值及点B 关于x 轴对称点P 的坐标，并在x 轴上找一点Q ，使得AQ +QB 最短，求出点Q 的坐标；(2) 平移抛物线，记平移后点A 的对应点为A ′，点B 的对应点为B ′，点C (-2，0)和点D (-4，0)是x 轴上的两个定点．① 当抛物线向左平移到某个位置时，A ′C +CB ′ 最短，求此时抛物线的函数解析式； ② 当抛物线向左或向右平移时，是否存在某个位置，使四边形A ′B ′CD 的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．2y ax =2y ax =4x。

--完整版学习资料分享----lAl第六章 将军饮马“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

模型1 定直线与两定点 模型 作法 结论当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使PA+PB 最小。

连接AB 交直线l 于点P ，点P 即为所求作的点。

PA+ PB 的最小。

--完整版学习资料分享----lBAll BAl P当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA+PB 最小。

作点B 关于直线l 的对称点B ′，连接AB ′交直线于点P ，点P 即为所求作的点。

PA+PB 的最小值为AB ′。

当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA PB -最大。

连接AB 并延长交直线l 于点P ，点P 即为所求作的点。

PA PB -的最大值为AB 。

--完整版学习资料分享----llA当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使PA PB -最大。

作点B 关于直线l 的对称点B ′，连接AB ′并延长交直线于点P ，点P 即为所求作的点。

PA PB -的最大值为AB ′。

模型实例--完整版学习资料分享----PDCB A例1．如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，则PD+PE 的最小值为 。

例2．如图，已知△ABC 为等腰直角三角形，AC=BC=4，∠BCD=15°，P 为CD 上的动点，则PA PB -的最大值是多少？ 热搜精练1．如图，在△ABC 中，AC=BC=2，∠ACB-90°，D 是BC 边的中点，E 是AB 边上一动点，则EC+ED 的最小值是 。

2．如图，点C 的坐标为（3，y ），当△ABC 的周长最短时，求y 的值。