12将军饮马常用模型

将军饮马问题的11个模型及例题将军饮马问题是一个经典的逻辑问题，涉及到将军如何用有限数量的马和酒到达目的地。

本文将介绍将军饮马问题的11个模型及相应的例题。

1. 直线模型将军与目的地之间没有障碍物，可以直线前进。

此时，将军只需将马拉到目的地即可。

例题1：将军与目的地之间距离为10公里，马的速度为每小时5公里，将军能否在2小时内到达目的地？2. 单个障碍物模型在将军与目的地之间存在一个障碍物，将军可以绕过该障碍物。

例题2：将军与目的地之间距离为15公里，马的速度为每小时4公里，障碍物位于距离将军起点5公里处，将军能否在3小时内到达目的地？3. 多个障碍物模型在将军与目的地之间存在多个障碍物，将军需要逐一绕过这些障碍物。

例题3：将军与目的地之间距离为20公里，马的速度为每小时6公里，障碍物位于距离将军起点分别为5公里、10公里和15公里的位置，将军能否在4小时内到达目的地？4. 跳跃模型将军可以让马跳过障碍物，从而直接到达目的地。

例题4：将军与目的地之间距离为12公里，马的速度为每小时8公里，将军在距离起点6公里处设置一个障碍物，将军能否在2小时内到达目的地？5. 限时模型将军需要在规定的时间内到达目的地。

例题5：将军与目的地之间距离为30公里，马的速度为每小时10公里，将军需要在3小时内到达目的地，是否可能？6. 守备模型目标地点有守备军，将军需要巧妙规避守备军。

例题6：将军与目的地之间距离为25公里，马的速度为每小时7公里，目的地有一支守备军位于距离目标地点10公里处，将军能否在4小时内到达目的地？7. 短平快模型将军不借助马匹，直接徒步走到目的地。

例题7：将军与目的地之间距离为8公里，将军的步行速度为每小时2公里，将军能否在4小时内到达目的地？8. 时间窗模型将军只能在规定时间范围内到达目的地。

例题8：将军与目的地之间距离为18公里，马的速度为每小时6公里，将军需要在3小时到4小时之间到达目的地，是否可能？9. 兵变模型将军需要利用敌军马匹达到目的地。

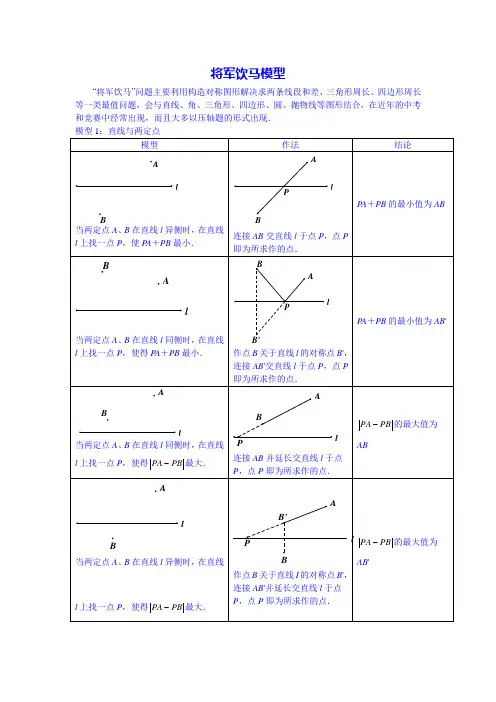
将军饮马模型“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现． 模型1：直线与两定点模型作法结论lB A当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使P A ＋PB 最小．lPAB连接AB 交直线l 于点P ，点P即为所求作的点．P A ＋PB 的最小值为ABl AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得P A ＋PB 最小．lPB'AB作点B 关于直线l 的对称点B '， 连接AB '交直线l 于点P ，点P 即为所求作的点．P A ＋PB 的最小值为AB 'l AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得PA PB -最大．lPAB连接AB 并延长交直线l 于点P ，点P 即为所求作的点．PA PB -的最大值为ABlAB当两定点A 、B 在直线l 异侧时，在直线l 上找一点P ，使得PA PB -最大．l B'AB P作点B 关于直线I 的对称点B '，连接AB '并延长交直线l 于点P ，点P 即为所求作的点．PA PB -的最大值为AB 'l AB当两定点A 、B 在直线l 同侧时，在直线l 上找一点P ，使得PA PB -最小．l PAB连接AB ，作AB 的垂直平分线交直线l 于点P ，点P 即为所求作的点．PA PB -的最小值为0模型实例例1：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，则PD ＋PE 最小值是 ．EBC ADP解答：如图所示，∵点B 与点D 关于AC 对称，∴当点P 为BE 与AC 的交点时，PD ＋PE 最小，且线段BE 的长． ∵正方形ABCD 的面积为12，∴其边长为23∵△ABE 为等边三角形，∴BE ＝AB ＝23PD ＋PE 的最小值为3例2：如图，已知△ABC 为等腰直角三角形，AC ＝BC ＝4，∠BCD ＝15°，P 为CD 上的动点，则PA PB -的最大值是多少？DPPA'B解答：如图所示，作点A 关于CD 的对称点A ′，连接A ′C ，连接A ′B 并延长交CD 于点P ，则点P 就是PA PB -的值最大时的点，PA PB -＝A ′B ．∵△ABC 为等腰直角三角形，AC ＝BC 等于4，∴∠ACB ＝90°． ∵∠BCD ＝15°，∴∠ACD ＝75°．∵点A 、A ′关于CD 对称，∴AA ′⊥CD ，AC ＝CA ′， ∵∠ACD ＝∠DCA ′＝75°，∴∠BCA ′＝60°．∵CA ′＝AC ＝BC ＝4，∴△A ′BC 是等边三角形，∴A ′B ＝BC ＝4．∴PA PB -的最大值为4． 练习1．如图，在△ABC 中，AC ＝BC ＝2，∠ACB ＝90°，D 是BC 边的中点，E 是AB 边上一动点，则EC ＋ED 的最小值是 ．DACB E解：解：过点C 作CO ⊥AB 于O ，延长CO 到C '，使O C '=OC ，连接D C '，交AB 于E ，连接C 'B ，此时DE+CE=DE+E C '=D C '的值最小．连接B C '，由对称性可知∠C 'BE=∠CBE=45°，∴∠CB C '=90°，∴B C '⊥BC ， ∠BC C '=∠B C 'C=45°，∴BC=B C '=2，∵D 是BC 边的中点，∴BD=1， 根据勾股定理可得：D C '=5，故EC+ED 的最小值是5． 2．如图，点C 的坐标为（3，y ），当△ABC 的周长最短时，求y 的值．xyB (2,0)A (0,3)O解：解：（1）作A 关于x=3的对称点A′，连接A′B 交直线x=3与点C ． ∵点A 与点A′关于x=3对称，∴AC=A′C ．∴AC+BC=A′C+BC ．当点B 、C 、A′在同一条直线上时，A′C+BC 有最小值，即△ABC 的周长有最小值． ∵点A 与点A′关于x=3对称，∴点A′的坐标为（6，3）．设直线BA′的解析式y=kx+b，将点B和点A′的坐标代入得：k＝34，b＝−32．∴y=34x-32．将x=3代入函数的解析式，∴y的值为3 43．如图，正方形ABCD中，AB＝7，M是DC上的一点，且DM＝3，N是AC上的一动点，求|DN－MN|的最小值与最大值．C解：解：当ND=NM时，即N点DM的垂直平分线与AC的交点，|DN-MN|=0，因为|DN-MN|≤DM，当点N运动到C点时取等号，此时|DN-MN|=DM=3，所以|DN-MN|的最小值为0，最大值为3于D ，点C 、点D 即为所求．PB OAQ点P 、Q 在∠AOB 内部，在OB 边上找点D ，OA 边上找点C ，使得四边形PQDC 周长最小．分别作点P 、Q 关于OA 、OB 的对称点P ′、Q ′，连接P ′Q ′，分别交OA 、OB 于点C 、D ，点C 、D 即为所求．PC ＋CD ＋DQ 的最小值为P ′Q ′，所以四边形PQDC 周长的最小值为PQ ＋P ′Q ′模型实例如图，∠AOB=30°，∠AOB 内有一定点P ，且10OP =.在OA 上有一点Q ，OB 上 一点R ．若立△PQR 周长最小，则最小周长是多少？解答如图，作点P 分别关于OA 、OB 的对称点E 、F ，连接EF ，分别交OA 、OB 于点Q 、R ，连接OE 、OF 、PE 、PF .EQ OP =，FR RP =．△PQR 的周长的最小值为EF 的长.由对称性可得∠EOQ=∠POQ ，∠FOR=∠POR ， ∠EOF=2∠AOB=60°． △EOF 是正三角形．10EF OE OP ===．即△PQR 周长最小值为10.模型2/角与定点1．已知，40MON °?，P 为MON Ð内一定点，A 为OM 上的点，B 为ON 上的点，当△PAB 的周长取最小值时：OBAP(1)找到A 、B 点，保留作图痕迹；(2)求此时APB Ð等于多少度.如果∠MON =θ，∠APB 又等于多少度？ON1.解答（1）做点P 分别关于OM ON 、的对称点E F 、，连接EF 分别交OM ON 、于点A B 、．点A B 、即为所求，此时△PAB 的周长最小．（２）∵点E 与点P 关于直线OM 对称，点F 与点P 关于ON 对称， ∴∠E ＝∠APE ，∠F =∠BPF ，∠CPD =180°-∠MON =140°． ∴在△EFP 中，∠E +∠F =180°-140°=40°， ∴∠CPA +∠BPD =40°．∴∠APB =100°．如果∠MON =θ， ∴∠CPD =180°-θ，∠E +∠F =θ． 又∵∠PAB =2∠E ，∠PBA =2∠F ∴∠PAB +∠PBA =2（∠E +∠F ）=2θ ∴∠APB =180°-2θ．ONE2．如图，四边形中ABCD ，110BAD °?,90B D °??，在BC 、CD 上分别找 一点M 、N ，使△AMN 周长最小，并求此时+AMN ANM ∠∠的度数．A DBMN2．解答如图，作点A关于BC的对称点A'，关于CD的对称点A''，连接A A'''与BC、CD的交点即为所求的点M、N．此时△AMN周长最小．∵∠BAD=110°，∴∠A'+∠A''=180°-110°=70°．由轴对称的性质得：∠A'=∠A AM'，∠A''=∠A AN''，∴∠AMN+∠ANM=2(∠A'+∠A'')=2×70°=140°．3．如图，在x轴上找一点C，在y轴上找一点D，使AD CD BC++最小，并求直线CD的解析式及点C、D的坐标．yxOB(3,1)A(1,3)3．解答作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A B''分别交x轴、y轴于点C、D，此时AD CD BC++最小．由对称性可知A'（-1,3），B'（3，-1）．易求得直线A B''的解析式为2y x=-+，即直线CD的解析式2y x=-+．当0y=时，2x=，∴点C坐标为（2,0）．当0x=时，2y=，∴点D坐标为（0,2）．xy (1，3)(3，1)OB 'BA 'AD C4．如图，20MON°?，A 、B 占分别为射线OM 、ON 上两定点，且2OA =，4OB =，点P 、Q 分别为射线OM 、ON 上两动点，当P 、Q 运动时，线段AQ PQ PB ++ 的最小值是多少？ONMAB4．解答作A 点关于ON 的对称点A '，点B 关于OM 的对称点B '，连接A B ''，分别交OM ON 、于点P Q 、，连接OA '、OB '．则AQ PQ PB A Q PQ PB A B ''''++=++=，此时AQ PQ PB ++最小． 由对称可知，PB PB '=，AQ A Q '=，2OA OA '==，4OB OB '==，20MOB NOA MON ''∠=∠=∠=︒． 60A OB ''∠=︒．作A D '⊥OB '于点D ， 在Rt △ODA '中，∴1OD =，3A D '= ∴413B D '=-=，23A B ''= ∴AQ PQ PB ++的最小值是23．模型作法结论如图，在直线l上找M、N两点(M在左)，使得AM＋MN＋NB最小，且MN＝d.将A向右平移d个单位到A′，作A′关于l的对称点A"，连接A"B与直线l交于点N，将点N向左平移d个单位即为M，点M，N即为所求.AM＋MN＋NB的最小值为A"B＋d如图，l1∥l2，l1、l2间距离为d，在l1、l2分别找M、N两点，使得MN⊥l1，且AM＋MN＋NB最小．将A向下平移d个单位到A，连接A′B交直线l2于点N，过点N作MN⊥l1，连接AM.点M、N即为所求．AM＋MN＋NB的最小值为A'B＋d.例题：在平面直角坐标系中，矩形OABC如图所示，点A在x轴正半轴上，点C在y轴正半轴上，且OA＝6，OC＝4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF＝2.当四边形BDEF的周长最小时，求点E的坐标．解答：如图，将点D向右平移2个单位得到D'(2，2)，作D'关于x轴的对称点D"(2，－2)，连接BD"交x轴于点F，将点F向左平移2个单位到点E，此时点E和点F为所求作的点，且四边形BDEF周长最小.理由：∵四边形BDEF的周长为BD＋DE＋EF＋BF，BD与EF是定值.∴BF＋DE最小时，四边形BDEF周长最小，∵BF＋ED＝BF＋FD'＝BF＋FD"＝BD"ABl2l1A′NMABl2l1BAlM NA′A"BAld设直线BD "的解析式为y ＝kx ＋b ，把B (6，4)，D "(2，－2)代入，得6k ＋b ＝4，2k ＋b ＝－2，解得k ＝32，b ＝－5，∴直线BD "的解析式为y ＝32x －5．令y ＝0，得x ＝103，∴点F 坐标为(103，0)．∴点E 坐标为(43，0)．练习1．在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，A (3，0)，B (0，4)，D 为边OB 的中点． (1)若E 为边OA 上的一个动点，求△CDE 的周长最小值；(2)若E 、F 为边OA 上的两个动点，且EF ＝1，当四边形CDEF 的周长最小时，求点E 、F 的坐标．解答：(1)如图，作点D 关于x 轴的对称点D '，连接CD '与x 轴交于点E ，连接DE ，由模型可知△CDE 的周长最小．∵在矩形OACB 中，OA ＝3，OB ＝4，D 为OB 的中点， ∴D (0，2)，C (3，4)，D '(0，－2).设直线CD '为y ＝kx ＋b ，把C (3，4)，D '(0，－2)代入， 得3k ＋b ＝4，b ＝－2，解得k ＝2，b ＝－2， ∴直线CD '为y ＝2x －2. 令y ＝0，得x ＝1， ∴点E 的坐标为(1，0). ∴OE ＝1，AE ＝2.利用勾股定理得CD ＝13，DE ＝5，CE ＝25， ∴△CDE 周长的最小值为13＋35．(2)如图，将点D 向右平移1个单位得到D '(1，2)，作D '关于x 轴的对称点D ″(1，－2)，连接CD ″交x 轴于点F ，将点F 向左平移1个单位到点E ，此时点E 和点F 为所求作的点，且四边形CDEF 周长最小．理由：∵四边形CDEF 的周长为CD ＋DE ＋EF ＋CF ，CD 与EF 是定值，∴DE ＋CF 最小时，四边形BDEF 周长最小，∴DE ＋CF ＝D 'F ＋CF ＝FD ″＋CF ＝CD ″， 设直线CD ″的解析式为y ＝kx ＋b ，把C (3，4)，D (1，－2)代入，得3k ＋b ＝4，k ＋b ＝－2，解得k ＝3，b ＝－5．∴直线CD ″的解析式为y ＝3x －5， 令y ＝0，得x ＝53，∴点F 坐标为(53，0)，∴点E 坐标为(23，0)．112．村庄A 和村庄B 位于一条小河的两侧，若河岸彼此平行，要架设一座与河岸垂直的桥，桥址应如何选择，才使A 与B 之间的距离最短？解答：设l 1和l 2为河岸，作BD ⊥l 2，取BB '等于河宽，连接AB '交l 1于C 1，作C 1C 2⊥l 2于C 2， 则A →C 1→C 2→B 为最短路线，即A 与B 之间的距离最短.AB l 2l 1。

“将军饮马”常见模型及18道典型习题何为将军饮马？2000多年以前。

古希腊的亚历山大城里住着一位睿智的数学家海伦。

一天，城里来了一位将军，听闻海伦盛名，特来向他请教一个问题。

将军说，每天早上，他都骑着马儿从营帐出发，到河边让马儿饮水，然后，再去河岸同一侧的一块草地上带着马儿去吃草，问题时，在河岸的哪个具体位置喝水，行程最短？海伦略做沉思，给出了将军最佳方案。

此之谓“将军饮马”。

最佳方案为何？且阅下文：一、将军饮马常见的5种模型：1、一动两定（和最小）：如图，点A是将军和马居住的营帐，点B是一块指定的草地，一条小河L潺潺流过，P是将军带着马儿喝水的地方，P点在何处时，将军和马儿走过的路PA+PB的值最小？解析：做A点关于L的对称点A’，连接A’B，与L的交点即为P点。

为什么这时PA+PB最小？假设L上有一点M（与P点不重合）。

∵A点与A’关于L对称∴AP=A’P；AM=A’M；∴AP + BP =A’P +BP =A’B而AM + BM = A’M +MB在△A’MB中，两边之和大于第三边∴A’B < A’M +MB；而M为L上任一点（与P点不重合）。

∴动点P在A’B与L交点处时AP+BP最小。

2、一定两动：如图，点A是将军和马居住的营帐，小河L1依然像上题中一样潺潺流过，P是将军带着马儿喝水的地方，不同的是，这次吃草的地方不在是一个指定的点，而是L2所代表的一片草地，Q则是将军骑马吃草的地方，水足草饱以后，将军和马儿会再回到营帐。

那么，P点、Q点在何处时，将军走过的路AP+PQ+QA的值最小？解析：做A点关于L1的对称点A’；做A点关于L2的对称点A‘’；连接A’A‘’，与L1和L2的交点即为P、Q。

为什么此时，AP+PQ+AQ的和最小？假设L1上有点M（不与P重合）、L2上有点N（不与Q重合）。

∵A点与A’关于L1对称；A点与A‘’关于L2对称。

∴AP=A’P；AQ=A”Q；AM=A’M；AN=A”N；∴AP+PQ+AQ = A’P+PQ+A”Q =A’A”；AM+MN+AN = A’M+MN+A”N在四边形A’MNA”中：A’M+MN+A”N >A’A”∴P、Q位于A’A”与L1和L2的交点处时，AP+PQ+AQ的和最小。

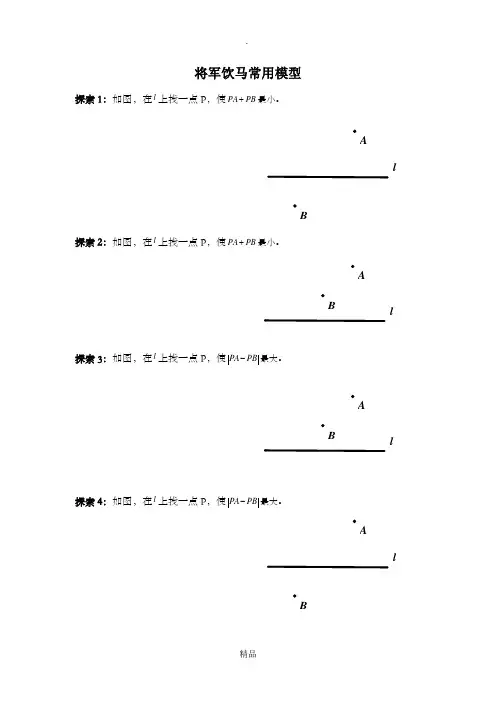
将军饮马常用模型
探索1：如图，在l 上找一点P ，使PA PB +最小。

l
A
B
探索2：如图，在l 上找一点P ，使PA PB +最小。

l
A B
探索3：如图，在l 上找一点P ，使PA PB -最大。

l
A B
探索4：如图，在l 上找一点P ，使PA PB -最大。

l
A
B
探索5：如图，在l上找一点P，使PA PB
最小。

A
l
B
探索6：如图，点P在锐角AOB
∠的内部，在OB边上求作一点D，在OA边上求作一点C，使PCD
∆的周长最小。

探索7：如图，点P在锐角AOB
∠的内部，在OB边上求作一点D，在OA边上求作一点C，使PD CD
+的周长最小。

探索8：如图，点C、D在锐角AOB
∠的内部，在OB边上求作一点F，在OA边上求作一点E，使CEFD的周长最小。

如有侵权请联系告知删除，感谢你们的配合！
如有侵权请联系告知删除，感谢你们的配合！。

当两淀点A 、R 在克罐/何侧时，在亞线』上携一点几便|阳一户创最大°将军饮马”三种模型"将军饮马"问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

晋两定点A.U 在点线F 异創时-在肖践f 上找一点Pt 使PA+PB 锻小*述接也交h 纱/于点P.点卩閒为所求作的点.肖两远点上B 在直雜I 同测时,在直刻上拥一点P,使PA+PB 最小'作庖U 芸于宜线F 的对称点V ■连楼AB'交直线于点P.点P 即为用求作的点"―二I \PA-P^\荊卩址大值洵丽。

连接班并延长交直戦』十点几点卩即为所求作的点。

当两定点仏k 在直找门司侧时，在直线』上找一点人使PA-PB\^扎作点B 关于直统』的对称点B'h 谨接恋’井延快交宜鏡于点巴点F 即为所求作的点。

皓论PAPI1的颯小°PA-PB 的盘小值为AB'□冋-卿的最大值为上的动点，则户创的圮大值是多少？A ■B ■\A\PA-PB\的 1当两定点限廿在宜线/同删时，在直线丿上找--点片使f4-砂|最小“ 叫连接馭作■-朋的垂直平分钱交直线f 于点P ，点卩即沟所求作的点-最小值为叽模型实例例1一如图"止厅形的面积是1氛是等边三博形，点E 在止方刑ABCI ）内“在对角纯蚯上有一点卩*则PD+FE 的艮小值为°^12.如圜已S11AABC 为辱展宜角匸角形…怔-氏=4”ZBCD 15".P 拘匚D热搜掃练I.如虱^AABC 中「ZACB-fJO 3，乃是就边的中点，II 是屈边b -动直+则LCIED 的最小悄是°])2・如图.点C的坐标为（3,y）,当△ABC的周长最短时，求丿的值。

3.如图.正方形ABCD中,AB-7,M是DCI：的一点，且DM-3,N是AC上的一动点.求|DN-MN|的嚴小值与战大值.△PCD 周氏最小为点P 在ZAOB 的内部，在0B 上找点D,在0A 上找点C,使得△PCD 周长最小。

、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦? 一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题.将军每天从军营A 出发，先到河边饮马，然后再去河岸同侧的军营B 开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它. 从此以后，这个被称为“将军饮马” 的问题便流传至今.【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1:在定直线I上找一个动点P,使动点P到两个定点A与B的距离之和最小，即PA+PB最小.作法：连接AB 与直线I 的交点Q,Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB 最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB,与直线I的交点Q P为直线I上任意一点例2 :在定直线I上找一个动点P,使动点P到两个定点A与B的距离之和最小即PA+PB 的和最小.关键:找对称点作法：作定点B关于定直线I的对称点C,连接AC，与直线I的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC,与直线I的交点Q P为直线I上任意一点，在"PAC中，由三角形三边关系可知：AP+P&AC （当且仅当PQ重合时取=）2.两动一定型例3 :在/ MON 的内部有一点A,在0M上找一点B,在ON上找一点C,使得△ BAC周长最短.作法：作点A关于0M的对称点A',作点A关于ON的对称点A''，连接A' A',与0M交于点B,与ON 交于点C,连接AB AC, △ABC即为所求.原理：两点之间，线段最短例4:在/MON的内部有点A和点B,在OM上找一点C,在ON上找一点D,使得四边形周长最短.作法：作点A关于OM的对称点A,作点B关于ON的对称点B'，连接A B '，与交于点C,与ON交于点D,连接AC, BD AB,四边形ABCD即为所求.原理：两点之间，线段最短3.两定两动型最值例5:已知A B是两个定点，在定直线I上找两个动点M与N,且MN长度等于定长d （动点M位于动点N 左侧），使AM+MN+N 的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A,作A'关于直线I的对称点A'',连接A''B,交直线I于点N,将点N 向左平移长度d, 得到点M作法二：作点A关于直线I的对称点A,将点A1向右平移长度d得到点A2,连接A B ,交直线I于点Q, 将点Q向左平移长度d,得到点Q。

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1.两点之间，线段最短；2.三角形两边之和大于第三边，两边之差小于第三边；3.中垂线上的点到线段两端点的距离相等；4.垂线段最短.基本模型1.已知：如图，定点A、B分布在定直线l两侧；要求：在直线l上找一点P，使PA+PB的值最小解：连接AB交直线l于点P，点P即为所求,PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB，即AP´+BP´>AP+BP ∴P为直线AB与直线l的交点时，PA+PB最小.2.已知：如图，定点A和定点B在定直线l的同侧要求：在直线l上找一点P，使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A´，连接A´B交l于P，点P即为所求；理由：根据轴对称的性质知直线l为线段AA´的中垂线，由中垂线的性质得：PA=PA´，要使PA+PB最小，则需PA´+PB值最小，从而转化为模型1.3.已知：如图，定点A、B分布在定直线l的同侧（A、B两点到l的距离不相等）要求：在直线l上找一点P，使︱PA-PB︱的值最大解：连接BA并延长，交直线l于点P，点P即为所求；理由：此时︱PA-PB︱=AB，在l上任取异于点P的一点P´，连接AP´、BP´，由三角形的三边关系知︱P´A-P´B︱<AB，即︱P´A-P´B︱<︱PA-PB︱4. 已知：如图，定点A、B分布在定直线l的两侧（A、B两点到l的距离不相等）要求：在直线l上找一点P，使︱PA-PB︱的值最大解：作点B关于直线l的对称点B´，连接B´A并延长交于点P，点P即为所求；理由：根据对称的性质知l 为线段BB ´的中垂线，由中垂线的性质得：PB=PB ´，要使︱PA-PB ︱最大，则需︱PA-PB ´︱值最大 ，从而转化为模型3.典型例题1-1如图，直线y=x+4与x 轴、y 轴分别交于点A 和点B ，点C 、D 分别为线段AB 、OB 的中点，点P 为OA 上一动点，当PC+PD 最小时，点P 的坐标为_________，此时PC+PD 的最小值为_________.【分析】符合基本模型2的特征，作点D 关于x 轴的对称点D'，连接CD'交x 轴于点P ，此时PC+PD 值最小，由条件知CD 为△BAO 的中位线，OP 为 △CDD'的中位线，易求OP 长，从而求出P 点坐标；PC+PD 的最小值即CD'长，可用勾股定理（或两点之间的距离公式，实质相同）计算.【解答】连接CD ，作点D 关于x 轴的对称点D ′，连接CD ′交x 轴于点P ，此时PC+PD 值最小．令y=x+4中x=0，则y=4，∴点B 坐标（0，4）；令y=x+4中y=0，则x+4=0，解得：x=﹣6，∴点A 的坐标为（﹣6，0）．∵点C 、D 分别为线段AB 、OB 的中点，∴CD 为△BAO 的中位线， ∴CD ∥x 轴，且CD=21AO=3，∵点D ′和点D 关于x 轴对称，∴O 为DD ′的中点，D ′（0，-1），∴OP 为△CDD ′的中位线，∴OP=21CD=23，∴点P 的坐标为（﹣，0）．在Rt △CDD ′中，CD ′=22D D CD '+=2243+=5，即PC+PD 的最小值为5.【小结】还可用中点坐标公式先后求出点C 、点P 坐标；若题型变化，C 、D 不是AB 和OB 中点时，则先求直线CD ′的解析式，再求其与x 轴的交点P 的坐标.典型例题1-2如图，在平面直角坐标系中，已知点A 的坐标为（0，1），点B 的坐标为（，﹣2），点P 在直线y=﹣x 上运动，当|PA ﹣PB|最大时点P 的坐标为_________，|PA ﹣PB|的最大值是_________.【分析】符合基本模型4的特征，作A 关于直线y=﹣x 对称点C ，连接BC ，可得直线BC 的方程；求得BC 与直线y=﹣x 的交点P 的坐标；此时|PA ﹣PB|=|PC ﹣PB|=BC 取得最大值，再用两点之间的距离公式求此最大值.【解答】作A 关于直线y=﹣x 对称点C ，易得C 的坐标为（﹣1，0）；连接BC ，可得直线BC的方程为y=﹣54x ﹣54，与直线y=﹣x 联立解得交点坐标P 为（4，﹣4）；此时|PA﹣PB|=|PC ﹣PB|=BC 取得最大值，最大值BC=2223)2()1(-++=241； 【小结】“两点一线”大多考查基本模型2和4，需作一次对称点，连线得交点.变式训练1-1已知菱形OABC 在平面直角坐标系的位置如图所示，顶点A （5，0），OB=4，点P 是对角线OB 上的一个动点，D （0，1），当CP+DP 最短时，点P 的坐标为（ ）A ．（0，0）B ．（1，）C ．（，）D ．（，）变式训练1-2如图，菱形ABCD 中，对角线AC 和BD 交于点O ，AC=2，BD=2,E 为AB 的中点，P 为对角线AC 上一动点，则PE+PB 的最小值为__________.变式训练1-3如图，已知直线y=x+1与y轴交于点A，与x轴交于点D，抛物线y=x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．（1）求该抛物线的解析式；（2）在抛物线的对称轴上找一点M，使|AM﹣MC|的值最大，求出点M的坐标.拓展模型1.已知：如图，A为锐角∠MON外一定点；要求：在射线OM上找一点P，在射线ON上找一点Q，使AP+PQ的值最小.解：过点A作AQ⊥ON于点Q，AQ与OM相交于点P，此时，AP+PQ最小；理由：AP+PQ≧AQ，当且仅当A、P、Q三点共线时，AP+PQ取得最小值AQ，根据垂线段最短，当AQ⊥ON时，AQ最小.2.已知：如图，A为锐角∠MON内一定点；要求：在射线OM上找一点P，在射线ON上找一点Q，使AP+PQ的值最小.解：作点A关于OM的对称点A′，过点A′作AQ⊥ON于点Q，A′Q交OM于点P，此时AP+PQ最小；理由：由轴对称的性质知AP=A′P，要使AP+PQ最小，只需A′P+PQ最小，从而转化为拓展模型13.已知：如图，A为锐角∠MON内一定点；要求：在射线OM上找一点P，在射线ON上找一点Q，使△APQ的周长最小解：分别作A点关于直线OM的对称点A1,关于ON的对称点A2，连接 A1A2交OM于点P，交ON于点Q，点P和点Q即为所求，此时△APQ周长最小，最小值即为线段A1A2的长度；理由：由轴对称的性质知AP=A1P，AQ=A2Q，△APQ的周长AP+PQ+AQ=A1P+PQ+A2Q，当A1、P、Q、A2四点共线时，其值最小.4. 已知：如图，A、B为锐角∠MON内两个定点；要求：在OM上找一点P，在ON上找一点Q，使四边形APQB的周长最小解：作点A关于直线OM的对称点A´，作点B关于直线ON的对称点B´，连接A´B´交OM于P，交ON于Q，则点P、点Q即为所求，此时四边形APQB周长的最小值即为线段AB和A´B´的长度之和；理由：AB长为定值，由基本模型将PA转化为PA´,将QB转化为QB´，当A´、P、Q、B´四点共线时，PA´+PQ+ QB´的值最小，即PA+PQ+ QB的值最小.5.搭桥模型已知：如图，直线m∥n,A、B分别为m上方和n下方的定点，（直线AB不与m垂直）要求：在m、n之间求作垂线段PQ，使得AP+PQ+BQ最小.分析：PQ为定值，只需AP+BQ最小，可通过平移，使P、Q“接头”，转化为基本模型解：如图，将点A沿着平行于PQ的方向，向下平移至点A′，使得AA′=PQ，连接A′B交直线n于点Q，过点Q作PQ⊥n，交直线m于点P，线段PQ即为所求，此时AP+PQ+BQ最小.理由：易知四边形QPAA′为平行四边形，则QA′=PA，当B、Q、A′三点共线时，QA′+BQ最小，即AP+BQ最小，PQ长为定值，此时AP+PQ+BQ最小.6.已知：如图，定点A、B分布于直线l两侧，长度为a(a为定值)的线段PQ在l上移动（P在Q左边）要求：确定PQ的位置，使得AP+PQ+QB最小分析：PQ为定值，只需AP+QB的值最小，可通过平移，使P、Q“接头”，转化为基本模型解：将点A沿着平行于l的方向，向右移至A´，使AA´=PQ=a,连接A´B交直线l于点Q，在l上截取PQ=a（P在Q左边），则线段PQ即为所求，此时AP+PQ+QB的最小值为A´B+PQ，即A´B+a理由：易知四边形APQA´为平行四边形，则PA=QA´，当A´、Q、B三点共线时，QA´+QB最小，即PA+QB最小，又PQ长为定值此时PA+PQ+QB值最小.7.已知：如图，定点A、B分布于直线l的同侧，长度a(a为定值)的线段PQ在l上移动（P在Q左边）要求：确定PQ的位置，使得四边形APQB周长最小分析：AB长度确定，只需AP+PQ+QB最小，通过作A点关于l的对称点，转化为上述模型3解：作A点关于l的对称点A´，将点A´沿着平行于l的方向，向右移至A´´，使A´A´´=PQ=a，连接A ´´B交l 于Q ，在l 上截取QP=a （P 在Q 左边），线段PQ 即为所求，此时四边形APQB 周长的最小值为A ´´B+AB+PQ ，即A ´´B+AB+a典型例题2-1如图，在矩形ABCD 中，AB=10，BC=5，若点M 、N 分别是线段AC 、AB 上的两个动点，则BM+MN 的最小值为 ．【分析】符合拓展模型2的特征，作点B 关于AC 的对称点E ，再过点E 作AB 的垂线段，该垂线段的长即BM+MN 的最小值，借助等面积法和相似可求其长度.【解答】作点B 关于AC 的对称点E ，再过点E 作EN ⊥AB 于N ，则BM+MN=EM+MN ，其最小值即EN 长；∵AB=10，BC=5，∴AC=22BC AB +=55，等面积法求得AC 边上的高为55510⨯=25，∴BE=45， 易知△ABC ∽△ENB ，∴，代入数据解得EN=8． 即BM+MN 的最小值为8．【小结】该类题的思路是通过作对称，将线段转化，再根据定理、公理连线或作垂线；可作定点或动点关于定直线的对称点，有些题作定点的对称点易解，有些题则作动点的对称点易解.典型例题2-2如图，∠AOB=60°，点P是∠AOB内的定点且OP=，点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（）A．B．C．6 D．3【分析】符合拓展模型3的特征；作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，此时△PMN周长最小，其值为CD长；根据对称性连接OC、OD，分析条件知△OCD是顶角为120°的等腰三角形，作底边上高，易求底边CD.【解答】作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=OC=，CH=OH=，∴CD=2CH=3．即△PMN周长的最小值是3；故选：D．【小结】根据对称的性质，发现△OCD是顶角为120°的等腰三角形，是解题的关键，也是难点.典型例题2-3如图，已知平行四边形ABCO，以点O为原点，OC所在的直线为x轴，建立直角坐标系，AB交y轴于点D，AD=2，OC=6，∠A=60°，线段EF所在的直线为OD的垂直平分线，点P为线段EF上的动点，PM⊥x轴于点M点，点E与E′关于x轴对称，连接BP、E′M．（1）请直接写出点A坐标为，点B坐标为；（2）当BP+PM+ME′的长度最小时，请求出点P的坐标.【分析】（1）解直角三角形求出OD，BD的长即可解决；（2）符合“搭桥模型”的特征；首先证明四边形OPME′是平行四边形，可得OP=EM，PM是定值，PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小，此时P点为直线OB与EF的交点，结合OB的解析式可得P点坐标；【解答】（1）在Rt△ADO中，∵∠A=60°，AD=2，∴OD=2•tan60°=2，∴A（﹣2，2），∵四边形ABCO是平行四边形，∴AB=OC=6，∴DB=6﹣2=4，∴B（4，2）（2）如图，连接OP．∵EF垂直平分线段OD，PM⊥OC，∴∠PEO=∠EOM=∠PMO=90°，∴四边形OMPE是矩形，∴PM=OE=，∵OE=OE′，∴PM=OE′，PM∥OE′，∴四边形OPME′是平行四边形,∴OP=EM，∵PM是定值，∴PB+ME′=OP+PB的值最小时，BP+PM+ME′的长度最小，∴当O、P、B共线时，BP+PM+ME′的长度最小，∵直线OB的解析式为y=x，∴P（2，）．【小结】求没有公共端点的两条线段之和的最小值，一般通过作对称和平移（构造平行四边形）的方法，转化为基本模型.典型例题2-4如图所示，在平面直角坐标系中，Rt△AOB的顶点坐标分别为A（﹣2，0），O（0，0），B（0，4），把△AOB绕点O按顺时针方向旋转90°，得到△COD．（1）求C、D两点的坐标；（2）求经过A、B、D三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上取两点E、F（点E在点F的上方），且EF=1，使四边形ACEF的周长最小，求出E、F两点的坐标．【分析】符合拓展模型7的特征，通过作对称、平移、连线，可找出E、F点，结合直线的解析式和抛物线的对称轴可解出E、F坐标.【解答】（1）由旋转的性质可知：OC=OA=2，OD=OB=4,∴C点的坐标是（0，2），D点的坐标是（4，0），（2）设所求抛物线的解析式为y=ax2+bx+c，4a-2b+c=0由题意，得 16a+4b+c=0c=4解得a=-b=1，c=4，∴所求抛物线的解析式为y=-；（3）只需AF+CE最短，抛物线y=-的对称轴为x=1，将点A向上平移至A1（﹣2，1），则AF=A1E，作A1关于对称轴x=1的对称点A2（4，1），连接A2C，A2C与对称轴交于点E，E为所求，可求得A2C的解析式为y=-，当x=1时，y=，∴点E的坐标为(1,)，点F的坐标为(1,)．【小结】解决此类题的套路是“对称、平移、连线”；其中，作对称和平移的顺序可互换.变式训练2-1几何模型：条件：如图1，A，B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA+PB的值最小．方法：作点A关于直线l的对称点A’，连接A’B交l于点P，即为所求.（不必证明）模型应用：（1）如图2，已知平面直角坐标系中两定点A（0，﹣1）和B（2，﹣1），P为x轴上一动点，则当PA+PB的值最小是点P的横坐标是，此时PA+PB= ．（2）如图3，正方形ABCD的边长为4，E为AB的中点，P是AC上一动点，连接BD，由正方形对称性可知，B与D关于直线AC对称．连接ED交AC于P，则PB+PE的最小值是．（3）如图4，在菱形ABCD中，AB=10，∠DAB=60°，P是对角线AC上一动点，E，F分别是线段AB和BC上的动点，则PE+PF的最小值是．（4）如图5，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E．F分别是AG，AD上的两个动点，则EF+ED的最小值是．变式训练2-2如图，矩形ABCD中，AD=15，AB=10，E为AB边上一点，且DE=2AE，连接CE与对角线BD交于F；若P、Q分别为AB边和BC边上的动点，连接EP、PQ和QF；则四边形EPQF周长的最小值是___________.变式训练2-3如图，已知直线l 1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=4，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ= ．变式训练2-4如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．（1）求经过A、B、C三点的抛物线的解析式；（2）当BE经过（1）中抛物线的顶点时，求CF的长；（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ=1，要使四边形BCPQ 的周长最小，求出P、Q两点的坐标．中考真题1.要在街道旁建奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使A、B到它的距离之和最短？小聪以街道为x轴，建立了如图所示的平面直角坐标系，A点坐标为（0，3），B点坐标为（6，5），则A、B两点到奶站距离之和的最小值是．2.如图，矩形ABOC 的顶点A 的坐标为（﹣4，5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是（ ） A ．（0，）B ．（0，）C ．（0，2）D ．（0，）3.如图，在矩形ABCD 中，AB=5，AD=3，动点P 满足S △PAB =31S 矩形ABCD ，则点P 到A 、B 两点距离之和PA+PB 的最小值为（ ） A ． B ． C ．5 D ．4.已知抛物线y=x 2+1具有如下性质：该抛物线上任意一点到定点F （0，2）的距离与到x 轴的距离始终相等，如图，点M 的坐标为（，3），P 是抛物线y=x 2+1上一个动点，则△PMF 周长的最小值是（ ） A ．3 B ．4C ．5D ．65.如图，点A （a ，3），B （b ，1）都在双曲线y=上，点C ，D ，分别是x 轴，y 轴上的动点，则四边形ABCD 周长的最小值为（ ） A ．B ．C ．D ．6.如图，在Rt △ABC 中，∠C=90°，AC=3，BC=4，D 、E 分别是AB 、BC 边上的动点，则AE+DE 的最小值为（ ）A．B．C．5 D．7.如图，Rt△ABC中，∠BAC=90°，AB=3，AC=6，点D，E分别是边BC，AC上的动点，则DA+DE的最小值为．8.如图，等腰△ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为．9.如图，菱形ABCD的边长为6，∠ABC=120°，M是BC边的一个三等分点，P是对角线AC上的动点，当PB+PM的值最小时，PM的长是（）A．B．C．D．10.如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为（）A．B．C．D．611.如图，在平面直角坐标系中，反比例函数y=（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点．△OMN的面积为10．若动点P在x轴上，则PM+PN 的最小值是（）A．6B．10 C．2D．212.如图，△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是形，P、E、F分别为线段AB、AD、DB上的任意点，则PE+PF的最小值是．13.如图，已知抛物线y=x2+bx+c与直线y=x+3交于A，B两点，交x轴于C、D两点，连接AC、BC，已知A（0，3），C（﹣3，0）．（1）求此抛物线的解析式；（2）在抛物线对称轴l上找一点M，使|MB﹣MD|的值最大，并求出这个最大值；（3）点P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P，使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．14.如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．15.如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣1，0），B（3，0），C（0，3）三点．（1）求抛物线的解析式及顶点M的坐标；（2）连接AC、BC，N为抛物线上的点且在第四象限，当S△NBC=S△ABC时，求N点的坐标；（3）在（2）问的条件下，过点C作直线l∥x轴，动点P（m，3）在直线l上，动点Q（m，0）在x轴上，连接PM、PQ、NQ，当m为何值时，PM+PQ+QN的和最小，并求出 PM+PQ+QN 和的最小值．16.如图，直线y=5x+5交x轴于点A，交y轴于点C，过A，C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B．（1）求二次函数的表达式；（2）连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND 长度的最大值；（3）若点H为二次函数y=ax2+4x+c图象的顶点，点M（4，m）是该二次函数图象上一点，在x轴、y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F，E的坐标．17.如图1，已知抛物线y=（x﹣2）（x+a）（a＞0）与x轴从左至右交于A，B两点，与y轴交于点C．（1）若抛物线过点T（1，﹣），求抛物线的解析式；（2）在第二象限内的抛物线上是否存在点D，使得以A、B、D三点为顶点的三角形与△ABC相似？若存在，求a的值；若不存在，请说明理由．（3）如图2，在（1）的条件下，点P的坐标为（﹣1，1），点Q（6，t）是抛物线上的点，在x轴上，从左至右有M、N两点，且MN=2，问MN在x轴上移动到何处时，四边形PQNM 的周长最小？请直接写出符合条件的点M的坐标．18.如图，对称轴为直线x=2的抛物线经过A（﹣1，0），C（0，5）两点，与x轴另一交点为B．已知M（0，1），E（a，0），F（a+1，0），P是第一象限内抛物线上的动点．（1）求此抛物线的解析式；（2）当a=1时，求四边形MEFP的面积的最大值，并求此时点P的坐标；（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．19.探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2=他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：x=，y=．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：；拓展：（3）如图3，点P（2，n）在函数y=x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．20.如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．21.如图①，在平面直角坐标系中，OA=6，以OA为边长作等边三角形ABC，使得BC∥OA，且点B、C落在过原点且开口向下的抛物线上．（1）求这条抛物线的解析式；（2）在图①中，假设一动点P从点B出发，沿折线BAC的方向以每秒2个单位的速度运动，同时另一动点Q从O点出发，沿x轴的负半轴方向以每秒1个单位的速度运动，当点P 运动到A点时，P、Q都同时停止运动，在P、Q的运动过程中，是否存在时间t，使得PQ⊥AB，若存在，求出t的值，若不存在，请说明理由；（3）在BC边上取两点E、F，使BE=EF=1个单位，试在AB边上找一点G，在抛物线的对称轴上找一点H，使得四边形EGHF的周长最小，并求出周长的最小值．本人所著《初中几何模型与解题通法》已发行，可在当当、淘宝和京东搜索购买特色：1.由一线名师编写，更专业权威，各地历年中考压轴题几乎都能在书中找到对应的模型和方法，甚至出现大量高度类似题。

将军饮马的六种模型将军饮马问题是一个经典的最优化问题，常见的有六种模型。

一、六大模型1.给定直线l和直线l的异侧两点A、B，在直线l上求一点P，使PA+PB最小。

2.给定直线l和直线l的同侧两点A、B，在直线l上求一点P，使PA+PB最小。

3.给定∠MON内一点P，在OM、ON上分别作点A、B，使△PAB的周长最小。

4.给定∠MON内的两点P、Q，在OM、ON上分别作点A、B，使四边形PAQB的周长最小。

5.给定∠MON外的一点A，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

6.给定∠MON内的一点A，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

二、常见题目Part1、三角形1.在等边△ABC中，AB=6，AD⊥BC，E是AC上的一点，M是AD上的一点，AE=2，求EM+EC的最小值。

解：连接BE，交AD于点M，则ME+MD最小。

过点B作BH⊥AC于点H，则EH=AH–AE=3–2=1.在直角△BHE中，BE=√(BH^2+HE^2)=√(3^2+1^2)=√10.因此，EM+EC=BE+BC-2AE=√10+6-2×2=√10+2.2.在锐角△ABC中，AB=√2，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？解：作点B关于AD的对称点B'，过点B'作B'E⊥AB于点E，交AD于点F，则线段B'E长就是BM+MN的最小值。

在XXX△AEB'中，根据勾股定理得到，B'E=√2.因此，XXX√2.3.在△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN值最小，则这个最小值是多少？解：作AB关于AC的对称线段AB'，过点B'作B'N⊥AB，垂足为N，交AC于点M，则B'N=MB'+MN=MB+MN。

将军饮马问题16大模型解析将军饮马问题，常见于教科书，也常用于实际生活。

这类题目最简单的方法就是画图像，但有些题目不会画图像怎么办呢？这里我来介绍一下16种模型。

解析一：当每位同学找出16种图形时，给每种图形做一个记号，不妨称之为一个象限。

我们先按照记号放入将军饮马问题的正确答案中，再对应题目要求去掉一个错误答案。

如上图中有： 1、 0、 2、3、 4、 5、 6、 7、 8、 9、 10、 11、 12、 13、 14、 15、16。

现在我们要找到除了这些外的那种图形。

解析二：此题中的关键是： 1、问号必须比周围颜色浅2、和周围颜色一样3、比其他任何颜色都要深4、不能被周围的任何颜色包围着5、不在画面上6、被画面上的任何颜色包围着7、两个单一色的棋子只能摆成一行。

8、两个单一色的棋子可以摆成任意形状9、最后剩下两个棋子没有形状，那么我们再找一个单一色棋子，将其加进去即可。

因为单一色可以组合成任意形状，所以我们要找的那个棋子的颜色不需要固定。

我们从原始棋子开始找起，第一步：如果还有空位，则代表该颜色无法加入棋子；第二步：如果还有棋子未被占据，则代表该颜色能够加入棋子；第三步：如果没有可以加入的空位，则代表该颜色不能加入棋子。

如下图，有四个可以加入的位置。

因为每一个颜色都有两种可以加入的情况，那么最终结果就是： 2、 4、6、 7。

从而得到解题思路：即可从黑白棋子中各选一个加入其余两个已经加入棋子的空格，再把剩余两个棋子放在新空位上即可。

8、两个单一色的棋子只能摆成一行，我们只需要想办法使得摆出的两个棋子一起摆成一条线即可。

9、最后剩下两个棋子没有形状，那么我们再找一个单一色棋子，将其加进去即可。

因为单一色可以组合成任意形状，所以我们要找的那个棋子的颜色不需要固定。

我们从原始棋子开始找起，第一步：如果还有空位，则代表该颜色无法加入棋子；第二步：如果还有棋子未被占据，则代表该颜色能够加入棋子；第三步：如果没有可以加入的空位，则代表该颜色不能加入棋子。

将军饮马模型一、背景知识：【传说】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【问题原型】将军饮马造桥选址费马点【涉及知识】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平移；【解题思路】找对称点，实现折转直二、将军饮马问题常见模型1.两定一动型：两定点到一动点的距离和最小例1：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB 最小.作法：连接AB，与直线l的交点Q，Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB最小，且最小值等于AB.原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在⊿PAB中，由三角形三边关系可知：AP+PB≧AB(当且仅当PQ重合时取﹦)例2：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.关键：找对称点作法：作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所要寻找的点，即当动点P跑到了点Q处，PA+PB和最小，且最小值等于AC.原理：两点之间，线段最短证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在⊿PAC中，由三角形三边关系可知：AP+PC≧AC(当且仅当PQ重合时取﹦)2.两动一定型例3：在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短．作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM 交于点B，与ON交于点C，连接AB，AC，△ABC即为所求．原理：两点之间，线段最短例4：在∠MON的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短．作法：作点A关于OM的对称点A’，作点B关于ON的对称点B’，连接A’ B’，与OM交于点C，与ON交于点D，连接AC，BD，AB，四边形ABCD即为所求．原理：两点之间，线段最短3.两定两动型最值例5：已知A、B是两个定点，在定直线l上找两个动点M与N，且MN长度等于定长d（动点M位于动点N左侧），使AM+MN+NB的值最小.提示：存在定长的动点问题一定要考虑平移作法一：将点A向右平移长度d得到点A’，作A’关于直线l的对称点A’’，连接A’’B，交直线l于点N，将点N向左平移长度d，得到点M。

将军饮马问题的11个模型及例题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（将军饮马问题的11个模型及例题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为将军饮马问题的11个模型及例题的全部内容。

将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1。

两点之间，线段最短;2。

三角形两边之和大于第三边，两边之差小于第三边;3。

中垂线上的点到线段两端点的距离相等；4。

垂线段最短。

基本模型1.已知:如图，定点A、B分布在定直线l两侧;要求:在直线l上找一点P,使PA+PB的值最小解:连接AB交直线l于点P，点P即为所求，PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB,即AP´+BP´〉AP+BP∴P为直线AB与直线l的交点时，PA+PB最小.2.已知：如图，定点A和定点B在定直线l的同侧要求：在直线l上找一点P，使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A´，连接A´B交l于P，点P即为所求；理由：根据轴对称的性质知直线l为线段AA´的中垂线，由中垂线的性质得：PA=PA´，要使PA+PB最小,则需PA´+PB值最小，从而转化为模型1.3.已知：如图，定点A、B分布在定直线l的同侧(A、B两点到l的距离不相等）要求：在直线l上找一点P,使︱PA—PB︱的值最大解：连接BA并延长，交直线l于点P,点P即为所求；理由：此时︱PA—PB︱=AB,在l上任取异于点P的一点P´，连接AP´、BP´，由三角形的三边关系知︱P´A-P´B︱<AB，即︱P´A—P´B︱〈︱PA—PB︱4。